晶体的对称性教程

晶体的对称实验原理
晶体的对称实验原理是指在晶体学中用来确定晶体对称元素和确定晶体点群的
一种实验方法。

晶体的对称元素是指晶体中具有对称操作的元素，包括旋转轴、平面镜面、反演中心和滑移面。

晶体学家通过对晶体进行一系列对称实验，可以确定晶体中存在的对称元素，从而确定晶体点群和空间群。

对称实验的具体步骤如下：
1. 测定晶体外形：通过测量晶体的外形和尺寸，可以初步了解晶体的对称性。

2. 测定晶体的物理性质：晶体的物理性质，如光学性质、电学性质等，与晶体的对称性有关。

通过测定这些物理性质，可以推断晶体的对称元素。

3. 观察晶体的X射线衍射图样：通过观察晶体的X射线衍射图样，可以得到晶体的间距、面索引和晶体的对称元素。

4. 观察晶体的旋转显微镜图样：通过旋转显微镜观察晶体在不同旋转角度下的图样，可以确定晶体的旋转轴、反演中心和滑移面。

5. 测定晶体的点群和空间群：通过以上实验结果，可以确定晶体的点群和空间群。

这些对称实验原理和方法在晶体学中起着重要的作用，对于研究晶体的物理性质、结构和应用都具有重要意义。

第一章晶体的对称性§1-1 晶体内部结构的周期性---点阵与晶格大家都知道晶体内部原子(分子、离子和原子团等，以后称质点)的排列是规则的，具有一定的周期性，这是晶体的主要特点。

不同晶体中的质点在空间中的排列规律是不同的，有许多种排列方式。

因此，在对晶体进行研究时，为了归类方便，常将构成晶体的实际质点抽象成纯粹的几何点，并称之为阵点。

这样的阵点在空间中周期性规则排列并有相同的周围环境。

这种阵点的空间排列就称为空间点阵，或晶体点阵，也称布拉法格子，简称点阵或晶格，共有14种。

§1-2 晶体的宏观对称性---点对称操作晶体内部结构不仅具有周期性，还具有比较复杂的对称性。

实际上，晶体宏观性质和外形的对称性都是其内部结构对称性的反映，与其有着密切关系。

应该说，人们最初认识晶体，是从它们丰富多彩又有规则的外部形状开始的，后来才逐步认识到，晶体外形上的规则性及其宏观性质的对称性，是与其内部微观结构的对称性密切相关的。

在本节及以下几节中，通过对晶体的宏观对称性的描述，引进群的初步概念，给出晶体的32个点群，并依据晶体对称性特征，区分晶类和晶系。

1．晶体的宏观对称性。

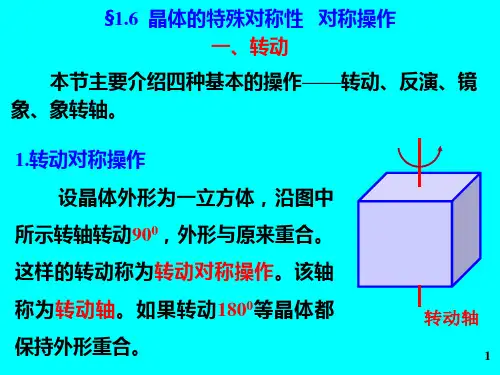
晶体外形上（宏观上）的规律性，突出表现在晶面的对称排列上。

如：把立方体的岩盐晶体绕其中心轴每转900后，晶体自身就会重合，而把六面柱体的石英晶体绕其柱轴每转600后，晶体亦会自身重合。

这里提到的绕轴转动称旋转操作，是一种点对称操作。

通常把经过某种点对称操作后晶体自身重合的性质称为晶体的宏观对称性。

描述晶体宏观对称性的方法，就是列举使其自身重合的所有点对称操作。

为了明确对称性和对称操作的概念，先给出以下概念：●相等图形。

如花瓣。

●等同图形。

如左右手。

相等图形属于等同图形，但等同图形不一定是相等图形。

●对称图形。

由两个或两个以上的等同图形构成的并在空间有规律排列的图形称对称图形。

2．对称性。

对称图形中各等同部分在空间排列的特殊规律性称对称性。

化学晶体对称性操作方法化学晶体的对称性操作是描述晶体结构中存在的各类对称性操作的方法。

对称性操作可以帮助我们研究和理解化学晶体的结构和性质。

下面我将详细介绍几种常见的对称性操作方法。

1. 旋转对称性操作旋转对称性操作是指将晶体结构围绕某个旋转轴进行旋转，使得旋转前后晶体结构完全重合。

旋转轴根据旋转角度的不同尽可能地进行分类，即2倍旋转轴、3倍旋转轴、4倍旋转轴等。

例如，围绕二倍旋转轴旋转180度可以使晶体结构不变。

在晶体学中，通常用符号n来表示旋转轴，如2倍旋转轴用2表示，3倍旋转轴用3表示。

2. 反射对称性操作反射对称性操作是指将晶体结构通过镜面进行翻转，使得镜面两侧的晶体结构完全重合。

反射镜面可以是垂直平面、水平平面或倾斜平面，根据其位置和方向可分为不同的反射面。

在晶体学中，通常以hkl指数来表示反射面，其中hkl为该反射面的法线方向。

反射对称性操作常常与旋转对称性操作结合使用，形成复合对称性操作。

3. 傍轴对称性操作傍轴对称性操作是指将晶体结构按照某个傍轴进行旋转，使得沿着傍轴方向的晶体结构重复周期性地出现。

傍轴包括，n倍傍轴（n为整数），以及基于六方晶系或立方晶系的三倍傍轴。

傍轴对称性操作可以是绕轴旋转和镜面反射操作的组合。

4. 滑移对称性操作滑移对称性操作是指将晶体结构平行于某个平面上滑动一个特定的偏移量，使得滑移后的晶体结构与滑移前完全重合。

滑移对称性操作对于晶体中平面的分子或离子的排列非常重要，及其对晶体的结构和性质产生显著影响。

5. 旋转反射对称性操作旋转反射对称性操作是指将晶体结构旋转到特定的角度，然后在镜面上进行翻转。

这种对称性操作通常出现在晶体的中心对称结构中，例如立方晶系和六方晶系。

总之，对称性操作是描述晶体结构中旋转、反射、滑移等各类对称操作的方法。

借助对称性操作，我们能够更好地理解晶体的结构和性质，并且为进一步研究和应用晶体提供了基础。

通过研究晶体对称性操作，我们可以发现晶体结构中的规律和现象，为新材料的设计合成和性质预测提供重要的参考依据。

第章第四章晶体的微观对称性原子或原子团位置的对称性叫做微观对称性宏观对称性微观对称性晶体3微观对称性和宏观对称性的主要区别微观对称性和宏观对称性的主要区别：1、宏观对称性对称元素必须相交一点，微观对称性中宏观对称性对称元素必须相交一点微观对称性中对称元素不须交于一点，可以在三维空间无限分布。

2、宏观对称性中对称元素只考虑方向，微观对称性中需要考虑对称元素的相互位置关系。

性中需要考虑对称元素的相互位置关系4点阵反映了晶体结构的周期性，这种周期性也就是点阵的平移复原的特性。

对于点阵，连接任意两个阵点的位置矢量：个阵点的位置矢量R= ma+ nb+ pc，进行平移可以使点阵复原，表现在晶体结构上就是使在三维空间无限伸展的相同部分得以重复。

R可使在三维空间无限伸展的相同部分得以重复以定义为晶体微观结构平移的方向矢量以定义为晶体微观结构平移的方向矢量。

微观对称元素= 宏观对称元素+ )平移(平移轴、螺旋轴、滑移面)5平移对称性;平移轴;平移群;I P6F C (A, B)14个布喇菲点阵→ 14个平移群三斜晶系: 简单布喇菲点阵:单斜晶系：简单布喇菲点阵，底心布喇菲点阵7a'=a b'=a'=a b'=bb c'=a +c bb c'=（a +c ）/2正交晶系简单体心面心和底心点阵正交晶系：简单、体心、面心和底心点阵四方晶系：体心和简单四方点阵三角晶系：简单三角点阵8六角晶系：简单六角点阵立方晶系：简单、面心和体心立方点阵2、螺旋对称轴A: 4; B: 4金刚石0,10,10.50751;30.50.250.75B0.50.250.75A 0,10,10,10.59n=3s=0,τ=0,3次旋转轴s=0=0s=1, τ=T/3, 3,次螺旋轴,右螺旋;,,1s=2, τ=T/3, 3次螺旋轴，左螺旋。

,,次螺旋轴螺旋215n 4次旋转轴n=4s=0，4次旋转轴；11/4T s=1, τ=1/4T ，右螺旋轴41；22/4T 双螺旋轴s=2, τ=2/4T ，中性螺旋轴42，双螺旋轴；s=3左螺旋轴s=3, τ=3/4T ，左螺旋轴43。