实验二 典型系统的时域响应分析实验仿真报告答案
- 格式:doc
- 大小:234.88 KB
- 文档页数:10
典型环节的时域响应实验报告一、实验要求了解和掌握各典型环节的传递函数及模拟电路图,观察和分析各典型环节的响应曲线。
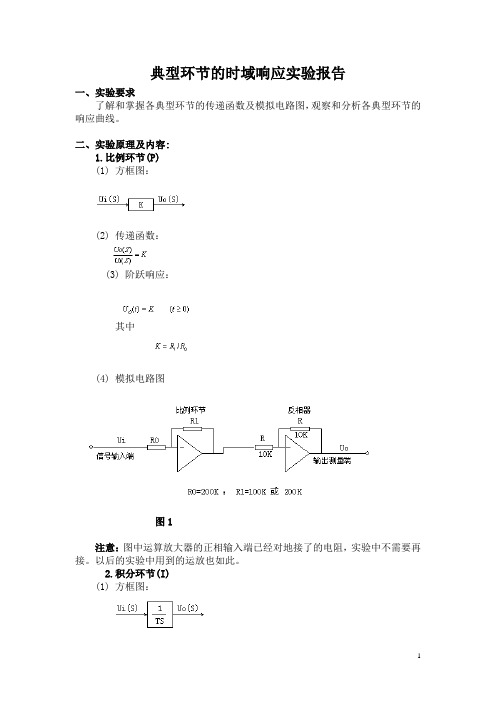
二、实验原理及内容:1.比例环节(P)(1) 方框图:(2) 传递函数:(3) 阶跃响应:其中(4) 模拟电路图图1注意:图中运算放大器的正相输入端已经对地接了的电阻,实验中不需要再接。
以后的实验中用到的运放也如此。
2.积分环节(I)(1) 方框图:(2) 传递函数(3) 阶跃响应:其中(4)模拟电路图:图23.比例积分环节(PI) (1) 方框图:(2)传递函数:(3) 阶跃响应:其中(4)模拟电路图:图34.惯性环节(T) (1) 方框图:(2) 传递函数:(3) 阶跃响应其中(4) 模拟电路图:图45.比例微分环节(PD)(1) 方框图:(2) 传递函数:(3) 阶跃响应:其中为单位脉冲函数,这是一个面积为t的脉冲函数,脉冲宽度为零,幅值为无穷大,在实际中是得不到的。
(4) 模拟电路图:图56.比例积分微分环节(PID)(1) 方框图:(2) 传递函数:(3) 阶跃响应:其中为单位脉冲函数,(4) 模拟电路图:图 6三、实验步骤1. 按比例环节的模拟电路图将线接好,检查无误后开启设备电源。
2. 将信号源单元的“ST”端插针与“S”端插针用“短路块”短接。
由于每个运放单元均设置了锁零场效应管,所以运放具有锁零功能。
调节调幅和调频电位器,使得“OUT”端输出的方波幅值为1V,周期为10s左右。
3. 将2中的方波信号加至环节的输入端Ui,用示波器的“CH1”和“CH2”表笔分别监测模拟电路的输入Ui端和输出U0端,观测输出端的实际响应曲线U0(t),记录实验波形及结果。
4. 改变几组参数,重新观测结果。
5. 用同样的方法分别搭接积分环节、比例积分环节、比例微分环节、惯性环节和比例积分微分环节的模拟电路图。
观测这些环节对阶跃信号的实际响应曲线,分别记录实验波形及结果。
四、实验曲线及结论1.比例环节 (P)(1)当R0=200K,R1=100K时, 图形如下:(2)当R0=200K、R1=200K时,图形如下:结论:对于比例环节的放大系数,其影响因素为R1、R0电阻的比值,其比值越大,放大系数越大。

典型环节的时域响应的实验报告.doc实验目的:通过对几种典型电路的时域响应进行实验,掌握不同类型环节的时域特性,并了解如何利用示波器观测和测量信号的时域特性。
实验器材和材料:1.示波器2.函数发生器3.电容4.电阻5.电感6.直流电源实验原理:在实验中将会涉及到三种基本电路环节:电容、电阻和电感。
它们的特性分别如下:电容:存储电荷,并在电场作用下产生电压。
在一定时间内,当外加电压改变时,电容内积累的电荷量也会发生相应变化,产生电流。
电阻:在电路中引入能够消耗电能的元件,对通过其的电流施加一定阻阻碍作用,从而产生电势降,转化成功率消耗的过程。
电感:存储能量的元件,具有感抗作用,对交变电压的响应速度较慢,产生电压滞后和电压峰值下降等现象。
实验步骤:1.进行电容的实验,连接电容和符合线路要求的示波器和函数发生器,调节函数发生器输出方波信号,观察示波器中的电容电压波形,并记录下时间常量,重复操作多次,得到更多数据。
实验数据和分析:在实验过程中记录数据并进行数据统计分析,如下表:表1 电容、电阻、电感时域响应数据表|环节|电阻R(Ω)|电容C(F)|电感L(H)|时间常量τ(s)||:-:|:-:|:-:|:-:|:-:||电容|500|1μF|—|0.0005||电阻|1k|—|—|0.001||电感|—|—|200μH|0.0001|通过数据可以看出,不同环节的时间常量不同,电容的时间常量最大,电感的时间常量最小。
这是由于电容对变动快速响应,而电感则对变化的响应速度较慢。
实验结论:经过实验数据的分析,可以得出以下结论:1.电容环节的时间常量比电阻、电感短。
4.不同环节的时间常量与电路元件特性有关,不同元件的响应速度不同。
实验中可以利用示波器等工具对时间常量进行测量,进而了解电路环节的时域特性,这对于设计电路、优化电路性能具有重要作用。

工程大学实验报告专业班号组别 01 教师同组者(个人)(1)分别绘出)/(2s rad n =ω,ζ分别取0,0.25,0.5,1.0和2.0时的单位阶跃响应曲线,分析参数ζ对系统的影响,并计算ζ=0.25时的时域性能指标ss s p r p e t t t ,,,,σ。
(2)绘制出当ζ=0.25, n ω分别取1,2,4,6时单位阶跃响应曲线,分析参数n ω对系统的影响。
(3)系统的特征方程式为010532234=++++s s s s ,试用二种判稳方式判别该系统的稳定性。
(4)单位负反馈系统的开环模型为 )256)(4)(2()(2++++=s s s s K s G 试分别用劳斯稳定判据和赫尔维茨稳定判据判断系统的稳定性,并求出使得闭环系统稳定的K 值围。
三、 实验结果及分析1.可以用两种方法绘制系统的阶跃响应曲线。
(1)用函数step( )绘制MATLAB 语言程序:>> num=[ 0 0 1 3 7];>> den=[1 4 6 4 1 ];>>step(num,den);>> grid;>>xlabel('t/s');ylabel('c(t)');title('step response');MATLAB 运算结果:(2)用函数impulse( )绘制MATLAB 语言程序:>> num=[0 0 0 1 3 7];>> den=[1 4 6 4 1 0];>> impulse(num,den);>> grid ;>> xlabel('t/s');ylabel('c(t)');title('step response'); MATLAB 运算结果:2. (1))/(2s rad n =ω,ζ分别取0,0.25,0.5,1.0和2.0时的单位阶跃响应曲线的绘制:MATLAB语言程序:>> num=[0 0 4];>> den1=[1 0 4];>> den2=[1 1 4];>> den3=[1 2 4];>> den4=[1 4 4];>> den5=[1 8 4];>> t=0:0.1:10;>> step(num,den1,t);>> grid>> text(2,1.8,'Zeta=0'); holdCurrent plot held>> step(num,den2,t);>> text (1.5,1.5,'0.25');>> step(num,den3,t);>> text (1.5,1.2,'0.5');>> step(num,den4,t);>> text (1.5,0.9,'1.0');>> step(num,den5,t);>> text (1.5,0.6,'2.0');>> xlabel('t');ylabel('c(t)'); title('Step Response ') ; MATLAB运算结果:实验结果分析:从上图可以看出,保持)/(2s rad n =ω不变,ζ依次取值0,0.25,0.5,1.0和2.0时, 系统逐渐从欠阻尼系统过渡到临界阻尼系统再到过阻尼系统,系统的超调量随ζ的增大而减小,上升时间随ζ的增大而变长,系统的响应速度随ζ的增大而变慢,系统的稳定性随ζ的增大而增强。

中南大学典型系统的时域响应和稳定性分析实验报告实验介绍:本实验以中南大学典型系统为研究对象,通过构建数学模型和实际建模结果,分析系统的时域响应和稳定性,以及初步探讨系统的性能和优化方法。
实验步骤:1、对中南大学典型系统进行数学建模,并得到系统的传递函数。
2、通过Matlab对系统的传递函数进行分析,得到系统的时域响应。
3、分析系统特征方程的根,判断系统的稳定性。
4、探讨系统的性能指标,并初步探讨系统的优化方法。
实验结果:1、数学模型及传递函数:根据中南大学典型系统的构成,我们可以得到其传递函数为:$$G(s) = \frac{Y(s)}{X(s)}=\frac{K}{s(T_1s+1)(T_2s+1)}$$2、时域响应分析:阶跃响应脉冲响应可以看出,在系统输入为阶跃信号时,系统的响应随着时间的增加逐渐趋于稳定;在系统输入为脉冲信号时,系统的响应在一定时间范围内会有一个稳定的振荡。
3、稳定性分析:我们根据系统的特征方程$$1+G(s)=0$$得到特征方程为:$$s^3+T_1T_2s^2+(T_1+T_2)s+K=0$$我们通过Matlab计算特征方程的根,得到系统的特征根分别为:$-0.0327\pm0.6480j$和$-2.4341$。
根据根的位置,我们可以判断系统的稳定性。
由于系统的根都在左半平面,因此系统是稳定的。
4、性能指标和优化方法:本实验中,我们主要关注系统的稳定性和响应速度等性能指标。
在实际应用中,我们可以通过调整系统控制参数,如增益$K$和时间常数$T_1$和$T_2$等,来优化系统的性能。
结论:本实验通过对中南大学典型系统进行数学建模和实际响应分析,得到了系统的传递函数、阶跃响应和脉冲响应等数学模型,并根据特征方程的根判断了系统的稳定性。
在探讨系统性能指标和优化方法的基础上,我们可以进一步探究系统的优化方案,并为实际控制应用提供参考。
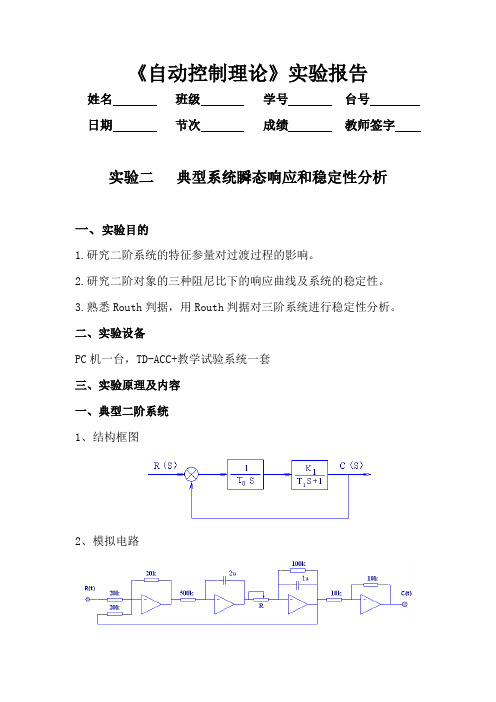
《自动控制理论》实验报告姓名班级学号台号日期节次成绩教师签字实验二典型系统瞬态响应和稳定性分析一、实验目的1.研究二阶系统的特征参量对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉Routh判据,用Routh判据对三阶系统进行稳定性分析。
二、实验设备PC机一台,TD-ACC+教学试验系统一套三、实验原理及内容一、典型二阶系统1、结构框图2、模拟电路3、理论分析 开环传函: )1(/)1()()(101101+=+=S T S T k S T S T k S H S G 系统的开环增益: 01/T k K =当s T 10= ,s T 1.01= ,R k /1001= , R k T k K /100/101=== 时 系统的开环传递函数为:)11.0(/100)()(+=S S RS H S G 系统的闭环传递函数为: RS S RR S S R S H S G S G S W /100010/1000/100)11.0(/100)()(1)()(2++=++=+=系统闭环传递函数标准式为: 2222)(n n nS S S W ωξωω++= 二式比较得: R n /10002=ω 102=n ξωR n /1010=ω R/10105=ξ当R=10k 时: 5.0/10105==Rξ0 < ξ < 1 , 当R=20k 时: 707.0/10105==Rξ 0 < ξ < 1 当R=40k 时: 1/10105==Rξ1=ξ ,当R=100k 时: 58.1/10105==Rξ ξ > 12.1 R=10Kp t =0.375S, s t =1.117S ,%p σ近似为零理论值p t = 0.363S, s t = 1.0S ,%p σ=12.8% 由此可以分析,理论值与实际值接近。
R=20Kp t =0.650S, s t 无法看出,%p σ近似为零理论值p t =0.444S ,s t =0.651S ,%p σ=1% 由此分析,理论值与实际值近似相等。

实验名称:一二阶系统的电子模拟及时域响应测试课程名称:自动控制原理实验目录(一)实验目的 (3)(二)实验内容 (3)(三)实验设备 (3)(四)实验原理 (3)(五)一阶系统实验结果 (3)(六)一阶系统实验数据记录及分析 (7)(七)二阶系统实验结果记录 (8)(八)二阶系统实验数据记录及分析 (11)(九)实验总结及感想............................................................................错误!未定义书签。
图片目录图片1 一阶模拟运算电路 (3)图片2 二阶模拟运算电路 (3)图片3 T=0.25仿真图形 (4)图片4 T=0.25测试图形 (4)图片5 T=0.5仿真图形 (5)图片6 T=0.5测试图形 (5)图片7 T=1仿真图形 (6)图片8 T=1测试图形 (6)图片9 ζ=0.25s仿真图形 (8)图片10 ζ=0.25s测试图形 (8)图片11 ζ=0.5s仿真图形 (9)图片12 ζ=0.5s测试图形 (9)图片13 ζ=0.8s仿真图形 (10)图片14 ζ=0.8s测试图形 (10)图片15 ζ=1s仿真图形 (11)图片16 ζ=1s测试图形 (11)表格目录表格1 一阶系统实验结果 (7)表格2 二阶系统实验结果 (11)一二阶系统的电子模拟及时域响应测试(一)实验目的1.了解一、二阶系统阶跃响应及其性能指标与系统参数之间的关系。
2.学习在电子模拟机上建立典型环节系统模型的方法。
3.学习阶跃响应的测试方法。
(二)实验内容1.建立一阶系统的电子模型,观测并记录在不同时间常数T时的跃响应曲线,并测定其过渡过程时间TS。
2.建立二阶系统的电子模型,观测并记录在不同阻尼比ζ时的跃响应曲线,并测定其超调量σ%及过渡过程时间TS。
(三)实验设备HHMN电子模拟机,实验用电脑,数字万用表(四)实验原理一阶系统:在实验中取不同的时间常数T,由模拟运算电路,可得到不同时间常数下阶跃响应曲线及不同的过渡时间。
实验一测试系统的时域响应【实验目的】1.了解MATLAB软件的基本特点和功能,熟悉其界面、菜单和工具条,熟悉MATLAB程序设计结构及M文件的编制;2.掌握线性系统模型的计算机表示方法;3.掌握求线性定常连续系统时域输出响应的方法,求得系统的时域响应曲线;4. 了解Simulink 的使用。
【实验指导】一、模型的建立:在线性系统理论中,一般常用的数学模型形式有:(1)传递函数模型;(2)状态空间模型;(3)零极点增益模型这些模型之间都有着内在的联系,可以相互进行转换.1、传递函数模型若已知系统的传递函数为:对线性定常系统,式中s的系数均为常数,且an不等于零,这时系统在MATLAB中可以方便地由分子和分母系数构成的两个向量唯一地确定出来,这两个向量分别用num和den表示.num=[cm,c,m-1,…,c1,c0]den=[an,an-1,…,a1,a0]注意:它们都是按s的降幂进行排列的.则传递函数模型建立函数为:sys=tf(num,den).2、零极点增益模型(略)3、状态空间模型(略)二、模型的转换在一些场合下需要用到某种模型,而在另外一些场合下可能需要另外的模型,这就需要进行模型的转换.三、模型的连接1、并联:parallel[num,den]=parallel(num1,den1,num2,den2)%将并联连接的传递函数进行相加.2、串联:series[num,den]=series(num1,den1,num2,den2)%将串联连接的传递函数进行相乘.3、反馈:feedback[num,den]=feedback(num1,den1,num2,den2,sign)%可以得到类似的连接,只是子系统和闭环系统均以传递函数的形式表示.当sign=1时采用正反馈;当sign= -1时采用负反馈;sign缺省时,默认为负反馈.4、闭环:cloop(单位反馈)[numc,denc]=cloop(num,den,sign)%表示由传递函数表示的开环系统构成闭环系统,sign意义与上述相同.四、线性连续系统的时域响应1 求取线性连续系统的阶跃响应函数为(step) 基本格式为:step(sys) step(num,den)【实验内容】1. 典型一阶系统的传递函数为 11)(+=s s G τ;τ为时间常数,试绘出当τ=0.5、1、 2、4、6、8、时该系统的单位阶跃响应曲线。
系别:机电工程学院专业:课程名称:自动控制原理实验班级:姓名:学号:组别:实验名称:典型系统的时域响应和稳定性分析实验时间:学生成绩:教师签名:批改时间:一、目的要求1.研究二阶系统的特征参量 (ξ、ωn) 对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉 Routh 判据,用 Routh 判据对三阶系统进行稳定性分析。
二、实验设备PC机一台,TD—ACC教学实验系统一套三、实验原理及内容1.典型的二阶系统稳定性分析(1) 结构框图:如图 1.2-1 所示。
图1.2-2(2) 对应的模拟电路图:如图 1.2-2 所示。
图1.2-2系别:机电工程学院专业:课程名称:自动控制原理实验班级:姓名:学号:组别:实验名称:实验时间:学生成绩:教师签名:批改时间:(3) 理论分析系统开环传递函数为:;开环增益:(4) 实验内容先算出临界阻尼、欠阻尼、过阻尼时电阻 R 的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。
在此实验中(图 1.2-2),系统闭环传递函数为:其中自然振荡角频率:2.典型的三阶系统稳定性分析(1) 结构框图:如图 1.2-3 所示。
系别:机电工程学院专业:课程名称:自动控制原理实验班级:姓名:学号:组别:实验名称:实验时间:学生成绩:教师签名:批改时间:图 1.2-3(2)模拟电路图:如图 1.2-4 所示。
图 1.2-4(3)理论分析:系统的特征方程为:(4)实验内容:实验前由 Routh 判断得 Routh 行列式为:系别:机电工程学院专业:课程名称:自动控制原理实验班级:姓名:学号:组别:实验名称:实验时间:学生成绩:教师签名:批改时间:为了保证系统稳定,第一列各值应为正数,所以有五、实验步骤1.将信号源单元的“ST”端插针与“S”端插针用“短路块”短接。
由于每个运放单元均设臵了锁零场效应管,所以运放具有锁零功能。
实验二典型系统的时域响应分析1. 实验目的1) 通过用MATLAB 及SIMULINK 对控制系统的时域分析有感性认识。
2) 明确对于一阶系统,单位阶跃信号、单位斜坡信号以及单位脉冲信号的响应曲线图。
3) 对于二阶系统阶跃信号的响应曲线图以及不同阻尼比、不同自然角频率取值范围的二阶系统曲线比较图。
4) 利用MATLAB 软件来绘制高阶控制系统的零极点分布图,判断此系统是否有主导极点,能否用低阶系统来近似,并将高阶系统与低阶系统的阶跃响应特性进行比较5)编制简单的M文件程序。
2. 实验仪器PC计算机一台,MATLAB软件1套3. 实验内容1)一阶系统的响应(1) 一阶系统的单位阶跃响应在SIMULINK 环境下搭建图1的模型,进行仿真,得出仿真曲线图。
理论分析:C(s)=1/[s(0.8s+1)]由拉氏反变换得h(t)=1-e^(-t/0.8) (t>=0)由此得知,图形是一条单调上升的指数曲线,与理论分析相符。
(2) 一阶系统的单位斜坡响应在SIMULINK环境下搭建图2的模型,将示波器横轴终值修改为12进行仿真,得出仿真曲线图。
理论分析:C(s)=1/[s^2(4s+1)]可求的一阶系统的单位斜坡响应为c(t)=(t-4)+4e^(-t/4) e(t)=r(t)-c(t)=4-4e^(-t/4) 当t=0时,e(t)=0,当趋于无穷时,误差趋于常值4.3)一阶系统的单位脉冲响应在medit 环境下,编译一个.m 文件,利用impulse()函数可以得出仿真曲线图。
此处注意分析在SIMULINK 环境中可否得到该曲线图。
理论分析:C (s )=5/(0.8s+2)=(5/2)/(0.4s+1)可求的g(t)=6.25e^(-t/0.4),是一个单调递减的函数。
两种环境下得到的曲线图不一致。
2)二阶系统的单位阶跃响应二阶系统的闭环传递函数标准形式为 2222)(nn n s s s G ωζωω++= 其阶跃响应可以分以下情况解出①当0=ζ时,系统阶跃响应为 )cos(1)(t t c n ω-=②当10<<ζ时,系统阶跃响应为 )sin(111)(2θωζζω+--=-t e t c d tn其中ζζθ/121-=-tg ,21ζωω-=n d③当1=ζ时,系统阶跃响应为 t n n e t t c ωω-+-=)1(1)(④当1>ζ时,系统阶跃响应为 ⎪⎪⎭⎫ ⎝⎛---=21221121)(λλζωλλt t ne e t c 其中121---=ζζλ,122-+-=ζζλ (1)自然角频率1=n ω选取不同阻尼比=ζ0,0.2,0.4,0.6,0.8,1.0,2.0,用MATLAB得到二阶系统阶跃响应曲线。