经纬仪三轴误差
- 格式:doc
- 大小:551.50 KB
- 文档页数:16

经纬仪测量误差分析水平角测量误差1.仪器误差仪器误差的来源可分为两方面。
一是仪器制造加工不完善的误差,如度盘刻划的误差及度盘偏心差等。
前者可采用度盘不同位置进行观测(按180°/n计算各测回度盘起始读数)加以削弱;后者采用盘左盘右取平均值予以消除。
其次是仪器校正不完善的误差,其视准轴不垂直于横轴及横轴不垂直于竖轴的误差,可采用盘左盘右取平均值予以消除。
但照准部水准管不垂直于竖轴的误差,不能用盘左盘右的观测方法消除。
因为,水准管气泡居中时,水准管轴虽水平,竖轴却与铅垂线间有一夹角θ,水平度盘不在水平位置面倾斜一个θ角,用盘左盘右来观测,水平度盘的倾角θ没有变动,俯仰望远镜产生的倾斜面也未变,而且瞄准目标的俯仰角越大,误差影响也越大,因此测量水平角时观测目标的高差较大时,更应注意整平。
2.观测误差(1)对中误差观测时若仪器对中不精确,致使度盘中心与测站中心O不重合而偏至O′,OO′的距离e称为测站偏心距,此时测得的角值β′与正确角值β之差△β′即为对中不良所产生的误差,由图可知:△β=β-β′=δ1+δ2。
因偏心距e是一小值,故δ1和δ2应为一小角,于是把e近似地看作一段小圆弧,所以得:△β=δ1+δ2=ep〞(1/d1+1/d2)式中:d1、d2——水平角两边的边长;e——测站偏心距;p〞=206265″。
由上式可知,对中误差与偏心距e成正比,与边长d1和d2成反比。
例如,e=3mm、d1=d2=100m,则△β=12.4″;如果d1= d2 =50m,则△β=24.8″。
故当边长较短时,应认真进行对中,使e值较小,减少对中误差的影响。
(2)整平误差观测时仪器未严格整平,竖轴将处于倾斜位置,这种误差与上面分析的水准管轴不垂直于竖轴的误差性质相同。
由于这种不能采用适当的观测方法加以消除,当观测目标的竖直角越大其误差影响也越大,故观测目标的高差较大时,应特别注意仪器的整平,一般每测回观测完毕,应重新整平仪器再进行下一个测回的观测。


实验三 精密经纬仪轴系误差检验一、实习目的掌握高低点法测定经纬仪水平轴误差、视准轴误差检验的操作程序与成果整理方法。
二、实习要求1.每个实习小组完成一套合格的检验成果。
2.总结出如何能准确而又迅速地设置高、低两个目标。
3.所测得的水平角和垂直角各项限差均应达到要求,否则应重测。
三、仪器及工具学时:4每组借用J 2型经纬仪一台(带脚架)、测尺一把、记录板一块。
自备铅笔、小刀、小三角板或直尺、记录表格等。
四、实习步骤1.实习前要认真复习有关内容,弄清检验原理与方法。
2.弄清水平角和垂直角观测程序与记录格式,并记住各项限差规定。
3.实习内容:(1)设置目标:在距仪器5m 以外的地方设置两个目标,一为高点,一为低点。
两点应大致在同一铅垂直线上,用仪器观测两点的垂直角的绝对值应不小于3°,其绝对值应大致相等,其差值不得超过30″(设置目标时,可用仪器指挥)。
(2)测定方法a .观测高低两点的水平角6个测回,每测回间更换水平度盘和测微器,其值按下式计算:)()()(m 21121180-+-⨯+-︒j m j i j ω 式中,m 为测回数(等于6);i 为度盘最小分格值(T3仪器,i =4′;J2仪器,i =20′)。
对于J2型仪器,每测回更换水平度盘和测微器,其值计算为: )21(600)1(10)1(180-"+-⨯'+-︒j m j j m 观测限差:2c 变化按高、低点方向分别比较,在整个测定中,其变化值不得超过6″;各测回角度值互差应小于3″。
对超出限差的测回须重测。
b .观测高、低点的垂直角高α和低α,用中丝法测三测回。
垂直角和指标差互差均不超过10″,超限测回应重测。
c .最后结果计算:水平轴误差:αctg C C i )(21低高-=视准轴误差: αcos )(21低高C C C +=式中:∑-=n R L n C 1)(21高高,∑-=n R L n C 1)(21低低,)(21低高ααα-= 限差:i 的绝对值,对于J 1型仪器不应超过10″,J 2型仪器不应超过15″。

3.3经纬仪的三轴误差3.3.1视准轴误差 1产生原因2视准轴误差对水平方向观测的影响⑴水平轴H H ',竖盘位于H 端。
⑵OZ 正确的视准轴所划出的垂直照准平面是M OZT '。
⑶当视准轴有误差C ,并偏向于竖盘一端时(设此时为正,反之为负),视准轴所描绘的是一个园锥面1PM Z O '。
⑷当用正确的视准轴OZ 瞄准目标P 时,垂直照准平面就必需以OZ 为轴(逆)转一个角度C OM M ∆='∠,C ∆就是视准轴误差C 对水平方向观测值的影响。
求C 与C ∆的关系。
以O 为球心,OH 为半径作单位球面,通过H 点作一个大园弧H HPT ',得直角球面三角形ZTP ,按球面三角形正弦公式有:)90sin(90sin sin sin α-=∆C C由于C ∆和C 都是很小的角,可以C C C C ∆=∆=sin ,sin ,得:αcos CC =∆ (3-25) 3视准轴误差对水平方向观测影响的规律⑴C ∆随目标垂直角的增大而增大,当C C =∆=时0α为最小值。
⑵由盘左和盘右的观测方向值求平均值,可以消除视准轴误差对水平方向观测的影响,而得到正确的方向值。
盘左C L L ∆-=0 (3-26)倒镜盘右C R R ∆+=0 (3-27)取盘左、盘右读数的平均数可得到正确的读数)(21R L A += (3-28)4计算2C 的作用一测回中各观测方向2C 互差的大小,在一定程度上反映了观测成果的质量。
3.3.2水平轴倾斜误差 1产生原因2水平轴倾斜误差对水平方向观测的影响⑴H H '仪器水平轴正确位置,视准轴OZ 划出的是个垂直平面M OZ '。
⑵11H H '仪器水平轴倾斜了i 角后的不正确位置,此时视准轴也跟着倾斜i 角后在Z O ',它划出的是个倾斜平面M Z O ''。
⑶以O 为球心,OH 为半径作单位球面。

三轴机床允许的误差
1. 位置精度,三轴机床在加工过程中所能达到的位置精度是一个重要的指标。
通常来说,机床的位置精度受到机床本身结构、导轨、传动系统等因素的影响。
一般来说,机床的位置精度可以通过国际标准ISO 230-1来进行评定,通常要求在几微米到几十微米之间。
2. 重复定位精度,重复定位精度是指机床在多次加工中,同一位置的加工精度能否保持一致。
这个指标也受到机床本身结构、传动系统、控制系统等因素的影响。
在实际应用中,重复定位精度一般要求在几微米到几十微米之间。
3. 直线度和平行度,对于三轴机床来说,轴线的直线度和轴线之间的平行度也是重要的误差指标。
这些误差会直接影响到加工零件的质量和精度。
总的来说,三轴机床允许的误差是一个综合考虑机床精度、使用要求、加工材料等多个因素的结果。
在实际应用中,需要根据具体的加工要求和机床性能来进行评估和控制。
同时,也需要通过定期的维护和保养来保证机床的精度和稳定性。
精密水准测量误差水准测量,又称几何水准测量。
是确定地面点高程或地面点间高差的基本方法,是其它高程测量的基础。
精密水准测量的误差来源有三个:一是测量仪器误差;二是观测者受地理条件限制而造成的人为误差即外界条件误差;三是观测误差。
在主要误差来源中,一、三项误差的影响基本上具有系统误差的性质,而第二项造成的测量误差为偶然误差。
一、水准测量的误差分析水准测量误差有仪器误差、观测误差和外界条件的影响。
1.仪器误差之一是水准仪的望远镜视准轴不平行于水准管轴所产生的误差仪器虽在测量前经过校正,仍会存在残余误差。
因此造成水准管气泡居中,水准管轴居于水平位置而望远镜视准轴却发生倾斜,致使读数误差。
这种误差与视距长度成正比。
观测时可通过中间法(前后视距相等)和距离补偿法(前视距离和等于后视距离总和)消除。
针对中间法在实际过程中的控制,立尺人是关键,通过应用普通皮尺测距离,之后立尺,简单易行。
而距离补偿法不仅繁琐,并且不容易掌握。
1.1 照准轴与管水准轴不平行的误差:望远镜照准轴与管水准器水准轴不平行而产生的i角误差,是仪器误差的主要来源,这是因为i角误差不可能彻底校正;而人眼又不可能使气泡严格居中。
所以观测时i角误差一定会存在。
设后视和前视的i角分别为i1和i2,视线长度分别为D1和D2,如图1-1,则有:图1-1δ1=(i″1/ρ″)* D1δ2=(i″2/ρ″)* D2a′=a+δ1b′=b+δ2由观测值算得h为:h= a′- b′=(a-b)+ (i″1/ρ″)* D1-(i″2/ρ″)* D2一般情况下,基本上i1=i2 ,则为:h=(a-b)+ (D1- D2)* i /ρ″所以,为了使i角误差尽可能的小一些,D1- D2应尽量小。
亦即前后视距尽量相等,以减弱i角影响。
2.仪器误差之二是水准尺误差主要包含尺长误差(尺子长度不准确)、刻划误差(尺上的分划不均匀)和零点差(尺的零刻划位置不准确),对于较精密的水准测量,一般应选用尺长误差和刻划误差小的标尺。
角度观测的误差来源作者:周晓林角度观测的误差来源多种多样,这些误差来源对角度观测精度的影响又各不相同。
现将其几种主要误差来源介绍如下。
一、仪器检校不完善和制造加工不完备引起的误差(一)仪器检校不完善引起的误差经纬仪经过检验校正后,通常只能在一定程度上满足某些几何条件,达到规定的限差要求,而不可能检校得十分彻底,因为限差本身就是一种宽容度。
因此检校后的仪器仍然有残存误差,这些残存误差必将影响角度观测的精度,其中:1.照准轴误差(照准轴与水平轴正交的残存误差)和水平轴误差(水平轴与坚轴正交的残存误差),可以通过盘左、盘右观测,取一测回方向中数的方法,消除其对水平角观测方向值的影响。
2.竖轴误差(竖轴与经纬仪照准部管水准轴正交的残存误差),不能通过盘左、盘右观测取中数的方法消除其对水平角观测方向值的影响。
只能通过校正尽量减少残存误差,每测回观测前仔细整平仪器,倾斜角大的测站更要特别注意仪器整平等方法削弱其影响。
照准轴误差、水平轴误差和竖轴误差是经纬仪的三个主轴误差,通常称为三轴误差,它是仪器误差的主要组成部分,必须予以充分重视。
(二)仪器制造加工不完备引起的误差仪器制造加工不完备的误差,如水平度盘偏心(即水平度盘旋转中心与度盘刻划中心不一致,其对度盘读数的影响称为水平度盘偏心差),竖盘偏心(即竖盘旋转中心与度盘刻划中心不一致,当仪器为单指标时其对度盘读数的影响称为竖盘偏心差),照准部偏心(即照准部旋转中心与水平度盘刻划中心不重合,其对水平度盘读数的影响称为照准部偏心差),度盘刻划误差(即度盘刻划不匀均的误差),水平度盘与坚轴不正交等,这些仪器误差不能通过一般地仪器检校减小其影响,其中:1.照准部偏心差和水平度盘偏心差。
此两项可以通过盘左、盘在观测,取一测回水平角观测方向值中数的方法消除。
2.水平度盘刻划误差。
此误差一般较小,且呈周期性变化,故可通过按规定配置各测回零方向的度盘位置的方法减弱其影响。
3.单指标经纬仪竖盘偏心差。
§3.4 精密光学经纬仪的仪器误差及其检验和校正前面几节具体介绍了光学经纬仪的主要部件及其相互关系。
仪器的制造和安装不论如何精细,也不可能完全满足理论上对仪器各部件及其相互几何关系的要求,加之在仪器使用过程中产生的磨损、变形,以及外界条件对仪器的影响,必然给角度测定结果带来误差影响。
这种因仪器结构不能完全满足理论上对各部件及其相互关系的要求而造成的测角误差称为仪器误差。
仪器误差包括三轴误差(视准轴误差、水平轴倾斜误差、垂直轴倾斜误差),照准部旋转误差,分划误差(水平度盘分划误差、测微盘分划误差)以及光学测微器行差等。
本节将介绍这些误差的产生原因,消除或减弱其影响的措施及检验方法。
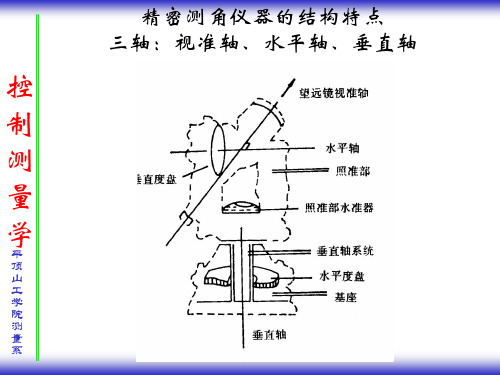
3.4.1 三轴误差由§3.1知,经纬仪的三轴(视准轴、水平轴、垂直轴)之问在测角时应满足一定的几何关系,即视准轴与水平轴正交,水平轴与垂直轴正交,垂直轴与测站铅垂线一致。
当这些关系不能满足时,将分别引起视准轴误差、水平轴倾斜误差、垂直轴倾斜误差。
1.视准轴误差(1)视准轴误差及其产生原因望远镜的物镜光心与十字丝中心的连线称为视准轴。
假设仪器已整置水平(即垂直轴与测站铅垂线一致),且水平轴与垂直轴正交,仅由于视准轴与水平轴不正交——即实际的视准轴与正确的视准轴存在夹角C ,称为视准轴误差。
如图3—26。
当实际的视准轴偏向垂直度盘一侧时,C 为正值,反之C 为负值。
产生视准轴误差的原因是由于安装和调整不正确,使望远镜的十字丝中心偏离了正确的位置,造成视准轴与水平轴不正交,从而产生了视准轴误差。
此外,外界温度的变化也会引起视准轴的位置变化,产生视准轴误差。
(2)视准轴误差对观测方向值的影响及消除影响的方法视准轴误差C 对观测方向值的影响C ∆为αcos C C =∆ (3-10) 式中:α为观测目标的垂直角。
由C ∆的表达式可知:1)C ∆的大小不仅与C 的大小成正比,而且与观测目标的垂直角α有关。
当α越大时,△C 也越大,反之就越小;当α=0时,C ∆=C 。
2)盘左观测时,实际视准轴位于正确视准轴的左侧,使正确的方向值L 0比含有视准轴误差的实际方向值L 小C ∆,即C L L ∆-=0纵转望远镜,以盘右观测同一目标时,实际视准轴在正确视准轴的右侧,显然此时对方向值的影响恰好和盘左时的数值相同,符号相反,即正确的方向值较有误差的方向值R 大,故图3-26 视准轴误差C R R ∆+=0取盘左与盘右的中数,得)(21)(2100R L R L +=+ (3-11) 可以看出:视准轴误差对观测方向值的影响,在望远镜纵转前后,大小相等,符号相反。
因此,取盘左与盘右的中数可以消除视准轴误差的影响。
3)观测一个角度时,如果两个方向的垂直角相等,则视准轴误差的影响可在半测回角 度值中得到消除。
即使垂直角不相等,如果差异不大且接近于0°,其影响也可以忽略。
4)望远镜纵转前后,同一方向的盘左、盘右观测值之差为C R L ∆=±-2180 (3-12)视准轴与水平轴的关系是机械的结合,在短时间内,可以认为C 是常值。
由(3-11)式可知,若各个方向的垂直角a 很小,且相差不大时,2△C 近似等于2C ,亦可认为是常值。
因此,可将上式写成:C R L 2180=±- (3-13)2C 通常被称为二倍照准差。
(3)计算2C 的作用及校正2C 的方法在短暂的观测时间里,视准轴受温度等外界因素的影响所产生的变化是很小的。
在观测过程中,2C 变动的主要原因是观测照准读数等偶然误差的影响。
因此,计算2C 并规定其变化范围可以作为判断观测质量的标准之一。
另外,2C 的常值部分对观测结果是没有影响的,有影响的仅是它的变动部分。
但是,2C 数值过大时,对记簿计算不太方便,因此2C 绝对值过大时需校正。
2C 的绝对值对于J 07 J 1型仪器应不大于20″,J 2型仪器应不大于30″。
校正2C 的方法如下:首先选择一个垂直角接近于0°的目标,用盘左、盘右观测出2C 值,若2C 值的绝对值大于《规范》规定的限差,应进行2C 的校正。
对于无目镜测微器的仪器,先按R 0=R+C (或L 0=L —C )算出正确读数。
然后用测微盘对准正确读数的不足度盘一格的零数,再用水平微动螺旋使水平度盘的上下分划像重合,使水平度盘读数等于R 0或L 0,此时望远镜的十字丝中心偏离目标影像。
再用十字丝网校正螺旋使十字丝照准目标。
不同类型的仪器,其十字丝校正螺旋亦不尽相同,如图3-27所示。
校正时,应注意校正螺旋的对抗性,应先松开一个再紧另一个。
校正后,通常应再检测一次,直到达到目的为止。
2.水平轴倾斜误差(1)水平轴倾斜误差及产生原因当视准轴与水平轴正交,且垂直轴与测站铅垂线一致时,仅由于水平轴与垂直轴不正交使水平轴倾斜一个小角i ,称为水平轴倾斜误差,见图3-28。
引起水平轴倾斜误差的主要原因是:在仪器安装、调整时不完善,致使仪器水平轴两支架不等高;或者水平轴两端的直径不相等。
(2)水平轴倾斜误差对观测方向值的影响及消除影响的方法水平轴倾斜误差i 对观测方向值的影响i ∆为图3-27 十字丝校正螺旋αtan ⋅=∆i i (3-14)式中:α为观测目标的垂直角。
由i ∆的表达式可知:1)i ∆的大小不仅与i 的大小成正比,而且与观测目标的垂直角α有关,当α越接近于90°,i ∆亦越大,当α=0°时,则i ∆=0°2)上述情况为盘左时,由于水平轴倾斜,使视准轴偏向垂直度盘一侧,正确的方向值L 0较有误差的方向值L 小i ∆,即i L L ∆-= 0 (3-15)纵转望远镜,在盘右位置观测时,正确读数较有误差的读数为大,故i R R ∆+=0 (3-16)取盘左和盘右读数的中数,得)(21)(2100R L R L +=+ 上式说明,水平轴倾斜误差对观测方向值的影响,在盘左和盘右读数中,可以得到消除。
3)观测一个角度时,如果两个方向的垂直角相差不大且接近于0°时,水平轴倾斜误差在半测回角度值中可以得到减弱或消除。
4)在望远镜纵转前后,同一方向上的盘左和盘右的观测值之差i R L ∆=±-2180 (3-17)这说明,即使没有视准轴误差存在,但由于有水平轴倾斜误差的存在,使得同一方向的 盘左和盘右读数之差值中,仍含有水平轴倾斜误差的影响。
在山区,一个测站上的各个观测方向的垂直角相差较大,如果视准轴误差和水平轴误差同时存在时,则有i C R L ∆+∆=±-22180 (3-18)这样,就不便于利用2C 的变化来判断观测成果的质量。
所以,对仪器的i 角的大小要加以限制,《规范》规定,J 07、J 1型仪器的i 角不得超过±10″,J 2型仪器不得超过±15″。
若超过限差,应对仪器进行校正。
(3)水平轴倾斜误差的检验1)检验公式式(3-18)为视准轴误差与水平轴倾斜误差同时存在时的盘左和盘右读数之差,即i C R L ∆+∆=±-22180将式(3-10)和式(3-14)代入上式,为书写简单,省去“±180°”(下同),得ααtan 2cos 2⋅+=-i C R L (3-19) 若观测目标的垂直角α>0°时,称之为高点。
在盘左和盘右位置观测高点时,则高高高ααtan 2cos 2)(⋅+=-i C R L (3-20) 若观测目标的垂直角α<0°时,称之为低点。
观测低点时,有低低低ααtan 2cos 2)(⋅+=-i C R L (3-21) 图3-28 水平轴倾斜误差在设置高点和低点时,若使ααα==低高把式(3-20)与式(3-21)相加和相减,可分别得到[][]⎪⎪⎩⎪⎪⎨⎧---=-+-=ααcot )()(41cos )()(41低高低高R L R L i R L R L C (3-22) 若对高点和低点均观测n 个测回,则有[][]⎪⎪⎩⎪⎪⎨⎧-∑--∑=-∑+-∑=ααcot )()(41cos )()(41低高低高R L R L ni R L R L n C (3-23) 令⎪⎪⎩⎪⎪⎨⎧-∑=-∑=低低高高)(21)(21R L n C R L n C (3-24) 则⎪⎪⎩⎪⎪⎨⎧-=+=ααcot 21cos 21)()(低高低高C C i C C C (3-25) 这就是高低点法检验视准轴误差及水平轴倾斜误差的公式。
2)检验方法此项检验可在室内或室外进行。
在室内检验时,可用两个照准器(任何装有十字丝的仪器均可)作为照准目标。
在室外检验时,可在距仪器5 m 以外的地方设置两个目标。
对两个目标位置的要求是:高点和低点应大致在同一方向上,两目标的垂直角的绝对值 应不小于3°且大致相等,其差值不得超过30″。
检验步骤是:观测高点和低点间的水平角6测回,并在各测回间均匀分配度盘。
在观测过程中,同一测回不得改变照准部的旋转方向,即半数测回顺时针方向旋转照准部,半数测回逆转。
观测限差是:各测回角度值互差,J 07、J 1型仪器应小于±3″;J 2型仪器不得超过±8″。
2C 变化,高点和低点的分别比较,J 07、J 1型仪器不得超过±8″,J 2型仪器不得超过±10″。
观测高点和低点的垂直角,用中丝法观测3个测回,垂直角、指标差的互差不得超过10″(各种类型的仪器要求相同)。
若有超限者,应进行重测。
检验示例见表3-2和表3-3。
顺便指出,当水平轴倾斜误差超限需要对仪器进行校正时,应由仪器检修人员进行。
所 以,此项误差的校正不再叙述。
3.垂直轴倾斜误差(1)垂直轴倾斜误差及其产生的原因当仪器三轴问的关系均已正确时,由于仪器未严格整置水平,而使仪器垂直轴偏离测站 铅垂线一个微小的角度v ,称为垂直轴倾斜误差。
如图3-29,OV 为与测站铅垂线一致的垂直轴位置,与之正交的水平轴为HH 1,O V ′为与测站铅垂线不一致即倾斜一个小角v 的垂直 轴的位置,水平轴也随之倾斜至H ′H 1′,位置。
这样,与水平轴正交的视准轴也偏离了正确位置,当其绕水平轴俯仰时形成的照准面将不是垂直照准面,而是倾斜照准面,从而给水平方向观测带来误差。
表3-2 水平轴不垂直于垂直轴之差的测定(一)高、低两点间水平角的测定仪器:北光J 07 No :71001 1974年5月3日注:120°位置为划去测回不采用,重测于后。
⎪⎪⎩⎪⎪⎨⎧+=⋅⨯=-=+=⋅⨯=-=∑∑"05.56.60621)(21"59.51.67621)(2111低低高高R L n C R L n C n n表3-3 水平轴不垂直于垂直轴之差的测定(二)高、低两点间垂直角的测定仪器:北光J 07 №:71001 1974年5月3日 照准点测回 读 数 指标差 垂直角 盘 左 盘 右° ′ ″ ° ′ ″ ° ′ ″ ° ′ ″ 高点Ⅰ92 00 01.3 87 58 56.8 01.4 02.7 56.6 113.4 -03.9 +4 00 09.3 Ⅱ 92 00 01.3 87 58 57.0 01.3 02.6 57.2 114.2 -03.2 +4 00 08.4 Ⅲ 92 00 00.3 87 58 56.600.2 00.5 57.0 113.6 -05.9+4 00 06.9 中数 + 4 00 08.2低点I87 58 57.8 92 00 00.1 58.1 115.9 00.2 00.3 -03.8 -4 00 04.4 Ⅱ 87 58 59.1 92 00 00.2 59.3 118.4 00.3 00.5 -01.1 -4 00 02.1 Ⅲ 87 58 58.2 92 00 00.658.5 116.7 00.5 01.1 -02.2-4 00 04.4 中数 -4 00 03.6 a =4 00 05.9注:水平轴不垂直于垂直轴之差:"86.32948.14)"05.5"59.5(21cot 21=⨯-+=-=α)(低高C C i (2)垂直轴倾斜误差对观测方向值的影响如图3-30,当垂直轴与测站铅垂线一致时,与之正交的水平轴HH 1处于水平位置,若照准部绕垂直轴旋转一周,水平轴HH 1将始终处于水平面H 1MHM 1上。