模式识别课后习题答案

人工智能之模式识别_北京理工大学中国大学mooc课后章节答案期末考试题库2023年1.采用非线性激活函数可以实现感知器解决非线性分类问题。

参考答案:错误2.下列关于最大池化的说法中错误的是？参考答案:LeNet采用的是最大池化方法3.填充树法由顶向底的方法和由底向顶填充相反。

参考答案:正确4.语言可以是无限的但是句子必须是有限的。

参考答案:正确5.文法是由下列哪些参数构成的？参考答案:起始符S_终止符V_T_非终止符V_N_产生式P6.感知器算法应用什么方法求解准则函数的最优值？参考答案:梯度下降法7.下列关于对比散度算法的说法中错误的是？参考答案:深度信念网中多层受限玻尔兹曼机同时通过对比散度算法完成预训练8.下列选项中，属于模式识别系统的环节是？参考答案:分类器训练_模式采集_分类决策_预处理与特征生成9.分类器函数的VC维h越大，将使下列选项中的哪些数据发生变化？参考答案:置信风险越大_结构风险越大_分类器泛化能力越差10.利用SVM将低维空间中的非线性问题映射到高维空间，存在哪些问题？参考答案:不确定需要映射到多少维的空间上，非线性问题才会转化为线性问题_如何找到合适的映射函数φ_增加计算量，可能会因为维数灾难无法解决11.本课程中介绍的与句法模式识别相关的基本概念有？参考答案:字母表_句子（链）_文法_语言12.下列选项中属于贝叶斯分类器的特点的是？参考答案:分类决策存在错误率_先验概率已知，以新获得的信息对先验概率进行修正13.贝叶斯分类器的训练，是从样本集数据中估计出____。

参考答案:类条件概率_先验概率14.下列选项中属于特征降维的优点的是？参考答案:降低模式识别任务的复杂度_提升分类决策的正确率_用更少的代价设计出更加优秀的模式识别系统15.下列说法中正确的是？参考答案:聚类结果受特征选取和聚类准则的影响_数据聚类没有预先分好类的样本集_聚类结果受各特征量纲标尺的影响_数据聚类没有已知的分类决策规则16.设计一个组合分类器需要满足什么要求？参考答案:每个基分类器的训练集和训练结果要有差异_组合分类器需要重点考虑方差和偏差_基分类器的分类正确率大于50%17.下列选项中属于决策树分类器的特点的是？参考答案:需选择分支后两个子节点纯度最高的特征作为一个节点的测试特征_速度快，分类决策规则明确_未考虑特征间的相关性_有监督学习方法18.下列选项中属于Adaboost算法的特点的是？参考答案:异常数据（离群点）影响大_不易实现并行化训练_只能解决二分类问题_算法的组合过程能减小偏差19.下列选项中属于反馈型神经网络的是？参考答案:Hopfield网络_受限玻尔兹曼机20.调节以下哪些部分可以对神经网络的性能造成影响？参考答案:权值_激活函数_隐层单元_阈值21.下列选项中关于前馈网络和反馈网络的说法中正确的是？参考答案:前馈网络输出不作用在网络的输入中_前馈网络为静态网络_反馈网络下一时刻的输出与上一时刻的输出有关_反馈网络为动态网络22.下列选项中属于BP网络的不足的是？参考答案:容易陷入局部极小值_全连接网络计算大_隐层神经元数量难以确定_无法做到深度很深，会产生梯度消失23.下列选项中属于深度学习的特点的是？参考答案:需要大量样本进行训练_逐层抽象，发现数据集的特征_是层数较多的大规模神经网络_需要大规模并行计算能力的支持24.利用链式求导法则需要哪些信息？参考答案:损失函数与网络输出向量之间的函数关系_激活函数输出对净激励的导数25.深度信念网不能用于图像识别的原因是？参考答案:深度信念网为一维向量输入，不能直接用于二位图像_需要进行认知－重构的双向计算，学习速度不够快_受限玻尔兹曼机的层间全连接，权值数量太多26.Jp作为类内、类间可分性的概率距离度量时应该满足下列选项中哪些条件？参考答案:当两类完全不可分时，Jp等于0_当两类完全可分时，Jp取得最大值27.特征选择的算法包括以下哪些？参考答案:分支定界法_顺序后退法_穷举法_顺序前进法28.特征降维的方法包括特征选择和特征提取。

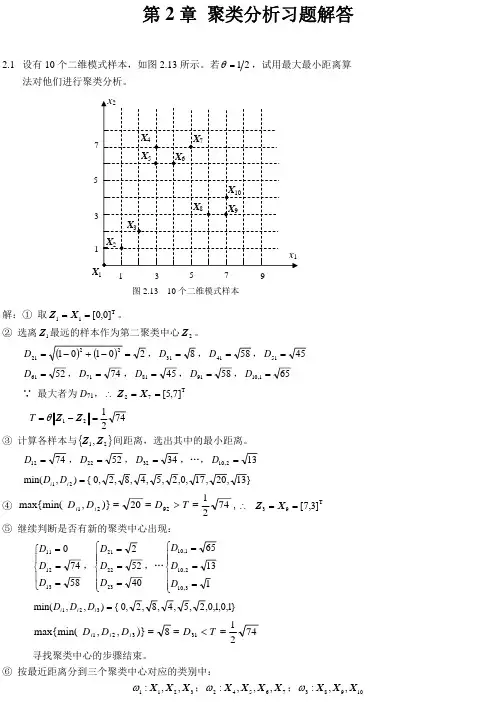
模式识别习题及答案模式识别习题及答案【篇一：模式识别题目及答案】p> t，方差?1?（2,0）-1/2??11/2??1t，第二类均值为，方差，先验概率??（2,2）?122???1??1/21??-1/2p(?1)?p(?2)，试求基于最小错误率的贝叶斯决策分界面。

解根据后验概率公式p(?ix)?p(x?i)p(?i)p(x)，(2’)及正态密度函数p(x?i)?t(x??)?i(x??i)/2] ,i?1,2。

(2’) i?1基于最小错误率的分界面为p(x?1)p(?1)?p(x?2)p(?2)，(2’) 两边去对数，并代入密度函数，得(x??1)t?1(x??1)/2?ln?1??(x??2)t?2(x??2)/2?ln?2(1) (2’)1?14/3-2/3??4/32/3??1由已知条件可得?1??2，?1，?2??2/34/3?，(2’)-2/34/31设x?(x1,x2)t，把已知条件代入式（1），经整理得x1x2?4x2?x1?4?0，(5’)二、（15分）设两类样本的类内离散矩阵分别为s1??11/2?, ?1/21?-1/2??1tt,各类样本均值分别为?1?，?2?，试用fisher准（1,0）（3,2）s2-1/21??（2,2）的类别。

则求其决策面方程，并判断样本x?解：s?s1?s2??t20?(2’) ??02?1/20??-2??-1?*?1w?s()?投影方向为12?01/22?1? (6’) ???阈值为y0?w(?1??2)/2??-1-13 (4’)*t2?1?给定样本的投影为y?w*tx??2-1?24?y0，属于第二类(3’) ??1?三、（15分）给定如下的训练样例实例 x0 x1 x2 t(真实输出) 1 1 1 1 1 2 1 2 0 1 3 1 0 1 -1 4 1 1 2 -1用感知器训练法则求感知器的权值，设初始化权值为w0?w1?w2?0；1 第1次迭代2 第2次迭代（4’）（2’）3 第3和4次迭代四、（15分）i. 推导正态分布下的最大似然估计；ii. 根据上步的结论，假设给出如下正态分布下的样本，估计该部分的均值和方差两个参数。

模式识别（山东联盟）智慧树知到课后章节答案2023年下青岛大学青岛大学第一章测试1.关于监督模式识别与非监督模式识别的描述正确的是答案:非监督模式识别对样本的分类结果是唯一的2.基于数据的方法适用于特征和类别关系不明确的情况答案:对3.下列关于模式识别的说法中,正确的是答案:模式可以看作对象的组成成分或影响因素间存在的规律性关系4.在模式识别中，样本的特征构成特征空间，特征数量越多越有利于分类答案:错5.在监督模式识别中，分类器的形式越复杂，对未知样本的分类精度就越高答案:错第二章测试1.下列关于最小风险的贝叶斯决策的说法中正确的有答案:条件风险反映了对于一个样本x采用某种决策时所带来的损失;最小风险的贝叶斯决策考虑到了不同的错误率所造成的不同损失;最小错误率的贝叶斯决策是最小风险的贝叶斯决策的特例2.我们在对某一模式x进行分类判别决策时，只需要算出它属于各类的条件风险就可以进行决策了。

答案:对3.下面关于贝叶斯分类器的说法中错误的是答案:贝叶斯分类器中的判别函数的形式是唯一的4.当各类的协方差矩阵相等时，分类面为超平面，并且与两类的中心连线垂直。

答案:错5.当各类的协方差矩阵不等时，决策面是超二次曲面。

答案:对第三章测试1.概率密度函数的估计的本质是根据训练数据来估计概率密度函数的形式和参数。

答案:对2.参数估计是已知概率密度的形式，而参数未知。

答案:对3.概率密度函数的参数估计需要一定数量的训练样本，样本越多，参数估计的结果越准确。

答案:对4.下面关于最大似然估计的说法中正确的是答案:在最大似然函数估计中，要估计的参数是一个确定的量。

;在最大似然估计中要求各个样本必须是独立抽取的。

;最大似然估计是在已知概率密度函数的形式，但是参数未知的情况下，利用训练样本来估计未知参数。

5.贝叶斯估计中是将未知的参数本身也看作一个随机变量，要做的是根据观测数据对参数的分布进行估计。

答案:对第四章测试1.多类问题的贝叶斯分类器中判别函数的数量与类别数量是有直接关系的。

“模式识别(三).PDF”课件课后上机选做作业参考解答(武大计算机学院袁志勇, Email: yuanzywhu@) 上机题目：两类问题，已知四个训练样本ω1={(0,0)T,(0,1)T}；ω2={(1,0)T,(1,1)T}使用感知器固定增量法求判别函数。

设w1=(1,1,1)Tρk=1试编写程序上机运行(使用MATLAB、 C/C++、C#、JA V A、DELPHI等语言中任意一种编写均可)，写出判别函数，并给出程序运行的相关运行图表。

这里采用MATLAB编写感知器固定增量算法程序。

一、感知器固定增量法的MATLAB函数编写感知器固定增量法的具体内容请参考“模式识别(三).PDF”课件中的算法描述，可将该算法编写一个可以调用的自定义MATLAB函数：% perceptronclassify.m%% Caculate the optimal W by Perceptron%% W1-3x1 vector, initial weight vector% Pk-scalar, learning rate% W -3x1 vector, optimal weight vector% iters - scalar, the number of iterations%% Created: May 17, 2010function [W iters] = perceptronclassify(W1,Pk)x1 = [0 0 1]';x2 = [0 1 1]';x3 = [1 0 1]';x4 = [1 1 1]';% the training sampleWk = W1;FLAG = 0;% iteration flagesiters = 0;if Wk'*x1 <= 0Wk =Wk + x1;FLAG = 1;endif Wk'*x2 <= 0Wk =Wk + x2;FLAG = 1;endif Wk'*x3 >= 0Wk=Wk-x3;FLAG = 1; endif Wk'*x4 >= 0Wk =Wk -x4; FLAG = 1; enditers = iters + 1; while (FLAG) FLAG = 0; if Wk'*x1 <= 0Wk = Wk + x1; FLAG = 1; endif Wk'*x2 <= 0Wk = Wk + x2; FLAG = 1; endif Wk'*x3 >= 0 Wk = Wk - x3; FLAG = 1; endif Wk'*x4 >= 0 Wk = Wk - x4; FLAG = 1; enditers = iters + 1; endW = Wk;二、程序运行程序输入：初始权向量1W , 固定增量大小k ρ 程序输出：权向量最优解W , 程序迭代次数iters 在MATLAB 7.X 命令行窗口中的运行情况： １、初始化1[111]T W = 初始化W 1窗口界面截图如下：２、初始化1kρ=初始化Pk 窗口界面截图如下：３、在MATLAB 窗口中调用自定义的perceptronclassify 函数由于perceptronclassify.m 下自定义的函数文件，在调用该函数前需要事先[Set path…]设置该函数文件所在的路径，然后才能在命令行窗口中调用。

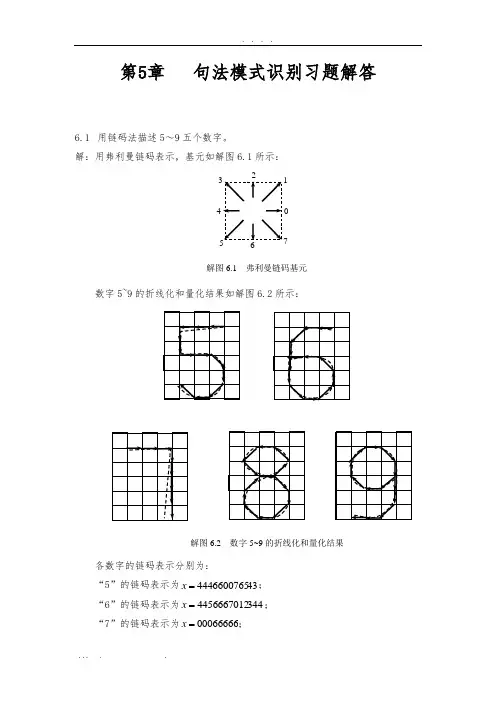
第5章 句法模式识别习题解答6.1 用链码法描述5～9五个数字。

解：用弗利曼链码表示，基元如解图6.1所示：数字5~9的折线化和量化结果如解图6.2所示：各数字的链码表示分别为：“5”的链码表示为434446600765=x ； “6”的链码表示为3444456667012=x ； “7”的链码表示为00066666=x ；0 17解图6.1 弗利曼链码基元解图6.2 数字5~9的折线化和量化结果“8”的链码表示为21013457076543=x ； “9”的链码表示为5445432107666=x 。

6.2 定义所需基本基元，用PDL 法描述印刷体英文大写斜体字母“H ”、“K ”和“Z ”。

解：设基元为：用PDL 法得到“H ”的链描述为)))))(~((((d d c d d x H ⨯+⨯+=；“K ”的链描述为))((b a d d x K ⨯⨯+=； “Z ”的链描述为))((c c g x Z ⨯-=。

6.3 设有文法),,,(S P V V G T N =，N V ，T V 和P 分别为},,{B A S V N =，},{b a V T =：P ①aB S →，②bA S →，③a A →，④aS A →⑤bAA A →，⑥b B →，⑦bS B →，⑧aBB B → 写出三个属于)(G L 的句子。

解：以上句子ab ，abba ，abab ，ba ，baab ，baba 均属于)(G L 。

bcadeabba abbA abS aB S ⇒⇒⇒⇒ ① ⑦ ② ③ab aB S ⇒⇒ ① ⑥ ba bA S ⇒⇒② ③ abab abaB abS aB S ⇒⇒⇒⇒ ① ⑦ ① ⑥baab baaB baS bA S ⇒⇒⇒⇒ ② ④ ① ⑥baba babA baS bA S ⇒⇒⇒⇒② ④ ② ③6.4 设有文法),,,(S P V V G T N =，其中},,,{C B A S V N =，}1,0{=T V ，P 的各生成式为①A S 0→，②B S 1→，③C S 1→ ④A A 0→，⑤B A 1→，⑥1→A ⑦0→B ，⑧B B 0→，⑨C C 0→，⑩1→C问00100=x 是否属于语言)(G L ？ 解：由可知00100=x 属于语言)(G L 。

模式识别习题及答案模式识别习题及答案模式识别是人类智能的重要组成部分，也是机器学习和人工智能领域的核心内容。

通过模式识别，我们可以从大量的数据中发现规律和趋势，进而做出预测和判断。

本文将介绍一些模式识别的习题，并给出相应的答案，帮助读者更好地理解和应用模式识别。

习题一：给定一组数字序列，如何判断其中的模式？答案：判断数字序列中的模式可以通过观察数字之间的关系和规律来实现。

首先，我们可以计算相邻数字之间的差值或比值，看是否存在一定的规律。

其次，我们可以将数字序列进行分组，观察每组数字之间的关系，看是否存在某种模式。

最后，我们还可以利用统计学方法，如频率分析、自相关分析等，来发现数字序列中的模式。

习题二：如何利用模式识别进行图像分类？答案：图像分类是模式识别的一个重要应用领域。

在图像分类中，我们需要将输入的图像分为不同的类别。

为了实现图像分类，我们可以采用以下步骤：首先，将图像转换为数字表示，如灰度图像或彩色图像的像素矩阵。

然后，利用特征提取算法，提取图像中的关键特征。

接下来，选择合适的分类算法，如支持向量机、神经网络等，训练模型并进行分类。

最后，评估分类结果的准确性和性能。

习题三：如何利用模式识别进行语音识别？答案：语音识别是模式识别在语音信号处理中的应用。

为了实现语音识别，我们可以采用以下步骤：首先，将语音信号进行预处理，包括去除噪声、降低维度等。

然后，利用特征提取算法，提取语音信号中的关键特征，如梅尔频率倒谱系数（MFCC）。

接下来，选择合适的分类算法，如隐马尔可夫模型（HMM）、深度神经网络（DNN）等，训练模型并进行语音识别。

最后，评估识别结果的准确性和性能。

习题四：如何利用模式识别进行时间序列预测？答案：时间序列预测是模式识别在时间序列分析中的应用。

为了实现时间序列预测，我们可以采用以下步骤：首先，对时间序列进行平稳性检验，确保序列的均值和方差不随时间变化。

然后，利用滑动窗口或滚动平均等方法，将时间序列划分为训练集和测试集。

题1：在一个10类的模式识别问题中，有3类单独满足多类情况1，其余的类别满足多类情况2。

问该模式识别问题所需判别函数的最少数目是多少？答：将10类问题可看作4类满足多类情况1的问题，可将3类单独满足多类情况1的类找出来，剩下的7类全部划到4类中剩下的一个子类中。

再在此子类中，运用多类情况2的判别法则进行分类，此时需要7*（7-1）/2=21个判别函数。

故共需要4+21=25个判别函数。

题2：一个三类问题，其判别函数如下：d1(x)=-x1, d2(x)=x1+x2-1, d3(x)=x1-x2-11.设这些函数是在多类情况1条件下确定的，绘出其判别界面和每一个模式类别的区域。

2.设为多类情况2，并使：d12(x)= d1(x), d13(x)= d2(x), d23(x)= d3(x)。

绘出其判别界面和多类情况2的区域。

3.设d1(x), d2(x)和d3(x)是在多类情况3的条件下确定的，绘出其判别界面和每类的区域。

答：三种情况分别如下图所示：1．2．3．题3：两类模式，每类包括5个3维不同的模式，且良好分布。

如果它们是线性可分的，问权向量至少需要几个系数分量？假如要建立二次的多项式判别函数，又至少需要几个系数分量？（设模式的良好分布不因模式变化而改变。

）答：（1）若是线性可分的，则权向量至少需要14N n =+=个系数分量； （2）若要建立二次的多项式判别函数，则至少需要5!102!3!N ==个系数分量。

题4：用感知器算法求下列模式分类的解向量w : ω1: {(0 0 0)T, (1 0 0)T, (1 0 1)T, (1 1 0)T} ω2: {(0 0 1)T, (0 1 1)T, (0 1 0)T, (1 1 1)T}解：将属于2w 的训练样本乘以(1)-，并写成增广向量的形式x1=[0 0 0 1]',x2=[1 0 0 1]',x3=[1 0 1 1]',x4=[1 1 0 1]';x5=[0 0 -1 -1]',x6=[0 -1 -1 -1]',x7=[0 -1 0 -1]',x8=[-1 -1 -1 -1]';迭代选取1C =，(1)(0,0,0,0)w '=，则迭代过程中权向量w 变化如下：(2)(0 0 0 1)w '=；(3)(0 0 -1 0)w '=；(4)(0 -1 -1 -1)w '=；(5)(0 -1 -1 0)w '=；(6)(1 -1 -1 1)w '=；(7)(1 -1 -2 0)w '=；(8)(1 -1 -2 1)w '=；(9)(2 -1 -1 2)w '=； (10)(2 -1 -2 1)w '=；(11)(2 -2 -2 0)w '=；(12)(2 -2 -2 1)w '=；收敛所以最终得到解向量(2 -2 -2 1)w '=，相应的判别函数为123()2221d x x x x =--+。

可编辑修改精选全文完整版题1：设有如下三类模式样本集ω1，ω2和ω3,其先验概率相等,求Sw 和Sb ω1：{（1 0)T, (2 0) T, (1 1） T} ω2：｛（—1 0）T, （0 1) T ， （-1 1) T}ω3：｛（-1 -1）T ， （0 -1） T ， (0 -2） T ｝解：由于本题中有三类模式，因此我们利用下面的公式：b S =向量类模式分布总体的均值为C ,))()((00031m m m m m P t i i i i --∑=ω，即：i 31i i 0m )p(E{x }m ∑===ωi m 为第i 类样本样本均值⎪⎪⎪⎪⎭⎫⎝⎛=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎪⎪⎭⎫⎝⎛=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎭⎫⎝⎛--+⎪⎭⎫⎝⎛-⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛=--=⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+--=⎪⎪⎪⎪⎭⎫⎝⎛--=⎥⎦⎤⎢⎣⎡---++-=⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡++-+-=⎪⎪⎪⎪⎭⎫ ⎝⎛=⎥⎦⎤⎢⎣⎡++++=∑=81628113811381628112181448144811681498149814981498116814481448112131911949119497979797949119491131)m m )(m m ()(P S 919134323131323431m 343121100131m 323211010131m ;313410012131m t 0i 0i 31i i b10321ω；333t(i)(i)k k w i i i i i i i i 1i 11111S P()E{(x-m )(x-m )/}C [(x m )(x m )33361211999271612399279Tk ωω====•==--⎡⎤⎡⎤--⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎣⎦⎣⎦∑∑∑题2:设有如下两类样本集，其出现的概率相等： ω1:{(0 0 0)T , (1 0 0) T ， （1 0 1） T ， （1 1 0) T ｝ω2：{(0 0 1）T , （0 1 0） T , （0 1 1） T , (1 1 1） T ｝用K-L 变换，分别把特征空间维数降到二维和一维，并画出样本在该空间中的位置.解:把1w 和2w 两类模式作为一个整体来考虑，故0 1 1 1 0 0 0 1 0 0 0 1 0 1 1 1 0 0 1 0 1 0 1 1x ⎛⎫ ⎪= ⎪ ⎪⎝⎭0.5{}0.50.5m E x ⎛⎫⎪== ⎪ ⎪⎝⎭协方差矩阵0.25 0 0{()()} 0 0.25 0 0 0 0.25x C E x m x m ⎛⎫ ⎪'=--= ⎪ ⎪⎝⎭从题中可以看出，协方差矩阵x C 已经是个对角阵，故x C 的本征值1230.25λλλ===其对应的本征向量为： 1231000,1,0001φφφ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭若要将特征空间维数降到二维,因本题中三个本征值均相等，所以可以任意选取两个本征向量作为变换矩阵,在这里我们取1φ和2φ，得到100100⎛⎫⎪Φ= ⎪ ⎪⎝⎭。