下载文档原格式
第一章参考答案习题1-1（P9）1、（1）]5,2(；（2）]2,2[-；（3）]34,32[；（4）),1()3,(+∞-⋃--∞；2、（1）不同，定义域不同；（2）相同；（3）不同，定义域不同；（4）不同，定义域不同；3、（1）}1,2{±≠-≥x x x 且；（2）Ｒ；（3）Ｒ；（4）]3,1[-；（5）),1(+∞-；（6）R ；4、x x x f x xx f x x x f f f -=++-=++=-==222)1(,231)1(,23)(,0)1(,2)0(； 5、⎩⎨⎧>≤=--=-==1,41,)1(,1)2(,4)2(,1)0(x x x x f f f f ；6、（1）偶函数；（2）奇函数；（3）偶函数；（4）偶函数；7、略； 8、32π； |9、（1）31-=x y ；（2）11-+=x x y ；（3）21-=-x e y ；（4）yyy -=12log ；10、（1）x y 3sin =；（2）13-≤≤-u ，不能构成复合函数；（3）x y 2cos 2+=；11、（1）x u u y tan ,2==；（2）2,,x v v e u e y u =-==； （3）x v v u u y sin ,,arcsin ===；（4）2,1,1,ln 3x t t v v u u y =+=+==；12、略；13、⎪⎩⎪⎨⎧>-=<=0,10,00,1)]([x x x x g f ，⎪⎩⎪⎨⎧>=<=-1,1,11,)]([1x e x x e x f g ；习题1-2（P13） （1）0；（2）0；（3）2；（4）∞；（5）0；（6）2； 习题1-3（P17） .1、（1）0；（2）8；（3）4-；（4）21；（5）0；（6）∞； 2、解：)(lim )(lim ,7)12(lim )(lim ,3lim )(lim 333333x f x f x x f x x f x x x x x x +-++--→→→→→→≠=+===显然所以)(lim 3x f x →不存在3、证明：)(lim )(lim ,1lim lim ,1lim lim 00000x f x f x xx x xx xx x x x x x x +-++--→→→→→→≠==-=-=显然所以xx x 0lim→不存在习题1-4（P19）（1）9；（2）0；（3）2；（4）0；（5）49；（6）6；（7）2；（8）21；（9）x 2；（10）3； （11）32；（12）31；（13）0；（14）2-；（15）322；（16）2；（17）41；（18）6；'习题1-5（P24）1、（1）3；（2）25；（3）34；（4）0；（5）2；（6）1； （7）x x x x x n nn n n n =⋅=∞→∞→22sin lim2sin 2lim ； （8）xx x x xx xx x x x x x 203030sin cos cos 1lim sin sin cos sin lim sin sin tan lim ⋅-=-=-→→→ 21sin cos )2()2(2sin 2lim sin cos 2sin 2lim 2222220220=⋅⋅⋅⋅=⋅=→→xxx x x x x x x x x x ；2、（1）e 1；（2）4e ；（3）e1；（4）21221)21()21(lim )21(lim 1)121(lim e tt t x t x tt t t x x =+⋅+=++=++-⋅∞→-∞→∞→令 21221)121()121(lim )121(lim e xxx xx x x =++⋅++=++-⋅+∞→∞→； （5）2-e ；（6）e1；《习题1-6（P28）1、（1）无穷大；（2）无穷小；（3）无穷小；（4）无穷大；2、当1→x 时函数无穷大，当∞→x 时函数无穷小；3、（1）0；（2）0；4、2322x x x x --是比高阶的无穷小； 5、（1）同阶；（2）同阶；（3）等价；6、（1）原式⎪⎩⎪⎨⎧<∞=>==→mn m n mn x x m nx ,,1,0lim 0；（2）原式44lim 220==→x x x ；（3）原式2323lim 0-=-=→x x x ；习题1-7（P33） 1、（1）1=x ，跳跃间断点；（2）2-=x ，无穷间断点；（3）0=x ，可去间断点； 、（4）1=x 可去间断点，3=x ，无穷间断点； 2、不连续；3、连续区间：),2()2,3()3,(+∞⋃-⋃--∞，21)(lim 0=→x f x ，58)(lim 3-=-→x f x ，∞=→)(lim 2x f x 4、函数在定义域]2,0[内连续；5、（1）2221e e +-；（2）22sin lim cos 2cos sin 2lim )cos(22sin lim 444-=-=-=-→→→x x x x x x x x x ππππ； 6、证明：设x e x f x3)(-=，显然)(x f 在]1,0[上连续因为0)3)(01()1()0(<--=⋅e f f ，由零点存在定理知，至少存在一点)1,0(0∈x ，使0)(0=x f ，即0300=-x e x所以方程x e x3=在区间)1,0(内至少有一个实根。
2024 年全国高中数学联赛福建赛区预赛 暨 2024 年福建省高中数学竞赛试卷参考答案(考试时间: 2024 年 6 月 22 日上午 9:00-11:30, 满分 160 分)一、填空题 (共 10 小题, 每小题 6 分, 满分 60 分. 请直接将答案写在题中的横线上) 1. 在 △ABC 中,已知 AB =4,BC =2,AC =2√3 ,若动点 P 满足 |CP⃗⃗⃗⃗⃗ |=1 ,则 AP ⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ 的最大值为 . 【答案】 5【解答】取 AB 中点 O ,则AP ⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ =PA ⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ =14[(PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ )2−(PA ⃗⃗⃗⃗⃗ −PB ⃗⃗⃗⃗⃗ )2]=14[(2PO ⃗⃗⃗⃗⃗ )2−BA⃗⃗⃗⃗⃗ 2]=PO ⃗⃗⃗⃗⃗ 2−14×42=PO ⃗⃗⃗⃗⃗ 2−4由 AB =4,BC =2,AC =2√3 ,知 AB 2=CA 2+CB 2 ,于是 CA ⊥CB . 所以 CO =12AB =2 .又 |CP⃗⃗⃗⃗⃗ |=1 ,所以 |PO ⃗⃗⃗⃗⃗ | 的最大值为 CO +1=3 . 所以 AP⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ 的最大值为 32−4=5 . 2. 已知 z 1,z 2,z 3 为方程 z 3=−i 的三个不同的复数根,则 z 1z 2+z 2z 3+z 3z 1= . 【答案】 0【解答】设 z =x +yi (x,y ∈R ) 为方程 z 3=−i 的复数根, 则 z 3=(x +yi )3=x 3+3x 2(yi )+3x (yi )2+(yi )3=−i . 即 x 3+3x 2yi −3xy 2−y 3i =−i,x 3−3xy 2+(3x 2y −y 3)i =−i . 由 x,y ∈R ,得 {x 3−3xy 2=03x 2y −y 3=−1,解得 {x 1=0y 1=1 , {x 2=√32y 2=−12,{x 3=−√32y 3=−12.于是 z 1=i, z 2=√32−12i, z 3=−√32−12i . 所以 z 2+z 3=(√32−12i)+(−√32−12i)=−i ,z 2z 3=(√32−12i)(−√32−12i)=(−12i)2−(√32)2=−14−34=−1.因此 z 1z 2+z 2z 3+z 3z 1=z 1(z 2+z 3)+z 2z 3=i ×(−i )−1=0 .3. 设a=66⋯6⏟10个6,b=33⋯3⏟6个3,则a,b的最大公约数为 .【答案】 33【解答】用(x,y)表示正整数x,y的最大公约数.则(a,b)=(66⋯6⏟10个6,33⋯3⏟6个3)=(33⋯3⏟10个3,33⋯3⏟6个3)=3(11⋯1⏟10个1,11⋯1⏟6个1) .设m=11⋯1⏟10个1, n=11⋯1⏟6个1,则由m=11⋯1⏟10个1=104×11⋯1⏟6个1+1111 ,可知(m,n)=(1111,11⋯1⏟6个1) .同理可得, (m,n)=(1111,11⋯1⏟6↑1)=(11,1111)=(11,11)=11 .所以(a,b)=3(m,n)=33 .4. 某校三个年级举办乒乓球比赛, 每个年级选派 4 名选手参加比赛. 组委会随机将这 12 名选手分成 6 组, 每组 2 人, 则在上述分组方式中每组的 2 人均来自不同年级的概率为 .【答案】64385【解答】设三个年级为甲、乙、丙.12名选手随机分成6组,每组2人的分组方式有: C122C102C82C62C42C22A66=11×9×7×5×3×1种.下面考虑每组的2人均来自不同年级的分组情形.先考虑甲年级4名选手的配对方式: 由于每组2人均来自不同年级, 因此需从乙, 丙两个年级中每个年级各取 2 名选手与甲年级的 4 名选手配对. 故有C42×C42×A44=36×24种方式.再考虑余下 4 人的配对方式,此时乙、丙年级各有 2 人,其分组方式有2×1种.所以每组的 2 人均来自不同年级的分组方式有36×24×2种.所以每组的 2 人均来自不同年级的概率为36×24×211×9×7×5×3×1=64385.5. 如图,在棱长为 6 的正方体ABCD−A1B1C1D1中,点E,F分别为 AB,BC 的中点,点 G 在棱 CC 1 上. 若平面 EFG 与底面 ABCD 所成角的余弦值为 3√1717,则平面 EFG 截正方体 ABCD −A 1B 1C 1D 1 所得截面多边形的周长为 . 【答案】 6√13+3√2【解答】如图,以 D 为原点,射线 DA,DC,DD 1 分别为 x 轴, y 轴,(第 5 题图) z 轴非负半轴建立空间直角坐标系.(第 5 题答题图)则 E (6,3,0),F (3,6,0) . 设 G (0,6,t ) ,则 EF ⃗⃗⃗⃗⃗ =(−3,3,0) , EG ⃗⃗⃗⃗⃗ =(−6,3,t ) . 设 m ⃗⃗ =(x,y,z ) 为平面 EFG 的一个法向量,则{m ⃗⃗ ⋅EF⃗⃗⃗⃗⃗ =−3x +3y +0=0m ⃗⃗ ⋅EG⃗⃗⃗⃗⃗ =−6x +3y +tz =0 ,于是 m ⃗⃗ =(t,t,3) 为平面 EFG 的一个法向量.又 n ⃗ =(0,0,1) 为平面 ABCD 的一个法向量,且平面 EFG 与底面 ABCD 所成角的余弦值 为 3√1717, 所以 |cos⟨m ⃗⃗ ,n ⃗ ⟩|=|m⃗⃗⃗ ⋅n ⃗ |m ⃗⃗⃗ |⋅|n ⃗ ||=√2t 2+9⋅1=3√1717. 结合 t >0 ,解得 t =2 . 所以 G (0,6,2),CG =2 .延长 EF 交直线 DC 于点 M ,由 E,F 分别为 AB,BC 的中点,知点 M 在 DC 延长线上, 且 CM =3 . 由 CG DD 1=26=39=MCMD 知, M,G,D 1 三点共线.于是 GD 1 是截面多边形的一条边.延长 FE 交直线 DA 于点 N ,连接 D 1N 交 AA 1 于点 P ,则 D 1P 也是截面多边形的一条边. 另由AN =3=12A 1D 1 可知, AP =12A 1P ,所以 AP =2,A 1P =4 .连接 PE ,则五边形 EFGD 1P 为平面 EFG 截正方体 ABCD −A 1B 1C 1D 1 所得的截面多边形. 易知 EF =√32+32=3√2,FG =√32+22=√13,GD 1=√42+62=2√13 ,D 1P =√62+42=2√13, PE =√22+32=√13.所以截面五边形的周长为 6√13+3√2 .注: 作 CH ⊥EF 与 H ,则 GH ⊥EF,∠GHC 为二面角 G −EF −D 的平面角,于是 tan∠GHC =CGCH =3√22=2√23,因此 CG =2 。
一、 计算下列各题（每小题4分，共16分） （1） 已知8)()(20=⋅'⎰dx x f x f ，且0)0(=f 求)(x f .（2） 设函数)1sin(sin 1cos )1(2cos )sin(-++--+=y x x y y xy z ，求)1,0(|dz（3） 设函数),(y x z 满足222=∂∂yz及x x z x z y ='=)0,(,1)0,(，求),(y x z . （4） 交换二重积分的次序⎰⎰11-||1),(x dy y x f dx .（5） 设曲面4:222=++∑z y x ，求第一类曲面积分⎰⎰∑++dS y x xy )2(22.一、（1）令C dx x f =⎰2)(,则x Cx f C x f 8)(8)(=⇒='，两端求定积分得 Cxdx C dx x f C 168)(220===⎰⎰，则4±=C ，故x x f 2)(±=. （2）3cos )sin 1(cos 3cos )sin 13cos sin ()1,(0200)1,0(=+=+==∂∂===x x x x xx x dx d dx x dz x z1)]1sin(1[)1cos()1()]1sin(1[))1sin(11(),0(1211)1,0(-=-+----+-=-+--==∂∂===y y y y y y y y y dy d dyy dz yzdy dx dy y z dx x z dz -=∂∂+∂∂=3cos |)1,0()1,0()1,0( （3）由)(2222x y yzy z ϕ+=∂∂⇒=∂∂，再由x x z y =')0,(得x x =)(ϕ， x y y x z y +='2),(，)()2(),(2x xy y dy x y y x z φ++=+=⎰，再由1)0,(=x z 得 1)(=x φ，因此1),(2++=xy y y x z .厦门大学第十一届“景润杯”数学竞赛试卷（理工类）竞赛日期 2014年6月7日(4) ⎰⎰⎰⎰⎰⎰--=-=1011-1||11-||1),(),(),(yyx x dx y x f dy dy y x f dx dy y x f dx .(5)ππ64244)(0)2(222222=⨯⨯=+++=++⎰⎰⎰⎰∑∑dS z y x dS y xxy .二、（10分）设函数⎪⎩⎪⎨⎧>-≤=+0)1(0)(222x x b x e x f xa ax 在点0=x 处连续，问常数)0(,>b b a 取何值时，定积分⎰-21)(ln dx x f 取最小值，并求最小值.解：由)(x f 在点0=x 处连续可得)0()(lim 0f x f x =+→,即1)1(lim 20=-+→x b x ， 由此可得1=b .于是⎩⎨⎧≠>-≤+=⎪⎩⎪⎨⎧>-≤=+1,0|1|ln 20)(ln ,0)1(0)(22222x x x x x a ax x f x x x e x f xa ax ，从而⎰⎰⎰-++=--20012221|1|ln 2)()(ln dx x dx x a ax dx x f)(|1|ln 23121202a I dx x a a 记⎰-++-=令03221)(=+-='a a I 得驻点43=a ，且032)43(>=''I ，故在43=a 处，积分取最小值。
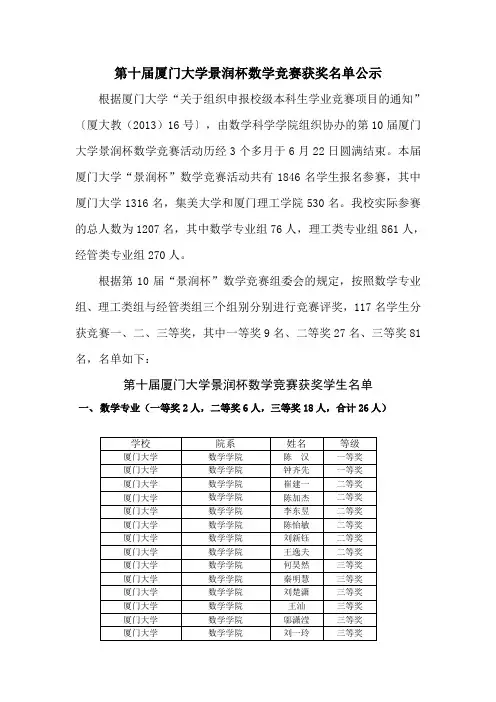
第十届厦门大学景润杯数学竞赛获奖名单公示根据厦门大学“关于组织申报校级本科生学业竞赛项目的通知”〔厦大教（2013）16号〕，由数学科学学院组织协办的第10届厦门大学景润杯数学竞赛活动历经3个多月于6月22日圆满结束。
本届厦门大学“景润杯”数学竞赛活动共有1846名学生报名参赛，其中厦门大学1316名，集美大学和厦门理工学院530名。
我校实际参赛的总人数为1207名，其中数学专业组76人，理工类专业组861人，经管类专业组270人。
根据第10届“景润杯”数学竞赛组委会的规定，按照数学专业组、理工类组与经管类组三个组别分别进行竞赛评奖，117名学生分获竞赛一、二、三等奖，其中一等奖9名、二等奖27名、三等奖81名，名单如下：
第十届厦门大学景润杯数学竞赛获奖学生名单
一、数学专业（一等奖2人，二等奖6人，三等奖18人，合计26人）
二、理工专业组（一等奖4人，二等奖12人，三等奖36人，合计52人）
三、经管专业组（一等奖3人，二等奖9人，三等奖27人，合计39人）
厦门大学数学科学学院
2013.6.25。
2023年厦门大学强基计划数学试题考试时间6月12日1．1w z =变换将复平面()z x yi =+上的直线1x =变换为W 平面()w p qi =+上的曲线C ,求曲线C 围成的面积是_______.2.在(1,1)-上任取个2数,求两数之和小于0.4的概率是_______.3.若椭圆22221x y a b +=的内接等腰三角形ABC 的疷边平行于x 轴，求ABC ∆的面积最大值_______.4.已知11()sin ,()248x f x g x x π==-，求()()f x g x =在[]420-，上所有根的和_______.5.已知,m n 为整数，若二元函数(,)f m n 满足4(,)(1,)(1,)(f m n f m n f m n f m =++-+ ,1)(,1)n f m n ++-，则称(,)f m n 为兔函数。
下列哪些是兔函数（1）22(,)f m n m n =-；（2）(1),(,)0,m m n f m n m n ⎧-==⎨≠⎩；（3）(,)sin()2v m f m n e π=，其中4b b e e -+=6.已知正整数,a b 互素，问22a b +和ab 是否互素？7.已知1221,,2n n n x a x b x x x ++===-，则2023x =______,前2023项和是______。
8.从1到100中至少取______个数才能保证一定存在2个数互素？9.n 位选手进行围棋单循环比赛，即两人之间恰进行一场比赛。
已知现在已经进行了12场比赛，其中6人已赛3场，剩下的选手，，平均比赛场次小于3场，则n 的最小值为______。
2022年厦门大学强基计划数学试题解析1. 答案4π解析：22222222111,111,111111()24bi z bi w bi b b p q b b p q p b p q -=+==++-∴==++∴+=+∴-+= 所以围成的面积为4π。
前三届高数竞赛预赛试题（非数学类）（参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。
）2009年 第一届全国大学生数学竞赛预赛试卷 一、填空题（每小题5分，共20分）1．计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令v x u y x ==+,，则v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=，v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=10210d 1)ln (1ln d )d ln 1d 1ln (u u u u u u u u u u v v u uv u u u u u ⎰-=12d 1u uu （*） 令u t -=1，则21t u -=dt 2d t u -=，42221t t u +-=，)1)(1()1(2t t t u u +-=-，⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 151651322153=⎥⎦⎤⎢⎣⎡+-=t t t 2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解:令⎰=20d )(x x f A ，则23)(2--=A x x f ，A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。
因此3103)(2-=x x f 。
3．曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解:因平面022=-+z y x 的法向量为)1,2,2(-，而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ，故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行，因此，由x z x =，y z y 2=知0000002),(2,),(2y y x z x y x z y x ====，即1,200==y x ，又5)1,2(),(00==z y x z ，于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ，即曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。
一、 求下列各题极限（每小题5分，共15分）（1） 求极限 20(32sin )3lim tan x xx x x→+-. 原式2ln(1sin )3222000022(1sin )1ln(1sin )e 133lim3lim lim lim x x x x x x x x x x x x x x +→→→→+-+-=⋅== 02sin 23lim 3x xx →==.另解：原式ln(32sin )ln32200e [ln(32sin )ln 3]lim lim x x x x x e x x e x xξ+→→-+-== 0012sin 2sin 2limlim 33x x x x x x η→→===. （两次应用拉格朗日中值定理） 其中ξ在ln(32sin )ln 3x x x +与之间，η在(32sin )3x +与之间.(1) 设12121,2,(2,3,)n n n x x x x x n --===+=，求极限1lim n nx →∞. 解：将递推的数列等式12n n n x x x --=+看成是二阶常系数的齐次差分方程 其特征方程为210λλ--=，其特征根为12λλ==，故此差分方程的通解为1122n n n x c c λλ=+，其中12,c c 为常数，其特解可由121,2x x ==定出,由于12lim,lim 0n n n n λλ→∞→∞=+∞=，所以 112211lim lim 0n nn n n x c c λλ→∞→∞==+. 另解：由题设条件知，对1n ∀>，0n x >，且120n n n x x x ---=>，即{}n x 严格单增，所以1212n n n n x x x x ---=+<，112n n x x ->，即有 2112n n x x -->， 故 211121213333()()()2222n n n n n n n x x x x x x ------=+>>>>= 厦门大学第十二届“景润杯”数学竞赛试卷（理工类）竞赛日期 2015年5月30日所以 1110limlim 03()2n n n n x →∞→∞-≤≤=，即1lim 0n n x →∞=.（3）设可微函数()f x 满足 0()lim 1x f x x→=，求t +→.解：由 0()lim1x f x x→= 得(0)0,(0)1f f '==. 记2]2f y dy f dy +=2t⎰lim t tt t ++→→=330()()222lim lim tuttt t t uf u du uf u du tt ππ+++→→→===⎰⎰200()()(0)lim lim (0)3333t t tf t f t f f t t ππππ++→→-'====. 二、（8分）设函数()f u 可导，且满足1()()caf x bf x x+=，其中,,a b c 是常数，且||||a b ≠，求(())f f x 的导数.解：由1()()(1)1()()(2)c af x bf x xaf bf x cx x ⎧+=⎪⎪⎨⎪+=⎪⎩, (1)(2)a b ⨯-⨯，得22()()aca b f x bcx x-=-，即22()()()c a f x bx a b x =--令 22()()c a u bx a b x =--，则222()()du c ab dx a b x=--- [(())][()]()d f f x d f u du duf u dx du dx dx'=⋅=⋅222222()()()()c a c ab b a b u a b x=--⋅---- (代入u ) 2222222222()[()]()()c a a b a a bx b b a b c x x--=-++-. 三、（8分）设函数()f x 在[0,1]上有连续的导数，且(0)(1)0f f '==，证明至少存在一点(0,1)ξ∈，使得()()f f ξξ'=.证明：构造辅助函数()()x F x e f x -=，则()F x 在[0,1]上连续可导，且()[()()]x F x e f x f x -''=-，1(0)(0),(1)(1),F f F e f -'''==-若对(0,1),()0x F x '∀∈≠，则有下面两种情况 (i)对(0,1),()0x F x '∀∈>，此时()F x ，(1)(0)0F F >=，1(1)0e f ->，从而(1)0F '<，这与1(1)lim ()0x F F x -→''=≥矛盾， (ii) 对(0,1),()0x F x '∀∈<，此时()F x ，(1)(0)0F F <=，1(1)0e f -<，从而(1)0F '>，这与1(1)lim ()0x F F x -→''=≤矛盾。
从而至少存在一点(0,1)ξ∈，使得()()f f ξξ'=. 四、（8分） 证明不等式 sin (1)(01)xx x x ππ>-<<证明：设sin ()(1)(01)xF x x x x ππ=--<<()cos 21F x x x π'=+-，令()0,F x '= 解得驻点为10,,12x =2()2sin (sin )F x x x πππππ''=-=-，(0)(1)20F F ''''==>1()202F π''=-<，故01x =和是()F x 的极小值点，12x =是()F x 的极大值点。
由罗尔定理，在区间1(0,)2上，2()(sin )F x x πππ''=-仅有唯一的一个零点1ξ，当10x ξ<<时，()0F x ''>，当112x ξ<<时，()0F x ''<，又1(0)()02F F ''==,因此在1(0,)2上，()0F x '>，从而在1(0,)2上，()F x 单增，且()(0)0F x F >=类似地，由罗尔定理，在区间1(,1)2上，2()(sin )F x x πππ''=-仅有唯一的一个零点2ξ，当212x ξ<<时，()0F x ''<，当21x ξ<<时，()0F x ''>，又1()(1)02F F ''==，因此在1(,1)2上，()0F x '<，从而()F x 在1(,1)2上单减，且()(1)0F x F >=，综上所述，()F x 在区间(0,1)上恒大于零，即()F x 在[0,1]上的最小值为(0)0F =，即()0,(0,1)F x x >∀∈，从而不等式成立。
五、设(),g()f x x 是[,]a b 上的连续函数，且对[,]x,y a b ∀∈有[()()][g()g()]0f x f y x y --≤ （称()g()f x x 与具有反序性）（i ） 证明：()()()()g();bb baaaf x dxg x dx b a f x x dx ⋅≥-⎰⎰⎰（ii ） 利用（i ）证：若()f x 是[0,1]上的连续函数，且对[0,1]x ∀∈有0()1f x ≤<，则11100()()1()1()f x dx f x dx f x f x dx≥--⎰⎰⎰. 证：(i)由[()()][g()g()]0f x f y x y --≤ 得()g()()g()()g()()g()f x x f y y f x y f y x +≤+不等式两端在D 上求二重积分，其中{(,)|,}D x y a y b a x b =≤≤≤≤，即()g()()g()()g()()g()DDD Df x x dxdy f y y dxdy f x y dxdy f y x dxdy +≤+⎰⎰⎰⎰⎰⎰⎰⎰即 ()()g()()g()b bba a ab a f x x dx f x dx x dx -≤⎰⎰⎰ （ii ）由于()1()f x f x -与1()f x -在上[0,1]具有反序性，则由（i ） 11110000()()()(1())(1())1()1()f x f x f x dx f x dx dx f x dx f x f x =-≤---⎰⎰⎰⎰1100()[1()]1()f x dx f x dx f x ≤⋅--⎰⎰因为11()0f x dx ->⎰，所以 11100()()1()1()f x dx f x dx f x f x dx≥--⎰⎰⎰. 六、（10分）已知曲线2C :3(1)y xz y ⎧=⎨=-⎩，在纵坐标为1y =的点处的切线为L ，∏是通过L 且与曲面22:4x y z ∑+=相切的平面，求∏的方程.解：若以y 为参数，曲线C 的参数方程为2C :3(1)x y y y z y ⎧=⎪=⎨⎪=-⎩，C 在对应1y =点(1,1,0)处的切向量为1{(),,()}{2,1,3}|{2,1,3}y x y y z y y ='''==，所以C 在点(1,1,0)处的切线L 的方程为11213x y z--==，或者 210330x y y z -+=⎧⎨--=⎩过L 的平面束方程为(33)(21)0y z x y λ--+-+=， 即(32)30x y z λλλ+--+-= （1）记22(,,)4F x y z x y z =+-，设∏与曲面∑的切点为0000()M x ,y ,z ，则曲面∑在点0000()M x ,y ,z 处的法向量为000{,,}{2,2,4}M M M FF F x y xyz∂∂∂=-∂∂∂，由于所求的平面∏与∑相切，因此λ应满足0321224x y λλ--==-， 由此可得，002,64x y λλ==-且2220001()51294z x +y λλ==-+, (0M 在∑上) 又因为0000()M x ,y ,z 也应在∏上，将其代入（1）得222(32)(64)(5129)30λλλλλλ+----++-=，即 251160λλ-+=解得61,5λ=，因而得到所求的∏的平面方程为 20x y z +--=或63590x y z +--=.七、（10分）设,a b 分别是函数2()|cost |dt x xf x π+=⎰在[0,]π上的最大值和最小值，L 是连接原点与点(1,0)A 的位于第一象限内的光滑曲线，并且与线段OA 围成的闭区域D 的面积为1，求关于坐标的曲线积分.(3sin )d (cos )d x x LI by e y x ax e y y =++++⎰（其中L 为逆时针方向）解：先确定,a b ，再计算I .由()f x 的积分表达式 sin cos 02()|sin ||cos |sin cos 2x x x f x x x x x x πππ⎧-≤<⎪⎪'=-=⎨⎪+≤≤⎪⎩， 于是()0f x '=的根为3,44x ππ=，并且3334242444242()|cost |dt |cost |dt sin |sin |24f x x πππππππππππ==+=-=⎰⎰⎰33342424442423()|cost |dt |cost |dt sin |sin |24f x x πππππππππππ==+=-=⎰⎰⎰ 22200(0)|cost |dt costdt sin |1f x πππ====⎰⎰333222()|cost |dt costdt sin |1f x πππππππ==-=-=⎰⎰所以3max{(),(),(0),()}44a f f f f πππ==3min{(),(),(0),()}244b f f f f πππ==-(3(2sin )d cos )d x x LI y e y x e y y =++++⎰ （由格林公式）cos )[3(2sin ]{}x x De y y e y dxdy x y ∂+∂++=-∂∂⎰⎰(3(2sin )d cos )d x x OAy e y x e y y -+-+++⎰12)32)35Ddxdy dx =--=--=-⎰⎰⎰.八、（10分）设幂级数0n n n a x ∞=∑的系数满足012,1,1n n a na a n n -==+-≥，求此幂级数的和函数()S x .解：设0()nn n S x a x ∞==∑，则11()n n n S x na x ∞-='=∑，由条件11n n na a n -=+-，有11111111()(1)()()n n nn n n n n n S x a xn xS x nx S x x nx ∞∞∞∞----===='=+-=+=+∑∑∑∑2()()()1(1)x xS x x S x x x '=+=+--解此一阶线性微分方程，得1()1x S x ce x=+-. 由(0)2S =，得1c =，故 1()1x S x e x=+-. 九、（12分）设L 是过原点，方向为(,,)αβγ（其中2221αβγ++=）的直线，均匀椭球2222221x y z a b c++≤（其中0c b a <<<，密度为1）绕L 旋转（1）求其转动惯量；（2）其转动惯量关于方向(,,)αβγ的最大值和最小值.解：（1）设旋转轴L 的方向向量为(,,)αβγ，椭球内任意一点(,,)P x y z 到旋转轴L 的距离的平方为222222222[(,,)(,,)]()d x y z x y z x y z x y z αβγαβγ=++-⋅=++-++ 222222(1)(1)(1)222x y z xy yz xz αβγαββγγα=-+-+----由积分区域的对称性，[222]0xy yz xz dxdydz αββγγαΩ++=⎰⎰⎰，其中222222{(,,)|1}x y z x y z a b cΩ=++≤，而22222223222214(1)d 15aay z x a a b c a x a bc x dxdydz x dx dydz x bc x a ππ-+≤--Ω==-=⎰⎰⎰⎰⎰⎰⎰同理332244,1515ab c abc y dxdydz z dxdydz ππΩΩ==⎰⎰⎰⎰⎰⎰ 所求的转动惯量为22222224[(1)(1)(1)]15abc I d dxdydz a b c παβγΩ==-+-+-⎰⎰⎰. （2）设考虑目标函数22222(1)(1)(1)ab c αβγ-+-+-在约束条件2221αβγ++=下的条件极值. 设拉格朗日函数为222222222(,,,)(1)(1)(1)(1)L a b c αβγλαβγλαβγ=-+-+-+++-令2222222()0,2()0,2()0,1L a L b L c αβγαλβλγλαβγ=-==-==-=++= 求得极值点为 222123(1,0,0,),(0,1,0,),(0,0,1,)Q a Q b Q c ±±±通过比较可知，当(,,)(0,0,1)αβγ=±时，即绕z 轴转动惯量最大，即22max 4()15abc I a b π=+，当(,,)(1,0,0)αβγ=±时，即绕x 轴转动惯量最小，即22min 4()15abc I b c π=+.十、（9分）在不断抽打下，陀螺会飞快地旋转，但当一旦停止对它进行抽打，它也就不再转动而停下来.设陀螺材质均匀，且旋转体所占的立体区域为222{()|()2},0}x,y,z x y z a a aΩ=+≤≤>，试求当陀螺停止转动后，在稳定平衡状态下它的中心轴与水平地面的夹角θ.如图（轴截面）(其中A 为陀螺停止转动后，在稳定平衡状态下与地平面的接触点)解：首先求陀螺的质心坐标.由于陀螺材质均匀的旋转体，所以它的 质心就是几何体的形心，根据对称性可知， 必有0x y ==，而zdvz dvΩΩ=⎰⎰⎰⎰⎰⎰22302za aD azdv dz dxdy dz a ππΩ===⎰⎰⎰⎰⎰⎰⎰22240423za aD az zdv zdz dxdy dz a ππΩ===⎰⎰⎰⎰⎰⎰⎰.所以有陀螺的质心坐标为 44G(0,0,)3a π.当陀螺停止转动后，在稳定平衡状态下时，它的质心到水平地面的距离应达到最短。
