当前位置：文档之家 › 3.3 泰勒公式与函数的高阶多项式逼近ppt

3.3 泰勒公式与函数的高阶多项式逼近ppt

  • 格式：ppt
  • 大小：409.50 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

高等数学课件3-3泰勒公式

高等数学课件3-3泰勒公式
n
n 1
Rn( 2 ) n( n 1)( 2 x0 )
( 2在x0与1之间)
如此下去,经过( n 1) 次后,得
Rn ( x ) ( x x0 )
n1

R
n 1!
( 在 x0与 n之间 ,也在 x 0 与 x 之间)
$3-3Taylor公式 9
( n1 ) n
$3-3Taylor公式 2
例如, 当 x 很小时, e 1 x , ln( 1 x ) x
x
ye
ye
x
x
y x
y ln(1 x )
y 1 x
o o
$3-3Taylor公式 3
不足: 1、精确度不高； 2、误差不能估计. 问题:
寻找函数 P ( x ) ,使得 f ( x ) P ( x ) ,
两函数 Rn ( x ) 及 ( x x 0 )
n1
在以 x 0 及 x 为
端点的区间上满足柯西中值定理的条件,得
Rn ( x ) ( x x0 )
n1

Rn ( x ) Rn ( x0 ) ( x x0 )
n1
0 ( 1 在 x 0 与 x 之间 )

R n ( 1 ) ( n 1 )( 1 x 0 )
f
(4)
(0) 0,
… ，
f
(n)
( 0 ) 依次取 0， ，， 1 . 1 0 -
若令n=2m,则
sin x x x
3

x
5

x
7
m 1 … ( 1)
x
2 m 1
3!
5!
7!

泰勒公式与函数的高阶多项式逼近

泰勒公式与函数的高阶多项式逼近

y
y f ( x)
Pn ( x0 ) f ( x0 )
2.若有相同的切线
Pn( x0 ) f ( x0 )
3.若弯曲方向相同
y pn ( x )
Pn( x0 ) f ( x0 )
o
x0
x
( x0 ) ( k 0,1,2,, n) 则 Pn ( x ) 与 f ( x ) 在 x0 附近有较高的接近程度 .
[ln( 1 x )]
( n 1)
( 1) n! ( x 1)n1
n
k 1 k
ln( 1 x ) ( 1)
k 1
n
( 1) x x . n1 k ( n 1)( 1)
n
n1
( 介于0 与 x 之间 )
带有拉格朗日型余项
的 麦克劳林公式 .
f ( x0 ) Pn ( x ) f ( x0 ) f ( x0 )( x x0 ) ( x x0 ) 2 2! f ( n ) ( x0 ) ( x x0 ) n n!
Pn ( x )称为函数f ( x )在x0的n次泰勒多项式 .
Pn ( x )完全由f ( x )惟一确定！
(1 x ) 1 x

( 1)
2! ( 1)( n 1) n n x o( x ) ; n!
( R )
x2
1 2 n n 1 x x x o( x ) . 1 x
2 cos x 3 例 3 计算 lim . 4 x 0 x 1 4 x2 2 4 解 e 1 x x o( x ) 2! e
f ( k ) (0) k f ( n1) ( x ) n1 x x k! ( n 1)!

泰勒公式及函数逼近

泰勒公式及函数逼近

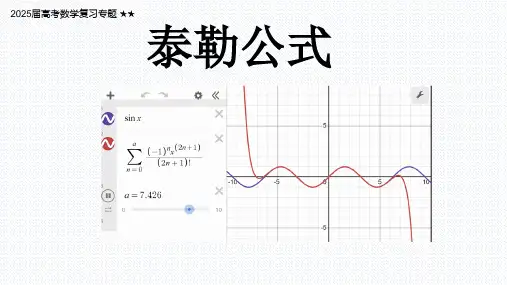
及它的 n 阶泰勒多项式的图形。 ( n 1 , 3 , 5 , , 13 ) 故输入命令如下：
f( x ) sin x
t
Table Normal Series Sin x , x, 0, i
PrependTo t, Sin x ;
Pi, Pi
, i, 1, 13, 2
;
Plot Evaluate t , x,
上述语句中的函数“PrependTo[t,Sin[x]]” sinx 添加到表t中。运行后得到图 是表示把函数 3-1。
3 2 1
-3
-2
-1 -1 -2 -3
1
2
3
图3-1
为了使图形比较更加生动，下面我们作出 sinx 和它的某一阶泰勒多项式的同一坐标系下的比较 图，并且在图中红色曲线表示函数 f( 的 x ) sin x 图形，蓝色曲线表示泰勒多项式的图形。命令如 下：
3 2 1
2
1
-3
-2
-1 -1 -2 -3
1
2
3
-3
-2
-1
1
2
3
-1
-2
1
1
0.5
0.5
-3
-2
-1
1
2
3
-3
-2
-1
1
2
3
-0.5
-0.5
-1
-1
1
1
0.5
0.5
-3
-2
-1
1
2
3
-3
-2
-1
1
2
3
-0.5
-0.5
-1
图3－2
-1
（2）扩大显示区间范围，以观察在偏离展开点 x 0 时泰勒多项式对函数的逼近情况。 显然，我们只要把上一个程序中的绘图命令中的 x 范围由 [ , ]分别改到 [ 2 ,2 ] ，并相应增 加阶数。故输入如 下命令：

D3_3泰勒公式(PPT)-文档资料

D3_3泰勒公式(PPT)-文档资料

称为麦克劳林( Maclaurin )公式 . 例1. 求 y ln cos x 在 x 处的带有拉格朗日余项 的2阶 4 泰勒公式. 解: 要求到3阶导数
目录
上页
下页
返回
结束
1 2 f ln ln 2, 2 4 2
2
f x tan x f 1 4
f ( x) f ( x0 ) f ( x0 )( x x0 )
x 的一次多项式
y
y f ( x)
p1 ( x)
特点:
f ( x0 ) f ( x0 )
O
x0 x
x
目录
上页
下页
返回
结束
为了提高精确度，我们考虑用n次多项式来近似 f ( x)
pn ( x) a0 a1 ( x x0 ) a2 ( x x0 ) 2 an ( x x0 ) n f x a0 f ( x0 ), 要求满足
3 5
f
(k )
f 0 1,
f 0 0, f 0 1,
π (0) sin k 2 4 f 0 0,

2 m 1 x x x sin x x (1) m1 R2m ( x) (2m 1) ! 3! 5!
f x sec x f 2, f x 2sec2 x tan x 4 2 1 ln cos x ln 2 x x 4 2 4 3 1 2 sec tan x 3 4
f ( x0 ) ( x x0 ) 2 f ( x0 ) f ( x0 )( x x0 ) 2! f (3) ( ) ( x x0 )3 3!

3-3泰勒公式98788

3-3泰勒公式98788

Rn(x)f(n (n 1)1())!(xx0)n1(在 x0与 x之 间 )
f(x )P nx R n (x )
称为按 (xx0)的幂展开的n阶泰勒公式.
其 中 P n f((x x )0 ) kn f0(fx (0 k ) k )( (!x x 0)x (0 x ) x f0 2 )( k ! x 0 )(x x 0 )2
由计算可知当 n = 9 时上式成立, 因此
e11 1 1 2.718281
2!
9!
例3 写 出 sin x 的 麦 克 劳 林 公 式 .
解 f (k)(x) sin(xk )
2
f (k)(0)sink
2


0,
(1
)
m
1
,
k2m(m1,2, k2m1
f(x)f(0 ) ff (nn()0 !(0))x x n f(nn1)(1x! ) xn1
三、简单应用
麦克劳林(Maclaurin)公式
f(x ) f(0 ) f(0 )x f(0 )x 2 f(n )(0 )x n f(n 1 )(x )x n 1
n次泰勒多项式 余项
an ?
设 P n(x)a0a1(xx0)a2(xx0)2
求an ?
an(xx0)n
(1)
假设 P n ( k ) ( x 0 ) f ( k ) ( x 0 ) ,k 0 , 1 ,2 ,n ( 2 )
对(1)求各阶导数,再分别将(2)式代入,得 P n ( x a ) 0 ,f af( n( x x 0 ) 0 n) 1,!a f 1 f( (nx )0 (f) x( (0x x ) 0)x ,a 0 ) 2 f 2 1 ! 2 ( ! x f0 ) (( x x 0 ),x 0 ) 2

高等数学(第二版)上册课件：泰勒公式

高等数学(第二版)上册课件：泰勒公式

分析
近 1.若在 x0点相交
似 程
Pn (x) f (x0)
度 越
2.若有相同的切线
来
越 好
Pn' (x) f ' (x0)
3.若弯曲方向相同
Pn'' (x) f '' (x0 )
y
y f (x)
0 x0
x
（1） 求 n 次近似多项式
Pn (x0) f (x0)
p'n (x0 )
f
' n
所以
f (x) 8 10(x 1) 9(x 1)2 6(x 1)3 (x 1)4
【例3.3.4】 求 f (x) ex2 的带有佩亚诺余项麦克劳林展开式
解
因为 ex 1 x x2 xn o(xn1)
2!
n!
用 x2代替公式中的 x，即得
ex2 1 x2 x4 x2n o(x2n2 )
2!
n!
【例3.3.1】 求 f (x) ex 的n阶麦克劳林展开式
解 由于 f ' (x) f ''(x) f (n) (x) ex，
所以 f '(0) f ''(0) f (n) (0) 1 ，
取拉格朗日余项，得麦克劳林展开式为
ex 1 x x2 xn e x xn1
则误差 R(x)= f (x) P(x)
设函数 f (x)在含有 x0 的开区间 (a, b) 内具有直到 (n+1) 阶导数，P(x) 为
多项式函数
pn(x)
a 1
(x
x0
)
a2
(x
x0
)2
an(x x0)n

2025届高考数学复习专题--泰勒公式在高中数学中的应用 课件(共17张PPT)

2025届高考数学复习专题 ★★
泰勒公式
泰勒公式
➢ 什么是泰勒公式 ➢ 泰勒公式的应用：
@证明不等式 @求参数范围 @比较大小
➢ 什么是泰 勒公式
泰勒公式，是一个用函数在某点的信息描述其附近取值的公式。 如果函数满足一定的条件，泰勒公式可以用函数在某一点的各阶 导数值做系数构建一个多项式来近似表达这个函数。 泰勒公式得名于英国数学家布鲁克·泰勒，他在1712年的一封信 里首次叙述了这个公式。泰勒公式是为了研究复杂函数性质时经 常使用的近似方法之一，也是函数微分学的一项重要应用内容。
1 1 x2 cosx 1 1 x2 1 x4
2!
2! 4!
（请证明上面不等式）
站得更高，高山也矮小！
2
@求参数范围
证明不等式常用：
g(x) cosx 1 x2 1． 2
（1）当 a＝1 时，求证：当 x≥0 时，f（x）≥0；
对于x 0
（2）若 f（x）+g（x）≥0 在[0，+∞）上恒成立，求 a 的取值范围．
ex 1 x 1 x2 2!
x 1 x2 ln(1 x) x 2
x 1 x3 sin x x 3!
x 1 x2 ln(1 x) x 2
x 1 x3 sin x x 3!

1 1 x2 cosx 1 1 x2 1 x4
2!
2! 4!
（请证明上面不等式）
➢ 泰勒公式的应用：例 2：设函数 f (x) x(ex 1) ax2 ,当 x 0 时， f (x) 0 ,求 a 的取值范围. @求参数范围
泰勒公式
泰勒公式产生背景：
常见函数的泰勒展开式
泰勒展开式 记忆方法
特别地，有
切线放缩

《泰勒公式》PPT课件


Rn ( x)
M (n 1) !
x x0
n1
二、泰勒定理
f (x)
f (x0 )
f ( x0 )( x
x0)
f ( x0 ) ( x 2!
x0 )2
Hale Waihona Puke f (n)( x0 ) ( x n!
x0 )n
Rn ( x)
其中
Rn ( x)
f (n1) ( )
( (n 1) !
x
x0
)n1
(
)
(n 1)! (n 1)!
在x与x0之间
二、泰勒定理
若 f (x)在包含 x0的某开区间 (a,b) 内具有
直 到 n 1 阶的导数 , 则当 x (a , b) 时, 有
f (x)
f (x0)
f ( x0 )( x
x0)
f ( x0 ) ( x 2!
x0 )2
f (n)( x0 ) ( x n!
如何确定Pn ( x)？——确定系数a0 , a1 , , an
f (k ) ( x0 ) Pn(k ) ( x0 ) (k 0,1, 2, , n)
设
函
数
f
(
x
)在
含
有
x
的
0
开
区
间(
a
,
b
)内
具
有
1至
(
n
1)阶
导
数
f ( x0 ) Pn ( x0 ) a0
f ( x0 ) Pn ( x0 ) a1
x0 )n
Rn ( x)
①
其中
Rn ( x)
f (n1) ( )

3,3泰勒公式-52页PPT精品文档


f ( x0) +
f ( x0 )( x - x0 ) +
f
( x0 2!
)
(x
-
x0 )2
+
+
f
(n) ( x0 n!
)
(x
-
x0 )n
+
Rn
(
x)
其中 Rn( x) =
f (n+1)( ) ( x
(n + 1)!
-
x0 )n+1(
在
x0与
x之间).
上页 下页
泰勒公式
证明: 由 假 设 , R n ( x )在 ( a ,b )内 具 有 直 到 ( n + 1 ) 阶
L+f(nn )(!x0)(x-x0)n=kn=0 f(kk)(!x0)(x-x0)k
称f为 (x)按 (x-x0)的幂展 n次近开 似多的 项式 .
f(x)=kn =0f(kk )(!x0)(x-x0)k+R n(x)
称f为 (x)按 (x-x0)的幂展 n阶泰 开 勒公的 式.
R n(x)=fn (n + + 1)1 (!)(x-x 0)n + 1(在 x 0 与 x 之 )间
x
以直代曲
f ( x ) = f ( x 0 ) + f ( x 0 ) x - ( x 0 ) + o ( x - x 0 )
例 如 ,当 x很 小 时 ,ex1+x,ln1+ (x)x
（如下图）
上页 下页
泰勒公式
以直代曲
y = ex
y = ex
y=x
y=1+x

泰勒公式ppt课件精选全文完整版

令n=2m，于是有
sin x
x
x3 3!
x5 5!
(1)m1 x2m1 (2m 1)
!
R2m
(
x)
其中 R2m (x)
s(in1()mxcos2(m2x1) ) x2m1 (0 1)
(2m 1) !
精选编辑ppt
18
机动 目录 上页 下页 返回 结束
类似地,可得
cos x
1 x2 2!
x4 4!
f (k)( x0 )
n!an f (n) ( x0 ). (k 0,1,2,, n)
代入 Pn ( x)中得
Pn ( x)
f ( x0 )
f ( x0 )( x x0 )
f
( x0 2!
)
(
x
x0
)2f(n)( x n!)(x
x0
)n
精选编辑ppt
10
机动 目录 上页 下页 返回 结束
三、泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x) 在含有 x0 的某个开区间(a, b) 内具有直到(n 1) 阶的导数,则
当 x在(a,b)内时, f ( x)可以表示为( x x0 )的一个 n次多项式与一个余项Rn ( x)之和:
f (x)
f ( x0 )
精选编辑ppt
16
机动 目录 上页 下页 返回 结束
例1:求函数 f (x) ex 的n阶麦克劳林展开式.
解:因为 f'x f''x fn x e x ，
所以 f0 f'0 f''0 fn 0 1 .
故
ex
1 x x2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

( n 1)!
拉格朗日型余项
( 介于 x 与 x0 之间)
（） 1 式称为 f ( x ) 在 x0 点带有 拉格朗日型余项 的 泰勒公式 . 证明略
特别，当 x0 0 时, 有
f ( x)
k 0 n
f
(k )
( 0)

x
k
f
( n 1 )
( x )
k!
( n 1)!
(k )
( x0 ) f
(k )
( x0 ) ( k 0,1,2, , n) 则
Pn ( x ) 与 f ( x ) 在 x0 附近有较高的接近程度 .
假设 pn
(k )
( x0 ) f
(k )
( x0 ) ， ( k 0,1,2, , n)
2 n
pn ( x ) a0 a1 ( x x0 ) a2 ( x x0 ) an ( x x0 )
寻找一个在 x0 附近与 f ( x ) 尽可能
n
接近的n 次多项式:
pn ( x ) a0 a1 ( x x0 ) an ( x x0 )
怎样构造 pn ( x )（如何确定它的系数） ？
使得在 x0 附近 Pn ( x ) 与 f ( x ) 很接近！
pn ( x ) a0 a1 ( x x0 ) a2 ( x x0 ) an ( x x0 )
推广了的微分中值定理 .
如 对 一 固 的 果 某 个 定
n， M 0,
x U ( x0 )
Rn ( x ) f
有
(n1)
f
( )
( n1)
(x) M .
n1
则
n1
( n 1 )!
( x x0 )
M
x x0
( n 1 )!
,
lim
Rn ( x ) ( x x0 )
2
n
分
析
近 似 程 度 越 来 越 好
1.若在 x 0 点相交
y
y f ( x)
Pn ( x0 ) f ( x0 )
2.若有相同的切线
Pn ( x0 ) f ( x0 )
y pn ( x )
3.若弯曲方向相同
Pn( x0 ) f ( x0 )
o
x0
x

如果 pn
f ( x)

k 0
n
f
(k )
( 0)
x o( x )
k n
.
k!
称为带有皮亚诺型
余项的 麦克劳林公式 .
二. 函数的高阶多项式逼近
f ( x ) e x 的 n 阶麦克劳林公式. 例1 求
解


f ( x ) f ( x ) f
( n)
( x) e ,
x
( n)
f ( x0 ) 2!
( x0 )
n!
( x x0 )
n
Pn ( x )称为函数 ( x )在x0的n次泰勒多项式 f .
Pn ( x )完全由f ( x )惟一确定！
） 定理1（泰勒中值定理 若函数 f ( x ) 在 U ( x0 )
具有直到n 1 阶的导数，则 x U ( x0 ) ，有
a0 f ( x0 ), 1 a1 f ( x0 ), 2!a2 f ( x0 ),
,
n!a n f
( n)
( x0 ) . a k
f
(k )
( x0 )
k!
( k 0,1, , n)
( x x0 )
2
Pn ( x ) f ( x0 ) f ( x0 )( x x0 ) f
( n)
f (0) f (0) f (0) f
( n 1)
(0) 1
注意到 f
(x ) e
x
n
x
代入公式,得
e
x
n1
e 1 x
x
x
2


2!
n!
( n 1)!
x
(0 1).
例 2 求函数 f ( x ) cos x 的 n 阶麦克劳林公式
n 1
x
n
o( x ) ;
n
2
3
n
带有 皮亚诺型 余项 的 麦克劳林公式 .
[ln( 1 x )]
( n1)

( 1) n!
n
( x 1)
k 1
n1
k
ln( 1 x )
( 1)
k 1
n
x

( 1)
n
x
n1 n1
k
( n 1)( 1)
.
( 介于 0 与 x 之间)
x
n 1
( 0 1)
拉格朗日型余项 的 麦克劳林公式 称为带有 麦克劳林( Maclaurin,1698-1746，英国 ) 注意: 在（1）中，当 n 0 时, 即
.
f ( x ) f ( x0 ) f ( )( x x0 ) ( 在 x0 与 x 之间 )
泰勒公式 1） （ 也称为含有高阶导数的
3.3 泰勒公式与函数的高阶多项式逼近
一. 泰勒公式 问题的提出：
附近时，有
f ( x ) f ( x0 ) f ( x0 )( x x0 ) o( x x0 )
泰勒（Taylor ） 1685 1731 , 英国 .
如果 f ( x ) 在点 x0 可微，则当 x 在 x0
.
解
f
(n)
( x ) cos( x
n 2
), f
(n)
( 0 ) cos(
(4)
n 2
)
f ( 0 ) 0 , f ( 0 ) 1 , f ( 0 ) 0 , f
2 4 2n
( 0 ) 1,
)
x
2n2
cos x 1
x

x
( 1)
带有 拉格朗日型余项
的
麦克劳林公式 .
(1 x )

1 x
( 1)
2!
x
2

n n

( 1)( n 1)
n!
x o( x ) ;
( R )
1 1 x
1 x x x o( x ) .
2
n
n
例3
计算 lim
f ( x ) f ( x0 ) f ( x0 )( x x0 ) f ( x0 ) 2!
n
( x x0 )
2

其中 Rn ( x )
f
f
( n)
( x0 )
( )
n!
( n 1 )
( x x0 ) Rn ( x ) （ ） 1
( x x0 )
n 1
n
n
n
0.
在不需要余项的精确
表达式时， n 阶泰勒公式可写为：
f ( x)

k 0
f
(k )
( x0 )
k!
( x x0 ) o[( x x0 ) ] .
k n
称为带有皮亚诺（Peano,1858-1932,意大利）
型余项的 泰勒公式 .
特别， x0 0 时, 有 当
x0
e
x
2
2 cos x 3 x
4
.
4
解
e
x
2
1 x
2
1 2!
x
4
x o( x )
4
cos x 1
x
2

o( x )
4
2!
4!

e
x
2
2 cos x 3 (
7 x o( x )
4 4
1 2!
2
7 12
1 4!
) x o( x )
4 4
n
x
cos( x
2n 2
2!
4!
( 2 n )!
2 ( 2 n 2 )! (0 1)
cos x 1
x
2

x
4
( 1)
n
x
2n
o( x
2n
)
2!
4!
( 2 n )!
常用函数的麦克劳林公式
e
x
1 x
x
2

x
n
o( x );
n
f 的线性近似 f ( x ) L( x ) ,
L( x )
所产生的误差是：
比 x x0 高阶的无穷小 ( x x0 ).
设 f ( x ) 在 x0 点具有直到n 阶的导数 .
问题: 办法:
能否用高次多项式 pn ( x ) f ( x ) ,
使误差 : Rn ( x ) f ( x ) Pn ( x ) 可以估计！
2!
sin x x x
3
n!
x
5

( 1)
n
x
2 n1
3!
5!
( 2n 1)!
o( x
2 n1
) ;
cos x 1
x
2

x
4
( 1)
n
x
2n