简述 x2 检验的注意事项。
- 格式:docx
- 大小:10.74 KB
- 文档页数:2

医学统计学名词解释及问答题1、总体(population ):是根据研究目的确定的同质研究对象的全体。
2、样本(sample):从总体中抽取的一部分有代表性的个体。
3、同质(homogeneity):是指所研究的观察对象具有某些相同的性质或特征。
4、变异(variation ):指同质个体的某项指标之间的差异。
5、参数(parameter):反映总体特征的指标称为参数。
6、统计量(statistic ):通过样本资料计算出来的相应指标称为统计量。
7、抽样误差(sampling error ):由随机抽样造成的样本指标与总体指标之间、样本指标与样本指标之间的差异。
8、概率(probability ):某事件发生的可能性大小。
9、正态分布(normal distribution ):高峰位于均数处,中间高两边低,左右完全对称地下降,但永远不与横轴相交的钟形曲线。
10、平均数(average):是描述一组同质变量值的平均水平或集中趋势的指标。
11、中位数(median):将一组数据由小到大排列,位于中间位置的观测值。
12、医学参考值范围(medical referenee range):又称正常值范围,医学上常将包括绝大多数正常人的某项指标的波动范围称为该指标的正常值范围。
13、方差(varianee ):是各个数据与平均数之差的平方的平均数。
14、标准差(standard deviation ):是各数据偏离平均数的距离的平均数,它是离均差平方和平均后的方根,用b 表示。
15、标准误(standard error ):样本均数的标准差,等于原变量总体标准差除以例数的平方根,用以说明均数抽样误差的大小。
16、均数的抽样误差(sampling error of mean ):由个体差异和抽样所导致的样本均数与样本均数之间,样本均数与总体均数之间的差异。
17、假设检验(hypothesis testing ):先对总体做出某种假设,然后根据样本信息来推断其是否成立的一类统计方法的总称。

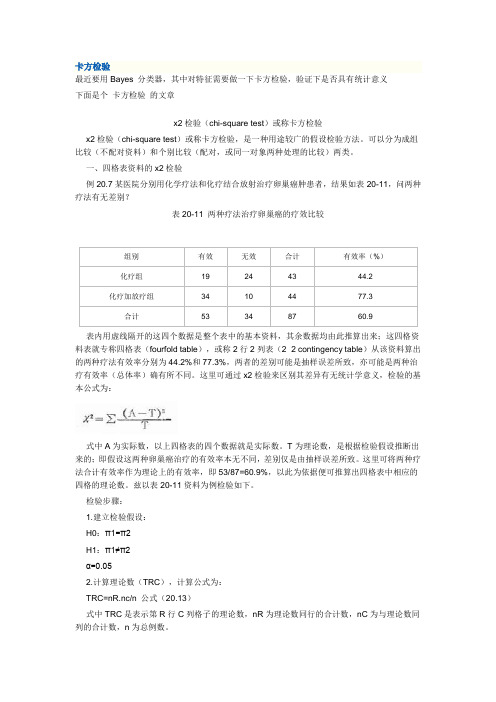
表内用虚线隔开的这四个数据是整个表中的基本资料,其余数据均由此推算出来;这四格资料表就专称四格表(fourfold table),或称2行2列表(2×2 contingency table)从该资料算出的两种疗法有效率分别为44.2%和77.3%,两者的差别可能是抽样误差所致,亦可能是两种治疗有效率(总体率)确有所不同。
这里可通过x2检验来区别其差异有无统计学意义,检验的基本公式为:式中A为实际数,以上四格表的四个数据就是实际数。
T为理论数,是根据检验假设推断出来的;即假设这两种卵巢癌治疗的有效率本无不同,差别仅是由抽样误差所致。
这里可将两种疗法合计有效率作为理论上的有效率,即53/87=60.9%,以此为依据便可推算出四格表中相应的四格的理论数。
兹以表20-11资料为例检验如下。
检验步骤:1.建立检验假设:H0:π1=π2H1:π1≠π2α=0.052.计算理论数(TRC),计算公式为:TRC=nR.nc/n 公式(20.13)式中TRC是表示第R行C列格子的理论数,nR为理论数同行的合计数,nC为与理论数同列的合计数,n为总例数。
因为上表每行和每列合计数都是固定的,所以只要用TRC式求得其中一项理论数(例如T1.1=26.2),则其余三项理论数都可用同行或同列合计数相减,直接求出,示范如下:T1.1=26.2T1.2=43-26.2=16.8T2.1=53-26.2=26.8T2.2=44-26.2=17.23.计算x2值按公式20.12代入4.查x2值表求P值在查表之前应知本题自由度。
按x2检验的自由度v=(行数-1)(列数-1),则该题的自由度v=(2-1)(2-1)=1,查x2界值表(附表20-1),找到x20.001(1)=6.63,而本题x2=10.01即x2>x20.001(1),P<0.01,差异有高度统计学意义,按α=0.05水准,拒绝H0,可以认为采用化疗加放疗治疗卵巢癌的疗效比单用化疗佳。


X2检验第七章 X2检验Chi-square testX2分布——计数资料第⼀节四格表资料的X2检验⼀、X2检验的基本思想1、X2分布(1)X2分布是⼀种连续型分布:X2分布(chi-square distribution)只有⼀个参数,即⾃由度。
当⾃由度V《2时,曲线呈L形随着V的增加,曲线逐渐趋于对称当⾃由度V—00⽆穷时,X2分布趋近正态分布(2)X2分布的⼀个基本性质是它的可加性:(X1+X2)——X2 (V1+V2)(3)X2 分布的界值:X2值愈⼤,P值愈⼩;反之,X2值愈⼩,P值愈⼤。
2、X2检验的基本思想四格表(fourfold table)资料PearsonX2——X2={Σ(A-T)2/T } V =(⾏数-1)(列数-1)A为实际频数(actual frequency)T为理论频数(theoretical frequency)——根据检验假设H0:π1=π2确定的。
T(RC)=nRnC/nT(RC)为第R⾏(row)第C列(column)的理论频数,nR为相应⾏的合计,nC为相应列的合计,n为总列数。
X2值反映了实际频数与理论频数的吻合程度。
3、X2检验的步骤H0::π1=π2,即试验组与对照组——总体有效率相等H1::π1≠π2,即——————————————不等ɑ=0.05——T值——V——P值⼆、四格表资料X2检验的专⽤公式X2=(ad-bc)2n/(a+b)(a+c)(d+b)(d+c)a,b,c,d为四格表的实际频数;(a+b)(a+c)(d+b)(d+c)是周边合计数;n为总例数,n=a+b+c+d. 四格表资料X2检验的校正公式三、X2C=(Iad-bcI-n/2)2n/(a+b)(a+c)(d+b)(d+c)(1)当n》40且所有的T》5时,⽤X2检验的基本公式或四格表资料X2检验的专有公式;(2)当n》40但有1《T《5时,⽤四格表资料X2检验的校正公式。

x2检验或卡方检验和校正卡方检验的计算x2检验(chi-square test)或称卡方检验x2检验(chi-square test)或称卡方检验,是一种用途较广的假设检验方法。
可以分为成组比较(不配对资料)和个别比较(配对,或同一对象两种处理的比较)两类。
一、四格表资料的x2检验例20.7某医院分别用化学疗法和化疗结合放射治疗卵巢癌肿患者,结果如表20-11,问两种疗法有无差别?表20-11 两种疗法治疗卵巢癌的疗效比较组别有效无效合计有效率(%)化疗组19 24 43 44.2 化疗加放疗组34 10 44 77.3合计53 34 87 60.9表内用虚线隔开的这四个数据是整个表中的基本资料,其余数据均由此推算出来;这四格资料表就专称四格表(fourfold table),或称2行2列表(2×2 contingency table)从该资料算出的两种疗法有效率分别为44.2%和77.3%,两者的差别可能是抽样误差所致,亦可能是两种治疗有效率(总体率)确有所不同。
这里可通过x2检验来区别其差异有无统计学意义,检验的基本公式为:式中A为实际数,以上四格表的四个数据就是实际数。
T为理论数,是根据检验假设推断出来的;即假设这两种卵巢癌治疗的有效率本无不同,差别仅是由抽样误差所致。
这里可将两种疗法合计有效率作为理论上的有效率,即53/87=60.9%,以此为依据便可推算出四格表中相应的四格的理论数。
兹以表20-11资料为例检验如下。
检验步骤:1.建立检验假设:H0:π1=π2H1:π1≠π2α=0.052.计算理论数(TRC),计算公式为:TRC=nR.nc/n 公式(20.13)式中TRC是表示第R行C列格子的理论数,nR为理论数同行的合计数,nC为与理论数同列的合计数,n为总例数。
第1行1列: 43×53/87=26.2第1行2列: 43×34/87=16.8第2行1列: 44×53/87=26.8第2行2列: 4×34/87=17.2以推算结果,可与原四项实际数并列成表20-12:表20-12 两种疗法治疗卵巢癌的疗效比较因为上表每行和每列合计数都是固定的,所以只要用TRC式求得其中一项理论数(例如T1.1=26.2),则其余三项理论数都可用同行或同列合计数相减,直接求出,示范如下:T1.1=26.2T1.2=43-26.2=16.8T2.1=53-26.2=26.8T2.2=44-26.2=17.23.计算x2值按公式20.12代入4.查x2值表求P值在查表之前应知本题自由度。
卫⽣统计学试卷(含答案)卫⽣统计学试卷姓名:__________ 考试时间:_______ ___(本⼤题满分40分,每⼩题1分)1. 算术均数适⽤于:( )A. 偏态分布资料B. 分布类型不明的资料C. 对数正态分布资料D. 以上都不是E. 正态分布资料2. 某医⽣在进⾏科室病例资料统计时,拟⽤算术平均数表⽰平均⽔平,应当选⽤什么样的资料:( )A. 性质不同的变量值B. 差异相同的变量值C. 性质相同的变量值D. 个体差异较⼤的变量值E. 个体差异较⼩的变量值3. 均数与标准差适⽤于:( )A. 正态分布B. 正偏态分布C. 不对称分布D. 偏态分布E. 负偏态分布4. 样本含量的估计是( )。
A. 不必估计,调查整个总体最好B. 保证研究结论具有⼀定可靠性的前提下确定的最少例数C. 经济条件允许的情况下,越多越好D. 时间允许的情况下,越多越好E. 根据实际情况,能选多少是多少5. 标化后的总死亡率:( )A. 它反映了事物实际发⽣的强度B. 以上都不对C. 它反映了实际⽔平D. 它不随标准选择的变化⽽变化E. 仅仅作为⽐较的基础,它反映了⼀种相对⽔平6. 下⾯说法中不正确的是( )。
A. 抽样误差的⼤⼩⼀般⽤标准误来表⽰B. 好的抽样设计⽅法,可避免抽样误差的产⽣C. 没有个体差异就不会有抽样误差D. 抽样误差是由抽样造成的样本统计量与总体参数间的差别及样本统计量间的差别E. 医学统计资料主要来⾃统计报表、医疗⼯作记录、专题调查或实验等7. 计算某⾎清⾎凝抑制抗体滴度的平均⽔平,宜⽤:( )A. 四分位数B. ⼏何均数C. 相对数D. 中位数E. 均数8. 变异系数是表⽰资料的:( )A. 对称分布B. 平均⽔平C. 相对变异D. 集中趋势E. 变异数9. 统计上所说的样本是指:( )A. 总体中的每⼀个个体B. 按照随机原则抽取总体中有代表性部分C. 按照研究者要求抽取总体中有意义的部分D. 有意识的抽取总体中有典型部分E. 随意抽取总体中任意部分10. ⼀群7岁男孩⾝⾼标准差为5cm,体重标准差为3kg,则⼆者变异程度⽐较:( )A. ⾝⾼变异⼩于体重B. ⾝⾼变异不等于体重C. ⾝⾼变异等于体重D. ⽆法⽐较E. ⾝⾼变异⼤于体重11. 某数值变量资料的分布性质未明,要计算集中趋势指标,下列适宜的指标是:( )A. GB. CvC. XD. SE. M12. t<t0.05(v),统计上可认为:( )A. B、两样本均数,差别⽆显著性B. 两总体均数,差别有显著性C. 两样本均数,差别有显著性D. 两总体均数,差别⽆显著性E. 以上均不是13. 下列关于统计表的要求,叙述错误的是:( )A. 不宜有竖线及斜线B. 标题位于表的上⽅中央C. 线条要求三线式或四线式D. 备注不必列⼊表内E. ⽆数字时可以不填14. 四个样本率作⽐较,x2>x20.01(3),可以认为:( )A. 各总体率不同或不全相同B. 各总体率均不相同C. 样本率与总体率均不相同D. 各样本率均不相同E. 各样本率不同或不全相同15. 计算标化率的⽬的是:( )A. 起加权平均的作⽤B. 使率能更好的代表实际⽔平C. 使⼤的率变⼩,D. 消除资料内部构成不同的影响,使率具有可⽐性E. 使⼩的率变⼤16. 四格表资料在哪种情况下作χ2检验不必校正( )。
简述 x2 检验的注意事项
引言
x2 检验(Chi-Square Test)是一种常用的统计方法,用于检验两个或多个分类变量之间是否存在相关性。
它是统计学中最常用的非参数检验之一,通常适用于已知样本的多个标称变量之间的关系推断。
在进行 x2 检验时,有一些注意事项需要被考虑。
注意事项一:样本量要求
在进行 x2 检验时,每个分类变量的样本数量应该足够大,以确保结果的有效性。
通常,每个分类变量的样本数量应不少于5。
注意事项二:数据类型
x2 检验通常适用于标称变量,即具有无序分类的变量。
因此,在进行 x2 检验之前,需要将待分析的变量进行适当的编码或转换,以确保其符合 x2 检验的前提条件。
注意事项三:独立性假设
x2 检验的基本假设是各个分类变量之间的无关性,即独立性假设。
在进行 x2 检验前,需要对该假设进行明确的说明,并确认其是否合理。
注意事项四:数据整理
在进行 x2 检验之前,需要对数据进行适当的整理和汇总。
通常,可以使用交叉制表(cross-tabulation)的方法,将不同分类变量的数据整理为一个列联表(contingency table)。
这样可以方便计算各个分类变量之间的卡方值和 p 值。
注意事项五:计算结果的解读
x2 检验的计算结果包括卡方值和 p 值。
卡方值用于衡量观察值与期望值之间的差异程度,而 p 值表示了观察到的差异在统计学上的显著性。
通常,较大的卡方值和较小的 p 值意味着分类变量之间存在显著的相关性。
注意事项六:多重比较问题
在进行多个分类变量之间的 x2 检验时,需要注意多重比较问题。
如果进行了多个检验,需要对 p 值进行校正,以控制整体的错误率。
注意事项七:样本的代表性
在进行 x2 检验时,样本的代表性非常重要。
样本应该可以代表总体,并且应该从总体中随机选择,以减少选择偏倚和非随机误差的影响。
注意事项八:结论的谨慎性
x2 检验只能判断分类变量之间是否存在相关性,不能确定因果关系。
因此,在得出结论时应保持谨慎,并考虑其他变量和因素的可能影响。
结论
x2 检验是一种常用的统计方法,用于检验两个或多个分类变量之间是否存在相关性。
在进行 x2 检验时,需要注意样本量的要求、数据类型、独立性假设、数据整理、计算结果解读、多重比较问题、样本的代表性以及结论的谨慎性。
只有在遵守这些注意事项的前提下,才能保证 x2 检验的有效性和可靠性。