下载文档原格式
整数与小数课标要求1.能熟练掌握整数、小数的数位顺序表，理解计数单位的大小，掌握十进制计数法。
2.能正确、熟练的读、写整数和小数，把一个整数改写成用“万”“亿”作单位的数，会用“四舍五入”法求近似数，并能根据不同的要求求小数的近似数。
3.理解小数的性质，能运用小数的性质化简和改写小数。
4.掌握整数、小数大小比较的方法，能正确、熟练的比较大小。
5.掌握正、负数的意义、读写方法和大小比较，会用正、负数表示日常生活中的量。
考点1 数位和计数单位1.在35096400中，“9”在（）位上，百万位上的数字是（）。
2. 10个0.1是（）。
3.6.78是（）为小数，计数单位是（），它有（）个这样的计数单位。
4.计算：6.79=6×1+7×（）+9×（）。
5. 判断：（1）个位、十位、百位、千位等都是计数单位。
（）（2）在小数中的小数部分，最大的计数单位是十分位。
（）6. 选择：（1）在上古时期，没有“数”的概念，人们打猎每获一只猎物就用一个小石子表示。
等到获得很多猎物时，就把若干个小石子换成一个大石子，表示这里的大石子相当于我们现在的（）。
A.位数B.数位C.计数单位（2）1.34中的“3”可用（）图中的涂色部分表示。
（3）有个整数，从右往左数，第6位上的数字是“8”，这个8表示（）A.8个“一”B.八个“6”C.8个“万”D.8个“十万”考点2 读数、写数、改写和求近似数7.中国国家大剧院占地总面积为118900平方米，综合投资额达2688000000元，横线上的数分别读作（）和（）。
8.中国国家图书馆馆舍面积是十七万平方米，居世界第二位；藏书二千一百六十万册，居世界第五位。
第一条横线上的数写作（），第二条横线上的数写作（）。
9.用3个5和2个0组成一个五位数，要求这个五位数的2个0都要读出来，则组成的五位数是（）。
10.一个九位数，最高位是8，十万位和千位上是2，其余数位上都是0，这个数写作（），读作（）。
人教版小升初数学复习资料精髓版（一）整数和小数1.整数和自然数像…-3, -2, -1, 0, 1, 2, 3, …这样数统称为（整数）。
整数个数是（无限）。
数物体时候,用来体现物体个数0,1,2,3…叫做（自然数）。
自然数是整数（一某些）。
（“1”）是自然数单位。
最小自然数是（ 0 ）。
2、小数小数体现就是十分之几, 百分之几, 千分之几……数, 一位小数可体现为十分之几数, 两位小数可体现为百分之几数, 三位小数可体现为千分之几数 ……熟记: =0.2 = 0.4 = 0.6 =0.841=0.25 43= 0.75 81= 0.125 83=0.37585=0.625 87=0.875 小数点右边第一位是（十分位）,计数单位是（十分之一）;第二位是（百分位）,计数单位是（百分之一）……小数某些有几种数位,就叫做几位小数。
如3.305是（ 三 ）位小数3.整数、小数读法和写法:读整数时注意先分级再读数。
读小数时注意小数某些顺次读出每个数位上数。
写数时注意写好后, 一定要读一读仔细校对。
为了读写以便,常常把较大数改写成用“万”或“亿”作单位数。
如只规定“改写”, 成果应是精确数。
=（ ）亿如规定“省略”万（亿）背面尾数, 成果应是近似数。
≈（）亿4.小数性质: 小数末尾添上0或者去掉0,小数大小不变.5.小数点向右(左)移动一位、两位、三位……本来数就扩大(缩小)10倍、100倍、1000倍……6.正数、负数0既不是正数也不是负数, 0是正数和负数分界点。
负数＜0＜正数两个负数比较, 负号背面数越大这个数反而越小。
-6.8＜-0.4 -2＞-10（二）因数和倍数1.因数和倍数一种数最小因数是1, 最大因数是它自身。
一种数因数个数是有限。
一种数最小倍数是它自身, 没有最大倍数。
一种数倍数个数是无限。
为了以便, 在研究因数和倍数时候, 咱们所说数指是整数（一般不波及0）2.奇数、偶数自然数中, 是2倍数数叫做偶数（0也是偶数）, 不是2倍数数叫做奇数。
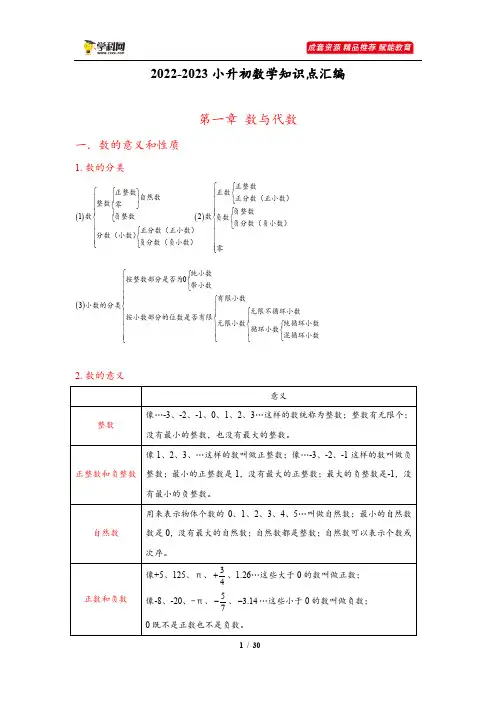
2022-2023小升初数学知识点汇编第一章 数与代数一．数的意义和性质1.数的分类()()()1203正整数正数正整数自然数正分数（正小数）整数零负整数数数负整数负数负分数（负小数）正分数（正小数）分数（小数）负分数（负小数）零纯小数按整数部分是否为带小数有限小数小数的分类无限不循环小数按小数部分的位数是否有限无限小数纯循环小数循环小数混循环小数2.数的意义分数把单位“1”平均分为若干份，表示这样的一份或几份的数叫做分数。
小数把单位“1”平均分成10份、100份、1000份…，这样的一份或几份可以用分母是10、100、1000、…的分数来表示，也可以用小数来表示。
百分数表示一个数是另一个数的百分之几的数叫做百分数，也叫做百分率或百分比。
3.数位整数部分小数点小数部分…亿级 万级 个级数位… 千亿位 百亿位 十亿位亿位千万位 百万位 十万位万位 千位 百位 十位 个位· 十分位 百分位 千分位万分位 …计数单位 … 千亿 百亿 十亿 亿千万 百万 十万 万 千 百 十 个十分之一 百分之一 千分之一 万分之一…4.性质二.数的读写三.数的改写1.四舍五入（≈）在求近似数时，如果被舍去部分的首位数字小于5，就直接舍去；如果被舍去部分的首位数字等于5或大于5，就在保留部分的末位上加1。
要求把小数保留到哪一位，先看这一位后一位上的数字，再按“四舍五入”法省略。
2.多位数改写为“万”、“亿”…（1）直接改写：改写为“万”，小数点左移4位，后面加万；改写为“亿”，小数点左移8位，后面加亿；（2）近似改写：先四舍五入省略掉“万”或“亿”后面的尾数，再在后面加“万”或“亿”。
3.假分数、带分数、整数互化（1）⇒假分数整数、带分数≠÷⋅⋅⋅⋅⋅⋅⇒余数余数零，则假分数=商分子分母=商余数分母余数=零，则假分数=商（2）⇒带分数假分数×带分数整数部分带分数分母+带分数分子假分数=带分数分母4.小数、分数、百分数互化（1）⇒小数分数先改写成分母是10、100、1000…的分数，再约分；（2）⇒分数小数分子÷分母；（3）⇒小数百分数先把小数点右移两位，再添加“%”；（4）⇒百分数小数先把小数点左移两位，再去掉“%”；（5）⇒分数百分数先把分数化成小数，再写成百分数；（6）⇒百分数分数先写成分数，再约分。
2023年小学六年级小升初数学专题复习（1）——整数四则混合运算¤¤知知识识归归纳纳总总结结一、整数的认识知识归纳1. 整数：像-2，-1，0，1，2这样的数称为整数在整数中，零和正整数统称为自然数．-1、-2、-3、…、-n、…（n为非零自然数）为负整数．则正整数、零与负整数构成整数．2. 整数分类：常考题型例：正数和负数都是整数．×．（判断题）分析：整数包括正整数、负整数、0．解：整数包括正整数、负整数、0．所以正数和负数都是整数，是错误的．故答案为：×．点评：根据整数的意义整数包括正整数、负整数、0，强调整数包括0．二、整数四则混合运算知识归纳1．加、减、乘、除四种运算统称四则运算．（1）加法的意义：把两个（或几个）数合并成一个数的运算叫做加法．（2）减法的意义：已知两个加数的和与其中的一个加数求另一个加数的运算叫做减法．减法中，已知的两个加数的和叫做被减数，其中一个加数叫做减数，求出的另一个加数叫差．（3）乘法的意义：一个数乘以整数，是求几个相同加数的和的简便运算，或是求这个数的几倍是多少．（4）除法的意义：已知两个因数的积与其中一个因数求另一个因数的运算叫做除法．在除法中，已知的两个因数的积叫做被除数，其中一个因数叫做除数，求出的另一个因数叫商．四则运算分为二级，加减法叫做第一级运算，乘除法叫做第二级运算．2．方法点拨：运算的顺序：在一个没有括号的算式里，如果只含有同一级运算，要从左往右依次计算；如果含有两级运算，要先算第二级运算，再算第一级运算．在有括号的算式里，要先算括号里的，再算括号外的．例1：72-4×6÷3如果要先算减法，再算乘法，最后算除法，应选择（）A、72-4×6÷3B、（72-4）×6÷3C、（72-4×6）÷3分析：72-4×6÷3的计算顺序是先算乘法，再算除法，最后算减法，要把减法提到第一步，需要只给减法加上小括号．解：72-4×6÷3如果要先算减法，再算乘法，最后算除法，应为：（72-4）×6÷3；故选：B．点评：本题考查了小括号改变运算顺序的作用，看清楚运算顺序，是把哪一种运算提前计算，在由此求解．例2：由56÷7=8，8+62=70，100-70=30组成的综合算式是（）A、100-62+56÷7；B、100-（56÷7+62）；C、不能组成分析：由于56÷7=8，8+62=70，则将两式合并成一个综合算式为56÷7+62=70，又100-70=30，则根据四则混合运算的运算顺序，将56÷7=8，8+62=70，100-70=30组成的综合算式是：100-（56÷7+62）．解：根据四则混合运算的运算顺序可知，将56÷7=8，8+62=70，100-70=30组成的综合算式是：100-（56÷7+62）．故选：B．点评：本题考查了学生根据分式及四则混合运算的运算顺序列出综合算式的能力．¤¤典典型型例例题题精精析析1．你能用两种方法表示出256这个数吗？【分析】明确数字在什么数位上和这个数的计数单位，它就表示几个这样的数字单位；可知：256表示由2个百、5个十和6个一组成；还表示256个一；由此解答即可．【解答】解：256表示由2个百、5个十和6个一组成；还表示256个一．【点评】此题考查了整数的认识，注意基础知识的积累．2．800可以看成个百，也可以看成个十，也可以看成个一．【分析】百位上是几，就表示有几个“百”，十位上是几，就表示有几个“十”，个位上是几，就表示有几个“一”，相邻的计数单位之间的进率是10，据此解答即可．【解答】解：800可以看成8个百，也可以看成80个十，也可以看成800个一．故答案为：8，80，800．【点评】掌握整数各个数位上的数表示的意义，是解答的关键．3．（1）一个计数器的最右边一位是个位．如果在这个计数器的右起第十位上拨9颗珠，拨出的数表示9个；（2）700400是由个万和个一组成的．（3）1枚1元硬币大约重6克，一万枚1元硬币大约重千克，一百万枚1元硬币大约重千克．【分析】（1）最右边是个位，从个位向左数9位，看第10位是什么位，进而可知表示的计数单位；（2）700400先分级可知这个数是七十万零四百，由70个万和400个一组成；（3）用6克乘上10000，就是一万枚硬币是多少克，然后换算成千克即可；1亿是1万个1万，用一万枚硬币的重量乘上10000就是一亿枚硬币的重量，然后再换算单位即可．【解答】解：（1）从右往左第10位是十亿位，上面的9表示9个十亿；（2）700400是由70个万和400个一组成的．（3）6×10000＝60000（克）；60000克＝60千克；1亿里面有10000个一万；60×10000＝600000（千克）；600000千克＝600吨．故答案为：十亿，70，400；60，600．【点评】本题考查了计数单位和数位，要熟记数位和计数单位，知道计数单位之间的进率．4．在说的对的同学下面的（）里面“√”．【分析】根据题意对各选项进行依次分析、进而判断即可．【解答】解：3030中两个3所在的数位不同，所以表示的意义就不同；1899后面的一个数1900，不是2000；8个十和7个千组成的数是7080，不是7800；故答案为：【点评】此题考查了整数的认识，注意平时基础知识的积累．5．一家银行的保险柜上的密码锁是四位数，千位上的数字比个位上的数字大3，百位上的数字比十位上的数字小3，四个数字都不相同，四个数字的和比25大，这个密码是多少？【分析】已知这四个数字都不相同，四个数字的和比25大，其中千位上的数字比个位上的数字大3，百位上的数字比十位上的数字小3，当千位数字是9时，个位数字是9﹣3＝6，此时若十位上的数字是8，则百位数字是8﹣3＝5，由于9+5+8+6＝28＞25，符合题意，所以四位数9586可能是密码；若此时十位上的数字是7，则百位数字是7﹣3＝4，由于9+4+7+6＝26＞25，符合题意，所以四位数9746可能是密码；当千位数字是8时，个位数字是8﹣3＝5，此时若十位上的数字是9，则百位数字是9﹣3＝6，由于8+6+9+65＝28＞25，符合题意，所以四位数8695可能是密码；当千位数字是7时，个位数字是7﹣3＝4，此时若十位上的数字是9，则百位数字是9﹣3＝6，由于7+6+9+4＝26＞25，符合题意，所以四位数7694可能是密码；据此解答．【解答】解：根据题意，当千位数字是9时，个位数字是9﹣3＝6，此时若十位上的数字是8，则百位数字是8﹣3＝5，由于9+5+8+6＝28＞25，符合题意，所以四位数9586可能是密码；若此时十位上的数字是7，则百位数字是7﹣3＝4，由于9+4+7+6＝26＞25，符合题意，所以四位数9746可能是密码；当千位数字是8时，个位数字是8﹣3＝5，此时若十位上的数字是9，则百位数字是9﹣3＝6，由于8+6+9+65＝28＞25，符合题意，所以四位数8695可能是密码；当千位数字是7时，个位数字是7﹣3＝4，此时若十位上的数字是9，则百位数字是9﹣3＝6，由于7+6+9+4＝26＞25，符合题意，所以四位数7694可能是密码；所以这个密码可能是9586或9476或8695或7694，答：这个密码是9586或9476或8695或7694．【点评】此题解答关键是求出这四个数字的平均数，进而确定各位上的数字．6．在□里填上合适的数．1÷□+0÷28+28÷1+□×28＝□+28＝29【分析】1÷□+0÷28+28÷1+□×28是先同时计算三个除法和乘法，再算加法，先把能够计算出结果的部分进行计算，再进一步求解．【解答】解：1÷□+0÷28+28÷1+□×28＝1÷□+28+□×28＝□+28所以1÷□＝□，那么第一个□应是1，即1÷1＝1；□×28＝0，所以第二个□应是0，即0×28＝0；这时算式就是1÷1+0÷28+28÷1+0×28＝1÷1+28+0×28＝1+28＝29故答案为：1，0，1．【点评】解决本题先计算出已知的部分，再根据算式的结果进一步推算．7．森林医生，（将不对的改正过来）126﹣96÷3＝30+3＝10381+120﹣272＝400﹣272＝128【分析】①先算除法，再算减法；②先算加法，再算减法．【解答】解：126﹣96÷3＝30+3＝10 （×）改正：126﹣96÷3＝126﹣32＝94②381+120﹣272＝400﹣272＝128（×）改正：381+120﹣272＝501﹣272＝229【点评】此题考查整数四则混合运算顺序，分析数据找到正确的计算方法．8．脱式计算．（能简算的要简算）29+12÷45+38；813÷7+17×613；2﹣613÷926﹣23；125×（56+34 ）+45．【分析】（1）先算除法，再按照从左向右的顺序进行计算；（2）先算除法和乘法，再算加法；（3）先算除法，再按照从左向右的顺序进行计算；（4）先算小括号里面的加法，再算乘法，最后算括号外面的加法．【解答】解：（1）29+12÷45+38＝29++38＝29+38＝67；（2）813÷7+17×613＝116+10421＝10537；（3）2﹣613÷926﹣23＝2﹣﹣23＝﹣1﹣23＝﹣24；（4）125×（56+34 ）+45＝125×90+45＝11250+45＝11295．【点评】考查了整数和分数四则混合运算，注意运算顺序和运算法则，然后再进一步计算．9．列式计算（1）96减去35的差，乘63与25的和，积是多少？（2）480除以6的商，加上20，再除以25，得多少？【分析】（1）最后求得是积，一个因数是96减去35的差，另一个因数是63与25的和；（2）先求480除以6的商，加上20求得和，再用和除以25得出答案即可．【解答】解：（1）（96﹣35）×（63+25）＝61×88＝5368答：积是5368．（2）（480÷6+20）÷25＝（80+20）÷25＝100÷25＝4答：得4．【点评】列式计算的关键是理解语言叙述的运算顺序，正确理解题意，列式计算即可．10．小明把一个数乘6看错了，结果把这个数除以6，接着他想再加上19，却又减去了19，出了这样的差错后，得数就变成36．假设小明不出错，正确的得数应该是多少？【分析】逆着结果向前推出原来的数：36加上19，是原数除以6得到，乘6得原数，再进一步列出正确算式计算即可．【解答】解：（36+19）×6＝55×6＝330；330×6+19＝1980+9＝1999；答：正确的得数应该是1999．【点评】此题考查混合运算的顺序是计算准确的前提，注意运算过程中的数字和运算符号．11．有一个四位数，个位上的数是7，和个位相邻的数位上的数字比个位上的数字少3，百位上的数字是十位上的数字的2倍，千位数字和个位数字的积是35。
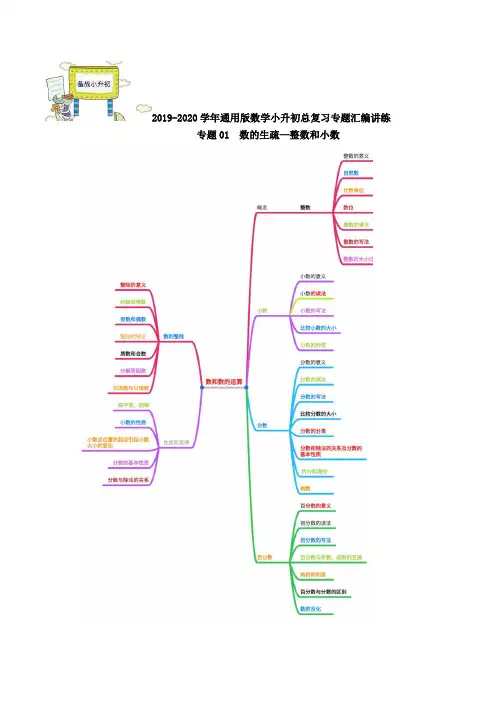
2019-2020学年通用版数学小升初总复习专题汇编讲练专题01 数的生疏—整数和小数（一）整数1、整数的意义自然数和0都是整数。
2、自然数我们在数物体的时候，用来表示物体个数的1，2，3……叫做自然数。
一个物体也没有，用0表示。
0也是自然数。
3、计数单位一（个）、十、百、千、万、十万、百万、千万、亿……都是计数单位。
其中“一”是计数的基本单位。
10个1是10，10个10是100……每相邻两个计数单位之间的进率都是10。
这样的计数法叫做十进制计数法。
4、数位计数单位依据肯定的挨次排列起来，它们所占的位置叫做数位。
5、整数的读法：从高位到低位，一级一级地读。
读亿级、万级时，先依据个级的读法去读，再在后面加一个“亿”或“万”字。
每一级末尾的0都不读出来，其它数位连续有几个0都只读一个零。
6、整数的写法：从高位到低位，一级一级地写，哪一个数位上一个单位也没有，就在那个数位上写0。
7、一个较大的多位数，为了读写便利，经常把它改写成用“万”或“亿”作单位的数。
有时还可以依据需要，省略这个数某一位后面的数，写成近似数。
⑴精确数：在实际生活中，为了计数的简便，可以把一个较大的数改写成以万或亿为单位的数。
改写后的数是原数的精确数。
例如把 1254300000 改写成以万做单位的数是 125430 万；改写成以亿做单位的数 12.543 亿。
⑵近似数：依据实际需要，我们还可以把一个较大的数，省略某一位后面的尾数，用一个近似数来表示。
例如： 1302490015 省略亿后面的尾数是 13 亿。
⑶四舍五入法：求近似数，看尾数最高位上的数是几，比5小就舍去，是5或大于5舍去尾数向前一位进1。
这种求近似数的方法就叫做四舍五入法。
8、整数大小的比较：位数多的那个数就大，假如位数相同，就看最高位，最高位上的数大，那个数就大；最高位上的数相同，就看下一位，哪一位上的数大那个数就大。
以此类推。
一、整数的生疏（2019秋•丰台区期末）如图中，最接近242万的点是()A．A B．B C．C D．D【变式1-1】（2019秋•巩义市期末）关于数的生疏，下面说法正确的是()A．最小的自然数是1，全部的自然数都是整数B．个位，十位，百位⋯⋯都是计数单位C．算盘上的1颗上珠表示5【变式1-2】（2019秋•朝阳区期末）图中不是14的是()A．B．C．二、整数的读法和写法（2017秋•汝城县期末）一个数由8个亿，4个百万，3个十组成，这个数写作8 0400 0030．【变式2-1】（2017秋•新晃县期末）宏伟的万里长城是世界上最宏大的建筑之一，全长约6300000米，读作六百三十万，改写成用“万”作单位的数是万米．其中“6”在位上，表示．【变式2-2】（2019春•射阳县月考）一个十位数，最高位上的数字是最大的一位数，亿位上的数字比最高位上的数字少7，万位上的数字是亿位上的数字的4倍，其他数位上的数字都是0，这个数是多少？三、整数的改写和近似数（2017秋•保定期中）假如96□30097≈万，那么□里可以填的数是()A．0B．1C．3D．5【变式3-1】（2015秋•祁阳县校级期中）49□98750≈万，在□里可以填的数字是() A．最小是4B．最小是5C．最大是4【变式3-2】（2017春•十堰期末）东风日产有一款车售价10.96万元，横线上的数改写成以“元”做单位的数是109600元，四舍五入保留整数约是万元．四、整数大小的比较（2017秋•惠来县校级月考）比较下面各组数的大小．100000〇9999956070000〇6707万2812000〇2809800199999〇200000〇200001．【变式4-1】（2016春•江苏校级期末）将下面各数依据从小到大的挨次排列．390万21302400 4001234 780998 3800670780998<<<<．【变式4-2】（2016春•江苏校级期末）在横线里填上“>”或“<”．314400<32万649800006500000250300000000249400000000630826083239805089377905021270104250212710259870．（二）小数1、小数的意义把整数1平均分成10份、100份、1000份……得到的格外之几、百分之几、千分之几……可以用小数表示。
温馨提示：图片放大更清晰小明在计算 5.a ＋b.9时，错算成了8.a ＋b.6，结果是10，那么5.a ＋b.9＝( )。
答案：7.3解析：8.a ＋b.6，结果是10，由此可知a ＋6＝10，8＋b ＝9，分别求出a 、b ，再代入5.a ＋b.9进行计算即可。
8.a ＋b.6，结果是10小升初数学通用版《小数四则运算》精准讲练所以a＋6＝10，8＋b＝9即a＝4，b＝15.a＋b.9＝5.4＋1.9＝7.3美心蛋糕房制作一种蛋糕，每个需要0.42kg面粉，李师傅用4kg面粉可以做10个这样的蛋糕。
( )答案：×解析：根据题意可列算式40.42，若将0.42按照“四舍五入”的原则估算，则估得的结果为10，但根据实际情况，每个蛋糕使用的面粉质量不能少估，因此答案不合理。
由分析可知，李师傅用4kg面粉可以做9个这样的蛋糕。
原题说法错误。
故答案为：×求24个偶数的平均数，保留一位小数的数是15.9，若保留两位小数的数应该是（）。
A．15.91 B．15.92 C．15.93 D．19.94答案：B解析：先求出这24偶数的平均数保留两位小数的最大值和最小值，这24个偶数的和一定为偶数，再根据“这组数据的和＝平均数×数据个数”求出满足条件的这24个偶数的和，最后利用“平均数＝这组数据的和÷数据个数”求出商保留两位小数的值，据此解答。
平均数保留一位小数的数是15.9，平均数保留两位小数的最小值为15.85，保留两位小数的最大值为15.94。
24个偶数和的最小值为：15.85×24＝380.424个偶数和的最大值为：15.94×24＝382.5624个偶数的和一定为偶数，则24个偶数的和为382。
382÷24≈15.92故答案为：B宁波市“十四五”规划纲要指出，实施乡村产业振兴行动，到2025年农村居民人均可支配收入达到5.5万元，比2020年的2倍少2.3万元。
专题1 整数和小数1.数的分类。
2.整数的意义。
像…， - 3， - 2， - 1，0，1，2，3，…这样的数统称为整数。
没有最小的整数，也没有最大的整题。
整数的个数是无限的。
3.正整数和负整数的意义。
像1，2，3，…这样的数叫作正整数；像 - 1， - 2， - 3，…这样的数叫作负整数。
最小的正整数是1，没有最大的正整数；最大的负整数是 - 1，没有最小的负整数。
4.自然数的意义。
用来表示物体个数的0，1，2，3，4，5，…叫自然数。
1是自然数的基本单位，除0以外，每个自然数都是由若干个1组成的。
0是最小的自然数，没有最大的自然数。
一个自然数有两个方面的意义:一是用来表示事物的多少，称为基数；二是用来表示事物的次序，称为序数。
例如:“5个鸡蛋”中的“5”是表示事物的多少，是基数；“第5排”中的“5”就是序数。
5.正数和负数的意义。
像16， + 4 9 ，0.65，…这些大于0的数叫作正数；像 - 18， - 0.9， -60，…这些小于0的数叫作负数。
“ - ”叫负号。
0既不是正数，也不是负数。
【小提升】0的作用：①表示起点，如直尺上的0；②占位作用；③作为界限，如“零上温度与零下温度的分界”；④表示没有。
6.小数的意义。
把整数“1”平均分成10份、100份、1000份…这样的一份或几份可以用知识梳理分母是10、100、1000…的分数来表示，也可以用小数来表示。
7.小数的分类。
（1）纯小数和带小数:整数部分是0的小数叫作纯小数，纯小数小于1；整数部分不是0的小数叫作带小数，带小数大于1。
（2）有限小数和无限小数:小数部分的位数是有限的小数，叫作有限小数；小数部分的位数是无限的小数，叫作无限小数。
如4.28是有限小数，π是无限小数。
（3）循环小数:一个小数，从小数部分的某一位起，一个数字或者几个数字依次不断地重复出现，这样的小数叫作循环小数。
循环小数都是无限小数。
（4）循环节:在一个循环小数的小数部分中，依次不断重复出现的数字，叫作这个循环小数的循环节。
第1讲：整数的认识姓名：班级：得分：考点1：整数的意义和分类▒考点归纳1．整数的意义和分类。
(1）像-3，-2，-1，0，1，2，3……这样的数统称为整数没有最小的整数，也没有最大的整数，整数的个数是无限的。
(2)整数可以分为正整数、0、负整数。
(3）用来表示物体个数的0，1，2，3，4……叫自然数。
2.整数数位顺序表。
3.计数单位、数位和位数。
计数单位:一(个)、十、百、千……都是计数单位。
数位:各个计数单位所在的位置叫作数位。
位数:一个自然数含有几个数位，它就是几位数。
※易错提示：0既不是正数也不是负数。
区别数位和位数：如:2024含有四个数位,则2024就是四位数。
▒例题精选例1：一个数由6个亿、6个千万、6个万、6个百和6个一组成，这个数写作(它是一个( )位数。
解析：根据数的组成写数时，可以先简写一个数位顺序表，再对应各数位写上计数单位的个数，即6个亿、6个千万、6个万、6个百、6个一分别对应亿位、千万位、万位、百位、个位写6，其他数位上一个计数单位也没有，都写0占位。
这个数的最高位是亿位，它是一个九位数。
解答：660060606 九▒ 举一反三11.在-3、4.5、25 、2、0中，( )是正数,( )是负数，( )既不 是正数也不是负数。
2. 65020600中的“5”表示( )。
A.5个百B.5个十万C. 5个百万D.5个百亿3.在上古时期，人们没有“数”的概念。
打猎时，每收获一只猎物就用一个小石子表示，等到收获到很多猎物时，就用一个大石子代替若干个小石子，这里的大石子就相当于( )。
A.数位B.数级 C ．位数 D.计数单位考点2：整数的读写▒考点归纳1．整数的读法。
先把数分级，再从高位到低位，一级一级地读。
亿级和万级都按个级的读法来读，再在后面加上一个“亿”字或“万”字。
每-级末尾的0都不读，每一级中间有一个0或连续几个0，都只读一个“零”。
2．整数的写法。
从高位起，一级一级地写，哪个数位上没有计数单位，就在那个数位上写0占位。
提高版（通用）2022-2023学年小升初数学精讲精练专题汇编讲义第1讲整数和小数知识精讲知识点一：整数1.整数的意义和分类：像-3，-2，-1，0，1，2，3，…这样的数统称为（整数）。
整数分为正整数、0、负整数（整数也可以分为自然数和负整数）【提示】0既不是正数，也不是负数2.整数的读法：读一个多位数，从高级到低级，一级一级地读。
每级都按照个级的读法来读，读亿级、万级时，必须加上“亿”字或“万”字。
每级末尾的“0"都不读，其他数位有一个或连续几个“0"的都只读一个零。
（读数时，可以先画出分级线，再读数，这样可以快速、准确地读出一个多位数3.整数的写法：写数时，按从高位到低位的顺序，一级一级地写。
亿级和万级都按个级的写法来写。
哪个数位上一个单位也没有，就在那一位上写0（写完后，画上分级线检查，每一级都只能写四位，不要多写或少写0）４.整数的大小比较:○1比较两个整数的大小，首先数一下多位数的位数，位数多的大于位数少的○2如果位数相同，就比较最高位，最高位上的数大的那个数就大；最高位上的数相同，次高位上的数大那个数就大，如果还相同，则继续依次比较，直到比较出大小为止。
５．整数的改写和近似数一个较大的多位数，为了读写方便，常常把它改写成用“万”或“亿”作单位的数。
有时还可以根据需要，省略这个数某一位后面的数，写成近似数。
（１）数的改写：①把整万、整亿数改写成用“万”或“亿”作单位的数：把万位或亿位后面的4个0或个0去掉，换成一个“万”字或“亿”字就可以了②把非整万、整亿数改写成用“万”或“化”作单位的数：先把原数的小数点向左移动4位或8位（小数部分末尾是0的要划掉），再在数的后面写上“万”字或“亿”字，中间用“=”连接（２）近似数：省略尾数改写成近似数：先用“四舍五入”法省略万位或亿位后面的尾数，再在数的后面写上“万”或“亿”字，中间用约等号连接【提示】近似数常用词：精确到哪位小数、保留几位小数等。
ａ.四舍五入法：要省略的尾数的最高位上的数是４或者比4小，就把尾数去掉；如果尾数的最高位上的数是５或者比５大，就把尾数舍去，并向它的前一位进１。
例如：省略345900万后面的尾数约是35万。
省略4725097420亿后面的尾数约是47亿。
ｂ.进一法：在取近似数时，不管多余部分上的数量是多少，都向前进1。
这种求近似数的方法，叫做进一法。
ｃ.去尾法：在取近似数时，不管多余部分上的数量是多少，一概去掉。
这种求近似数的方法，叫做去尾法。
知识点二：小数1.小数的意义：把整数1平均分成10份、100份、1000份…得到的十分之几、百分之几、千分之几…可以用小数表示。
一位小数表示十分之儿，两位小数表示百分之几，三位小数表示千分之几….2.小数的计数单位：整数部分小数点。
小数部分…亿级万级个级数位…千亿位百亿位十亿位亿位千万位百万位十万位万位千位百位十位个位十分位百分位千分位万分位…计数单位千亿百亿十亿亿千万百万十万万千百十个十分之一百分之一千分之一万分之一3.小数的分类：按小数部分的不同情况小数可分为有限小数和无限小数①有限小数：小数部分的位数是有限的.例如：134.56，9.001，2.222是有限小数②无限小数：小数部分的位数是无限的.无限小数分为无限循环小数和无限不循环小数。
○3循环小数：小数部分从某一位起，一个数字或几个数字依次不断地重复出现，这样的小数，叫做循环小数。
例如：0.3333…，1．242424…，9.0531531531…○4循环节：一个循环小数的小数部分，依次不断重复出现的数字叫做这个循环小数的循环节。
例如：33.333…的循环节是“3”，记作33.3。
；4.32727…的循环节是“27”，记4.32。
7。
；0.1809809…的循环节是“809”，记作0.18。
09。
○5无限不循环小数：一个没有循环节的无限小数，叫做无限不循环小数。
无限不循环小数也叫做无理数。
例如： ＝3.1415926…是无限不循环小数。
【提示】循环小数一定是无限小数，不要误以为小数部分有重复出现的数就是循环小数4.小数的读法：读小数时，小数的整数部分按整数的读法来读，小数点读作“点”，小数部分按照顺序读出每一个数位上的数字。
【提示】小数部分不要按照整数的读法来读。
5.小数的写法：写小数时，整数部分按照整数的写法来写，小数点写在个位右下角，小数部分顺次写出每一个数位上的数字【提示】整数部分是零的写作”0”6.小数的基本性质：小数的末尾添上0或者去掉0，小数的大小不变。
【提示】把一个小数写成指定位数的小数，大小不变，而计数单位和意义都不同。
7.小数的大小比较：先比较整数部分，整数部分大的那个小数就大；如果整数部分相同，就比较十分位，十分位大的那个小数就大；如果十分位相同，就比较百分位，百分位大的那个小数就大，直到比较出大小为止8.小数点的移动规律（1）小数点向右移动一位，原数就扩大到原数的10倍移动两位，原数就扩大到原数的100倍移动三位，原数就扩大到原数的1000倍（2）小数点向左移动一位，小数就缩小10倍，即小数就缩小到原数的十分之一；移动两位，小数就缩小100倍，即小数就缩小到原数的百分之一；移动三位，小数就缩小1000倍，即小数就缩小到原数的千分之一；……（3）小数点移动要记牢右移扩大、左移缩小移动一（二、三、……）位是10（100、1000……）倍，位数不够“0”补位。
9.小数的近似数：01.保留整数，表示精确到个位，就是要把小数部分省略，要看十分位，如果十分位的数字大于或等于5则向前一位进一。
如果小于五则舍去02.保留一位小数，表示精确到十分位，就要把第一位小数以后的部分全部省略，这时要看小数的第二位，如果第二位的数字比5小则全部舍。
反之，要向前一位进一。
03.保留两位小数，表示精确到百分位，就要把第二位小数以后的部分全部省略，这时要看小数的第三位，如果第三位的数字比5小则全部舍。
反之，要向前一位进一。
04.为了读写的方便，常把不是整万或整亿的数改写成用“万”或“亿”作单位的数。
改写成“万”作单位的数就是小数点向左移4位，即在万位的右边点上小数点，在数的后面加上“万”字。
改写成“亿”作单位的数就是小数点往左移8位即在亿位的右边点上小数点，在数的后面加上“亿”字。
注意：带上单位。
然后再根据小数的性质把小数末尾的零去掉即可提高达标百分练一、精挑细选（共5题；每题2分，共10分）1．（2分）（2022·潼关）每个空瓶最多可以装0.48千克的香油，王老师要把7.56千克的香油装在这样的瓶子里，至少需要（）个这样的瓶子。
A．14 B．15 C．16 D．18 2．（2分）（2022·泾县）下列各数中，只读出一个零的是（）。
A．3002166 B．1.200 C．78650003 D．0.05 3．（2分）（2022·即墨）一个小数的小数点向右移动1位，再向左移动3位，这个小数（）。
A．扩大到原来的10倍B．缩小到原来的1 10C．扩大到原来的100倍D．缩小到原来的1 1004．（2分）（2021·承德）某停车场的收费标准是：半小时内（含半小时）免费；半小时以上，每过1小时收费8元，不足1小时按1小时算。
李叔叔缴费24元，他的停车时间可能是（）。
A．9：55-12：25 B．12：30-14：30 C．11：25~14：45 5．（2分）（2020·三门峡）报社将一定的奖金分发给征文活动获奖者，其中一等奖学金是二等的2倍，二等奖学金是3等的1.5倍，如果一、二、三等奖学各评选两人，那么一等奖获得者将得2400元奖金；如果一等奖只评选一人，二、三等奖各评选两人，那么一等奖的奖金是（）A．2800元B．3000元C．3300元D．4500元二、判断正误（共5题；每题2分，共10分）6．（2分）（2022·灵武）一个自然数乘以一个比1大的数，积一定是大于这个自然数。
（）7．（2分）（2022·阳西）6.1和6.10的大小相等，计数单位也相同。
（）8．（2分）（2022六下·伊川期末）一个小数的小数点先向左移动两位，再向右移动一位，这个小数缩小到了原来的110。
（）9．（2分）（2021·文山）3500÷800＝35÷8＝4……3。
（）10．（2分）在一个数的末尾添上2个零，这个数就扩大到原来的100倍。
（）三、仔细想，认真填（共8题；每空1分，共12分）11．（2分）（2022·海港）截至2021年12月8日，中国快递年业务量首次突破100000000000件。
相当于去年全国每个人至少收到了71件快件，可以铺满17045个天安门广场，首尾相连能绕地球748圈。
中国快递的突飞猛进，映射出中国速度、中国活力。
横线上的数读作，改写成用“亿”作单位的数是。
12．（2分）（2022·罗湖）来自国家卫健委数据显示截至6月12日，全国新冠疫情确诊病例为3399959人，横线上的数读作，用四舍五入法省略万位后面的位数是万。
13．（2分）（2022·开平）林老师是一名运动爱好者，他每天用“微信运动”记录自己走路的步数，2021年，他累计走3036984步，横线上的数读作，用“四舍五入”法省略万后面的尾数，改写成用“万”作单位约是万步。
14．（1分）（2022·西城）数学中的黄金分割比（约为0.618：1）应用广泛，一些音乐家喜欢在创作乐曲时将节奏的转折点安排在全曲的黄金分割点处。
按照这种做法，如果是89节的乐曲，就用89×0.618≈55，那么转折点应设在55节处；如果是50节的乐曲，转折点应设在节处。
（结果用四舍五入法保留整数）15．（1分）（2022六下·龙里期末）用一张长1米、宽8分米的硬纸板（如图所示）剪半径为4厘米的小圆，一共能剪出个这样的圆形。
16．（1分）（2022六下·竞赛）计算：2.89×47+1.53-1.4×1.1+24×0.11+288×0.53-0.1= 。
（2022六下·巧家期中）甲乙两数之差是14，两数之和是56，甲数是，（2分）17．乙数是。
18．（1分）（2021·重庆）小明骑自行车以每小时20公里的速度由A城市直奔B城市，同时小强以每小时15公里的速度由B开往A．如果有一只鸟，以30公里每小时的速度与他们同时起动，碰到另一个人时就按相反的方向返回去飞，就这样依次在两人之间来回地飞，如果AB相距14公里，那么这只小鸟飞行了公里。
四、综合提升（共3题；共6分）19．（6分）（2021·盐田）2021年5月11日，第七次全国人口普查数据显示：（1）（2分）全国人口共1411780000人，把横线上的数改写成用“亿”作单位的数是亿；（2分）其中男性人口为7.2334亿人，横线上的数中的数字“2”表示2个；（2）（2分）女性人口为68844万人，横线上的数“四舍五入”到亿位约是亿。
