高中期末数学复习题

一、选择题1．已知1,0()1,0ax x f x x x x +≤⎧⎪=⎨->⎪⎩，则下列关于[()]1y f f x =+的零点的判断正确的是（ ） A ．当0a >时，有4个零点，当0a <时，有1个零点；B ．当0a >时，有3个零点，当0a <时，有2个零点；C ．无论a 为何值，均有2个零点；D ．无论a 为何值，均有4个零点．2．已知函数()21,04,0x x f x x x ⎧+≤=⎨>⎩，若函数()y f x a =-有3个不同的零点1x ，2x ，3x （123x x x <<），则123a x x x ++的取值范围是( ) A ．()2,0-B ．[]2,0-C ．[]2,0-D ．(]2,0- 3．若函数()22f x x x a =--有4个零点，则实数a 的取值范围为（ ）A ．01a <≤B ．10a -<<C ．0a =或1a >D ．01a << 4．集合{}1002,x x xx R =∈的真子集的个数为（ ） A ．2B ．4C ．6D ．7 5．设52a -=，5log 2b =，8log 5c =，则（ ） A ．a b c <<B ．b c a <<C ．c b a <<D ．c a b << 6．如图是指数函数①y =x a ；②y =x b ；③y =c x ；④y =d x 的图象，则a ，b ，c ，d 与1的大小关系是（ ）A ．a <b <1<c <dB ．b <a <1<d <cC ．1<a <b <c <dD ．a <b <1<d <c 7．下列各函数中，表示相等函数的是（ ）A ．lg y x =与21lg 2y x = B ．211x y x -=-与1y x =+C ．21y x =-与1y x =-D ．y x =与log x a y a =(0a >且1a ≠)8．已知函数223,()11,x x x a f x ax x a⎧--≥⎪=⎨-<⎪⎩，对于任意两个不相等的实数1x ，2x R ∈，都有不等式()()()12120x x f x f x -->⎡⎤⎣⎦成立，则实数a 取值范围是（ ）A ．[)3,+∞B ．[]0,3C ．[]3,4D ．[]2,4 9．已知函数()3221x f x x =-+，且()()20f a f b ++<，则（ ） A ．0a b +< B ．0a b +>C ．10a b -+>D ．20a b ++< 10．已知集合{}11M x Z x =∈-≤≤，{}Z (2)0N x x x =∈-≤，则如图所示的韦恩图中的阴影部分所表示的集合为（ ）A ．{}0,1B ．{}1,2-C ．{}1,0,1-D ．1,0,1,2 11．若{}|28A x Z x =∈≤<，{}5|log 1B x R x =∈<，则R A C B ⋂的元素个数为（ ）A ．0B ．1C ．2D ．3 12．已知集合{}1A x x =>，{}1B x x =≥，则（ ）A ．A ⊆B B ．B ⊆AC ．A∩B=φD ．A ∪B=R 二、填空题13．已知()32,,x x a f x x x a⎧≤=⎨>⎩，若存在实数b ，使函数()()g x f x b =-有两个零点，则a的取值范围是________．14．已知函数22()1()x x f x x e a x e a R =++∈有四个零点，则实数a 的取值范围是________．15．函数()log 31a y x =+-.（0a >且1a ≠）的图像恒过定点A ，若点A 在直线 10mx ny ++=上（其中m ，0n >），则12m n+的最小值等于__________. 16．有以下结论： ①将函数x y e =的图象向右平移1个单位得到1x y e-=的图象； ②函数()x f x e =与()g x lnx =的图象关于直线y =x 对称③对于函数()x f x a =(a >0,且1a ≠)，一定有()()121222f x f x x x f ++⎛⎫≤ ⎪⎝⎭④函数()22log (2)f x x x =-+的图象恒在x 轴上方. 其中正确结论的序号为_________.17．函数y x =+______．18．已知函数()f x 的值域为[]0,4（2,2x ），函数()1=-g x ax ，2,2x ，[]12,2x ∀∈-，总[]02,2x ∃∈-，使得()()01g x f x =成立，则实数a 的取值范围为________________.19．若关于x 的方程2210ax x ++=的解集有唯一子集 ，则实数a 的取值范围是_____. 20．若不等式34x b -<的解集中的整数有且仅有5,6，则b 的取值范围是______.三、解答题21．已知函数(2),()(1),x x a x a f x a x x a-≥⎧=⎨-<⎩，其中a 为实数，且0a ≠． （1）当1a =-时，求函数()f x 的单调区间；（2）若方程()0f x =仅有一个实数根，求实数a 的取值范围．22．随着科技的发展，智能手机已经开始逐步取代传统PC 渗透进入了人们娱乐生活的各个方面，我们的生活已经步入移动互联网时代.2020年，某手机企业计划将某项新技术应用到手机生产中去，为了研究市场的反应，计划用一年时间进行试产､试销.通过市场分析，生产此款手机全年需投入固定成本280万，每生产x (千部)手机，需另投入成本()C x 万元，且210200,050()100008019450,50.x x x C x x x x ⎧+<<⎪=⎨+-≥⎪⎩，由市场调研知，每部手机售价0.8万元，且全年内生产的手机当年能全部销售完.（1）求出2020年的利润()W x (万元)关于年产量x (千部)的函数关系式(利润=销售额-成本)；（2）2020年产量为多少(千部)时，企业所获利润最大？最大利润是多少？23．定义在D 上的函数()f x ，如果满足：对任意x D ∈，存在常数0M >，都有()f x M ≤成立，则称()f x 是D 上的“有上界函数”，其中M 称为函数()f x 的上界．已知函数11()139x xf x a ⎛⎫⎛⎫=+⋅+ ⎪ ⎪⎝⎭⎝⎭． （1）当12a =-时，求函数()f x 在(,0)-∞上的值域，并判断函数()f x 在(,0)-∞上是否为“有上界函数”，请说明理由；（2）若函数()f x 在[0,)+∞上是以4为上界的“有上界函数”，求实数a 的取值范围． 24．已知函数()log (0,1)a f x x a a =>≠，且(4)(2)1f f -=.（1）求函数()f x 的表达式；（2）判断函数()(2)(2)g x f x f x =++-的奇偶性，并说明理由.25．已知函数()0k y x k x =+>在区间(单调递减，在区间)+∞单调递增． （1）求函数2y x x=+在区间(),0-∞的单调性；（只写出结果，不需要证明） （2）已知函数()()2131x ax f x a x ++=∈+R ，若对于任意的x N *∈，有()5f x ≥恒成立，求实数a 的取值范围．26．关于x 的不等式22(21)(2)0x a x a a -+++->，223()0x a a x a -++<的解集分别为M 和N（1）试求M 和N ；（2）若M N ⋂=∅，求实数a 的取值范围．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】按0a >和0a <分类讨论[()]1y f f x =+的零点个数，即确定[()]10f f x +=的解的个数，可得正确选项．【详解】0x >时，1()f x x x=-是增函数，()(,)f x ∈-∞+∞，此时()f x m =对任意m R ∈均有一解． 0x ≤时，若0a >，()1f x ax =+是增函数，()(,1]f x ∈-∞，此时()f x m =在1m 时有一解，1m 时无解，若0a <，()1f x ax =+是减函数，()[1,)f x ∈+∞，此时()f x m =在m 1≥时有一解，1m <时无解，由[())10f f x +=得[()]1f f x =-，设()1f t =-，则0a >时，()1f t =-的解为2t a =-和12t =，20a -<，51012-<<，因此2()f x a =-有两解，51()2f x -=有两解，共4解． 0a <时，()1f t =-只有一解5112t -=<，51()2f x -=只有一解， ∴函数[()]1y f f x =+在0a >时，有4个零点，当0a <时，有1个零点． 故选：A ．【点睛】关键点点睛：本题考查函数的零点，解题方法是转化与化归思想，转化为方程[()]10f f x +=的解．通过换元法，先求得()1f t =-的解，若0t 是其解，再求0()f x t =的解，从而得出结论．2．D解析：D【分析】作出函数()f x 的图象，由函数()f x 的图象与直线y a =的交点得123,,x x x 的范围与关系，从而可求得123a x x x ++的取值范围． 【详解】函数()y f x a =-的零点就是函数()y f x =的图象与直线y a =的交点的横坐标，作出函数()y f x =的图象，作出直线y a =，如图，由图可知122x x +=-，由241x =得12x =（12x =-舍去），∴3102x <≤，234x a =， ∴23123334224(2,0]x a x x x x x ++=-+=-+∈-． 故选：D ．【点睛】本题考查函数的零点，解题关键是掌握转化与化归思想，函数零点转化为函数图象与直线的交点，由数形结合思想确定零点的性质，得出结论．3．D解析：D【分析】令0f x ，可得22x x a -=，作出()22g x x x =-的图象，令直线y a =与()g x 的图象有4个交点，可求出实数a 的取值范围.【详解】令0f x ，则22x x a -=，构造函数()22g x x x =-，作出()g x 的图象，如下图，()g x 在()0,2上的最大值为()1121g =-=，当01a <<时，直线y a =与()g x 的图象有4个交点，所以函数()f x 有4个零点，实数a 的取值范围为01a <<.故选：D.【点睛】本题考查函数的零点，注意利用数形结合方法，考查学生的计算求解能力，属于中档题. 4．D解析：D【分析】分析指数函数2x y =与幂函数100y x =的图像增长趋势，当0x <时，有1个交点；当0x >时，有2个交点；即集合{}1002,x x x x R =∈有3个元素，所以真子集个数为3217-=【详解】分析指数函数2x y =与幂函数100y x=的图像增长趋势， 当0x <时，显然有一个交点； 当0x >时，当1x =时，110021>；当2x =时，210022<；故()1,2x ∈时，有一个交点；分析数据发现，当x 较小时，100y x =比2x y =增长的快；当x 较大时，2x y =比100y x =增长的快，即2x y =是爆炸式增长，所以还有一个交点.即2x y =与100y x =的图像有三个交点，即集合{}1002,x x x x R =∈有3个元素，所以真子集个数为3217-=故选：D.【点睛】结论点睛：本题考查集合的子集个数，集合A 中含有n 个元素，则集合A 的子集有2n 个，真子集有()21n -个，非空真子集有()22n -个. 5．A解析：A【分析】 由551112,2332log -<<<，8152log >，即可得出a ，b ，c 的大小关系. 【详解】 52112243--<=<，11325551152532log log log =<<=，12881582log log >=， a b c ∴<<.故选：A【点睛】本题主要考查了指数函数、对数函数的单调性，对数的运算性质，还考查了转化求解问题的能力，属于中档题.6．B解析：B【分析】根据指数函数的图象与性质可求解.【详解】根据函数图象可知函数①y =x a ；②y =x b 为减函数，且1x =时，②y =1b <①y =1a ， 所以1b a <<，根据函数图象可知函数③y =c x ；④y =d x 为增函数，且1x =时，③y =c 1>④y =d 1， 所以1c d >>故选：B【点睛】本题主要考查了指数函数的单调性，指数函数的图象，数形结合的思想，属于中档题. 7．D解析：D【分析】本题可依次判断四个选项中函数的定义域、对应关系、值域是否相同，即可得出结果.【详解】A 项：函数lg y x =定义域为()0,∞+，函数21lg 2y x =定义域为{}0x x ≠，A 错误；B 项：函数211x y x -=-定义域为{}1x x ≠，函数1y x =+定义域为R ，B 错误； C 项：函数21y x =-值域为[)1,-+∞，函数1y x =-值域为R ，C 错误；D 项：函数y x =与函数log x a y a =(0a >且1a ≠)定义域相同，对应关系相同，D 正确.故选：D【点睛】方法点睛：判断两个函数是否相同，首先可以判断函数的定义域是否相同，然后判断两个函数的对应关系以及值域是否相同即可，考查函数定义域和值域的求法，是中档题. 8．C解析：C【分析】根据题意，可得()f x 在R 上为单调递增函数，若x a ≥时为增函数，则3a ≥，若x a <时为增函数，则0a >，比较x=a 处两函数值的大小，即可求得答案，【详解】因为()()()12120x x f x f x -->⎡⎤⎣⎦，所以()f x 在R 上为单调递增函数，当x a ≥时，2()23f x x x =--的图象如图所示：因为()f x 在R 上为单调递增函数，所以3a ≥，当x a <时，()11f x ax =-为增函数，所以0a >，且在x=a 处222311a a a --≥-，解得4a ≤，综上34a ≤≤，故选：C.【点睛】解题的关键是熟悉分段函数单调性的求法，根据单调性，先分析分段点两侧单调性，再比较分段点处函数值的大小即可，考查推理分析，化简计算的能力，属中档题.9．A解析：A【分析】求得函数的单调性，构造奇函数利用单调性得解【详解】由函数单调性性质得：3y x =，21x y =+在R 上单调递增 所以()3221x f x x =-+在R 上单调递增， 令函数()()321121x x g x f x x -=+=-+，()()0g x g x +-= 则函数()g x 为奇函数，且在R 上单调递增，故()()20f a f b ++<()()g a g b ⇔<-0a b a b ⇔<-⇔+<．故选:A【点睛】构造奇函数利用单调性是解题关键.10．B解析：B【分析】阴影部分可以用集合M N 、表示为()()M N C M N ⋃⋂，故求出M N 、、M N ⋃，M N ⋂即可解决问题．【详解】解：由题意得，{}1,0,1M =-，{}0,1,2N ={}1,0,1,2M N ⋃=-，{}0,1M N ⋂=阴影部分为()(){}1,2M N C M N ⋃⋂=-故选B【点睛】本题考查用韦恩图表示的集合的运算，解题时要能用集合的运算表示出阴影部分． 11．D解析：D【分析】化简集合A 、B ，根据补集与交集的定义写出R A B ，即可得出结论．【详解】集合{|28}{2A x Z x =∈<=，3，4，5，6，7}， 51{||log |1}{|5}5B x R x x R x =∈<=∈<<， 1{|5R B x R x∴=∈或5}x ， {5R A B ∴=，6，7}．∴其中元素个数为3个．故选：D ．【点睛】本题考查了集合的化简与运算问题，是基础题．12．A解析：A【分析】根据数轴判断两集合之间包含关系.【详解】 因为{}1A x x =>，{}1B x x =≥，所以A ⊆B ，选A. 【点睛】本题考查集合之间包含关系，考查基本判断分析能力. 二、填空题13．【分析】由有两个零点可得有两个零点即与的图象有两个交点则函数在定义域内不能是单调函数结合函数图象可求的范围【详解】有两个零点有两个零点即与的图象有两个交点由可得或①当时函数的图象如图所示此时存在满足 解析：()(),01,-∞⋃+∞【分析】由()()g x f x b =-有两个零点可得()f x b =有两个零点，即()y f x =与y b =的图象有两个交点，则函数在定义域内不能是单调函数，结合函数图象可求a 的范围【详解】()()g x f x b =-有两个零点，()f x b ∴=有两个零点，即()y f x =与y b =的图象有两个交点，由32x x =可得，0x =或1x =①当1a >时，函数()f x 的图象如图所示，此时存在b ，满足题意，故1a >满足题意②当1a =时，由于函数()f x 在定义域R 上单调递增，故不符合题意③当01a <<时，函数()f x 单调递增，故不符合题意④0a =时，()f x 单调递增，故不符合题意⑤当0a <时，函数()y f x =的图象如图所示，此时存在b 使得，()y f x =与y b =有两个交点综上可得，0a <或1a >故答案为：()(),01,-∞⋃+∞【点睛】本题考察了函数的零点问题，渗透了转化思想，数形结合、分类讨论的数学思想． 14．【分析】由题意可得有四个不等实根设求得导数和单调性可得极值画出图象即可得到所求范围【详解】函数有四个零点由不为零点即即有有四个不等实根设①当时令在区间上单调递增且使得则函数在区间上单调递减在区间上单 解析：1a e e -<--【分析】 由题意可得1(||)||x x a x e x e -=+有四个不等实根，设1()(||)||x xg x x e x e =+，求得导数和单调性，可得极值，画出图象，即可得到所求范围．【详解】 函数22()1()x x f x x e a x e a R =++∈有四个零点由(0)1f =，0x =不为零点即()0f x =即有1x x a x e x e -=+有四个不等实根 设1()x xg x x e x e =+ ①当0x >时，1()x x g x xe xe =+，()2222(1)11()(1)x x x xx x e x g x x e x e x e +-+'=+-= 令22()1x h x x e =-，222()220x x h x xe x e '=+>()h x ∴在区间(0,)+∞上单调递增，且2(0)10,(1)10h h e =-<=->∴0(0,1)x ∈，使得()0220010x h x x e =-=()0g x '∴<⇒00x x <<，0()0g x x x '>⇒>则函数()g x 在区间()00,x 上单调递减，在区间()0,x +∞上单调递增，且()min 0()2g x g x ==②当0x <时，1()xx g x xe xe =--导数为()2222(1)11()(1)x x x x x x e x g x x e x e x e +-+'=-++= 令22()1x x x e ϕ=-，2()2(1)xx x x e ϕ'=-+ ()010x x ϕ'>⇒-<<，()01x x ϕ'<⇒<-所以函数()x ϕ在区间(),1-∞-上单调递减，在区间(1,0)-上单调递增()min 21()110x eϕϕ=-=->，即22()01x x x e ϕ->=在区间(,0)-∞上成立 即()010g x x '>⇒-<<，()01g x x '<⇒<- 则函数()g x 在区间(),1-∞-上单调递减，在区间(1,0)-上单调递增且1x =-时，()g x 取得极小值1e e -+画出函数()g x 的图象，可得1a e e -->+即1a e e -<--时，1(||)||x xa x e x e -=+有四个不等实根，即函数()f x 有四个零点 故答案为：1a e e -<--【点睛】本题考查函数的零点个数问题解法，注意运用数形结合思想方法和导数判断单调性、极值，考查运算能力，属于中档题．15．8【分析】根据函数平移法则求出点得再结合基本不等式即可求解【详解】由题可知恒过定点又点在直线上故当且仅当时取到等号故的最小值等于8故答案为：8【点睛】本题考查函数平移法则的使用基本不等式中1的妙用属 解析：8【分析】根据函数平移法则求出点A ()2,1--，得21m n +=，再结合基本不等式即可求解【详解】由题可知，()log 31a y x =+-恒过定点()2,1--，又点A 在直线 10mx ny ++=上，故21m n +=，()121242448n m m n m n m n m n⎛⎫+=++=++≥+= ⎪⎝⎭，当且仅当122n m ==时取到等号，故12m n+的最小值等于8 故答案为：8【点睛】 本题考查函数平移法则的使用，基本不等式中“1”的妙用，属于中档题16．②③④【分析】①根据图象的平移规律直接判断选项；②根据指对函数的对称性直接判断；③根据指数函数的图象特点判断选项；④先求的范围再和0比较大小【详解】①根据平移规律可知的图象向右平移1个单位得到的图象解析：②③④【分析】①根据图象的平移规律，直接判断选项；②根据指对函数的对称性，直接判断；③根据指数函数的图象特点，判断选项；④先求22x x -+的范围，再和0比较大小.【详解】①根据平移规律可知xy e =的图象向右平移1个单位得到1x y e -=的图象，所以①不正确；②根据两个函数的对称性可知函数()x f x e =与()g x lnx =的图象关于直线y =x 对称，正确；③如下图，设1a >，122x x f +⎛⎫⎪⎝⎭对应的是曲线上横坐标为122x x +的点C 的纵坐标，()()122f x f x +是线段AB 的中点D 的纵坐标，由图象可知()()121222f x f x x x f ++⎛⎫≤ ⎪⎝⎭，同理，当01a <<时，结论一样，故③正确；④2217721244x x x ⎛⎫-+=-+≥> ⎪⎝⎭ 根据函数的单调性可知()222log 2log 10x x -+>=，所以函数()22log (2)f x x x =-+的图象恒在x 轴上方，故④正确.故答案为：②③④【点睛】思路点睛：1.图象平移规律是“左＋右－”，相对于自变量x 来说，2.本题不易判断的就是③，首先理解122x x f +⎛⎫ ⎪⎝⎭和()()122f x f x +的意义，再结合图象判断正误. 17．【分析】利用换元法将函数换元构造出新函数由新函数的定义域结合二次函数的性质求出最值即可得到值域【详解】设则所以原函数可化为：由二次函数性质当时函数取最大值2由性质可知函数无最小值所以值域为：故答案为 解析：(],2-∞【分析】利用换元法将函数换元构造出新函数，由新函数的定义域结合二次函数的性质求出最值即可得到值域.【详解】 设)10t x t =-≥，则21x t =-，所以原函数可化为：()2210y t t t =-++≥， 由二次函数性质，当1t =时，函数取最大值2，由性质可知函数无最小值，所以值域为：(],2-∞.故答案为：(],2-∞.【点睛】本题考查换元法求函数值域，当函数解析式中含有根式时，一般考虑换元法，用换元法时要注意一定写出新变量数的取值范围.18．【分析】依题意分析的值域A 包含于的值域B 再对分类讨论得到的值域列关系计算即可【详解】因为总使得成立所以的值域A 包含于的值域B 依题意A=又函数因此当时不满足题意；当时在上递增则故即得；当时在上递减则故 解析：55,,22⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭ 【分析】依题意分析()f x 的值域A 包含于()g x 的值域B ，再对a 分类讨论得到()g x 的值域，列关系计算即可.【详解】因为[]12,2x ∀∈-，总[]02,2x ∃∈-，使得()()01g x f x =成立，所以()f x 的值域A 包含于()g x 的值域B ，依题意A =[]0,4，又函数()1=-g x ax ，2,2x ，因此，当0a =时，{}1B =-，不满足题意；当0a >时，()g x 在[]2,2-上递增，则[][]21,210,4B a a =---⊇，故210214a a --≤⎧⎨-≥⎩，即得52a ≥； 当0a <时，()g x 在[]2,2-上递减，则[][]21,210,4B a a =---⊇，故210214a a -≤⎧⎨--≥⎩，即得52a ≤-. 综上，实数a 的取值范围为55,,22⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭. 故答案为：55,,22⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭. 【点睛】本题考查了恒成立问题、函数的值域，以及利用包含关系求参数范围问题，属于中档题. 19．【分析】由题意知关于的方程无实数解可得出由此可解出实数的取值范围【详解】由题意知关于的方程无实数解当时原方程为解得不合乎题意；当时则有解得综上所述实数的取值范围是故答案为：【点睛】本题考查利用集合的 解析：()1,+∞【分析】由题意知，关于x 的方程2210ax x ++=无实数解，可得出00a ≠⎧⎨∆<⎩，由此可解出实数a 的取值范围.【详解】由题意知，关于x 的方程2210ax x ++=无实数解.当0a =时，原方程为210x +=，解得12x =-，不合乎题意；当0a ≠时，则有440a ∆=-<，解得1a >.综上所述，实数a 的取值范围是()1,+∞.故答案为：()1,+∞.【点睛】本题考查利用集合的子集个数求参数，将问题转化为方程无实解是解题的关键，考查分类讨论思想的应用，属于中等题.20．【分析】先求得不等式的解集根据不等式的解集中的整数有且仅有得出不等式组即可求解得到答案【详解】由题意不等式即解得要使得不等式的解集中的整数有且仅有则满足解得即实数的取值范围是故答案为【点睛】本题主要 解析：[]16,17【分析】 先求得不等式34x b -<的解集4433b b x -++<<，根据不等式34x b -<的解集中的整数有且仅有5,6，得出不等式组44534673b b -+⎧≤<⎪⎪⎨+⎪<≤⎪⎩，即可求解，得到答案. 【详解】 由题意，不等式34x b -<，即434x b -<-<，解得4433b b x -++<<， 要使得不等式34x b -<的解集中的整数有且仅有5,6， 则满足44534673b b -+⎧≤<⎪⎪⎨+⎪<≤⎪⎩，解得1617b ≤≤，即实数b 的取值范围是[]16,17. 故答案为[]16,17.【点睛】本题主要考查了绝对值不等式的求解，以及集合的应用，其中解答中正确求解绝对值不等式，根据题设条件得到不等式组是解答的关键，着重考查了分析问题和解答问题的能力，属于中档试题.三、解答题21．（1）函数()f x 的单调减区间为(],1-∞-，增区间()1,-+∞；（2）1a ≤且0a ≠．【分析】（1）当1a =-时，(2),1()(1),1x x x f x x x +≥-⎧=⎨--<-⎩，进而可得函数的单调区间；（2）令()0f x =，分别解出x ，由方程()0f x =仅有一个实数根，列出不等式解出实数a 的取值范围．【详解】（1）当1a =-时，(2),1()(1),1x x x f x x x +≥-⎧=⎨--<-⎩， 则函数()f x 的单调减区间为(],1-∞-，增区间()1,-+∞；（2）令()0f x =，当x a ≥时，解得0x =或2x a =；当x a <时，解得1x =；方程()0f x =仅有一个实数根，则021a a a a ≤⎧⎪<⎨⎪≤⎩或021a a a a >⎧⎪≥⎨⎪≤⎩或021a a a a >⎧⎪<⎨⎪>⎩，解得1a ≤且0a ≠．【点睛】方法点睛：本题考查分段函数的单调性，考查函数与方程思想，关于分段函数的理解，需要有：分段函数是指自变量在两个或两个以上不同的范围，有不同的对应法则的函数； 分段函数是一个函数;分段函数的定义域是各段函数定义域的并集，值域也是各段函数值域的并集．22．（1）210600280,050()100009170,50x x x W x x x x ⎧-+-<<⎪=⎨⎛⎫-++≥ ⎪⎪⎝⎭⎩；（2）2020年产量为100(千部)时，企业所获利润最大最大利润是8970万元.【分析】（1）分050x <<与50x ≥写出分段函数的解析式即可；（2）分两段分别求函数的最大值，比较两个值的大小，即可求出函数的最大值.【详解】（1）当050x <<时，()22()8001020028010600280W x x x x x x =-+-=-+- 当50x ≥时，1000010000()80080194502809170W x x x x x x ⎛⎫⎛⎫=-+--=-++ ⎪ ⎪⎝⎭⎝⎭ 210600280,050()100009170,50x x x W x x x x ⎧-+-<<⎪∴=⎨⎛⎫-++≥ ⎪⎪⎝⎭⎩ （2）若050x <<，2()10(30)8720W x x =--+，当30x =时，max ()8720W x =万元若50x ≥，10000()917091708970W x x x ⎛⎫=-++≤-= ⎪⎝⎭， 当且仅当10000x x=时，即100x =时，max ()8970W x =万元.因为89708720>.所以2020年产量为100(千部)时，企业所获利润最大，最大利润是8970万元.答（1）210600280,050()100009170,50x x x W x x x x ⎧-+-<<⎪=⎨⎛⎫-++≥ ⎪⎪⎝⎭⎩ （2）2020年产量为100(千部)时，企业所获利润最大最大利润是8970万元.【点睛】关键点点睛：在实际问题中分类讨论求出函数的解析式，求最大值时，要分别求自变量在不同区域的最值，然后比较大小，得出函数的最值.23．（1）值域为3,2⎛⎫+∞⎪⎝⎭，不是“有上界函数”；理由见解析；（2）(,2]-∞ 【分析】（1）把12a =-代入函数的表达式，令13x t ⎛⎫= ⎪⎝⎭，可得1t >，可求出2112y t t =-+的值域，即为()f x 在(,0)-∞的值域，结合“有上界函数”的定义进行判断即可；（2）由题意知，()4f x ≤对[0,)x ∈+∞恒成立，令13xt ⎛⎫= ⎪⎝⎭，可得(0,1]t ∈，整理得3a t t ⎛⎫≤- ⎪⎝⎭对(0,1]t ∈恒成立，只需min 3a t t ⎛⎫≤- ⎪⎝⎭即可. 【详解】 （1）当12a =-时，111()1239x x f x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭， 令13x t ⎛⎫= ⎪⎝⎭，0x <，1t ∴>，2112y t t =-+， 2112y t t =-+在(1,)+∞上单调递增，111232y -∴>+=， 即()f x 在(,0)-∞的值域为3,2⎛⎫+∞ ⎪⎝⎭， 故不存在常数0M >，使()f x M ≤成立．∴函数()f x 在(,0)-∞上不是“有上界函数”（2）由题意知，()4f x ≤对[0,)x ∈+∞恒成立，令13x t ⎛⎫= ⎪⎝⎭，0x ≥，(0,1]t ∴∈， 214at t ∴++≤对(0,1]t ∈恒成立，即3a t t ⎛⎫≤-⎪⎝⎭对(0,1]t ∈恒成立，设3()g t t t=-，易知()g t 在(0,1]t ∈上递减， ()g t ∴在(0,1]t ∈上的最小值为(1)2g =． ∴min ()2a g t ≤=，∴实数a 的取值范围为(,2]-∞【点睛】本题考查新定义，考查函数的值域与最值，考查学生的推理能力与计算求解能力，属于中档题.24．（1）2()log f x x =（2）偶函数.见解析【分析】（1）根据(4)(2)1f f -=，代入到函数的解析式中可求得2a =，可求得函数()f x 的解析式; （2）由函数()f x 的解析式，求得函数()g x 的解析式，先求得函数()g x 的定义域，再由函数的奇偶性的判断方法证得函数的奇偶性.【详解】（1）因为()log (0,1)a f x x a a =>≠，且(4)(2)1f f -=，所以log 4log 21a a -=，即log 21a =.，解得2a =，所以2()log f x x =;（2）因为()log a f x x =，所以22()log (2)log (2)g x x x =++-,由2020x x +>⎧⎨->⎩,得22x -<<,所以()g x 的定义域为()22-，， 又因为22()log (2)log (2)()g x x x g x -=-++=，所以22()log (2)log (2)g x x x =++-为偶函数.【点睛】本题考查对数函数的函数解析式的求解，函数的奇偶性的证明，属于基础题.25．（1）在区间(,-∞的单调递增，在区间()的单调递减；（2）2,3⎡⎫-+∞⎪⎢⎣⎭． 【分析】（1）利用对勾函数的性质，直接写出结论即可；（2）利用不等式恒成立的关系，把问题从()5f x ≥恒成立，转化为对于任意的x N *∈，21351x ax x ++≥+恒成立，利用参变分离的方法，等价于()85a x x x *⎛⎫≥-+∈ ⎪⎝⎭N ，然后，根据对勾函数的性质进行求解即可 【详解】解：（1）因为函数k y x x =+()0k >在(单调递减，在)+∞单调递增，所以，当2k =时函数2y x x =+在(单调递减，在)+∞单调递增． 易知函数2y x x =+为奇函数，所以函数y x x =+在区间(,-∞的单调递增；在区间()的单调递减．（2）由题意，对任意的x N *∈，有()5f x ≥恒成立， 即对于任意的x N *∈，21351x ax x ++≥+恒成立， 等价于()85a x x x *⎛⎫≥-+∈ ⎪⎝⎭N ． 设()()8g x x x x*=+∈N ，易知，当且仅当8x x=，即x =()g x 取得最小值，由题设知，函数()g x 在(0,上单调递减，在()+∞上单调递增． 又因为x N *∈，且()26g =，()1733g =，而()()23g g >， 所以当3x =时，()min 173g x =． 所以81725533x x ⎛⎫-+≤-=- ⎪⎝⎭，即23a ≥-， 故所求实数a 的取值范围是2,3⎡⎫-+∞⎪⎢⎣⎭．【点睛】 关键点睛：解题的关键在于，利用参变分离法，把问题转化为证明()85a x x x *⎛⎫≥-+∈ ⎪⎝⎭N 恒成立，进而利用对勾函数性质求解，属于中档题 26．（1）(,1)(2,)M a a =-∞-⋃++∞，集合N 见解析；（2）[1,2]-.【分析】（1）对两个不等式进行因式分解，分类讨论即可得解；（2）结合（1）的结论进行分类讨论求解.【详解】（1）22(21)(2)0x a x a a -+++->即()()()120x a x a ---+>所以(,1)(2,)M a a =-∞-⋃++∞；223()0x a a x a -++<即()()20x a x a --<当1a >或0a <时，2(,)N a a =；当01a <<时，2(,)N a a =；当1a =或0a =时，N =∅；（2）分类讨论：当1a =或0a =时，N =∅，符合题意；当01a <<时，2(,)N a a =，M N ⋂=∅， 即212a a a a ≥-≤+⎧⎨⎩，2102a a a a -+≥≤+⎧⎨⎩恒成立，所以01a <<符合题意； 当1a >或0a <时，212a a a a ≥-≤+⎧⎨⎩解得：12a -≤≤，所以[)(]1,01,2a ∈-， 综上所述：[1,2]a ∈-【点睛】此题考查求二次不等式的解集，关键在于准确进行因式分解并分类讨论，根据两个集合的交集为空集求参数的取值范围，考查分类讨论思想.。

高中数学复习题集及答案近几年来，高中数学的学习逐渐变得日益重要。

数学不仅是高考的一大重要科目，同时也是培养学生逻辑思维和解决问题能力的关键学科之一。

为了帮助广大高中学生更好地复习数学知识，我们准备了一份高中数学复习题集及答案，希望能为同学们的学习提供一点帮助。

题目一：求解二次方程1. 解方程$x^2+5x+6=0$。

解答：首先，观察方程可知，二次方程的通常形式为$ax^2+bx+c=0$。

将给定方程与通常形式进行比较，可以得到$a=1$，$b=5$，$c=6$。

根据韦达定理可得：\[\Delta = b^2-4ac = 5^2-4\times1\times6 = 1\]因为$\Delta > 0$，所以方程有两个不相等的实根。

根据二次方程的求根公式可得：\[x = \frac{-b\pm\sqrt{\Delta}}{2a} = \frac{-5\pm\sqrt{1}}{2} = -3, -2\]所以方程$x^2+5x+6=0$的解是$x=-3, -2$。

题目二：等差数列求和2. 求等差数列$3, 6, 9, 12, \ldots, 99$的前20项和。

解答：根据题意可知，该等差数列的首项$a=3$，公差$d=6-3=9-6=12-9=\ldots=3$。

为了求出该等差数列的前20项和，我们需要先求出其第20项$A_{20}$。

根据等差数列的通项公式可得：\[A_n = a + (n-1)d\]带入$a=3$和$d=3$可得：\[A_{20} = 3 + (20-1)\times3 = 3 + 19\times3 = 3 + 57 = 60\]所以等差数列的第20项为$A_{20} = 60$。

接下来，利用等差数列的求和公式可得前20项和$S_{20}$：\[S_{20} = \frac{n}{2}(a+A_n) = \frac{20}{2}(3+60) = 10\times63 = 630\]所以等差数列$3, 6, 9, 12, \ldots, 99$的前20项和为630。

高中高三数学下册期末测试试题习题大全平面及其基本性质．平面图形直观图的画法．平行直线．对应边分别平行的角．异面直线所成的角．异面直线的公垂线．异面直线的距离．直线和平面平行的判定与性质．直线和平面垂直的判定与性质．点到平面的距离．斜线在平面上的射影．直线和平面所成的角．三垂线定理及其逆定理．平行平面的判定与性质．平行平面间的距离．二面角及其平面角．两个平面垂直的判定与性质．多面体．正多面体．棱柱．棱锥．球．考试要求（1）掌握平面的基本性质，会用斜二测的画法画水平放置的平面图形的直观图;能够画出空间两条直线、直线和平面的各种位置关系的图形，能够根据图形想像它们的位置关系．（2）掌握两条直线平行与垂直的判定定理和性质定理，掌握两条直线所成的角和距离的概念，对于异面直线的距离，只要求会计算已给出公垂线时的距离．（3）掌握直线和平面平行的判定定理和性质定理；掌握直线和平面垂直的判定定理和性质定理；掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念掌握三垂线定理及其逆定理．（4）掌握两个平面平行的判定定理和性质定理，掌握二面角、二面角的平面角、两个平行平面间的距离的概念，掌握两个平面垂直的判定定理和性质定理．（5）会用反证法证明简单的问题．（6）了解多面体、凸多面体的概念，了解正多面体的概念．（7）了解棱柱的概念，掌握棱柱的性质，会画直棱柱的直观图．（8）了解棱锥的概念，掌握正棱锥的性质，会画正棱锥的直观图．（9）了解球的概念，掌握球的性质，掌握球的表面积、体积公式．（B）．直线、平面、简单几何体考试内容：平面及其基本性质．平面图形直观图的画法．平行直线．直线和平面平行的判定与性质．直线和平面垂直的判定．三垂线定理及其逆定理．两个平面的位置关系．空间向量及其加法、减法与数乘．空间向量的坐标表示．空间向量的数量积．直线的方向向量．异面直线所成的角．异面直线的公垂线．异面直线的距离．直线和平面垂直的性质．平面的法向量．点到平面的距离．直线和平面所成的角．向量在平面内的射影．平行平面的判定和性质．平行平面间的距离．二面角及其平面角．两个平面垂直的判定和性多面体．正多面体．棱柱．棱锥．球．考试要求：（1）掌握平面的基本性质。

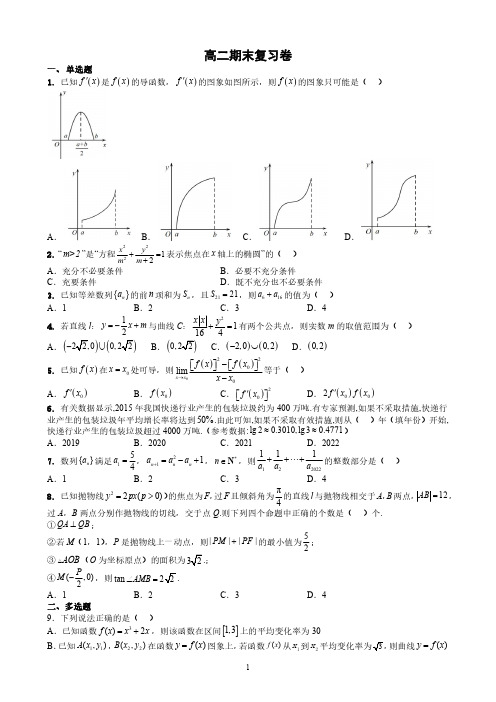
高二期末复习卷一、单选题1.已知()f x '是()f x 的导函数，()f x '的图象如图所示，则()f x 的图象只可能是（）A．B．C．D．2.“m>2”是“方程22212x ym m +=+表示焦点在x 轴上的椭圆”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3.已知等差数列{}n a 的前n 项和为n S ，且2121S =，则616a a +的值为（）A ．1B ．2C ．3D ．44.若直线l ：12y x m =-+与曲线C ：21164x x y +=有两个公共点，则实数m 的取值范围为（）A．()(0,- B．(0,C ．()()2,00,2-⋃D ．()0,25.已知()f x 在0x x =处可导，则()()02200lim x x f x f x x x →-⎡⎤⎡⎤⎣⎦⎣⎦-等于（）A ．()0f x 'B ．()0f x C ．()20f x '⎡⎤⎣⎦D ．()()002f x f x '6.有关数据显示,2015年我国快递行业产生的包装垃圾约为400万吨.有专家预测,如果不采取措施,快递行业产生的包装垃圾年平均增长率将达到50%.由此可知,如果不采取有效措施,则从（）年（填年份）开始,快递行业产生的包装垃圾超过4000万吨.（参考数据:lg 20.3010,lg 30.4771≈≈）A ．2019B ．2020C ．2021D ．20227.数列{}n a 满足154a =，211n n n a a a +=-+，*n ∈N ，则122022111a a a +++ 的整数部分是（）A ．1B ．2C ．3D ．48.已知抛物线22(0)y px p =>）的焦点为F ，过F 且倾斜角为π4的直线l 与抛物线相交于A ，B 两点，12AB =，过A ，B 两点分别作抛物线的切线，交于点Q .则下列四个命题中正确的个数是（）个.①QA QB ⊥；②若M （1，1），P 是抛物线上一动点，则||||PM PF +的最小值为52；③AOB （O为坐标原点）的面积为；④(,0)2PM -，则tan AMB ∠=A ．1B ．2C ．3D ．4二、多选题9．下列说法正确的是（）A ．已知函数3()2f x x x =+，则该函数在区间[]1,3上的平均变化率为30B ．已知11(,)A x y ，22(,)B x y 在函数()y f x =图象上，若函数()f x 从1x 到2x则曲线()y f x =的割线AB 的倾斜角为3πC ．已知直线运动的汽车速度V 与时间t 的关系是221V t =-，则2t =时瞬时加速度为7D ．已知函数()f x x =，则(9.05) 3.008f ≈10．在底面边长为2、高为4的正四棱柱1111ABCD A B C D -中，O 为棱1A A 上一点，且111,4A O A A P Q =､分别为线段1111B D A D ､上的动点，M 为底面ABCD 的中心，N 为线段AQ 的中点，则下列命题正确的是（）A ．CN 与QM 共面B ．三棱锥A DMN -的体积为43C ．PQ QO +的最小值为322D ．当11113D Q D A = 时，过,,A Q M 三点的平面截正四棱柱所得截面的周长为()82103+11．数列{}n a 满足1a a =，2131n n n a a a +=--，则下列说法正确的是（）A ．若1a ≠且2a ≠，数列{}n a 单调递减B ．若存在无数个自然数n ，使得1n n a a +=，则1a =C ．当2a >或1a <时，{}n a 的最小值不存在D ．当3a =时，121111,12222n a a a ⎛⎤++⋅⋅⋅⋅⋅⋅+∈ ⎥---⎝⎦12．设F 是抛物线2:4C y x =的焦点，直线:1l x ty =+与抛物线C 交于,A B 两点，O 为坐标原点，则下列结论正确的是（）A ．||4AB ≥B ．OA OB ⋅可能大于0C ．P 为抛物线上异于A 、B 的点，直线l 与准线交于点T ，当0,t A >为第一象限的点时，若APB α∠=，PF 平分APB ∠，则π2APT +∠=αD ．若在抛物线上存在唯一一点Q (异于,)A B ，使得QA QB ⊥则3t =±三、填空题13．若()f x 为可导函数，且()()0121lim 14x f x f x→--=-，则过曲线()y f x =上点()()1,1f 处的切线斜率为______．14．对于数列{}n a ，若1,n n a a +是关于x 的方程2103n n x c x -+=的两个根，且12a =，则数列{}n c 所有项的和为________．15．法国数学家加斯帕•蒙日被称为“画法几何创始人”、“微分几何之父”.他发现与椭圆相切的两条互相垂直的切线的交点的轨迹是以该椭圆中心为圆心的圆，这个圆称为该椭圆的蒙日圆.若椭圆()2222:10x y a b a bΓ+=>>的蒙日圆为2223:2C x y a +=，过C 上的动点M 作Γ的两条切线，分别与C 交于P ，Q 两点，直线PQ 交Γ于A ，B 两点，则下列说法，正确的有______.①椭圆Γ的离心率为22②MPQ 面积的最大值为232a③M 到Γ的左焦点的距离的最小值为()22a-④若动点D 在Γ上，将直线DA ，DB 的斜率分别记为1k ，2k ，则1212k k =-16．已知数列{}n a 的通项公式为4152nn n a +⎛⎫=-⋅ ⎪⎝⎭，设数列{}n a 的最大项和最小项分别为,M N ，则M N +=______.四、解答题17．已知椭圆()2222:10x y C a b a b+=>>的四个顶点构成的四边形的面积为12．(1)求椭圆C 的标准方程；(2)过椭圆C 右焦点且倾斜角为135︒的直线l 交椭圆C 于M 、N 两点，求MN 的值．18．已知双曲线2222:1(0,0)x y C a b a b -=>>，四点12346,,4,,4,333M M M M ⎛⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭中恰有三点在C 上．(1)求C 的方程；(2)过点(3,0)的直线l 交C 于P ，Q 两点，过点P 作直线1x =的垂线，垂足为A ．证明：直线AQ 过定点．19．如图1，在等腰直角三角形ABC 中，4AC BC ==，D 是AC 的中点，E 是AB 上一点，且DE AB ⊥.将ADE V 沿着DE 折起，形成四棱锥-P BCDE ，其中点A 对应的点为点P ，如图2.(1)在图2中，在线段PB 上是否存在一点F ，使得CF ∥平面PDE ？若存在，请求出PFPB的值，并说明理由；若不存在，请说明理由；(2)在图2中，平面PBE 与平面PCD 所成的锐二面角的大小为3π，求四棱锥-P BCDE 的体积.20．在①11a =，525S =；②35a =，917a =；③416S =，864S =这三个条件中任选一个补充在下面的横线上并解答.已知等差数列{}n a 满足________.(1)求数列{}n a 的通项公式；(2)求数列{3}n n a ⋅的前n 项和.n T (如果选择多个条件分别解答，按第一个解答计分)21．在一个有穷数列的每相邻两项之间插入这两项的和，形成新的数列，我们把这样的操作称为该数列的一次“Z 拓展”．如数列1，2第1次“Z 拓展”后得到数列1，3，2，第2次“Z 拓展”后得到数列1，4，3，5，2．设数列a 、b 、c 经过第n 次“Z 拓展”后所得数列的项数记为n P ，所有项的和记为n S ．(1)求1P 、2P ；(2)若2023n P ≥，求n 的最小值；(3)是否存在实数a 、b 、c ，使得数列{}n S 为等比数列？若存在，求a 、b 、c 满足的条件；若不存在，说明理由．21．记数列{}n a 的前n 项和为111,2,34n n n n S a S S a ++=+=-.(1)求{}n a 的通项公式；(2)设2log n n n b a a =，记{}n b 的前n 项和为n T .若2(1)2n t n T -+≤对于2n ≥且*N n ∈恒成立，求实数t 的取值范围.22．已知抛物线的顶点为原点，焦点F 在x轴的正半轴，F 到直线20x +=的距离为54.点()2,2N ，不过点N 的直线l 与抛物线交于两点,A B ，且2NA NB k k +=-.(1)求抛物线方程及抛物线的准线方程(2)求证：直线AB 过定点，并求该定点坐标.高二期末复习卷(答案)一、单选题1.已知()f x '是()f x 的导函数，()f x '的图象如图所示，则()f x 的图象只可能是（）2.“m>2”是“方程22212x y m m +=+表示焦点在x 轴上的椭圆”的（）A ．充分不必要条件B ．必要不充分条件3.已知等差数列{}n a 的前n 项和为n S ，且2121S =，则616a a +的值为（）A ．1B ．2C ．3D ．4【答案】B【分析】根据等差数列前n 项和公式以及等差数列的性质，可得2121S =与616a a +的关系式，即可求得结果.4.若直线l ：12y x m =-+与曲线C ：21164x x y +=有两个公共点，则实数m 的取值范围为（）A ．()(0,-B ．(0,2,00,2-⋃0,2如图可知，当直线l 介于直线12y x =-和与曲线C 有两个公共点．设1l 的方程为012y x m =-+，()00m >，则有联立220116412x yy x m⎧+=⎪⎪⎨⎪=-+⎪⎩，消去x 并整理得2y 由()2200Δ4840m m =--=，解得022m =故m 的取值范围为()0,22．故选：B ．5.已知()f x 在0x x =处可导，则()()02200lim x x f x f x x x →-⎡⎤⎡⎤⎣⎦⎣⎦-等于（）A ．()0f x 'B ．()0f x C ．()20f x '⎡⎤⎣⎦D ．()()002f x f x '业产生的包装垃圾年平均增长率将达到50%.由此可知,如果不采取有效措施,则从（）年（填年份）开始,快递行业产生的包装垃圾超过4000万吨.（参考数据:lg 20.3010,lg 30.4771≈≈）7.数列{}n a 满足154a =，211n n n a a a +=-+，*n ∈N ，则122022111a a a +++ 的整数部分是（）8.已知抛物线22(0)y px p =>）的焦点为F ，过F 且倾斜角为π4的直线l 与抛物线相交于A ，B 两点，12AB =，过A ，B 两点分别作抛物线的切线，交于点Q .则下列四个命题中正确的个数是（）个.①QA QB ⊥；②若M （1，1），P 是抛物线上一动点，则||||PM PF +的最小值为52；③AOB （O 为坐标原点）的面积为；④(,0)2PM -，则tan AMB ∠=二、多选题9．下列说法正确的是（）A ．已知函数3()2f x x x =+，则该函数在区间[]1,3上的平均变化率为30B ．已知11(,)A x y ，22(,)B x y 在函数()y f x =图象上，若函数()f x 从1x 到2x 则曲线()y f x =的割线AB 的倾斜角为3πC V 与时间t 的关系是221V t =-，则2t =时瞬时加速度为7D ．已知函数()f x =，则(9.05) 3.008f ≈【答案】BD10．在底面边长为2、高为4的正四棱柱1111ABCD A B C D -中，O 为棱1A A 上一点，且11,4A O A A P Q =､分别为线段1111B D A D ､上的动点，M 为底面ABCD 的中心，N 为线段AQ 的中点，则下列命题正确的是（）A ．CN 与QM 共面B ．三棱锥A DMN -的体积为43C ．PQ QO +的最小值为2D ．当11113D Q D A = 时，过,,A Q M 三点的平面截正四棱柱所得截面的周长为83对于C ，如图2，展开平面点P ，交11A D 与点Q ，则此时对于D ，如图3，取11113D H D C =uuuu r uuuu r共面，即过,,A Q M 三点的正四棱柱的截面为梯形，且12233QH AC ==，所以平面截正四棱柱所得截面的周长为故选:ACD.11．数列{}n a 满足1a a =，1n n n +=--，则下列说法正确的是（）A ．若1a ≠且2a ≠，数列{}n a 单调递减B ．若存在无数个自然数n ，使得1n n a a +=，则1a =C ．当2a >或1a <时，{}n a 的最小值不存在D ．当3a =时，121111,12222n a a a ⎛⎤++⋅⋅⋅⋅⋅⋅+∈ ⎥---⎝⎦【答案】ACD【分析】A 选项，根据()2110n n n a a a +=--<-求出1n a ≠，再由21311n n n a a a +=--≠求出2n a ≠，从而得到1a ≠且2a ≠，数列{}n a 单调递减，A 正确；B 选项，可举出反例；与抛物线C 交于两点，O 为坐标原点，则下列结论正确的是（）A ．||4AB ≥B ．OA OB ⋅可能大于0C ．P 为抛物线上异于A 、B 的点，直线l 与准线交于点T ，当0,t A >为第一象限的点时，若APB α∠=，PF 平分APB ∠，则π2APT +∠=α对于D 选项，因QA QB ⊥，则Q 为以因()()1122,,A x y B x y ，，1222y y t +=，212212x xt +=+，2AB 则以AB 为直径的圆的方程为(22x t -将其与2:4C y x =联立，消去x 化简得：注意到()4228166448y t y ty +---4y =()()2244412yty yty =--++，由题可得，联立方程有2440y ty --=，其判别式恒大于0，则24120y ty ++=的判别式216t -故选：ACD【点睛】关键点点睛：本题为直线与抛物线综合题为常用手段；对于C 选项，在抛物线中有很多的等量关系与成比例的关系分解因式处理.三、填空题13．若()f x 为可导函数，且()()121lim14x f x f x→--=-，则过曲线()y f x =上点()()1,1f 处的切线斜率为14．对于数列n a ，若1,n n a a +是关于x 的方程203n n x c x -+=的两个根，且12a =，则数列{}n c 所有项的和为________．【答案】92##4.5种情况进行分类讨论，利用分组和法来求得n T ，进而可利用极限求得“数列所有项的和”.15．法国数学家加斯帕•蒙日被称为“画法几何创始人”、“微分几何之父”.他发现与椭圆相切的两条互相垂直的切线的交点的轨迹是以该椭圆中心为圆心的圆，这个圆称为该椭圆的蒙日圆.若椭圆()2222:10x y a b a bΓ+=>>的蒙日圆为2223:2C x y a +=，过C 上的动点M 作Γ的两条切线，分别与C 交于P ，Q 两点，直线PQ 交Γ于A ，B 两点，则下列说法，正确的有______.①椭圆Γ②MPQ 面积的最大值为232a③M到Γ的左焦点的距离的最小值为(2a④若动点D 在Γ上，将直线DA ，DB 的斜率分别记为1k ，2k ，则1212k k =-16．已知数列{}n a 的通项公式为52n n a +⎛⎫=-⋅ ⎪⎝⎭，设数列{}n a 的最大项和最小项分别为,M N ，则四、解答题17．已知椭圆()2222:10x y C a b a b+=>>的四个顶点构成的四边形的面积为12．18．已知双曲线2222:1(0,0)x yC a ba b-=>>，四点12346,,4,,3M M M M⎛⎛⎛-⎝⎭⎝⎭⎝⎭中恰有三点在C上．(1)求C的方程；将ADEV沿着DE折起，形成四棱锥-P BCDE，其中点A对应的点为点P，如图2.(1)在图2中，在线段PB 上是否存在一点F ，使得CF ∥平面PDE ？若存在，请求出PFPB的值，并说明理由；若不存在，请说明理由；(2)在图2中，平面PBE 与平面PCD 所成的锐二面角的大小为3π，求四棱锥-P BCDE 的体积.3PB 理由如下：过点C 作CH ED ⊥，垂足为H ，在PE 上取一点M ，使得13PM PE =，连接因为13PM PE =，13PF PB =，所以FM 建立空间直角坐标系，设PEB θ∠=，则()2,0,0D -，()22,2,0C -，(P 则()2,2,0DC =- ，(2,2cos DP = 设平面PCD 的法向量为(),,m x y z =，则220,22cos 2sin m DC x y m DP x y θθ⎧⋅=-+=⎪⎨⋅=+⋅+⎪⎩取sin x θ=，则sin y θ=，cos z θ=-所以()sin ,sin ,cos 1m θθθ=--，，948153线上并解答.已知等差数列{}n a满足________.(1)求数列{}n a的通项公式；(2)求数列{3}na⋅的前n项和.n Tn一次“Z拓展”．如数列1，2第1次“Z拓展”后得到数列1，3，2，第2次“Z拓展”后得到数列1，4，3，5，2．设数列a、b、c经过第n次“Z拓展”后所得数列的项数记为n P，所有项的和记为n S．(1)求1P 、2P ；(2)若2023n P ≥，求n 的最小值；(3)是否存在实数a 、b 、c ，使得数列{}n S 为等比数列？若存在，求a 、b 、c 满足的条件；若不存在，说明n 项和为111n n n n ++(1)求{}n a 的通项公式；(2)设2log n n n b a a =，记{}n b 的前n 项和为n T .若2(1)2n t n T -+≤对于2n ≥且*N n ∈恒成立，求实数t 的取值范围.【答案】(1)2nn a =(2)8t ≤【分析】（1）利用n a 与n S 的关系证得数列{}n a 是等比数列，从而求得2n n a =；22．已知抛物线的顶点为原点，焦点F 在x 轴的正半轴，F 到直线20x +=的距离为4.点2,2N ，不过点N 的直线l 与抛物线交于两点,A B ，且2NA NB k k +=-.(1)求抛物线方程及抛物线的准线方程。

【压轴题】⾼中必修⼆数学下期末试题（含答案）【压轴题】⾼中必修⼆数学下期末试题(含答案)⼀、选择题1．△ABC 的内⾓A 、B 、C 的对边分别为a 、b 、c.已知5a =，2c =，2cos 3A =，则b= A ．2B ．3C ．2D ．32．设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S = A ．5B ．7C ．9D ．113．已知集合{}{}2|320,,|05,A x x x x R B x x x N =-+=∈=<<∈，则满⾜条件A CB ??的集合C 的个数为（）A ．1B ．2C ．3D ．44．已知集合{}22(,)1A x y x y =+=，{}(,)B x y y x ==，则A B I 中元素的个数为（） A ．3B ．2C ．1D ．05．某三棱锥的三视图如图所⽰，则该三棱锥的体积为（）A ．20B ．10C ．30D ．606．设正项等差数列的前n 项和为，若，则的最⼩值为 A ．1 B ．C ．D ．7．已知1sin 34πα??-= ，则cos 23πα??+= （）A ．58-B ．58C ．78-D ．788．已知函数21(1)()2(1)a x x f x x x x x ?++>?=?-+≤在R 上单调递增，则实数a 的取值范围是 A ．[]0,1B ．(]0,1C ．[]1,1-D ．(]1,1-9．函数()lg ||f x x x =的图象可能是（）A ．B ．C ．D ．10．已知0.6log 0.5a =，ln0.5b =，0.50.6c =，则（） A ．a c b >> B ．a b c >>C ．c a b >>D ．c b a >>11．设n S 为等差数列{}n a 的前n 项和，若3243S S S =+，12a =，则5a = A ．12-B ．10-C ．10D ．1212．如图，在△ABC 中, 13AN NC =u u u v u u u v ,P 是BN 上的⼀点,若29AP m AB AC ??→??→??→=+,则实数m 的值为( )A ．B ．C ．19D ．⼆、填空题13．在ABC △中，若223a b bc -= ，sin 23sin C B = ，则A 等于__________． 14．已知函数()3sin(2)cos(2)(||)2 f x x x π=---<的图象关于y 轴对称,则()f x 在区[6π-,5]12π上的最⼤值为__. 15．已知ABC V ，135B o∠=，22,4AB BC ==，求AB AC ?=u u u r u u u r______．16．函数()12x f x =-的定义域是__________． 17．如图，在矩形中，为边的中点，1AB =，2BC =，分别以A 、D 为圆⼼，1为半径作圆弧EB 、EC （在线段AD 上）.由两圆弧EB 、EC 及边所围成的平⾯图形绕直线旋转⼀周，则所形成的⼏何体的体积为 .18．若圆x 2＋y 2＝4和圆x 2＋y 2＋4x －4y ＋4＝0关于直线l 对称，则直线l 的⽅程为____________．19．若()1,x ∈+∞，则131y x x =+-的最⼩值是_____． 20．在△ABC 中，85a b ==，，⾯积为12，则cos 2C =______．三、解答题21．设ABC ?的内⾓A 、B 、C 所对的边分别为a 、b 、c ，且4cos ,25B b ==. （1）当π6A =时，求a 的值；（2）当ABC ?的⾯积为3时，求a+c 的值． 22．已知x ，y ，()0,z ∈+∞，3x y z ++=．（1）求111x y z++的最⼩值（2）证明：2223x y z ≤++．23．已知数列{}n a 是等⽐数列，24a =，32a +是2a 和4a 的等差中项. （1）求数列{}n a 的通项公式；（2）设22log 1n n b a =-，求数列{}n n a b 的前n 项和n T . 24．已知数列{}n a 满⾜11a =，()121n n na n a +=+，设nn a b n=．（1）求123b b b ，，；（2）判断数列{}n b 是否为等⽐数列，并说明理由；（3）求{}n a 的通项公式．25．以原点为圆⼼，半径为r 的圆O 222:()0O x y r r +=>与直线380x --=相切. （1）直线l 过点(6)-且l 截圆O 所得弦长为43l l 的⽅程；（2）设圆O 与x 轴的正半轴的交点为M ，过点M 作两条斜率分别为12,k k 12,k k 的直线交圆O 于,A B 两点，且123k k ?=-，证明：直线AB 恒过⼀个定点，并求出该定点坐标.26．如图，平⾏四边形ABCD 中，E ，F 分别是BC ，DC 的中点，G 为BF 与DE 的交点，若AB a =u u u v v ,AD b =u u u v v ，试以a v ，b v 为基底表⽰DE u u u v 、BF u u uv 、CG u u u v ．【参考答案】***试卷处理标记，请不要删除⼀、选择题 1．D 解析：D 【解析】【分析】【详解】由余弦定理得，解得（舍去），故选D.【考点】余弦定理【名师点睛】本题属于基础题,考查内容单⼀,根据余弦定理整理出关于b 的⼀元⼆次⽅程,再通过解⽅程求b.运算失误是基础题失分的主要原因,请考⽣切记！2．A解析：A【解析】1353333,1a a a a a ++===，5153355()25522S a a a a =+=?==，选A. 3．D解析：D 【解析】【分析】【详解】求解⼀元⼆次⽅程，得{}()(){}2|320,|120,A x x x x x x x x =-+=∈=--=∈R R {}1,2=，易知{}{}|05,1,2,3,4B x x x =<<∈=N .因为A C B ??，所以根据⼦集的定义，集合C 必须含有元素1,2，且可能含有元素3,4，原题即求集合{}3,4的⼦集个数，即有224=个，故选D. 【点评】本题考查⼦集的概念，不等式，解⼀元⼆次⽅程.本题在求集合个数时，也可采⽤列举法.列出集合C 的所有可能情况，再数个数即可.来年要注意集合的交集运算，考查频度极⾼.4．B解析：B 【解析】试题分析：集合中的元素为点集，由题意，可知集合A 表⽰以()0,0为圆⼼，1为半径的单位圆上所有点组成的集合，集合B 表⽰直线y x =上所有的点组成的集合，⼜圆221x y +=与直线y x =相交于两点,22? ??，22??-- ? ???，则A B I 中有2个元素.故选B.【名师点睛】求集合的基本运算时，要认清集合元素的属性(是点集、数集或其他情形)和化简集合，这是正确求解集合运算的两个先决条件.集合中元素的三个特性中的互异性对解题影响较⼤，特别是含有字母的集合，在求出字母的值后，要注意检验集合中的元素是否满⾜互异性.5．B解析：B 【解析】【分析】根据三视图还原⼏何体，根据棱锥体积公式可求得结果. 【详解】由三视图可得⼏何体直观图如下图所⽰：可知三棱锥⾼：4h =；底⾯⾯积：1155322S == ∴三棱锥体积：1115410332V Sh ==??=本题正确选项：B 【点睛】本题考查棱锥体积的求解，关键是能够通过三视图还原⼏何体，从⽽准确求解出三棱锥的⾼和底⾯⾯积. 6．D解析：D 【解析】【分析】先利⽤等差数列的求和公式得出，再利⽤等差数列的基本性质得出，再将代数式和相乘，展开后利⽤基本不等式可求出的最⼩值.【详解】由等差数列的前项和公式可得，所以，，由等差数列的基本性质可得，，所以，，当且仅当，即当时，等号成⽴，因此，的最⼩值为，故选：D.【点睛】本题考查的等差数列求和公式以及等差数列下标性质的应⽤，考查利⽤基本不等式求最值，解题时要充分利⽤定值条件，并对所求代数式进⾏配凑，考查计算能⼒，属于中等题。

高中数学总复习练习题专题47 任意角和弧度制一、选择题1．（2019·广西高一期末（文））150o 化成弧度制为（ ） A.56πB.4π C.23π D.3π 【答案】A【解析】由题意可得51501501806ππ=⨯=o，故选：A. 2．把85π-化为角度是（ ） A.96-o B.144-oC.288-oD.576-o【答案】C【解析】由题意，根据角度制和弧度制的互化，可得8818028855π-=-⨯=-o o . 故选：C.3．下列角的终边与37o 角的终边在同一直线上的是（ ） A.37-o B.143oC.379oD.143-o【答案】D【解析】与37o 角的终边在同一直线上的角可表示为37180k +⋅o o ，k Z ∈，当1k =-时，37180143-=-o o o ，所以，143-o 角的终边与37o 角的终边在同一直线上. 故选：D ．4．与468-o 角的终边相同的角的集合是（ ）A.{}360456,k k Z αα=⋅+∈ooB.{}360252,k k Z αα=⋅+∈ooC.{}36096,k k Z αα=⋅+∈ooD.{}360252,k k Z αα=⋅-∈oo【答案】B【解析】因为4682360252-=-⨯+o o o ，所以252o 角与468-o 角的终边相同，所以与468-o 角的终边相同的角的集合为{}360252,k k Z αα=⋅+∈o o. 故选：B ．5．如果角α的终边上有一点()0,3P -，那么α（ ）A.是第三象限角B.是第四象限角C.是第三或第四象限角D.不是象限角【答案】D【解析】因为点P 在y 轴的负半轴上，即角α的终边落在y 轴的非正半轴上，所以α不是象限角． 故选：D.6．已知角α的终边落在x 轴的非负半轴上，则角2α的终边落在（ ） A.x 轴的非负半轴上 B.x 轴上 C.y 轴的非负半轴上 D.y 轴上【答案】B【解析】由题意，知()360k k Z α=⋅∈o，则()1802k k Z α=⋅∈o .当k 为偶数时，设()2k n n Z =∈，则3602n α=⋅o ，此时，角2α的终边在x 轴的非负半轴上； 当k 为奇函数时，设()21k n n Z =+∈，则()()211801803602n n n Z α=+⋅=+⋅∈o o o ，此时，角2α的终边在x 轴的非正半轴上. 综上所述，角2α的终边在x 轴上.故选：B ．7．（2019·河南高一期末）已知一个扇形的圆心角为56π，半径为3．则它的弧长为（ ） A.53πB.23π C.52πD.2π 【答案】C【解析】由扇形弧长公式得：55362L r ππα==⨯= 本题正确选项：C8．（2019·山东高一期末）下列各角中，与角6π终边相同的角是（ ） A.136π-B.116π-C.116πD.196π【答案】B 【解析】角6π终边相同的角可以表示为2,()6a k k Z ππ=+∈，当1k =-时，6a 11π=-，所以答案选择B 9．若角α的顶点与原点重合，始边与x 轴的非负半轴重合，则集合{}1804518090,k k k Z αα⋅+≤≤⋅+∈oooo中的角α的终边在图中的位置（阴影部分）是（ ）A. B. C. D.【答案】C【解析】当k 为偶数时，设()2k n n Z =∈，则有3604536090n n α⋅+≤≤⋅+o o o o ，角α的终边在介于4590o o :角终边所在的区域；当k 为奇数时，设()21k n n Z =+∈，则有360225360270n n α⋅+≤≤⋅+o o o o ，角α的终边在介于225270o o :角终边所在的区域.故选：C.10．若2弧度的圆心角所对的弧长为4，则这个圆心角所在的扇形的面积为（ ） A ．4 B ．2C ．4πD ．2π【答案】A【解析】由已知得，=24l θ=，，又因为弧长l R θ=，所以扇形的半径=2R ，所以面积11=42=422S lR =⋅⋅．选A ．11．（2019·安徽高三月考（文））已知某扇形的面积为22.5cm ，若该扇形的半径r ，弧长l 满足27cm r l +=，则该扇形圆心角大小的弧度数是（ ）A.45B.5C.12D.45或5 【答案】D【解析】据题意，得27,1 2.5,2l r lr +=⎧⎪⎨=⎪⎩解得5,22r l ⎧=⎪⎨⎪=⎩或1,5,r l =⎧⎨=⎩所以45l r =或5.故选D . 12．（2019·湖北高三月考（文））《九章算术》是我国古代的数学巨著，其中《方田》章给出了计算弧田面积所用的经验公式为：弧田面积12=⨯（弦×矢+矢2），弧田（如图阴影部分所示）是由圆弧和弦围成，公式中的“弦”指圆弧所对的弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角为23π，矢为2的弧田，按照上述方法计算出其面积是( )A.2+43B.13+2C.2+83D.4+83【答案】A 【解析】如图，由题意可得23AOB π∠=， 在Rt AOD ∆中，,36AOD DAO ππ∠=∠=，所以2OB OD =，结合题意可知矢2OB OD OD =-==，半径4OB =， 弦2216443AB AD ==-= 所以弧田面积12=（弦⨯矢+矢2）21(4322)4322=+=， 故选A. 二、填空题13．（2019·上海交大附中高一开学考试）2018°是第________象限角. 【答案】三【解析】20185360218=⨯+o o o Q ，又218o 是第三象限角，所以2018o 也是第三象限角. 故答案为：三.14．（2019·上海市吴淞中学高一期末）圆心角为60︒的扇形，它的弧长为2π，则该扇形所在圆的半径为______. 【答案】6 【解析】263l r r r παπ===∴=故答案为：615．（2018·江西高一期末）扇形的半径为1cm ，圆心角为30°，则该扇形的弧长为________cm 【答案】6π【解析】圆弧所对的圆心角为30°即为6π弧度，半径为1cm 弧长为l ＝|α|•r 6π=⨯16π=（cm ）．故答案为：6π． 16．（2019·上海市复兴高级中学高一月考）若角α与角3-2π终边相同（始边相同且为x 轴正半轴），且302πα≤＜，则=α______． 【答案】2π 【解析】因为角α与角32π-终边相同（始边相同且为x 轴正半轴）， 所以322k παπ=-，k ∈Z ， 又因302πα≤<， 所以当1k =时，2πα=.故答案为：2π 三、解答题17．如图所示，用弧度制表示顶点在原点，始边重合于x 轴的非负半轴，终边落在阴影部分的角的集合.【答案】(1) {α|＋2k π<α<＋2k π，k ∈Z}；(2) {α|－＋2k π<α≤＋2k π，k ∈Z}；(3){α|k π≤α≤＋k π，k ∈Z}；(4) {α|＋k π<α<＋k π，k ∈Z}. 【解析】 (1)将阴影部分看成是由OA 逆时针转到OB 所形成， 故满足条件的角的集合为{α|＋2kπ<α<＋2kπ，k∈Z}．(2)若将终边为OA 的一个角改写为－，此时阴影部分可以看成是OA 逆时针旋转到OB 所形成，故满足条件的角的集合为{α|－＋2kπ<α≤＋2kπ，k∈Z}．(3)将图中x 轴下方的阴影部分看成是由x 轴上方的阴影部分旋转πrad 而得到，所以满足条件的角的集合为{α|kπ≤α≤＋kπ，k∈Z}．(4)与第(3)小题的解法类似，将第二象限阴影部分旋转πrad 后可得到第四象限的阴影部分．所以满足条件的角的集合为{α|＋kπ<α<＋kπ，k∈Z}．18．已知1570α=-o ，2750α=o，135βπ=，23βπ=-． （1）将12,αα用弧度制表示出来，并指出它们各自的终边所在的象限；（2）将12,ββ用角度制表示出来，并在720,180⎡⎤--⎣⎦o o内找出与它们终边相同的所有角．【答案】（1）1196πα=-终边位于第二象限，2256πα=终边位于第一象限； （2）12108,60ββ==-o o，与1β终边相同的角为252-o 和612-o ，与2β终边相同的角为420-o .【解析】（1）由题意，根据角度制与弧度制的互化公式，可得：1195705701806ππα=-=-⨯=-o oo， 2257507501806ππα==⨯=o o o， 又由1195466ππαπ=-=-+，所以1α与角56π的终边相同，所以1α终边位于第二象限；225466ππαπ==+，所以2α与角6π的终边相同，所以2α终边位于第第一象限.（2）根据角度制与弧度制的互化公式，可得131085βπ==o ，2603βπ=-=-o ， 根据终边相同角的表示，可得与1β终边相同的角为1360108,k k Z θ=⨯+∈o o，当1k =-时，1360108252θ=-+=-o o o ；当2k =-时，12360108612θ=-⨯+=-o o o. 与2β终边相同的角为236060,k k Z θ=⨯-∈o o ，当1k =-时，136060420θ=--=-o o o.19．在角的集合{}|9045,k k αα︒︒=+∈Z g， （1）有几种终边不同的角？（2）写出区间(180,180)︒︒-内的角？ （3）写出第二象限的角的一般表示法．【答案】(1) 4种．(2) 135,45,45,135︒︒︒︒--．(3) 360135,k k ︒︒+∈Z g ．【解析】（1）由题知9045,k k α︒︒=+∈Z g ，令0,1,2,3k =，则45,135,225,315α︒︒︒︒=， ∴在给定的角的集各中，终边不同的角共有4种． （2）由1809045180,k k ︒︒︒︒-<+<∈Z g ，得53,22k k -<<∈Z ，∴2,1,0,1k =--， ∴在区间(180,180)︒︒-内的角有135,45,45,135︒︒︒︒--． （3）由（1）知，第二象限的角可表示为360135,k k ︒︒+∈Z g ．20．已知扇形面积为225cm ，当扇形的圆心角为多大时，扇形的周长取得最小值？ 【答案】当扇形的圆心角为2时，扇形的周长取得最小值．【解析】设扇形的半径为R ，弧长为l ，扇形的周长为y ，则2y l R =+． 由题意，得1252lR =，则50l R =，故502522(0)y R R R R R ⎛⎫=+=+> ⎪⎝⎭． 利用函数单调性的定义，可得当05R <…时，函数502y R R=+是减函数； 当5R >时，函数502y R R=+是增函数． 所以当5R =时，y 取得最小值20，此时10l =，2lRα==， 即当扇形的圆心角为2时，扇形的周长取得最小值．21．（2019·宁夏银川一中高一期中）已知在半径为的圆中，弦的长为.（1）求弦所对的圆心角的大小；（2）求圆心角所在的扇形弧长及弧所在的弓形的面积. 【答案】（1）（2）【解析】（1）由于圆的半径为，弦的长为，所以为等边三角形，所以.（2）因为，所以.，又，所以.22．已知一扇形的中心角为α，所在圆的半径为R ．（1）若,6cm 3R απ== ，求该扇形的弧长l ． （2）若扇形的周长为12cm ，问当α多大时，该扇形有最大面积？并求出这个最大面积．【答案】（1）2π； （2）2α=，扇形的最大面积为29cm . 【解析】（1）由扇形的弧长公式，可得该扇形的弧长为623l R παπ==⨯=；（2）由题意，扇形的周长为12cm ，所以212R l +=，可得122l R =-， 又由扇形的面积公式，可得2211(122)6(3)922S lR R R R R R ==-=-+=--+, 当3R =时，扇形的面积取得最大值，此时最大面积为29S cm =， 此时1226l R =-=，即36R αα=⨯=，解得2α=.。

高中期末数学试题及答案一、选择题（每题3分，共30分）1. 下列函数中，哪一个是奇函数？A. y = x^2B. y = x^3C. y = x^4D. y = x^5答案：B2. 已知集合A={1, 2, 3}，B={2, 3, 4}，则A∩B等于？A. {1, 2, 3}B. {2, 3}C. {1, 4}D. {1, 2, 3, 4}答案：B3. 若a > 0，b < 0，则下列不等式中正确的是？A. a + b > 0B. ab > 0C. a - b > 0D. ab < 0答案：D4. 已知圆的方程为(x-2)^2 + (y-3)^2 = 9，圆心坐标为？A. (2, 3)B. (-2, -3)C. (2, -3)D. (-2, 3)答案：A5. 函数y = 2^x的反函数是？A. y = log2(x)B. y = 2^(-x)C. y = log(x/2)D. y = 2^x答案：A6. 已知等差数列{an}的首项a1=2，公差d=3，则a5等于？A. 14B. 17C. 20D. 23答案：A7. 已知向量a=(1, 2)，b=(-2, 4)，则向量a与向量b的点积为？A. -2B. 0C. 2D. 4答案：B8. 已知双曲线方程为x^2/a^2 - y^2/b^2 = 1，其中a=2，b=1，则该双曲线的渐近线方程为？A. y = ±x/2B. y = ±2xC. y = ±x/√2D. y = ±√2x答案：A9. 已知函数f(x) = x^2 - 4x + 3，求f(0)的值？A. 3B. 4C. 5D. 6答案：A10. 已知三角形ABC的三边长分别为a, b, c，且a^2 + b^2 = c^2，该三角形为？A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形答案：B二、填空题（每题4分，共20分）11. 已知函数f(x) = x^2 - 6x + 8，求该函数的顶点坐标为______。

模块一复习测试题二一．选择题（共10小题）1．若集合{|15}A x N x =∈,a =则下面结论中正确的是( ) A ．{}a A ⊆B ．a A ⊆C ．{}a A ∈D ．a A ∉2．已知实数1a >,1b >,则4a b +是22log log 1a b ⋅的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件3．若命题“[0x ∀∈,3],都有220x x m --≠ “是假命题,则实数m 的取值范围是( ) A ．(-∞,3]B ．[1-,)+∞C ．[1-,3]D ．[3,)+∞4．若函数2()44f x x x m =--+在区间[3,5)上有零点,则m 的取值范围是( ) A ．(0,4)B ．[4,9)C ．[1,9)D ．[1,4]5．已知2x >,则12y x x =+-的( ) A ．最小值是2 B ．最小值是4 C ．最大值是2 D ．最大值是46．已知函数12x y +=的图象与函数()y f x =的图象关于直线0x y +=对称,则函数()y f x =的反函数是( )A ．21log ()y x =--B ．2log (1)y x =--C ．12x y -+=-D ．12x y -+=7．已知cos()3παα+=为锐角）,则sin (α= )A B C D8．设函数()sin f x x x =,[0x ∈,2]π,若01a <<,则方程()f x a =的所有根之和为()A ．43π B ．2π C ．83π D ．73π 二．多选题（共4小题）9．若集合M N ⊆,则下列结论正确的是( ) A ．MN N =B ．M N N =C ．()M M N ∈D ．()M N N ⊆10．下列说法中正确的有( )A ．不等式2a b ab +恒成立B ．存在a ,使得不等式12a a+成立 C ．若a ,(0,)b ∈+∞,则2b a a b+ D ．若正实数x ,y 满足21x y +=,则218x y+ 11．已知函数||()1x f x x =+,则( ) A ．()f x 是奇函数B ．()f x 在[0,)+∞上单调递增C ．函数()f x 的值域是(,1)[0-∞-,)+∞D ．方程2()10f x x +-=有两个实数根12．下列选项中,与11sin()6π-的值相等的是( ) A ．22cos 151︒-B ．cos18cos 42sin18sin 42︒︒-︒︒C ．2sin15sin 75︒︒D ．tan30tan151tan30tan15o oo o+-三．填空题（共4小题）13．化简32a b-= （其中0a >,0)b >．14．高斯是德国的著名数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设x R ∈,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,例如:[ 3.4]4-=-,[2.7]2=．已知函数21()15x x e f x e =-+,则函数[()]y f x =的值域是 ． 15．若1lgx lgy +=,则25x y+的最小值为 ． 16．若42x ππ<<,则函数32tan 2tan y x x =的最大值为 ．四．参考解答题（共8小题） 17．已知0x >,0y >,且440x y +=． （Ⅰ）求xy 的最大值; （Ⅱ）求11x y+的最小值． 18．已知函数2()21f x x ax a =--+,a R ∈．（Ⅰ）若2a =,试求函数()(0)2f x y x x=>的最小值; （Ⅱ）对于任意的[0x ∈,2],不等式()f x a 成立,试求a 的取值范围; （Ⅲ）存在[0a ∈,2],使方程()2f x ax =-成立,试求x 的取值范围． 19．解方程 （1）231981xx-=（2）444log (3)log (21)log (3)x x x -=+++20．设函数33()sin cos 2323x x f x ππ=-． （1）求()f x 的最小正周期;（2）若函数()y g x =与()y f x =的图象关于x 轴对称,求当[0x ∈,3]2时,()y g x =的最大值．21．已知函数()cos()(0,0,||)2f x A x B A πωϕωϕ=++>><的部分图象如图所示．（Ⅰ）求()f x 的详细解析式及对称中心坐标;（Ⅱ）先将()f x 的图象纵坐标缩短到原来的12,再向右平移6π个单位,最后将图象向上平移1个单位后得到()g x 的图象,求函数()y g x =在3[,]124x ππ∈上的单调减区间和最值．22．已知函数2()3sin 2cos 12xf x x =-+． （Ⅰ）若()23()6f παα=+,求tan α的值;（Ⅱ）若函数()f x 图象上所有点的纵坐标保持不变,横坐标变为原来的12倍得函数()g x 的图象,且关于x 的方程()0g x m -=在[0,]2π上有解,求m 的取值范围．模块一复习测试题二参考正确答案与试题详细解析一．选择题（共10小题）1．若集合{|15}A x N x =∈,a =则下面结论中正确的是( ) A ．{}a A ⊆B ．a A ⊆C ．{}a A ∈D ．a A ∉【详细分析】利用元素与集合的关系直接求解．【参考解答】解:集合{|15}{0A x N x =∈=,1,2,3},a =a A ∴∉．故选:D ．【点评】本题考查命题真假的判断,是基础题,解题时要认真审题,注意元素与集合的关系的合理运用．2．已知实数1a >,1b >,则4a b +是22log log 1a b ⋅的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件【详细分析】根据充分必要条件的定义以及基本不等式的性质判断即可． 【参考解答】解:1a >,1b >, 2log 0a ∴>,2log 0b >,2a b ab +,4a b +,故4ab ,222222222log log log ()log 4log log ()[]()1222a b ab a b +⋅==,反之,取16a =,152b =,则1522224log log log 16log 215a b ⋅=⋅=<, 但4a b +>,故4a b +是22log log 1a b ⋅的充分不必要条件, 故选:A ．【点评】本题考查了充分必要条件,考查基本不等式的性质,是一道基础题．3．若命题“[0x ∀∈,3],都有220x x m --≠ “是假命题,则实数m 的取值范围是( ) A ．(-∞,3]B ．[1-,)+∞C ．[1-,3]D ．[3,)+∞【详细分析】直接利用命题的否定和一元二次方程的解的应用求出结果．【参考解答】解:命题“[0x ∀∈,3],都有220x x m --≠ “是假命题,则命题“[0x ∃∈,3],使得220x x m --= “成立是真命题, 故222(1)1m x x x =-=--． 由于[0x ∈,3],所以[1m ∈-,3]． 故选:C ．【点评】本题考查的知识要点:命题的否定的应用,一元二次方程的根的存在性的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型．4．若函数2()44f x x x m =--+在区间[3,5)上有零点,则m 的取值范围是( ) A ．(0,4)B ．[4,9)C ．[1,9)D ．[1,4]【详细分析】判断出在区间[3,5)上单调递增,(3)0(5)0f f ⎧⎨>⎩得出即1090m m -⎧⎨->⎩即可．【参考解答】解:函数2()44f x x x m =--+,对称轴2x =,在区间[3,5)上单调递增 在区间[3,5)上有零点,∴(3)0(5)0f f ⎧⎨>⎩即1090m m -⎧⎨->⎩ 解得:19m <, 故选:C ．【点评】本题考查了二次函数的单调性,零点的求解方法,属于中档题． 5．已知2x >,则12y x x =+-的( ) A ．最小值是2 B ．最小值是4 C ．最大值是2 D ．最大值是4【详细分析】直接利用不等式的基本性质和关系式的恒等变换的应用求出结果． 【参考解答】解:已知2x >,所以20x ->,故11222(2)2422y x x x x x =+=-++-=--（当3x =时,等号成立）． 故选:B ．【点评】本题考查的知识要点:不等式的基本性质,关系式的恒等变换,主要考查学生的运算能力和转换能力及思维能力,属于基础题．6．已知函数12x y +=的图象与函数()y f x =的图象关于直线0x y +=对称,则函数()y f x =的反函数是( )A ．21log ()y x =--B ．2log (1)y x =--C ．12x y -+=-D ．12x y -+=【详细分析】设(,)P x y 为()y f x =的反函数图象上的任意一点,则P 关于y x =的对称点(,)P y x '一点在()y f x =的图象上,(,)P y x '关于直线0x y +=的对称点(,)P x y ''--在函数12x y +=的图象上,代入详细解析式变形可得．【参考解答】解:设(,)P x y 为()y f x =的反函数图象上的任意一点, 则P 关于y x =的对称点(,)P y x '一点在()y f x =的图象上,又函数()y f x =的图象与函数12x y +=的图象关于直线0x y +=对称,(,)P y x ∴'关于直线0x y +=的对称点(,)P x y ''--在函数12x y +=的图象上,∴必有12x y -+-=,即12x y -+=-,()y f x ∴=的反函数为:12x y -+=-;故选:C ．【点评】本题考查反函数的性质和对称性,属中档题7．已知cos()3παα+=为锐角）,则sin (α= )A B C D 【详细分析】由11sin sin[()]33ααππ=+-,结合已知及两角差的正弦公式即可求解．【参考解答】解:cos()3παα+=为锐角）,∴1sin()3απ+=,则11111sin sin[()]sin())33233ααππαπαπ=+-=++,1(2=-,=故选:C ．【点评】本题考查的知识点是两角和与差的余弦公式,诱导公式,难度不大,属于基础题．8．设函数()sin f x x x =,[0x ∈,2]π,若01a <<,则方程()f x a =的所有根之和为( )A ．43π B ．2π C ．83π D ．73π 【详细分析】把已知函数详细解析式利用辅助角公式化积,求得函数值域,再由a 的范围可知方程()f x a =有两根1x ,2x ,然后利用对称性得正确答案．【参考解答】解:1()sin 2(sin )2sin()23f x x x x x x π=+=+=+,[0x ∈,2]π,()[2f x ∴∈-,2],又01a <<,∴方程()f x a =有两根1x ,2x ,由对称性得12()()33322x x πππ+++=,解得1273x x π+=．故选:D ．【点评】本题考查两角和与差的三角函数,考查函数零点的判定及应用,正确理解题意是关键,是基础题．二．多选题（共4小题）9．若集合M N ⊆,则下列结论正确的是( ) A ．MN N =B ．M N N =C ．()M M N ∈D ．()M N N ⊆【详细分析】利用子集、并集、交集的定义直接求解． 【参考解答】解:集合M N ⊆,∴在A 中,M N M =,故A 错误;在B 中,M N N =,故B 正确;在C 中,()M M N ⊆,故C 错误;在D 中,M N N N =⊆,故D 正确．故选:BD ．【点评】本题考查了子集、并集、交集定义等基础知识,考查运算求解能力,属于基础题． 10．下列说法中正确的有( )A ．不等式2a b ab +恒成立B ．存在a ,使得不等式12a a+成立 C ．若a ,(0,)b ∈+∞,则2b a a b+ D ．若正实数x ,y 满足21x y +=,则218x y+ 【详细分析】结合基本不等式的一正,二定三相等的条件检验各选项即可判断．【参考解答】解:不等式2a b ab +恒成立的条件是0a ,0b ,故A 不正确;当a 为负数时,不等式12a a+成立．故B 正确; 由基本不等式可知C 正确;对于212144()(2)4428y x y x x y x y x y x y x y+=++=+++=, 当且仅当4y x x y =,即12x =,14y =时取等号,故D 正确． 故选:BCD ．【点评】本题考查基本不等式的应用,要注意应用条件的检验．11．已知函数||()1x f x x =+,则( ) A ．()f x 是奇函数B ．()f x 在[0,)+∞上单调递增C ．函数()f x 的值域是(,1)[0-∞-,)+∞D ．方程2()10f x x +-=有两个实数根【详细分析】根据函数的奇偶性判断A ,根据函数的单调性判断B ,结合图象判断C ,D 即可．【参考解答】解:对于||:()()1x A f x f x x --=≠--+,()f x 不是奇函数,故A 错误; 对于:0B x 时,1()111x f x x x ==-++在[0,)+∞递增,故B 正确; 对于C ,D ,画出函数()f x 和21y x =-的图象,如图示:,显然函数()f x 的值域是(,1)[0-∞-,)+∞,故C 正确,()f x 和21y x =-的图象有3个交点,故D 错误;故选:BC ．【点评】本题考查了函数的单调性,奇偶性问题,考查数形结合思想,转化思想,是一道中档题．12．下列选项中,与11sin()6π-的值相等的是( ) A ．22cos 151︒-B ．cos18cos 42sin18sin 42︒︒-︒︒C ．2sin15sin 75︒︒D ．tan30tan151tan30tan15o oo o+- 【详细分析】求出11sin()6π-的值．利用二倍角的余弦求值判断A ;利用两角和的余弦求值判断B ;利用二倍角的正弦求值判断C ;利用两角和的正切求值判断D ．【参考解答】解:111sin()sin(2)sin 6662ππππ-=-+==． 对于A ,22cos 1531cos30o -=︒=对于B ,1cos18cos42sin18sin 42cos(1842)cos602︒︒-︒︒=︒+︒=︒=; 对于C ,12sin15sin 752sin15cos15sin302︒︒=︒︒=︒=; 对于D ,tan30tan15tan(3015)tan 4511tan30tan15o oo o+=︒+︒=︒=-．∴与11sin()6π-的值相等的是BC ． 故选:BC ．【点评】本题考查三角函数的化简求值,考查诱导公式、倍角公式及两角和的三角函数,是基础题．三．填空题（共4小题）13．化简32a b -= a （其中0a >,0)b >．【详细分析】根据指数幂的运算法则即可求出．【参考解答】解1311132322()b b bb ⨯=== 原式2111()3322a b a ---==,故正确答案为:a ．【点评】本题考查了指数幂的运算,属于基础题．14．高斯是德国的著名数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设x R ∈,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,例如:[ 3.4]4-=-,[2.7]2=．已知函数21()15x x e f x e =-+,则函数[()]y f x =的值域是 {1-,0,1} ．【详细分析】先利用分离常数法将函数化为92()51x f x e =-+,进而求出()f x 的值域,再根据[]x 的定义可以求出[()]f x 的所有可能的值,进而得到函数的值域．【参考解答】解:212(1)212192()215151551x x x x x x e e f x e e e e+-=-=-=--=-++++, 0x e >,11x e ∴+>,∴2021x e <<+,∴19295515x e -<-<+, 即19()55f x -<<,①当1()05f x -<<时,[()]1f x =-, ②当0()1f x <时,[()]0f x =,③当91()5f x <<时,[()]1f x =, ∴函数[()]y f x =的值域是:{1-,0,1},故正确答案为:{1-,0,1}．【点评】本题主要考查了新定义运算的求解,关键是能通过分离常数的方式求得已知函数的值域,是中档题．15．若1lgx lgy +=,则25x y+的最小值为 2 ． 【详细分析】根据对数的基本运算,结合不等式的解法即可得到结论．【参考解答】解:1lgx lgy +=,1lgxy ∴=,且0x >,0y >,即10xy =, ∴25251022210x y x y +=, 当且仅当25x y =,即2x =,5y =时取等号, 故正确答案为:2【点评】本题主要考查不等式的应用,利用对数的基本运算求出10xy =是解决本题的关键,比较基础．16．若42x ππ<<,则函数32tan 2tan y x x =的最大值为 16- ．【详细分析】直接利用三角函数的性质和关系式的恒等变换的应用及二次函数的性质的应用求出结果．【参考解答】解:若42x ππ<<,则tan (1,)x ∈+∞, 另22tan tan 21tan x x x=-, 设tan x t =,(1)t >, 则422222244416111111()()24t y t t t t ===-----,当且仅当t =时,等号成立．故正确答案为:16-．【点评】本题考查的知识要点:三角函数关系式的变换,关系式的变换和二次函数的性质,主要考查学生的运算能力和转换能力及思维能力,属于中档题．四．参考解答题（共8小题）17．已知0x >,0y >,且440x y +=．（Ⅰ）求xy 的最大值; （Ⅱ）求11x y+的最小值． 【详细分析】（1）由已知得,40424x y xy =+=解不等式可求,（2）由题意得,11111()(4)40x y x y x y +=++,展开后结合基本不等式可求． 【参考解答】解:（1）0x >,0y >,40424x y xy ∴=+=当且仅当4x y =且440x y +=即20x =,5y =时取等号,解得,100xy ,故xy 的最大值100．（2）因为0x >,0y >,且440x y +=．所以111111419()(4)(5)(540404040y x x y x y x y x y +=++=+++=, 当且仅当2x y =且440x y +=即403x =,203y =时取等号, 所以11x y +的最小值940． 【点评】本题考查了基本不等式在求最值中的应用,属于中档题18．已知函数2()21f x x ax a =--+,a R ∈．（Ⅰ）若2a =,试求函数()(0)2f x y x x =>的最小值; （Ⅱ）对于任意的[0x ∈,2],不等式()f x a 成立,试求a 的取值范围;（Ⅲ）存在[0a ∈,2],使方程()2f x ax =-成立,试求x 的取值范围．【详细分析】（Ⅰ）对式子变形后,利用基本不等式即可求得结果;（Ⅱ）先由题设把问题转化为:2210x ax --对于任意的[0x ∈,2]恒成立,构造函数2()21g x x ax =--,[0x ∈,2],利用其最大值求得a 的取值范围;（Ⅲ）由题设把问题转化为:方程21a x =-在[0a ∈,2]有解,解出x 的范围．【参考解答】解:（Ⅰ）当2a =时,2()41111()22212222f x x x y x x x x -+===+-⨯-=-（当且仅当1x =时取“= “),1min y ∴=-;（Ⅱ）由题意知:221x ax a a --+对于任意的[0x ∈,2]恒成立,即2210x ax --对于任意的[0x ∈,2]恒成立,令2()21g x x ax =--,[0x ∈,2],则(0)10(2)340g g a =-⎧⎨=-⎩,解得:34a , a ∴的取值范围为3[4,)+∞; （Ⅲ）由()2f x ax =-可得:210x a -+=,即21a x =-, [0a ∈,2],2012x ∴-,解得:11x -,即x 的取值范围为[1-,1]．【点评】本题主要考查基本不等式的应用、函数的性质及不等式的解法,属于中档题．19．解方程 （1）231981x x -= （2）444log (3)log (21)log (3)x x x -=+++【详细分析】（1）直接利用有理指数幂的运算法则求解方程的解即可．（2）利用对数运算法则,化简求解方程的解即可．【参考解答】解:（1）231981x x -=,可得232x x -=-,（2分） 解得2x =或1x =;（4分）（2）444log (3)log (21)log (3)x x x -=+++,可得44log (3)log (21)(3)x x x -=++,3(21)(3)x x x ∴-=++,（2分）得4x =-或0x =,经检验0x =为所求．（4分）【点评】本题考查函数的零点与方程根的关系,对数方程的解法,考查计算能力．20．设函数3()cos 323x x f x ππ=-． （1）求()f x 的最小正周期;（2）若函数()y g x =与()y f x =的图象关于x 轴对称,求当[0x ∈,3]2时,()y g x =的最大值． 【详细分析】（1）利用辅助角公式化积,再由周期公式求周期;（2）由对称性求得()g x 的详细解析式,再由x 的范围求得函数最值．【参考解答】解:（1）3()cos sin()32333x x f x x ππππ=-=-． ()f x ∴的最小正周期为263T ππ==;（2）函数()y g x =与()y f x =的图象关于x 轴对称,()()3sin()33x g x f x ππ∴=-=-． [0x ∈,3]2,∴[333x πππ-∈-,]6π, sin()[33xππ∴-∈,1]2,()[g x ∈,3]2． ∴当[0x ∈,3]2时,()y g x =的最大值为32． 【点评】本题考查sin()y A x ωϕ=+型函数的图象和性质,考查三角函数最值的求法,是中档题．21．已知函数()cos()(0,0,||)2f x A x B A πωϕωϕ=++>><的部分图象如图所示． （Ⅰ）求()f x 的详细解析式及对称中心坐标;（Ⅱ）先将()f x 的图象纵坐标缩短到原来的12,再向右平移6π个单位,最后将图象向上平移1个单位后得到()g x 的图象,求函数()y g x =在3[,]124x ππ∈上的单调减区间和最值．【详细分析】（Ⅰ）由函数的图象的顶点坐标求出A ,B ,由周期求出ω,由特殊点的坐标求出ϕ的值,可得函数的详细解析式,再根据余弦函数的图象的对称性,得出结论． （Ⅱ）由题意利用函数sin()y A x ωϕ=+的图象变换规律,正弦函数的单调性、定义域和值域,得出结论．【参考解答】解:（Ⅰ）由函数()cos()(0,0,||)2f x A x B A πωϕωϕ=++>><的部分图象知: 1(3)22A --==,1(3)12B +-==-,72212T πππωω-==⇒=, ()2cos(2)1f x x ϕ∴=+-,把点(,1)12π代入得:cos()16πϕ+=, 即26k πϕπ+=,k Z ∈． 又||2πϕ<,∴6πϕ=-,∴()2cos(2)16f x x π=--． 由图可知(,1)3π-是其中一个对称中心, 故所求对称中心坐标为:(,1)32k ππ+-,k Z ∈． （Ⅱ）先将()f x 的图象纵坐标缩短到原来的12,可得1cos(2)62y x π=--的图象,再向右平移6π个单位,可得11cos(2)sin 2222y x x π=--=- 的图象, 最后将图象向上平移1个单位后得到1()sin 22g x x =+的图象． 由22222k x k ππππ-++,k Z ∈,可得增区间是[4k ππ-,]4k ππ+,当3[,]124x ππ∈时,函数的增区间为[,]124ππ． 则32[,]62x ππ∈,当22x π=即,4x π=时,()g x 有最大值为32, 当322x π=,即34x π=时,()g x 有最小值为11122-+=-． 【点评】本题主要考查由函数sin()y A x ωϕ=+的部分图象求详细解析式,由函数的图象的顶点坐标求出A 、B ,由周期求出ω,由特殊点的坐标求出ϕ的值,余弦函数的图象的对称性．函数sin()y A x ωϕ=+的图象变换规律,正弦函数的单调性、定义域和值域,属于中档题．22．已知函数2()2cos 12x f x x =-+．（Ⅰ）若()()6f παα=+,求tan α的值; （Ⅱ）若函数()f x 图象上所有点的纵坐标保持不变,横坐标变为原来的12倍得函数()g x 的图象,且关于x 的方程()0g x m -=在[0,]2π上有解,求m 的取值范围． 【详细分析】（Ⅰ）利用三角恒等变换,化简()f x 的详细解析式,根据条件,求得tan α的值． （Ⅱ）根据函数sin()y A x ωϕ=+的图象变换规律,求得()g x 的详细解析式,再利用正弦函数的定义域和值域,求得()g x 的范围,可得m 的范围．【参考解答】解:（Ⅰ）2()2cos 1cos 2sin()26x f x x x x x π-+-=-,()()6f παα=+,∴sin()6παα-=,∴1cos 2ααα-=,即cos αα-=,∴tan α=（Ⅱ）把()f x 图象上所有点横坐标变为原来的12倍得到函数()g x 的图象, 所以函数()g x 的详细解析式为()(2)2sin(2)6g x f x x π==-, 关于x 的方程()0g x m -=在[0,]2π上有解, 等价于求()g x 在[0,]2π上的值域, 因为02x π,所以52666x πππ--, 所以1()2g x -,故m 的取值范围为[1-,2]．【点评】本题主要考查三角恒等变换,函数sin()y A x ωϕ=+的图象变换规律,正弦函数的定义域和值域,属于中档题．。

一、选择题1．若正数x，y满足21yx+=，则2xy+的最小值为（）A．2 B．4 C．6 D．82．已知正数x，y满足1431x y+=+，则x y+的最小值为（）A．53B．2 C．73D．63．设变量,x y、满足约束条件236y xx yy x≤⎧⎪+≥⎨⎪≥-⎩，则目标函数2z x y=+的最大值为（）A．2 B．3 C．4 D．94．如图，地面四个5G中继站A、B、C、D ，已知()62kmCD=+，30ADB CDB∠=∠=︒，45DCA∠=︒，60ACB∠=︒，则A、B两个中继站的距离是（）A．3km B．10km C10km D．62km 5．ABC∆的内角A，B，C的对边分别为a，b，c，已知2b=，6Bπ=，4Cπ，则ABC∆的面积为（）A．223+B31C．232D316．设ABC的内角A，B，C的对边分别是a，b，c.已知2cos0b a C-=，()sin3sinA A C=+，则2bca=（）A7B14C．23D67．在ABC中，角A，B，C的对边分别为a，b，c，若22tan tanB Cb c=，则ABC的形状为（）A．等腰三角形或直角三角形B．等腰直角三角形C．等腰三角形D．直角三角形8．已知实数x ，y 满足2402401x y x y y -+≥⎧⎪+-≤⎨⎪≥-⎩，则2x y +的最大值为（ ）A ．2B ．8C ．11D ．139．数列{}n a 的前n 项和为()21n S n n =-（*n ∈N ），若173a a ka +=，则实数k 等于（ ） A ．2B ．3C ．269D．25910．已知递增的等差数列{}n a 的前n 项和为n S ，175a a ⋅=，266a a +=，对于n *∈N ，不等式1231111+++⋅⋅⋅+<nM S S S S 恒成立，则整数M 的最小值是（ ） A ．1B ．2C ．3D ．411．若{}n a 是等比数列，其公比是q ，且546,,a a a -成等差数列，则q 等于( ) A ．－1或2B ．1或－2C ．1或2D ．－1或－212．在等比数列{}n a 中，若1234531a a a a a ++++=，2345662a a a a a ++++=，则通项n a 等于（ ） A ．12n -B ．2nC ．12n +D ．22n -二、填空题13．已知实数x ，y 满足约束条件010x y x y x -≤⎧⎪+≤⎨⎪⎩，则23x y z +=的最大值__________.14．若x >1，y >1，且a b x y xy ==，则a +4b 的最小值为___________. 15．设ABC 的内角A ，B ，C 所对的边长分别为a ，b ，c ，且3cos 2cos a C c A b ⋅=⋅+，则()tan A C -的最大值为__________.16．在ABC 中，角A ，B ，C 的对边a ，b ，c 为三个连续自然数，且2C A =，则a =_______．17．如图，测量河对岸的塔高AB 时，可以选与塔底B 在同一水平面内的两个观测点,C D ，测得15BCD ︒∠=，30CBD ︒∠=，152m CD =，并在C 处测得塔顶A 的仰角为45︒，则塔高AB =______m ．18．在ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，若4a =，2c =，60B =︒，则b = ，C = ．19．数列{}n a 中，已知22a =，21n n n a a a ++=+，若834a =，则数列{}n a 的前6项和为______．20．在数列{}n a 中，11a =()*1n =∈N ；等比数列{}n b 的前n 项和为2n n S m =-．当n *∈N 时，使得n n b a λ≥恒成立的实数λ的最小值是_________．三、解答题21．已知函数()()()23f x x a x =-+. （1）当72a >-时，解关于x 的不等式()46f x x >+； （2）若关于x 的方程()80f x +=在(–),1∞上有两个不相等实根，求实数a 的取值范围. 22．已知0a >，0b >.（1）求证：()2232a b b a b +≥+；（2）若2a b ab +=，求ab 的最小值.23．在ABC 中a ，b ，c 分别为内角A ，B ，C 所对的边，若()()2sin 2sin sin 2sin sin a A B C b C B c =+++.（1）求A 的大小； （2）求sin sin B C +的最大值.24．ABC 是等边三角形，点D 在边AC 的延长线上，且AD =3CD ，BD，求AD 的值和sin ∠ABD 的值25．在①数列{}n a 为递增的等比数列，且2312a a +=，②数列{}n a 满足122n n S S +-=，③数列{}n a 满足1121222n n n n a a a na -++++=这三个条件中任选一个，补充在下面问题中，再完成解答．问题：设数列{}n a 的前n 项和为n S ，12a =，__________． （1）求数列{}n a 的通项公式； （2）设2221log log n n n b a a +=⋅，求数列{}n b 的前n 项和n T ．26．已知等比数列{}n a 的公比3q =，并且满足2a ，318a +，4a 成等差数列. （1）求数列{}n a 的通项公式； （2）设数列{}n b 满足31log n n nb a a =+，记n S 为数列{}n b 的前n 项和，求使2220n S n ->成立的正整数n 的最小值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】 由21y x +=，对2x y +乘以21y x+=，构造均值不等式求最值 .【详解】22242248x y x xy y x y xy ⎛⎫⎛⎫+=++=+++≥+= ⎪ ⎪⎝⎭⎝⎭，当且仅当421xy xy y x⎧=⎪⎪⎨⎪+=⎪⎩，即412x y =⎧⎪⎨=⎪⎩时，等号成立，∴min28x y ⎛⎫+= ⎪⎝⎭.故选：D 【点睛】利用基本不等式求最值时，要注意其必须满足的三个条件：“一正、二定、三相等” (1) “一正”就是各项必须为正数；(2)“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；(3)“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方．如果等号成立的条件满足不了，说明函数在对应区间单调，可以利用单调性求最值或值域．2．B解析：B 【分析】化简114[(1)]()131x y x y x y +=++⨯+-+，再利用基本不等式求解. 【详解】由题得1114(1)1[(1)]31[(1)]()1331x y x y x y x y x y +=++-=++⨯-=++⨯+-+ 1141(5)1(5)123131y x x y y +=++-≥+-=++ 当且仅当1x y ==时取等.所以x y +的最小值为2. 故选：B 【点睛】方法点睛：利用基本不等式求最值时，常用到常量代换，即把所求代数式中的某一常量换成已知中的代数式，再利用基本不等式求解.3．D解析：D 【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得结论. 【详解】画出满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩的可行域，如图，画出可行域ABC ∆，(2,0)A ，(1,1)B ，(3,3)C ， 平移直线2z x y =+，由图可知，直线2z x y =+经过(3,3)C 时 目标函数2z x y =+有最大值，2z x y =+的最大值为9.故选D. 【点睛】本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.4．C解析：C 【分析】由正弦定理得求得AC 、BC 长，再由余弦定理得AB 长可得答案. 【详解】由题意可得75DAC ∠=︒，45DBC ∠=︒， 在ADC 中，由正弦定理得()362sin 223sin sin 75CD ADCAC DAC+⨯⋅∠===∠︒， 在BDC 中，由正弦定理得()162sin 231sin 22CD BDC BC DBC+⨯⋅∠===+∠，在ACB △中，由余弦定理得2222cos AB AC BC AC BC ACB =+-⨯⨯⋅∠()()()22123312233112=++-⨯⨯+⨯=，所以10km AB =. 故选：C. 【点睛】本题考查了正弦定理、余弦定理解三角形的应用.5．B解析：B 【解析】试题分析：根据正弦定理，，解得，，并且，所以考点：1．正弦定理；2．面积公式．6．D解析：D 【分析】根据正弦定理把角化边，可得3a b =，进一步得到2cos 3C =，然后根据余弦定理，可得6c b =，最后可得结果.【详解】 在ABC ∆中，sin sin a b A B=，由()sin 3sin()3sin 3sin A A C B B π=+=-=，所以3a b =①，又2cos 0b a C -=②，由①②可知：2cos 3C =，又2222cos 23a b c C ab +-==③，把①代入③化简可得：c =，则()2293bc b a b ==， 故选：D. 【点睛】本题考查正弦定理、余弦定理的综合应用，难点在于将c 用b 表示，当没有具体数据时，可以联想到使用一个参数表示另外两个参数，属于中档题.7．A解析：A 【分析】由三角函数恒等变换的应用，正弦定理化简已知等式可得sin 2sin 2B C =，可得22B C =，或22B C π+=，解得B C =，或2B C π+=，即可判断ABC ∆的形状．【详解】22tan tan B Cb c =， ∴22sin sin cos cos B C b B c C =，由正弦定理可得：22cos cos b cb Bc C=，可得：cos cos b B c C =，可得sin cos sin cos B B C C =，可得：sin 2sin 2B C =，22B C ∴=，或22B C π+=，B C ∴=，或2B C π+=，ABC ∆∴的形状为等腰三角形或直角三角形． 故选：A ． 【点睛】本题主要考查了三角函数恒等变换的应用，正弦定理在解三角形中的应用，考查了转化思想，属于基础题．8．C解析：C 【分析】根据条件作出可行域，根据图形可得出答案. 【详解】由实数x ，y 满足2402401x y x y y -+≥⎧⎪+-≤⎨⎪≥-⎩，作出可行域，如图.设2z x y =+，则化为2y x z =-+ 所以z 表示直线2y x z =-+在y 轴上的截距.2401x y y -+=⎧⎨=-⎩可得()6,1A --，2401x y y +-=⎧⎨=-⎩可得()61B -， 根据图形可得，当直线2y x z =-+过点()61B -，时截距最大， 所以2z x y =+的最大值为11. 故选：C【点睛】方法点睛：解决线性规划问题的实质是把代数问题几何化，即数形结合思想.需要注意的是：一，准确无误地作出可行域;二，画目标函数所对应的直线时，要注意让其斜率与约束条件中的直线的斜率进行比较，避免出错;三，一般情况下，目标函数的最大值或最小值会在可行域的端点或边界上取得.9．C解析：C 【分析】由已知结合递推公式可求n a ，然后结合等差数列的通项公式即可求解. 【详解】因为()21n S n n =-， 所以111a S ==，当2n ≥时，()()()12112343n n n a S S n n n n n -=-=----=-，111a S ==适合上式，故43n a n =-，因为173a a ka +=， ∴1259k +=， 解可得269k = 故选：C. 【点睛】本题主要考查了由数列前n 项和求数列的通项公式，考查来了运算能力，属于中档题.10．C解析：C 【分析】先求出等差数列的1a 和d ，由等差数列前n 项和公式得n S ，把1nS 拆成两项的差，用裂项相消法求得和12111nS S S +++，在n 变化时，求得M 的范围，得出结论． 【详解】∵{}n a 是等差数列，∴17266a a a a +=+=，由171765a a a a +=⎧⎨=⎩解得1715a a =⎧⎨=⎩或1751a a =⎧⎨=⎩，又{}n a 是递增数列，∴1715a a =⎧⎨=⎩，715127163a a d --===-， 1(1)(1)(2)233n n n n n n n S na d n --+=+=+=， 121113331324(2)n S S S n n +++=+++⨯⨯+3111111112324112n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-+- ⎪ ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦31119311122124212n n n n ⎛⎫⎛⎫=+--=-+ ⎪ ⎪++++⎝⎭⎝⎭94<， 由不等式1231111+++⋅⋅⋅+<n M S S S S 恒成立，得94M ≥，∴最小的整数3M =． 故选：C ． 【点睛】本题考查不等式恒成立问题，考查等差数列的性质，等差数列的通项公式和前n 项和公式，裂项相消法求和，本题属于中档题．11．A解析：A 【解析】分析：由546,,a a a -成等差数列可得5642a a a -+=，化简可得()()120q q +-=，解方程求得q 的值. 详解：546,,a a a -成等差数列，所以5642a a a -+=，24442a q a q a ∴-+=，220q q ∴--=，()()120q q ∴+-=，1q ∴=-或2，故选A.点睛：本题考查等差数列的性质，等比数列的通项公式基本量运算，属于简单题. 等比数列基本量的运算是等比数列的一类基本题型，数列中的五个基本量1,,,,,n n a q n a S ，一般可以“知二求三”，通过列方程组所求问题可以迎刃而解，解决此类问题的关键是熟练掌握等比数列的有关性质和公式，并灵活应用.12．A解析：A 【详解】设等比数列{a n }的公比为q ，∵a 1+a 2+a 3+a 4+a 5=31,a 2+a 3+a 4+a 5+a 6=62， ∴q=2，∴a1(1+q+q 2+q 3+q 4)=31， 则a 1=1， 故an=2n−1. 故选A.二、填空题13．【分析】先作出不等式组对应的可行域再通过数形结合求出的最大值即得解【详解】由题得不等式组对应的可行域是如图所示的阴影三角形区域设它表示斜率为纵截距为的直线系要求的最大值即求的最大值当直线经过点时直线 解析：9【分析】先作出不等式组对应的可行域，再通过数形结合求出2x y +的最大值即得解. 【详解】由题得不等式组对应的可行域是如图所示的阴影三角形区域，设12,22m m x y y x =+∴=-+，它表示斜率为12-，纵截距为2m的直线系， 要求23x y z +=的最大值即求m 的最大值.当直线122m y x =-+经过点(0,1)A 时，直线的纵截距2m最大，m 最大. 此时max 022m =+=， 所以23x y z +=的最大值为239=.故答案为：9 【点睛】方法点睛：线性规划问题一般用图解法，其步骤如下： （1）根据题意，设出变量,x y ； （2）列出线性约束条件；（3）确定线性目标函数(,)z f x y =；（4）画出可行域（即各约束条件所示区域的公共区域）； （5）利用线性目标函数作平行直线系()(y f x z =为参数）；（6）观察图形，找到直线()(y f x z =为参数）在可行域上使z 取得欲求最值的位置，以确定最优解，给出答案。

江苏高中数学复习题# 江苏高中数学复习题## 一、选择题1. 函数的奇偶性：若函数\( f(x) = x^2 - 4x + 3 \)，判断该函数的奇偶性。

2. 不等式的解集：解下列不等式：\( |x - 1| + |x + 2| < 4 \)。

3. 数列的通项公式：已知等差数列的第3项为10，第5项为14，求该数列的通项公式。

4. 三角函数的化简：化简下列三角函数式：\( \frac{1 - \cos^2 \theta}{\sin^2\theta} \)。

5. 导数的应用：若函数\( f(x) = 3x^3 - 2x^2 - 6x + 1 \)，求其在\( x = 1 \)处的切线斜率。

## 二、填空题1. 复数的模：设复数\( z = 2 - i \)，求\( |z| \)。

2. 立体几何体积：一个正方体的边长为3，求其体积。

3. 概率的计算：若一个袋子中有5个红球和3个蓝球，随机取出2个球，求至少有一个红球的概率。

4. 矩阵的运算：设矩阵\( A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \)，求\( A^2 \)。

5. 函数的单调性：若函数\( f(x) = 2x - \ln x \)在\( x > 1 \)上单调递增，求其导数\( f'(x) \)。

## 三、解答题1. 解析几何：已知椭圆\( \frac{x^2}{9} + \frac{y^2}{4} = 1 \)，求过点(2,0)的切线方程。

2. 函数的极值：求函数\( f(x) = x^3 - 3x^2 - 9x + 5 \)在区间[-2, 4]上的极值。

3. 数列的求和：求等比数列\( 3, 6, 12, ... \)的前10项和。

4. 向量的运算：已知向量\( \vec{a} = (3, -1) \)，\( \vec{b} = (2, 4) \)，求向量\( \vec{a} \)与\( \vec{b} \)的点积。

一、选择题1．第24届国际数学大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如图，会标是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形的一个锐角为θ，且πsin 2sin 52θθ⎛⎫++= ⎪⎝⎭.若在大正方形内随机取一点，则该点取自小正方形区域的概率为（ ）.A ．14B ．15C ．25D ．352．从单词“book ”的四个字母中任取2个，则取到的2个字母不相同的概率为（ ） A ．13B ．12C ．23D ．343．算盘是中国传统的计算工具，其形长方，周为木框，内贯直柱，俗称“档”，档中横以梁，梁上两珠，每珠作数五，梁下五珠，每珠作数一.算珠梁上部分叫上珠，梁下部分叫下珠.例如：在十位档拨上一颗上珠和一颗下珠，个位档拨上一颗上珠，则表示数字65.若在个､十､百位档中随机选择一档拨一颗上珠，再随机选择两个档位各拨一颗下珠，则所拨数字为奇数的概率为（ ）A ．13B ．49C ．59D ．234．设向量()()1,,a x y x y R =-∈，若1a ≤，则y x ≥的概率为（ ） A ．14B ．1142π- C ．114π-D ．3142π+ 5．执行如图所示的程序框图，结果是（ ）A．11 B．12 C．13 D．14 6．下列赋值语句正确的是 ()A．S＝S＋i2B．A＝－AC．x＝2x＋1 D．P＝7．执行如图所示的程序框图，若输出的结果为48，则输入k的值可以为A．6B．10C．8D．4) 8．执行如图所示程序框图，当输入的x为2019时，输出的y(A ．28B ．10C ．4D ．29．某农业科学研究所分别抽取了试验田中的海水稻以及对照田中的普通水稻各10株，测量了它们的根系深度（单位：cm ），得到了如图所示的茎叶图，其中两竖线之间表示根系深度的十位数，两边分别是海水稻和普通水稻根系深度的个位数，则下列结论中不正确的是（ ）A ．海水稻根系深度的中位数是45.5B ．普通水稻根系深度的众数是32C ．海水稻根系深度的平均数大于普通水稻根系深度的平均数D ．普通水稻根系深度的方差小于海水稻根系深度的方差10．已知变量,x y 之间的线性回归方程为0.47.6=-+y x ，且变量,x y 之间的一组相关数据如表所示，则下列说法错误的是（ ）A ．变量,x y 之间呈现负相关关系B ．m 的值等于5C ．变量,x y 之间的相关系数0.4=-rD ．由表格数据知，该回归直线必过点()9,411．PM2.5是指空气中直径小于或等于2.5微米的颗粒物（也称可入肺颗粒物），为了探究车流量与PM2.5的浓度是否相关，现采集到某城市周一至周五某时间段车流量与PM2.5浓度的数据如下表：根据上表数据，用最小二乘法求出y 与x 的线性回归方程是（ ）参考公式：121()()()niii ni i x x y y b x x ==--=-∑∑，a y b x =-⋅；参考数据：108x =，84y =；A ．0.6274ˆ.2yx =+ B ．0.7264ˆ.2y x =+ C ．0.7164ˆ.1y x =+ D ．0.6264ˆ.2y x =+ 12．有一个同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经统计，得到一个卖出的热饮杯数与当天气温的对比表：根据上表数据确定的线性回归方程应该是（ ）A ．ˆ 2.352147.767yx =-+ B ．ˆ 2.352127.765yx =-+ C ．ˆ 2.35275.501yx =+D ．ˆ 2.35263.674yx =+ 二、填空题13．甲、乙两人进行象棋比赛，采取五局三胜制（不考虑平局，先赢得三场的人为获胜者，比赛结束）.根据前期的统计分析，得到甲在和乙的第一场比赛中，取胜的概率为0.5，受心理方面的影响，前一场比赛结果会对甲的下一场比赛产生影响，如果甲在某一场比赛中取胜，则下一场取胜率提高0.1，反之，降低0.1，则甲以3:1取得胜利的概率为______________.14．如图所示，分别以,,A B C 为圆心，在ABC 内作半径为2的三个扇形，在ABC内任取一点P ，如果点P 落在这三个扇形内的概率为13，那么图中阴影部分的面积是____________.15．从1，2，3，4中任取两个不同的数，则取出的2个数之差的绝对值小于或等于2的概率为__________．16．执行如图所示的程序框图，输出S 的值为___________.17．用秦九韶算法求多项式()5432357911f x x x x x x =+-+-+当4x =时的值为____________.18．如图是一个算法的流程图，则输出的a 的值是___________．19．为了了解2100名学生早晨到校时间，计划采用系统抽样的方法从全体学生中抽取容量为100栋样本，则分段间隔为__________．20．已知一组数据：5.7，5.8，6.1，6.4，6.5，则该数据的方差是__________．三、解答题21．从广安市某中学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm 和195cm 之间，将测量结果按如下方式分成八组：第一组[)155160,，第二组[)160165,，...，第八组[)190,195，如图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4人.（1）求第七组的频率；（2）估计该校800名男生的身高的中位数。

一、选择题1．关于x 的方程2||10x a x ++=有4个不同的解，则实数a 的取值范围是（ ） A ．()(),22,-∞-+∞B ．(],2-∞-C ．(),2-∞-D ．()2,+∞2．函数1,(0)()0,(0)x x f x x x ⎧+≠⎪=⎨⎪=⎩，关于x 的方程2()()0f x bf x c ++=有5个不等的实数根的充分必要条件是（ ） A ．2b <-且0c >B ．2b >-且0c <C ．2b <-且0cD ．2b ≥-且0c3．若直角坐标平面内的两点P 、Q 满足条件：①P 、Q 都在函数()y f x =的图象上；②P 、Q 关于原点对称，则称点对[]P Q 、是函数()y f x =的一对“友好点对”（点对[]P Q 、与[]Q P 、看作同一对“友好点对”）．已知函数22(0)()2(0)x x f x x x x ⎧≤=⎨->⎩，则此函数的“友好点对”有（ ） A ．4对 B ．3对 C ．2对 D ．1对4．若关于x 的不等式34log 2xa x -≤在10,2x ⎛⎤∈ ⎥⎝⎦恒成立，则实数a 的取值范围是（ ） A ．1,14⎡⎫⎪⎢⎣⎭B ．10,4⎛⎤ ⎥⎝⎦C ．3,14⎡⎫⎪⎢⎣⎭D ．30,4⎛⎤ ⎥⎝⎦5．已知函数()()3,<1log ,1aa x a x f x x x ⎧--=⎨≥⎩的值域．．是R ，那么实数a 的取值范围是（ ） A ．31,2⎛⎤ ⎥⎝⎦B ．()1,+∞C ．()()0,11,3D ．3,32⎡⎫⎪⎢⎣⎭6．已知函数()sin 2f x x x =-，且()0.3231ln ,log ,223a f b f c f ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，则以下结论正确的是 A ．c a b >>B ．a c b >>C ．a b c >>D ．b a c >>7．已知()f x 在[],x a b ∈的最大值为M ，最小值为m ，给出下列五个命题：（ ） ①若对任何[],x a b ∈都有()p f x ≤，则p 的取值范围是(],m -∞. ②若对任何[],x a b ∈都有()p f x ≤，则p 的取值范围是(],M -∞. ③若关于x 的方程()p f x =在区间[],a b 有解，则p 的取值范围是[],m M . ④若关于x 的不等式()p f x ≤在区间[],a b 有解，则p 的取值范围是(],m -∞.⑤若关于x 的不等式()p f x ≤在区间[],a b 有解，则p 的取值范围是(],M -∞. A ．4B ．3C ．2D ．18．已知函数()f x 的定义域为R ,对任意的 12,x x <都有1212()(),f x f x x x -<-且(3)4,f =则(21)2f x x ->的解集为( )A ．(2,)+∞B ．(1,)+∞C ．(0,)+∞D ．(1,)-+∞9．已知函数()113sin 22f x x x ⎛⎫=+-+ ⎪⎝⎭，则122018201920192019f f f ⎛⎫⎛⎫⎛⎫++⋅⋅⋅+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭（ ） A ．2018 B ．2019 C ．4036D ．403810．下图中的阴影部分，可用集合符号表示为（ ）A ．()()U U A B ⋂ B ．()()U UA BC ．()UA BD ．()UA B ⋂11．已知集合{}|10A x x =-<，{}2|20B x x x =-<，则AB =（ ）A ．{}|0x x <B ．{}|1x x <C ．{}1|0x x <<D ．{}|12x x <<12．已知集合{0,1,2,3,4},{|21,}A B x x n n A ===+∈，则A B 等于（ ）A ．{}1,3,5B ．{}3C ．{}5,7,9D ．{}1,3二、填空题13．若函数244y ax a x =+-存在零点，则实数a 的取值范围是______． 14．2019年1月1日起新的个人所得税法开始实施，依据《中华人民共和国个人所得税法》可知纳税人实际取得工资、薪金（扣除专项、专项附加及依法确定的其他）所得不超过5000元（俗称“起征点”）的部分不征税，超出5000元部分为全月纳税所得额.新的税率表如表：2019年1月1日后个人所得税税率表 全月应纳税所得额 税率（%） 不超过3000元的部分 3 超过3000元至12000元的部分10个人所得税专项附加扣除是指个人所得税法规定的子女教育、继续教育、大病医疗、住房贷款利息、住房租金和赡养老人等六项专项附加扣除.其中赡养老人一项指纳税人赡养60岁（含）以上父母及其他法定赡养人的赡养支出，可按照以下标准扣除：纳税人为独生子女的，按照每月2000元的标准定额扣除；纳税人为非独生子女的，由其与兄弟姐妹分摊每月2000元的扣除额度，每人分摊的额度不能超过每月1000元.某纳税人只有一个姐姐，且两人仅符合规定中的赡养老人的条件，如果他在2020年5月份应缴纳个人所得税款为180元，那么他当月的工资、薪金税后所得是_____元. 15．已知函数()f x 的定义域是[1,1]-，则函数(21)()ln(1)f xg x x -=-的定义域是________.16．已知12512.51000x y ==，则11x y＝_____.17．设函数f (x )满足：对任意的x 1，x 2∈R 都有(x 1－x 2)[f (x 1)－f (x 2)]>0，则f (－3)与f (－π)的大小关系是________．18．定义在R 上的奇函数()f x 在(0,)+∞上是增函数，又(3)0f -=，则不等式()0xf x <的解集为______．19．若集合2{|(2)20,A x x a x a =-++-<x ∈Z }中有且只有一个元素，则正实数a 的取值范围是________20．已知集合(){}21210,,A x a x x a R x R =-++=∈∈，若集合A 至多有两个子集，则a 的取值范围是__________.三、解答题21．某化工厂一种溶液的成品，生产过程的最后工序是过滤溶液中的杂质，过滤初期溶液含杂质为2%，每经过一次过滤均可使溶液杂质含量减少一半，记过滤次数为*()x x N ∈时溶液杂质含量为y（1）分别求出1次过滤、2次过滤以后的溶液杂质含量1y ，2y 的值． （2）写出y 与x 的函数关系式（要求写出定义域）（3）按市场要求，出厂成品杂质含量不能超过0.02%，问至少经过几次过滤才能使产品达到市场要求？(参考数据：lg2=0.301)22．某市出租汽车的收费标准如下：在3km 以内（含3km ）的路程统一按起步价7元收费，超过3km 以外的路程按2.4元/km 收费.而出租汽车一次载客的运输成本包含以下三个部分：一是固定费用，约为2.3元；二是燃油费，约为1.6元/km ；三是折旧费，它与路程的平方近似成正比，且当路程为20km 时，折旧费为0.1元.现设一次载客的路程为x km. （1）试将出租汽车一次载客的收费F 与成本C 分别表示为x 的函数；（2）若一次载客的路程不少于2km ，则当x 取何值时，该市出租汽车一次载客每千米的收益y 取得最大值？（每千米收益计算公式为)F Cy x-=23．已知函数()2()log log 2(0,1)a a f x x x a a =-->≠. （1）当2a =时，求(2)f ； （2）求解关于x 的不等式()0f x >；（3）若[2,4],()4x f x ∀∈≥恒成立，求实数a 的取值范围. 24．函数()2lg 34y x x=-+的定义域为M ，x M ∈，求()2234x x f x +=-⨯的最值.25．已知函数()f x =+ （1）求()f x 的定义域和值域； （2）设()h x =231()42h x m am ≤-对于任意[1,1]x ∈-及任意[1,1]a ∈-都恒成立，求实数m 的取值范围．26．已知全集U =R ，集合{}2450A x x x =--≤，{}2124x B x -=≤≤．（1）求()UAB ；（2）若集合{}4,0C x a x a a =≤≤>，且满足C A A =，C B B =，求实数a 的取值范围．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】由2||10x a x ++=可得1a x x =--，转化为y a =与()1g x x x=--的图象有4个不同的交点，作出()1g x x x=--，数形结合即可求解. 【详解】由2||10x a x ++=可得22111||||x x a x x x x----===--， 令()1g x x x=--，若关于x 的方程2||10x a x ++=有4个不同的解， 则y a =与()1g x x x=--的图象有4个不同的交点， ()1g x x x=--是偶函数， 当0x <时()()()111x x x x x x g x --=---=+-=， ()1g x x x=+在(),1-∞-单调递增，在()1,0-单调递减， 所以()1g x x x=+的图象如图所示： 当1x =-时()max 1121g x =-+=--，若y a =与()1g x x x=--的图象有4个不同的交点， 由图知2a <-， 故选：C 【点睛】方法点睛：已知函数有零点(方程有根)求参数值(取值范围)常用的方法： （1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围； （2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决；（3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解.2．C解析：C 【分析】首先根据题中所给的方程的根进行分析，得到五个根的情况，从而判断出0c ，之后利用()f x b =-有四个根，结合函数图象求得结果. 【详解】当0x =时()0f x =，当0x =为()()20f x bf x c ++=的一个根时可得0c.所以()()20fx bf x c ++=即()()20f x bf x +=有4个不同的根， ()0f x ≠，()f x b ∴=-有4个根.0x ≠时()11122f x x x x x x x=+=+≥=，图象如图所示：由图可知22b b ->⇒<-. 综上可得2,0b c <-=. 故选：C. 【点睛】该题考查的是有关根据函数零点的个数判断参数的取值范围的问题，充要条件的判断，在解题的过程中，注意数形结合思想的应用，属于中档题目.3．C解析：C 【分析】由题意，设点(,)P x y ，则Q 的坐标为(,)x y --，结合22(0)()2(0)x x f x x x x ⎧≤=⎨->⎩，转化为此函数的“友好点对”的个数即方程222x x x --=-在0x >时的解的个数，从而作图解答 【详解】解：由题意，设点(,)P x y ，则Q 的坐标为(,)x y --，因为22(0)()2(0)x x f x x x x ⎧≤=⎨->⎩，所以此函数的“友好点对”的个数即方程222x x x --=-在0x >时的解的个数， 作2x y -=-与22y x x =-的图像如图所示，两函数图像有两个交点，所以此函数的“友好点对”有2对故选：C【点睛】此题考查学生对新定义的理解能力及作图能力，属于中档题4．A解析：A【分析】转化为当10,2 x⎛⎤∈ ⎥⎝⎦时，函数342xy=-的图象不在log ay x=的图象的上方，根据图象列式可解得结果.【详解】由题意知关于x的不等式34log2xax-≤在10,2x⎛⎤∈ ⎥⎝⎦恒成立，所以当10,2x⎛⎤∈ ⎥⎝⎦时，函数342xy=-的图象不在log ay x=的图象的上方，由图可知0111log22aa<<⎧⎪⎨≥⎪⎩，解得114a≤<.故选：A【点睛】关键点点睛：利用函数342xy =-的图象与函数log a y x =的图象求解是解题关键. 5．A解析：A 【分析】当0＜a ＜1时，当1≥x 时，log 0a y x =≤，则当1x <时，()3y a x a =--的值域必须要包含()0,+∞，，当1a >时，当1≥x 时，[)log 0a y x =∈+∞，，则当1x <时，()3y a x a =--的值域必须要包含()0-∞，,从而可得答案. 【详解】由题意，()f x 的值域为R ，当0＜a ＜1时，当1≥x 时，log 0a y x =≤，所以当1x <时，()3y a x a =--的值域必须要包含()0,+∞，当1x <时，()3y a x a =--单调递增，()332y a x a a =--<- 所以不满足()f x 的值域为R .当1a >时，当1≥x 时，[)log 0a y x =∈+∞，， 所以当1x <时，()3y a x a =--的值域必须要包含()0-∞，, 若3a =时，当1x <时，3y a =-=-，不满足()f x 的值域为R .若3a >时，当1x <时，()3y a x a =--单调递减，()332y a x a a =-->- 所以不满足()f x 的值域为R .若13a <<时，当1x <时，()3y a x a =--单调递增，()332y a x a a =--<- 要使得()f x 的值域为R ，则320a -≥，即32a ≤ 所以满足条件的a 的取值范围是：312a <≤， 故选：A ． 【点睛】关键点睛：本题考查根据函数的值域求参数的范围，解答本题的关键是当0＜a ＜1时，当1≥x 时，log 0a y x =≤，则当1x <时，()3y a x a =--的值域必须要包含()0,+∞，，当1a >时，当1≥x 时，[)log 0a y x =∈+∞，，则当1x <时，()3y a x a =--的值域必须要包含()0-∞，，属于中档题. 6．D解析：D 【解析】因为()cos 20f x x '=-<，所以函数()sin 2f x x x =-的单调递减函数，又因为0.3213log 0,ln ln 1,12232e <<=<<，即0.3213log ln 232<<，所以由函数的单调性可得：0.3213(log )(ln )(2)32f f f >>，应选答案D ．7．B解析：B 【分析】这是一个对不等式恒成立，方程或不等式解集非空的理解，概念题．对各个选项分别加以判断，在①②中，得出①正确②错误，④⑤中得出⑤正确④错误，而不难发现③是一个真命题，由此可得正确答案. 【详解】对任何x ∈[a ，b]都有()p f x ≤，说明p 小于等于()f x 的最小值，①是正确的; 由于①正确，所以②是一个错误的理解，故不正确;关于x 的方程p =f (x ）在区间[a ，b ]上有解，说明p 应属于函数f (x ）在[a ，b ]上的值域[m ，M ]内，故③是正确的;关于x 的不等式p ≤f (x ）在区间[a ，b ]上有解，说明p 小于或等于的最大值，所以④是错误的，而⑤是正确的 正确的选项应该为①③⑤ 故选： B. 【点睛】关键点点睛：本题考查了命题的真假判断与应用，属于基础题．不等式或方程解集非空，只要考虑有解;而不等式恒成立说明解集是一切实数，往往要考虑函数的最值了．8．A解析：A 【分析】由题可得[][]1122()()0f x x f x x ---<,可构造函数()()F x f x x =-是R 上的增函数,原不等式可转化为()()213F x F ->,再结合增函数的性质可求出答案. 【详解】 由题意,[][]121211221122()()()()()()0f x f x x x f x x f x x f x x f x x -<-⇔-<-⇔---<, 因为12,R x x ∈且12,x x <所以函数()()F x f x x =-是R 上的增函数.()3(3)31F f =-=,因为(21)2(21)(21)1f x x f x x ->⇔--->,所以()()213F x F ->, 则213x ->,解得2x >. 故选:A.【点睛】本题考查了函数的单调性的应用,构造函数()()F x f x x =-是解决本题的关键,属于中档题.9．A解析：A 【分析】根据函数解析式可验证出()()12f x f x +-=，采用倒序相加法可求得结果. 【详解】()11113sin 22f x x x ⎛⎫-=-+-+ ⎪⎝⎭，()()12f x f x ∴+-=，令122018201920192019S f f f ⎛⎫⎛⎫⎛⎫=++⋅⋅⋅+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 则201712019201922018019S f f f ⎛⎫⎛⎫⎛⎫=++⋅⋅⋅+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 两式相加得：222018S =⨯，2018S ∴=. 故选：A . 【点睛】本题考查倒序相加法求和的问题，解题关键是能够根据函数解析式确定()()1f x f x +-为常数.10．C解析：C 【分析】图中阴影部分是集合A 与集合B 的补集的交集. 【详解】图中阴影部分是集合A 与集合B 的补集的交集，所以图中阴影部分，可以用()UA B 表示. 【点睛】本题考查了用韦恩图表示集合间的关系，考查了学生概念理解，数形结合的能力，属于基础题.11．C解析：C 【分析】求出A 、B 中不等式的解集确定出A 、B ，找出A 与B 的交集即可． 【详解】集合{}{}|10|1A x x x x =-<=<，集合{}{}2|20|02B x x x x x =-<=<<，所以A B ={}1|0x x <<.故选：C【点睛】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．12．D解析：D 【分析】首先求得集合B ，然后进行交集运算即可. 【详解】由题意可得：{}1,3,5,7,9B =，则{}1,3A B =.故选D . 【点睛】本题主要考查集合的表示方法，交集的定义与运算等知识，意在考查学生的转化能力和计算求解能力.二、填空题13．【分析】将函数存在零点转化为与图像有交点作出图像观察图像得出实数的取值范围【详解】解：设则函数存在零点等价于与图像有交点如图：函数的图像恒过点当其和函数的图像相切时有解得由图像可知所以所以与的图像有解析：30,⎡⎤⎢⎥⎣⎦【分析】将函数244y ax a x =+--存在零点转化为()()4f x a x =+与2()4g x x =-图像有交点，作出图像，观察图像得出实数a 的取值范围. 【详解】解：设()()4f x a x =+，2()4g x x =-，则函数244y ax a x =+--存在零点等价于()()4f x a x =+与2()4g x x =-图像有交点， 如图：函数()()4f x a x =+的图像恒过点(4,0)-，当其和函数2()4g x x =-2=，解得3a =±，由图像可知，0a >，所以3a =， 所以()()4f x a x =+与()g x =03a ≤≤.故答案为：⎡⎢⎣⎦. 【点睛】本题考查函数零点问题的研究，关键是将零点问题转化为函数图像的交点问题，考查数形结合的思想，是中档题.14．9720【分析】按题意从最低纳税额开始计算最高纳税同时考虑到专项附加扣除后可得【详解】设他的工资是元工资是8000元时纳税为由于他有专项附加扣1000元因此他工资是9000元时纳税90元纳税后收入为解析：9720 【分析】按题意从最低纳税额开始计算最高纳税，同时考虑到专项附加扣除后可得． 【详解】设他的工资是x 元，工资是8000元时纳税为30003%90⨯=，由于他有专项附加扣1000元，因此他工资是9000元时，纳税90元，(9000)10%18090x -⨯=-，9900x =，纳税后收入为9900－180＝9720（元）． 故答案为：9720． 【点睛】本题考查函数的应用，解题时根据分段函数的意义分段计算纳税额即可得．解题关键是正确理解题意，弄懂工资收入与纳税额之间的关系．15．【分析】由函数的定义域是即结合函数的解析式列出不等式组即可求解【详解】由题意函数的定义域是即则函数有意义则满足解得解得即函数的定义域是故答案为：【点睛】本题主要考查了抽象函数定义域的求解以及对数函数 解析：(0,1)【分析】由函数()f x 的定义域是[1,1]-，即11x -≤≤，结合函数的解析式(21)()ln(1)f xg x x -=-，列出不等式组12111011x x x -≤-≤⎧⎪->⎨⎪-≠⎩，即可求解. 【详解】由题意，函数()f x 的定义域是[1,1]-，即11x -≤≤，则函数(21)()ln(1)f x g x x -=-有意义，则满足12111011x x x -≤-≤⎧⎪->⎨⎪-≠⎩ ，解得0110x x x ≤≤⎧⎪<⎨⎪≠⎩，解得01x <<，即函数(21)()ln(1)f xg x x -=-的定义域是(0,1).故答案为：(0,1). 【点睛】本题主要考查了抽象函数定义域的求解，以及对数函数的性质的应用，其中解答中熟记抽象函数的定义域的求解方法，以及对数函数的性质是解答的关键，着重考查推理与运算能力.16．【分析】根据指数与对数之间的关系求出利用对数的换底公式即可求得答案【详解】∵∴∴∴故答案为：【点睛】本题考查了指数与对数之间的关系掌握对数换底公式:是解本题的关键属于基础题解析：13【分析】根据指数与对数之间的关系,求出,x y ,利用对数的换底公式,即可求得答案. 【详解】∵12512.51000x y ==， ∴12512.51000100011log 1000,log 1000log 125log 12.5x y ====，∴1000100011log 125,log 12.5x y==， ∴1000111log 103x y -==. 故答案为：13. 【点睛】本题考查了指数与对数之间的关系.掌握对数换底公式:log log log c a c bb a=是解本题的关键.属于基础题.17．f(－3)>f(－π)【解析】由得是上的单调递增函数又解析：f (－3)>f (－π)【解析】由()()1212()[]0x x f x f x >－－ 得()f x 是R 上的单调递增函数，又3(3)()f f ππ>∴>－－，－－ ．18．【分析】由条件确定原点两侧函数的单调性和零点由函数的草图确定不等式的解集【详解】在R 上是奇函数且在上是增函数∴在上也是增函数由得由得作出的草图如图所示：则或由图象得所以或所以的解集为故答案为：【点睛 解析：(3,0)(0,3)-⋃【分析】由条件确定原点两侧函数的单调性和零点，由函数()f x 的草图确定不等式的解集. 【详解】()f x 在R 上是奇函数，且()f x 在(0,)+∞上是增函数，∴()f x 在(,0)-∞上也是增函数，由(3)0f -=，得(3)0f =，由(0)(0)f f =--，得(0)0f =， 作出()f x 的草图，如图所示：()0xf x <，则0()0x f x >⎧⎨<⎩ 或0()0x f x <⎧⎨>⎩，由图象得，所以03x <<或30x -<<，所以()0xf x <的解集为(3,0)(0,3)-⋃． 故答案为：(3,0)(0,3)-⋃． 【点睛】本题考查函数奇偶性、单调性的综合应用，考查数形结合思想，灵活作出函数的草图是解题关键．属于中档题．19．【分析】由f （x ）＝x2﹣（a+2）x+2﹣a ＜0可得x2﹣2x+1＜a （x+1）﹣1即直线在二次函数图像的上方的点只有一个整数1则满足题意结合图象即可求出【详解】f （x ）＝x2﹣（a+2）x+2﹣解析：12(,]23【分析】由f （x ）＝x 2﹣（a +2）x +2﹣a ＜0可得x 2﹣2x +1＜a （x +1）﹣1，即直线在二次函数图像的上方的点只有一个整数1，则满足题意，结合图象即可求出． 【详解】f （x ）＝x 2﹣（a +2）x +2﹣a ＜0， 即x 2﹣2x +1＜a （x +1）﹣1， 分别令y ＝x 2﹣2x +1，y＝a（x+1）﹣1，易知过定点（﹣1，﹣1），分别画出函数的图象，如图所示：∵集合A＝{x∈Z|f（x）＜0}中有且只有一个元素，即点（0，0）和点（2,1）在直线上或者其直线上方，点（1,0）在直线下方，结合图象可得∴10 {120 311aaa-≤--≤＜，解得12＜a23≤故答案为（12，23]【点睛】本题考查了二次函数的性质以及参数的取值范围，考查了转化思想和数形结合的思想，属于中档题20．或【分析】分集合为或有且仅有一个元素两种情况进行求解其中当集合有且仅有一个元素时注意对方程的二次项系数分和两种情况进行分别求解即可【详解】由题意可得集合为或有且仅有一个元素当时方程无实数根所以解得当解析：2a≥或1a=【分析】分集合A为φ或有且仅有一个元素两种情况进行求解,其中当集合A有且仅有一个元素时,注意对方程()21210a x x-++=的二次项系数分10a-=和10a-≠两种情况进行分别求解即可.【详解】由题意可得,集合A为φ或有且仅有一个元素,当Aφ=时,方程()21210a x x-++=无实数根,所以()21024110a a -≠⎧⎨∆=-⨯-⨯<⎩, 解得2a >,当集合A 有且只有一个元素时,方程()21210a x x -++=有且只有一个实数根,当10a -=,即1a =时,方程有一根12x =-符合题意;当10a -≠,即1a ≠时,判别式()224110a ∆=-⨯-⨯=,解得2a =;综上可知a 的取值范围为:2a ≥或1a =. 故答案为:2a ≥或1a = 【点睛】本题考查利用分类讨论思想求解方程根的个数问题;其中当一个方程的二次项系数含有参数,考虑其根的个数问题时,一定要注意对方程的二次项系数分为0和不为0两种情况进行讨论；属于中档题.三、解答题21．（1）1%，0.5%；（2）211()50x y =⨯，*x ∈N ；（3）7． 【分析】 （1）1次过滤后，11502⨯，2次过滤后，1115022⨯⨯，化简即可； （2）由每经过一次过滤均可使溶液杂质含量减少一半得12%(1)2xy =⨯-，*x ∈N ；（3）结合lg20.301=，解不等式11()0020.2%5x ⨯，即可得到x 的范围． 【详解】（1）1次过滤后，溶液杂质含量1110.011%502y =⨯==， 2次过滤后，溶液杂质含量21110.0050.5%5022y =⨯⨯==； （2）因为每经过一次过滤均可使溶液杂质含量减少一半，所以过滤次数为*()x x N ∈时溶液杂质含量111222%(1)()50x x y =⨯-=⨯，*x ∈N ．（3）设至少应过滤x 次才能是产品达到市场要求，则11()0020.2%5x ⨯， 即0121()10x ，所以121lg2100 6.7lg 2lgx=≈， 又*x ∈N ，所以7x ，即至少应过滤7次才能使产品达到市场要求． 【点睛】与实际应用相结合的题型也是高考命题的动向，这类问题的特点是通过现实生活的事例考查书本知识，解决这类问题的关键是耐心读题、仔细理解题，只有吃透题意，才能将实际问题转化为数学模型进行解答.22．（1）7,032.40.2,3x F x x <≤⎧=⎨->⎩，212.3 1.6(0)4000C x x x =++>；（2）100km. 【分析】（1）根据在3km 以内（含3km ）的路程统一按起步价7元收费，超过3km 以外的路程按2.4元/km 收费求得F ，设折旧费2z kx =，由路程为20km 时，折旧费为0.1元.代入求得k ，再根据运输成本包含固定费用，二是燃油费和折旧费求得C . （2）根据F Cy x-=，结合（1）求得y ，再根据分段函数的最值的求法求解. 【详解】（1）由题意得：7,037 2.4(3),3x F x x <≤⎧=⎨+->⎩，.即7,032.40.2,3x F x x <≤⎧=⎨->⎩.设折旧费2z kx =，将(20,0.1)代入， 得0.1400k =，解得14000k =. 所以212.3 1.6(0)4000C x x x =++>. （2）因为F Cy x-=， 所以 4.7 1.6,2340002.50.8,34000x x x y x x x ⎧--≤≤⎪⎪=⎨⎛⎫⎪-+> ⎪⎪⎝⎭⎩，当3x >时，由基本不等式，得0.80.75y ≤-=， 当且仅当100x =时取等号.当23x ≤≤时，由y 在[2,3]上单调递减， 当2x =时，得max 10.750.752000y =-<. 综上所述，该市出租汽车一次载客路程为100km 时，每千米的收益y 取得最大值. 【点睛】方法点睛：(1)很多实际问题中，变量间的关系不能用一个关系式给出，这时就需要构建分段函数模型，如出租车的票价与路程的函数就是分段函数．(2)求函数最值常利用基本不等式法、导数法、函数的单调性等方法．在求分段函数的最值时，应先求每一段上的最值，然后比较得最大值、最小值．23．（1）2-；（2）当1a >时，()0f x >的解集为()210,,a a ⎛⎫+∞ ⎪⎝⎭，当01a <<时；()210,,a a ⎛⎫+∞ ⎪⎝⎭（3）(3,11,22⎫⎤⎪⎢⎦⎪⎣⎭.【分析】（1）将2a =直接代入解析式计算即可.（2）将()2()log log 20a a f x x x =-->整理为()()log 2log 10a a x x -+>，解得log 1<-a x 或log 2a x >，再对a 讨论即可解不等式.（3）将问题转化为min ()4f x ≥，分别分1a >和01a <<讨论，求()f x 最小值，令其大于4，即可求解.【详解】（1）当2a =时，()()222log log 2f x x x =--()21122f ∴=--=-（2）由()0f x >得：()()()2log log 2log 2log 10a a a a x x x x --=-+>log 1a x ∴<-或log 2a x >当1a >时，解不等式可得：10x a <<或2x a > 当01a <<时，解不等式可得：1x a>或20x a <<综上所述：当1a >时，()0f x >的解集为()210,,a a ⎛⎫+∞ ⎪⎝⎭；当01a <<时，()0f x >的解集为()210,,aa ⎛⎫+∞ ⎪⎝⎭（3）由()4f x ≥得：()()()2log log 6log 3log 20a a a a x x x x --=-+≥log 2a x ∴≤-或log 3a x ≥①当1a >时，()max log log 4a a x =，()min log log 2a a x =2log 42loga a a -∴≤-=或3log 23log a a a ≥=，解得：1a <≤②当01a <<时，()max log log 2a a x =，()min log log 4a a x =2log 22log a a a -∴≤-=或3log 43log a a a ≥=，解得：12a ≤<综上所述：a 的取值范围为(31,2⎫⎤⎪⎦⎪⎣⎭【点睛】本题主要考查了复合函数的单调性、考查函数的最值和恒成立问题、考查分类讨论的思想，属于中档题. 24．最大值为43，无最小值. 【分析】首先根据对数真数大于0，解不等式2340x x -+>求出定义域M ，然后利用换元法，即可求出函数()f x 的最值． 【详解】由2340x x -+>，解得1x <或3x >，所以(,1)(3,)M =-∞+∞，22()234423(2)x x x x f x +=-⨯=⨯-⨯，令2x t =，由x M ∈得02t <<或8t >，则原函数可化为2224()433()33g t t t t =-=--+，其对称轴为23t =，所以当02t <<时，4()(4,]3g t ∈-；当8t >时，()(,160)g t ∈-∞-．所以当23t =，即223log x =时，()g t 取得最大值43，即函数()f x 取得最大值43，函数()g t 无最小值，故函数()f x 无最小值．【点睛】本题主要考查函数定义域的求法及换元法求函数最值．25．（1）定义域为[1,1]-，值域为2]（2）1m ≤-或1m ≥ 【分析】（1）由1010x x +≥⎧⎨-≥⎩可得定义域，先求出2()f x 的值域，再开方求出()f x 的值域；（2）换元，令t =2]∈，根据对勾函数的单调性求出2()()4t h x g t t ==+的最大值，则不等式转化为21310244am m -+-≥对任意[1,1]a ∈-都恒成立，利用一次函数的图象列式可解得结果. 【详解】 （1）由函数有意义得1010x x +≥⎧⎨-≥⎩，解得11x -≤≤，所以函数()f x 的定义域为[1,1]-，因为22()2f x ==+[2,4]∈，又()0f x ≥，所以()2]f x ∈.（2）()h x ==令t =2]∈，则22t =-，所以2()()4t h x g t t ==+14t t=+， 因为()g t在2]上递增，所以当2t =时，()g t 取得最大值221(2)244g ==+，即max 1()4h x =， 所以不等式231()42h x m am ≤-对于任意[1,1]x ∈-恒成立，转化为2311424m am -≥对任意[1,1]a ∈-都恒成立，即21310244am m -+-≥对任意[1,1]a ∈-都恒成立， 所以2213102441310244m m m m ⎧+-≥⎪⎪⎨⎪-+-≥⎪⎩，即2232103210m m m m ⎧+-≥⎨--≥⎩，解得113113m m m m ⎧≤-≥⎪⎪⎨⎪≤-≥⎪⎩或或，所以1m ≤-或1m ≥. 【点睛】结论点睛：本题考查不等式的恒成立与有解问题，可按如下规则转化： ①若()k f x ≥在[,]a b 上恒成立，则max ()k f x ≥； ②若()k f x ≤在[,]a b 上恒成立，则min ()k f x ≤； ③若()k f x ≥在[,]a b 上有解，则min ()k f x ≥； ④若()k f x ≤在[,]a b 上有解，则max ()k f x ≤； 26．（1）()U {|12A x B x =-≤<或45}x <≤．（2）514a ≤≤． 【分析】（1）解不等式确定集合,A B ，然后由集合运算法则计算； （2）由C A A =，C B B =，得B C A ⊆⊆，利用包含关系可得参数满足的不等关系，从而得出结论．【详解】（1）{}2450{|15}A x x x x x =--≤=-≤≤，{}2124{|022}{|24}x B x x x x x -=≤≤=≤-≤=≤≤．∴{|2UB x x =<或4}x >，∴()U{|12Ax B x =-≤<或45}x <≤．（2）∵C A A =，C B B =，∴B C A ⊆⊆，∴12445aa-≤≤⎧⎨≤≤⎩，解得514a≤≤．【点睛】关键点点睛：本题考查集合的综合运算，考查集合的包含关系．集合的运算中确定集合中的元素是解题关键．本题有两个结论值得注意：C A A C A=⇔⊆，C B B=B C⇔⊆．。

章末复习一、知识导图二、要点归纳1.圆的方程(1)圆的标准方程：(x－a)2＋(y－b)2＝r2.(2)圆的一般方程：x2＋y2＋Dx＋Ey＋F＝0(D2＋E2－4F>0).2.点和圆的位置关系设点P(x0，y0)及圆的方程(x－a)2＋(y－b)2＝r2.(1)(x0－a)2＋(y0－b)2>r2⇔点P在圆外.(2)(x0－a)2＋(y0－b)2<r2⇔点P在圆内.(3)(x0－a)2＋(y0－b)2＝r2⇔点P在圆上.3.直线与圆的位置关系设直线l与圆C的圆心之间的距离为d，圆的半径为r，则d>r⇒相离；d＝r⇒相切；d<r⇒相交.4.圆与圆的位置关系设C1与C2的圆心距为d，半径分别为r1与r2，则位置关系外离外切相交内切内含图示d与r1，r2的d>r1＋r2d＝r1＋r2|r1－r2|<d<r1＋r2d＝|r1－r2| d<|r1－r2|关系(1)求相交两圆的弦长时，可先求出两圆公共弦所在直线的方程，再利用相交两圆的几何性质和勾股定理来求弦长.(2)过圆C1：x2＋y2＋D1x＋E1y＋F1＝0与圆C2：x2＋y2＋D2x＋E2y＋F2＝0的交点的直线方程为(D1－D2)x＋(E1－E2)y＋F1－F2＝0.5.空间直角坐标系(1)建立的空间直角坐标系要遵循右手法则，空间上的任意一点都与有序实数组(x，y，z)一一对应.(2)空间中P1(x1，y1，z1)，P2(x2，y2，z2)之间的距离|P1P2|＝(x1－x2)2＋(y1－y2)2＋(z1－z2)2.(3)可利用“关于谁对称，谁保持不变，其余坐标相反”的方法来求空间直角坐标系下的对称点.题型一圆的方程例1一个圆和已知圆x2＋y2－2x＝0相外切，并与直线l：x＋3y＝0相切于M(3，－3)点，求该圆的方程.考点题点解∵圆C与圆x2＋y2－2x＝0相外切，故两个圆心之间的距离等于半径的和，又∵圆C与直线l：x＋3y＝0相切于M(3，－3)点，可得圆心与点M(3，－3)的连线与直线x＋3y＝0垂直，其斜率为 3.设圆C的圆心为(a，b)，则⎩⎪⎨⎪⎧ b ＋3a －3＝3，(a －1)2＋b 2＝1＋|a ＋3b |2.解得a ＝4，b ＝0，r ＝2或a ＝0，b ＝－43，r ＝6，∴圆C 的方程为(x －4)2＋y 2＝4或x 2＋(y ＋43)2＝36.反思感悟 求圆的方程主要是根据圆的标准方程和一般方程，利用待定系数法求解，采用待定系数法求圆的方程的一般步骤：第一步：选择圆的方程的某一形式.第二步：由题意得a ，b ，r (或D ，E ，F )的方程(组).第三步：解出a ，b ，r (或D ，E ，F ).第四步：代入圆的方程.注：解题时充分利用圆的几何性质可获得解题途径，减少运算量，例如：圆的切线垂直于经过切点的半径；圆心与弦的中点连线垂直于弦；当两圆相交时，连心线垂直平分两圆的公共弦；当两圆相切时，连心线过切点等.跟踪训练1 (1)如图所示，圆C 与x 轴相切于点T (1,0)，与y 轴正半轴交于两点A ，B (B 在A 的上方)，且|AB |＝2，则圆C 的标准方程为____________________.答案 (x －1)2＋(y －2)2＝2解析 取AB 的中点D ，连接CD ，AC ，则CD ⊥AB .由题意知，|AD |＝|CD |＝1，故|AC |＝|CD |2＋|AD |2＝2，即圆C 的半径为 2.又因为圆C 与x 轴相切于点T (1,0)，所以圆心C (1，2)，故圆的标准方程为(x －1)2＋(y －2)2＝2.(2)求半径为10，圆心在直线y ＝2x 上，被直线x －y ＝0截得的弦长为42的圆的方程. 解 设圆的方程为(x －a )2＋(y －b )2＝r 2，则圆心坐标为(a ，b )，半径r ＝10，圆心(a ，b )到直线x －y ＝0的距离d ＝|a －b |2， 由半弦长，弦心距，半径组成的直角三角形得，d 2＋⎝⎛⎭⎫4222＝r 2， 即(a －b )22＋8＝10， ∴(a －b )2＝4，又∵b ＝2a ，∴a ＝2，b ＝4或a ＝－2，b ＝－4，故所求圆的方程是(x －2)2＋(y －4)2＝10或(x ＋2)2＋(y ＋4)2＝10.题型二 直线与圆、圆与圆的位置关系例2 (1)已知圆M ：x 2＋y 2－2ay ＝0(a >0)截直线x ＋y ＝0所得线段的长度是22，则圆M 与圆N ：(x －1)2＋(y －1)2＝1的位置关系是( )A.内切B.相交C.外切D.相离考点题点答案 B解析 由垂径定理得⎝⎛⎭⎫a 22＋(2)2＝a 2，解得a 2＝4， ∴圆M ：x 2＋(y －2)2＝4， ∴圆M 与圆N 的圆心距d ＝(0－1)2＋(2－1)2＝ 2.∵2－1<2<2＋1，∴两圆相交.(2)已知直线l ：x －3y ＋6＝0与圆x 2＋y 2＝12交于A ，B 两点，过A ，B 分别作l 的垂线与x 轴交于C ，D 两点，则|CD |＝________.考点题点答案 4解析 联立⎩⎨⎧ x －3y ＋6＝0，x 2＋y 2＝12，消去x 得y 2－33y ＋6＝0， 解得⎩⎨⎧ x ＝－3，y ＝3或⎩⎨⎧x ＝0，y ＝2 3. 不妨设A (－3，3)，B (0,23)，则过点A 且与直线l 垂直的直线方程为3x ＋y ＋23＝0，令y ＝0得x C ＝－2.同理得过点B 且与l 垂直的直线与x 轴交点的横坐标x D ＝2，∴|CD |＝4.反思感悟 直线与圆、圆与圆的主要题型为：①位置关系的判断，②弦长问题，③求圆的方程.解决问题的方法主要有两种，一种代数法，一种几何法.跟踪训练2 (1)圆(x ＋1)2＋y 2＝2的圆心到直线y ＝x ＋3的距离为( )A.1B.2C. 2D.2 2考点题点答案 C(2)设直线y ＝x ＋2a 与圆C ：x 2＋y 2－2ay －2＝0相交于A ，B 两点，若|AB |＝23，则圆C 的面积为________.考点题点答案 4π解析 x 2＋y 2－2ay －2＝0，即x 2＋(y －a )2＝a 2＋2，则圆心为C (0，a ).又|AB |＝23，C 到直线y ＝x ＋2a 的距离为|0－a ＋2a |2， 所以⎝⎛⎭⎫2322＋⎝ ⎛⎭⎪⎫|0－a ＋2a |22＝a 2＋2， 得a 2＝2，所以圆C 的面积为π(a 2＋2)＝4π.题型三 对称问题例3 从点B (－2,1)发出的光线经x 轴上的点A 反射，反射光线所在的直线与圆x 2＋y 2＝12相切，求点A 的坐标.考点题点解 点B (－2,1)关于x 轴对称的点为B ′(－2，－1)，易知反射光线所在直线的斜率存在，设反射光线所在的直线方程为y ＋1＝k (x ＋2)，即kx －y ＋2k －1＝0.由题意，得|0－0＋2k －1|k 2＋1＝12， 化简得7k 2－8k ＋1＝0，解得k ＝1或k ＝17， 故所求切线方程为x －y ＋1＝0或x －7y －5＝0.令y ＝0，则x ＝－1或x ＝5.所以A 点的坐标为(－1,0)或(5,0).反思感悟 (1)对称的两种类型即轴对称与中心对称.(2)准确把握对称的几何性质.(3)圆的对称图形关键是圆心的对称，其半径不变.跟踪训练3 若圆C 的半径为1，其圆心与点(1,0)关于直线y ＝x 对称，则圆C 的标准方程为________________________________________________________________________. 答案 x 2＋(y －1)2＝1解析 由题意知圆C 的圆心为(0,1)，半径为1，所以圆C 的标准方程为x 2＋(y －1)2＝1.题型四 圆中的最值问题例4 圆x 2＋y 2＋2ax ＋2ay ＋2a 2－1＝0与x 2＋y 2＋2bx ＋2by ＋2b 2－2＝0的公共弦长的最大值为( )A.2 2B.2C. 2D.1考点 与圆有关的最值问题题点 与圆的几何性质有关的最值答案 B解析 由题意得，两圆的标准方程分别为(x ＋a )2＋(y ＋a )2＝1和(x ＋b )2＋(y ＋b )2＝2，两圆的圆心坐标分别为(－a ，－a )，(－b ，－b )，半径分别为1，2，则当公共弦为圆(x ＋a )2＋(y ＋a )2＝1的直径时，公共弦长最大，最大值为2.反思感悟 与圆有关的最值问题包括(1)求圆O 上一点到圆外一点P 的最大距离、最小距离：d max ＝|OP |＋r ，d min ＝||OP |－r |.(2)求圆上的点到某条直线的最大、最小距离：设圆心到直线的距离为m ，则d max ＝m ＋r ，d min＝|m －r |.(3)已知点的运动轨迹是(x －a )2＋(y －b )2＝r 2，求①y x ；②y －m x －n；③x 2＋y 2等式子的最值，一般是运用几何法求解.跟踪训练4 已知P 是直线3x ＋4y ＋8＝0上的动点，P A ，PB 是圆x 2＋y 2－2x －2y ＋1＝0的两条切线，A ，B 是切点，C 是圆心，那么四边形P ACB 的面积的最小值为________. 考点 与圆有关的最值问题题点 与面积有关的最值答案 2 2解析 圆x 2＋y 2－2x －2y ＋1＝0的圆心为C (1,1)，半径为1，由题意知，当圆心C 到点P 的距离最小时(即为圆心到直线的距离)，四边形的面积最小，又圆心到直线的距离d ＝|3＋4＋8|32＋42＝3， ∴|P A |＝|PB |＝d 2－r 2＝22，∴S 四边形P ACB ＝2×12|P A |r ＝2 2.1.以点(－3,4)为圆心，且与x 轴相切的圆的方程是( )A.(x －3)2＋(y ＋4)2＝16B.(x ＋3)2＋(y －4)2＝16C.(x －3)2＋(y ＋4)2＝9D.(x ＋3)2＋(y －4)2＝9考点 圆的标准方程题点 求与某直线相切的圆的标准方程答案 B2.已知圆C 与直线x －y ＝0和x －y －4＝0都相切，圆心在直线x ＋y ＝0上，则圆C 的方程为( )A.(x ＋1)2＋(y －1)2＝2B.(x －1)2＋(y ＋1)2＝2C.(x －1)2＋(y －1)2＝2D.(x ＋1)2＋(y ＋1)2＝2题点 求圆的标准方程答案 B3.两圆x 2＋y 2－6x ＋16y －48＝0与x 2＋y 2＋4x －8y －44＝0的公切线的条数为( )A.4B.3C.2D.1考点 圆与圆的位置关系题点 两圆的位置关系与其公切线答案 C解析 两圆的标准方程分别为(x －3)2＋(y ＋8)2＝121；(x ＋2)2＋(y －4)2＝64，则两圆的圆心与半径分别为C 1(3，－8)，r 1＝11；C 2(－2,4)，r 2＝8.圆心距为|C 1C 2|＝(3＋2)2＋(－8－4)2＝13.∵r 1－r 2<|C 1C 2|<r 1＋r 2，∴两圆相交，则公切线共2条.4.经过两个定点A (a,0)，A 1(a ，a )，且圆心在直线y ＝13x 上的圆的方程为________________________.答案 ⎝⎛⎭⎫x －32a 2＋⎝⎛⎭⎫y －a 22＝a 22 解析 圆过点A (a,0)，A 1(a ，a )，则圆心在直线y ＝a 2上. 又圆心在直线y ＝13x 上， 所以圆心坐标为⎝⎛⎭⎫32a ，a 2，则半径r ＝⎝⎛⎭⎫a －32a 2＋⎝⎛⎭⎫－a 22＝22|a |， 故圆的方程为⎝⎛⎭⎫x －32a 2＋⎝⎛⎭⎫y －a 22＝a 22. 5.已知直线x －my ＋3＝0和圆x 2＋y 2－6x ＋5＝0.(1)当直线与圆相切时，求实数m 的值；(2)当直线与圆相交，且所得弦长为2105时，求实数m 的值. 考点 直线和圆的位置关系解 (1)因为圆x 2＋y 2－6x ＋5＝0可化为(x －3)2＋y 2＝4，所以圆心坐标为(3,0)，r ＝2. 因为直线x －my ＋3＝0与圆相切， 所以|3＋3|1＋(－m )2＝2， 解得m ＝±2 2.(2)圆心(3,0)到直线x －my ＋3＝0的距离为d ＝|3＋3|1＋(－m )2.由24－⎝ ⎛⎭⎪⎫|3＋3|1＋(－m )22＝2105， 得2＋2m 2＝20m 2－160，即m 2＝9.故m ＝±3.。

高中数学必修第一册《一元二次函数、方程和不等式》期末复习专项训练一、单选题l. (2022·四川绵阳·高一期末〉下列结论正确的是（〉A.若的b，则。

c>bc c.若。

＞b，则。

＋c>b+cl I B.若α＞b，则－〉－a D D.着。

＞b，则。

2> b22.(2022·辽宁·新民市第一高级中学高一期末〉已知α＜b<O，则（〉A.a2 <abB.ab<b2C.a1 <b1D.a2 >b i3.(2022·陕西汉中·高一期末〉若关于工的不等式，咐2+2x+m>O的解集是R，则m的取值范围是（〉A.(I, +oo)B.(0, I〕C.( -J, I)D.(J, +oo)4.(2022·广东珠海高一期末〉不等式。

＋l)(x+3)<0的解集是（〉A.RB.②c.｛对－3<x<-I} D.{xi x<-3，或x>-l}5. (2022·四川甘孜·高一期末〉若不等式似2+bx-2<0的解集为｛xl-2<x<I｝，则。

÷b=( )A.-2B.OC.ID.26. (2022·湖北黄石·商一期末〉若关于X的不等式x2-ax’＋7＞。

在（2,7）上有实数解，则α的取值范围是（〉A.（唱，8)B.（叫8] c.（叫2./7) D.（斗）7.(2022·新疆乌市一中高一期末〉已知y=(x-m)(x-n)+2022(n> m），且α，β（α〈别是方程y=O的两实数根，则α，β，111,n的大小关系是（〉A.α＜m<n＜βC.m＜α〈β＜nB.m＜α＜n＜βD.α＜m＜β＜n8.(2022·浙江·杭州四中高一期末〉已失11函数y＝κ－4+...2....(x>-1），当x=a时，y取得最小值b，则。

第三章 函数的概念与性质考试时间120分钟，满分150分．一、单项选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．函数y ＝x 2＋1的值域是( B ) A ．[0，＋∞) B ．[1，＋∞) C ．(0，＋∞)D ．(1，＋∞)[解析] 由题意知，函数y ＝x 2＋1的定义域为R ，则x 2＋1≥1，∴y ≥1. 2．已知f (12x －1)＝2x －5，且f (a )＝6，则a 等于( B )A ．－74B ．74C ．43D ．－43[解析] 设12x －1＝t ，则x ＝2t ＋2，t ∈R ，∴f (t )＝2(2t ＋2)－5＝4t －1，∴f (x )＝4x －1.由f (a )＝6得4a －1＝6，即a ＝74.3．(2019·山东烟台高一期中测试)已知函数y ＝f (x )的部分x 与y 的对应关系如下表：则f [f (4)]A ．－1 B ．－2 C ．－3D ．3[解析] 由图表可知，f (4)＝－3，∴f [f (4)]＝f (－3)＝3.4．已知幂函数f (x )＝x α的图象过点(2，12)，则函数g (x )＝(x －2)f (x )在区间[12，1]上的最小值是( C )A ．－1B ．－2C ．－3D ．－4[解析] 由已知得2α＝12，解得α＝－1，∴g (x )＝x －2x ＝1－2x 在区间[12，1]上单调递增，则g (x )min ＝g (12)＝－3，故选C ．5．(2019·吉林榆树一中高一期中测试)已知函数f (x －1)＝x 2－3，则f (2)的值是( B ) A ．－2B ．6C．1 D．0[解析]解法一：令x－1＝2，则x＝3，∴f(2)＝32－3＝6.解法二：令x－1＝t，则x＝t＋1，∴f(t)＝(t＋1)2－3＝t2＋2t－2，∴f(2)＝22＋2×2－2＝6.6．(2019·吉林乾安七中高一期测试)已知函数f(x)＝(m－1)x2＋(m－2)x＋m2－7m＋12为偶函数，则m的值是(B)A．1 B．2C．3 D．4[解析]由题意得m－2＝0，∴m＝2.7．“龟兔赛跑”讲述了这样一个故事：领先的兔子看着缓缓爬行的乌龟，骄傲起来，睡了一觉，当它醒来时发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点．用s1和s2分别表示乌龟和兔子所行的路程，t为时间，s为路程，则下列图象中与故事情节相吻合的是(D)[解析]根据题意：s1是匀速运动，路程一直在增加，s2有三个阶段：开始是路程增加，中间睡觉，路程不变；醒来时发现乌龟快到终点了急忙追赶，路程增加；但是乌龟还是先到终点，即s1在s2上方，故选D．8．已知定义在R上的奇函数f(x)满足f(x－4)＝－f(x)且在区间[0,2]上是增函数，则(D)A．f(－1)<f(3)<f(4) B．f(4)<f(3)<f(－1)C．f(3)<f(4)<f(－1) D．f(－1)<f(4)<f(3)[解析]因为f(x)是R上的奇函数，所以f(0)＝0，又f(x)满足f(x－4)＝－f(x)，则f(4)＝－f(0)＝0，又f(x)＝－f(－x)且f(x－4)＝－f(x)，所以f(3)＝－f(－3)＝－f(1－4)＝f(1)，又f (x )在区间[0,2]上是增函数，所以f (1)>f (0)，即f (1)>0，所以f (－1)＝－f (1)<0，f (3)＝f (1)>0，可得f (－1)<f (4)<f (3)，故选D ． 二、多项选择题(本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多个选项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得3分)9．下列幂函数中，其图象过点(0,0)，(1,1)，且为偶函数的是( BD )A ．y ＝x 12B ．y ＝x 2C ．y ＝x－14D ．y ＝x 4[解析] 由题设知该幂函数为偶函数，且幂指数大于0，故选BD ．10．若奇函数f (x )在[3,7]上是增函数，且最小值是1，则它在[－7，－3]上( AB ) A ．是增函数 B ．最大值是－1 C ．是减函数D ．最小值是－1[解析] ∵奇函数在对称区间上的单调性相同，最值互为相反数．∴y ＝f (x )在[－7，－3]上有最大值－1且为增函数．故选AB ．11．已知f (x )＝3－2|x |，g (x )＝x 2－2x ，F (x )＝⎩⎪⎨⎪⎧g (x )(若f (x )≥g (x ))f (x )(若f (x )<g (x ))，则F (x )( BC )A ．最小值－1B ．最大值为7－27C ．无最小值D ．无最大值[解析] 作出F (x )的图象，如图实线部分，知有最大值而无最小值，且最大值不是3，故选BC ．12．已知f (x )是定义在[0，＋∞)上的函数，根据下列条件，可以断定f (x )是增函数的是( CD )A ．对任意x ≥0，都有f (x ＋1)>f (x )B ．对任意x 1，x 2∈[0，＋∞)，且x 1≥x 2，都有f (x 1)≥f (x 2)C ．对任意x 1，x 2∈[0，＋∞)，且x 1－x 2<0，都有f (x 1)－f (x 2)<0D ．对任意x 1，x 2∈[0，＋∞)，且x 1≠x 2，都有f (x 1)－f (x 2)x 1－x 2>0[解析] 根据题意，依次分析选项：对于选项A ，对任意x ≥0，都有f (x ＋1)>f (x )，不满足函数单调性的定义，不符合题意；对于选项B ，当f (x )为常数函数时，对任意x 1，x 2∈[0，＋∞)，都有f (x 1)＝f (x 2)，不是增函数，不符合题意；对于选项C ，对任意x 1，x 2∈[0，＋∞)，且x 1－x 2<0，都有f (x 1)－f (x 2)<0，符合题意；对于选项D ，对任意x 1，x 2∈[0，＋∞)，设x 1>x 2，若f (x 1)－f (x 2)x 1－x 2>0，必有f (x 1)－f (x 2)>0，则函数在[0，＋∞)上为增函数，符合题意．三、填空题(本大题共4小题，每小题5分，共20分．) 13．(2019·陕西黄陵中学高一期末测试)函数f (x )＝4－2x ＋1x ＋1的定义域是__{x |x ≤2且x ≠－1}__.[解析] 由题意得⎩⎪⎨⎪⎧4－2x ≥0x ＋1≠0，解得x ≤2且x ≠－1，∴函数f (x )的定义域为{x |x ≤2且x ≠－1}．14．已知f (x )＝⎩⎪⎨⎪⎧2x ，x >0，f (x ＋1)，x ≤0，则f (－43)＋f (43)等于__4__.[解析] ∵f (x )＝⎩⎪⎨⎪⎧2x ，x >0，f (x ＋1)，x ≤0，∴f (－43)＝f (－43＋1)＝f (－13)＝f (－13＋1)＝f (23)＝23×2＝43，f (43)＝2×43＝83，∴f (－43)＋f (43)＝43＋83＝4.15．已知幂函数f (x )＝x α的图象经过点(9,3)，则f (12)＝2，函数f (1x －1)的定义域为__(0,1]__.[解析] 幂函数f (x )的图象经过点(9,3)，所以3＝9α，所以α＝12，所以幂函数f (x )＝x ，故f (12)＝22，故1x－1≥0，解得0<x ≤1.16．设α∈{1,2,3，－1}，则使y ＝x α为奇函数且在(0，＋∞)上单调递增的α的值为__1或3__.[解析] 当α＝1时，y ＝x 为奇函数，且在R 上单调递增，满足题意；当α＝2时，y ＝x 2为偶函数不满足题意；当α＝3时，y ＝x 3为奇函数，且在R 上单调递增，满足题意；当α＝－1时，y ＝1x为奇函数，但在(0，＋∞)上单调递减，不满足题意．四、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分)已知函数f (x )＝ax ＋b ，且f (1)＝2，f (2)＝－1. (1)求f (m ＋1)的值；(2)判断函数f (x )的单调性，并用定义证明．[解析] (1)由f (1)＝2，f (2)＝－1，得a ＋b ＝2,2a ＋b ＝－1，即a ＝－3，b ＝5，故f (x )＝－3x ＋5，f (m ＋1)＝－3(m ＋1)＋5＝－3m ＋2.(2)f (x )在R 上是减函数．证明：任取x 1<x 2(x 1，x 2∈R )，则f (x 2)－f (x 1)＝(－3x 2＋5)－(－3x 1＋5)＝3x 1－3x 2＝3(x 1－x 2)，因为x 1<x 2，所以f (x 2)－f (x 1)<0，即函数f (x )在R 上单调递减． 18．(本小题满分12分)已知函数f (x )＝3－axa －1(a ≠1)． (1)若a >0，求f (x )的定义域；(2)若f (x )在区间(0,1]上单调递减，求实数a 的取值范围．[解析] (1)当a >0且a ≠1时，由3－ax ≥0得x ≤3a ，即函数f (x )的定义域是(－∞，3a ]．(2)当a －1>0，即a >1时，要使f (x )在(0,1]上单调递减，则需3－a ×1≥0，此时1<a ≤3. 当a －1<0，即a <1时，要使f (x )在(0,1]上单调递减，则需－a >0，且3－a ×1≥0，此时a <0.综上所述，所求实数a 的取值范围是(－∞，0)∪(1,3]．19．(本小题满分12分)某商品在近30天内每件的销售价格P (元)和时间t (天)的函数关系为P ＝⎩⎪⎨⎪⎧t ＋20，0<t <25，－t ＋100，25≤t ≤30(t ∈N *)．设商品的日销售量Q (件)与时间t (天)的函数关系为Q ＝40－t (0<t ≤30，t ∈N *)，求这种商品的日销售金额的最大值，并指出日销售金额最大时是第几天．[解析] 设日销售金额为y 元，则y ＝PQ ，所以y ＝⎩⎪⎨⎪⎧－t 2＋20t ＋800(0<t <25，t ∈N *)，t 2－140t ＋4 000(25≤t ≤30，t ∈N *). 当0<t <25且t ∈N *时，y ＝－(t －10)2＋900， 所以当t ＝10时，y max ＝900.①当25≤t ≤30且t ∈N *时，y ＝(t －70)2－900， 所以当t ＝25时，y max ＝1 125.②结合①②得y max ＝1 125.因此这种商品日销售金额的最大值为1 125元，且在第25天日销售金额最大．20．(本小题满分12分)已知二次函数f (x )的最小值为1，且f (0)＝f (2)＝3. (1)求f (x )的解析式；(2)若f (x )在区间[2a ，a ＋1]上不单调，求实数a 的取值范围．[解析] (1)由f (0)＝f (2)知二次函数f (x )关于直线x ＝1对称，又函数f (x )的最小值为1， 故可设f (x )＝a (x －1)2＋1，由f (0)＝3，得a ＝2. 故f (x )＝2x 2－4x ＋3.(2)要使函数不单调，则2a <1<a ＋1， 则0<a <12.故实数a 的取值范围(0，12)．21．(本小题满分12分)如果函数y ＝f (x )(x ∈D )满足： ①f (x )在D 上是单调函数；②存在闭区间[a ，b ]⊆D ，使f (x )在区间[a ，b ]上的值域也是[a ，b ]． 那么就称函数y ＝f (x )为闭函数．试判断函数y ＝x 2＋2x 在[－1，＋∞)内是否为闭函数．如果是闭函数，那么求出符合条件的区间[a ，b ]；如果不是闭函数，请说明理由．[解析] 设x 1，x 2是[－1，＋∞)内的任意两个不相等的实数，且－1≤x 1<x 2，则有f (x 2)－f (x 1)＝(x 22＋2x 2)－(x 21＋2x 1)＝(x 22－x 21)＋2(x 2－x 1)＝(x 2－x 1)(x 1＋x 2＋2)． ∵－1≤x 1<x 2，∴x 2－x 1>0，x 1＋x 2＋2>0. ∴(x 2－x 1)(x 1＋x 2＋2)>0. ∴f (x 2)>f (x 1)．∴函数y ＝x 2＋2x 在[－1，＋∞)内是增函数． 假设存在符合条件的区间[a ，b ]，则有⎩⎪⎨⎪⎧ f (a )＝a f (b )＝b ，即⎩⎪⎨⎪⎧a 2＋2a ＝ab 2＋2b ＝b. 解得⎩⎪⎨⎪⎧ a ＝0b ＝0或⎩⎪⎨⎪⎧ a ＝0b ＝－1或⎩⎪⎨⎪⎧ a ＝－1b ＝0或⎩⎪⎨⎪⎧a ＝－1b ＝－1.又∵－1≤a <b ，∴⎩⎪⎨⎪⎧a ＝－1b ＝0.∴函数y ＝x 2＋2x 在[－1，＋∞)内是闭函数，符合条件的区间是[－1,0]．22．(本小题满分12分)已知函数y ＝x ＋tx 有如下性质：如果常数t >0，那么该函数在(0，t )上是减函数，在[t ，＋∞)上是增函数．(1)已知f (x )＝4x 2－12x －32x ＋1，x ∈[0,1]，利用上述性质，求函数f (x )的单调区间和值域；(2)对于(1)中的函数f (x )和函数g (x )＝－x －2a ，若对任意x 1∈[0,1]，总存在x 2∈[0,1]，使得g (x 2)＝f (x 1)成立，求实数a 的值．[解析] (1)y ＝f (x )＝4x 2－12x －32x ＋1＝2x ＋1＋42x ＋1－8，设u ＝2x ＋1，x ∈[0,1]，∴1≤u ≤3，则y ＝u ＋4u －8，u ∈[1,3]．由已知性质得，当1≤u ≤2，即0≤x ≤12时，f (x )单调递减，所以单调减区间为[0，12]；当2≤u ≤3，即12≤x ≤1时，f (x )单调递增，所以单调增区间为[12，1]；由f (0)＝－3，f (12)＝－4，f (1)＝－113，得f (x )的值域为[－4，－3]．(2)g (x )＝－x －2a 为减函数，故g (x )∈[－1－2a ，－2a ]，x ∈[0,1]．由题意知，f (x )的值域是g (x )的值域的子集，∴⎩⎪⎨⎪⎧－1－2a ≤－4，－2a ≥－3，∴a ＝32.。

2020-2021学年湖北省荆门市钟祥实验中学高二（下）期末数学复习练习试卷（8）一、选择题：本大题10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是满足题目要求的.A ．12B ．1C ．32D ．21．（5分）设m ∈R ，且2m 1−i+1-i 是实数，则m =（ ）A ．{x |x ≤0}B ．{x |2≤x ≤4}C ．{x |0≤x <2或x >4}D ．{x |0<x ≤2或x ≥4}2．（5分）已知全集为R ，集合A ={x |（12）x ≤1}，B ={x |x 2-6x +8≤0}，则A ∩（∁R B ）=（ ）A ．①②B ．①③C ．②③D ．③④3．（5分）给出下列结论：①“a >b ”是“a 2>b 2”的充分条件；②若p ：∀x ∈R ，x 2+2x +2>0，则￢p ：∃x 0∈R ，x 02+2x 0+2≤0；③“若m >0，则方程x 2+x -m =0有实数根”的否命题是“若m ≤0，则方程x 2+x -m =0没有实数根”；④若p∧q 是假命题，则p 、q 均为假命题．则其中正确结论的序号是（ ）A ．[-13，5]B ．[-13，7]C ．[0，7]D ．[5，7]4．（5分）已知变量x ,y 满足约束条件V Y Y W Y Y X x −y +2≥0x +y −4≤0x −2y −1≤0，则目标函数z =2x +y 的取值范围是（ ）A ．-10B ．10C ．-6D ．65．（5分）执行如图所示的程序框图，输出的S 值为（ ）二、填空题:本大题共5小题，每小题5分，共25分.答错位置，书写不清，模棱两可均不得分.A ．2B ．2C ．22D ．306．（5分）在△ABC 中，内角A 、B 、C 的对边分别是a 、b 、c ,若cosB =34，sinC =2sinA ，且S △ABC =74，则b =（ ）√√√√A ．1B ．2C ．3D ．47．（5分）对于非零向量a 、b ，给出以下结论：①若a ∥b ，则a 在b 方向上的投影为|a |；②若a ⊥b ，则a •b =（a •b ）2；③若a •c =b •c ，则a =b ；④若|a |=|b |，且a ，b 同向，则a >b ．其中所有正确结论的个数是（ ）→→→→→→→→→→→→→→→→→→→→→→→→→A ．m ≥4或m ≤-2B ．m ≥2或m ≤-4C ．-2<m <4D ．-4<m <28．（5分）已知x >0，y >0，若2y x +8x y>m 2+2m 恒成立，则实数m 的取值范围是（ ）A ．相交B ．内切C ．外切D ．相离9．（5分）（文科做）双曲线x 2a 2−y 2b 2=1的左焦点为F 1，顶点为A 1，A 2，P 是该双曲线右支上任意一点，则分别以线段PF 1，A 1A 2为直径的两圆一定是（ ）A ．（0，6]B ．（0，7]C ．（6，7]D ．（6，7）10．（5分）已知函数f （x ）=V W X |lgx |，x >0x +7，x ≤0，若关于x 的方程f （x 2+2x ）=a 有6个不相等的实根，则实数a 的取值范围是（ ）11．（5分）计算：sin 256π+cos 263π+tan （-274π）= ．三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.12．（5分）若一个几何体的三视图如图，则此几何体的体积为 ．13．（5分）若a =21（x -1x 2）dx ,则（x -a x ）10的展开式中常数项为 ．∫14．（5分）在Rt △ABC 中，若∠C =90°，AC =b ,BC =a ,则△ABC 外接圆半径r =a 2+b 22．运用类比方法，若三棱锥的三条侧棱两两互相垂直且长度分别为a ,b ,c ,则其外接球的半径R = ．√15．（5分）某工厂产生的废气经过过滤后排放，过滤过程中废气的污染指数量Pmg /L 与时间th 间的关系为P =P 0e -kt ．如果在前5个小时消除了10%的污染物，则10小时后还剩 %的污染物．16．（12分）已知函数f （x ）=3sinωxcosωx +cos 2ωx +m （ω>0，x ∈R ）的最小正周期为π，最大值为2．（Ⅰ）求ω和m 值；（Ⅱ）求函数f （x ）在区间[0，π2]上的取值范围．√17．（12分）已知数列{a n }是公差不为0的等差数列，满足S 3=9，且a 1，a 2，a 5成等比数列．（Ⅰ）求数列{a n }的通项公式；（Ⅱ）设b 1=a 1，b n +1-b n =2a n （n ∈N *），求数列{b n }的通项公式．18．（12分）某班有12名男生和18名女生参加综合素质测试，所得分数的茎叶图如图，若成绩在75分以上（包括75分）定义为“优秀”，成绩在75分以下（不包括75分）定义为“非优秀”．（Ⅰ）如果用分层抽样的方法从“优秀”和“非优秀”中共抽取5人，再从这5人中选2人，那么至少有一人是“优秀”的概率是多少？（Ⅱ）若从所有“优秀”中选3人参加综合素质展示活动，用ξ表示所选学生中女生的人数，写出ξ的分布列，并求ξ的数学期望．19．（12分）如图，在四棱锥P -ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD =DC ，E 是PC 的中点，作EF ⊥PB 交PB 于点F ．（1）证明：PA ∥平面EDB ；（2）证明：PB⊥平面EFD；（3）求二面角C-PB-D的大小．（m≠-20．（13分）设点A、B的坐标分别为（0，1），（0，-1），直线AM、BM相交于点M，且它们的斜率之积是常数-1m+11）．（Ⅰ）求点M的轨迹C的方程；交曲线C于点P，Q，是否存在m,使得以PQ为直径的圆恒过点A？若存在，求m的值；若不存在，请说明（Ⅱ）设直线l：y=kx-13理由．x2+ax-lnx（a∈R）21．（14分）设函数f（x）=1−a2（Ⅰ）当a=1时，求函数f（x）的极值；（Ⅱ）当a≥2时，讨论函数f（x）的单调性；（Ⅲ）若对任意a∈（2，3）及任意x1，x2∈[1，2]，恒有ma+ln2>|f（x1）-f（x2）|成立，求实数m的取值范围．。

高中数学复习题（含答案）一、单选题1．不等式(5)(4)18x x -+≥的解集是（ ） A ．[]1,2-B ．[]2,1-C ．(][],12,-∞-+∞ D ．(][),21,-∞-+∞2．函数13x y -=的值域为（ ） A ．(],3-∞B ．(]0,1C ．(]0,3D ．(]1,33．函数22y x x =-，[]1,3x ∈-的值域为（ ） A ．[]0,3B ．[]1,3-C ．[]1,0-D ．[]1,34．已知函数()()2,11,1x x f x f x x ⎧<⎪=⎨-≥⎪⎩，则()2log 7f =（ ）A ．32B ．74C ．D ．945．已知函数()g x 的定义域为R ，对任意实数m 、n 都有()()()2022g m n g m g n +=++，且函数()()22022x x f x g x -=+的最大值为p ，最小值为q ，则p q +=（ ）A ．2-B ．2022C ．2022-D ．4044-6．已知()log 83a y ax =-在[]12，上是减函数，则实数a 的取值范围是（ ） A ．0,1 B ．41,3⎛⎫⎪⎝⎭ C ．4,43⎡⎫⎪⎢⎣⎭D ．（1,+∞）7．已知213alog <，(0a >且1)a ≠，则a 的取值范围为（ ） A ．31,2⎛⎫⎪⎝⎭ B ．2,13⎛⎫ ⎪⎝⎭ C ．()30,11,2⎛⎫⋃ ⎪⎝⎭ D ．()20,1,3⎛⎫⋃+∞ ⎪⎝⎭8．已知21()f x x ax x=+-，若对任意12[2,,)x x ∈+∞，当12x x ≠时恒有()()1212121f x f x x x x x ->-，则实数a 的取值范围是（ ） A ．[2,)-+∞B ．[4,)-+∞C ．(,2]-∞D ．(,4]-∞9．三星堆遗址被称为20世纪人类最伟大的考古发现之一，其出土文物是宝贵的人类文化遗产，在人类文明发展史上占有重要地位．2021年，“沉睡三千年，一醒惊天下”的三星堆遗址的重大考古发现再一次惊艳世界．为推测文物年代，考古学者通常用碳14测年法推算（碳14测年法是根据碳14的衰变程度计算出样品的大概年代的一种测量方法）．2021年，考古专家对某次考古的文物样本上提取的遗存材料进行碳14年代测定，检测出碳14的残留量约为初始量的66%，已知碳14的半衰期是5730年（即每经过5730年，遗存材料的碳14含量衰减为原来的一半）．以此推算出该文物大致年代是（ ）（参考数据：log 190.7034≈-，log 346.4634≈-） A ．公元前1600年到公元前1500年 B ．公元前1500年到公元前1400年 C ．公元前1400年到公元前1300年 D ．公元前1300年到公元前1200年10．已知函数()ln ln(2)f x x x =+-，则A ．y =()f x 的图像关于点（1,0）对称B ．()f x 在（0,2）单调递减C ．y =()f x 的图像关于直线x =1对称D ．()f x 在（0,2）单调递增11．已知函数221,1(){(2),1x x f x x x -≤=->，函数()y f x a =-有四个不同的的零点1x ，2x ，3x ，4x ，且1234x x x x <<<，则（ ）A ．a 的取值范围是(0,12) B ．21x x -的取值范围是(0,1)C ．342x x +=D ．12342212x x x x +=+ 二、多选题12．若1a b c >>>，则（ ）A ．33a b >B ．a b b c +>+C ．c b a< D ．22ac bc >13．下列函数中是偶函数，且在(1,)+∞为增函数的是（ ）A ．()||f x x =B ．2()23f x x x =--C ．2()2||1f x x x =--D ．1,0()1,0x x f x x x -+<⎧=⎨+>⎩ 14．已知:p x y >，则下列条件中是p 成立的必要条件的是（ ）A ．22x y >B ．33x y >C ．11x y> D ．332x y -+>15．已知函数(),0()23,0x a x f x a x a x ⎧<⎪=⎨-+≥⎪⎩，满足对任意12x x ≠，都有()()1212f x f x x x -<-0成立，则a 的取值不可以是（ ）A ．34B ．54C ．13D ．1616．已知函数()2431x f x =-+，则（ ） A ．()34f x << B ．()()6f x f x +-=C ．()3f x -为偶函数D ．()f x 的图象关于点()0,3中心对称17．已知函数()f x 的定义域为R ，且满足()()()()2log 1,012,0x x f x f x f x x ⎧-≤⎪=⎨--->⎪⎩，则下列结论中正确的是（ ）A ．()11f -=B ．()20231f =-C ．()()8102f f +=D ．()f x 在[]2023,2023-上有675个零点参考答案：1．A【分析】将不等式化为220x x --≤，根据一元二次不等式的解法即可求解. 【详解】原不等式可化为220x x --≤，即(2)(1)0x x -+≤，解得12x -≤≤. 所以不等式的解集为[]1,2-. 故选：A 2．C【分析】11，结合指数函数的单调性，即可得到函数函数13y =的值域.【详解】∵0，∴11，∴1033<≤.故选：C 3．B【分析】求出函数的对称轴，结合二次函数的最值和对称轴的关系进行求解即可． 【详解】解：函数的对称轴为1x =，[]1,3x ∈-，∴当1x =时，函数取得最小值121y =-=-，当3x =或=1x -时函数取得最大值123=+=y ， 即函数的值域为[]1,3-， 故选：B ． 4．B【分析】直接根据分段函数解析式代入求值即可； 【详解】解：()()2,11,1x x f x f x x ⎧<⎪=⎨-≥⎪⎩，222log 4log 7log 8<<，即()2log 72,3∈()()()22log 7log 72222227log 7log 71log 72224f f f -∴=-=-=== 故选：B 5．D【分析】由()()()2022g m n g m g n +=++，分别令0m n ==，m n =-，得到()2022g x +是奇函数，进而得到2022f x是奇函数求解.【详解】解：因为函数()g x 的定义域为R ，对任意实数m 、n 都有()()()2022g m n g m g n +=++，令0m n ==，得02022g ，令m n =-，得()()202220220g n g n ++-+=， 所以()2022g x +是奇函数，设()h x =因为()()2022h x h x x -==--+，所以()h x 是奇函数， 所以2022f x是奇函数，又因为奇函数的最大值和最小值互为相反数， 所以202220220p q +++=，即4044p q +=-， 故选：D 6．B【分析】令83t ax =-，由于底数0a >，故t 为减函数，再根据复合函数“同增异减”性质判断，结合真数大于0的特点即可求解a 的取值范围【详解】因为0a >，所以83t ax =-为减函数，而当1a >时，log a y t =是增函数，所以()log 83a y ax =-是减函数，于是1a >；由830ax ->，得83a x<在[]1,2上恒成立，所以min 8843323a x ⎛⎫<== ⎪⨯⎝⎭. 故选：B 7．D【分析】直接分a 大于1和大于0小于1两种情况讨论再结合函数的单调性即可求解． 【详解】解：因为：21log 3a a log a <=， 当1a >时，须23a <，所以1a >； 当01a <<时，21log 3aa log a <=，解得203a >>． 综上可得：a 的取值范围为：()20,1,3⎛⎫+∞ ⎪⎝⎭．故选：D ． 8．B【分析】依题意，设12x x <，则()()1212122111x x f x f x x x x x --<=-，即函数()()1g x f x x=+在[2,)+∞上单调递增，再根据二次函数的性质解答即可.【详解】解：对任意的12[2,,)x x ∈+∞，都有()()1212121f x f x x x x x ->-，即()()222212112212121212121211x x x ax x ax x x a x x x x x x x x x x ⎛⎫⎛⎫-+--+--+-+ ⎪ ⎪⎝⎭⎝⎭=--()12121211x x a x x x x =+++>， 所以，()12a x x >-+，1x 、[)22,x ∈+∞且12x x ≠，所以，124x x +>，则()124x x -+<-，因此，4a ≥-. 故选：B . 9．B【分析】设时间经过了x 年，则573010.662x ⎛⎫= ⎪⎝⎭，结合参考数据计算得到答案.【详解】设时间经过了x 年，则573010.662x⎛⎫= ⎪⎝⎭，即()57360.50.66x=，573657365736573657360.50.50.50.50.5log 0.66log 66log 100log 662log 10x ==-=-219034.734634.43435⨯-==. 343240254111=--.故选：B. 10.C【详解】因为()(2)2ln 2ln(2)0f x f x x x +-=+-≠ ，所以A 错；1122()012(2)x f x x x x x x -=-==⇒=∴--' B ，D 错 因为()(2)f x f x =- ，所以C 对，选C.11．D【分析】将问题转化为()f x 与y a =有四个不同的交点，应用数形结合思想判断各交点横坐标的范围及数量关系，即可判断各选项的正误.【详解】()y f x a =-有四个不同的零点1x 、2x 、3x 、4x ，即()f x a =有四个不同的解．()f x 的图象如下图示，由图知：1201,01a x x <<<<<，所以210x x ->，即21x x -的取值范围是(0,＋∞)． 由二次函数的对称性得：344x x +=，因为121221x x -=-，即12222x x +=，故12342212x x x x +=+． 故选：D 12．ABC【分析】根据不等式的性质进行逐项判断.【详解】对于选项A ：因为1a b >>，所以33a b >，A 正确； 对于选项B ：因为a c >，所以a b b c +>+，B 正确； 对于选项C ：因为1a b c >>>，所以1c ab a a<=<，C 正确； 对于选项D ：当0c =时，22ac bc =，D 错误． 故选：ABC 13．ACD【分析】根据题意，依次分析选项中函数的奇偶性与单调性，综合即可得答案． 【详解】解：根据题意，依次分析选项：对于A ，()||f x x =，偶函数，且在(1,)+∞为增函数，符合题意； 对于B ，2()23f x x x =--，不是偶函数，不符合题意； 对于C ，2()2||1f x x x =--，是偶函数，在1(,)4+∞上为增函数，故在(1,)+∞为增函数，符合题意；对于D ，1,0()1,0x x f x x x -+<⎧=⎨+>⎩，是偶函数，且在(1,)+∞为增函数，符合题意；故选：ACD ． 14．BD【分析】利用特殊值判断AC ，根据指数函数的单调性判断B ，利用基本不等式判断D ；【详解】解：当0x =，1y =-，满足x y >，但22x y >不成立，故A 错误； 因为x y >，3x y =在定义域上单调递增，所以33x y >，故B 正确； 当2x =，1y =时，满足x y >，但11x y>不成立，故C 错误； 因为30x >，30y ->，则33x y -+≥x y >，所以0x y ->，所以31x y ->所以2>，所以332x y -+>，故D 正确； 故选：BD 15．AB【分析】根据条件知()f x 在R 上单调递减，从而得出012031a a a <<⎧⎪-<⎨⎪≤⎩，求a 的范围即可得出答案．【详解】∵()f x 满足对任意12x x ≠，都有()()1212f x f x x x -<-0成立，∴()f x 在R 上是减函数，∴00120(2)03a a a a a <<⎧⎪-<⎨⎪-⨯+≤⎩，解得103a <≤，∴a 的取值范围是10,3⎛⎤⎥⎝⎦．故选：AB ． 16．BD【分析】对A ，由31x +的范围得到131x+的范围，进而求出函数的值域；对B ，通过运算()()f x f x +-即可得到答案；对C ，根据函数奇偶性的定义即可判断；对D ，结合C 中的推理即可判断答案.【详解】对A ，因为31(1,)x +∈+∞,则1(0,1)31x ∈+，2(2,0)31x -∈-+， 所以2()4(2,4)31x f x =-∈+.A 错误； 对B ，22()()443131x x f x f x -+-=-+-++ 11332828263131332x x x x x x---++⎛⎫=-+=-⋅= ⎪++++⎝⎭.B 正确；对C ，记231()()31,R 3131x x x F x f x x -=-=-=∈++，311331()()311331x x x x xx F x F x ------===-=-+++，则函数()3f x -为奇函数.C 错误； 对D ，由C 可知，()3f x -为奇函数，则()3f x -的图象关于点(0,0)对称，所以()f x 的图象关于点(0,3)中心对称.D 正确. 故选：BD. 17．ABD【分析】根据解析式可直接求得()1f -的值，判断A ；根据0x >时的性质，利用变量代换，推出此时函数的周期，结合解析式，即可求值，判断B ，C ；利用函数周期以及(0)0f =，推出(3)0f =，即可推出()(3)(6)(9)(12)(2022)00f f f f f f =======，即可判断D.【详解】对于A ，()21log 21f -==，A 正确；对于B ，当0x >时，()(1)(2)f x f x f x =---，即(2)(1)()f x f x f x +=+-， 则(3)(2)(1)f x f x f x +=+-+，即得(3)()f x f x +=-， 则(6)(3)()f x f x f x +=-+=，即0x >时，6为()f x 的周期；()22023(33761(1)(1)(0)1)0log 2f f f f f =⨯+=--=-=-=，B 正确； 对于C ，由B 的分析可知()8(2)(1)(0)(1)1f f f f f ==-=--=-，()(4)(3)(2)(1)10f f f f f ==-=-(0)(1)1f f =-+-=， 故()()8100f f +=，C 错误；对于D ，当0x <时，11x ->,()2()log 10f x x =->，此时函数无零点； 由于(0)0f =，则()(5)(4)(4)(3)(4)(3)(0)06f f f f f f f f =-=--=-==， 故(3)0f =，则()(3)(6)(9)(12)(2022)00f f f f f f =======，由于20223674=⨯，故()f x 在[]2023,2023-上有675个零点，D 正确， 故选：ABD。

河南省洛阳市栾川县实验高中2024年高三下学期期末复习检测试题（一模）数学试题请考生注意：1．请用2B 铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。

写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知函数2211()log 13||f x x x ⎛⎫=+++⎪⎝⎭，则不等式(lg )3f x >的解集为（ ）A ．1,1010⎛⎫⎪⎝⎭B ．1,(10,)10⎛⎫-∞⋃+∞ ⎪⎝⎭C ．(1,10)D ．1,1(1,10)10⎛⎫⋃⎪⎝⎭2．一物体作变速直线运动，其v t -曲线如图所示，则该物体在1s~6s 2间的运动路程为（ ）m ．A ．1B ．43C ．494D ．23．已知函数()cos sin 2f x x x =，下列结论不正确的是（ ） A ．()y f x =的图像关于点(),0π中心对称 B ．()y f x =既是奇函数，又是周期函数C ．()y f x =的图像关于直线2x π=对称D ．()y f x =的最大值是324．在平面直角坐标系xOy 中，已知角θ的顶点与原点O 重合，始边与x 轴的非负半轴重合，终边落在直线2y x =上，则3sin 22πθ⎛⎫+= ⎪⎝⎭（ ） A ．45B ．45-C ．35D ．355．已知函数()ln(1)f x x ax =+-，若曲线()y f x =在点(0,(0))f 处的切线方程为2y x =，则实数a 的取值为（ ） A ．-2B ．-1C ．1D ．26．1777年，法国科学家蒲丰在宴请客人时，在地上铺了一张白纸，上面画着一条条等距离的平行线，而他给每个客人发许多等质量的，长度等于相邻两平行线距离的一半的针，让他们随意投放.事后，蒲丰对针落地的位置进行统计，发现共投针2212枚，与直线相交的有704枚.根据这次统计数据，若客人随意向这张白纸上投放一根这样的针，则针落地后与直线相交的概率约为（ ） A ．12πB ．3πC ．2πD ．1π7．在棱长为2的正方体ABCD −A 1B 1C 1D 1中，P 为A 1D 1的中点，若三棱锥P −ABC 的四个顶点都在球O 的球面上，则球O 的表面积为（ ） A ．12πB ．21π2C ．41π4D ．10π8．已知函数2()e (2)e xx f x t t x =+--（0t ≥），若函数()f x 在x ∈R 上有唯一零点，则t 的值为（ ）A ．1B ．12或0 C ．1或0 D ．2或09．已知函数()2tan()(0)f x x ωω=>的图象与直线2y =的相邻交点间的距离为π，若定义{},max ,,a a ba b b a b ⎧=⎨<⎩，则函数()max{()h x f x =，()cos }f x x 在区间3,22ππ⎛⎫⎪⎝⎭内的图象是( ) A ． B ．C ．D ．10．ABC ∆ 的内角,,A B C 的对边分别为,,a b c ，已知22cos a c b A +=，则角B 的大小为（ ） A ．23π B ．3π C ．6π D ．56π 11．若两个非零向量a 、b 满足()()0a b a b +⋅-=，且2a b a b +=-，则a 与b 夹角的余弦值为（ ） A ．35B ．35±C ．12D ．12±12．已知等比数列{}n a 的前n 项和为n S ，若11a =，且公比为2，则n S 与n a 的关系正确的是（ ） A ．41n n S a =-B ．21n n S a =+C ．21n n S a =-D ．43n n S a =-二、填空题：本题共4小题，每小题5分，共20分。