§1.2.2矩形的性质与判定

格式：doc
大小：44.62 KB
文档页数：2

下载文档原格式

1.2矩形的性质与判定+课件+2023-2024学年北师大版数学九年级上册

B．AC＝BD
C．AD＝AB
D．∠BAD＝∠ADC
2．如图，BO是Rt△ABC斜边上的中线，延长BO到点D，使DO＝BO，
连接AD，CD．四边形ABCD是矩形吗?请说明理由．
解：四边形ABCD是矩形．理由如下：
∵BO是Rt△ABC斜边上的中线，
∴OA＝OC＝OB＝OD．
∴四边形ABCD是平行四边形，且AC＝BD．
∴DE∥AC，DF∥AB．
∴四边形AEDF是平行四边形．
又∠A＝90°，
∴四边形AEDF是矩形．
典例3
如图，在□ ABCD是矩形ABCD中，∠ACB＝90°，过点D作
DE⊥BC交BC的延长线于点E．求证：四边形ACED是矩形．
证明：∵四边形ABCD为平行四边形，
∴AD∥BC．
∴∠DAC＝∠ACB＝90°．
不一定成立的是( C )
A．AB∥CD
B．AC＝BD
C．AC⊥BD
D．OA＝OC
变式1
矩形具有而平行四边形不一定具有的性质是( C )
A．对角相等
B．对边相等
C．对角线相等
D．对角线互相平分
典例2
如图，在矩形ABCD中，E是CD边的中点．求证：AE＝BE．
证明：∵四边形ABCD是矩形，
∴AD＝BC，∠D＝∠C＝90°．

∴∠ABD＝ ∠ABC，∠ABE＝ ∠ABP．
∵∠ABC＋∠ABP＝180°，

∴∠ABD＋∠ABE＝ ×180°＝90°，

即∠DBE＝90°．
∵AE⊥BE，AD⊥BD，
∴∠E＝∠D＝90°．
∴四边形AEBD是矩形．
1．如图，四边形ABCD的对角线AC与BD相交于点O，下列条件中，能

北师大版九年级数学上册1.2.2矩形的性质与判定优秀教学案例

3.小组合作：我组织学生进行小组合作，让他们共同探讨矩形的性质和判定方法。这种小组合作的学习方式不仅能够培养学生的团队合作和沟通能力，还能够促进他们之间的互相学习和共同进步。
4.反思与评价：在课堂的最后阶段，我组织学生进行反思，让他们回顾本节课所学的矩形的性质和判定方法，巩固知识。同时，我设计相关的练习题目，让学生进行实践操作，检验他们对矩形性质和判定方法的掌握程度。这种反思与评价的教学策略能够培养学生的自我评估和自我改进能力，提高他们的学习效果。
北师大版九年级数学上册1.2.2矩形的性质与判定优秀教学案例
一、案例背景
本节课的教学内容是北师大版九年级数学上册1.2.2矩形的性质与判定。矩形是初中数学中的重要几何图形之一，它具有独特的性质和判定方法。在本节课中，学生需要掌握矩形的性质，包括对角线相等、四个角都是直角等，同时还需要学习如何判定一个四边形是矩形。
在教学过程中，我以实际生活中的情境为导入，让学生观察教室的黑板，发现黑板是一个矩形。通过这个实例，让学生初步感知矩形的性质，并激发他们对本节课的学习兴趣。接着，我引导学生通过小组合作、讨论交流的方式，探索矩形的性质和判定方法。在学生掌握矩形的性质后，我组织学生进行实践操作，让他们运用所学知识解决实际问题，如测量教室的长和宽等。
（四）反思与评价
1.在课堂的最后阶段，组织学生进行反思，让他们回顾本节课所学的矩形的性质和判定方法，巩固知识。
2.设计相关的练习题目，让学生进行实践操作，检验他们对矩形性质和判定方法的掌握程度。
3.教师对学生的学习情况进行评价，及时给予肯定和鼓励，提高他们的学习积极性和自信心。
作为一名特级教师，我深知教学策略的重要性。在教学过程中，我将根据学生的实际情况，灵活运用各种教学策略，以激发学生的学习兴趣，培养他们的几何思维和问题解决能力，提高他们的学习效果。同时，我还会注重学生的情感态度与价值观的培养，让他们在愉快的氛围中学习和成长。

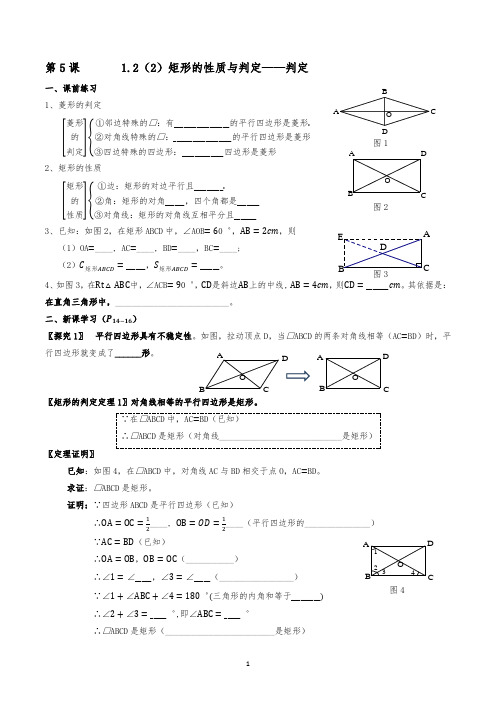
第5课1.2(2)矩形的性质与判定

第5课 1.2（2）矩形的性质与判定——判定一、课前练习 1、菱形的判定[菱形的判定]{①邻边特殊的□：有_________________的平行四边形是菱形.②对角线特殊的□：__________________的平行四边形是菱形③四边特殊的四边形：_____________四边形是菱形2、矩形的性质[矩形的性质]{①边：矩形的对边平行且_________. ②角：矩形的对角______，四个角都是_______③对角线：矩形的对角线互相平分且_______3、已知：如图2，在矩形ABCD 中，∠AOB =60゜，AB =2cm ，则（1）OA =____, AC =____, BD =____，BC =____; （2）C 矩形ABCD =______，S 矩形ABCD =______。

4、如图3，在Rt △ABC 中，∠ACB =90゜，CD 是斜边AB 上的中线, AB =4cm ，则CD =_______cm 。

其依据是：在直角三角形中，__________________________。

二、新课学习（P 14−16）〖探究1〗平行四边形具有不稳定性。

如图，拉动顶点D ，当□ABCD 的两条对角线相等（AC =BD ）时，平行四边形就变成了______形。

〖矩形的判定定理1〗对角线相等的平行四边形是矩形。

∵在□ABCD 中，AC =BD （已知）∴□ABCD 是矩形（对角线____________________________是矩形）〖定理证明〗已知：如图4，在□ABCD 中，对角线AC 与BD 相交于点O ，AC =BD 。

求证：□ABCD 是矩形。

证明：∵四边形ABCD 是平行四边形（已知）∴OA =OC =12____, OB =OD =12____（平行四边形的_______________）∵AC =BD （已知）∴OA =OB ，OB =OC （___________）∴∠1=∠_____，∠3=∠_____（_________________） ∵∠1+∠ABC +∠4=180゜(三角形的内角和等于_________) ∴∠2+∠3=_____゜,即∠ABC =_____゜∴□ABCD 是矩形（_________________________是矩形）CAB DO OABCD图2EDCBA图1图3BAOCDDC OAB图4432BAOCD1☆巩固练习一4、（1）有_______________的平行四边形是矩形。

矩形的判定ppt课件

解：∵四边形 ABCD 是平行四边形，
1
1
∴ OA = OC = AC，OB = OD = BD.
2
2
又∵ OA = OD，
∴ AC = BD.
∴ 四边形 ABCD 是矩形.
∴∠BAD = 90°.
又∵∠OAD = 50°，∴∠OAB = 40°.
C
D
O
A
B
任务二
有三个角是直角的四边形是矩形
想一想一个四边形至少有几个角是直角时，是矩形？
已知：如图，在四边形 ABCD 中，∠A =∠B =∠C = 90°.
求证：四边形 ABCD 是矩形.
证明：∵ ∠A =∠B =∠C = 90°，
∴∠A +∠B = 180°，∠B +∠C = 180°.
A
D
B
C
∴ AD∥BC，AB∥CD.
∴ 四边形 ABCD 是平行四边形.
∴ 四边形 ABCD 是矩形.
1.2 .2 矩形的性质与判定
复习
1.矩形的定义
2.矩形的性质
任务一
对角线相等的平行四边形是矩形
如图，是一个平行四边形活动框架，拉动一对不相邻的顶点时，平
行四边形的形状会发生变化.
（1）随着∠α 的变化两条对角线的长度将发生怎样的变化？
（2）当两条对角线的长度相等时平行四边形有什么特征？由此你
能得到一个怎样的猜想？
任务一
对角线相等的平行四边形是矩形
已知：如图，在□ ABCD中，AC，DB 是它的两条对角线，且 AC =
DB. 求证：□ ABCD 是矩形.
证明：∵四边形 ABCD 是平行四边形，
∴ AB = DC，AB∥DC.

1.2.2矩形的性质与判定(教师)

九年级数学导学案课题： 1.2.2矩形的性质与判定学习目标 1.进一步掌握矩形的定义与性质。

2.经历探索矩形的判定方法的过程，进一步了解和体会说理的基本方法.3.在探索活动过程中发展学生的探究意识。

兴趣.学习重点 1.矩形判定方法的探索与理解学习过程一、自主学习 1.什么是矩形？ 2. 矩形的性质有哪些？二、合作探究1. 观察下图平行四边形变化（1）随着∠α的变化，两条对角线的长度分别是怎样变化的？（2）当两条对角线的长度相等时，平行四边形有什么特征？你能得出一个怎样的猜想？结论：对角线的平行四边形是矩形请你尝试证明你的结论：已知：平行四边形ABCD 中，两条对角线AC ，BD 相交于点O ，AC=BD求证：平行四边形ABCD 是矩形主备：授课：日期：次数：2.我们知道，矩形的四个角都是直角。

反过来，一个四边形至少有几个角是直角时，这个四边形就是矩形？请证明你的结论，并与同伴交流结论：的四边形是矩形请你尝试证明你的结论：3.你有什么方法检查你家（或教室）刚安装的门框是不是矩形？如果仅有一根较长的绳子，你怎样检查？请说明检查方法的合理性，与同伴交流三、互动展示（学生在独立思考的基础上小组交流，并选代表展示）1.如图在平行四边形ABCD 中，两条对角线AC ，BD 相交于点O ， △AOB 是等边三角形AB=4 cm ．求平行四边形ABCD 的面积。

四、达标测试1、课本P16“随堂练习”（在导学案背后完成）五、课堂小结与反思你通过本节课的探索解决了哪些问题？还有那些困惑？有哪些新的发现、想法？六、课堂延伸、布置作业、预习思考1、必做题：课本P16习题1.5 第1、2题。

2、选做题：课本P16习题1.5 第3题。

3、预习：课本P16--19“矩形的性质与判定”的应用。

七、复议、二次备课、教后反思。

北师大版数学九年级上册矩形的性质与判定(第2课时矩形的判定)课件(共26张)

｛AP=DP ∵ AB=PC ， BP=PC ∴△ABP≌△DCP（SSS）， ∴∠D=∠A， ∵∠D+∠A=180°， ∴∠D=∠A=90°， ∵四边形ABCD是平行四边形， ∴平行四边形ABCD是矩形．
7.如图， ABCD的四个内角的平分线相交于点E、F、G、H. 求证：EG = FH.
证明：∵四边形ABCD是平行四边形，∴AD∥BC， ∴∠BAD+∠ABC=180°．又∵AH，BH分别平分∠BAD，∠ABC， ∴∠DAE=∠BAE= ∠DAB，∠CBG=∠ABG= ∠ABC， ∴∠BAE+∠ABG= （∠DAB +∠ABC ）=90°， ∴∠AHB=90°，同理可证∠EFG=90°，∠HEF=90°， ∴四边形EFGH为矩形，∴EG=FH．
∴∠ABC+∠DCB=180°.
∴∠ABC=∠DCB
=
1 2
×180°=90°.
∴□ABCD是矩形.(矩形的定义)
2．矩形的四个角都是直角，反过来，一个四边形至少有几个角是直角时，这个四边形才是矩形呢？请证明你的结论，并与同伴交流．
归纳结论：有三个角是直角的四边形是矩形．
已知:如图,在四边形ABCD中,
已知:如图,在□ABCD中,对角线AC=BD.
求证:平行四边形ABCD是矩形.
分析:要证明□ABCD是矩形,只要证明有一个角是直角即可.
证明: ∵四边形ABCD是平行四边形. A
D
∴AB=CD,AB∥CD.
又∵AC=DB,BC=CB.
∴ △ABC≌△DCB.
B
C
∴∠ABC=∠DCB.
又∵AB∥CD.
巩固练习
1．如图，四边形ABCD的对角线互相平分，要使它变为矩形，需要添加的条件是( D )

1.2.2矩形判定

三、群学:我们小组出现问题有哪些，原因是什么，易错点是什么？
四、展示（展示时要读题，讲用到的知识点，讲思路、重点、易错点或问题的变式等）
五、检测：
1．下列说法正确的是（）．
（A）有一组对角是直角的四边形一定是矩形（B）有一组邻角是直角的四边形一定是矩形
（C）对角线互相平分的四边形是矩形（D）对角互补的平行四边形是矩形
八年级数学导学案
课题
1.2.2矩形的性质与判定
学习目标
1．能运用综合法证明矩形判定定理。
2．体会证明过程中所运用的归纳概括以及转化等数学思想方法。
一、知识链接：
知识链接：
矩形具有一般平行四边形的所有性质，它还具有特殊的性质：
矩形的四个角_______。矩形的对角线_______。
二、探究Байду номын сангаас知
（一）自主学习：阅读课本14页—15页，试着解决以下问题：
⑵摆放成如图②的四边形，则这时窗框的形状是形，根据的数学道理是：；
⑶将直角尺靠紧窗框的一个角（如图③），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图④），说明窗框合格，这时窗框是形，根据的数学道理是：；
4．已知点A、B、C、D在同一平面内，有6个条件：①AB∥CD，②AB=CD，③BC∥AD，④BC=AD，
求证：四边形ACBE为矩形．
本节思维导图：
本节思维导图：
2．下列条件中，不能判定四边形ABCD为矩形的是（）．
A．AB∥CD，AB=CD，AC=BD B．∠A=∠B=∠D=90°
C．AB=BC，AD=CD，且∠C=90°D．AB=CD，AD=BC，∠A=90°
3．工人师傅做铝合金窗框分下面三个步骤进行：
⑴先截出两对符合规格的铝合金窗料（如图①），使AB＝CD，EF＝GH；

矩形的性质与判定

又∵BM＝EM，∴DN＝EM.∵AB∥CD， ∴∠ABO＝∠CDO.∴∠MBO＝∠NDO. ∴ME∥DN.
∴四边形DEMN是平行四边形．
∵BD＝2AB，BD＝2BO，∴AB＝OB.又∵M是AO的中点，∴BM⊥AO. ∴∠AMB＝∠EMN＝90°. ∴四边形DEMN是矩形． ∵AB＝5，DN＝BM＝EM＝4，∴AM＝3＝MO. ∴MN＝6. ∴矩形DEMN的面积为6×4＝24.
理由如下： ∵△ABC 是等腰三角形且 AD⊥BC，
A
E N
∴BD = CD,
F
又∵ADCE是矩形，∴AE = CD，AE∥CD，
∴BD=AE, BD∥AE,
B
D
C
∴四边形 ABDE 是平行四边形.
探究新知
A 直角三角形斜边上的中
线等于斜边的一半。 B
符号语言：
∵ Rt△ABC，O是AC的中点
∴
BO=
(2)当AB=DC时，求证：AEFD是矩形.
B (2)证明：∵四边形ABED和四边形AFCD都是平行四边形，
E
F
C
∴DE=AB，AF=DC.
又AB=DC，
∴DE=AF.
又∵四边形AEFD是平行四边形，
A
D
四边形判定条件
平行四边形有一个角是直角
对角线相等
B
O
C
判定菱形的常见思路：
四条边都相等
四边形判定平行四边形一组邻边相等
条件
对角线互相垂直
菱形
随堂练习
1. 已知：如图，四边形 ABCD 由两个全等的等边三角形 ABD 和 CBD 组成，M，N 分别是 BC 和 AD 的中点. 求证：四边形BMDN是矩形.

1.2.2矩形的性质与判定(教案)

此外，实践活动环节，学生们对矩形在实际生活中的应用表现出浓厚兴趣。这让我意识到，将生活实例融入教学，能够激发学生的学习兴趣和积极性。因此，在之后的教学中，我会继续挖掘与课程相关的生活案例，让学生在学习过程中感受到数学的实用性和趣味性。
同时，我也发现部分学生在解决矩形相关问题时，仍然存在思维定式，不能灵活运用所学知识。为了帮助学生克服这一问题，我打算在课后加强个别辅导，针对不同学生的特点，引导他们运用多种方法解决问题，提高他们的解题能力。
1.培养学生的几何直观与空间想象能力：通过探究矩形的性质与判定，使学生在观察、操作、思考中形成对矩形几何特征的直观认识，提高空间想象力。
2.培养学生的逻辑推理能力：在探究矩形性质与判定的过程中，训练学生运用逻辑思维，通过推理、证明等方式掌握矩形的性质及其应用。
3.培养学生的数学建模能力：通过解决与矩形相关的实际问题，让学生学会运用所学知识构建数学模型，培养解决实际问题的能力。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解矩形的基本概念。矩形是有一个角是直角的平行四边形，具有对边平行且相等、对角相等、四个角都是直角的特点。它在几何学中具有重要地位，广泛应用于日常生活和建筑等领域。
2.案例分析：接下来，我们来看一个具体的案例。通过分析一个矩形物体的性质，了解矩形在实际中的应用，以及它如何帮助我们解决问题。
（2）矩形的判定方法：掌握至少三种判定矩形的方法，并能运用到实际问题中。
-举例：通过具体练习题，让学生练习如何根据直角、对角线相等、对边平行等条件判断一个四边形是否为矩形。
2.教学难点
（1）矩形的性质推导：理解并掌握矩形对角线互相平分、相等的性质，以及矩形是轴对称图形的证明。
-难点解释：这部分内容需要学生具备一定的逻辑推理和几何证明能力，教师应通过直观演示和逐步引导，帮助学生理解性质背后的几何原理。

北师大版九年级数学上1.2 矩形的性质与判定 (共39张PPT)

直角三角形斜边上的中线等于斜边的一半.
2.明确定理：直角三角形性质定理：直角三角形斜边上的
中线等于斜边的一半.
推理格式：在△ABC中， ∵∠ABC=90°，AO=CO， BO 1 AC.
2
3.定理证明
D
思路：（1）造全等：
延长BO至点D，使OD=OB，连接AD.
先证△BOC≌△DOA（SAS），
解：∵四边形ABCD是平行四边形， ∴OA=OC，OB=OD. 又∵△ABO是等边三角形， ∴OA=OB=AB=4. ∴OA=OC=OB=OD=4. ∴AC=BD=2OA=2×4=8.
∴□ABCD是矩形（对角线相等的平行四边形是矩形）.
∴∠ABC=90°（矩形的四个角都是直角）. 在Rt△ABC中，由勾股定理，得 AB2 + BC 2 = AC 2 ,
• 9、要学生做的事，教职员躬亲共做；要学生学的知识，教职员躬亲共学；要学生守的规则，教职员躬亲共守。21.9.821.9.8Wednesday, September 08, 2021 • 10、阅读一切好书如同和过去最杰出的人谈话。10:15:0210:15:0210:159/8/2021 10:15:02 AM • 11、只有让学生不把全部时间都用在学习上，而留下许多自由支配的时间，他才能顺利地学习……（这）是教育过程的逻辑。21.9.810:15:0210:15Sep-218-Sep-21 • 12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。10:15:0210:15:0210:15Wednesday, September 08, 2021
证明：∵AD平分∠BAC，AN平分∠CAM，
∟
CAD = 1 BAC，CAN = 1 ∠CAM.

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.矩形是轴对称图形，它有______条对称轴．
2.在矩形ABCD中，对角线AC，BD相交于点O，若对角线AC=10cm，边BC= 8cm，则△ABO的周长为________．
3.矩形是特殊的平行四边形，怎样判定一个平行四边形是矩形呢?
请同学们说出最基本的方法：（用定义）.
二、合作学习：
1.知识点一：探究“对角线相等的平行四边形是矩形.”
2.△ABC中，点O是AC边上一动点，过O点作直线MN//BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F，
（1）试说明EO=OF的理由.
（2）当点O运动到何处时，四边形AECF是矩形？并说明你的结论.
【教（学）后反思】
已知：在四边形ABCD中∠A=∠B=∠C=90°
求证：四边形ABCD矩形
证明：∵∠A+∠B+∠C+∠D=度
而∠A=∠B=∠C=90度
∴∠D=︒
∴===
∴四边形ABCD是平行四边形（）
∴四边形ABCD矩形（）
归纳：矩形的判定定理
1.有一个角是直角的平行四边形是矩形.
2.对角线相等的平行四边形是矩形.
3.三个角都是直角的四边形是矩形.
定边六中九年级数学科导学案（总第5课时）
主备人：王广锋领导审核：班级姓名组号
课题:§1.2.2矩形的性质与判定
反思栏
反思栏
【学习目标】
1.探索并掌握矩形的判定定理.
2.会应用矩形判定定理进行证明.
【学习重难点】
1.重点：掌握矩形的判定定理及其应用.
2.难点：会、自主学习：
【作业设计】
一、书面作业：
习题1.5第1、2题.
二、家庭作业：
1．工人师傅做铝合金窗框分下面三个步骤进行：
（1）先截出两对符合规格的铝合金窗料（如图①），使AB＝CD，EF＝GH；
(2)摆放成如图②的四边形，则这时窗框的形状是形，根据的数学道理是：；
(3)将直角尺靠紧窗框的一个角（如图③），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图④），说明窗框合格，这时窗框是形，根据的数学道理是：
如图在□ABCD中，对角线AC、BD相交于O，如果AC=BD
求证：□ABCD是矩形.
证明：□ABCD是平行四边形
∴AB=CD，AB∥CD（）
∴∠ABC+∠DCB=180
三、课堂巩固：
1.如图，□ABCD中，AB= 6，BC= 8，AC= 10，
求证:□ABCD是矩形.
2.如上图已知：□ABCD的AC、BD对角线相交于O，△AOB是等边三角形，AB=4cm,求这个平行四边形的面积.
3.已知：如图，在□ABCD中，M是AD边的中点，且MB=MC.
M
D
A
求证：四边形ABCD是矩形.
C
B
三、课堂小结
本节课你有什么收获和困惑？请谈一谈.
在△ABC和△DCB中
=
=
=
∴△ABC≌△DCB（）
∴∠ABC=∠DCB
∴∠ABC=
∴□ABCD是矩形（）
2.知识点二：探究“三个角都是直角的四边形是矩形.”