圆柱认识及展开图概述
- 格式:ppt
- 大小:4.44 MB
- 文档页数:79

圆柱的侧面展开图及其与底面之间的关系
问题(1)导入圆柱的侧面展开后是什么形状?(教材19页例2)
过程讲解
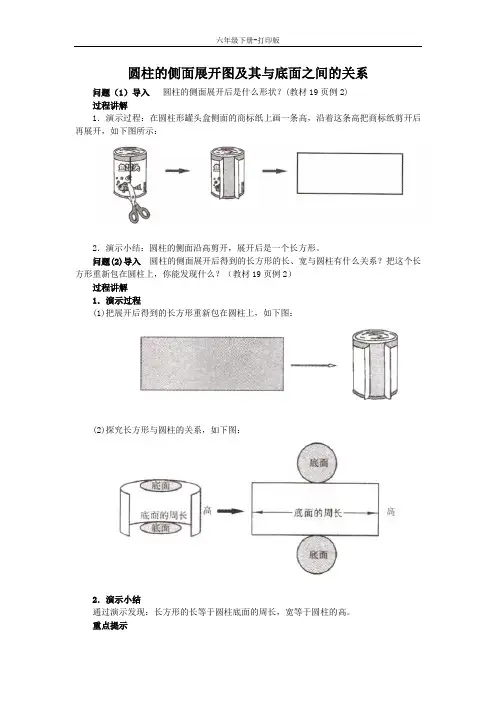
1.演示过程:在圆柱形罐头盒侧面的商标纸上画一条高,沿着这条高把商标纸剪开后再展开,如下图所示:
2.演示小结:圆柱的侧面沿高剪开,展开后是一个长方形。
问题(2)导入圆柱的侧面展开后得到的长方形的长、宽与圆柱有什么关系?把这个长方形重新包在圆柱上,你能发现什么?(教材19页例2)
过程讲解
1.演示过程
(1)把展开后得到的长方形重新包在圆柱上,如下图:
(2)探究长方形与圆柱的关系,如下图:
2.演示小结
通过演示发现:长方形的长等于圆柱底面的周长,宽等于圆柱的高。
重点提示
当圆柱的底面周长和高相等时,沿高剪开的侧面展开后是一个正方彤。
归纳总结
圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),这个长。
方形(或正方形)的长(或边长)等于圆柱的底面周长,宽(或边长)等于圆柱的商。




完整版)球体和圆柱体的展开图1.引言本文将介绍球体和圆柱体的展开图。
展开图是一种将三维图形展开成二维平面的技术,以便更好地理解和研究该图形的表面特征和结构。
球体和圆柱体是常见的三维图形,其展开图可以帮助我们更好地理解它们的形态和关系。
2.球体的展开图球体是一种由无数个点组成的几何体,其所有的点到中心点的距离相等。
球体的展开图是将球体切开并展开成一个平面图形。
具体步骤如下:1.首先,我们选择球体上的一个点作为球心。
2.然后,我们从球心到球体表面上的任意一点画一条直线,这条线即为球体的一条切线。
3.我们将这条切线作为线段,并沿着球体的表面将该线段绕着球心旋转到与原位置相重合,形成一个等长的弧。
4.重复步骤2和步骤3,直到我们绕过整个球体。
5.最后,将所有的弧按照它们在球体上的排列顺序连接起来,就得到了球体的展开图。
球体的展开图是一个平面圆形图形,它展示了球体的所有表面特征和结构。
该图形上的每一点代表了球体上的一个点,而每一条弧代表了球体上的一条切线。
3.圆柱体的展开图圆柱体是一个由两个平行且相等圆组成的几何体。
圆柱体的展开图是将圆柱体展开成一个矩形。
具体步骤如下:1.首先,我们选择圆柱体的一个圆作为底面圆,将其展开成一个半径等于底面圆的弧。
2.接着,我们将圆柱体展开使得底面圆的两个半径相对,再将这两条半径绕着底面圆的轴线旋转到与原位置相重合,形成两个等长的直线段。
3.重复步骤1和步骤2,直到我们绕过整个圆柱体。
4.最后,将所有的直线段按照它们在圆柱体上的排列顺序连接起来,就得到了圆柱体的展开图。
圆柱体的展开图是一个矩形,它展示了圆柱体的所有表面特征和结构。
该图形上的每一点代表了圆柱体上的一个点,而每一条直线段代表了圆柱体上的一条半径。
4.结论球体和圆柱体的展开图是将这两种常见的三维图形展开成了二维平面图形。
通过展开图,我们可以更好地理解和研究球体和圆柱体的形态和关系。
展开图将复杂的三维图形简化为了平面图形,使我们更容易分析和计算这些图形的各种特性。





圆柱的认识1. 简介圆柱是一种具有柱形结构的几何体,由两个平行的圆面和一个连接两个圆面的侧面组成。
圆柱是常见的几何体之一,广泛应用于工程、建筑、数学等领域。
2. 基本属性圆柱具有以下基本属性: - 高度(Height):圆柱的两个平行圆面之间的距离称为高度。
- 半径(Radius):圆柱的平行圆面的半径相等,称为圆柱的半径。
- 直径(Diameter):圆柱的平行圆面的直径相等,是半径的两倍。
3. 圆柱的公式根据圆柱的基本属性,可以得到以下公式:3.1 圆柱的体积圆柱的体积(Volume)可以通过以下公式计算:V = π * r^2 * h其中,V表示圆柱的体积,π是圆周率(约等于3.14159),r表示圆柱的半径,h表示圆柱的高度。
3.2 圆柱的表面积圆柱的表面积(Surface Area)可以通过以下公式计算:A = 2πr^2 + 2πrh其中,A表示圆柱的表面积,π是圆周率,r表示圆柱的半径,h表示圆柱的高度。
4. 应用领域圆柱在各个领域都有广泛的应用,以下是一些典型的应用案例:4.1 工程建筑圆柱可以用于建筑物的结构设计,如水塔、烟囱等。
圆柱的稳定结构使其成为承载大量重量的理想选择。
4.2 数学几何圆柱是数学几何学中的一个重要概念,通过研究圆柱的特性和性质,可以推导出许多几何学定理和公式,对数学学科的发展起到促进作用。
4.3 食品加工食品加工行业中常使用圆柱形的容器如罐子、桶子等进行存储和包装,圆柱形状可以最大限度地节省空间,提高存储效率。
5. 总结圆柱是一种常见的几何体,具有独特的形状和特性。
通过了解圆柱的基本属性和公式,可以更好地理解和应用圆柱在各个领域中的作用。
无论在工程、建筑、数学还是食品等领域,对圆柱的认识都是至关重要的。
希望通过本文档的介绍,对圆柱的认识有所加深,能够在实际应用中更好地运用圆柱的知识。