圆柱和圆锥的侧面展开图

圆柱和圆锥的侧面展开图（四）2006-8-1 13:35页面功能【字体：大中小】【打印】【关闭】圆锥侧面展开图(扇形)中的各元素与圆锥的各元素之间的关系极为密切，即扇形的半径是圆锥的母线，扇形的弧长是圆锥底面圆的周长。

因此我们要重视空间图形与平面图形的互相转化。

教学步骤（一）明确目标在小学，同学们除了学习圆柱之外还学习了一个几何体——圆锥，在生活中我们也常常遇到圆锥形的物体，涉及到这些物体表面积的计算．这些圆锥形物体的表面积是怎样计算出来的？这就是本节课“7.21圆锥的侧面展开图”所要研究的内容。

（二）整体感如和圆柱一样，圆锥也是日常生活或实践活动中常见物体，在学生学过圆柱的有关计算后，进一步学习圆锥的有关计算，不仅对培养学生的空间观念有好处，而且能使学生体会到用平面几何知识可以解决立体图形的计算，为学习立体几何打基础。

圆锥的侧面展开图不仅用于圆锥表面积的计算，而且在生产中常用于画图下料上，因此圆锥侧面展开图是本课的重点。

本课首先在小学已具有圆锥直观感知的基础上，用直角三角形旋转运动的观点给出圆锥的一系列概念，然后利用圆锥的模型，把其侧面展开，使学生认识到圆锥的侧面展开图是一个扇形，并能将圆锥的有关元素与展开图扇形的有关元素进行相互间的转化，最后应用圆锥及其侧面展开图之间对应关系进行计算。

（三）教学过程［幻灯展示生活中常遇的圆锥形物体，如：铅锤、粮堆、烟囱帽］前面屏幕上展示的物体都是什么几何体？［安排回忆起的学生回答：圆锥］在小学我们已学过圆锥，哪位同学能说出圆锥有哪些特征？安排举手的学生回答：圆锥是由一个底面和一个侧面围成的，圆锥的底面是一个圆，侧面是一个曲面，从圆锥的顶点到底面圆的距离是圆锥的高。

［教师边演示模型，边讲解］：大家观察Rt，绕直线SO旋转一周得到的图形是什么？［安排中下生回答：圆锥］大家观察圆锥的底面，它是Rt 的哪条边旋转而成的？［安排中下生回答：OA］圆锥的侧面是Rt的什么边旋转而得的？［安排中下生回答，斜边］，因圆锥是Rt绕直线SO旋转一周得到的，与圆柱相类似，直线SO应叫做圆锥的什么？［安排中下生回答：轴］大家观察圆锥的轴SO应具有什么性质？［安排学生稍加讨论，举手发言：圆锥的轴过底面圆的圆心，且与底面圆垂直，轴上连接圆锥顶点与底面圆心的线段就是圆锥的高。

(2019年1月最新最细）2019全国中考真题解析考点汇编☆圆柱、圆锥的侧面展开图一、选择题1. （2019江苏无锡，4，3分）已知圆柱的底面半径为2cm ，高为5cm ，则圆柱的侧面积是（ ）A ．20cm 2B ．20πcm 2C ．10πcm 2D ．5πcm 2考点：圆柱的计算。

分析：圆柱的侧面积=底面周长×圆柱的高，据此即可求解． 解答：解：圆柱的底面周长是：2×2π=4πcm ，则圆柱的侧面积是：4π×5=20πcm 2． 故选B ．点评：本题主要考查了圆柱侧面积的计算方法．2. （2019内蒙古呼和浩特，3，3）已知圆柱的底面半径为1，母线长为2，则圆柱的侧面积为（ ）A 、2B 、4C 、2πD 、4π 考点：圆柱的计算． 专题：计算题．分析：圆柱侧面积=底面周长×高． 解答：解：圆柱沿一条母线剪开，所得到的侧面展开图是一个矩形，它的长是底面圆的周长，即2π，宽为母线长为2cm ，所以它的面积为4πcm 2．故选D ．点评：本题考查了圆柱的计算，掌握特殊立体图形的侧面展开图的特点，是解决此类问题的关键．3. （2019四川广安，6，3分）如图所示，圆柱的底面周长为6cm ，AC 是底面圆的直径，高BC ＝ 6cm ，点P 是母线BC 上一点且PC ＝23BC ．一只蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离是（ ）A ．（64π+）cm B ．5cm C ． D ．7cm考点：圆柱的表面展开图，勾股定理 专题：圆柱的表面展开图、勾股定理分析：画出该圆柱的侧面展开图如图所示，则蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离为线段AP 的长．在Rt △ACP 中，AC ＝()632cm =，PC ＝23BC ＝4cm ，所以()5AP cm ==．解答：B点评：解决这类问题要善于将空间图形转化为平面图形，采用“化曲为直”的方法，利用圆柱体的表面展开图，把求最短距离问题转化为求两点之间的线段的长度问题．4. （2019新疆乌鲁木齐，7，4）露露从纸上剪下一个圆形和一个扇形的纸片（如图），用它们恰好能围成一个圆锥模型，若圆的半径为1．扇形的圆心角等于120°，则此扇形的半径为（ ）A 、3B 、6错误！未找到引用源。

九年级数学教案圆柱和圆锥的侧面展开图一、教学目标素质教育目标（一）知识教学点1.使学生了解圆柱的特征，了解圆柱的侧面、底面、高、轴、母线、过轴的截面等概念，了解圆柱的侧面展开图是矩形.2.使学生会计算圆柱的侧面积或全面积.（二）能力训练点1.通过圆柱形成过程的教学，培养学生观察能力、抽象思维能力和概括能力；2.通过圆柱侧面积的计算，培养学生正确、迅速的运算能力；3.通过实际问题的教学，培养学生空间想象能力，从实际问题中抽象出数学模型的能力.（三）德育渗透点1.通过圆柱的实物观察及有关概念的归纳向学生渗透“真知产生于实践”的观点；3.通过圆柱侧面展开图的教学，向学生渗透化曲面为平面，化立体图形为平面图形的“转化”的观点；4.通过圆柱轴截面的教学，向学生渗透“抓主要矛盾、抓本质”的矛盾论的观点.（四）美育渗透点重点·难点·疑点及解决办法1.重点：（1）圆柱的形成手段和圆柱的轴、母线、高等概念及其特征；（2）会用展开图的面积公式计算圆柱的侧面积和全面积.2.难点：对侧面积计算的理解.3.疑点及解决方法：学生对圆柱侧面展开图的长为什么是底面圆的周长有疑虑，为此教学时用模型展开，加强直观性教学.二、教学步骤（一）明确目标在小学，大家已学过圆柱，在生活中我们也常常遇到圆柱形的物体，涉及到圆柱形物体的侧面积和全面积的计算问题如何计算呢这就是今天“7.21圆柱的侧面展开图”要研究的内容。

（二）整体感知圆柱是生产、生活实际中常遇到的几何体，它是怎样形成的，如何计算它的表面积为了回答上述问题，首先在小学已具有直观感知的基础上，用矩形旋转、运动的观点给出圆柱体有关的一系列概念，然后利用圆柱的模型将它的侧面展开，使学生认识到圆柱的侧面展开图是一个矩形，并能将这矩形的长与宽跟圆柱的高（或母线）、底面圆半径找到相互转化的对应关系.最后应用对应关系和面积公式进行计算.〔三〕教学过程（幻灯展示生活中常遇的圆柱形物体，如：油桶、铅笔、圆形柱子等），前面展示的物体都是圆柱.在小学，大家已学过圆柱，哪位同学能说出圆柱有哪些特征（安排举手的学生回答：圆柱的两个底面都是圆面，这两个圆相等，侧面是曲面.）（教师演示模型并讲解）：大家观察矩形ABCD，绕直线AB旋转一周得到的图形是什么（安排中下生回答：圆柱）.大家再观察，圆柱的上、下底是由矩形的哪些线段旋转而成的（安排中下生回答：上底是以A为圆心，AD旋转而成的，下底是以B为圆心，BC旋转而成的.）上、下底面圆为什么相等（安排中下生回答：因矩形对边相等，所以上、下底半径相等，所以上、下底面圆相等.）大家再观察，圆柱的侧面是矩形ABCD的哪条线段旋转而成的（安排中下生回答：侧面由DC旋转而成的.）矩形ABCD绕直线AB旋转一周，直线用叫做圆柱的轴，CD叫做圆柱的母线.圆柱侧面上平行于轴的线段都叫做圆柱的母线.矩形的另一组对边AD、BC是上、下底面的半径。

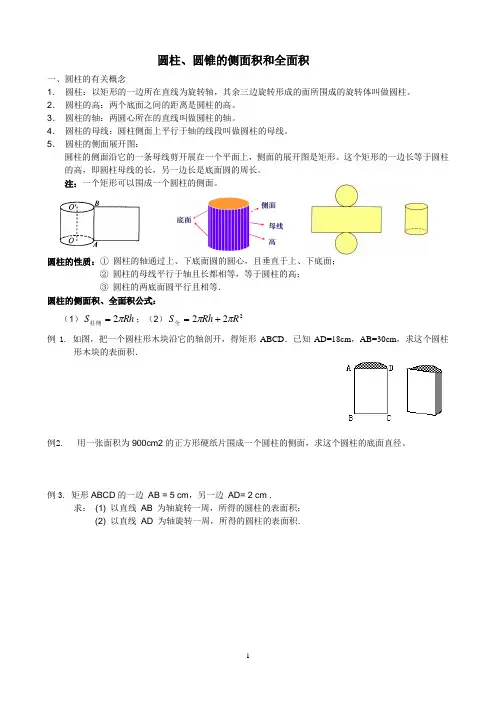
圆柱、圆锥的侧面积和全面积 一、圆柱的有关概念1． 圆柱：以矩形的一边所在直线为旋转轴，其余三边旋转形成的面所围成的旋转体叫做圆柱。

2． 圆柱的高：两个底面之间的距离是圆柱的高。

3． 圆柱的轴：两圆心所在的直线叫做圆柱的轴。

4． 圆柱的母线：圆柱侧面上平行于轴的线段叫做圆柱的母线。

5． 圆柱的侧面展开图：圆柱的侧面沿它的一条母线剪开展在一个平面上，侧面的展开图是矩形。

这个矩形的一边长等于圆柱的高，即圆柱母线的长，另一边长是底面圆的周长。

注：一个矩形可以围成一个圆柱的侧面。

圆柱的性质：① 圆柱的轴通过上、下底面圆的圆心，且垂直于上、下底面；② 圆柱的母线平行于轴且长都相等，等于圆柱的高；③ 圆柱的两底面圆平行且相等．圆柱的侧面积、全面积公式：（1）Rh S π2=柱侧；（2）222R Rh S ππ+=全例1. 如图，把一个圆柱形木块沿它的轴剖开，得矩形ABCD ．已知AD=18cm ，AB=30cm ，求这个圆柱形木块的表面积．例2. 用一张面积为900cm2的正方形硬纸片围成一个圆柱的侧面，求这个圆柱的底面直径。

例3. 矩形ABCD 的一边 AB = 5 cm ，另一边 AD= 2 cm .求： (1) 以直线 AB 为轴旋转一周，所得的圆柱的表面积；(2) 以直线 AD 为轴旋转一周，所得的圆柱的表面积.二、圆锥的有关概念1．圆锥：以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体叫做圆锥。

2．圆锥的高：从圆锥的顶点到底面的距离是圆锥的高。

3．圆锥的母线：我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线。

注：圆锥的母线长都相等。

4．圆锥的侧面展开图：如果把一个圆锥的侧面沿它的一条母线剪开，展在一个平面上，那么它的展开图是一个扇形。

这个扇形的半径是圆锥的母线长，弧长是圆锥底面圆的周长。

（1）l = 20，r=12（2）h =12, r=5（3）l = 10, h = 8你能帮小明的妈妈算一算至少需多少平方米的材料吗？例5. 小明的妈妈做的圣诞老人的帽子满足以下条件,请你求出帽子侧面展开图的圆心角θ（r、h、l分别是圆锥的底面半径、高线、母线长）（1）l= 2，r = 1 则θ=________；（2）h=3, r=4 则θ=__________。

24.4.2 圆柱、圆锥的侧面展开图及其计算教学目标（一）知识教学目标1．使学生了解圆柱的特征，了解圆柱的侧面、底面、高、轴、母线、过轴的截面等概念，了解圆柱的侧面展开图是矩形．2．使学生会计算圆柱的侧面积或全面积．3．使学生了解圆锥的特征，了解圆锥的侧面、底面、高、轴、母线、过轴的截面等概念，了解圆锥的侧面展开图是扇形。

4．使学生会计算圆锥的侧面积或全面积。

（二）能力训练目标1．通过圆柱、圆锥形成过程的教学，培养学生观察能力、抽象思维能力和概括能力；2．通过圆柱、圆锥侧面积的计算，培养学生正确、迅速的运算能力；3．通过实际问题的教学，培养学生空间想象能力，从实际问题中抽象出数学模型的能力．教学重点·难点·1．重点：（1）圆柱的形成和圆柱的轴、母线、高等概念及其特征；（2）会用展开图的面积公式计算圆柱、圆锥的侧面积和全面积．2．难点：圆柱、圆锥的侧面积计算的理解．教学过程一、复习导入在小学，大家已学过圆柱，在生活中我们也常常遇到圆柱形的物体，涉及到圆柱形物体的侧面积和全面积的计算问题如何计算呢？圆柱是生产、生活实际中常遇到的几何体，它是怎样形成的，如何计算它的表面积？（展开图是一个矩形，并能将这矩形的长与宽跟圆柱的高（或母线）、底面圆半径找到相互转化的对应关系．最后应用对应关系和面积公式进行计算．）二、新课学习（一）圆柱学习（幻灯展示生活中常遇的圆柱形物体，如：油桶、铅笔、圆形柱子等），前面展示的物体都是圆柱．在小学，大家已学过圆柱，哪位同学能说出圆柱有哪些特征？（教师演示模型并讲解）：大家观察矩形ABCD，绕直线AB旋转一周得到的图形是什么？大家再观察，圆柱的上、下底是由矩形的哪些线段旋转而成的？上、下底面圆为什么相等？圆柱的侧面是矩形ABCD的哪条线段旋转而成的？矩形ABCD绕直线AB旋转一周，直线用叫做圆柱的轴，CD叫做圆柱的母线．圆柱侧面上平行于轴的线段都叫做圆柱的母线．矩形的另一组对边AD、BC是上、下底面的半径。

24.4弧长和扇形面积一．弧长：公式： .探究：如图，用一根铁丝能弯成一个半径为9cm ，圆心角为︒100的圆弧，求铁丝的长相关思路：⑴︒360圆心角的圆的周长公式为 ；⑵︒1的圆心角所对的弧长为 ；⑶︒n 的圆心角所对的弧长为 .解答：二．练习：1．已知扇形的圆心角为︒120，半径为6，则扇形的弧长是（ ）A ．π3B ．π4C ．π5D ．π62.已知一条弧长为l ，它所对圆心角的度数为︒n ，则这条弦所在圆的半径为（ ）． Ａ．180ln π Ｂ．πn l 180 Ｃ．πn l 360 Ｄ．n lπ1803.一条弧所对的圆心角是︒90，半径是R ，则这条弧的长是 ．4.︒75的圆心角所对的弧长是π5.2cm ，则此弧所在圆的半径为 cm .5． 如图，两个大小一样的传送轮连接着一条传送带，求这条传送带的长三．扇形面积：探究：如图，在半径为为9cm 的圆中剪去一个圆心角为︒100的扇形，求此扇形的面积.相关思路：⑴︒360圆心角的圆的面积公式为 ；⑵︒1的圆心角的扇形面积为 ；⑶︒n 的圆心角的扇形面积为 ；⑷︒n 的圆心角的扇形面积可用其弧长、半径表示为 .解答：四．练习：1．半径为3，圆心角为︒120的扇形的面积为 .2.扇形的圆心角为︒210，弧长是π28，则扇形的面积为 ．3．扇形的弧长为6π，面积为12π，则此扇形的半径为 .4．扇形的面积为π32，半径为2，则此扇形的圆心角为 .5．若扇形的圆心角为︒120，弧长为π6cm ，则这个扇形的面积为 ．6．一个扇形的半径等于一个圆的半径的2倍，且面积相等．则这个扇形的圆心角为 ．7.一个扇形的弧长为π20cm ，面积为π2402cm ，则此扇形的圆心角为.如图，水平放置的圆柱形排水管道的截面半径是m 6.0，其中水面高m 3.0.求截面上有水部分的面积.8．如图，已知在扇形AOB 中，若︒=∠45AOB ，cm AD 4=，弧π3=CD cm ，求图中阴影部分的面积．1．（2013•佛山）如图，圆锥的侧面展开图是一个半圆，求母线AB 与高AO 的夹角．参考公式：圆锥的侧面积S=πrl，其中r 为底面半径，l 为母线长．2．（2011•陕西）一天，数学课外活动小组的同学们，带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度，来评估这些坑道对河道的影响，如图是同学们选择（确保测量过程中无安全隐患）的测量对象，测量方案如下：①先测出沙坑坑沿的圆周长34.54米；②甲同学直立于沙坑坑沿的圆周所在的平面上，经过适当调整自己所处的位置，当他位于B 时恰好他的视线经过沙坑坑沿圆周上一点A 看到坑底S （甲同学的视线起点C 与点A ，点S 三点共线），经测量：AB=1.2米，BC=1.6米．根据以上测量数据，求圆锥形坑的深度（圆锥的高）．（π取3.14，结果精确到0.1米）3．（2011•杭州）在△ABC中，AB= 3，AC= 2，BC=1．（1）求证：∠A≠30°；（2）将△ABC绕BC所在直线旋转一周，求所得几何体的表面积．4．（2009•青海）如图，一个圆锥的高为33cm，侧面展开图是半圆．求：（1）圆锥的母线长与底面半径之比；（2）求∠BAC的度数；（3）圆锥的侧面积（结果保留π）．5．（2008•庆阳）附加题：对于本试卷第19题：“图中△ABC外接圆的圆心坐标是”．请再求：（1）该圆圆心到弦AC的距离；（2）以BC为旋转轴，将△ABC旋转一周所得几何体的全面积．（所有表面面积之和）6．（2008•南通）铁匠王老五要制作一个圆锥体模型，操作规则是：在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆，使得扇形围成圆锥的侧面时，圆恰好是该圆锥的底面．他们首先设计了如图所示的方案一，发现这种方案不可行，于是他们调整了扇形和圆的半径，设计了如图所示的方案二．（两个方案的图中，圆与正方形相邻两边及扇形的弧均相切．方案一中扇形的弧与正方形的两边相切）请你帮助他算一算可以吗？（1）请说明方案一不可行的理由；（2）判断方案二是否可行？若可行，请确定圆锥的母线长及其底面圆半径；若不可行，请说明理由7．（2007•庆阳）如图，一个直角三角形两条直角边分别为3cm 和4cm ，以斜边AB 所在直线为轴旋转一周得到一个几何体，在虚线框内画出这个几何体的草图，求这个几何体的表面积．8．（2006•芜湖）在一次科学探究实验中，小明将半径为5cm 的圆形滤纸片按图1所示的步骤进行折叠，并围成圆锥形．（1）取一漏斗，上部的圆锥形内壁（忽略漏斗管口处）的母线OB 长为6cm ，开口圆的直径为6cm ．当滤纸片重叠部分三层，且每层为41圆时，滤纸围成的圆锥形放入该漏斗中，能否紧贴此漏斗的内壁（忽略漏斗管口处），请你用所学的数学知识说明；（2）假设有一特殊规格的漏斗，其母线长为6cm ，开口圆的直径为7.2cm ，现将同样大小的滤纸围成重叠部分为三层的圆锥形，放入此漏斗中，且能紧贴漏斗内壁．问重叠部分每层的面积为多少？9．（2006•攀枝花）如图，圆锥的底面半径r=3cm ，高h=4cm ．求这个圆锥的表面积．（π取3.14）10．（2005•山西）下图是一纸杯，它的母线AC和EF延长后形成的立体图形是圆锥．该圆锥的侧面展开图形是扇形OAB．经测量，纸杯上开口圆的直径为6cm，下底面直径为4cm，母线长EF=8cm．求扇形OAB的圆心角及这个纸杯的表面积．（面积计算结果用π表示）．11．（2003•宁波）已知扇形的圆心角为120°，面积为300πcm2．（1）求扇形的弧长；（2）若将此扇形卷成一个圆锥，则这个圆锥的轴截面面积为多少？12．（2003•淮安）如图，扇形OAB的圆心角为120°，半径为6cm．（1）请用尺规作出扇形的对称轴（不写作法，但应保留作图痕迹）；（2）若将此扇形围成一个圆锥的侧面（不计接缝），求圆锥的高．1．（2008•庆阳）下图是某几何体的展开图．（1）这个几何体的名称是；（2）画出这个几何体的三视图；（3）求这个几何体的体积．（π取3.14）2．（2006•烟台）如图1，O 为圆柱形木块底面的圆心，过底面的一条弦AD ，沿母线AB 剖开，得剖面矩形ABCD ，AD=24cm ，AB=25cm ．若弧AmD 的长为底面周长的32，如图2所示． （1）求⊙O 的半径；（2）求这个圆柱形木块的表面积．（结果可保留π和根号）3．（2006•丽水）如下示意图，是我市香菇培植场常见的半地下室栽培棚，它由两部分组成，地上部分为半圆柱形四周封闭的塑料薄膜保温棚；地下部分为长方体的培植室，室内长30米，宽1.2米的地面上存放菌棒培育香菇．（1）地下培植室内按标准排放菌棒，宽排放8袋，长每米排放4排，求能排放多少袋香菇菌棒？（2）要建这样的保温棚约需多少平方米的塑料薄膜？（不计余料及埋在土里的塑料薄膜，结果精确到0.1平方米）4．（2006•安徽）附加题：如图是某工件的二视图，按图中尺寸求工件的表面积．5．（2004•宁波）如图，矩形ABCD 中，AB=1，若直角三角形ABC 绕AB 旋转所得圆锥的侧面积和矩形ABCD 绕AB 旋转所得圆柱的侧面积相等，求BC 的长．9．（2002•安徽）如图，是一个几何体的二视图，求该几何体的体积．（π取3.14）6．（2004•杭州）要在如图所示的一个机器零件（尺寸单位：mm ）表面涂上防锈漆，请你帮助计算一下这个零件的表面积．3．（2010•宜宾）将半径为5的圆（如图1）剪去一个圆心角为n °的扇形后围成如图2所示的圆锥，则n 的值等于 ．11．（2006•安徽）如图是某工件的三视图，求此工件的全面积．4．（2009•永州）问题探究：（1）如图①所示是一个半径为23，高为4的圆柱体和它的侧面展开图，AB 是圆柱的一条母线，一只蚂蚁从A 点出发沿圆柱的侧面爬行一周到达B 点，求蚂蚁爬行的最短路程．（探究思路：将圆柱的侧面沿母线AB 剪开，它的侧面展开图如图①中的矩形ABB ′A ′，则蚂蚁爬行的最短路程即为线段AB ′的长）；（2）如图②所示是一个底面半径为32，母线长为4的圆锥和它的侧面展开图，PA 是它的一条母线，一只蚂蚁从A 点出发沿圆锥的侧面爬行一周后回到A 点，求蚂蚁爬行的最短路程；（3）如图③所示，在②的条件下，一只蚂蚁从A 点出发沿圆锥的侧面爬行一周到达母线PA 上的一点，求蚂蚁爬行的最短路程．6．（2007•庆阳）如图，一个直角三角形两条直角边分别为3cm 和4cm ，以斜边AB 所在直线为轴旋转一周得到一个几何体，在虚线框内画出这个几何体的草图，求这个几何体的表面积．7．（2007•荆州）如图，不透明圆锥体DEC 放在水平面上，在A 处灯光照射下形成影子．设BP 过底面圆的圆心，已知圆锥体的高为23m ，底面半径为2m ，BE=4m ．（1）求∠B 的度数；（2）若∠ACP=2∠B ，求光源A 距水平面的高度．（答案用含根号的式子表示）10．（2006•贵阳）如图，这是一个由圆柱体材料加工而成的零件，它是以圆柱体的上底面为底面，在其内部“掏取”一个与圆柱体等高的圆锥体而得到的，其底面直径AB=12cm ，高BC=8cm ，求这个零件的表面积．（结果保留π）。

数学教案－圆柱和圆锥的侧面展开图第一课时素质教育目标（一）知识教学点1．使学生了解圆柱的特征，了解圆柱的侧面、底面、高、轴、母线、过轴的截面等概念，了解圆柱的侧面展开图是矩形．2．使学生会计算圆柱的侧面积或全面积．（二）能力训练点1．通过圆柱形成过程的教学，培养学生观察能力、抽象思维能力和概括能力；2．通过圆柱侧面积的计算，培养学生正确、迅速的运算能力；3．通过实际问题的教学，培养学生空间想象能力，从实际问题中抽象出数学模型的能力．（三）德育渗透点1．通过圆柱的实物观察及有关概念的归纳向学生渗透“真知产生于实践”的观点；2．通过应用圆柱展开图进行计算，解决实际问题，向学生渗透理论联系实际的观点；3．通过圆柱侧面展开图的教学，向学生渗透化曲面为平面，化立体图形为平面图形的“转化”的观点；4．通过圆柱轴截面的教学，向学生渗透“抓主要矛盾、抓本质”的矛盾论的观点．（四）美育渗透点通过学习新知，使学生领略主体图形美与平面图形美的联系，提高学生对美的认识层次．重点·难点·疑点及解决办法1．重点：（1）圆柱的形成手段和圆柱的轴、母线、高等概念及其特征；（2）会用展开图的面积公式计算圆柱的侧面积和全面积．2．难点：对侧面积计算的理解．3．疑点及解决方法：学生对圆柱侧面展开图的长为什么是底面圆的周长有疑虑，为此教学时用模型展开，加强直观性教学．教学步骤（一）明确目标在小学，大家已学过圆柱，在生活中我们也常常遇到圆柱形的物体，涉及到圆柱形物体的侧面积和全面积的计算问题如何计算呢？这就是今天“7．21圆柱的侧面展开图”要研究的内容。

（二）整体感知圆柱是生产、生活实际中常遇到的几何体，它是怎样形成的，如何计算它的表面积？为了回答上述问题，首先在小学已具有直观感知的基础上，用矩形旋转、运动的观点给出圆柱体有关的一系列概念，然后利用圆柱的模型将它的侧面展开，使学生认识到圆柱的侧面展开图是一个矩形，并能将这矩形的长与宽跟圆柱的高（或母线）、底面圆半径找到相互转化的对应关系．最后应用对应关系和面积公式进行计算．〔三〕教学过程（幻灯展示生活中常遇的圆柱形物体，如：油桶、铅笔、圆形柱子等），前面展示的物体都是圆柱．在小学，大家已学过圆柱，哪位同学能说出圆柱有哪些特征？（安排举手的学生回答：圆柱的两个底面都是圆面，这两个圆相等，侧面是曲面．）（教师演示模型并讲解）：大家观察矩形ABCD，绕直线AB旋转一周得到的图形是什么？（安排中下生回答：圆柱）．大家再观察，圆柱的上、下底是由矩形的哪些线段旋转而成的？（安排中下生回答：上底是以A为圆心，AD旋转而成的，下底是以B为圆心，BC旋转而成的．）上、下底面圆为什么相等？（安排中下生回答：因矩形对边相等，所以上、下底半径相等，所以上、下底面圆相等．）大家再观察，圆柱的侧面是矩形ABCD的哪条线段旋转而成的？（安排中下生回答：侧面由DC旋转而成的．）矩形ABCD绕直线AB旋转一周，直线用叫做圆柱的轴，CD叫做圆柱的母线．圆柱侧面上平行于轴的线段都叫做圆柱的母线．矩形的另一组对边AD、BC是上、下底面的半径。