理论力学第三章习题答案

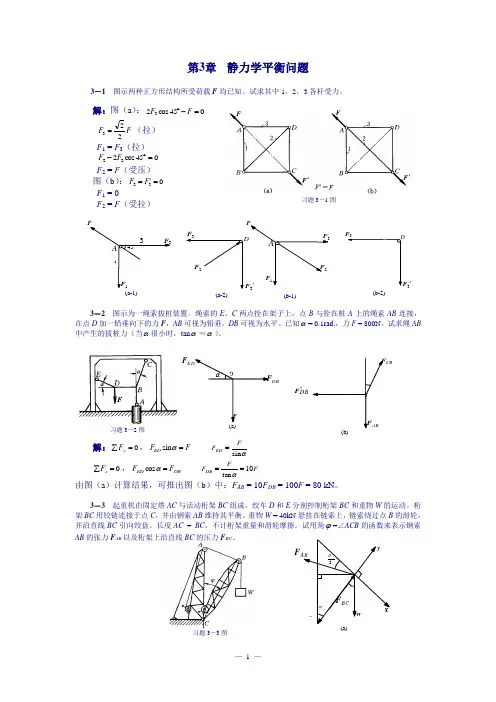
F DBCBDBF '习题3－3图第3章 静力学平衡问题3－1 图示两种正方形结构所受荷载F 均已知。

试求其中1，2，3各杆受力。

解：图（a ）：045cos 23=-︒F FF F 223=（拉） F 1 = F 3（拉） 045cos 232=︒-F F F 2 = F （受压） 图（b ）：033='=F F F 1 = 0F 2 = F （受拉）3－2 图示为一绳索拔桩装置。

绳索的E 、C 两点拴在架子上，点B 与拴在桩A 上的绳索AB 连接，在点D 加一铅垂向下的力F ，AB 可视为铅垂，DB 可视为水平。

已知α= 0.1rad.，力F = 800N 。

试求绳AB 中产生的拔桩力（当α很小时，tan α≈α）。

解：0=∑y F ，F F ED =αsin αs i nFF ED = 0=∑x F ，DB ED F F =αcos F FF DB 10tan ==α由图（a ）计算结果，可推出图（b ）中：F AB = 10F DB = 100F = 80 kN 。

3－3 起重机由固定塔AC 与活动桁架BC 组成，绞车D 和E 分别控制桁架BC 和重物W 的运动。

桁架BC 用铰链连接于点C ，并由钢索AB 维持其平衡。

重物W = 40kN 悬挂在链索上，链索绕过点B 的滑轮，并沿直线BC 引向绞盘。

长度AC = BC ，不计桁架重量和滑轮摩擦。

试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。

(b-1)习题3－1图(a-1)(a-2)'3(b-2)习题3－2图F习题3-5图习题3－4图 解：图（a ）：0=∑x F ，0sin 2cos=-ϕϕW F AB ，2sin2ϕW F AB =0=∑y F ，02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3－4 杆AB 及其两端滚子的整体重心在G 点，滚子搁置在倾斜的光滑刚性平面上，如图所示。

理论力学课后习题第三章解答3.1解 如题3.1.1图。

均质棒受到碗的弹力分别为，棒自身重力为。

棒与水平方向的夹角为。

设棒的长度为。

由于棒处于平衡状态，所以棒沿轴和轴的和外力为零。

沿过点且与轴平行的合力矩为0。

即：①②③ 由①②③式得：④ 又由于即⑤ 将⑤代入④得：图题1.3.11N ,2N G θl x y A z 0sin 2cos 21=-=∑θθN N F x0cos 2sin 21=-+=∑G N N Fyθθ0cos 22=-=∑θlG c N M i ()θθ22cos 1cos 22-=c l ,cos 2c r =θrc 2cos =θ3.2解 如题3.2.1图所示，均质棒分别受到光滑墙的弹力，光滑棱角的弹力，及重力。

由于棒处于平衡状态，所以沿方向的合力矩为零。

即①由①②式得：所以()cr c l 2224-=o图题1.3.21N 2N G y 0cos 2=-=∑G N Fyθ0cos 22cos 2=-=∑θθlG d N M z ld=θ3cos 31arccos ⎪⎭⎫ ⎝⎛=l d θ3.3解 如题3.3.1图所示。

棒受到重力。

棒受到的重力。

设均质棒的线密度为。

由题意可知，整个均质棒沿轴方向的合力矩为零。

3.4解 如题3.4.1图。

轴竖直向下，相同的球、、互切，、切于点。

设球的重力大小图题1.3.32AB i G ag ρ=1i G bgρ=2ρz ()BH BF G OD G M z --⋅=∑21sin θ=0sin cos 2sin 2=⎪⎭⎫ ⎝⎛--θθρθρa b gb a ga aba b 2tan 22+=θ图题1.3.4Ox A B C B C D为，半径为，则对、、三个球构成的系统来说，在轴方向的合力应为零。

即：①对于球，它相对于过点与轴平行的轴的合力矩等于零。

即：②由式得：3.5解 如题3.5.1图。

梯子受到地面和墙的弹力分别为，，受地面和墙的摩擦力分别为，。

《理论⼒学》习题三答案讲解《理论⼒学》习题三答案⼀、单项选择题（本⼤题共30⼩题，每⼩题2分，共60分）1. 求解质点动⼒学问题时，质点的初始条件是⽤来（ C ）。

A 、分析⼒的变化规律； B 、建⽴质点运动微分⽅程； C 、确定积分常数； D 、分离积分变量。

2. 在图1所⽰圆锥摆中，球M 的质量为m ，绳长l ，若α⾓保持不变，则⼩球的法向加速度为（ C ）。

A 、αsin g ；B 、αcos g ；C 、αtan g ；D 、αtan gc 。

3. 已知某点的运动⽅程为2bt a S +=（S 以⽶计,t 以秒计，a 、b 为常数），则点的轨迹为（ C ）。

A 、是直线；B 、是曲线；C 、不能确定；D 、抛物线。

4. 如图2所⽰距地⾯H 的质点M ，具有⽔平初速度0v ，则该质点落地时的⽔平距离l 与（ B ）成正⽐。

A 、H ；B 、H ；C 、2H ；D 、3H 。

5. ⼀质量为m 的⼩球和地⾯碰撞，开始瞬时的速度为1v ，碰撞结束瞬时的速度为2v（如图3），若v v v ==21，则碰撞前后质点动量的变化值为（ A ）。

A 、mv ；B 、mv 2 ；C 、mv 3；D 、 0。

6. ⼀动点作平⾯曲线运动，若其速率不变，则其速度⽮量与加速度⽮量（ B ）。

A 、平⾏； B 、垂直； C 、夹⾓随时间变化； D 、不能确定。

7. 三棱柱重P ，放在光滑的⽔平⾯上，重Q 的匀质圆柱体静⽌释放后沿斜⾯作纯滚动，则系统在运动过程中（ A ）。

A 、沿⽔平⽅向动量守恒，机械能守恒；B 、动量守恒，机械能守恒；C 、沿⽔平⽅向动量守恒，机械能不守恒；D 、均不守恒。

图1图2图38. 动点M 沿其轨迹运动时，下列⼏种情况中，正确的应该是（ A ）。

A 、若始终有a v⊥，则必有v 的⼤⼩等于常量；B 、若始终有a v⊥，则点M 必作匀速圆周运动； C 、若某瞬时有v ∥a ，则点M 的轨迹必为直线；D 、若某瞬时有a 的⼤⼩为零，且点M 作曲线运动，则此时速度必等于零。

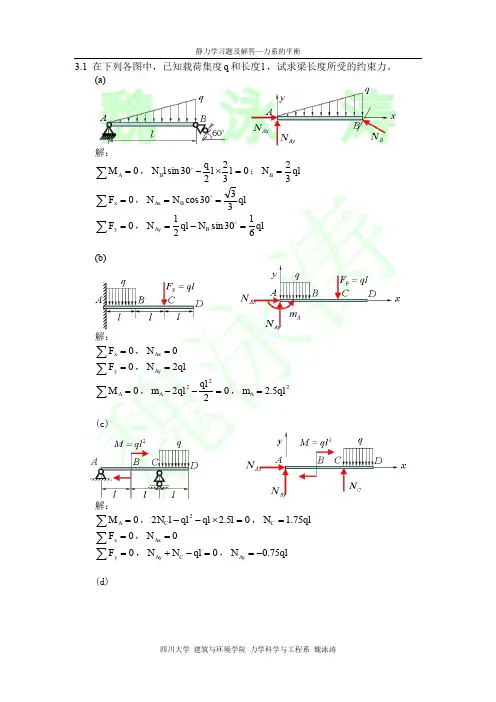
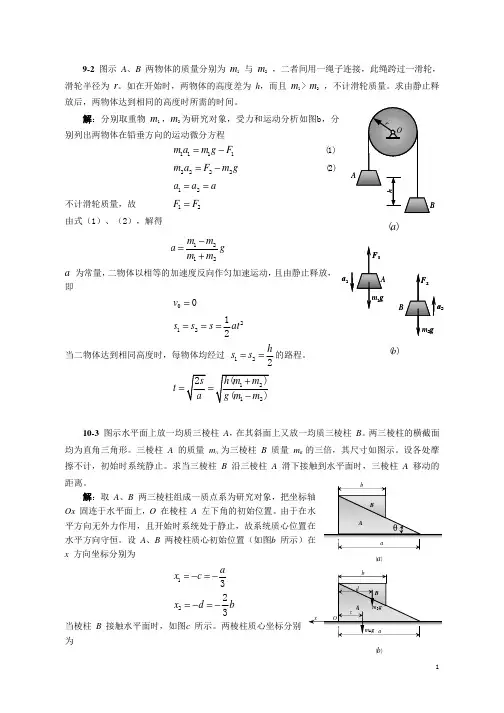
第三章作业答案3-6 力系中，=100 N，=300 N，F=200 N，各力作用线的位置如图3-6 所示。

试将力系向原点O 简化。

图3-63-11 水平圆盘的半径为r，外缘C 处作用有已知力F。

力F 位于铅垂平面内，且与C 处圆盘切线夹角为60°，其他尺寸如图3-11a 所示。

求力F 对x，y，z 轴之矩。

图3-11解（1）方法1，如图3-11b 所示，由已知得（2）方法23-14 图3-14a 所示空间桁架由杆1，2，3，4，5 和6 构成。

在节点A 上作用1 个力F，此力在矩形ABDC 平面内，且与铅直线成45°角。

ΔEAK =ΔFBM。

等腰三角形EAK，FBM和NDB 在顶点A，B 和D 处均为直角，又EC=CK=FD=DM。

若F=10 kN，求各杆的内力。

图3-14解(1) 节点 A 为研究对象，受力及坐标如图3-14b 所示（2）节点B 为研究对象，受力如图3-14b 所示3-19 图3-19a 所示6 杆支撑1 水平板，在板角处受铅直力F 作用。

设板和杆自重不计，求各杆的内力。

图3-19解截开6 根杆，取有板的部分为研究对象，受力如图3-19b 所示。

3-22 杆系由球铰连接，位于正方体的边和对角线上，如图3-22a 所示。

在节点D 沿对角线LD 方向作用力。

在节点C 沿CH 边铅直向下作用F。

如球铰B，L 和H 是固定的，杆重不计，求各杆的内力。

图3-22解（1）节点D 为研究对象，受力如图3-22b 所示（2）节点C 为研究对象，受力如图3-22b 所示3-25 工字钢截面尺寸如图3-25a 所示，求此截面的几何中心。

图3-25解把图形的对称轴作轴x，如图3-25b 所示，图形的形心C 在对称轴x 上，即第五章作业答案5-3 如图5-3 所示，半圆形凸轮以等速= 0.01m/s沿水平方向向左运动，而使活塞杆AB 沿铅直方向运动。

当运动开始时，活塞杆A 端在凸轮的最高点上。

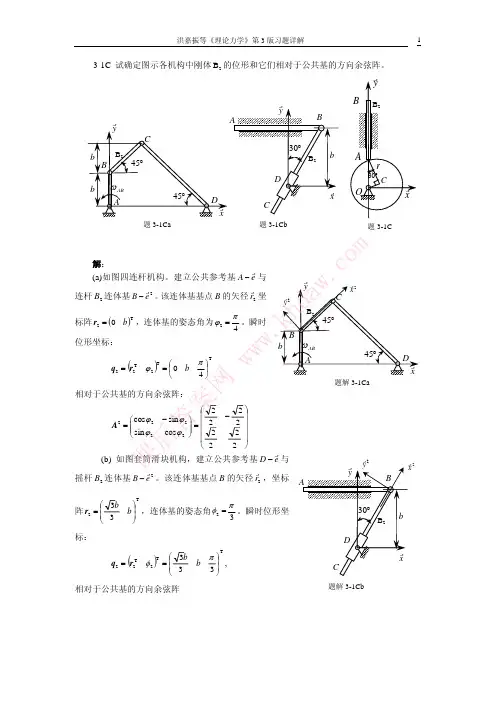
动力学第三章部分习题解答3－3 取套筒B 为动点，OA 杆为动系 根据点的复合运动速度合成定理r e a v v v +=可得：l v v ω==e 0a 30cos ，l v v v BC B ω332a === 研究AD 杆，应用速度投影定理有：030cos D A v v =，l v D ω334=再取套筒D 为动点，BC 杆为动系，根据点的复合运动速度合成定理r D BC D v v v +=将上式在x 轴上投影有：r D BC D v v v +-=-，l v v v BC D D ω332r =+-=3－4 AB 构件（灰色物体）作平面运动， 已知A 点的速度s A O v A /0cm 4510==ωAB 的速度瞬心位于C ，应用速度瞬心法有：rad/s 23==AC v A AB ω BC v AB B ω=，设OB 杆的角速度为ω，则有rad/s 415==OB v B ω 设P 点是AB 构件上与齿轮I 的接触点， 该点的速度：CP v AB P ω=齿轮I 的角速度为：rad/s 61==r v PI ω a v e vr vA vDv rD v A vB P v CAB ωI ω3－6 AB 杆作平面运动，取A 为基点 根据基点法公式有：BA A B v v v +=将上式在AB 连线上投影，可得0,01==B O B v ω因此，041ωω==AB v A AB因为B 点作圆周运动，此时速度为零，因此只有切向加速度（方向如图）。

根据加速度基点法公式n t BA BAA B aaa a ++=将上式在AB 连线上投影，可得n060cos BA A B a a a +=-，r a B 205.2ω-=201231ωα-==B O a B B O （瞬时针）3－7 齿轮II 作平面运动，取A 为基点有nt BA BA A B a a a a ++= n t 1BA BA a a a a ++=将上式在x 投影有：n 1cos BA a a a -=-β由此求得：212n 2cos 2r a a r a BAII βω+==再将基点法公式在y 轴上投影有：2t2sin r a a II BA αβ==，由此求得22sin r a II βα=再研究齿轮II 上的圆心，取A 为基点n t n t2222A O AO A O O aaa aa++=+将上式在y 轴上投影有2sin 2t t 22βαa r a a II AO O ===， B vBAv A vAa Ba t BA an BA atBA anBA axyt2A Oa n 2AO a xyn 2O a t 2Oa由此解得：)(2sin 2121t 221r r a r r a OO O +=+=βα再将基点法公式在x 轴上投影有：n1n22A O O a a a -=- 由此解得：2cos 1n2a a a O -=β，又因为221n 212)(O O O r r a ω+= 由此可得：)(2cos 21121r r a a O O +-±=βω3－9 卷筒作平面运动，C 为速度瞬心， 其上D 点的速度为v ，卷筒的角速度为r R vDC v -==ω 角加速度为rR ar R v -=-== ωα 卷筒O 点的速度为：rR vRR v O -==ω O 点作直线运动，其加速度为 rR aRr R R v va O O -=-==研究卷筒，取O 为基点，求B 点的加速度。

第三章 非惯性参考系不识庐山真面目，只缘身在此山中。

地球的多姿多彩，宇宙的繁荣，也许在这里可以略见一斑。

春光无限，请君且放千里目，别忘了矢量语言在此将大放益彩。

【要点分析与总结】1 相对运动t r r r '=+t t dr dr dr dr dr r dt dt dt dt dtυω'''==+=++⨯ t r υυω''=++⨯()t dv dv d v r a dt dt dtω''+⨯==+222**22()t d r d r d dr r v r dt dt dt dtωωωω'''''=++⨯+⨯+⨯+⨯()2t a a r r v ωωωω''''=++⨯+⨯⨯+⨯t c a a a '=++〈析〉仅此三式便可以使“第心说”与“日心说”归于一家。

（1） 平动非惯性系 (0ω=)t a a a '=+ 即：()t ma F ma '=+-（2） 旋转非惯性系 (0t t a υ==)()2a a r r ωωωωυ''''=+⨯+⨯⨯+⨯2 地球自转的效应（以地心为参考点）2mr F mg m r ω=--⨯写成分量形式为：2sin 2(sin cos )2cos x y z mx F m y my F m x z mz F mg m y ωλωλλωλ⎧=+⎪=-+⎨⎪=-+⎩ 〈析〉坐标系选取物质在地面上一定点O 为坐标原点，x 轴指向南方，y 轴指向东方，铅直方向为 z 轴方向。

2mr F mg m r ω=--⨯ 为旋转非惯性系 ()2F mg mr m r m r m r ωωωω-=+⨯+⨯⨯+⨯在 ,rR ωω条件下忽略 m r ω⨯与 ()m r ωω⨯⨯所得。

正因如此，地球上的物体运动均受着地球自转而带来的科氏力 2m r ω-⨯的作用，也正是它导致了气旋，反气旋，热带风暴，信风，河岸右侧冲刷严重，自由落体，傅科摆等多姿多彩的自然现象。

第三章思考题解答3.1 答：确定一质点在空间中得位置需要3个独立变量，只要确定了不共线三点的位置刚体的位置也就确定了，故须九个独立变量，但刚体不变形，此三点中人二点的连线长度不变，即有三个约束方程，所以确定刚体的一般运动不需3n 个独立变量，有6个独立变量就够了.若刚体作定点转动，只要定出任一点相对定点的运动刚体的运动就确定了，只需3个独立变量；确定作平面平行运动刚体的代表平面在空间中的方位需一个独立变量，确定任一点在平面上的位置需二个独立变量，共需三个独立变量；知道了定轴转动刚体绕转动轴的转角，刚体的位置也就定了，只需一个独立变量；刚体的平动可用一个点的运动代表其运动，故需三个独立变量。

3.2 答物体上各质点所受重力的合力作用点即为物体的重心。

当物体的大小远小于地球的线度时物体上各质点所在点的重力加速度都相等，且方向彼此平行即重力场为均匀场，此时质心与重心重合。

事实上但物体的线度很大时各质点所在处g 的大小是严格相等，且各质点的重力都指向地心，不是彼此平行的，重心与质心不和。

答 当物体为均质时，几何中心与质心重合；当物体的大小远小于地球的线度时，质心与重心重合；当物体为均质且大小远小于地球的线度时，三者都重合。

3.4 答 主矢F 是力系各力的矢量和，他完全取决于力系中各力的大小和方向，故主矢不随简化中心的位置而改变，故而也称之为力系的主矢；简化中心的位置不同，各力对简化中心的位矢i r 也就不同则各力对简化中心的力矩也就不同，故主矩随简化中心的位置而变，被称之为力系对简化中心的主矩。

分别取O 和O '为简化中心，第i 个力i F 对O 和O '的位矢分别为i r 和i r '，则i r =i r '+O O '，故()()iii ii i O F O O r F r M ⨯'-'=⨯'=∑∑'()∑∑⨯'-⨯'=ii ii i F O O F r ∑⨯'+=ii o F O O M即o o M M ≠'主矢不变，表明刚体的平动效应不变，主矩随简化中心的位置改变，表明力系的作用对刚体上不同点有不同的转动效应，但不改变整个刚体的转动规律或者说不影响刚体绕质心的转动。

3-3在图示刚架中，已知kN/m3=mq，26=F kN，mkN10⋅=M，不计刚架自重。

求固定端A处的约束力。

mkN12kN60⋅===AAyAxMFF，，3-4杆AB及其两端滚子的整体重心在G点，滚子搁置在倾斜的光滑刚性平面上，如图所示。

对于给定的θ角，试求平衡时的β角。

Aθ3lGβGθBBFARF32lO解：解法一：AB为三力汇交平衡，如图所示ΔAOG中βsinlAO=，θ-︒=∠90AOG，β-︒=∠90OAG，βθ+=∠AGO由正弦定理：)90sin(3)sin(sinθβθβ-︒=+ll，)cos31)sin(sinθβθβ=+l即βθβθθβsincoscossincossin3+=即θβtantan2=)tan21arctan(θβ=解法二：：=∑x F，0sinR=-θGF A（1）=∑y F，0cosR=-θGF B（2）)(=∑FAM，0sin)sin(3R=++-ββθlFlG B（3）解（1）、（2）、（3）联立，得)tan21arctan(θβ=3-5 由AC 和CD 构成的组合梁通过铰链C 连接。

支承和受力如图所示。

已知均布载荷强度kN/m 10=q ，力偶矩m kN 40⋅=M ，不计梁重。

kN 15kN 5kN 40kN 15===-=D C B A F F F F ；；；解：取CD 段为研究对象，受力如图所示。

0)(=∑F CM，024=--q M F D ；kN 15=D F取图整体为研究对象，受力如图所示。

0)(=∑F AM ，01682=--+q M F F D B；kN 40=B F0=∑yF ，04=+-+D BAyF q F F ；kN 15-=Ay F0=∑x F ，0=AxF3-6如图所示，组合梁由AC 和DC 两段铰接构成，起重机放在梁上。

已知起重机重P1 = 50kN ，重心在铅直线EC 上，起重载荷P2 = 10kN 。

如不计梁重，求支座A 、B 和D 三处的约束反力。