4电路化简

一、陈述 对任意含源单口网络N，都可以用一个电压源 与一个电阻相串联来等效。 R0 i i + + 即 + 等效 u N u u oc _ _ _
电压源的电压等于该网络的开路电压uoc， 这个电阻等于从此单口网络两端看进去，当网 络内部所有独立源均置零(No)时的等效电阻R0 i =0
+
4.6 戴维南定理
7Ω
10Ω
例（2） a 44 b
20 60 60
20
20 60
22
结论 只含电阻单口网络 等效为一个电阻
只含 电阻
R
2.含独立源电路 1V 例(1)
+
_
2
3
0.5A
0.2A 5
0.5A
5
5 0.3A
+ 1.5V _
结论 含独立源单口网络 等效为实际电压源 或实际电流源 含独立 源和电 阻电路
试用电压源与电流源等效变换的方 法计算2电阻中的电流。
1 2A
解:
I
1 3 2A 2A 6
1
3 + 6V –
6 + – 12V (a)
1 2
(b)
– 2V 2
I + +
由图(d)可得
82 I A 1A 2 2 2
2 2 +
2 2 4A
–
8V (d)
(c)
+
– 2V 2
第四章
分解方法及单口网络
——用等效化简的方法分析电路
本章的主要内容： 1、分解、等效的概念； 2、二端网络的等效化简，实际电源 的等效变换 ; 3、置换、戴维南、诺顿定理， 最大功率传递定理； 4、三端网络T形和形的等效变换。

数字电路逻辑代数化简
数字电路是现代电子设备中的重要组成部分，它们由逻辑门和
触发器等基本元件组成，用于处理和传输数字信号。

在数字电路中，逻辑代数化简是一项重要的技术，它可以帮助简化逻辑电路的设计，减少元件的数量，提高电路的性能和可靠性。

逻辑代数化简是利用布尔代数的原理，通过逻辑运算的规则，
将复杂的逻辑表达式简化为最简形式的过程。

这个过程可以通过代
数方法、卡诺图法等多种技术来实现。

逻辑代数化简的目标是找到
一个等价的最简化的逻辑表达式，以实现电路的最小化设计。

在数字电路的设计中，逻辑代数化简具有以下重要作用：
1. 减少元件数量，通过逻辑代数化简，可以将逻辑表达式简化
为最简形式，从而减少电路中的逻辑门数量，降低成本和功耗。

2. 提高电路性能，简化后的逻辑电路通常具有更快的响应速度
和更小的延迟，从而提高电路的性能。

3. 减少设计复杂性，简化后的逻辑表达式更易于理解和维护，
减少了设计的复杂性，提高了电路的可靠性。

逻辑代数化简是数字电路设计中不可或缺的一环，它的应用可以使电路设计更加高效和可靠。

随着数字电路的不断发展和应用，逻辑代数化简技术也将继续发挥重要作用，为电子设备的性能提升和成本降低提供强大支持。

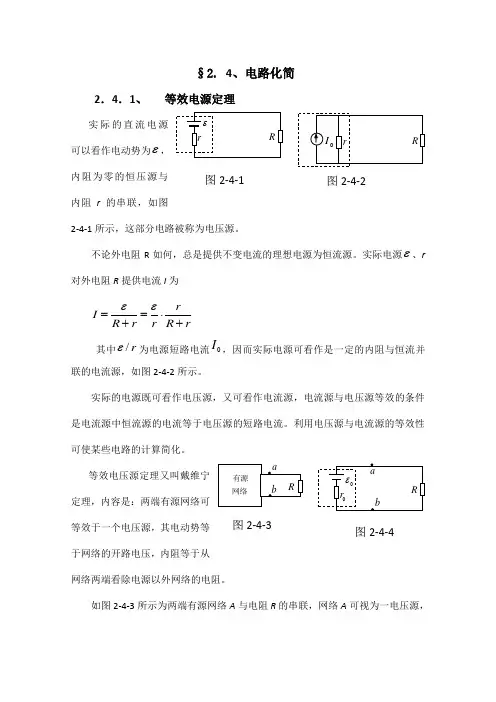
§2. 4、电路化简2．4．1、 等效电源定理实际的直流电源可以看作电动势为ε，内阻为零的恒压源与内阻r 的串联，如图2-4-1所示，这部分电路被称为电压源。

不论外电阻R 如何，总是提供不变电流的理想电源为恒流源。

实际电源ε、r 对外电阻R 提供电流I 为r R rr r R I +⋅=+=εε其中r /ε为电源短路电流0I ，因而实际电源可看作是一定的内阻与恒流并联的电流源，如图2-4-2所示。

实际的电源既可看作电压源，又可看作电流源，电流源与电压源等效的条件是电流源中恒流源的电流等于电压源的短路电流。

利用电压源与电流源的等效性可使某些电路的计算简化。

等效电压源定理又叫戴维宁定理，内容是：两端有源网络可等效于一个电压源，其电动势等于网络的开路电压，内阻等于从网络两端看除电源以外网络的电阻。

如图2-4-3所示为两端有源网络A 与电阻R 的串联，网络A 可视为一电压源，Rrε图2-4-10I rR图2-4-2abR网络有源图2-4-3Rr 0εab图2-4-4等效电源电动势0ε等于a 、b 两点开路时端电压，等效内阻0r 等于网络中除去电动势的内阻，如图2-4-4所示。

等效电流源定理 又叫诺尔顿定理，内容是：两端有源网络可等效于一个电流源，电流源的0I 等于网络两端短路时流经两端点的电流，内阻等于从网络两端看除电源外网络的电阻。

例4、如图2-4-5所示的电路中，Ω=Ω=Ω=Ω=Ω===0.194,5.432,0.101,0.12,5.01,0.12,0.31R R R R r r V V εε （1）试用等效电压源定理计算从电源()22r 、ε正极流出的电流2I ；（2）试用等效电流源定理计算从结点B 流向节点A 的电流1I 。

分析： 根据题意，在求通过2ε电源的电流时，可将ABCDE 部分电路等效为一个电压源，求解通过1R 的电流时，可将上下两个有源支路等效为一个电流源。

解： （1）设ABCDE 等效电压源电动势0ε，内阻0r ，如图2-4-6所示，由等效电压源定理，应有VR R R r R 5.1132111=+++=εε()Ω=+++++=5321132110R R R r R R r R r电源00r 、ε与电源22r 、ε串联，故Ar R r I 02.0240022-=+++=εε2I ＜0，表明电流从2ε负极流出。

数
字
电
子
技
术
1、代入规则 在任何一个含有变量A的逻辑代数等式中， 在任何一个含有变量A的逻辑代数等式中，如果将所有 出现A的地方代之一个逻辑函数，则等式仍然成立。 出现A的地方代之一个逻辑函数，则等式仍然成立。 1： B（A+C） 现将A用函数 用函数（ 代替， 例1： B（A+C）= BA+BC ，现将A用函数（ A+D ）代替， 证明： 成立。 证明：等式 B [（ A+D ）+C ]= B（A+D）+BC 成立。 （ （ ） 证：等式左边 B [（ A+D ）+C ]= BA+BD+BC （ 等式右边 B（A+D）+BC = BA+BD+BC （ ）
2、化简逻辑函数的标准（得到最简与或式） 、化简逻辑函数的标准（得到最简与或式）
（1）变量数要最少； 变量数要最少； 与项（乘积项）数要最少。 （2）与项（乘积项）数要最少。
3、逻辑函数化简，通常遵循以下几条原则： 、逻辑函数化简，通常遵循以下几条原则：
(1)逻辑电路所用的门要最少； (1)逻辑电路所用的门要最少； 逻辑电路所用的门要最少 各个门的输入端要尽量少； （2）各个门的输入端要尽量少； （3）逻辑电路所用的级数要尽量少； 逻辑电路所用的级数要尽量少； （4）逻辑电路能可靠地工作。 逻辑电路能可靠地工作。
数
字
电
子
技
术
一、逻辑代数的基本公式、定律； 逻辑代数的基本公式、定律； 二、逻辑代数的三个规则; 逻辑代数的三个规则; 三、逻辑代数的公式化简法。 逻辑代数的公式化简法。
数
字
电
子

101
0
110
0
1 2020/8/14 1 1
1
14
练习：三变量表决逻辑真值表填入卡诺图
ABC
Y
000
0
001
0
010
0
011
1
100
0
101
1
110
1
111
1
2020/8/14
15
（2）从最小项表达式画卡诺图 把表达式中所有的最小项在对应的小方块中填
入1，其余的小方块中填入0。
例4： 画出函数Y(A、B、C、D)= ∑m(0,3,5,7,9,12,15) 的卡诺图。
① 无关项的概念
对应于输入变量的某些取值下，输出函数的值可 以是任意的(随意项、任意项)，或者这些输入变量的 取值根本不会（也不允许）出现(约束项)，通常把这 些输入变量取值所对应的最小项称为无关项或任意项， 在卡诺图中用符号“×”表示，在标准与或表达式中用 ∑d（ ）表示。
例：当8421BCD码作为输入变量时，禁止码1010～ 1111这六种状态所对应的最小项就是无关项。
相邻 相邻
② 几何相邻的必须
逻辑相邻：变量的 取值按00、01、11、 10的顺序（循环码 ） 排列 。
图1-11 三变量卡诺图的画法
2020/8/14
12
不 相邻
相邻
相邻
图1-12 四变量卡诺图的画法
正确认识卡诺 图的“逻辑相邻”： 上下相邻，左右相 邻，并呈现“循环 相邻”的特性，它 类似于一个封闭的 球面，如同展开了 的世界地图一样。
复习：
真值表--逻辑表达式（化简）--逻辑电路图
例：三变量表决逻辑 Y=？ 逻辑图？
2020/8/14

0 1 1 0
BC
F2
F = AB + C = AB + C = AB ⋅ C 1
F2 = BC + ABC = BC + ABC = BC ⋅ ABC 2、将 F1 和 F2 整体 化简(找公共项 找公共项） 找公共项
AB AB C 00 01 11 10 C 00 01 11 10 0 0 0 0 1 ABC 0 0 0 0 1 1 0 1 1 0 1 1 1 1 1 C
尾部代替因子 一个乘积项的尾部因子，可根据需要加以扩展，如果扩 展变量是属于头部内的变量，则该乘积项的值不变。扩展后 的因子，称为原乘积项尾部因子的代替因子。
Ei = abc = abac = abbc = ababc 头部因子可以随意放入尾部因子， 头部因子可以随意放入尾部因子，也可以从尾部因 子中取走。 子中取走。 即：尾部因子的反号可以任意伸长和缩短，伸长将头 部因子 放进去，缩短将头部因子取出来。
例： 证明： 证明： abc = abac = ab(a + c) = aba + abc = abc
abc = abbc = ab b + c = abc abc = ababc = ab a + b + c = abc
(
(
)
(a ⋅a = 0)
)
乘积项合并 如果两个或两个以上乘积项的头部完全相同，则这几个 乘机项可以合并为一个乘积项。 AB
例4:已知 F = ∑m(0,1,3,4,5)求F' 的最小项表达式。
F = B+ A C F' = B A + C = AB + BC
(
1 1 0 1 B = ABC + ABC + ABC A C = ∑m (0,1,5) F和F'号码数目相同，对应之和为7。 变量： F和F'之间的关系： 由此推广到 n 变量： ) F = ∑m (0,1,3,4,5) F( a, b, cL = ∑( i) 最小项编号

化简求值50道(你值得拥有)1.先化简，再求值：(+)/(÷)，其中x=-1.2.化简求值：(a^2+1)/(a-1)，a取-1、0、1、2中的一个数。

3.先化简，再求值：(√3-1)/(√3+1)。

4.先化简，再求值：(1-1/3+1/5-1/7+1/9)/(1+1/3+1/5+1/7+1/9)。

5.先化简，再求值：(1/(1+x)+x/(1-x^2)),其中x=(-1)+(-1)*tan60°。

6.先化简，再求值：(a^2+1)/(a^3-a)，其中a=-1.7.先化简，再求值：(1-x)/(x^2-x-1)，其中x满足x^2-x-1=0.8.先化简，再求值：(a+2)/(a^2+3a-1)，其中a满足a^2+3a-1=0.9.先化简，再求值：(x-max)/(x-min)，其中x为数据-1，-3，1，2的极差。

10.先化简，再求值：(√2+1)/(√2-1)。

11.化简求值：(1+√2)/(√2-1)。

12.先化简，再求值：(x^2-3)/(x-√3)。

13.先化简，再求值：(a+b)/(a-b)，其中a=-1，b=1+√2.14.先化简，再求值：(x+1)/(x^2-1)其中x≠-1.15.先化简，再求值：(x-2)/(x^2+1)，其中x=2.16.先化简，再从不等式2x-3<7的正整数解中选一个使原式有意义的数代入求值：(x+1)/(x-2)。

17.先化简，再求值：(1/x)+(x/1)，其中x的值为方程2x=5x-1的解。

18.先化简：(x^2-1)/(x+1)。

19.先化简，再求值：(√(x+3)-1)/(√(x+3)+1)，其中x=-1.20.先化简，再求值：(-2)/(x^2-4)，其中x=2.21.先化简，再求值：(1-a)/(a^2+2a+1)，其中a=-1/2.22.先化简，再求值：(-1)/(a^2-b^2)，其中a=1，b=-1.23.先化简代数式(-a)/(a^2+1)，再从1，2三个数中选择适当的数作为a的值代入求值。

＊选学内容：电路的化简方法★知识要点1. 稍复杂的混联电路的等效化简方法： (1) 电路化简时的原则：① 无电流的支路化简时可去除，为什么？ ② 等电势的点化简时可合并，为什么？ ③ 理想．．导线可任意长短； ④ 理想．．电流表可认为短路，理想．．电压表可认为断路； ⑤ 电压稳定．．的电容器可认为断路. (2) 常用等效化简方法： ① 电流分支法：a. 先将各结点用字母标上；b. 判定各支路元件的电流方向（若电路原无电压电流，可假设在总电路两端加上电压后判定）；c. 按电流流向，自左到右将各元件、结点、分支逐一画出；d. 将画出的等效电路图加工整理. ② 等势点排列法：a. 将各结点用字母标上；b. 判定各结点电势的高低（若原电路未加电压，可先假设加上电压）；c. 将各结点按电势高低自左到右排列，再将各结点间的支路画出；d. 将画出的等效电路图加工整理.注意：若能将以上两种方法结合使用，效果更好. 2. 含有电容器的直流电路的分析方法： (1) 电路稳定时，电容器是断路的，其两端电压等于所并联的电路两端的电压. (2) 电路的电流、电压变化时，将会引起电容器的充（放）电. 如果电容器两端电压升高，电容器将充电；如果电压降低，电容器将通过与并联的电路放电.★应用演练【例1】如右图所示，R 1=R 2=R 3= R 4=R ，求：电键S 闭合和开启时，A 、B 两端电阻之比. 解析：化简时可假设电键S 开启，而无电流的支路化简时可去除，等化简结束后再补上.方法（一）：用电流分支法化简电路.设A 点电势高于B 点电势，判断各支路上的电流情况：甲乙电流由A 经R 1到B 为第一支路；电流由A 经R 2到C ，再到B 为第二支路；电流由A 经R 3到D ，再经R 4到B 为第三支路. 沿电流方向画出电路图，然后在C 、D 间补上电键S （如图乙）.S 闭合：R 4短路，相当于R 1、R 2、R 3并联，故R AB =R/3.S 开启：相当于R 3、R 4串联后再和R 1、R 2并联，故12341111AB R R R R R =++'+，R AB ′=2R/5.∴R AB :R AB ′=5:6. 方法（二）：用等电势排列法化简电路. 设A 点电势高于B 点电势，判断电路上各点的电势情况：φA ＞φD ＞φC =φB .在A 、B 之间有三条支路并联：第一条为R 1；第二条为R 2；第三条为R 3和R 4的串联电路.由等电势的点化简时可合并可得：S 与R 4并联. 答案：5:6〖点评〗对于复杂的电路化简时应交替使用分支法和等势法 【例2】如右图所示，R 1=R 2=R 3=R 4=R ，则：A 、B 两端总电阻是多大？解析：方法（一）：用电流分支法化简电路.设A 点电势高于B 点电势，判断各支路上的电流情况（如A 图所示）. 沿电流方向画出电路图（如B 图所示），经整理得到C 图.故R AB =R 1＋R 并=R ＋R/3=4R/3.方法（二）：用等电势排列法化简电路. 设A 点电势高于B 点电势，判断电路上各点的电势情况(电势相同的点标相同的字母)：φA ＞φC ＞φB . 在A 、C 之间有R 1；在C 、B 之间有R 2、R 3、R 4三个电阻并联.★同步练习1. 如右图所示，AB 之间的总电阻为：甲图R AB = Ω；乙图R AB = Ω；丙图S 断开时R AB = Ω，S 闭合时R AB ′= Ω；丁图S 断开时R AB = Ω，S 闭合时R AB ′= Ω. 0、12/13、4、2、3、D 图乙甲丙丁A 图B 图C 图2. 用三个完全相同的金属环，将其相互垂直放置，并把相交点焊接起来成为如右图所示的球形骨架，如每个圆环的周长导线电阻阻值为4Ω，则A 、C 间的总电阻阻值R AC = Ω. 0.5 解析：设A 点接高电势，B 点接低电势. 由题目的对称性可推断出B 、D 、E 、F 各点的电势相等，因此B 、D 、E 、F 各点可合并为一点. 电路可简化为右图所示电路. 则A 、C 间的总电阻阻值R AC =(R/4)/4×2=R/8=0.5Ω.3. 如下图所示的电路，R 1=R 2=4Ω,R 3=R 4=2Ω,U AB =6V ,求：A. 安培表A 1和A 2的示数（不计安培表的内阻）； I A1=1.5A ；I A2=1.0AB. R 1与R 4两端电压之比. U 1:U 4=1:2解析：⑴ R 1、R 2与R 3相并联，再跟R 4相串联，其等效电路如右图所示. 根据并联电路的性质，可知R 1、R 2、R 3三个电阻并联的总电阻R 并，即：1231111R R R R =++并. ∴R 并=1Ω.根据欧姆定律，干路中电流为4ABU I R R =+并=2A.并联部分的电压为：U 并=I·R 并=2V . 则通过R 1、R 2、R 3的电流分别为：1U I R =并１＝0.5A ，22U I R =并＝0.5A ，33U I R =并＝1.0A.由图可知，安培表A 1的示数是通过R 2与R 3的电流之和，则有：I A1=I 2+I 3=1.5A. 安培表A 2的示数是通过R 1与R 2的电流之和，则有：I A2=I 1+I 2=1.0A. ⑵ 根据串联电路电压分配关系可知：1444R U 1U U U R ==并并＝２.－A2。

实验3 控制系统方框图化简
一、实验目的
掌握控制系统三类典型的连接结构及方框图的等效变换和化简。

二、实验基础知识
1、串联、并联和反馈连接是三种基本的连接方式，可直接对应代数方程中的三种运算。

利用这些基本运算公式，可求得各种组合下的传递函数。

环节串联后的总传递函数等于各个串联环节传递函数的乘积。

环节并联后的总传递函数等于各个并联环节传递函数的代数和。

2、相加点和引出点的移动
在结构图简化过程中，当系统中出现信号交叉时，需要移动相加点（亦称比较点、求和点）或引出点的位置，这时应注意保持移动前后信号传递的等效性，并注意以下两点：
①引出点与相加点互换太复杂，尽量不用。

②在等效交换过程中，一般尽可能和方框进行位置移动交换，相加点移向相加点，分支点移向分支点。

三、实验内容
试用结构图等效化简图1所示各系统的传递函数
()
()
C s R s 。

（a ） （b ）
(d)
(e)
四、实验报告要求
按照上述步骤进行实验，并按实验记录完成实验报告。

（2）吸收法
运用公式 A AB A 消去多余的项，其中，A、B可以是
任意一个复杂的逻辑式。例如：
Y1 AB AC DEB AB
Y2 AB ABC ABD AB D E AB AB C D D E AB
（3）消去法
运用公式 A AB A B 消去多余的因子。例如：
例如：逻辑函数Y的卡诺图。 Y ABCD ABCD ABCD ABCD
ABCD ABCD ABCD ABCD
（3）用卡诺图化简逻辑函数式 使用卡诺图化简逻辑函数所依据的原理是：具有相邻性 的最小项可以合并消去不同的因子。 ①2个相邻的最小项结合（用一个包围圈表示），可以消 去1个取值不同的变量而合并为1项，如下图所示。
00 01 11 10 00
01 11 10
②4个相邻的最小项结合（用一个包围圈表示），可以消 去2个取值不同的变量而合并为l项，如下图所示。
00 01 11 10 00
01 11 10
③8个相邻的最小项结合（用一个包围圈表示），可以消 去3个取值不同的变量而合并为l项，如下图所示。
00 01 11 10 00
②化简具有无关项的逻辑函数 在卡诺图中用×表示无关项。使用卡诺图化简逻辑函数 式时，要充分利用无关项可以当0也可以当1的特点，尽量扩 大卡诺圈，使逻辑函数式更简。
（2）卡诺图
卡诺图就是将n变量的全部最小项各用一个小方块表示，
并使具有逻辑相邻性的最小项在几何位置上也相邻的排列起 来所得的图形。下图所示为2到4变量最小项的卡诺图。
若要画出某一逻辑函数的卡诺图，只需将该逻辑函数式 化为最小项之和的标准形式后，在卡诺图中这些最小项对应 的位置上填入1，在其余的位置上填入0即可。
1．公式化简法

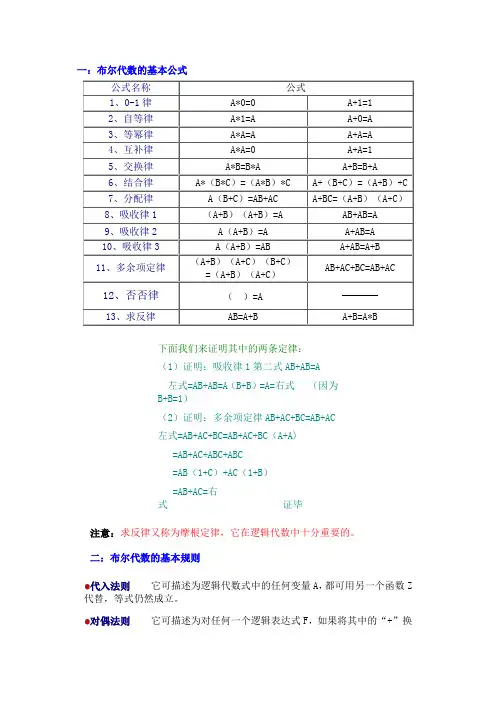
一：布尔代数的基本公式公式名称公式1、0-1律A*0=0 A+1=12、自等律A*1=A A+0=A3、等幂律A*A=A A+A=A4、互补律A*A=0 A+A=15、交换律A*B=B*A A+B=B+A6、结合律A*（B*C）=（A*B）*C A+（B+C）=（A+B）+C7、分配律A（B+C）=AB+AC A+BC=（A+B）（A+C）8、吸收律1（A+B）（A+B）=A AB+AB=A9、吸收律2A（A+B）=A A+AB=A10、吸收律3A（A+B）=AB A+AB=A+B11、多余项定律（A+B）（A+C）（B+C）=（A+B）（A+C）AB+AC+BC=AB+AC12、否否律（）=A13、求反律AB=A+B A+B=A*B下面我们来证明其中的两条定律：（1）证明：吸收律1第二式AB+AB=A左式=AB+AB=A（B+B）=A=右式（因为B+B=1）（2）证明：多余项定律AB+AC+BC=AB+AC左式=AB+AC+BC=AB+AC+BC（A+A)=AB+AC+ABC+ABC=AB（1+C）+AC（1+B）=AB+AC=右式证毕注意：求反律又称为摩根定律，它在逻辑代数中十分重要的。

二：布尔代数的基本规则代入法则它可描述为逻辑代数式中的任何变量A，都可用另一个函数Z 代替，等式仍然成立。

对偶法则它可描述为对任何一个逻辑表达式F，如果将其中的“+”换成“*”，“*”换成“+”“1”换成“0”，“0”换成“1”，仍保持原来的逻辑优先级，则可得到原函数F的对偶式G，而且F与G互为对偶式。

我们可以看出基本公式是成对出现的，二都互为对偶式。

反演法则有原函数求反函数就称为反演（利用摩根定律），我们可以把反演法则这样描述：将原函数F中的“*”换成“+”，“+”换成“*”，“0”换成“1”，“1”换成“0”；原变量换成反变量，反变量换成原变量，长非号即两个或两个以上变量的非号不变，就得到原函数的反函数。

第四章
组合逻辑设计原理
Combinational Logic Design Principle 第四讲 逻辑函数的卡诺图化简方法-1
你好，今天我们来学习如何化简函数。
4.3.3 Combinational Circuit Minimization
(组合电路的化简)
What is the Minimization? (什么是最简?)
化简的基础
X’·Y·Z’
X’·Y’·Z+X·Y’·Z=Y’·Z
X·Y·Z+X·Y’·Z=X·Z
化简: F = A,B,C,D ( 0, 2, 3, 5, 7, 8, 10, 11, 13 )
1、填图
AB
CD 00
2、圈组
A’·B·D 00 1
“圈”尽可能大
01
圈数尽可能少 方格可重复使用
11 1 10 1
3、读图
B’·C
B·C’·D
01 11 10
1
11
1
1
1
F(A,B,C,D) = B’·D’ B’·C+ B·C’·D+ A’·B·D
B’·D’
化简的步骤
• 填写卡诺图
• 圈组：找出可以合并的最小项
– 组(圈)数最少、每组(圈)包含的方块数最多 – 方格可重复使用，但至少有一个未被其它组圈过 – 圈组时应从合并数最小的开始
• 读图：写出化简后的乘积项
– 消掉既能为0也能为1的变量 – 保留始终为0或始终为1的变量
积之和形式： 0 反变量 1 原变量
Karnaugh Maps (卡诺图化简)
பைடு நூலகம்数最少 每项中的变量
数最少
卡诺图是逻辑函数真值表的图形表示。

电路化简2．4．1、 等效电源定理实际的直流电源可以看作电动势为ε，内阻为零的恒压源与内阻r 的串联，如图2-4-1所示，这部分电路被称为电压源。

不论外电阻R 如何，总是提供不变电流的理想电源为恒流源。

实际电源ε、r 对外电阻R 提供电流I 为r R rr r R I +⋅=+=εε其中r /ε为电源短路电流0I ，因而实际电源可看作是一定的内阻与恒流并联的电流源，如图2-4-2所示。

实际的电源既可看作电压源，又可看作电流源，电流源与电压源等效的条件是电流源中恒流源的电流等于电压源的短路电流。

利用电压源与电流源的等效性可使某些电路的计算简化。

等效电压源定理又叫戴维宁定理，内容是：两端有源网络可等效于一个电压源，其电动势等于网络的开路电压，内阻等于从网络两端看除电源以外网络的电阻。

如图2-4-3所示为两端有源网络A 与电阻R 的串联，网络A 可视为一电压源，等效电源电动势0ε等于a 、b 两点开路时端电压，等效内阻0r 等于网络中除去电动势的内阻，如图2-4-4所示。

等效电流源定理又叫诺尔顿定理，内容是：两端有源网络可等效于一个电流源，电流图2-4-1图2-4-2图2-4-3图2-4-4源的0I 等于网络两端短路时流经两端点的电流，内阻等于从网络两端看除电源外网络的电阻。

例4、如图2-4-5所示的电路中，Ω=Ω=Ω=Ω=Ω=Ω===0.194,5.43,0.52,0.101,0.12,5.01,0.12,0.31R R R R r r V V εε（1）试用等效电压源定理计算从电源()22r 、ε正极流出的电流2I ；（2）试用等效电流源定理计算从结点B 流向节点A 的电流1I 。

分析： 根据题意，在求通过2ε电源的电流时，可将ABCDE 部分电路等效为一个电压源，求解通过1R 的电流时，可将上下两个有源支路等效为一个电流源。

解： （1）设ABCDE 等效电压源电动势0ε，内阻0r ，如图2-4-6所示，由等效电压源定理，应有VR R R r R 5.11321110=+++=εε()Ω=+++++=5321132110R R R r R R r R r电源00r 、ε与电源22r 、ε串联，故Ar R r I 02.0240022-=+++=εε2I ＜0，表明电流从2ε负极流出。

一、普通编码器
特点： 特点：任何时刻只允许 输入一个编码信号。 输入一个编码信号。 例：3位二进制普通编 位 码器
输 I0 I1 I2 I3 I4 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0
电工理论与应用电子系
Digital Electronics Technology
2010-10-6
4.2 组合逻辑电路的分析与设计方法
一火灾报警系统，设有烟感、 例：一火灾报警系统，设有烟感、温感和紫外光感三种 类型的火灾探测器。为了防止误报警， 类型的火灾探测器。为了防止误报警，只有当其中有两种 或两种以上类型的探测器发出火灾检测信号时， 或两种以上类型的探测器发出火灾检测信号时，报警系统 产生报警控制信号。设计一个产生报警控制信号的电路。 产生报警控制信号。设计一个产生报警控制信号的电路。 分析设计要求， 解：(1)分析设计要求，设输入输出变量并逻辑赋值； 分析设计要求 设输入输出变量并逻辑赋值； 输入变量：烟感 温感B，紫外线光感C； 输入变量：烟感A 、温感 ，紫外线光感 ； 输出变量：报警控制信号 。 输出变量：报警控制信号Y。 逻辑赋值： 表示肯定， 表示否定。 逻辑赋值：用1表示肯定，用0表示否定。 表示肯定 表示否定
A+ A'B = A+ B
0 '0 '
0 ' 0' ' 0
Y2 = I 7 + I 6 + I 5 + I 4
电工理论与应用电子系 Digital Electronics Technology
实例： 实例： 74HC148

四、简答题
1.试述戴维南定理的求解步骤？如何把一个有源二端网络化为一个无源二端网络？在此过程中，有源二端网络内部的电压源和电流源应如何处理？
2.实际应用中，我们用高内阻电压表测得某直流电源的开路电压为225V，用足够量程的电流表测得该直流电源的短路电流为50A，问这一直流电源的戴维南等效电路？
3.负载上获得最大功率时，电源的利用率大约是多少？
20.求图示电路的戴维宁等效电路，并计算使RL的功率为最大的RL值和最大功率。
21.图示电路，IS=2A，R1=R2=4，若负载RL可变，当RL等于何值时负载获得最大功率，最大功率为多少？
22.应用等效变换求图示电路中的I的值。
23.应用戴维南定理求解图示电路中的电流I。
24.如图所示电路，若RL可变，RL为多大时可获得最大功率？此时Pmax为多少？
21.求线性有源二端网络内阻时： （1）无源网络的等效电阻法，应将电压源（开路、短路、保留）处理，将电流源（开路、短路、保留）处理；（2）外加电源法， 应将电压源（开路、短路、保留）处理，电流源（开路、短路、保留）处理；（3）开路电压和短路电流法，应将电压源（开路、短路、保留）处理，电流源（开路、短路、保留）处理。
10.当一个实际电流源（诺顿电路）开路时，该电源内部有无电流。
11.几个电压源串联的等效电压等于所有电压源的。
12.几个同极性的电压源并联，其等效电压等于。
13.几个电流源并联的等效电流等于代数和。
14.几个同极性电流源串联，其等效电流等于。
15.某元件与理想电压源并联，其等效关系为。
16.某元件与理想电流源串联，其等效关系为。
4.已知图示电路中电压U=4.5V，试应用已经学过的电路求解法求电阻R。
5.求解图示电路的戴维南等效电路。

G1
+ (+-)
A G1
G2 AG2
AG1 AG1+ AG2
++
1 G1
G2 AG2
A G1
1 G1
AG1 AG2
G2 + +
分支点移动 A G2
1 G2
AG1 AG1+ AG2 G1 + +
AG2
(2)反馈化成单位反馈
A+ -
G1 A G1 1 + G1G2
A1+
G2
-
G1
G1 G2 1+ G1G2
(3)根据因果关系，确定各个原始微分方程分中的输入量与 输出量，并将拉斯变换的结果表示成传递函数方框图的形 式；
(4)按信号的传递过程，依次将上述各个方框图连接起来， 构成整个系统的传递函数方框图，一般输入在左边，输出 在右边。
jik 04
2
例2： 绘制电枢控制式直流电动机的传递函数
方框图 。
R
i1 (t)
G1 +
G2 +
1 G3
-A
G3
Xo(s)
C
H2
H1
H3
Xi 1(s)
+
-
G1 +
G2
-
1 G3
G3 1+H2 G3
Xo(s)
C
略
H1
jik 04
15
X (s) 0 求 Xo(s) 。令
Xi2(s)
i1
Xi 1(s)
H3
+
-
-
G1 B +
G2
,
Xi

数电逻辑表达式化简摘要：1.数电逻辑表达式的概念与意义2.化简数电逻辑表达式的方法3.化简过程的实例演示4.化简后的表达式应用场景5.总结与展望正文：【1.数电逻辑表达式的概念与意义】在数字电子电路中，逻辑表达式是一种描述电路功能和逻辑关系的重要手段。

它采用布尔代数，通过运算符（如AND、OR、NOT等）连接变量，表示电路中各信号的逻辑关系。

化简数电逻辑表达式，就是将一个复杂的逻辑表达式转化为一个更简单、更容易理解和分析的形式。

【2.化简数电逻辑表达式的方法】化简数电逻辑表达式的常用方法有以下几种：1）代入法：将表达式中的一个变量用另一个变量表示，从而简化表达式。

2）乘法公式：利用乘法公式（如分配律、结合律等）简化表达式。

3）除法公式：利用除法公式（如分配律、结合律等）简化表达式。

4）德摩根定律：将表达式中的乘法项转化为加法项，或将加法项转化为乘法项。

5）卡诺图：将逻辑表达式转化为图形化表示，便于观察和化简。

【3.化简过程的实例演示】以一个简单的逻辑表达式为例：A ·B +C · D化简过程如下：1）利用乘法公式，将表达式转化为：(A · B) + (C · D)2）利用德摩根定律，将表达式转化为：A ·B +C ·D = A + B · C + D3）将表达式中的变量用另一个变量表示，得到简化后的表达式：A +B ·C + D【4.化简后的表达式应用场景】化简后的逻辑表达式更易于分析和设计数字电子电路。

在实际应用中，化简后的表达式可以帮助工程师快速了解电路的逻辑功能，简化电路分析与设计过程，提高工作效率。

【5.总结与展望】数电逻辑表达式的化简是数字电子电路设计与分析的重要环节。

掌握化简方法，善于运用乘法公式、德摩根定律等工具，能够将复杂的逻辑表达式简化，为电路设计提供便利。