人教版高中数学必修第一册四种命题2

【人教版】高一数学上册四种命题知识点学习是一个边学新知识边巩固的过程，对学知识一定要多加计划，这样才能进步。

因此，为大家整理了高一数学上册四种命题知识点，供大家参考。

【人教版】高一数学上册四种命题知识点【《四种命题》知识点】四种命题包括原命题、逆命题、否命题和逆否命题。

1、对于两个命题，如果一个命题的条件和结论分别是另外一个命题的结论和条件，那么这两个命题叫做互逆命题，其中一个命题叫做原命题，另外一个命题叫做原命题的逆命题。

2、对于两个命题，如果一个命题的条件和结论分别是另外一个命题的条件的否定和结论的否定，那么这两个命题叫做互否命题，其中一个命题叫做原命题，另外一个命题叫做原命题的否命题。

3、对于两个命题，如果一个命题的条件和结论分别是另外一个命题的结论的否定和条件的否定，那么这两个命题叫做互为逆否命题，其中一个命题叫做原命题，另外一个命题叫做原命题的逆否命题。

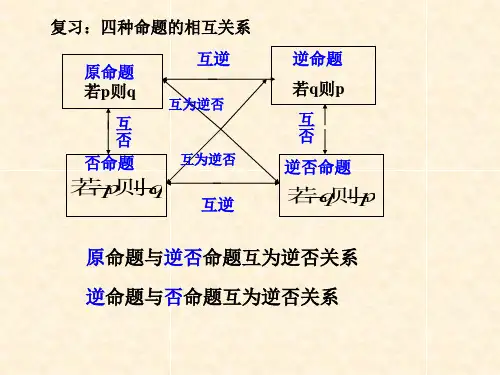
四种命题的相互关系1、四种命题的相互关系：原命题与逆命题互逆，逆命题与逆否命题互否，逆否命题与否命题互逆，否命题与原命题互否，原命题与逆否命题相互逆否，逆命题与否命题相互逆否。

2、四种命题的真假关系：(1)两个命题互为逆否命题，它们有相同的真假性。

(2)两个命题为互逆命题或互否命题，它们的真假性没有关系。

【同步练习题】1.命题“若A∩B=A,则A∪B=B”的否命题是( )A.若A∪B=B,则A∩B=A B.若A∩B≠A,则A∪B≠BC.若A∪B≠B,则A∩B≠A D.若A∪B≠B,则A∩B=A 答案：B解析：条件与结论要同时否定.2.关于命题“平行四边形的两组对边分别相等”,下列论述中,正确的是( )A.逆命题是假命题 B.否命题是假命题C.逆否命题是真命题 D.以上答案都不对答案：C解析：原命题为真命题,所以逆否命题为真命题.3.命题:“若a、b都是偶数,则a+b是偶数”的逆否命题是( )A.若a+b是偶数,则a、b都不是偶数B.若a+b是偶数,则a、b不都是偶数C.若a+b不是偶数,则a、b都不是偶数D.若a+b不是偶数,则a、b不都是偶数答案：D解析：注意“都是”的否定为“不都是”.4.用反证法证明“如果a b 0,那么”假设的内容应是( )A. = B. C. ≤ D. 且 =答案：C解析：“ ”的反面为“≤”.5.“相似三角形的周长相等”写成“若p则q”的形式为_________________.答案：若两三角形相似,则它们的周长相等解析：条件p:若两三角形相似,结论q:它们的周长相等.6.用反证法证明:“任何三角形至少有两个锐角”时,应假设_____________________.答案：三角形至多有一个锐角解析：即假设三角形只有一个锐角或一个锐角也没有.7.给定命题:已知a、b为实数,若x2+ax+b≤0的解集是空集,则a2-4b≤0,写出它的逆命题、否命题、逆否命题,并判断四个命题的真假.解：原命题:是假命题.逆命题:已知a、b为实数,若a2-4b≤0,则x2+ax+b≤0的解集是空集.假命题.否命题:已知a、b为实数,若x2+ax+b≤0的解集不是空集,则a2-4b 0.假命题.逆否命题:已知a、b为实数,若a2-4b 0,则x2+ax+b≤0的解集不是空集.假命题.能力提升踮起脚,抓得住!8.一个命题与它的逆命题、否命题、逆否命题这四个命题中( )A.真命题的个数一定是奇数B.真命题的个数一定是偶数C.真命题的个数可能是奇数也可能是偶数D.以上判断都不正确答案：B解析：原命题与逆否命题同真同假,逆命题与否命题同真同假.9.若命题p的否命题为r,命题r的逆命题为s,则s是p的逆命题t的( )A.逆否命题 B.逆命题C.否命题 D.原命题答案：C解析：由题知s是p的逆否命题,而t是p的逆命题,所以s是t的否命题.10.命题“若a b,则ac bc(a、b、c∈R)”与它的逆命题、否命题、逆否命题中,真命题的个数为__________________.答案:0解析：注意c∈R.知识点是同学们提高总体学习成绩的重要途径，高一数学上册四种命题知识点为大家巩固相关重点，让我们一起学习，一起进步吧!。

1.7 四种命题①课文三点专讲重点:(1)四种命题及其关系.原命题：若p 则q 逆命题：若p 则q否命题：若⌝p 则⌝q 逆否命题：若⌝q 则⌝p(2)四种命题的关系.四种命题的关系如下表所示:(3)命题真假的判定.互为逆否命题具有相同的真假性.(4)反证法.要证明某一结论A是正确的，但不直接证明，而是先去证明A的反面（非A）是错误的，从而断定A是正确的即反证法就是通过否定命题的结论而导出矛盾来达到肯定命题的结论，完成命题的论证的一种数学证明方法难点：反证法反证法的步骤：(1)假设命题的结论不成立，即假设结论的反面成立(2)从这个假设出发，通过推理论证，得出矛盾(3)由矛盾判定假设不正确，从而肯定命题的结论正确注意：可能出现矛盾四种情况：①与题设矛盾；②与反设矛盾；③与公理、定理矛盾④在证明过程中，推出自相矛盾的结论考点:(1)考察逆命题、否命题与逆否命题.(2)四种命题的相互关系.应用四个重要结论解题.(3)反证法.该方法较为适用的题型为:①命题简单明了,没有更多的公理概念等依据可供论证的命题; ②结论本身是以否定形式出现的一类命题; ③有关结论是以“至多……”或“至少……”的形式出现的一类命题; ④关于惟一性、存在性的命题; ⑤结论的反面比原结论更具体、更容易研究和掌握.②练功篇典型试题分析例1. 写出命题“在△ABC 中，若∠C ＝90°，则c 2＝a 2＋b 2”的逆命题，否命题和逆否命题，并指出它们的真假.分析:此题的原命题中“在△ABC 中”是前提，在写这类命题的逆命题、否命题和逆否命题时一般保持不变.解析：原命题是真命题.逆命题为“在△ABC 中，若c 2＝a 2＋b 2，则∠C ＝90°.为真命题.否命题为：“在△ABC 中，若∠C ≠90°，则c 2≠a 2＋b 2”，是真命题.逆否命题为：“在△ABC 中，若c 2≠a 2＋b 2，则∠C ≠90°，是真命题.例2. 判断下列命题的真假，并说明理由.(1)设a ，b ∈N *，如果a ＋b 是偶数，那么a 、b 都是偶数.(2)如果A ⊆B ，B ⊆C ，那么A ⊆C.(3)如果一元二次方程ax 2＋bx ＋c ＝0满足ac ＜0那么这个方程有实数根.(4)相似三角形一定是全等三角形.(5)合数必定是偶数.分析：在判断命题的真假时，应注意运用有关的概念、定理、公式等基本理论，对命题的条件和结论仔细分析，认真思考.并注意反例的运用. (1)取反例：a ＝1，b ＝3，（2）由集合的性质，可判定，(3)由ac ＜0⇒b 2－4ac ≥0，（4）相似三角形的对应边不一定相等，(5)反例：9是合数，但不是偶数.解析：(1)假命题.例如a ＝1，b ＝3，a ＋b ＝4为偶数.但a 、b 不是偶数.(2)真命题.设任x 0∈A ，∵A ⊆B .∴x 0∈B .又 ∵B ⊆C ，则x 0∈C .故A ⊆C 成立.(3)真命题.因方程中由ac ＜0⇒Δ＝b 2－4ac ≥0.故一元二次方程ax 2＋bx ＋c ＝0有实数根.(4)假命题.因相似三角形的对应边不一定相等.则不一定是全等三角形.(5)假命题.例如9是合数，但不是偶数.基础知识巩固1.有以下5个命题：（1）没有男生爱踢足球；（2）所有男生都不爱踢足球；（3）至少有一个男生不爱踢足球；（4）所有女生都爱踢足球；（5）所有男生都爱踢足球．其中命题（5）的否命题是 （ ）A ．（1）B ．（2）C ．（3）D ．（4）2.下面三个命题：（1）“若3=b ，则92=b ”的逆命题；（2）“全等三角形的面积相等”的否命题；（3）“若1≤c ，则022=++c x x 有实根”的逆否命题．其中真命题的个数是 ( )A ． 0B ． 1C ． 2 D.．33.命题“能被4整除的数一定是偶数”，等价命题是（）A.偶数一定能被4整除B.不能被4整除的数一定不是偶数C.不能被4整除的数不一定是偶数D.4.下列命题中，正确的是( )①“若x2+y2 =0,则x , y全是0”的否命题②“全等三角形是相似三角形”的否命题③“若m＞1,则mx2－2(m+1)x+(m－3)＞0的解集为R”的逆命题④若“a+5是无理数，则a是无理数”的逆否命题A.①②③B.①④C.②③④D.①③④5.用反证法证明命题的第二步中，得出的矛盾可以是与下列哪些内容产生的( )①命题已知②数学定义③定理，公理④推理、演算的规律A.①B.①③C.②D.①②③④6.用反证法证明命题“2＋3是无理数”时，假设正确的是( )A.假设2是有理数B.假设3是有理数C.假设2或3是有理数D.假设2+3是有理数7.给定下列命题：①“若k＞0，则方程x2＋2x－k＝0”有实数根；②“若a＞b，则a+c＞b+c”的否命题；③“矩形的对角线相等”的逆命题；④“若xy=0，则x、y中至少有一个为0”的否命题.其中真命题的序号是______.8.写出命题p：“若m＞0，则关于x的方程x2+x－m=0有实数根”的逆命题，否命题和逆命题，并分别判断它的真假.9.写出下列命题的否命题(1)有些三角形是直角三角形;(2)所有的质数都是奇数 .10.若x、y∈R+，且x+y＞2,求证：y x+1＜2与x y+1＜2中，至少有一个成立.③升级篇典型试题分析例3：写出命题“若x≥2且y≥3，则x＋y≥5”的逆命题、否命题，逆否命题.并判断其真假.分析：应注意分析清楚原命题的条件与结论，并充分利用四种命题的定义，还要注意条件和结论中“或”“且”“非”的否定的语句表述的准确性. 本题应注意理解掌握“p且q”的否定为“⌝p 或⌝q ”，“p 或q ”的否定为“⌝p 且⌝q ”.解析：原命题：“若x ≥2且y ≥3则x ＋y ≥5”为真命题.逆命题为：“若x ＋y ≥5，则x ≥2且y ≥3”，为假命题.否命题是：“若x ＜2或y ＜3，则x ＋y ＜5.”其为假命题.逆否命题是：“若x ＋y ＜5，则x ＜2或y ＜3”其为真命题.例4. 写出下列命题的否命题，并判断原命题及否命题的真假：(1)如果x ＞－3，那么x ＋8＞0(2)如果一个三角形的三边都相等，那么这个三角形的三角都相等.(3)矩形的对角线互相平分且相等.(4)相似三角形一定是全等三角形.分析：将原命题的条件和结论同时加以否定，便得到其否命题. 一个命题的否定应当包含除了本身以外的所有情况.如：“都相等”的否定应为“不都相等”，即至少有两个元素不相等；“p 或q ”与“⌝p 且⌝q ”互为否定；“一定是”的否定是“一定不是”.解析：(1)否命题是：“如果 x ≤－3，那么x ＋8≤0”原命题为真命题，否命题为假命题.(2)否命题是：“如果一个三角形的三边不都相等，那么这个三角形的三角不都相等. 原命题为真命题，否命题也为真命题.(3)否命题是：“如果四边形不是矩形，那么对角线不互相平分或不相等”.原命题是真命题，否命题也是真命题.(4)否命题是“不相似的三角形一定不是全等三角形.”原命题是假命题，否命题是真命题.知识应用与提升11. 给出以下四个命题：其中真命题是( )①“若x ＋y =0，则x ，y 互为相反数”的逆命题；②“全等三角形的面积相等”的否命题；③“若1-≤q ，则02=++q x x 有实根”的逆否命题；④“不等边三角形的三内角相等”的逆否命题．A ．①②B ．②③C ．①③D ．③④ 12. 命题“a 、b 都是偶数，则a +b 是偶数”的逆否命题为A.a +b 不是偶数，则a 、b 不都是偶数B.a +b 不是偶数，则a 、b 都不是偶数C.a 、b 不都是偶数，则a +b 不是偶数D.a 、b 都不是偶数，则a +b 不是偶数13. 用反证法证明命题“若整数n 的立方是偶数，则n 也是偶数”如下：假设n 是奇数，则n =2k +1(k 是整数)，n 3＝(2k ＋1)3＝______，与已知n 3是偶数矛盾，所以n 是偶数.14. 用反证法证明命题：“a ，b ∈N ，ab 可被5整除，那么a ，b 中至少有一个能被5整除”时，假设的内容应为（ ）A. a ，b 都能被5整除B. a ，b 都不能被5整除C. a ，b 不都能被5整除D. a 不能被5整除15. 给出下列命题：①命题“若b 2－4ac <0,则方程ax 2+bx +c =0(a ≠0)无实根”的否命题②命题“△ABC 中，AB =BC =CA ，那么△ABC 为等边三角形”的逆命题③命题“若a >b >0,则3a >3b >0”的逆否命题其中真命题的序号为__________.16. 写出下列命题的逆命题，并判断原命题和逆命题的真假.(1)若x 2＝1，则x ＝1.(2)对顶角相等.(3)等腰三角形的两腰相等.(4)x 2＋2x ＋8＞0的解集为空集.④闯关篇典型试题分析例5：若a 、b 、c 均为实数，且2222,2,2236a x y b y z c z x πππ=-+=-+=-+，求证：a 、b 、c 中至少有一个大于0．分析: 反证法是一种常用的数学方法，属于一种间接证法．当待证命题中出现“不可能”、“一定”、“至多”、“唯一”等词语时，常可考虑运用反证法．运用反证法时常见词语的否定方式有：“在”⇒“不在”；“是”⇒“不是”；“都是”⇒“不都是”；“大于”⇒“不大于”；“所有的…”⇒“至少有一个不…”；“至少一个” ⇒“一个也没有”；“任意一个”⇒“存在某个不…”，等等．证明: （用反证法）假设a 、b 、c 都不大于0，即0a ≤，0,0b c ≤≤，则有0a b c ++≤． 而222222236a b c x y y z z x πππ⎛⎫⎛⎫⎛⎫++=-++-++-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()()()222222x x y y z z π=-+-+-+()()()()2221113x y z π=-+-+-+-,所以 0a b c ++>，此与0a b c ++≤矛盾．故假设错误，从而原命题正确．评述:本题亦可直接转化为证明等价命题：0a b c ++>．．例6.若()22f x x ax a a =++-在[-1,1]上至少存在一点C 使()0f C >,求实数a 的取值范围.分析: 利用否命题来求解这一类问题,可以简化运算步骤,回避分类讨论.解析：该题可利用其否命题来解.该命题的否命题是: ()22f x x ax a a =++-在[-1,1]不存在点C 使()0f C >即对任意x ∈[-1,1], ()f x ≤0 .∴有()()1010f f ≤⎧⎪⎨-≤⎪⎩解之得11a a ≥≤-或故实数a的取值范围为()1a ∈- ..． 知识拔高与创新17. 否定结论“至多有两个解”的说法中，正确的是（ ）A.有一解B.有两解C.有三解D.至少有两解18. 已知两函数：2222132,3)31(2a x x y a ax x y ++=+--+=.求证：不论a 取怎样的实数，这两函数的图象至少有一个位于x 轴的上方.19. 已知a 、b 、c 是一组勾股数(即a 2＋b 2＝c 2)，求证：a 、b 、c 不可能都是奇数.20. 假设p 、q 都是奇数，求证：关于x 的方程x 2＋px ＋q ＝0无整数根.⑤行侠篇高考试题点击21.(2005江苏) 命题“若a ＞b ，则2a ＞2b －1”的否命题为 .22. (2004江苏)若命题p 的否命题为r ，命题r 的逆命题为s ，则s 是p 的逆命题t 的( )A.逆否命题 B.逆命题 C.否命题 D.原命题⑥娱乐广场开阔视野、趣味学习反证法小游戏三个古希腊哲学家，由于争论和天气炎热感到疲倦了，于是在花园里的一棵大树下躺下来休息一会，结果都睡着了这时一个爱开玩笑的人用炭涂黑了他们的前额三个人醒来以后，彼此看了看，都笑了起来但这并没引起他们之中任何一个人的担心，因为每个人都以为是其他两人在互相取笑这时其中有一个突然不笑了，因为他发觉自己的前额也给涂黑了答案：为了方便，用甲、乙、丙分别代表三个科学家，并不妨设甲已发觉自己的脸给涂黑了那么甲这样想：“我们三个人都可以认为自己的脸没被涂黑，如果我的脸没被涂黑，那么乙能看到（当然对于丙也是一样），乙既然看到了我的脸没给涂黑，同时他又认为他的脸也没给涂黑，那么乙就应该对丙的发笑而感到奇怪因为在这种情况下（甲、乙的脸都是干净的），丙是没有可笑的理由了然而现在的事实是乙对丙的发笑并不感到奇怪，可见乙是在认为丙在笑我由此可知，我的脸也给涂黑了这里应着重指出的是，甲并没有直接看到自己的脸是否给涂黑了，他是根据乙、丙两人的表情进行分析、思考，而说明了自己的脸给涂黑了简单地说，甲是通过说明脸被涂黑了的反面—没被涂黑是错误的，从而觉察了自己的脸被涂黑了因此这是一种间接的证明方法显然这种证明方法也是不可缺少的像这样，为了说明某一个结论是正确的，但不从正面直接说明，而是通过说明它的反面是错误的，从而断定它本身是正确的方法，就叫做“反证法“参考答案:1.7 四种命题1. C 解析：“所有”的否定是“至少有一个不”.2. Ｂ解析：（3）“若1≤c ，则022=++c x x 有实根”的逆否命题为真命题．3. D 解析：其逆否命题为“不是偶数一定不能被4整除”.4. B 解析：“若x 2+y 2 =0,则x , y 全是0”的否命题与若“a +5是无理数，则a 是无理数”的逆否命题为真命题.5. D 解析:反证法证明命题的第二步中，得出的矛盾的可以是所有的条件或相关的结论.6. D 解析: “2＋3是无理数”的否定是“2+3是有理数”.7. ①②④ 解析 ①Δ＝4－4(－k )＝4＋4k ＞0 ∴是真命题 ;②否命题为“若a ≤b ，则a +b ≤b +b ”是真命题;③逆命题“对角线相等的四边形是矩形”是假命题;④否命题：“若xy ≠0，则x 、y 都不为零”是真命题.8. 逆命题：“若关于x 的方程x 2+x －m=0有实数根，则m ＞0”；否命题：“m ≤0，则关于x 的方程x 2+x －m=0没有实数根”；逆否命题：“若关于x 的方程x 2+x －m=0没有实数根，则m ≤0”.当m ＞0时，△=1+4m ＞0，方程x 2+x －m=0必有两个不等实根，故原命题及逆否命题是真命题.当方程x 2+x －m=0，有实数根时，△=1+4m ≥0，m ≥－41，而不一定要＞0，故逆命题及否命题是假命题.9. 解析:(1)这是一个存在性命题,存在量词“有些”可以用“存在一个、至少有一个、某个”等词代替,故该命题的否命题为“所有三角形都不是直角三角形”.本题还可以写出它的逆否命题来判断原命题与否命题的真假.(2)这是一个全称命题,全称量词“所有的”可以用“任意的、对于一切、每一个”等词代替,故该命题的否命题为“存在一个质数不是奇数”或“所有的奇数不都是奇数”.10. 证明：假设都不成立，即yx +1≥2,x y +1≥2成立 ∵x ，y ∈R +,∴1+x ≥2y ,1+y ≥2x ,∴2+x +y ≥2x +2y ,∴x +y ≤2与已知x +y ＞2矛盾， ∴假设不成立，∴原结论成立.11. C 解析: “全等三角形的面积相等”的否命题；“不等边三角形的三内角相等”的逆否命题都是假命题.12. A 解析:命题“a 、b 都是偶数，则a +b 是偶数”的逆否命题为“a +b 不是偶数，则a 、b不都是偶数”13. 2(4k3＋6k2＋3k)＋1解析: (2k+1)3＝8k3＋12k2＋6k＋1＝2(4k3＋6k2＋3k)＋114. B解析:“a，b中至少有一个能被5整除”的否定是“a，b都不能被5整除”15. ①②③以上均为真命题.16. 分析：应先将原命题改写成“如果……，那么……的形式”然后再构造它的逆命题. 解析：(1)逆命题是“若x＝1，则x2＝1.”原命题为假命题，逆命题是真命题.(2)逆命题是“如果两个角相等，那么这两个角是对顶角”.原命题为真命题，逆命题为假命题.(3)逆命题是“如果一个三角形有两边相等，那么这个三角形是等腰三角形.”原命题是真命题，逆命题也是真命题.(4)逆命题是“空集是x2＋2x＋8＞0的解集”.原命题和逆命题都是假命题.17. C 解析: “至多有两个解”包括了无解、有一解、有两解三种情形,其否定可以选有三解.18.证明:假设这两函数的图象没有一个位于x轴的上方,则有22144(10,4120,a aa aa a⎧≤-≥⎧+-⎪⎪⇒⎨⎨-≥≤≤⎪⎪⎩⎩或此不等式组的解集为∅,所以假设不成立.故这两函数的图象至少有一个位于x轴的上方.19. 证明假设a、b、c都是奇数∵a、b、c是一组勾股数，∴a2＋b2＝c2 ①∵a、b、c都是奇数，∴a2、b2、c2也都是奇数 ∴a2＋b2是偶数这样①式的左边是偶数，右边却是奇数，得出自相矛盾的结论.∴a、b、b不可能都是奇数.20. 分析：此题中含有否定用“无”，可考虑用反证法，另外关于有无整数根，可从已知方程的判别式与根和系数的关系入手分析证明之.证法一：只有在Δ＝p2－4q＝（p－m）2时((p－m)2表示完全平方数,其中由－4q＝－2pm ＋m2可知m应为偶数)才可能有整数根.化简上式得出p与q的关系：q＝p·2m－（2m）2，因p是奇数，不论2m是怎样的整数，都可得q为偶数，这与已知q为奇数相矛盾，则判别式Δ的值不会是一个完全平方数，故方程无整数根.证法二：假设方程有整数根α，无论α是奇数还是偶数，都必有α2＋pα＋q为奇数，这与α2＋pα＋q＝0矛盾.故方程无整数根.21. 若122,-≤≤baba则解析：由题意原命题的否命题为“若122,-≤≤baba则”.22. B解析设p为“若A则B”，则r、s、t分别为“若﹁A则﹁B”“若﹁B则﹁A”“若B 则A”，故s是t的否命题.。

二简易逻辑（§1.7.1 四种命题）教学时间:第一课时课题: §1.7.1 四种命题的概念教学目标：1.理解四种命题的概念，掌握命题形式的表示.2.培养学生简单推理的思维能力.教学重点：四种命题的概念.教学难点：由原命题写出另外三种命题.教学方法：读、议、讲、练结合教学.教具准备：投影片1张教学过程：（I）复习回顾师：初中已学习过命题与逆命题的知识，请一位同学回答：什么叫做命题的逆命题？举例。

生：在两个命题中，如果第一个命题的条件是第二个命题的结论，且第一个命题的结论是第二个命题的条件，那么这两个命题叫做互为逆命题。

如“同位角相等，两直线平行”条件（题设）：同位角相等。

结论：两直线平行它的逆命题：两直线平行，同位角相等。

师：本节将进一步研究命题与其有关的命题的概念。

（II）讲授新课§1.7.1 四种命题的概念师：阅读课本P20—P30，思考下列问题：(1) 原命题、逆命题、否命题、逆否命题的定义分别是什么？(2) 原命题的形式表示为“若p则q”，则其它三种命题的形式如何表示？（教师在黑板上写出下列三个命题：）①两直线平行，同位角相等；②负数的平方是正数；③四边相等的四边形是正方形.师：请同学回答：什么叫做原命题？原命题的形式可如何表示？生：通常把所给的一个命题叫做原命题。

如果用p和q分别表示原命题的条件和结论，则原命题可表示：若p则q。

师：什么叫做逆命题初中已学过，那么原命题的逆命题的形式如何表示？生：原命题的逆命题的形式可表示为：若q则p.师：请写出黑板上第①个命题的逆命题.生：同位角相等，两直线平行。

师：什么叫做否命题？形式可如何表示？生：如果一个命题的条件和结论分别是原命题的条件和结论的否定，那么这两个命题叫做互否命题，这个命题叫做原命题的否命题.。

否命题的形式可表示为：若非p则非q.（注：教师强调，可书写为：若┐p则┐q.）师：写出黑板上命题①的否命题.生：两直线不平行，同位角不相等.师：什么叫做逆否命题？形式可如何表示？生：如果一个命题的条件和结论分别是原命题的结论和条件的否定，那么这两个命题叫做互为逆否命题，这个命题叫做原命题的逆否命题。

第二十一教时教材：四种命题的关系目的：要求学生理解四种命题的关系，并能利用这个关系判断命题的真假。

过程：一、复习：四种命题提问：说出命题“若两个三角形全等，则这两个三角形相似”的逆命题、否命题、逆否命题。

（解答略）二、1．接复习提问：原命题与逆否命题互逆否，否命题与逆命题互逆否，逆命题与逆否命题互逆。

小结：得表：Array2．如果原命题为真，则逆命题、否命题、逆否命题真假如何？例：原命题：“若a = 0 则ab = 0”是真命题逆命题：“若ab = 0 则a = 0”是假命题否命题：“若 a ≠ 0 则ab ≠ 0”是假命题逆否命题：“若ab ≠ 0 则 a ≠ 0”是真命题小结：原命题为真，逆命题不一定为真，否命题也不一定为真，逆否命题为真。

3．又例：若四边形ABCD为平行四边形，则对角线互相平分。

它的逆命题、否命题、逆否命题均为真。

三、例题：P32 例二（略）又例：命题“若x = y 则x2 = y2”写出它的逆命题、否命题、逆否命题，并判断它的真假。

解：逆命题：若x2 = y2则x = y （假，如x = 1, y = -1）否命题：若x≠ y 则x2≠ y2（假，如x = 1, y = -1）逆否命题：若x2 ≠ y2则x ≠ y （真）又例：写出命题：“若x + y = 5则x = 3且y = 2”的逆命题否命题逆否命题，并判断它们的真假。

解：逆命题：若x = 3 且y = 2 则x + y = 5 （真）否命题：若x+ y ≠ 5 则x ≠ 3且y≠2 （真）逆否命题：若x≠ 3 或y≠2 则x + y ≠5 （假）四、处理《课课练》30—31 16课五、作业：课本33—34习题1．7中3，4《课课练》16课余下部分。

原命题若p则q逆命题若q则p 互为逆互互逆否互四种命题(2)教学目的：12．理解反证法的基本原理；掌握运用反证法的一般步骤；并能用反证法证明一些命题；3授课类型：新授课课时安排：1课时教具：多媒体、实物投影仪内容分析：学生在初中数学中，学习过简单的命题(包括原命题与逆命题)知识，掌握了简单的推理方法(包括对反证法的了解)．由此，这一大节首先讲述四种命题及其相互关系，并且在初中的基础上，结合四种命题的知识，进一步讲解反证法．然后，通过假设干实例，讲述了充分条件、必要条件和充要条件的有关知识．这一大节的重点是充要条件．学习简易逻辑知识，主要是为了培养学生进行简单推理的技能，发展学生的思维能力，在这方面，逻辑联结词“或〞、“且〞、“非〞与充要条件的有关内容是十分必要的．〔初中数学中有关反证法的内容，要求比较低，并且基本没有涉及代数命题到高中数学学习反证法，一是要注意加强对有关代数命题的训练，二是教学要求要适当，对反证法的掌握，还有待于随着学习的深入，逐步提高教科书中反证法涉及代数命题的例、习题，是属于初中X围的，比较简单．因此，这些题目都可以用直接的方法进行证明，不一定用反证法，选取这些题，主要是为了让学生熟悉反证法〕反证法在初中教科书中指出：从命题结论的反面出发，引出矛盾，从而证明命题成立，教学过程：一、复习引入：四种命题及其形式原命题：假设p那么q；逆命题：假设q那么p；否命题：假设 p那么 q；逆否命题：假设 q那么 p.二、讲解新课：1．四种命题的相互关系互逆命题、互否命题与互为逆否命题都是说两个命题的关系，假设把其中一个命题叫做原命题时，另一个命题就叫做原命题的逆命题、否命题与逆否命题.因此，四种命题之间的相互关系，可用右以下图表示：2．四种命题的真假关系一个命题的真假与其他三个命题的真假有如下三条关系：①、原命题为真，它的逆命题不一定为真3．反证法：要证明某一结论A是正确的，但不直接证明，而是先去证明A的反面〔非A〕是错误的，从而断定A即反证法就是通过否定命题的结论而导出矛盾来达到肯定命题的结论，4．反证法的步骤：(1)(2)(3)注意：可能出现矛盾四种情况：①与题设矛盾；②与反设矛盾；③与公理、定理矛盾④在证明过程中，推出自相矛盾的结论三、X例例1．判断以下四种命题的真假原命题：假设四边形ABCD为平行四边形，那么对角线互相平分真逆命题：假设四边形ABCD对角线互相平分，那么它为平行四边形；真否命题：假设四边形ABCD不是为平行四边形，那么对角线不平分；真逆否命题：假设四边形ABCD对角线不平分，那么它不是平行四边形；真归纳小结：〔学生回答，教师整理补充〕(1)原命题为真，它的逆命题不一定为真；(2)原命题为真，它的否命题不一定为真；(3)结论：两个互为逆否的命题同真或同假(如原命题和它的逆否命题，逆命题和否命题)，其余情况那么不一定同真或同假〔如原命题和逆命题，否命题和逆否命题等〕，这时称互为逆否的两个命题等价，即原命题⇔例2．〔课本第32页例2〕设原命题是“当c>0时，假设a>b，那么ac>bc〞，写出它的逆命题、否命题与逆否命题，并分别判断它们的真假.分析：“当c>0时〞是大前提，写其他命题时应该保留，原命题的条件是a>b，结论是ac>bc.解：逆命题：当c>0时，假设ac>bc，那么a>b.它是真命题；否命题：当c>0时，假设a≤b，那么ac≤bc.它是真命题；逆否命题：当c>0时，假设ac≤bc，那么a≤b.它是真命题.练习：课本第32页 练习：1，2. 答案：1.(1)正确；(2)正确. 2.(1)逆命题：两个全等三角形的三边对应相等.逆命题为真； 否命题：三边不对应相等的两个三角形不全等.否命题为真； 逆否命题：两个不全等的三角形的三边不对应相等.逆否命题为真. (2)逆命题：假设a+c>b+c,那么a>b.逆命题为真.否命题：假设a ≤b,那么a+c ≤b+c.否命题为真.逆否命题：假设a+c ≤b+c ，那么a ≤b.逆否命题为真.例3．〔课本第32页例3〕用反证法证明：如果a>b>0，那么b a >.证明：假设a 不大于b ，那么或者a <b ,或者a =b .∵a>0，b>0，∴a <b ⇒a a <b a ，a b <b b⇒ab a <，b ab <⇒a<b ；a =b ⇒a=b.这些都同条件a>b>0矛盾，∴b a >.证法二〔直接证法〕()()b a b a b a -+=-， ∵a>b>0,∴a -b>0即()()0>-+b a b a ,∴0>-b a ∴b a > 例4〔课本第33页例4〕用反证法证明：圆的两条不是直径的相交弦不能互相平分. ：如图，在⊙O 中，弦AB 、CD 交于P ，且AB 、CD 不是直径. 求证：弦AB 、CD 不被P 平分.分析：假设弦AB 、CD 被P 平分，连结OP 后，可推出AB 、CD 都与OP 垂直，那么出现矛盾.证明：假设弦AB 、CD 被P 平分，由于P 点一定不是圆心O ，连结OP ，根据垂径定理的推论，有OP ⊥AB ，OP ⊥CD ，即过点P 有两条直线与OP 都垂直，这与垂线性质矛盾.∴弦AB 、CD 不被P 平分.四、小结：四种命题之间的相互关系和真假关系反证法的基本原理及其四个步骤五、练习：课本第33页 练习：1，2.提示：1.设b2-4ac ≤0，那么方程没有实数根，或方程有两个相等的实数根，得出矛盾.2.设∠B≥900，那么∠C+∠B≥1800，得出矛盾.补充题：1．命题“假设 x = y 那么 |x| = |y|〞写出它的逆命题、否命题、逆否命题，并判断解：逆命题：假设 |x| = |y| 那么 x = y 〔假，如 x = 1, y = -1〕否命题：假设 x ≠ y 那么 |x| ≠|y| 〔假，如 x = 1, y = -1〕逆否命题：假设 |x| ≠|y| 那么 x ≠ y 〔真〕2．写出命题：“假设 xy = 6那么 x = 3且 y = 2〞的逆命题否命题逆否命题，并判断解：逆命题：假设 x = 3 且 y = 2 那么 x + y = 5 〔真〕否命题：假设 x + y ≠ 5 那么 x ≠ 3且y≠2 〔真〕逆否命题：假设 x ≠ 3 或y≠2 那么 x + y ≠5 〔假〕六、作业：课本第33-34页习题1．7中3，4 ， 5.补充题：1．假设a2能被2整除，a是整数，求证：a也能被2整除.证：假设a不能被2整除，那么a必为奇数，故可令a=2m+1(m为整数),由此得a2=(2m+1)2=4m2+4m+1=4m(m+1)+1,此结果说明a2是奇数，这与题中的条件〔a2能被2整除〕相矛盾,∴a能被2整除.七、板书设计〔略〕八、课后记：小故事：三个古希腊哲学家，由于争论和天气炎热感到疲倦了，于是在花园里的一棵大树下躺下来休息一会，结果都睡着了.这时一个爱开玩笑的人用炭涂黑了他们的前额.三个人醒来以后，彼此看了看，都笑了起来.但这并没引起他们之中任何一个人的担心，因为每个人都以为是其他两人在互相取笑.这时其中有一个突然不笑了，因为他发觉自己的前额也给涂黑了.那么他是怎样觉察到的呢？你能想出来吗？答案：为了方便，用甲、乙、丙分别代表三个科学家，并不妨设甲已发觉自己的脸给涂黑了.那么甲这样想：“我们三个人都可以认为自己的脸没被涂黑，如果我的脸没被涂黑，那么乙能看到〔当然对于丙也是一样〕，乙既然看到了我的脸没给涂黑，同时他又认为他的脸也没给涂黑，那么乙就应该对丙的发笑而感到奇怪.因为在这种情况下〔甲、乙的脸都是干净的〕，丙是没有可笑的理由了.然而现在的事实是乙对丙的发笑并不感到奇怪，可见乙是在认为丙在笑我.由此可知，我的脸也给涂黑了.这里应着重指出的是，甲并没有直接看到自己的脸是否给涂黑了，他是根据乙、丙两人的表情进行分析、思考，而说明了自己的脸给涂黑了.简单地说，甲是通过说明脸被涂黑了的反面—没被涂黑是错误的，从而觉察了自己的脸被涂黑了.因此这是一种间接的证明方法.显然这种证明方法也是不可缺少的.像这样，为了说明某一个结论是正确的，但不从正面直接说明，而是通过说明它的反面是错误的，从而断定它本身是正确的方法，就叫做“反证法“.。