kernel(核函数学习)

kernel密度法（原创版）目录1.介绍 Kernel 密度估计法2.Kernel 密度法的原理3.Kernel 密度法的应用4.Kernel 密度法的优缺点正文一、介绍 Kernel 密度估计法Kernel 密度估计法是一种常用的非参数统计方法，用于估计连续型随机变量的概率密度函数。

该方法通过核函数将数据映射到高维空间，在高维空间中计算密度，再将密度映射回原空间。

Kernel 密度估计法具有较强的理论性质和实用性。

二、Kernel 密度法的原理Kernel 密度法的基本思想是利用核函数将原始数据映射到高维空间，然后使用高维空间中的数据计算密度。

核函数的选择和带宽的确定是Kernel 密度估计法的关键。

1.核函数：核函数是一种对称的函数，将原始数据映射到高维空间。

常用的核函数有高斯核、线性核、多项式核等。

2.带宽：带宽是核函数中的重要参数，决定了核函数的形状。

带宽越小，核函数越尖锐，估计的密度函数越接近真实密度函数；带宽越大，核函数越平缓，估计的密度函数越平滑。

三、Kernel 密度法的应用Kernel 密度法广泛应用于数据分析、信号处理、模式识别等领域，具有重要的实际意义。

1.数据分析：Kernel 密度法可以用于分析数据的分布特征，如均值、方差等。

2.信号处理：Kernel 密度法可以用于信号的滤波、去噪等。

3.模式识别：Kernel 密度法可以用于图像识别、语音识别等领域。

四、Kernel 密度法的优缺点1.优点：Kernel 密度法具有较强的理论性质，可以估计任意形状的密度函数；同时，Kernel 密度法具有较好的鲁棒性，能够处理含有异常值的数据。

机器学习算法调参技巧解读机器学习算法调参是提高模型性能的关键一步。

通过合理地调整算法的参数，可以使得模型更准确地对数据进行拟合，从而提高预测精度和泛化能力。

在本文中，我们将以逻辑回归和支持向量机为例，探讨机器学习算法调参的技巧和方法。

一、逻辑回归算法调参技巧解读逻辑回归是一种广泛应用于分类问题的机器学习算法。

在调参过程中，我们通常会关注以下几个参数：正则化参数lambda、学习率alpha 以及迭代次数iterations。

1. 正则化参数lambda正则化参数lambda的作用是缓解模型的过拟合问题。

过低的lambda值会导致模型在训练集上过拟合，而过高的lambda值则会导致欠拟合。

因此，我们可以通过交叉验证的方法来选择最合适的lambda 值。

2. 学习率alpha学习率alpha决定了每次参数更新的步长。

过大的学习率可能导致无法收敛，而过小的学习率则会导致收敛速度过慢。

在调参过程中，我们可以通过尝试不同的学习率来找到最合适的取值。

3. 迭代次数iterations迭代次数iterations指的是训练数据的遍历次数。

当迭代次数太少时，模型可能没有充分学习到数据的规律；而当迭代次数太多时，可能会导致过拟合。

因此，在调参过程中，我们可以通过观察模型在训练集和验证集上的表现来选择合适的迭代次数。

二、支持向量机算法调参技巧解读支持向量机是一种常用于分类和回归问题的机器学习算法。

在调参过程中，重要的参数包括：核函数类型kernel、正则化参数C以及gamma。

1. 核函数类型kernel核函数用于将低维数据映射到高维空间中，从而使数据更容易分类。

常见的核函数包括线性核函数、多项式核函数和高斯核函数等。

在实际调参中，我们可以通过对比不同核函数的表现来选择最适合的类型。

2. 正则化参数C正则化参数C控制着模型对误分类样本的惩罚程度。

较小的C值会使模型更加关注少数类别的分类准确性，而较大的C值则会平衡所有类别。

cuda 核函数使用在 CUDA 编程中，核函数（kernel function）是在 GPU 上执行的函数，用于并行计算。

以下是 CUDA 核函数的基本使用方式：定义核函数：核函数是一个在 GPU 上并行执行的函数，通常使用 __global__ 修饰符声明。

函数的参数表示线程的索引和数据。

以下是一个简单的核函数示例：__global__ void myKernel(int* input, int* output, int size) {int tid = blockIdx.x * blockDim.x + threadIdx.x;if (tid < size) {output[tid] = input[tid] * 2;}}启动核函数：在主机代码中，使用 CUDA 的启动语法来启动核函数。

以下是一个使用核函数的示例：cppCopy codeint main() {// 分配和初始化数据int size = 1000;int* hostInput = new int[size];int* hostOutput = new int[size];// 在 GPU 上分配内存int* deviceInput;int* deviceOutput;cudaMalloc((void**)&deviceInput, size * sizeof(int));cudaMalloc((void**)&deviceOutput, size * sizeof(int));// 将数据从主机复制到设备cudaMemcpy(deviceInput, hostInput, size * sizeof(int), cudaMemcpyHostToDevice);// 定义启动核函数的网格和线程块大小int blockSize = 256;int gridSize = (size + blockSize - 1) / blockSize;// 启动核函数myKernel<<<gridSize, blockSize>>>(deviceInput, deviceOutput, size);// 将结果从设备复制回主机cudaMemcpy(hostOutput, deviceOutput, size * sizeof(int), cudaMemcpyDeviceToHost);// 清理内存delete[] hostInput;delete[] hostOutput;cudaFree(deviceInput);cudaFree(deviceOutput);return 0;}核函数调用的语法：使用 <<<...>>> 语法来指定执行核函数的网格和线程块大小。

核函数摘要根据模式识别理论，低维空间线性不可分的模式通过非线性映射到高维特征空间则可能实现线性可分，但是如果直接采用这种技术在高维空间进行分类或回归，则存在确定非线性映射函数的形式和参数、特征空间维数等问题，而最大的障碍则是在高维特征空间运算时存在的“维数灾难”。

采用核函数技术可以有效地解决这样问题。

本文详细的介绍了几种核函数：多项式空间和多项式核函数，Mercer 核，正定核以及核函数的构造关键词：模式识别理论，核函数0引言核方法是解决非线性模式分析问题的一种有效途径，其核心思想是：首先，通过某种非线性映射将原始数据嵌入到合适的高维特征空间；然后，利用通用的线性学习器在这个新的空间中分析和处理模式。

相对于使用通用非线性学习器直接在原始数据上进行分析的范式，核方法有明显的优势：首先，通用非线性学习器不便反应具体应用问题的特性，而核方法的非线性映射由于面向具体应用问题设计而便于集成问题相关的先验知识。

再者，线性学习器相对于非线性学习器有更好的过拟合控制从而可以更好地保证泛化性能。

还有，很重要的一点是核方法还是实现高效计算的途径，它能利用核函数将非线性映射隐含在线性学习器中进行同步计算，使得计算复杂度与高维特征空间的维数无关。

核函数理论不是源于支持向量机的。

它只是在线性不可分数据条件下实现支持向量方法的一种手段.这在数学中是个古老的命题。

Mercer定理可以追溯到1909年，再生核希尔伯特空间(ReproducingKernel Hilbert Space, RKHS)研究是在20世纪40年代开始的。

早在1964年Aizermann等在势函数方法的研究中就将该技术引入到机器学习领域，但是直到1992年Vapnik等利用该技术成功地将线性SVMs推广到非线性SVMs时其潜力才得以充分挖掘。

核函数方法是通过一个特征映射可以将输入空间(低维的)中的线性不可分数据映射成高维特征空间中(再生核Hilbert空间)中的线性可分数据.这样就可以在特征空间使用SVM方法了.因为使用svm方法得到的学习机器只涉及特征空间中的内积，而内积又可以通过某个核函数(所谓Mercer 核)来表示，因此我们可以利用核函数来表示最终的学习机器.这就是所谓的核方法。

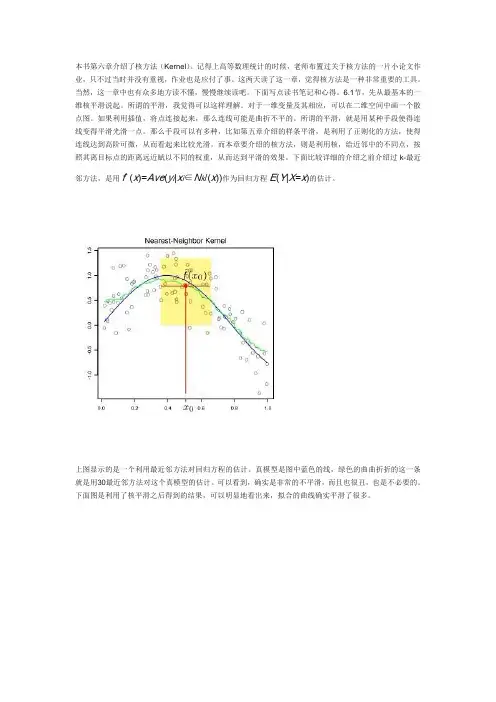
本书第六章介绍了核方法（Kernel）。

记得上高等数理统计的时候，老师布置过关于核方法的一片小论文作业，只不过当时并没有重视，作业也是应付了事。

这两天读了这一章，觉得核方法是一种非常重要的工具。

当然，这一章中也有众多地方读不懂，慢慢继续读吧。

下面写点读书笔记和心得。

6.1节，先从最基本的一维核平滑说起。

所谓的平滑，我觉得可以这样理解。

对于一维变量及其相应，可以在二维空间中画一个散点图。

如果利用插值，将点连接起来，那么连线可能是曲折不平的。

所谓的平滑，就是用某种手段使得连线变得平滑光滑一点。

那么手段可以有多种，比如第五章介绍的样条平滑，是利用了正则化的方法，使得连线达到高阶可微，从而看起来比较光滑。

而本章要介绍的核方法，则是利用核，给近邻中的不同点，按照其离目标点的距离远近赋以不同的权重，从而达到平滑的效果。

下面比较详细的介绍之前介绍过k-最近邻方法，是用fˆ(x)=Ave(y i|x i∈N k/(x))作为回归方程E(Y|X=x)的估计。

上图显示的是一个利用最近邻方法对回归方程的估计。

真模型是图中蓝色的线，绿色的曲曲折折的这一条就是用30最近邻方法对这个真模型的估计。

可以看到，确实是非常的不平滑，而且也很丑，也是不必要的。

下面图是利用了核平滑之后得到的结果，可以明显地看出来，拟合的曲线确实平滑了很多。

上面仅仅是一个核平滑的例子。

下面给出一维核平滑的一些具体的公式fˆ(x0)=∑Ni=1Kλ(x0,xi)yi∑Ni=1Kλ(x0,xi)这个就是利用核平滑对x0点的真实值的估计，可以看出，这其实是一个加权平均，相比起最近邻方法，这里的特殊的地方就是权重Kλ(x0,x)。

这个权重就称为核。

核函数有很多种，常用的包括Epanechnikov quadratic 核：Kλ(x0,x)=D(x−x0λ) with D(t)=34(1−t2),|t|<1这个图就是D(t)的图像，可以看出，随着离目标点的距离越来越远，所附加的权重也是平滑的越来越小。

核函数（kernelfunction）在接触反演、算法等⽅⾯的知识后，经常听到“核”这个字，它不像对原始变量的线性变换，也不像类似于机器学习中激活函数那样的⾮线性变换，对原始数据进⾏变换，就可以将复杂的问题简单化。

接下来，就让我们了解了解“核”这个东西。

参考链接：注，kernel function 与kernel function指的是同⼀个东西，可以这样理解：核⽅法只是⼀种处理问题的技巧，低维空间线性不可分可以在⾼维空间线性可分，但是⾼维空间的计算复杂度⼜很⼤，那么我们就把⾼维空间的计算通过低维空间的计算外加⼀些线性变换来完成。

还有，都说核⽅法与映射⽆关，怎么理解呢？核⽅法是⼀种技巧，不管怎么映射，我们都是⽤低维空间的计算来解决⾼维空间计算复杂的问题。

1. 问题描述给定两个向量(x_i)和(x_j)，我们的⽬标是要计算他们的内积\(I\) = <\(x_i\), \(x_j\)>。

现在假设我们通过某种⾮线性变换：\(\Phi : x \rightarrow \phi(x)\)把他们映射到某⼀个⾼维空间中去，那么映射后的向量就变成：\(\phi(x_i)\)和\(\phi(x_j)\)，映射后的内积就变成：\(I’\) = <\(\phi(x_j)\),\ (\phi(x_j)\)>。

现在该如何计算映射后的内积呢？传统⽅法是先计算映射后的向量\(\phi(x_i)\)和\(\phi(x_j)\)，然后再计算它俩的内积。

但是这样做计算很复杂，因为映射到⾼维空间后的数据维度很⾼。

⽐如，假设\(x_i\)和\(x_j\)在映射之后都是⼀个( \(1 \times 10000\))维的向量，那么他们的内积计算就需要做10000次加法操作和10000次乘法操作，显然复杂度很⾼。

于是，数学家们就想出⼀个办法：能不能在原始空间找到⼀个函数\(K(x_i,x_j)\)使得\(K(x_i,x_j) = <\phi(x_j),\phi(x_j)>\)呢？如果这个函数存在，那么我们只需要在低维空间⾥计算函数\(K(x_i,x_j)\)的值即可，⽽不需要先把数据映射到⾼维空间，再通过复杂的计算求解映射后的内积了。

⽀持向量机（四）--核函数⼀、核函数的引⼊问题1：SVM 显然是线性分类器。

但数据假设根本就线性不可分怎么办？解决⽅式1：数据在原始空间（称为输⼊空间）线性不可分。

可是映射到⾼维空间（称为特征空间）后⾮常可能就线性可分了。

问题2：映射到⾼维空间同⼀时候带来⼀个问题：在⾼维空间上求解⼀个带约束的优化问题显然⽐在低维空间上计算量要⼤得多，这就是所谓的“维数灾难”。

解决⽅式2：于是就引⼊了“核函数”。

核函数的价值在于它尽管也是讲特征进⾏从低维到⾼维的转换。

⼆、实例说明⽐如图中的两类数据，分别分布为两个圆圈的形状，不论是不论什么⾼级的分类器，仅仅要它是线性的。

就没法处理。

SVM 也不⾏。

由于这种数据本⾝就是线性不可分的。

从上图我们能够看出⼀个理想的分界应该是⼀个“圆圈”⽽不是⼀条线（超平⾯）。

假设⽤ 和 来表⽰这个⼆维平⾯的两个坐标的话，我们知道⼀条⼆次曲线（圆圈是⼆次曲线的⼀种特殊情况）的⽅程能够写作这种形式：注意上⾯的形式，假设我们构造另外⼀个五维的空间，当中五个坐标的值分别为 , , , , ，那么显然。

上⾯的⽅程在新的坐标系下能够写作：关于新的坐标 。

这正是⼀个超平⾯ 的⽅程！也就是说，假设我们做⼀个映射 。

将 依照上⾯的规则映射为 ，那么在新的空间中原来的数据将变成线性可分的，从⽽使⽤之前我们推导的线性分类算法就能够进⾏处理了。

这正是 Kernel ⽅法处理⾮线性问题的基本思想。

三、具体分析还记得之前我们⽤内积这⾥是⼆维模型，可是如今我们须要三维或者更⾼的维度来表⽰样本。

这⾥我们如果是维度是三。

那么⾸先须要将特征x 扩展到三维，然后寻找特征和结果之间的模型。

我们将这样的特征变换称作特征映射（feature mapping ）。

映射函数称作，在这个样例中我们希望将得到的特征映射后的特征应⽤于SVM 分类，⽽不是最初的特征。

这样，我们须要将前⾯公式中的内积从，映射到。

为什么须要映射后的特征⽽不是最初的特征来參与计算，⼀个重要原因是例⼦可能存在线性不可分的情况，⽽将特征映射到⾼维空间后，往往就可分了。

CUDA核函数参数解析CUDA是一种并行计算平台和编程模型，它允许开发者在GPU上进行高效的并行计算。

在CUDA中，核函数（Kernel Function）是在GPU上执行的并行计算任务的入口点。

核函数是由开发者编写的，用于对数据进行并行处理。

核函数的参数解析是指如何将参数传递给核函数，以及如何在核函数中使用这些参数。

在CUDA中，核函数的参数列表在其定义中指定，可以根据具体的应用需求进行自定义。

1.传递基本类型参数：核函数可以接受和使用标准的C/C++基本类型的参数，如整型、浮点型、布尔型等。

在调用核函数时，可以使用类似于C/C++函数调用的方式将这些参数传递给核函数。

2.传递指针参数：核函数可以接受指向全局内存或设备内存的指针参数。

在GPU上执行的核函数可以直接访问和修改全局内存和设备内存中的数据。

在调用核函数时，需要将数据复制到设备内存中，然后将指向设备内存的指针作为参数传递给核函数。

3.动态分配的设备内存：在核函数执行期间，可以动态使用cudaMalloc函数在设备内存中分配内存，然后在核函数中使用这些内存。

4.CUDAC++模板参数：核函数还可以使用CUDAC++模板参数。

这允许开发者根据具体的数据类型和算法需求进行参数化编程，以提高代码的复用性和性能。

5.线程索引和块索引：在核函数中，可以使用内置的线程索引和块索引来确定当前执行的线程和块的位置。

这些索引可以用于数据的划分、任务的调度、线程的协作等操作。

总结起来，CUDA核函数的参数解析可以涉及基本类型参数、指针参数、动态分配的设备内存、CUDAC++模板参数、线程索引和块索引等。

正确地解析核函数参数能够提高代码的性能和可维护性，使程序能够充分利用GPU的并行计算能力。

核函数方法简介（1）核函数发展历史早在1964年Aizermann等在势函数方法的研究中就将该技术引入到机器学习领域，但是直到1992年Vapnik等利用该技术成功地将线性SVMs推广到非线性SVMs时其潜力才得以充分挖掘。

而核函数的理论则更为古老，Mercer定理可以追溯到1909年，再生核希尔伯特空间(ReproducingKernel Hilbert Space, RKHS)研究是在20世纪40年代开始的。

（2）核函数方法原理核函数方法原理根据模式识别理论，低维空间线性不可分的模式通过非线性映射到高维特征空间则可能实现线性可分，但是如果直接采用这种技术在高维空间进行分类或回归，则存在确定非线性映射函数的形式和参数、特征空间维数等问题，而最大的障碍则是在高维特征空间运算时存在的“维数灾难”。

采用核函数技术可以有效地解决这样问题。

设x,z∈X,X属于R（n）空间,非线性函数Φ实现输入间X到特征空间F的映射,其中F属于R（m）,n<<m。

根据核函数技术有：K(x,z) =<Φ(x),Φ(z) >(1)其中：<, >为内积,K(x,z)为核函数。

从式(1)可以看出，核函数将m维高维空间的内积运算转化为n维低维输入空间的核函数计算，从而巧妙地解决了在高维特征空间中计算的“维数灾难”等问题，从而为在高维特征空间解决复杂的分类或回归问题奠定了理论基础。

根据模式识别理论，低维空间线性不可分的模式通过非线性映射到高维特征空间则可能实现线性可分，但是如果直接采用这种技术在高维空间进行分类或回归，则存在确定非线性映射函数的形式和参数、特征空间维数等问题，而最大的障碍则是在高维特征空间运算时存在的“维数灾难”。

采用核函数技术可以有效地解决这样问题。

设x,z∈X,X属于R（n）空间,非线性函数Φ实现输入间X到特征空间F的映射,其中F属于R（m）,n<<m。

根据核函数技术有：K(x,z) =<Φ(x),Φ(z) > (1)其中：<, >为内积,K(x,z)为核函数。

CUDA（Compute Unified Device Architecture）是由NVIDIA推出的并行计算架构，可以利用GPU（Graphics Processing Unit）进行高性能计算。

在CUDA中，核函数（kernel function）是在GPU上执行的并行函数，它可以由多个线程同时执行，以加速计算过程。

对于一些需要大量重复计算的任务，可以使用核函数内的for循环来实现并行化计算，从而提高计算效率。

1. 核函数的概念和作用核函数是在CUDA中执行的并行函数，可以由多个线程同时执行，以加速计算过程。

在核函数中，可以对数据进行并行处理，利用GPU的并行计算能力来加速计算任务。

核函数的使用可以极大地提高计算性能，尤其是对于需要重复计算的任务来说，可以实现更高效的并行计算。

2. 核函数内的for循环在核函数内部，通常需要对数据进行遍历和计算，而这些计算往往需要通过循环来实现。

在CUDA中，可以使用for循环来对数据进行并行处理，实现并行化计算。

在核函数内部使用for循环，可以将计算任务分配给多个线程来并行处理，以提高计算效率。

通过核函数内的for循环，可以充分利用GPU的并行计算能力，加速计算过程。

3. 实现核函数内的for循环要实现核函数内的for循环，首先需要了解GPU的并行计算模式。

在CUDA中，核函数内的每个线程都会处理一个数据元素，因此可以通过for循环将计算任务平均分配给每个线程来实现并行化计算。

还需要考虑数据的划分和线程的同步等问题，确保计算任务能够正确并且高效地并行化执行。

4. 示例代码下面是一个在核函数内实现for循环的示例代码：```c__global__ void parallel_for_loop(float* input, float* output, int N) {int tid = blockIdx.x * blockDim.x + threadIdx.x;for (int i = tid; i < N; i += blockDim.x * gridDim.x) {// 对数据进行计算output[i] = input[i] * 2;}}```在这个示例代码中，核函数`parallel_for_loop`内使用了for循环来处理数据。

kernel密度法
Kernel密度法是一种非参数化的概率密度估计方法，用于推断数据分布的形状。

它基于观测数据的位置和分布，通过在每个观测点周围放置核函数（通常是高斯核函数），来估计未知数据的概率密度。

Kernel密度法的基本思想是，在每个观测点上放置一个核函数，然后将所有核函数叠加在一起，以得到整体的概率密度估计。

具体计算时，核函数需要进行归一化，以确保概率密度的总和为1。

Kernel密度法的一个重要参数是带宽（bandwidth），它控制
了核函数的宽度。

带宽的选择对估计结果有很大影响，带宽太小可能导致过拟合，而带宽太大可能导致平滑过度。

Kernel密度法的优点是可以估计任意形状的概率密度函数，适用于各种类型的数据分布。

然而，它的缺点是计算复杂度高，特别是在高维数据和大样本量下。

此外，带宽的选择也很困难，对估计结果有很大影响。

总结起来，Kernel密度法是一种用于非参数化概率密度估计的方法，通过在每个观测点上放置核函数来推断未知数据的分布。

它的优点是适用于任意形状的数据分布，缺点是计算复杂度高和带宽选择困难。

柯西核函数1. 前言柯西核函数是机器学习中常用的一种核函数，它可以用于支持向量机、K近邻等算法中。

本文将详细介绍柯西核函数的定义、性质以及如何在Python中实现。

2. 柯西核函数的定义柯西核函数是一种径向基函数（RBF）的变体，它的定义如下：$$K(x_i, x_j) = \frac{1}{1 + \gamma ||x_i - x_j||^2}$$其中，$x_i$和$x_j$是输入数据点，$\gamma$是一个常数。

可以看出，柯西核函数与RBF核函数的主要区别在于分母上多了一个常数1。

3. 柯西核函数的性质柯西核函数具有以下性质：- 对称性：$K(x_i, x_j) = K(x_j, x_i)$；- 半正定性：对于任意$n$个数据点$x_1, x_2, ..., x_n$和实数$c_1,c_2, ..., c_n$，有$\sum_{i=1}^{n}\sum_{j=1}^{n}c_ic_jK(x_i,x_j) \ge 0$。

4. 如何在Python中实现柯西核函数下面给出一个Python实现柯西核函数的示例代码：```pythonimport numpy as npdef cauchy_kernel(X, gamma):n_samples = X.shape[0]K = np.zeros((n_samples, n_samples))for i in range(n_samples):for j in range(n_samples):K[i,j] = 1 / (1 + gamma * np.linalg.norm(X[i] - X[j])**2)return K```上述代码中，输入参数X是一个$n \times d$的矩阵，表示$n$个$d$维数据点。

gamma是柯西核函数中的常数。

输出结果K是一个$n \times n$的矩阵，表示每两个数据点之间的核函数值。

5. 柯西核函数的应用柯西核函数可以用于支持向量机、K近邻等算法中。

拉普拉斯核函数1. 什么是拉普拉斯核函数？拉普拉斯核函数（Laplacian Kernel Function）是一种常用的非线性核函数，在机器学习和图像处理中有着广泛的应用。

它的定义如下：$$K(x,y) = \exp(-\frac{\|x-y\|}{\sigma})$$其中，$\|x-y\|$表示欧几里得距离，也就是两个向量之间的差的模长。

$\sigma$是一个常数，常常由用户指定。

2. 拉普拉斯核函数的性质拉普拉斯核函数具有以下性质：(1) 对于所有的$x$和$y$，$\exp(-\frac{\|x-y\|}{\sigma})$始终为正数。

(2)当$x$和$y$相同时，$K(x,y)=1$。

(3)当$x$和$y$很远时，$\|x-y\|$趋近于无穷大，$K(x,y)$趋近于0。

(4) 拉普拉斯核函数是对称的，即$K(x,y)=K(y,x)$。

(5)当$\sigma$取值很小的时候，拉普拉斯核函数给予距离较近的样本更高的相似度，反之则给予距离较远的样本更高的相似度。

(6)当$\sigma$取值适当时，拉普拉斯核函数可以较好地捕捉数据之间的局部变化。

3. 拉普拉斯核函数的应用拉普拉斯核函数在机器学习和图像处理领域中有着广泛的应用。

下面举例说明：(1)在SVM分类器中，使用拉普拉斯核函数可以较好地处理非线性分类问题。

(2)在聚类分析中，使用拉普拉斯核函数可以较好地将数据聚集成密度较高的簇。

(3)在图像处理中，拉普拉斯核函数可以被用于实现边缘检测、图像去噪等。

(4)在自然语言处理中，拉普拉斯核函数可以被用于实现文本分类、情感分析等。

4. 拉普拉斯核函数的优缺点优点：(1)拉普拉斯核函数在处理非线性问题时较为有效。

(2)拉普拉斯核函数可以帮助机器学习算法更好地捕捉数据之间的局部变化，提高分类或回归的准确率。

(3)拉普拉斯核函数的运算速度较快。

缺点：(1)拉普拉斯核函数的性能与参数$\sigma$的取值有关，如果选取不当，则很容易出现过度拟合或者欠拟合的情况。

机器学习：SVM（核函数、⾼斯核函数RBF）⼀、核函数（Kernel Function）　1）格式K(x, y)：表⽰样本 x 和 y，添加多项式特征得到新的样本 x'、y'，K(x, y) 就是返回新的样本经过计算得到的值；在 SVM 类型的算法 SVC() 中，K(x, y) 返回点乘：x' . y'得到的值；　2）多项式核函数业务问题：怎么分类⾮线性可分的样本的分类？内部实现：1. 对传⼊的样本数据点添加多项式项；2. 新的样本数据点进⾏点乘，返回点乘结果；多项式特征的基本原理：依靠升维使得原本线性不可分的数据线性可分；升维的意义：使得原本线性不可分的数据线性可分；例：1. ⼀维特征的样本，两种类型，分布如图，线性不可分：2.3. 为样本添加⼀个特征：x2，使得样本在⼆维平⾯内分布，此时样本在 x 轴升的分布位置不变；如图，可以线性可分：4.　3）优点 / 特点不需要每次都具体计算出原始样本点映射的新的⽆穷维度的样本点，直接使⽤映射后的新的样本点的点乘计算公式即可；减少计算量减少存储空间1. ⼀般将原始样本变形，通常是将低维的样本数据变为⾼维数据，存储⾼维数据花费较多的存储空间；使⽤核函数，不⽤考虑原来样本改变后的样⼦，也不⽤存储变化后的结果，只需要直接使⽤变化的结果进⾏运算并返回运算结果即可；核函数的⽅法和思路不是 SVM 算法特有，只要可以减少计算量和存储空间，都可以设计核函数⽅便运算；对于⽐较传统的常⽤的机器学习算法，核函数这种技巧更多的在 SVM 算法中使⽤；　4）SVM 中的核函数svm 类中的 SVC() 算法中包含两种核函数：1. SVC(kernel = 'ploy')：表⽰算法使⽤多项式核函数；2. SVC(kernel = 'rbf')：表⽰算法使⽤⾼斯核函数；SVM 算法的本质就是求解⽬标函数的最优化问题；求解最优化问题时，将数学模型变形：　5）多项式核函数格式：from sklearn.svm import SVCsvc = SVC(kernel = 'ploy')思路：设计⼀个函数（ K(x i, x j) ），传⼊原始样本（x(i)、 x(j)），返回添加了多项式特征后的新样本的计算结果（x'(i) . x'(j)）；内部过程：先对 x i、x j添加多项式，得到：x'(i)、 x'(j)，再进⾏运算：x'(i) . x'(j)；1. x(i)添加多项式特征后：x'(i)；2. x(j)添加多项式特征后：x'(j)；3. x(i) . x(j)转化为：x'(i) . x'(j)；其实不使⽤核函数也能达到同样的⽬的，这⾥核函数相当于⼀个技巧，更⽅便运算；⼆、⾼斯核函数（RBF）业务问题：怎么分类⾮线性可分的样本的分类？　1）思想业务的⽬的是样本分类，采⽤的⽅法：按⼀定规律统⼀改变样本的特征数据得到新的样本，新的样本按新的特征数据能更好的分类，由于新的样本的特征数据与原始样本的特征数据呈⼀定规律的对应关系，因此根据新的样本的分布及分类情况，得出原始样本的分类情况。

Cauchy核函数（Cauchy Kernel Function）是一种在数学和物理中常用的函数，它描述了函数在无穷远处的奇异性质。

Cauchy核函数在信号处理、图像处理、物理和工程等领域都有广泛的应用。

Cauchy核函数的一般形式为：k(x, y) = 1 / (π(x² + y²))其中，x和y是两个变量，x²和y²分别表示它们的平方，π是圆周率。

Cauchy核函数具有以下特性：1. 奇函数：由于Cauchy核函数的分子是常数1，而分母中的x²和y²都是平方项，因此它是奇函数。

这意味着Cauchy核函数在原点对称，即对于任何点(x, y)，都有k(-x, -y) = k(x, y)。

2. 无穷大：当x或y趋于无穷大时，Cauchy核函数的值趋于无穷大。

这是因为分母中的x²和y²会趋于无穷大，使得整个函数的值变得非常小。

这种性质使得Cauchy核函数在处理一些特定问题时非常有用。

3. 零均值：Cauchy核函数的平均值为0，即对于任何区域内的所有点，Cauchy核函数的总和为0。

这是由于其奇函数的性质决定的。

4. 高斯积分：Cauchy核函数与高斯函数有密切关系。

高斯函数是一种在数学和物理中常用的概率分布函数，其概率密度函数形式为：f(x) = a * e ^ (-x² / 2)其中a是常数。

高斯积分可以用来计算高斯函数的数值，而Cauchy核函数可以用来计算高斯函数的积分。

在信号处理中，Cauchy核函数可以用于设计滤波器，实现图像的平滑、锐化等操作。

在图像处理中，Cauchy核函数可以用于实现图像的模糊、锐化、边缘检测等操作。

在物理和工程领域，Cauchy核函数可以用于描述物体在无穷远处的行为，如热传导、弹性力学等问题。

cuda 循环调用核函数-回复如何在CUDA中循环调用核函数CUDA是一种并行计算平台和编程模型，通常用于利用GPU进行高性能计算。

在使用CUDA进行编程时，循环调用核函数（kernel function）是一种常见的需求。

本文将一步一步地回答"如何在CUDA中循环调用核函数"这个问题，帮助读者了解和掌握这一技术。

第一步：编写核函数在开始循环调用之前，我们首先需要编写一个可重复执行的核函数。

核函数通常被设计为只处理输入数据中的一个小部分，例如一个块（block）或一个线程（thread）。

要使核函数可循环调用，需要确保输入数据的一致性和循环的正确停止条件。

一个常见的做法是使用循环索引（loop index）来确定处理的数据范围，例如使用threadIdx.x + blockIdx.x * blockDim.x 来计算全局索引。

第二步：确定线程层次结构在CUDA中，线程被组织成一个线程块（block）和一个线程网格（grid）的结构。

线程块中的线程可以通过共享内存（shared memory）进行通信和协作。

要循环调用核函数，我们需要确定线程块的数量和大小，以及核函数在线程块中处理的数据范围。

线程块的数量可以通过计算网格的大小和线程块的大小得到。

第三步：定义循环次数和停止条件在CUDA中实现核函数的循环调用通常需要定义循环次数和停止条件。

循环次数可以在主机代码中定义为一个常量或变量，也可以在核函数的输入参数中传递。

停止条件可以是循环次数达到指定值，或者根据处理的数据是否满足某个特定条件来确定。

在核函数中，可以使用条件语句（如if语句）来检查停止条件，并在满足条件时终止循环。

第四步：使用CUDA API进行循环调用在CUDA中，循环调用核函数通常使用CUDA API的调用方式。

首先，我们需要使用cudaMalloc()函数分配设备内存，用于存储输入和输出数据。

然后，我们可以使用cudaMemcpy()函数将主机内存中的数据复制到设备内存中。