常见曲线物极坐标方程
- 格式:ppt
- 大小:370.00 KB
- 文档页数:22

高考数学知识点解析极坐标系中的曲线与方程高考数学知识点解析:极坐标系中的曲线与方程在高考数学中,极坐标系中的曲线与方程是一个重要的知识点,对于同学们理解数学中的图形和解决相关问题具有重要意义。
首先,让我们来了解一下什么是极坐标系。
极坐标系是一种不同于我们常见的直角坐标系的坐标系统。
在极坐标系中,一个点的位置由极径和极角来确定。
极径表示点到极点的距离,极角则表示极轴(通常是 x 轴正半轴)到线段极点与该点连线的夹角。
那么,极坐标系中的曲线方程又是怎么一回事呢?简单来说,它是用极坐标的形式来描述曲线的数学表达式。
常见的极坐标曲线方程有很多,比如圆的极坐标方程。
当圆心在极点,半径为 r 时,圆的极坐标方程为ρ = r 。
这意味着,对于这个圆上的任意一点,其极径ρ 的值都是固定的 r 。
我们可以通过这个简单的方程,很直观地看出圆的特性。
再来说说直线的极坐标方程。
例如,过极点且与极轴夹角为α 的直线,其极坐标方程为θ =α 。
这个方程表明,在这条直线上的所有点,其极角都是固定的α 。
接下来,我们看看如何将极坐标方程转化为直角坐标方程。
这是解决很多问题的关键步骤。
设极坐标系中的一点为(ρ,θ),对应的直角坐标系中的点为(x,y),则有 x =ρcosθ,y =ρsinθ。
通过这两个关系式,我们可以将极坐标方程转化为直角坐标方程。
例如,极坐标方程ρ =2cosθ,将ρ =√(x²+ y²),cosθ = x /√(x²+ y²) 代入,经过一系列的化简和整理,可以得到直角坐标方程 x²+ y²= 2x ,进一步变形为(x 1)²+ y²= 1 ,这就是一个以(1,0)为圆心,半径为 1 的圆。
在解题过程中,我们常常需要根据具体问题的条件,选择使用极坐标系还是直角坐标系。
比如,当题目中涉及到一些与角度、距离有关的条件,或者图形具有明显的对称性时,使用极坐标系可能会更加简便。

极坐标常用方程极坐标是一种二维坐标系统,与我们常见的直角坐标系有所不同。
在极坐标系统中,一个点的位置由它的极径和极角确定,而不是由它的x坐标和y坐标确定。
极坐标常用方程是一种描述极坐标系中曲线的数学表达式,本文将介绍一些常见的极坐标常用方程。
矩形方程与极坐标方程转换要将直角坐标系中的一个方程转换为极坐标系中的方程,需要使用以下公式:•x = r * cos(θ)•y = r * sin(θ)其中,(x, y)是直角坐标系中的点,(r, θ)是极坐标系中的点。
举例来说,我们有一个方程 x^2 + y^2 = 4,要将它转换为极坐标系中的方程。
首先,我们可以使用换元法将直角坐标系中的x和y表示为极坐标系中的r和θ:* x = r * cos(θ) * y = r * sin(θ)将上述方程代入原方程,得到:* r^2 * cos^2(θ) + r^2 * sin^2(θ) = 4再进行化简,可以得到:* r^2 * (cos^2(θ) + sin^2(θ)) = 4 * r^2 = 4因此,极坐标系中的方程为 r = 2。
这个方程描述了以极径为2的圆。
常见的极坐标常用方程1.极坐标方程 r = a这是一个描述以极径为常数a的圆的方程。
圆心位于原点,半径为a。
2.极坐标方程r = a * cos(θ)这是一个描述以极径可变的半径为a * cos(θ)的螺线的方程。
3.极坐标方程r = a * sin(θ)这是一个描述以极径可变的半径为a * sin(θ)的螺线的方程。
4.极坐标方程r = a / cos(θ)这是一个描述以极径可变的半径为a / cos(θ)的双曲线的方程。
5.极坐标方程r = a / sin(θ)这是一个描述以极径可变的半径为a / sin(θ)的双曲线的方程。
6.极坐标方程r = a * e^(bθ)这是一个描述以极径可变的曲线的方程,其中a和b是常数,e是自然对数的底。
这个方程可以描述出多种不同的曲线,如指数增长曲线。

极坐标参数方程公式大全极坐标是一种描述平面上点的坐标系,它以原点为中心,以极径和极角两个参数来确定点在平面上的位置。
极坐标参数方程是用极坐标来表示的函数方程,它可以描述一条曲线在极坐标系下的形状。
下面是一些常见的极坐标参数方程公式。
1. 圆的极坐标参数方程圆是一种特殊的曲线,它的每个点到原点的距离都相等。
圆的极坐标参数方程可以表示为:r=a其中,a表示圆的半径。
2. 阿基米德螺线的极坐标参数方程阿基米德螺线是一种由数学家阿基米德创建的曲线,其极坐标参数方程可以表示为:$r=a+b\\theta$其中,a表示螺线的起始半径,b表示每转一圈半径增加的量,$\\theta$表示极角。
3. 双纽线的极坐标参数方程双纽线是一种具有两个回环的曲线,其极坐标参数方程可以表示为:$r^2=a^2\\cos(2\\theta)$其中,a表示双纽线的参数。
4. 渐开线的极坐标参数方程渐开线是一种非常具有特点的曲线,其极坐标参数方程可以表示为:$r=a\\theta$其中,a表示渐开线的参数。
5. 摆线的极坐标参数方程摆线是一种由在铅笔一端水平移动而形成的曲线,其极坐标参数方程可以表示为:$r=a(\\theta-\\sin\\theta)$其中,a表示摆线的参数。
6. 旋轮线的极坐标参数方程旋轮线是一种由相对运动的两个圆形组成的曲线,其极坐标参数方程可以表示为:$x=(r_1-r_2)\\cos\\theta+r_2\\cos(\\frac{r_1-r_2}{r_2}\\theta)$$y=(r_1-r_2)\\sin\\theta-r_2\\sin(\\frac{r_1-r_2}{r_2}\\theta)$其中,r1和r2分别表示两个圆的半径。
以上是一些常见的极坐标参数方程公式。
通过使用这些参数方程,我们可以在极坐标系下描述和绘制出各种曲线的形状。
极坐标系在数学、物理、工程等领域中有广泛的应用,对于研究曲线和解决问题非常有帮助。

极坐标方程表达式极坐标方程是描述平面上点的位置的一种常用表达方式。
它利用距离和角度来表示点的坐标,相比直角坐标系更适合描述圆的形状和对称性。
本文将介绍极坐标方程的表达式形式以及如何将其转换为直角坐标系。
同时,还将介绍极坐标方程在数学和物理中的应用。
极坐标方程表达式的一般形式为:$r = f(\\theta)$其中,r表示点到原点的距离,$\\theta$表示点与正 x 轴之间的角度,f是一个关于$\\theta$的函数。
极坐标方程的形式可以有很多种,取决于具体问题的性质。
以下是一些常见的极坐标方程的表达式。
1. 极坐标方程表示直线:$r = a\\sec(\\theta - \\alpha)$其中,a是一定的常数,$\\alpha$是直线与极轴之间的夹角。
2. 极坐标方程表示圆:$r = a$其中,a是圆的半径。
3. 极坐标方程表示椭圆:$r = \\frac{a(1 - e^2)}{1 - e\\cos(\\theta - \\alpha)}$其中,a是椭圆的长半轴,e是离心率,$\\alpha$是椭圆与极轴之间的夹角。
4. 极坐标方程表示双曲线:$r = \\frac{a(1 + e^2)}{1 + e\\cos(\\theta - \\alpha)}$其中,a是双曲线的长半轴,e是离心率,$\\alpha$是双曲线与极轴之间的夹角。
利用以上表达式,可以方便地描述出各种形状的曲线。
将极坐标方程转换为直角坐标系的表达式需要利用以下关系式:$x = r\\cos(\\theta)$$y = r\\sin(\\theta)$通过上述关系式,可以将极坐标方程中的$r$与$\\theta$表达式用$x$和$y$来表示,从而得到在直角坐标系中曲线的方程。
极坐标方程在数学和物理中有广泛的应用。
在数学中,它可以用来描述曲线和曲面的形状及其性质。
例如,极坐标方程可用于描述螺旋线、心形线等特殊曲线。
在物理中,极坐标方程可用于描述圆周运动、波动等循环性质的物理现象。

几种常见的极坐标方程好嘞,今天咱们聊聊极坐标方程,听起来有点高深,实际上跟咱们日常生活没啥区别,简简单单说白了就是用一个点的位置来描述事物。
这就像咱们出去约会,找人只需要说“我在咖啡馆”,而不是说“我在某个地方的某个角度上”。
极坐标就是这样,给了我们一个非常直接的方式来定位。
得提提极坐标系。
咱们想象一下,画一个平面,在中心点放个大圆圈,圆圈的中心就是原点,咱们常说的“坐标轴”。
从这个中心点出发,咱们可以用距离和角度来描述任何一个点。
距离就像咱们走到咖啡馆需要的路程,角度就像咱们转头去找人的方向。
说到这,真是让人想起小时候的游戏,东南西北一转,走到目标就是乐趣无穷。
接下来聊聊简单的极坐标方程,比如说,最基础的“圆”的方程。
这个方程特别简单,形如 ( r = a )。
这啥意思呢?就是不管你转到哪个角度,离原点的距离都是恒定的,a就是那个距离。
这就好比你和好朋友约好了,每次见面都在同样的咖啡馆,无论你们怎么转,始终在那个地方见面,真是让人感到温暖。
想象一下,那种“我在这儿,你在那儿”的默契,真是特别赞。
再说说“螺旋线”的方程,形如 ( r = a + btheta )。
这玩意儿可有意思了,随着你转动,离中心的距离也在变化。
就像是走在一条旋转的楼梯上,越走越远。
这就让我想起了小时候爬山的情景,一步一步往上走,虽然有点累,但越爬越高,心情也越愉快。
这种感觉,就像是追逐梦想,慢慢攀升,虽然有时会觉得累,但看着美丽的风景,心里就觉得特别值得。
然后就是“玫瑰线”的方程,这个就更加浪漫了,形如 ( r = a cos(ktheta) ) 或者 ( r = a sin(ktheta) )。
如果k是偶数,那就是两边各开一朵花;如果是奇数,那一朵花就会非常炫酷地绽放。
这就像爱情一样,有时候开得热烈,有时候平静如水。
生活中的每一个时刻都有它的色彩,犹如一朵盛开的玫瑰,既美丽又让人沉醉。
还有那“心形线”的方程,形如 ( r = a(1 sin(theta)) )。

极坐标方程公式大全极坐标是一种由半径和角度两个参数来描述点的坐标系统。
极坐标系常用于描述圆形、螺线等曲线,对于研究具有旋转对称性的问题非常有用。
在数学和物理学中,极坐标方程提供了描述极坐标系中各种曲线和图形的公式。
本文将介绍一些常见的极坐标方程公式。
圆的极坐标方程圆可以用极坐标方程表示为:r=a其中,a是圆的半径。
该公式表示了以原点为中心的圆,半径为a。
简单螺线的极坐标方程螺线是在极坐标系中以常数速率展开的曲线。
最常见的螺线是阿基米德螺线,其极坐标方程可以表示为:$r = a + b \\theta$其中,a和b是常数,$\\theta$ 是极角。
该公式描述了螺线的形状,a表示了螺线的起始半径,b表示了螺线的展开速率。
雪花曲线的极坐标方程雪花曲线是一种具有对称性的曲线,它由多个相互重叠的圆组成。
它的极坐标方程可以表示为:$r = a \\cdot \\sin(n \\theta)$其中,a和n是常数,$\\theta$ 是极角。
该公式描述了雪花曲线的形状,a控制着雪花曲线的大小,n控制着雪花曲线的复杂程度。
心形线的极坐标方程心形线是以两个相互重叠的圆为基础构成的曲线。
它的极坐标方程可以表示为:$r = a(1 - \\sin \\theta)$其中,a是常数,$\\theta$ 是极角。
该公式描述了心形线的形状,a控制着心形线的大小。
摆线的极坐标方程摆线是由一个悬挂的线上的一点在重力作用下运动形成的曲线。
摆线的极坐标方程可以表示为:$r = a - b \\cdot \\cos \\theta$其中,a和b是常数,$\\theta$ 是极角。
该公式描述了摆线的形状,a控制摆线的振幅,b控制摆线的周期。
总结极坐标方程提供了描述极坐标系中各种曲线和图形的公式。
本文介绍了圆、螺线、雪花曲线、心形线和摆线的极坐标方程。
每个公式都可以通过调整常数参数来控制图形的形状和大小。
极坐标方程的使用可以简化对特定曲线和图形的描述和分析,为研究具有旋转对称性的问题提供了便利。

1附录1 曲线的极坐标方程一. 极坐标我们知道,单元实函数()y f x =(x ∈()f D )的图形一般是平面上的一条曲线(段)L , 而()y f x =(x ∈()f D )就是L 的方程. 由给定曲线建立其方程是平面解析几何的基本任务之一,也是本课程所必须的. 但是,在直角坐标系中,对于许多曲线来说,要建立其方程是比较困难的,即使是常用曲线(如等速螺线)也是这样. 然而在极坐标系中,有些问题可以迎刃而解.极坐标也是人们确定平面上点的位置的常用方法. 例如,炮兵射击时,以大炮为基点,利用目标的方位角及目标到大炮的距离来确定目标的位置的. 在航海中也经常使用类似的方法.下面给出利用角和距离建立的坐标系——极坐标系.在平面内取定一点O ,称之为极点,引一条射线Ox ,称之为极轴. 再选定单位长度和角的正向(通常取逆时针方向)(见图F-1).图 F —1对于平面内任意一点M ,用ρ表示M 到O 的距离,即线段OM 的长度,θ表示从Ox 到OM 的角度. 其中ρ称为点M 的极径,θ称为点M 的极角,当M 为极点O 时,其极径0ρ=,其极角可取任意值. 于是平面上的任意一点就用一对有序实数表示出来了,有序对实数(, )ρθ称为点M 的极坐标.反过来,给定一对有序实数,ρθ(假定0ρ≥),以极点为顶点、极轴为始边作大小等于θ的角,在其终边上截取长为ρ的线段OM ,则M 是平面上极坐标为(, )ρθ的唯一的点.2极坐标为(, )ρθ的点M 也可表示为(,)M ρθ. 这样建立起来的坐标系称为极坐标系.例1 在极坐标系中画出下列各点:.()()()()()π5π4π5π2π1,,(2,0), 1.5,,3,,2,,3,.46333A B C D E F −解图 F —2注意:()()4π2π3,3,33D F −与是同一点.上例表明,平面上点的极坐标不是唯一的. 事实上,一个点的极坐标有无穷多,因为始边为Ox 、终边为OM 的角有无穷多个. 例如,()()()πππ2,,2,2π,2,2π444+−,以及()π2,2π()4k k +∀∈Z 等,都是同一点A 的极坐标.不仅如此, 在某些情况下,允许ρ取负值,是方便的. 当0ρ<时,点.(, )M ρθ可按下列规则确定:作射线OP ,在OP 的反向延长线上取一点M ,使得OM ρ=,则点M 就是极坐标为(, )ρθ的点(见图F —3 ).例如,上例中的点()π2,4A 也可以表示为()π2,(21)π()4M k k −++∀∈Z .3图F —3如果限定0, 02πρθ≥≤<(或πθπ−<≤),则除极点外,平面上的点与其极坐标就是一一对应的了.二. 曲线的极坐标方程在极坐标系中,曲线L 可以用含有极坐标ρ和θ这两个变量的方程(,)0F ρθ=来表示. 这种方程叫做曲线L 的极坐标方程. 此时,以这个方程的每一组解为坐标的点都在曲线L 上,然而曲线L 上每个点的极坐标有无穷多个,故可能不全满足这个方程,但其中至少有一个坐标能满足这个方程. 这一点是曲线的极坐标方程与直角坐标方程的不同之处.求曲线的极坐标方程的方法与步骤,同直角坐标方程类似,即视曲线为满足某种条件的点的集合(或动点的轨迹),将已知条件用曲线上点的即坐标ρ和θ的关系式表示出来,就得到曲线的极坐标方程.例2 (1)求从极点出发、倾角为π4的射线的极坐标方程;(2)求过极点且倾角为π4解 (1)设(,)M ρθ(图F —4),由条件得π4θ= (0ρ≥).图F —4这就是所求射线的方程,因为对于任意0ρ≥,坐标为()π,4ρ的点均在此射线上,另一方面,在此射线上的每一点都可用坐标()π,4ρ(0ρ∀≥)来4表示,故其至少有一个坐标满足方程π4θ= (0ρ≥).(2)易知所求直线的极坐标方程为π4θ= (ρ∀∈R )(见图F —4 ).图F —5例 3 求中心在极点、半径为 (0)a a >的圆的极坐标方程.解 设(,)M ρθ为圆上动点,由轨迹条件OM a =,得所求圆的方程为a ρ= (θ∀∈R ).如果限制02πθ≤<,则此圆上的点的极坐标与方程a ρ=(02πθ≤<)的解是一一对应的.图F —65例4 求圆心在点(,0) (0)a a >其中、半径为a 的圆的极坐标方程. 解 由条件知,圆心在极轴上,且圆经过极点O . 设圆与极轴的另一交点为A (见图F —7),则2OA a =.设(,)M ρθ是圆上任意一点,则OM MA ⊥,于是有 cos OM OA θ=. 所以此圆的极坐标方程为2cos a ρθ= (ππ22θ−≤≤).图F —6 例5 阿基米德螺线由极坐标方程a ρθ= (0a >为常数)确定的曲线,通常称为阿基米德螺线(或等速螺线).请画出基米德螺线. 解 在极坐标系中作图的方法和步骤,同直角坐标系中是一样的. 给出θ的一系列允许值,通过()ρρθ=算出ρ的对应值(可列成表格),再根据得到的有序数对在极坐标系中描出相应的点,然后依次将这些点连成平滑的曲线,便得到()ρρθ=的图形.对于a ρθ=(0a >为常数)有:O6图F —7如果允许ρ取负值,则当,ρθ是方程a ρθ=的解时,,ρθ−−也是a ρθ=的解. 因为在极坐标系中,点(,)ρθ−−与点(,)ρθ关于过极点且垂直于极轴的直线对称,故a ρθ=的图形也关于该直线对称. 同济P360(10)图中的实线表示,ρθ取正值时的螺线部分,而虚线表示,ρθ取负值时的螺线部分.阿基米德螺线可以看作按以下条件运动的动点M 的轨迹:以点O 为端点的射线l ,绕点O 作等角速度的转动,而l 上的点M 从O 出发沿l 作等速直线运动. 因此,阿基米德螺线也叫做等速螺线或等进螺线. 在机械传动的凸轮装置中,将绕定轴旋转的凸轮的轮廓设计为阿基米德螺线,以使从动杆作等速直线运动.例6 心脏线用同样的方法,可画出由极坐标方程(1cos )a ρθ=+ (0a >为常数)确定的曲线(见图F —8),称为心脏线 (或心形线),它是外摆线的一种.更多曲线的极坐标方程请见同济附录II7三. 直角坐标与极坐标的转换关系为了研究的方便,有时需将要曲线在一种坐标系下方程转化为另一种坐标系下的方程. 如图F —9所示,把直角坐标系 的原点为极点,Ox 轴的正半轴作为极 轴,并在两种坐标系中取相同的单位 长度.设M 为平面上任意一点,其直角 坐标为(,)x y ,极坐标为(,)ρθ. 则有“极—直”关系转换式:cos sin (0)x y ρθρθρ⎧≥⎨⎩==. 图F —9 由此也有关系转换式:,tan (0)yx x ρθ⎧=⎪⎨=≠⎪⎩在一般情况下,由tan θ确定θ时,可根据点M 所在的象限取最小正角. 例7 (1) 将点M 的极坐标()π5,6化为直角坐标; (2)将点P 的直角坐标()1−化为极坐标.解 (1)x = π55sin ,62y ==即点M 的直角坐标为)52.(2)2, tan ρθ====因为点P 在第三象限,而20,ρ=> 故最小正角为7π6θ=. 因此,P 的极坐标为()7π2,6.例8 化圆的直角坐标方程2220(0)x y ay a +−=>为极坐标方程.8解 将cos (0)sin x y ρθρρθ=⎧≥⎨=⎩2222cos sin 2sin a ρθρθρθ+−即 2sin a ρθ=(0θπ≤≤).图F —10*例9 广义极坐标变换co s n s i x a y b ρθρθ=⎧⎨=⎩将椭圆22221y x a b+=变换成极坐标系中的单位圆 1 (02π)ρθ=≤≤.习题F-11. 极坐标方程22cos 2 (0)a a ρθ=>的图形称为双纽线. 请描绘出双纽线.2. 指出下列极坐标方程表示什么曲线,并画图:(1)3ρ=; (2)π ()3θρ=−∞<<+∞;(3)cos 2ρθ=; (4)10sin ρθ=; (5)10(1cos )ρθ=+.。

极坐标方程公式大全1.点到原点的距离:r2.与正半轴的夹角:θ3.线段:r=ar=a表示距离原点为a的一个圆,其中a是一个常数。
如果a>0,圆心在极坐标系的原点;如果a<0,圆心在原点的反向。
4. 线段:r = a(1±sinθ)r = a(1±sinθ)表示一个心脏形状曲线,其中a是一个常数。
当a>0时,曲线是两半心脏形状;当a<0时,曲线是两半相反的心脏形状。
5. 线段:r = 1/a(1±cosθ)r = 1/a(1±cosθ)表示一个准一次曲线,其中a是一个常数。
当a>0时,曲线有两个极大值和一个极小值;当a<0时,曲线有一个极大值和两个极小值。
6. 线段:r = a±bcosθr = a±bcosθ表示一个椭圆形状曲线,其中a和b是常数。
当a=0时,曲线是一个标准椭圆;当a≠0时,曲线是一个偏心椭圆。
7. 线段:r = a±bsinθr = a±bsinθ表示一个双曲线形状曲线,其中a和b是常数。
当a>0时,曲线有两个分支;当a<0时,曲线只有一条分支。
8. 曲线:r = a(1-sinθ)r = a(1-sinθ)表示一个钟形曲线,其中a是一个常数。
9. 曲线:r = a(1+sinθ)r = a(1+sinθ)表示一个叶形曲线,其中a是一个常数。
10. 曲线:r = asin(nθ)r = asin(nθ)表示一个以原点为中心,顶点在极轴上,具有n个叶片的曲线,其中a和n是常数。
以上是一些常见的极坐标方程公式示例,用于描述平面上的点的坐标。
这些方程能够帮助我们更完整地了解点的位置和形状。
不同的极坐标方程可以描述出各种各样的曲线形状,从简单的圆形到复杂的心脏形状和叶形曲线,极坐标方程为我们提供了更灵活的表示平面上点的方式。

极坐标系下的曲线方程极坐标系是一种以极点为中心,以极轴为基准,描述平面上点位置的坐标系。
在极坐标系中,点的位置由两个参数r 和θ 描述,其中 r 表示点到极点的距离,θ 表示点与极轴的夹角。
极坐标系常用于描述环形物体、旋转对称图形等。
在极坐标系中,曲线的方程可以用极坐标参数 r 和θ 表示。
下面介绍几种常见的曲线方程。
1. 极轴和极点如果一个点的 r 坐标为 0,则该点位于极轴上;如果一个点的θ 坐标为 0,则该点位于极点上。
因此,极轴和极点可以用下面的方程表示:极轴:θ = k (k 为常数)极点:r = 02. 圆的方程在直角坐标系中,圆的方程为 (x-a)² + (y-b)² = r²,其中 (a,b) 表示圆心坐标,r 表示半径。
在极坐标系中,圆的方程可以表示为:r = a cos(θ) + b sin(θ)其中 (a,b) 表示圆心坐标,r 表示半径。
这个方程的具体形式可以通过将圆心坐标和半径代入得到。
例如,以圆心为 (2,3),半径为 4 的圆的方程为:r = 2 cos(θ) + 3 sin(θ) + 43. 椭圆的方程在直角坐标系中,椭圆的方程为 (x-a)²/a² + (y-b)²/b² = 1,其中(a,b) 表示椭圆中心坐标,a 和 b 分别表示横向半轴长度和纵向半轴长度。
在极坐标系中,椭圆的方程可以表示为:r = (a b) / √((b cos(θ))² + (a sin(θ))²)其中 (a,b) 表示椭圆中心坐标。
这个方程的具体形式可以通过将椭圆中心坐标代入得到。
例如,以中心为 (2,3),横向半轴长度为4,纵向半轴长度为 3 的椭圆的方程为:r = (12) / √(9 cos²(θ) + 16 sin²(θ))4. 双曲线的方程在直角坐标系中,双曲线的方程为 (x-a)²/a² - (y-b)²/b² = 1,其中(a,b) 表示双曲线中心坐标,a 和 b 分别表示横向半轴长度和纵向半轴长度。

千里之行,始于足下。
极坐标和参数方程知识点总结极坐标是一种表示平面上点位置的坐标系统,它是由点到原点的距离(称为极径)和点与极轴的夹角(称为极角)所确定的。
在极坐标系中,每个点的坐标可以表示为(r,θ)的形式,其中r为极径,θ为极角。
参数方程是一种用一对参数变量来表示曲线上的点的坐标的方法。
对于平面上的曲线,常用的参数方程形式为x=f(t)和y=g(t),其中t为参数变量,f(t)和g(t)分别表示x和y的函数关系。
以下是极坐标和参数方程的一些重要知识点总结:1. 极坐标的转换关系:- 直角坐标到极坐标的转换:x=r*cos(θ),y=r*sin(θ)- 极坐标到直角坐标的转换:r=sqrt(x^2+y^2),θ=tan^(-1)(y/x)2. 常见曲线的极坐标方程:- 直线:θ=常数- 圆:r=常数- 椭圆:r=a*b/sqrt(b^2*cos^2(θ)+a^2*sin^2(θ))3. 参数方程的表示方式:- 曲线方程:(x,y)=(f(t),g(t))- 曲线长度的计算公式:L=∫sqrt((dx/dt)^2+(dy/dt)^2)dt4. 参数方程的性质:- 曲线方向:随着参数变量的增大,曲线的运动方向- 曲线对称性:参数方程对称性特点取决于函数f(t)和g(t)的对称性第1页/共2页锲而不舍,金石可镂。
- 曲线切线方向:曲线上某点的切线方向由参数方程的导数决定5. 参数方程与极坐标之间的关系:- 参数方程可以转换为极坐标方程,极径r=f(t),极角θ=g(t)- 极坐标方程可以转换为参数方程,x=f(θ)*cos(θ),y=f(θ)*sin(θ)需要注意的是,极坐标和参数方程在一些问题中可以更方便地描述曲线的特性,而在其他问题中直角坐标系可能更适用。
因此,在应用中需要根据具体问题选择合适的坐标系表示。
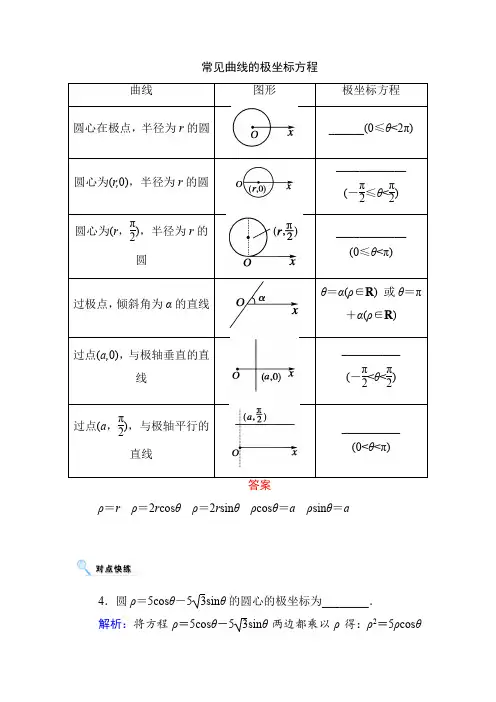
常见曲线的极坐标方程
答案
ρ=rρ=2r cosθρ=2r sinθρcosθ=aρsinθ=a
4.圆ρ=5cosθ-53sinθ的圆心的极坐标为________.
解析:将方程ρ=5cosθ-53sinθ两边都乘以ρ得:ρ2=5ρcosθ
-53ρsin θ,化成直角坐标方程为x 2+y 2-5x +53y =0.圆心的坐标
为⎝ ⎛⎭⎪⎫
52
,-532,化成极坐标为⎝ ⎛⎭⎪⎫5,5π3. 答案:⎝ ⎛
⎭
⎪⎫5,5π3(答案不唯一)
5.在极坐标系中,过点(1,0)并且与极轴垂直的直线方程是________,过(0,-1)与极轴平行的直线方程是________.
解析:过点(1,0)且与极轴垂直的直线,在直角坐标系中的方程为x =1,所以其极坐标方程为ρcos θ=1.过(0,-1)且与极轴平行的直线,在直角坐标系中是y =-1,所以其极坐标方程为ρsin θ=-1.
答案:ρcos θ=1 ρsin θ=-1
6.在极坐标系中,圆心在(2,π)且过极点的圆的方程是________. 解析:如图,O 为极点,OB 为直径,A (ρ,θ),则∠ABO =θ-90°,OB =22=ρ
sin (θ-90°)
,化简得ρ=-22cos θ.
答案:ρ=-22cos θ。
抛物线的极坐标方程表达式抛物线是数学中的一种曲线形状,常见于物理学和工程领域的问题中。
在笛卡尔坐标系中,抛物线的方程通常被表示为y=ax2+bx+c,其中a、b、c是常数。
然而,我们也可以使用极坐标系下的方程来表达抛物线。
极坐标系简介极坐标系是一种二维坐标系,它使用距离和角度来描述一个点的位置。
在极坐标系中,一个点的位置由极径(r)和极角($\\theta$)确定。
极径是点到原点的距离,可以是正数或零。
极角是点与正极轴(通常取为x轴正方向)的夹角,通常以弧度表示,范围是从0到 $2\\pi$。
极角为0表示正极轴的正方向,逆时针方向角度增加。
抛物线在极坐标系中的表示接下来我们将介绍如何用极坐标方程表示抛物线。
考虑一个抛物线的极坐标方程为 $r=f(\\theta)$。
在极坐标系中,抛物线的形状由函数 $f(\\theta)$ 决定。
为了得到具体的极坐标方程,我们将使用一种常见的方式,即将笛卡尔坐标系下的抛物线方程转化为极坐标系下的方程。
假设笛卡尔坐标系下的抛物线方程为y=ax2+bx+c。
首先,我们将笛卡尔坐标系中的点(x,y)转换为极坐标系中的点 $(r, \\theta)$:$r=\\sqrt{x^2+y^2}$$\\theta=\\arctan{\\frac{y}{x}}$接下来,我们将笛卡尔坐标系下的x和y代入极坐标系的转换公式中,得到:$r=\\sqrt{x^2+(ax^2+bx+c)^2}$$\\theta=\\arctan{\\frac{ax^2+bx+c}{x}}$经过整理和简化,我们可以得到抛物线在极坐标系中的方程表达式:$r=\\frac{1}{\\sqrt{1+a^2}}\\cdot\\frac{1}{4a}\\cdot\\frac{1}{\\sin^2{(\\fr ac{\\theta}{2})}}$这个极坐标方程描述了抛物线在极坐标系中的形状。
抛物线的性质抛物线在极坐标系中有一些特殊的性质。
极坐标方程所有公式一、极坐标系简介极坐标系是一种常用的二维坐标系统,通过角度和半径参数来描述平面上的点。
在极坐标系中,每个点可以用一个有序对(r, θ)表示,其中 r 代表点到坐标原点的距离(称为极径),θ 表示该点与指定方向的连线(通常为正 x 轴)之间的夹角(称为极角)。
可以将极坐标系与直角坐标系相互转换,极坐标系的公式可以用于描述很多几何和物理问题。
二、极坐标方程表达形式极坐标方程可以通过不同的表达形式来描述。
下面是常见的几种极坐标方程形式:1. 极径与极角的显式函数:以极径 r 和极角θ 作为变量,表示为r = f(θ)。
这种形式下,极径 r 是极角θ 的函数。
常见的例子有圆形方程 r = a(a 为常数)和椭圆方程 r = a(1 - e·cosθ)(a 和e 为常数)。
2. 极径与极角的参数方程:将极角θ 表示为 t 的函数,极径 r 表示为 t 的函数,表示为 r = f(t),θ = g(t)。
通常通过引入一个或多个参数 t 来描述曲线。
常见的例子有直线参数方程 r = a + bt (a 和 b 为常数),和螺旋线参数方程 r = at,θ = b t(a 和 b 为常数)。
3. 函数关系:将极径 r 和极角θ 表示为函数之间的关系,即F(r, θ) = 0。
这种形式下,极坐标方程可以看作是一个隐式方程。
常见的例子有椭圆方程 r^2 = a2·sin2(θ) + b2·cos2(θ)(a 和 b 为常数)和心形线方程r = a(1 + cosθ)(a 为常数)。
三、主要极坐标方程公式1. 圆的极坐标方程圆的极坐标方程为 r = a,其中 a 为常数。
这表示了以坐标原点为中心,半径为a 的圆。
2. 椭圆的极坐标方程椭圆的极坐标方程为 r = a(1 - e·cosθ),其中 a 和 e 为常数,a 表示椭圆的主轴长度,e 表示离心率。
当 e = 0 时,椭圆退化为圆。
极坐标方程必背公式在数学中,极坐标方程是描绘平面上点位置的一种方式。
与笛卡尔坐标系不同,极坐标使用极径和极角来表示点的位置,极径表示点到原点的距离,极角表示点与正半轴的夹角。
在学习和应用极坐标方程时,有一些必背的公式是十分重要的。
极坐标与直角坐标的转换公式直角坐标到极坐标的转换公式:极径 $r = \\sqrt{x^2 + y^2}$极角 $\\theta = \\arctan{\\frac{y}{x}}$极坐标到直角坐标的转换公式:$x = r \\cos{\\theta}$$y = r \\sin{\\theta}$这些公式允许我们在直角坐标系和极坐标系之间转换点的位置。
通过使用这些公式,我们可以将直角坐标系中的点转换为极坐标系表示,并将极坐标系中的点转换为直角坐标系表示。
这对于解决涉及圆的问题或极坐标方程的问题非常有用。
极坐标方程的标准形式极坐标方程的标准形式:$r = f(\\theta)$这里,r是极径,$\\theta$是极角,$f(\\theta)$是一个函数,表示极径与极角之间的关系。
极坐标方程的标准形式提供了一种描述点在极坐标系统中的位置的方法。
通过选择不同的函数$f(\\theta)$,我们可以得到不同形状的曲线。
下面介绍几种常见的极坐标方程的标准形式及其对应的曲线形状。
•极坐标方程:r=a这是一个简单的极坐标方程,表示半径为常数a的一个圆。
圆心位于极点。
•极坐标方程:$r = a \\cos{\\theta}$这是一个以极点为中心的半径为a的圆形。
它具有轴对称性,并且在极坐标系中形成一个闭合的环。
•极坐标方程:$r = a \\sin{\\theta}$这是一个以极点为中心的半径为a的圆形。
它具有轴对称性,并且在极坐标系中形成一个闭合的环。
•极坐标方程:$r = a \\theta$这是一个以极点为中心,半径按照极角$\\theta$线性增加的螺旋曲线。
它通常被称为阿基米德螺旋线。
高等数学18种曲线以下是高等数学中18种曲线的详细介绍:1.星形线:星形线是一种特殊的曲线,其极坐标方程为ρ=sinθ,直角坐标方程为x2+y2−x=0。
星形线是围绕原点对称的,并且在直角坐标系中呈现出类似于星形的形状。
2.心形线:心形线也是一种特殊的曲线,其极坐标方程为ρ=1+cosθ,直角坐标方程为x2+y2−2x=0。
心形线也是围绕原点对称的,并且在直角坐标系中呈现出类似于心形的形状。
3.摆线:摆线是一种在圆上运动的质点在直线上的轨迹曲线。
其极坐标方程为ρ=a+bθ,直角坐标方程为x=a(1−cos t)和y=b(1+sin t)。
摆线有许多有趣的性质,例如它的长度和圆的半径相等。
4.对数螺线:对数螺线是一种以原点为中心,向四周无限延伸的曲线。
其极坐标方程为ρ=eθ,直角坐标方程为x=et cos t和y=et sin t。
对数螺线的形状类似于螺壳,并且它的曲率随着半径的增长而逐渐减小。
5.双曲螺线:双曲螺线是一种在双曲线上运动的点在直线上的轨迹曲线。
其极坐标方程为ρ=a2−b2sinθ,直角坐标方程为x=a cosh t cosθ和y=b sinh t sinθ。
双曲螺线的形状类似于螺线,但是它的曲率是负的。
6.阿基米德螺线:阿基米德螺线是一种在平面内无限延伸的曲线,其极坐标方程为ρ=aθ,直角坐标方程为x=a(1−os t)和y=a(1+sin t)。
阿基米德螺线的形状类似于螺线,并且它的曲率随着半径的增长而逐渐减小。
7.伯努利双纽线:伯努利双纽线是一种特殊的曲线,其极坐标方程为ρ=±2a sin2θ,直角坐标方程为(x2+y2)2=4a2y2。
伯努利双纽线的形状类似于两个交叉的圆环,并且在不同的参数条件下表现出不同的性质。
8.三叶玫瑰线:三叶玫瑰线是一种具有三个叶子的特殊曲线,其极坐标方程为ρ=3a cosθ,直角坐标方程为x=3a cos3t和y=3a sin3t。
三叶玫瑰线的形状类似于三片叶子连接在一起,并且它的曲率随着半径的变化而变化。