下载文档原格式
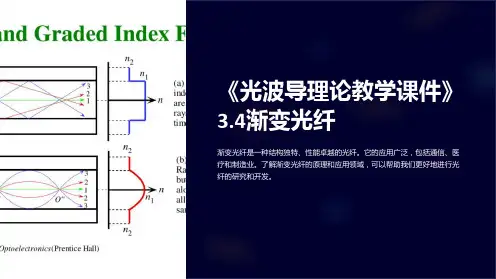
多模渐变型折射率光纤多模渐变型折射率光纤是一种新型的光纤通信技术，它采用局部折射率结构改变来提高光纤的传输性能和抗噪声能力。
该技术可以提供很大的优势，使得传输距离更远，速度更快，而且可以降低光纤的成本，而不需要考虑机箱安装等问题，同时还可以提高光纤的使用寿命和可靠性。
多模渐变型折射率光纤的原理多模渐变型折射率光纤采用局部折射率结构改变来提高光纤的传输性能和抗噪声能力，以满足长距离传输要求，其基本原理是局部折射率（lens）。
根据测定的折射率（refractive index）值的变化，可以制造出折射率逐渐变大或变小的光纤段，称为“折射率梯级”（refractive ladder）。
多模渐变型折射率光纤的折射率梯级以离散的形式串接，并在改变折射率梯级上实现多模传输，从而提高光纤传输性能和抗噪声能力。
多模渐变型折射率光纤的优点多模渐变型折射率光纤的优点在于它可以有效的改变光纤的折射率，改变传输距离，可以实现长距离传输。
同时，该技术的运行速度也得到改善，可以达到比传统折射率光纤更高的传输率。
此外，多模渐变型折射率光纤在环境敏感条件，如湿度、温度、电磁干扰等情况下，其传输特性仍然能够得到有效的改善，使得光纤的可靠性大大提高。
多模渐变型折射率光纤的应用多模渐变型折射率光纤的主要应用是在长距离通信领域，用于提高传输性能。
多模渐变型折射率光纤的出现，可以有效地改善传输距离，使长距离传输变得更加可行，另一方面，多模渐变型折射率光纤的出现也使得因特网的传输速度有了很大的提高。
此外，多模渐变型折射率光纤也广泛应用在宽带接入和网络服务等场合中。
结论多模渐变型折射率光纤是一种新型的光纤通信技术，可以有效的改变光纤的折射率，改变传输距离，实现长距离传输，也能够提高传输速度，提高光纤的使用寿命和可靠性，及抵抗环境的敏感性。
因此，多模渐变型折射率光纤受到广泛的关注，也被广泛的应用于长距离通信领域、宽带接入和网络服务等，具有非常重要的意义。
