固体物理化学 (第1章 气体)
- 格式:ppt
- 大小:295.00 KB
- 文档页数:24





物理化学主要公式第一章 气体的pVT 关系1.理想气体状态方程式nRT RT M m pV ==)/(或 RT n V p pV ==)/(m式中p ,V ,T 及n 单位分别为Pa ,m 3,K 及mol 。
m /V V n =称为气体的摩尔体积,其单位为m 3 · mol -1。
R =8.314510 J · mol -1 · K -1,称为摩尔气体常数。
此式适用于理想气体,近似地适用于低压的真实气体。
2.气体混合物 (1) 组成摩尔分数 y B (或x B ) = ∑AA B /n n体积分数 /y B m,B B *=V ϕ∑*AVy Am ,A式中∑AA n 为混合气体总的物质的量。
A m,*V 表示在一定T ,p 下纯气体A 的摩尔体积。
∑*AA m ,A V y 为在一定T ,p 下混合之前各纯组分体积的总和。
(2) 摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M式中 ∑=BB m m 为混合气体的总质量,∑=BB n n 为混合气体总的物质的量。
上述各式适用于任意的气体混合物。
(3)V V p p n n y ///B B B B *=== 式中p B 为气体B ,在混合的T ,V 条件下,单独存在时所产生的压力,称为B 的分压力。
*B V 为B 气体在混合气体的T ,p 下,单独存在时所占的体积。
3.道尔顿定律p B = y B p ,∑=BB p p上式适用于任意气体。
对于理想气体V RT n p /B B =4.阿马加分体积定律V RT n V /B B =*此式只适用于理想气体。
5.范德华方程RT b V V a p =-+))(/(m 2mnRT nb V V an p =-+))(/(22式中a 的单位为Pa · m 6 · mol -2,b 的单位为m 3 · mol -1,a 和b 皆为只与气体的种类有关的常数,称为范德华常数。

第一章气体的pVT性质1.1物质的体膨胀系数与等温压缩率的定义如下试推出理想气体的,与压力、温度的关系。
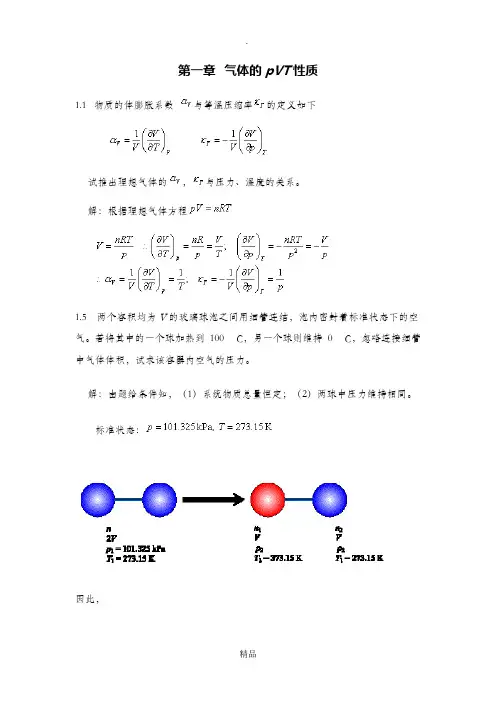
解:根据理想气体方程1.5两个容积均为V的玻璃球泡之间用细管连结,泡内密封着标准状态下的空气。
若将其中的一个球加热到100 C,另一个球则维持0 C,忽略连接细管中气体体积,试求该容器内空气的压力。
解:由题给条件知,(1)系统物质总量恒定;(2)两球中压力维持相同。
标准状态:因此,1.9 如图所示,一带隔板的容器内,两侧分别有同温同压的氢气与氮气,二者均可视为理想气体。
(1)保持容器内温度恒定时抽去隔板,且隔板本身的体积可忽略不计,试求两种气体混合后的压力。
(2)隔板抽取前后,H2及N2的摩尔体积是否相同?(3)隔板抽取后,混合气体中H2及N2的分压立之比以及它们的分体积各为若干?解:(1)等温混合后即在上述条件下混合,系统的压力认为。
(2)混合气体中某组分的摩尔体积怎样定义?(3)根据分体积的定义对于分压1.11 室温下一高压釜内有常压的空气,为进行实验时确保安全,采用同样温度的纯氮进行置换,步骤如下:向釜内通氮气直到4倍于空气的压力,尔后将釜内混合气体排出直至恢复常压。
重复三次。
求釜内最后排气至恢复常压时其中气体含氧的摩尔分数。
解:分析:每次通氮气后至排气恢复至常压p,混合气体的摩尔分数不变。
设第一次充氮气前,系统中氧的摩尔分数为,充氮气后,系统中氧的摩尔分数为,则,。
重复上面的过程,第n次充氮气后,系统的摩尔分数为,因此。
1.13 今有0 C,40.530 kPa的N2气体,分别用理想气体状态方程及van der Waals 方程计算其摩尔体积。
实验值为。
解:用理想气体状态方程计算用van der Waals计算,查表得知,对于N2气(附录七),用MatLab fzero函数求得该方程的解为也可以用直接迭代法,,取初值,迭代十次结果1.16 25 C时饱和了水蒸气的湿乙炔气体(即该混合气体中水蒸气分压力为同温度下水的饱和蒸气压)总压力为138.7 kPa,于恒定总压下冷却到10 C,使部分水蒸气凝结为水。

物理化学选择题复习题(优选.)第一章 气体pVT性质1.对于真实气体,当处于( )条件时,其行为与理想接近。
A.高温高压B.高温低压C.低温低压D.低温高压3.物质能以液态形式存在的最高温度是( )A.沸腾温度b TB.临界温度c TC.玻义尔温度B TD.凝固点温度f T4.对比温度是其所处的温度T 与( )比值。
A.玻义尔温度 B TB.临界温度 c TC. 沸腾温度b TD.273 K6.理想气体的微观模型是( )A.各种分子间的作用力相等,各种分子的体积大小相等B.所有分子都看作一个质点,它们具有相同的能量C.分子间无作用力,分子本身不占有体积D.处于临界温度以上的气体第一定律(第一组)1.热力学第一定律表达式为:U Q W ∆=+,其只适用于( )A.单纯的pVT 变化B.相变化C.化学变化D.封闭系统的任何变化2.( )组成的封闭系统的热力学能和焓仅仅是温度的函数。
A.理想溶液B.所有气体C.稀溶液D.理想气体3.公式,d d m p m H C T =的适用条件应该是( )A.等压过程B.恒外压过程C.无相变、无化学变化的恒压变温过程D.组成不变的均相系统的恒压过程4.公式,()V m U nC T ∆=∆适用条件应该是( )A.恒容过程B.等容过程C.无相变、无化学变化和'W =0且,V m C 为常数的恒容过程D.任何变化5.一定量的理想气体,从同一始态的压力1p 可逆膨胀到2p ,若将等温可逆膨胀后的体积与绝热可逆膨胀后的体积相比,则( )A.前者大于后者B.前者小于后者C.二者相等D.无法判断差别7.理想气体经绝热可逆膨胀,其压力与体积的关系为( )A.r pV =常熟B.11r pV nRT =C. 111r pV =D.无一定关系8.下面摩尔反应焓中,其中( )既为2H 的燃烧焓,又为2H O(l)生成焓。
A.2221H (g)+O (g)=H O(g)2B. 2222H (g)+O (g)=2H O(g)C.2221H (g)+O (g)=H O(l)2D. 2221H O(l)=H (g)+O (g)29.已知CO(g)和2H O(g)在298K 时标准摩尔生成焓分别为(CO,g)f m H θ∆=-111-1kJ mol ⋅和-242-1kJ mol ⋅,则反应22H O(g)+C(H (g)+CO(g)→石墨) 的摩尔反应焓为( )A.-353-1kJ mol ⋅B.-131-1kJ mol ⋅C.131-1kJ mol ⋅D.353-1kJ mol⋅ 第二组1.对于某一化学反应,若,r p m C ∆>0,则( )A.r m H ∆随T 升高而减小B. r m H ∆随T 升高而增大C. r m H ∆不随T 而变化D. r m H ∆随T 变化无规律2.某化合物的标准摩尔生成焓的定义是( )A.在298K 和100kPa 下由稳定单质生成1mol 化合物时焓变B.在温度T 和1atm 下由稳定单质生成1mol 化合物时焓变C.在1atm 下由单质生成1mol 化合物时的焓变D.在温度T 和各处于100kPa 下的纯的稳定单质生成1mol 处于100kPa 下和指定状态下的化合物时的焓变3.下列对于焓变的描述,正确的是( )A.系统的焓等于等压热B.系统的焓变等于过程的等压热C.系统的焓变等于系统的热D.系统的焓等于恒压和非体积功为零时过程的热4.热力学第一定律表达式为U Q W ∆=+,其只适用于( )A.敞开系统B.理想气体系统C.封闭系统D.孤立系统5.在一个恒容的绝热箱内有一绝热隔板,其两侧分别放有,,n T p 皆不相同的2N (g),若该气体可视为理想气体,则抽去隔板达到平衡,则混合过程的U ∆( ),W ( ),Q ( ),H ∆( )。


单选40道,多选10道,判断10道,填空20道。
单选:1.在任意T,P下,理想气体的压缩因子Z( )。
(A)>1(B)<1(C)=1(D)无一定变化规律答案:C2.在一定的T,P下,某真实气体的Vm,真实大于理想气体的Vm,理想,则该气体的压缩因子Z( )。
(A)>1(B)<1(C)=1(D)无法判断答案:A3.在以下临界点的描述中,哪条是错误的?( )(A)⎪⎭⎫⎝⎛∂∂VmpTc=0,⎪⎪⎭⎫⎝⎛∂∂2mVpTc=0(B)临界参数是pc、Vmc、Tc的统称(C)在pc、Vmc、Tc三个参数中,临界摩尔体积最容易测定(D)在临界点处,液体与气体的密度相同、摩尔体积相同答案:C4.CO2空钢瓶在工厂车间充气时(车间温度15°C)会发现,当充气压力表到达一定数值后就不再升高,而钢瓶的总重量却还在增加,其原因是( )。
(A)钢瓶容积增加(B)钢瓶中出现干冰(C)钢瓶中出现液态CO2(D)不知道答案:C5.在温度恒定为100℃、体积为2.0dm³的容器中含有0.035mol 的水蒸气H 2O(g)。
若向上述容器中再加入0.025mol 的液态水H 2O(l),则容器中的H 2O 必然是( )。
(A )液态(B )气态(C )气液两相平衡(D )无法确定其相态答案:B6.真实气体在( )的条件下,其行为与理想气体相近。
(A )高温高压(B )低温低压(C )低温高压(D )高温低压答案:D7.当真实气体的T 与其波义尔温度T B 为:T <T B 时,lim p→0[ð(pV m )ðp ]T( ); (A )>0(B )<0(C )=0(D )无法判断答案:B8.在温度恒定为25℃,体积恒定为25 dm 3的容器中,含有0.65 mol 的理想气体A , 0.35 mol 的理想气体B ;若向容器中再加人0.4 mol 的理想气体D , 则B 的分压力B p ( )。

第一章 理想气体1、理想气体:在任何温度、压力下都遵循P V=nRT 状态方程的气体。
2、分压力:混合气体中某一组分的压力。
在混合气体中,各种组分的气体分子分别占有相同的体积(即容器的总空间)和具有相同的温度。
混合气体的总压力是各种分子对器壁产生撞击的共同作用的结果。
每一种组分所产生的压力叫分压力,它可看作在该温度下各组分分子单独存在于容器中时所产生的压力B P 。
P y P B B =,其中∑=BBB B n n y 。
分压定律:∑=BB P P道尔顿定律:混合气体的总压力等于与混合气体温度、体积相同条件下各组分单独存在时所产生的压力的总和。
∑=BB V RT n P )/(3、压缩因子ZZ=)(/)(理实m m V V 4、范德华状态方程 RT b V V ap m m=-+))((2 nRT nb V Van p =-+))((225、临界状态(临界状态任何物质的表面张力都等于0)临界点C ——蒸气与液体两者合二为一,不可区分,气液界面消失; 临界参数:(1)临界温度c T ——气体能够液化的最高温度。
高于这个温度,无论如何加压 气体都不可能液化;(2)临界压力c p ——气体在临界温度下液化的最低压力; (3)临界体积c V ——临界温度和临界压力下的摩尔体积。
6、饱和蒸气压:一定条件下,能与液体平衡共存的它的蒸气的压力。
取决于状态,主要取决于温度,温度越高,饱和蒸气压越高。
7、沸点:蒸气压等于外压时的温度。
8、对应状态原理——处在相同对比状态的气体具有相似的物理性质。
对比参数:表示不同气体离开各自临界状态的倍数 (1)对比温度c r T T T /= (2)对比摩尔体积c r V V V /= (3)对比压力c r p p p /= 9、rr r c r r r c c c T Vp Z T V p RT V p Z =⋅=10、压缩因子图:先查出临界参数,再求出对比参数r T 和r p ,从图中找出对应的Z 。
物理化学主要公式及使用条件(上册)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN物理化学主要公式及使用条件第一章 气体的pVT 关系 主要公式及使用条件1. 理想气体状态方程式nRT RT M m pV ==)/(或 RT n V p pV ==)/(m式中p ,V ,T 及n 单位分别为Pa ,m 3,K 及mol 。
m /V V n =称为气体的摩尔体积,其单位为m 3 · mol -1。
R =8.314510 J · mol -1 · K -1,称为摩尔气体常数。
此式适用于理想气体,近似地适用于低压的真实气体。
2. 气体混合物 (1) 组成摩尔分数 y B (或x B ) = ∑AA B /n n体积分数/y B m,B B *=V ϕ∑*AVy Am ,A式中∑AA n 为混合气体总的物质的量。
Am,*V表示在一定T ,p 下纯气体A 的摩尔体积。
∑*AA m ,A V y 为在一定T ,p 下混合之前各纯组分体积的总和。
(2) 摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M式中 ∑=BB m m 为混合气体的总质量,∑=BB n n 为混合气体总的物质的量。
上述各式适用于任意的气体混合物。
(3)V V p p n n y ///B B B B *=== 式中p B 为气体B ,在混合的T ,V 条件下,单独存在时所产生的压力,称为B 的分压力。
*B V 为B 气体在混合气体的T ,p 下,单独存在时所占的体积。
3. 道尔顿定律p B = y B p ,∑=BB p p上式适用于任意气体。
对于理想气体V RT n p /B B =4. 阿马加分体积定律V RT n V /B B =*此式只适用于理想气体。
5. 范德华方程RT b V V a p =-+))(/(m 2mnRT nb V V an p =-+))(/(22式中a 的单位为Pa · m 6 · mol -2,b 的单位为m 3 · mol -1,a 和b 皆为只与气体的种类有关的常数,称为范德华常数。
第一章气体的pvT关系⑴波义尔定律:当n、T一定时,PV=常数⑵盖-吕萨克定律:当n、P一定时,V/T=常数⑶阿伏伽德罗定律:当T、P一定时,V/n=常数●⑷理想气体状态方程:PV=(m/M)RT= nRT或者或PVm=p(V/n)=RTR=8.314mol-1·K-1称为摩尔气体常数;T为华氏温度⑸摩尔分数:X B=n B/n总●⑹道尔顿定律:P B=P总X B;P总=P分⑺实际气体状态方程:PV=znRT(z为压缩因子)●⑻理想气体特征:①分子间无相互作用力②分子本身不占有体积第二章热力学第一定律热力学第一定律(能量守恒定律)●⑴系统:①隔离系统:无能量、无物质交换②★封闭系统:有能量、无物质交换(热力学基础;热力学研究对象)③敞开系统:有能量、有物质交换●⑵状态函数:P、V、T、U、H、G、A、S (P、T、C p, m、C V,m 为强度量,其他均为广度量) 状态函数特征:①有可微分性,能计算②只与始末状态有关●途径函数:Q、W●⑶热:系统从环境中吸热(Q>0);系统对环境做功(W<0)●⑷热力学能:△U=Q+W(封闭系统);U只是温度T的函数;只与首末有关非体积功的计算①气体向真空膨胀时体积功所的计算W=0②恒外压过程体积功W=-p(V2-V1)=-p△V③对于理想气体恒压变温过程W=-p△V=-nR△T④可逆过程体积功W=-p(v2-v1)●⑤理想气体恒温可逆过程体积功 W=-p(v2-v1)或者W=-nRTln(V1/V2)或者W=nRTln(p2/ p1)⑥理想气体绝热可逆过程体积功W=-p(v2-v1)=(-)γ= C p, m /C V,m(双原子气体为1.4)T2/T1=(V1/V2) 的γ-1次方;T2/T1=(P1/P2)的(γ-1)/γ次方;P2/P1=(V1/V2)的γ次方●⑦恒温膨胀可逆功最大,系统对环境作最大功;恒温可逆压缩,环境对系统做最小功⑧可逆相变体积功W=-pdV恒热容、恒压热,焓⑴焓定义:H=U + PV⑵焓变:△H=△U+△(pV)式中△(pV)为p V乘积的增量,只有在恒压下△(pV)=p(V2-V1)在数值上等于体积功。