真空中静电场1电场强度

静电场中电场强度的计算在物理学中，静电场是指由于电荷分布而形成的电场。

电场强度是描述电场强弱的物理量，通常用 E 表示，单位是 N/C（牛顿/库仑）。

本文将探讨如何计算静电场中的电场强度。

1. 点电荷的电场强度计算对于一个点电荷 q 在离其距离 r 的点 P 处的电场强度 E，可以通过库仑定律计算：E = k * (q / r^2)其中，k 是电场常数，取值为 9 × 10^9 Nm^2/C^2。

2. 均匀带电线的电场强度计算对于一条无限长的均匀带电线，其线密度为λ，可以使用以下公式计算点 P 处的电场强度 E：E = (k * λ) / (2πr)其中，r 是点 P 到线的距离。

3. 均匀带电平面的电场强度计算对于一个无限大、均匀带电的平面，其面密度为σ，可以使用以下公式计算点 P 处的电场强度 E：E = σ / (2ε)其中，ε 是真空中的介电常数，取值为8.85 ×10^-12 C^2/(Nm^2)。

4. 多个点电荷的电场强度计算如果存在多个点电荷，则可以使用叠加原理来计算总的电场强度。

假设有 n 个点电荷 q1, q2, ..., qn 在位置 r1, r2, ..., rn 上，那么在点 P 处的电场强度 E 总和为：E = k * (q1 / r1^2) + k * (q2 / r2^2) + ... + k * (qn / rn^2)5. 静电场中的电势能电场强度与电势能之间有着密切的关系。

在静电场中，电荷沿电场方向从点 A 移动到点 B 时，电场力做的功将转化为电势能的增加。

电场强度 E 与电势差ΔV 之间的关系可以表示为：ΔV = -∫E·dl其中，ΔV 表示点 A 到点 B 的电势差，这里取负号表示电场力与位移方向相反。

总结：静电场中的电场强度可以根据不同情况使用不同的计算公式。

对于点电荷，使用库仑定律；对于均匀带电线和平面，使用相应的公式；对于多个点电荷，使用叠加原理。

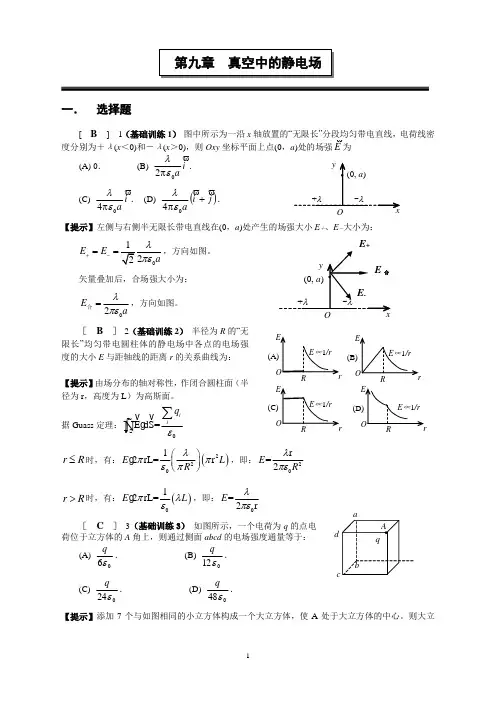
一． 选择题[ B ] 1（基础训练1） 图中所示为一沿x 轴放置的“无限长”分段均匀带电直线，电荷线密度分别为＋λ(x ＜0)和－λ(x ＞0)，则Oxy 坐标平面上点(0，a )处的场强E为(A) 0． (B) i a 02ελπ． (C) i a 04ελπ． (D)()j i a+π04ελ． 【提示】左侧与右侧半无限长带电直线在(0，a )处产生的场强大小E ＋、E －大小为：E E +-==矢量叠加后，合场强大小为：02E aλπε=合，方向如图。

［ B ］ 2（基础训练2） 半径为R 的“无限长”均匀带电圆柱体的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为：【提示】由场分布的轴对称性，作闭合圆柱面（半径为r ，高度为L ）为高斯面。

据Guass 定理：SE dS=iiq ε∑⎰r R ≤时，有：()22012rL=r E L R λππεπ⎛⎫ ⎪⎝⎭，即：20r =2E R λπε r R >时，有：()012rL=E L πλε ，即：0=2rE λπε ［ C ］ 3（基础训练3） 如图所示，一个电荷为q 的点电荷位于立方体的A 角上，则通过侧面abcd 的电场强度通量等于： (A)06εq ． (B) 012εq． (C) 024εq ． (D) 048εq ．【提示】添加7个与如图相同的小立方体构成一个大立方体，使A 处于大立方体的中心。

则大立方体的外表面构成一个闭合的高斯面。

由Gauss 定理知，通过该高斯面的电通量为qε。

另一方面，该高斯面可看成由24个面积与侧面abcd 相等的面组成，且具有对称性。

所以，通过侧面abcd 的电场强度通量等于24εq ［ D ］ 4（基础训练6） 在点电荷+q 的电场中，若取图中P 点处为电势零点 ， 则M 点的电势为 (A) a q 04επ． (B) a q 08επ． (C) a q 04επ-． (D) a q 08επ-．【提示】200248P a M M aq qU E dl dr r a πεπε-===⎰⎰［ B ］ 5（自测提高6）如图所示，两个同心的均匀带电球面，内球面半径为R 1、带电荷Q 1，外球面半径为R 2、带有电荷Q 2．设无穷远处为电势零点，则在内球面之内、距离球心为r 处的P 点的电势U 为：(A)rQ Q 0214επ+． (B) 20210144R Q R Q εεπ+π． (C) 0． (D) 1014R Q επ． 【提示】根据带电球面在球内外所激发电势的公式，以及电势叠加原理即可知结果。

静电场中的电场强度分布在物理学中，电场是一种非常重要的概念。

真空中的电场E可以定义为一个小试电荷在空间某一点所受到的电力F与试电荷量q之比，即E=F/q。

在静电场中，电场强度分布是一件重要的事情，它反映了电场在空间中的变化程度和方向。

关于静电场中的电场强度分布，我们将从其定义、性质和计算三个方面进行探讨。

首先，让我们看看静电场中电场强度的定义。

电场强度是描述电场在空间中强度的物理量，它由电荷产生，并在空间四处传播。

在静电场中，一个物体所受到的电力取决于这个位置的电场强度。

如果我们在静电场中放置一个试电荷，那么这个试电荷在电场的作用下会产生一个力，这个力的大小就是试电荷的电荷量乘以电场强度。

所以，电场强度可以理解为单位电荷所受到的电场力。

接着，我们需要理解静电场中电场强度的性质。

首先，电场具有方向性，电场方向是由正电荷指向负电荷。

其次，电场强度大小与电荷量和距离有关。

电荷量越大，电场强度越大；电荷和点的距离越近，电场强度越大。

最后，电场强度是一个矢量，也就是说，当有多个电荷同时存在时，某一点的电场强度等于各个电荷在这一点处产生的电场强度矢量之和。

再者，我们来看看如何计算静电场中的电场强度分布。

一般情况下，计算电场强度的公式是E=Q/(4πε0r²)，其中Q表示电荷电量，ε0表示真空的电介质常数，r表示距离。

在计算多个电荷产生的电场强度时，可以利用电场强度矢量的叠加性质，单独计算出每个电荷在某一点产生的电场强度，然后做矢量求和，即可得到总的电场强度。

在静电场中，电场强度分布主要受电荷的分布和距离的影响。

当电荷分布均匀时，电场强度在各个方向上都是一样的。

当电荷分布不均匀时，电场强度在不同的点上会有所不同。

加之电场强度还会随着距离的增加而减小，所以，在静电场中电场强度的分布情况即视电荷分布及其距离而定。

总的来说，静电场中的电场强度分布是一个重要的研究对象。

通过理解电场强度的定义、性质和计算方式，我们可以了解更多关于电场的知识，从而更好地利用电场这一物理现象。

静电场中的电场强度电场是物理学中一个重要的概念，用来描述电荷在空间中产生的力场。

在静电场中，电场强度是衡量电场强弱的物理量。

本文将详细介绍静电场中的电场强度的概念、计算方法以及应用。

1.电场强度的定义静电场中的电场强度表示单位正电荷所受到的电场力。

在某一位置上，电荷Q在周围产生了一个电场，电场强度E的大小和方向取决于位置和电荷大小。

电场强度的单位是牛顿/库仑(N/C)。

2.电场强度的计算方法在给定电荷分布的情况下，计算静电场中某一点的电场强度可以采用两种方法：叠加原理和连续电荷分布的积分。

2.1 叠加原理叠加原理指出，在由多个离散点电荷组成的电荷分布下，电场强度是这些点电荷产生的电场强度的矢量和。

根据叠加原理，可以将电荷Q分成n个小电荷dq，然后计算每个dq在某一点P产生的电场强度dE，最后对所有dq的电场强度进行叠加得到最终的电场强度E。

2.2 连续电荷分布的积分对于具有连续电荷分布的情况，可以使用积分的方法来计算电场强度。

根据库仑定律，连续电荷分布被视为无限小电荷元素，电场强度可以写作dE=k(dq/r^2)dr，其中k为电场常数，r为距离，dq为无限小电荷元素。

通过对整个电荷分布进行积分，可以得到最终的电场强度。

3.电场强度的应用电场强度在物理学和工程学中有广泛的应用。

3.1 静电势能电场强度和电荷之间的关系可以用来计算电场中电荷的势能。

当电荷在电场中移动时，电场对电荷做功，但由于电场是保守场，所以对电场中电荷所做的功可以表示为电荷的势能。

静电势能的计算公式为U=qV，其中U为势能，q为电荷量，V为电势。

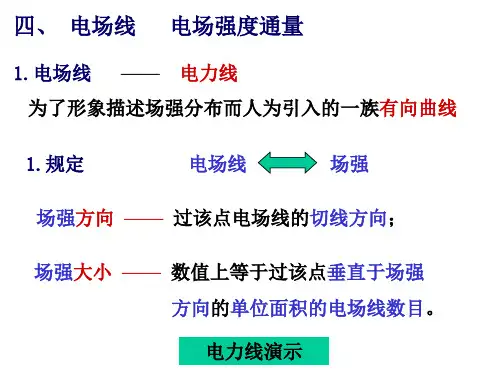
3.2 电场线和电势面电场强度的方向可以通过在每一点上绘制电场线来表示。

电场线是描述电场强度方向的曲线，其切线方向与电场强度的方向一致。

另外，电场强度和等势面垂直。

等势面是指在某一位置上电势相等的点连成的曲面。

3.3 静电力电场强度和电荷之间的关系可以用来计算电场中的静电力。

静电力的计算公式为F=qE，其中F为静电力，q为电荷量，E为电场强度。

w真空中的静电场基 本 要 求一、理解电场强度和电势这两个基本概念和它们之间的联系。

二、掌握反映静电场性质的两个基本定理——高斯定理和环流定理的重要意义及其应用。

三、掌握从已知的电荷分布求场强和电势分布的方法。

容 提 要一、真空中的库仑定律)(412210rr q q rF ⋅=πε库仑定律的适用条件：1. 点电荷；2. 电荷静止（或低速）。

二、电场和电场强度电场 电荷能够产生电场。

电场是一种客观存在的物质形态。

电场对外表现的性质：1. 对处于电场中的其他带电体有作用力；2. 在电场中移动其他带电体时，电场力要对它做功，这也表明电场具有能量。

电场强度的定义式0q F E =点电荷场强公式)(4120rr q r E ⋅⋅=πε场强叠加原理 电场中某点的场强等于每个电荷单独在该点产生的场强的叠加（矢量和）。

w几种常见带电体的场强1、电荷线密度为λ的无限长均匀带电直线外一点的场强a λE 02πε=2、电荷面密度为σ的无限大均匀带电平面外一点的场强2εσE =方向垂直于带电平面。

3、带电Q 、半径为R 的均匀带电导体球面或导体球的场强分布r<R 时， E =0r>R 时，0204r E r Qπε=4、带电Q 、体密度为ρ的均匀带电球体场强分布r<R 时，r E 304RQπε= r>R 时，0204r E r Q πε=三、电通量 高斯定理电场线（电力线）画法 1. 电场线上某点的切线方向和该点场强方向一致；2. 通过垂直于E 的单位面积的电场线的条数等于该点E 的大小。

电场线的性质 1. 两条电场线不能相交；2. 电场线起自正电荷（或无穷远处），止于负电荷（或无穷远处），电场线有头有尾，不是闭合曲线。

电场强度通量 ⎰⎰⋅=se d ΦS E电场强度通量也可形象地说成是通过该面积S 的电场线的条w数。

高斯定理 真空中静电场内，通过任意闭合曲面的电场强度通量等于该曲面所包围的电量的代数和的1/ε 0倍。

静电场和电场强度静电场和电场强度是电学中两个重要的概念。

理解和掌握这些概念对于我们理解电学现象以及应用电学原理具有重要的意义。

本文将介绍静电场和电场强度的定义、性质以及相关的计算方法。

一、静电场的定义静电场是物体之间由于电荷分布引起的一种力场。

当物体带有电荷时，周围空间中会产生电场，这个电场对其周围的其他电荷具有作用力。

静电场的作用力是电荷间相互作用的结果，遵循库仑定律。

静电场是一种矢量场，可以用箭头表示。

箭头的方向表示电场的方向，箭头的长度表示电场的强度。

静电场的强度用E表示。

二、电场强度的定义电场强度是描述一个点电荷周围电场的强度大小和方向的物理量。

电场强度可以通过单位正电荷所受到的力来定义。

对于位于电场中的一个点电荷，其受到的电场力与该点电荷带电量成正比，与电荷之间的距离的平方成反比。

这样，我们可以定义电场强度为单位正电荷所受到的力，即E=F/q，其中E表示电场强度，F表示电场力，q表示单位正电荷的电荷量。

电场强度也是一种矢量量，其方向与电场力的方向相同。

电场强度大小与电荷之间的距离的平方成反比，与电荷的大小成正比。

三、电场强度的性质1. 电场强度的方向是从正电荷指向负电荷，如果只有一个电荷，则电场强度的方向就是从该点电荷指向外部。

2. 电场强度大小与电荷的大小成正比，与距离的平方成反比。

3. 电场中的任意一点，电场强度是一个矢量量，可以用箭头表示，箭头的方向表示电场的方向，箭头的长度表示电场的强度。

4. 电场强度可以叠加，多个电场产生的电场强度在空间中的某一点是矢量和，即各向量和。

四、电场强度的计算方法根据电场强度的定义，我们可以通过公式E=F/q计算电场强度。

当电场的分布情况符合某种对称性时，我们可以采用高斯定律来计算电场强度。

高斯定律是静电学的重要定律，适用于由某个带电体产生的电场。

该定律指出，电场通过固定闭合曲面的总通量与该闭合曲面内的总电荷成正比。

五、结论静电场和电场强度是电学中的重要概念，在理解电学现象和应用电学原理上起着关键作用。