下载文档原格式
第六章 真空中的静电场一、 基本要求1．掌握静电场的电场强度和电势的概念以及电场强度的叠加原理和电势的叠加原理。
掌握电势与电场强度的积分关系。
能计算一些简单问题中的电场强度和电势。
2．理解静电场的规律：高斯定理和环路定理。
理解用高斯定理计算电场强度的条件和方法。
3．了解电偶极矩的概念。
能计算电偶极子在均匀电场中所受的力和力矩。
二、 基本内容1．点电荷当带电体的形状和大小与它们之间的距离相比可以忽略时，可以把带电体看作点电荷。
对点电荷模型应注意：（1）点电荷概念和大小具有相对意义，即它本身不一定是很小的带电体。
只要两个带电体的线度与它们之间距离相比可忽略，就可把它们简化为点电荷，另外，当场点到带电体的距离比带电体的线度大得多时也可以把带电体简化为点电荷。
（2）点电荷是由具体带电体（其形状没有限制）抽象出来的理想化模型，所以不能把点电荷当作带电小球。
（3）点电荷不同于微小带电体。
因带电体再小也有一定的形状和电荷分布，还可以绕通过自身的任意轴转动，点电荷则不同。
（4）一个带电体在一些问题中可简化为点电荷，在另一些问题中则不可以。
如讨论带电体表面附近的电性质时就不能把带电体简化为点电荷。
2．库仑定律02qq kr 0F r 其中，0r 由施力电荷指向受力电荷的单位矢量。
适用条件：真空中点电荷之间（相对观察者静止的电荷）的相互作用。
当空间有两个以上的点电荷同时存在时，作用在某一点电荷上的总静电力等于其它各点电荷单独存在时对该电荷所施静电力的矢量和——电场力的叠加原理。
3．电场强度矢量0q =E F ，电场中某点的电场强度等于单位电荷在该点所受的电场力。
0q 为正时，E 和电场力F 同方向，0q 为负时，E 的方向和F 方向相反。
（1）E 反映电场的客观性质，E 与试验电荷0q 的大小，电荷正负无关，也与0q 的存在与否无关。
（2）E 是一个矢量，一般地说，电场空间不同点处的场强不同，即()r =E E 。
第6章真空中的静电场习题及答案1.电荷为q 和2q 的两个点电荷分别置于x1m 和x1m 处。
一试验电荷置于x 轴上何处，它受到的合力等于零？解：根据两个点电荷对试验电荷的库仑力的大小及方向可以断定，只有试验电荷 q 位于点电荷 0q 的右侧，它受到的合力才可能为0，所以2qqqq00224(x 1)4(x1) ππ 00故x3222.电量都是q 的三个点电荷，分别放在正三角形的三个顶点。
试问：(1)在这三角形的中心放 一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都 为零)?(2)这种平衡与三角形的边长有无关系?解：(1)以A 处点电荷为研究对象，由力平衡知，q 为负电荷，所以2 4 1 π 0 q a 22 cos304 1 π 0 ( q 33qa 2 )3故qq3(2)与三角形边长无关。
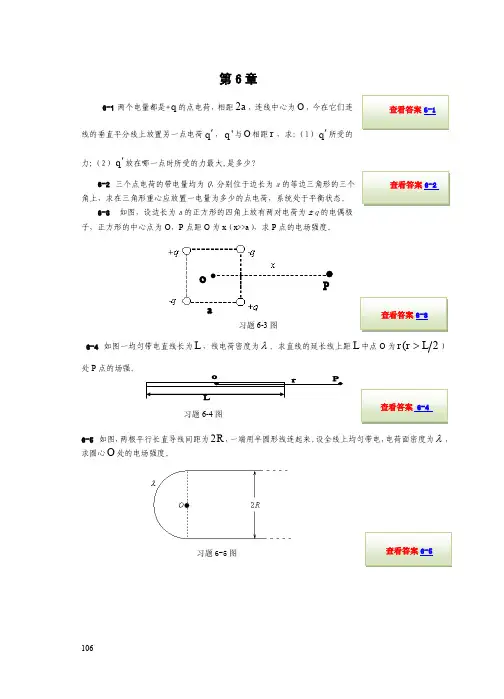
3.如图所示，半径为R 、电荷线密度为1的一个均匀带电圆环，在其轴线上放一长为l 、电荷线密度为2的均匀带电直线段，该线段的一端处于圆环中心处。
求该直线段受到的电场力。
解：先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取dqdl 1，dq 在带电圆环轴 线上x 处产生的场强大小为 dE 4 dq20(xRy2 )根据电荷分布的对称性知，yE0E zdEdEcos x41xdq 1R 3 22 2O(xR) 02xl式中：为dq 到场点的连线与x 轴负向的夹角。
E x4x 220(xR) 3 2dqzx21R R 1 x4x 2R2()3 2 2xR 2( 02 )3 2下面求直线段受到的电场力。
在直线段上取dqdx2，dq受到的电场力大小为Rx12dFxdxEdq32222(xR)0方向沿x轴正方向。
直线段受到的电场力大小为Rlx12FdxdF3202220xR)(11R1121/22R22lR方向沿x轴正方向。
4.一个半径为R的均匀带电半圆环，电荷线密度为。
求：（1）圆心处O点的场强；（2）将此带电半圆环弯成一个整圆后，圆心处O点场强。
作业6静电场六1．真空中有一均匀带电球体和一均匀带电球面，如果它们的半径和所带的电量都相等，则 它们的静电能之间的关系是[]。
A.球体的静电能等于球面的静电能B.球体的静电能大于球面的静电能C.球体的静电能小于面的静电能D.球体内的静电能大于球面内的静电能，球体外的静电能小于球面外的静电能答案：【B 】解：设带电量为Q 、半径为R ，球体的电荷体密度为。
由高斯定理，可以求得两种电荷分布的电场强度分布S EdS2r 2EQ 0 0， E Q 0 2r 0 2对于球体电荷分布：43 r 2r 3 E0，（rR ）； 122r300Q E ，（rR ）。
222r对于球壳电荷分布：/ E0，（rR ）； 1Q/ E ，（rR ）。
222r可见，球外：两种电荷分布下，电场强度相等；球内：球体电荷分布，有电场，球壳电荷分 布无电场。
静电场能量密度1 2 E2 两球外面的场强相同，分布区域相同，故外面静电能相同；而球体(并不是导体)内部也有电 荷分布，也是场分布，故也有静电能。
所以球体电荷分布时，球内的静电场能量，大于球面 电荷分布时，球内的静电场能量；球体电荷分布时，球外的静电场能量，等于球面电荷分布 时，球外的静电场能量。
2． C 和C 2两空气电容器串联起来接上电源充电，然后将1电源断开，再把一电介质板插入 []。
C 中，如图6-1所示，则1A. C 两端电势差减少，C 2两端电势差增大1B. C 两端电势差减少，C 2两端电势差不变1C. C 两端电势差增大，C 2两端电势差减小1D. C 两端电势差增大，C 2两端电势差不变1答案：【B 】解：电源接通时，给两个串联的电容器充电。
充电量是相同的，是为Q 。
则两个电容器的 电压分别为Q U ， 1 C 1U 2Q C 2电源断开后，C1插入电介质，两个电容器的电量不变，仍然都是Q。
但C1的电容增大，因此C1两端的电压降低；而C2不变，因此，C2两端的电压不变。
第六章 静电场习题6-1 电量都是q 的三个点电荷，分别放在正三角形的三个顶点。
试问：（1）在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡（即每个电荷受其他三个电荷的库仑力之和都为零）？（2）这种平衡与三角形的边长有无关系？解：（1）如图任选一点电荷为研究对象，分析其受力有1230F F F F =++=合 y 轴方向有()()21322002032cos 242433304q qQ F F F a a q q Q aθπεπεπε=+=+=+=合得 33Q q =-（2）这种平衡与三角形的边长无关。
6-2 两小球的质量都是m ，都用长为l 的细绳挂在同一点，它们带有相同电量，静止时两线夹角为2θ，如图所示。
设小球的半径和线的质量都可以忽略不计，求每个小球所带的电量。
解：对其中任一小球受力分析如图所示，有⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得 θπεθtan 4sin 20mg l q = 6-3 在氯化铯晶体中，一价氯离子Cl －与其最邻近的八个一价铯离子Cs +构成如图所示的立方晶格结构。
（1）求氯离子所受的库仑力；（2）假设图中箭头所指处缺少一个铯离子（称作晶格缺陷），求此时氯离子所受的库仑力。
（1）由对称性可知 F 1= 0（2）291222200 1.9210N 43q q e F r aπεπε-===⨯ 方向如图所示6-4 长l ＝15.0 cm 的直导线AB 上均匀地分布着线密度95.010C m λ-=⨯的正电荷。
试求：（1）在导线的延长线上与导线B 端相距1 5.0cm a =处P 点的场强；（2）在导线的垂直平分线上与导线中点相距2 5.0d cm =处Q 点的场强。
解：（1）如图所示，在带电直线上取线元x d ，其上电量q d 在P 点产生场强为20)(d π41d x a xE P -=λε2220)(d π4d x a x E E llP P -==⎰⎰-ελ]2121[π40l a l a +--=ελ)4(π220l a l -=ελ 用15=l cm ，9100.5-⨯=λ1m C -⋅，5.12=a cm 代入得21074.6⨯=P E 1C N -⋅ 方向水平向右（2）同理 2220d d π41d +=x xE Q λε 方向如图所示由于对称性可知⎰=l QxE 0d ，即Q E只有y 分量22222220dd d d π41d ++=x x xE Qyλε22π4d d ελ⎰==lQyQy E E ⎰-+2223222)d (d l l x x 2220d 4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅ 方向沿y 轴正向*6-5 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行，试计算通过此半球面的电场强度通量。
大学物理第六章静电场习题答案(总7页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第六章静电场习题6-1 电量都是q的三个点电荷，分别放在正三角形的三个顶点。
试问：（1）在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡（即每个电荷受其他三个电荷的库仑力之和都为零）（2）这种平衡与三角形的边长有无关系？解：（1）如图任选一点电荷为研究对象，分析其受力有1230F F F F=++=合y轴方向有()()21322232cos242433304q qQF F Fa aqq Qaθπεπεπε=+=+=+=合得33Q q=-（2）这种平衡与三角形的边长无关。
6-2 两小球的质量都是m，都用长为l的细绳挂在同一点，它们带有相同电量，静止时两线夹角为2θ，如图所示。
设小球的半径和线的质量都可以忽略不计，求每个小球所带的电量。
解：对其中任一小球受力分析如图所示，有⎪⎩⎪⎨⎧===22)sin2(π41sincosθεθθlqFTmgTe解得θπεθtan4sin2mglq=6-3 在氯化铯晶体中，一价氯离子Cl－与其最邻近的八个一价铯离子Cs+构成如图所示的立方晶格结构。
（1）求氯离子所受的库仑力；（2）假设图中箭头所指处缺少一个铯离子（称作晶格缺陷），求此时氯离子所受的库仑力。
（1）由对称性可知F1= 0（2）2912222001.9210N43q q eFr aπεπε-===⨯方向如图所示6-4 长l＝ cm的直导线AB上均匀地分布着线密度95.010C mλ-=⨯的正电荷。
试求：（1）在导线的延长线上与导线B端相距15.0cma=处P点的场强；（2）在导线的垂直平分线上与导线中点相距25.0d cm=处Q点的场强。
解：（1）如图所示，在带电直线上取线元x d，其上电量q d在P点产生场强为20)(d π41d x a xE P -=λε2220)(d π4d x a x E E llP P -==⎰⎰-ελ]2121[π40l a l a +--=ελ)4(π220l a l -=ελ 用15=l cm ，9100.5-⨯=λ1m C -⋅，5.12=a cm 代入得21074.6⨯=P E 1C N -⋅ 方向水平向右（2）同理 2220d d π41d +=x xE Q λε 方向如图所示由于对称性可知⎰=l Qx E 0d ，即Q E只有y 分量22222220dd d d π41d ++=x x x E Qyλε22π4d d ελ⎰==lQyQy E E ⎰-+2223222)d (d l l x x2220d 4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Q y Q E E 1C N -⋅ 方向沿y 轴正向*6-5 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行，试计算通过此半球面的电场强度通量。
第六章 真空中的静电场1、电量为－5×10-9 C 的试验电荷放在电场中某点时，受到 20×10-9 N 的向下的力，求该点的电场强度大小和方向。
解：由q E F = 得C N q F E /4105/1020/99-=⨯-⨯==--方向向上2、一个带负电荷的质点，在电场力作用下从A 点 经C 点运动到B 点，其运动轨迹如图所示．已知质点运动的速率是递减的，试定性画出电场E的方向。
解：速率是递减→τa 为负→切向力与v相反做曲线运动→有n a →受合力方向如图→即电场E-的方向3、一均匀静电场，电场强度()j i E 600400+=V ·m -1，求点a (3,2)和点b (1,0)之间的电势差U ab ．(点的坐标x ,y 以米计) 解：⎰⋅=baab l d E U)()600400(⎰+⋅+=baj dy i dx j i +=⎰13400dx ⎰2400dy=－2×103 V4、如图所示，真空中一长为L 的均匀带电细直杆，总电荷为q ，试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度．解：设杆的左端为坐标原点O ，x 轴沿直杆方向．带电直杆的电荷线密度为λ=q / L ，在x 处取一电荷元d q = λd x = q d x / L ，它在P 点的场强： ()204d d x d L qE -+π=ε()204d x d L L xq -+π=ε 2分总场强为 ⎰+π=Lx d L xL q E 02)(d 4－ε()d L d q +π=04ε 3分方向沿x 轴，即杆的延长线方向．-qEO5、A 、B 为真空中两个平行的“无限大”均匀带电平面，已知两平面间的电场强度大小为E 0，两平面外侧电场强度大小都为E 0/3，方向如图．求A 、B 两平面上的电荷面密度σA , σB ． 解：设电荷面密度为σA , σB由场强迭加原理，平面内、外侧电场强度由σA , σB 共同贡献： 外侧：32200E BA=+-εσεσ内侧：0022E BA=+εσεσ联立解得：3/200E Aεσ-= 3/400E Bεσ=6、半径为R 的半球面置于场强为E的均匀电场中，其对称轴与场强方向一致，如图所示．求通过该半球面的电场强度通量。
第6章 真空中的静电场 习题及答案1. 电荷为q +和q 2-的两个点电荷分别置于1=x m 和1-=x m 处。
一试验电荷置于x 轴上何处，它受到的合力等于零解：根据两个点电荷对试验电荷的库仑力的大小及方向可以断定，只有试验电荷0q 位于点电荷q +的右侧，它受到的合力才可能为0，所以200200)1(π4)1(π42-=+x qq x qq εε 故 223+=x2. 电量都是q 的三个点电荷，分别放在正三角形的三个顶点。
试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)(2)这种平衡与三角形的边长有无关系解：(1) 以A 处点电荷为研究对象，由力平衡知，q '为负电荷，所以2220)33(π4130cos π412a q q a q '=︒εε故 q q 33-=' (2)与三角形边长无关。
3. 如图所示，半径为R 、电荷线密度为1λ的一个均匀带电圆环，在其轴线上放一长为l 、电荷线密度为2λ的均匀带电直线段，该线段的一端处于圆环中心处。
求该直线段受到的电场力。
解：先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取dl dq 1λ=，dq 在带电圆环轴线上x 处产生的场强大小为)(4220R x dqdE +=πε根据电荷分布的对称性知，0==z y E E23220)(41 cos R x xdqdE dE x +==πεθ式中：θ为dq 到场点的连线与x 轴负向的夹角。
⎰+=23220)(4dq R x xE x πε 232210)(24R x R x +⋅=πλπε232201)(2R x xR +=ελ 下面求直线段受到的电场力。
在直线段上取dx dq 2λ=，dq 受到的电场力大小为dq E dF x =dx R x xR 2322021)(2+=ελλ方向沿x 轴正方向。
直线段受到的电场力大小为⎰=dF F dx R x xR l ⎰+=02322021)(ελλ2R Oλ1λ2lxyz()⎥⎦⎤⎢⎣⎡+-=2/12202111R l R R ελλ2 方向沿x 轴正方向。
4. 一个半径为R 的均匀带电半圆环，电荷线密度为λ。
求： （1）圆心处O 点的场强；（2）将此带电半圆环弯成一个整圆后，圆心处O 点场强。
解：（1）在半圆环上取ϕλλRd l dq ==d ，它在O 点产生场强大小为20π4R dq dE ε=ϕελd R0π4= ，方向沿半径向外根据电荷分布的对称性知，0=y Eϕϕελϕd RdE dE x sin π4sin 0==R d R E x 000π2sin π4ελϕϕελπ==⎰故 RE E x 0π2ελ==，方向沿x 轴正向。
（2）当将此带电半圆环弯成一个整圆后，由电荷分布的对称性可知，圆心处电场强度为零。
5．如图所示，真空中一长为L 的均匀带电细直杆，总电量为q ，试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度。
解：建立图示坐标系。
在均匀带电细直杆上取dx Lqdx dq ==λ，dq 在P 点产生的场强大小为 202044xdxx dq dE πελπε==，方向沿x 轴负方向。
故 P 点场强大小为 ⎰⎰+==Ld dP xdxdE E 204πελ ()L d d q+π=04ε方向沿x 轴负方向。
6. 一半径为R 的均匀带电半球面，其电荷面密度为σ，求球心处电场强度的大小。
解：建立图示坐标系。
将均匀带电半球面看成许多均匀带电细圆环，应用场强叠加原理求解。
在半球面上取宽度为dl 的细圆环，其带电量rdl dS dq πσσ2⋅=⋅=θθπσd R sin 22⋅=， dq 在O 点产生场强大小为（参见教材中均匀带电圆环轴线上的场强公式）23220)(4r x xdqdE +=πε ，方向沿x 轴负方向利用几何关系，θcos R x =，θsin R r =统一积分变量，得23220)(4r x xdqdE +=πε θθπσθπεd R RR sin 2cos 41230⋅=Lθθθεσd cos sin 20=因为所有的细圆环在在O 点产生的场强方向均沿为x 轴负方向，所以球心处电场强度的大小为⎰=dE E θθθεσπd cos sin 22/00⎰=04εσ= 方向沿x 轴负方向。
7. 一“无限大”平面，中部有一半径为R 的圆孔，设平面上均匀带电，电荷面密度为σ，如图所示。
试求通过小孔中心O 并与平面垂直的直线上各点的场强。
解：应用补偿法和场强叠加原理求解。
若把半径为R 的圆孔看作由等量的正、负电荷重叠而成，挖去圆孔的带电平面等效为一个完整的“无限大”带电平面和一个电荷面密度为σσ-='的半径为R 的带电圆盘，由场强叠加原理知，P 点的场强等效于“无限大”带电平面和带电圆盘在该处产生的场强的矢量和。
“无限大”带电平面在P 点产生的场强大小为12εσ=E ，方向沿x 轴正方向 半径为R 、电荷面密度σσ-='的圆盘在P 点产生的场强大小为（参见教材中均匀带电圆盘轴线上的场强公式）022εσ=E )1(22xR x +-，方向沿x 轴负方向故 P 点的场强大小为220212x R xE E E +=-=εσ方向沿x 轴正方向。
8. (1)点电荷q 位于一边长为a 的立方体中心，试求在该点电荷电场中穿过立方体的一个面的电场强度通量；(2)如果该场源点电荷移动到该立方体的一个顶点上，这时穿过立方体各面的电场强度通量是多少解：（1）由高斯定理0d εqS E s⎰=⋅ 求解。
立方体六个面，当q 在立方体中心时，每个面上电通量相等，所以通过各面电通量为6εqe =Φ （2）电荷在顶点时，将立方体延伸为边长a 2的立方体，使q 处于边长a 2的立方体中心，则通过边长a 2的正方形各面的电通量06εq e =Φ 对于边长a 的正方形，如果它不包含q 所在的顶点，则024εqe =Φ，如果它包含q 所在顶点，则0=Φe 。
9. 两个无限大的平行平面都均匀带电，电荷的面密度分别为1σ和2σ，试求空间各处场强。
解：如图所示，电荷面密度为1σ的平面产生的场强大小为12εσ=E ，方向垂直于该平面指向外侧 电荷面密度为2σ的平面产生的场强大小为2σ1σ22εσ=E ，方向垂直于该平面指向外侧 由场强叠加原理得两面之间，)(2121021σσε-=-=E E E ，方向垂直于平面向右 1σ面左侧，)(2121021σσε+=+=E E E ，方向垂直于平面向左 2σ面右侧，)(2121021σσε+=+=E E E ，方向垂直于平面向右 10. 如图所示，一球壳体的内外半径分别为1R 和2R ，电荷均匀地分布在壳体内，电荷体密度为ρ（0>ρ）。
试求各区域的电场强度分布。
解：电场具有球对称分布，以r 为半径作同心球面为高斯面。
由高斯定理∑⎰=⋅iSqS d E 01ε得i q r E ∑=⋅0214επ当1R r <时，0=∑i q ，所以 0=E当21R r R <<时，)3434(313R r q i ππρ-=∑，所以203133)(r R r E ερ-=当2R r >时，)3434(3132R R q i ππρ-=∑，所以2031323)(rR R E ερ-= 11. 有两个均匀带电的同心带电球面，半径分别为1R 和2R （12R R >），若大球面的面电荷密度为σ，且大球面外的电场强度为零。
求：（1）小球面上的面电荷密度；（2）大球面内各点的电场强度。
解:（1）电场具有球对称分布，以r 为半径作同心球面为高斯面。
由高斯定理∑⎰=⋅iSqS d E 01ε 得i q r E ∑=⋅0214επ当2R r >时，0=E ，0442122=⋅'+⋅=∑R R q i πσπσ，所以σσ212)R R （-=' （2）当1R r <时，0=∑i q ，所以0=E当21R r R <<时，222144R R q i πσπσ-=⋅'=∑，所以22)εσr R E （-=负号表示场强方向沿径向指向球心。
12. 一厚度为d 的无限大的带电平板，平板内均匀带电，其体电荷密度为ρ，求板内外的场强。
解：电场分布具有面对称性，取同轴闭合圆柱面为高斯面，圆柱面与平板垂直，设两底面圆到平板中心的距离均为x ，底面圆的面积为S ∆。
由高斯定理∑⎰=⋅iSqS d E 01ε 得=⋅⎰SS d E i q S E S E ∑=+∆⋅+∆⋅010ε 当2dx <时（平板内部），S x q i ∆⋅⋅=∑2ρ，所以 0ερx E =当2dx >（平板外部），S d q i ∆⋅⋅=∑ρ，所以2ερd E =13. 半径为R 的无限长直圆柱体均匀带电，体电荷密度为ρ，求其场强分布。
解：电场分布具有轴对称性，取同轴闭合圆柱面为高斯面，圆柱面高为l ，底面圆半径为r ，应用高斯定理求解。
i Sq rl E S E ∑=⋅=⋅⎰1π2d ε(1) 当R r <时，l r qi2πρ⋅=∑，所以 02ερr E =(2) 当R r >时，l R qi2πρ⋅=∑，所以rR E 022ερ=14.一半径为R 的均匀带电圆盘，电荷面密度为σ，设无穷远处为电势零点，求圆盘中心O 点的电势。
解：取半径为r 、dr 的细圆环rdr dS dq πσσ2⋅==，则dq 在O 点产生的电势为024εσπεdrrdq dV ==圆盘中心O 点的电势为dr dV V R⎰⎰==002εσ02εσR = 15. 真空中两个半径都为R 的共轴圆环，相距为l 。
两圆环均匀带电，电荷线密度分别是λ+和λ-。
取两环的轴线为x 轴，坐标原点O 离两环中心的距离均为2l，如图所示。
求x 轴上任一点的电势。
设无穷远处为电势零点。
解：在右边带电圆环上取dq ，它在x 轴上任一点P 产生的的电势为220)2/(4Rl x dqdV +-=πε右边带电圆环在P 产生的的电势为⎰⎰+-==+dq R l x dV V 220)2/(41πε220)2/(2Rl x R+-=ελ同理，左边带电圆环在P 产生的电势为220)2/(2Rl x RV ++-=-ελ由电势叠加原理知，P 的电势为02ελR V V V =+=-+-+-22)2/(1(R l x ))2/(122Rl x ++16. 真空中一半径为R 的球形区域内均匀分布着体电荷密度为ρ的正电荷，该区域内a 点离球心的距离为R 31，b 点离球心的距离为R 32。
求a 、b 两点间的电势差ab U解：电场分布具有轴对称性，以O 为球心、作半径为r 的同心球面为高斯面。
