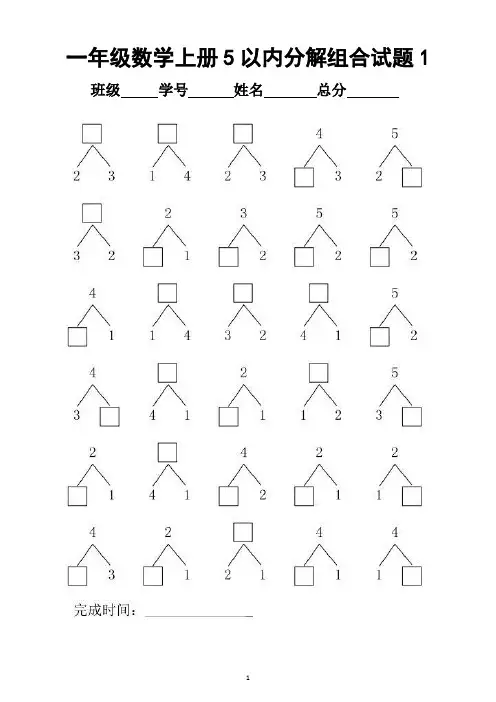
5以内数的分解组合练习题

一年级数学数的分成练习题简介：本文是针对一年级学生设计的数学练习题，主要涉及数字的分解及组合。

通过这些练习题，学生可以培养对数字的理解能力，提高计算能力和逻辑思维能力。

第一题：分解数字1. 将数字8分解成两个数的和，使得两个数的和最大。

2. 将数字12分解成两个互质的数的和。

3. 分解数字9，使得两个数的乘积最小。

第二题：组合数字1. 用数字1、2、3、4，能组成多少个各位不相同的两位数？2. 用数字1、2、3、4，能组合出哪些能被4整除的两位数？3. 用数字1、2、3、4，能组成多少个可以被3整除的三位数？第三题：数的分解与组合1. 用数字2、3、5，能组成多少个素数？2. 用数字4、5、6，能组成多少个不大于100的数？3. 用数字1、2、3、4，能组成多少个能被5整除的三位数，且每个数字只能使用一次？第四题：数的运算1. 用数字2、3，能通过加、减、乘、除运算，得到数字4吗？如果可以，给出所有可能的算式。

2. 用数字1、2、3、4组成一个等式，使得等式两边的结果相等。

3. 用数字7、9、1、2，通过加、减、乘、除运算，能得到数字8吗？如果可以，给出一个可能的算式。

第五题：进制转换1. 将二进制数1101转换成十进制数。

2. 将十进制数25转换成二进制数。

3. 将八进制数54转换成十进制数。

总结：通过上述练习题的实践操作，一年级的学生可以巩固数字的分解与组合的基本概念，培养他们的观察力和逻辑思维能力。

同时，适当引入数的运算和进制转换的练习，可以拓宽他们的数学思维，为进一步学习打下坚实的基础。

希望这些练习题能帮助学生们更好地理解和掌握数学中的基本概念和运算技巧。

1
9个
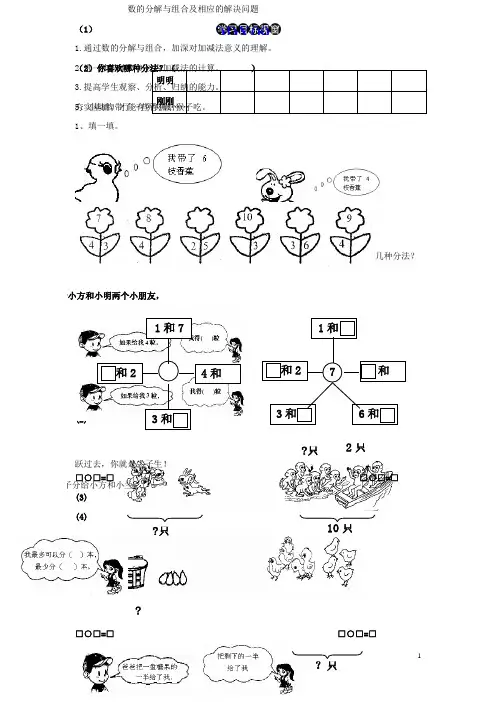
数的分解与组合及相应的解决问题
1.通过数的分解与组合，加深对加减法意义的理解。

2.
3.1、填一填。

2、在□里填合适的数。

3.
(2)
□○□=
□
□○□=□
(3)
(4)
□○□=□ □○□=□ （4）
（5）
（1）
（25
动物园一共有5只猴子，如果一只猴子吃1枝香蕉，他们带的香蕉够吗？你有几种分法？
豆给小方和小明两个小朋友，
跃过去，你就是尖子生！ 本子分给小方和小兰，
糖
9. 两棵树上共有麻雀12只，当有3只从第一棵树上飞到第二棵树上时，两棵树上的麻雀一
样多，你知道原来两棵树上各用多少只麻雀？
数的分解与组合及相应的解决问题
1.47 7 9 5
2.略
3.（1）4+2=6 （2）6+2=8
（3）9-4=5 （4）4+5=9
（5）5+5=10 （6）9-2=7
4.略
5. 两种，每个猴子分1个；每个猴子分2个。

6. 5 6
7.略
8. 8快
9.9只，3只
2。

学前分解练习题解决学前儿童的分解问题是培养他们数学思维和逻辑推理能力的重要一环。

本文将提供一些适合学前儿童的分解练习题，帮助他们提升数学技能和思维能力。

A. 分解数字在学前阶段，教授儿童分解数字是培养他们数学意识和操作能力的关键任务。

下面是一些有趣的练习题，可以帮助他们理解分解数字的概念。

1. 用点或线连接正确的数字分解方式：8 = □ + □a) 7 + 1b) 4 + 4c) 5 + 32. 选择正确的数字组合，使其总和为给定数字：a) 9 = □ + □b) 6 = □ + □ + □B. 分解集合练习分解集合可以帮助学前儿童理解数学中的集合概念和分类能力。

以下是几个适合学前儿童的练习题。

1. 将图中的形状分类为正方形或圆形：(图片：一些形状图案)2. 根据给定的物体，绘制图形进行分类，例如动物或交通工具：a) 猫b) 小汽车c) 鸟C. 分解图形学前儿童能够将图形分解为更小的部分，可以培养他们的空间想象力和图形认知能力。

以下是一些练习题可以帮助他们提升这些能力。

1. 将大图形分解成几个小图形并重组为大图形：(图片：一个图形被分解成几个小图形)2. 根据给定的几个形状，用它们组成一个新的大图形：(图片：给定几个小形状，组合成一个大图形)D. 分解操作通过分解操作，学前儿童可以掌握数学中的基本运算和操作。

以下是一些练习题可以帮助他们提升这方面的能力。

1. 用“+”或“-”计算下面的数学表达式：a) 6 + 2 = □b) 9 - 4 = □2. 用给定的数字和运算符号，填空使等式成立：a) □ + 2 = 8b) □ - 3 = 5总结：学前儿童在分解问题上的练习可以促进他们的数学思维和逻辑推理能力。

本文提供了一些适合学前儿童的分解练习题，帮助他们理解数字分解、集合分解、图形分解和基本计算操作等概念。

通过这些练习题的训练，学前儿童可以在数学方面取得更好的进展，并为将来的学习奠定坚实的基础。

幼⼉数学数的分解与组合练习题及答案幼⼉数学数的分解与组合练习题及答案 幼⼉数学数的分解与组合练习题及答案 1.通过数的分解与组合，加深对加减法意义的理解。

2.进⼀步熟练１０以内加减法的计算。

3.提⾼学⽣观察、分析、归纳的能⼒。

夯实基础，才能有所突破…… 1、填⼀填。

2、在□⾥填合适的'数。

3.看图列式 (1) (2) □○□=□□○□=□ (3) (4) □○□=□□○□=□ （4）（5） □○□=□□○□=□ 这是⼀座由课内通向课外的桥梁…… 4．妈妈买来了8个西红柿，分给明明和刚刚，他们俩可能得到⼏个？填⼀填。

明明 刚刚 （1） （2）你喜欢哪种分法？（） 5、⼩动物带了⼀些⾹蕉给猴⼦吃。

动物园⼀共有5只猴⼦，如果⼀只猴⼦吃1枝⾹蕉，他们带的⾹蕉够吗？你有⼏种分法？ 6、考考你 把9粒黄⾖给⼩⽅和⼩明两个⼩朋友， 7 跃过去，你就是尖⼦⽣！ 8．把4本本⼦分给⼩⽅和⼩兰， 9.爸爸分糖 这时盘⾥还剩2块，盘⾥原来有⼏块？ 9. 两棵树上共有⿇雀12只，当有3只从第⼀棵树上飞到第⼆棵树上时，两棵树上的⿇雀⼀样多，你知道原来两棵树上各⽤多少只⿇雀？ 答案 1.4 7 7 9 5 2. 略 3. （1）4+2=6 （2）6+2=8 （3）9-4=5 （4）4+5=9 （5）5+5=10 （6）9-2=7 4.略 5. 两种，每个猴⼦分1个；每个猴⼦分2个。

6. 5 67.略 8. 8快 9.9只，3只。

小学二年级数学分解练习题（正文开始）在小学二年级的数学学习中，学生们开始接触到分解数的概念。

分解数是将一个数拆分成若干个数的和的过程，通过分解数的练习，可以帮助学生们更好地理解数的结构和关系，提高他们的计算能力和数学思维能力。

下面是一些适合小学二年级的数学分解练习题，让我们一起来解答。

一、分解和组合1. 将数字7分解成两个比较的数字。

2. 用两个数字，组合出比较大的数字6。

二、分解整数3. 将数字12分解成两个整数。

4. 用两个整数，组合出数字15。

三、扩展分解5. 将数字18分解成两个整数，并且这两个整数之和再分解成两个整数。

6. 将数字24分解成两个整数，并且这两个整数之差再分解成两个整数。

四、分解与运算7. 将数字30分解成两个整数，并计算这两个整数的和。

8. 将数字56分解成两个整数，并计算这两个整数的积。

五、分解与问题解决9. 小明有10块钱，他买了两个相同的木棒，每个木棒的价钱是3块钱。

请帮小明计算一下，他还剩下多少钱？10. 小华有18个橙子，他想将这些橙子分成两堆，每堆橙子的数量一样，你知道每堆有几个橙子吗？六、挑战分解11. 用不重复的两个数字，组合出比较大的两位数，且这两位数的个位数是十位数的2倍。

12. 将数字36分解成两个整数，并且这两个整数之和再分解成两个整数，这两个整数的和是一位数。

以上是小学二年级数学分解练习题。

通过这些练习题的解答，学生们可以加深对分解数的理解，并培养他们的观察力、思维能力和计算能力。

希望学生们能够认真思考，积极解答，提升自己的数学水平。

（正文结束）。

小学数学分解组合练习题1. 一本书的页码用四个数字表示，其中不含有数字0，也不含有数字9。

问这本书最多有多少页？解析：由于不含有数字0和数字9，所以每一个数字都有8个选择（1, 2, 3, 4, 5, 6, 7, 8）。

设这本书的页数为abcd，那么a, b, c, d都有8个选择。

根据乘法原理，一共有8 * 8 * 8 * 8 = 8^4 = 4096 个可能。

因此，这本书最多有4096页。

2. 一家公司共有7个项目，现需要从中选择3个项目进行合作。

问有多少种选择方式？解析：由于需要选择3个项目，所以可以使用组合的方法进行计算。

C(7, 3)表示从7个项目中选择3个的组合数。

根据组合的计算公式，C(7, 3) = 7! / [(3!)(7-3)!] = (7 * 6 * 5) / (3 * 2 * 1) = 35。

因此，有35种选择方式。

3. 小明家有4种水果：苹果、香蕉、橙子和葡萄。

他每天从中选择2种水果搭配作为早餐水果。

问他一共有多少种早餐水果搭配方式？解析：小明每天从4种水果中选择2种水果，可以使用组合的方法进行计算。

C(4, 2)表示从4种水果中选择2种的组合数。

根据组合的计算公式，C(4, 2) = 4! / [(2!)(4-2)!] = (4 * 3) / (2 * 1) = 6。

因此，小明一共有6种早餐水果搭配方式。

4. 一个密码锁的密码为4位数，每一位数字从1-9中选择，且不允许重复。

问一共有多少种可能的密码？解析：由于每一位数字都有9个选择，且不允许重复，所以第一位有9种选择，第二位有8种选择，第三位有7种选择，第四位有6种选择。

根据乘法原理，一共有9 * 8 * 7 * 6 = 3024种可能的密码。

5. 一张纸被折叠3次，问一共有多少种不同的折叠方式？解析：每一次折叠都相当于在已有的折叠方式上新增一种可能性。

第一次折叠有1种方式，第二次折叠有2种方式，第三次折叠有4种方式。

数字的组合与分解练习题在数学学习中，数字的组合与分解是一个重要的基础概念。

通过组合与分解数字，可以深入理解数字的构成方式，拓展思维能力，并为解决实际问题提供帮助。

本文将为大家提供一些数字组合与分解的练习题，以帮助巩固相关概念和技巧。

题一：三位数的组合（1）某三位数的百位数字是3，十位数字是5，个位数字是7，它的值是多少？（2）取两个不同的数字组成最大的三位数，各位数字之和为15，这个三位数是多少？（3）用1、3、5、7四个数字，能组成多少个各位数字都不相同的三位数？解答：（1）根据题意，该三位数是由百位数字3、十位数字5、个位数字7组成，百位数字的实际值是3，十位数字的实际值是5，个位数字的实际值是7。

因此，该三位数的值是357。

（2）设百位数字为a，十位数字为b，个位数字为c。

根据题意，a + b + c = 15，并且要求取两个不同的数字组成最大的三位数。

由于最大的三位数首位数字最大，次位数字次之，所以尽可能取较大的数字。

因此，应取9、6作为百位和十位数字，个位数字为15-9-6=0。

所以，这个三位数是960。

（3）根据题意，各位数字都不相同，且是由1、3、5、7四个数字组成的三位数。

根据排列组合的原理，我们可以得知，百位数字有4种选择，十位数字有3种选择（因为不能重复使用百位数字），个位数字有2种选择（不能重复使用百位和十位数字）。

所以，用1、3、5、7四个数字，能组成4×3×2=24个各位数字都不相同的三位数。

题二：四位数的分解（1）将4279拆分成千位、百位、十位和个位数字。

（2）将9876按从大到小的顺序拆分成千位、百位、十位和个位数字。

（3）将3768按从小到大的顺序拆分成千位、百位、十位和个位数字。

解答：（1）将4279拆分成千位、百位、十位和个位数字，千位数字为4，百位数字为2，十位数字为7，个位数字为9。

（2）将9876按从大到小的顺序拆分成千位、百位、十位和个位数字，千位数字为9，百位数字为8，十位数字为7，个位数字为6。

幼儿园数学分解练习题一、分解组合：64649二、填写组成。

91215820∕﹨∕﹨∕﹨∕﹨∕﹨□ □ 10□ □0□二、计算：8+5= +7= +5=4+9=+7= +9=+5=+7=6+5=3+9=+7= +7=6+6= +5=9-3=7-4=-2=-5=9-4=6-2=8-3=18-5= 17-4=19-6=16-7= 17-8= 15-6= 12-7=25-8= 4-6= 2-15=-17= 3+8=7+6=数学练习一、计算题：4+5=3+6= +5=4+6= -3=3+4=3+8= +7=8-3= -5=7+5=8+8= +6=9-5=8+7=11+5= 13+6= 16-8=17-3=15+4=13+13=14+17= 18-12=17+15= 16+18=27-15=25-17=6+19=28+23=5-19=33-16=35+16= 7-9=34-16=24+15=38+6=-7=31-15=27+13=25+6=27+15=-8=+7=38-9=27+8=26-7=24-15=-7=35-17=四、计算。

+ = + = + = + = + = + = + = + 0 = 0 + = + =1 + 1 =1 + =一、比一比，看谁算的又对又快。

5+4= 0 - 0= +8= 15-5=9-7= 10+2=+6= 13+2= -3= 17-10= -6= 10+10= - 1 = 10-6= 11-3=10+5=6+6=5- = 10+1=4-=＋3＝＋5＝2＋1＝＋6＝5＋2＝＋3＝＋1＝＋7＝二、填空。

13591三、填相邻数36539326数学练习题一、填一填11 1 1 1 12六、下面的数字哪些是单数和双数1 10单数：双数：三、数数。

************************************* *** **五、连线。

628519632981493二、填写阿拉伯数字一十五二十二十二五十七三十六十二七十三三十六十五三、请将下面的物品分成二等分○□▽◇四、加法应用题明明买了5本小人书，妈妈又买了2本小人书给明明，明明现在一共有几本小人书？+ =五、减法应用题盘子里有10个草莓，小红一口气吃了6个草莓，现在盘子里还剩几个草莓？- =二、填空题：1、与10 相邻的两个数分别是和。

幼儿园宝宝分解练习题一．分解组合6∕﹨∕﹨∕﹨∕﹨∕﹨＼／∕﹨＼／ +3= +5= 1+9= +2=5 ＼／＼／106∕﹨∕﹨ 1 ＼／＼／9+8=+4= +4=+3= +4=+5= +1=+6=1) )10-2= -3= -5=9-1= 10-5=-4=5-3= -1=9-2= -6= 10-4=-3= -2=4-1= -5=-3=6-1= -3=6-4= 10-6=+=10 -= +5=1010-= -2= +6=+5=96-= -5=2+=84-=15-=三、填单、双、序、倒和倍数、____ ____ ____ ____ ____ ____ ____ 10 ____ _________ _____ 15_____ _____ 11_____、____ 10 ____ ____0 _____、____ ____ ____ 1____ ____ 1____ 、1 ____ _________ 11 ____ ____ 1____ 、11____ ____ _____ ____ 四、填相邻数102五、比较10比91比715比61比41 比618比91 10比9多比8多比4多比5多比8少比8多1比9多1 比多1比多1 六、看图计算★★★★★ ☆☆☆☆ += -= ◇◇◇◇◇◇◇◇◆◆ += -= 二、加减混合运算。

5+6=7+4=+9=8+9=+3=-4=+5=4=3= 10-2= +2= 10+0= 1+9= 13-4=6-2=-1= +9= +4= -0= 三、按顺序填空。

36比7少比5少1 比少1 12-5= -0=8-7=+8=5+6= +10= 2220135390434569751 9 51 48 四、按顺序填写奇数和偶数。

0 1 10 4261 1 11 297五、按下列得数从小到大排列出来。

3+1=6+3=5+2=3+3=2+3=6+4=1+1=+0=------- ------- ------------- ------ ------ ------ ----- 一、我会算9+6= 17-3=+2= 18+2= 11-3= 10-2= +0=+3=+8= 12+5= 14-8= 19-9= +3+2=-3+4=+3-5= 10-1-4=4数学练习题一、分解组合：9468二、填写组成。

一年级数学组合分解练习题题目：一年级数学组合分解练习题一、组合分解的概念及基本规则组合分解是数学中的一种基本概念和方法，用于将一个数或一个式子分解成多个因数的乘积或求多个数的和。

在一年级的数学学习中，组合分解是一个重要的内容，它可以帮助学生培养观察和逻辑思维能力。

下面我们通过练习题来巩固组合分解的基本规则。

二、练习题示例1. 将数字9组合分解成两个数的和。

解答：9可以拆分为5+4的形式。

2. 将数字12组合分解成三个数的和。

解答：12可以拆分为7+3+2的形式。

3. 将数字15进行组合分解，使得分解出的所有数字之和最小。

解答：15可以拆分为1+1+1+...+1+2的形式，其中共有15个1和1个2。

4. 将数字18进行组合分解，使得分解出的所有数字之和最大。

解答：18可以拆分为9+9的形式，此时分解出的数字和为18。

5. 求出10的全部组合分解形式。

解答：10可以拆分为1+9、2+8、3+7、4+6、5+5的形式。

三、综合练习1. 小明手中有15个苹果，他想把这些苹果分成三堆，每堆苹果数都不一样，那么他有几种不同的分堆方式？解答：根据题目要求，可以进行组合分解，将15拆分成三个数的和。

一种可能的分堆方式为：5+4+6。

2. 小红有12个玩具，她想分给三个朋友，每人至少分到一个，那么她有几种不同的分法？解答：类似于上一题，可以进行组合分解，将12拆分成三个数的和。

一种可能的分法为：1+1+10。

3. 小明和小红一共有20个糖果，他们想分给四个朋友，每人至少分到一个，那么他们有几种不同的分法？解答：将分法进行组合分解，其中的一个可能分法为：1+1+1+17。

四、总结通过以上练习题示例，我们可以看到组合分解在解决实际问题时的重要性。

它可以帮助我们将一个数或一个式子分解成多个因数的乘积或求多个数的和，从而更好地理解数的特性和数学规律。

在一年级的数学学习中，适量的组合分解练习可以帮助学生培养观察和逻辑思维能力，提高他们解决问题的能力。

01数的分解与组成基本概念Chapter分解与组成定义分解组成培养数感为加减法打基础解决实际问题030201数学中重要性及应用总数不变无论一个数如何分解，其总数始终保持不变。

例如，无论将5分解成哪两个数相加，其和始终是5。

分解方式多样5以内的数可以有多种分解方式，如5可以分解成2和3，也可以分解成1和4等。

组成数唯一虽然一个数可以有多种分解方式，但对于每一种分解方式，其组成数是唯一的。

例如，5分解成2和3后，2和3就是5的唯一的组成数。

分解与组成相互对应数的分解与组成是相互对应的，一个数的分解数就是其组成数，反之亦然。

例如，5的分解数2和3就是5的组成数。

5以内数分解与组成特点025的分解方法及实例演示Chapter按顺序逐步分解法01020304将5分解为1和4将5分解为2和3将5分解为3和2将5分解为4和1任意组合分解法不按特定顺序分解强调分解的多样性图形化表示方法使用实物或图形表示5的分解通过图形化表示加深理解实际生活应用举例分享场景组合场景购物场景035的组成方式及规律探究Chapter单一元素组成方式5个相同的元素相加例如5个1相加，即1+1+1+1+1=5。

单一元素重复5次例如一个元素重复5次，也可以表示成5。

1 2 3两个不同的元素组合三个不同的元素组合多于三个元素的组合多元素组合成5情况讨论规律性总结与发现奇偶性规律5是一个奇数，因此它不可能被分解成两个偶数相加。

分解方式有限性对于给定的一个数，其分解方式是有限的。

例如，5只能被分解成1和4、2和3等有限的几种方式。

分解与组成的可逆性如果一个数可以被分解成两个数相加，那么这两个数也可以组合成原来的数。

例如，5可以分解成2和3，那么2和3也可以组合成5。

创意性组合尝试数字与字母组合图形组合将数字与字母进行组合，例如用数字2和字母T过来的2，两者组合起来像生活中的实物组合04练习题巩固知识点掌握Chapter口头回答题目类型书面作业题目类型完成课本或练习册上的5的分解与组成相关练习题。

以内数的分解与组合练习题2的分成：2可以分成0和2，也可以分成1和1.2的组成：2可以由0和2组成，也可以由1和1组成。

2的分成变式：2减去1等于1，2减去0等于2.2的组成变式：1加上1等于2，0加上2等于2.3的分成与组合：3可以分成0和3，1和2，2和1，3和0.也可以由1、2组成，2、1组成，3、0组成。

3的分成变式：3减去0等于3，3减去1等于2，3减去2等于1，3减去3等于0.3的组合变式：1加上2等于3，2加上1等于3，3加上0等于3.4的分成与组合：4可以分成0和4，1和3，2和2，3和1，4和0.也可以由1、3组成，2、2组成，3、1组成，4、0组成。

4的分成变式：4减去0等于4，4减去1等于3，4减去2等于2，4减去3等于1，4减去4等于0.4的组合变式：1加上3等于4，2加上2等于4，3加上1等于4，4加上0等于4.5的分成和组合：5可以分成0和5，1和4，2和3，3和2，4和1，5和0.也可以由1、4组成，2、3组成，3、2组成，4、1组成，5、0组成。

二、5的组合1+4=5.2+3=5.3+2=5.4+1=51.4.2.3.3.2.4.15.5.5.5三、5的分成变式0-5=5.1-4=3.2-3=2.3-2=1.5-1=4.5-2=3.5-3=2.5-4=1四、5的组合变式1+4=5.2+3=5.3+2=5.4+1=5六、6的分成和组合一、6的分成6.6.6.6.6.66.5.4.3.2.11.2.3.4.5.6二、6的组合1+5=6.2+4=6.3+3=6.4+2=6.5+1=61.5.2.4.3.3.3.3.4.2.5.10.1.2.3.4.5三、6的分成变式0-6=6.1-5=4.2-4=2.3-3=0.4-2=2.5-1=4四、6的组合变式1+5=6.2+4=6.3+3=6.4+2=6.5+1=6七、7的分成和组合一、7的分成1+7=8.2+6=8.3+5=8.4+4=8.5+3=8.6+2=8.7+1=8.这是8的组合变式。

小学三年级数的分解练习题题目一：分解整数的加法和减法1. 将数11分解成两个整数的和，其中一个整数是6。

2. 将数18分解成两个整数的和，其中一个整数是12。

3. 将数15分解成两个整数的和，其中一个整数是8。

4. 将数23分解成两个整数的和，其中一个整数是16。

5. 将数29分解成两个整数的和，其中一个整数是21。

6. 将数36分解成两个整数的差，其中一个整数比另一个整数多6。

7. 将数45分解成两个整数的差，其中一个整数比另一个整数多18。

8. 将数56分解成两个整数的差，其中一个整数比另一个整数多24。

题目二：分解整数的乘法1. 用两个整数的乘法分解数24。

2. 用两个整数的乘法分解数40。

3. 用两个整数的乘法分解数56。

4. 用两个整数的乘法分解数72。

5. 用两个整数的乘法分解数90。

6. 用两个整数的乘法分解数28。

7. 用两个整数的乘法分解数48。

8. 用两个整数的乘法分解数64。

题目三：分解整数的除法1. 将数42分解成两个整数的商，其中一个整数是7。

2. 将数56分解成两个整数的商，其中一个整数是8。

3. 将数72分解成两个整数的商，其中一个整数是9。

4. 将数84分解成两个整数的商，其中一个整数是12。

5. 将数96分解成两个整数的商，其中一个整数是16。

6. 将数98分解成两个整数的商，其中一个整数是14。

7. 将数120分解成两个整数的商，其中一个整数是20。

8. 将数144分解成两个整数的商，其中一个整数是18。

题目四：综合分解练习1. 用加法、减法、乘法或除法的组合，将数36分解成两个整数的差，其中一个整数是12。

2. 用加法、减法、乘法或除法的组合，将数48分解成两个整数的和，其中一个整数是16。

3. 用加法、减法、乘法或除法的组合，将数60分解成两个整数的和，其中一个整数是20。

4. 用加法、减法、乘法或除法的组合，将数80分解成两个整数的和，其中一个整数是30。

小学数学分解与合成练习题一、分解与合成的概念及基本原则数学中的分解与合成是指将一个复杂的数或式子拆分成简单的数或式子，或者将简单的数或式子组合成一个复杂的数或式子。

这是解决数学问题中常用的方法之一。

在小学数学中，分解与合成是培养学生思维能力和解决问题能力的重要训练内容。

分解与合成的基本原则是根据问题的要求，将复杂问题分解成若干简单的部分进行逐步求解，或者将多个简单的部分合成为一个整体。

通过合理的分解与合成，可以将原本看似复杂的问题转化为更易解决的简单问题，从而帮助学生更好地理解数学概念和方法，培养他们的逻辑思维和问题分析能力。

二、数的分解与合成练习题1. 将数分解成因数的乘积：(1) 将60分解成两个素数的乘积的形式。

(2) 将96分解成两个不同的素数的乘积的形式。

(3) 将120分解成两个相邻自然数的乘积的形式。

(4) 将84分解成两个整数的积，使其中一个数是另一个数的因数。

(5) 将98分解成两个互质的数的乘积。

2. 将多项式进行因式分解：(1) 将多项式x^2 + 5x + 6分解成两个一次因式的乘积。

(2) 将多项式x^3 − x^2 − 6x分解成两个一次因式的乘积。

(3) 将多项式x^4 − 10x^2 + 9分解成两个二次因式的乘积。

(4) 将多项式x^3 + 8x^2 + 16x + 32分解成两个一次因式和一个二次因式的乘积。

三、分解与合成的解题思路和方法1. 数的分解与合成的解题思路：(1) 求一个数的所有因数，根据题目要求进行分解。

(2) 找出一个数的特殊性质，进行巧妙的分解与合成。

2. 多项式的因式分解的解题思路：(1) 提取公因式，将多项式变为一个公因式和一个因式相乘的形式。

(2) 使用平方差公式、平方和公式等进行分解与合成。

(3) 利用二次因式乘积法则，将多项式分解成两个一次因式的乘积。

四、分解与合成练习题的解答与详细步骤1. 数的分解与合成的解答：(1) 60 = 2 × 2 × 3 × 5(2) 96 = 2 × 2 × 2 × 2 × 3(3) 120 = 10 × 12 = 2 × 5 × 2 × 6 = 2 × 5 × 2 × (2 × 3) = 2 × 10 × 2 × 3 = 20 × 6(4) 84 = 2 × 42 = 2 × 2 × 21(5) 98 = 2 × 7 × 72. 多项式的因式分解的解答：(1) x^2 + 5x + 6 = (x + 2)(x + 3)(2) x^3 − x^2 − 6x = x(x− 3)(x + 2)(3) x^4 − 10x^2 + 9 = (x^2 − 9)(x^2 − 1) = (x− 3)(x + 3)(x− 1)(x + 1)(4) x^3 + 8x^2 + 16x + 32 = (x + 4)(x^2 + 4)五、练习题的拓展在练习题的基础上，可以进一步拓展学生思维，设计更具挑战性的题目。

小学一年级数学数的分解练习题【试卷】题目一：数的分解1. 将下列数分解成个位数和十位数之和：a) 35 = ___ + ___b) 48 = ___ + ___c) 21 = ___ + ___2. 将下列数分解成个位数和十位数之和，并用物品表示出来：a) 26 = ___ + ___，用26颗豆子表示b) 53 = ___ + ___，用53只小石头表示c) 39 = ___ + ___，用39块糖果表示3. 将下列两个数相加，然后将和分解成个位数和十位数之和：a) 17 + 25 = ___ + ___b) 39 + 48 = ___ + ___c) 51 + 63 = ___ + ___题目二：数的组合1. 从下列数中选出两个数相加，使结果等于给出的数：a) 25，选择两个数相加等于12，可以是 ___ + ___b) 37，选择两个数相加等于19，可以是 ___ + ___c) 45，选择两个数相加等于28，可以是 ___ + ___2. 从下列数中选择一个数，然后从另一列中选出一个数相加，使结果等于给出的数：a) 32，选择一个数，再选择一个数与之相加等于19，可以是 ___ + ___b) 47，选择一个数，再选择一个数与之相加等于25，可以是 ___ + ___c) 56，选择一个数，再选择一个数与之相加等于33，可以是 ___ + ___3. 利用下列数字组成两位数，并写出所有可能的组合：a) 3, 8 = ___ 或 ___b) 4, 5 = ___ 或 ___c) 6, 7 = ___ 或 ___题目三：数的识别1. 图中有多少个圆圈？写出答案：___[图：四个圆圈]2. 从下列数中选择出偶数：a) 25，偶数是 ___b) 38，偶数是 ___c) 41，偶数是 ___3. 读出下列两位数的个位数和十位数：a) 17，个位数是 ___，十位数是 ___b) 39，个位数是 ___，十位数是 ___c) 52，个位数是 ___，十位数是 ___题目四：数的排序1. 将下列数按照从小到大的顺序排列：a) 17，25，12，39 = ___，___，___，___b) 23，56，14，48 = ___，___，___，___c) 32，28，45，19 = ___，___，___，___2. 将下列数按照从大到小的顺序排列：a) 35，21，18，42 = ___，___，___，___b) 53，47，29，12 = ___，___，___，___c) 64，39，27，16 = ___，___，___，___3. 比较下列两位数的大小，用"<"或">"填空：a) 17 ___ 25b) 39 ___ 48c) 51 ___ 63【参考答案】（仅供参考）题目一：1. a) 30 + 5b) 40 + 8c) 20 + 12. a) 20 + 6b) 50 + 3c) 30 + 93. a) 10 + 20b) 30 + 40c) 50 + 10题目二：1. a) 25，可以是 7 + 5b) 37，可以是 9 + 8c) 45，可以是 9 + 62. a) 32，可以是 13 + 6b) 47，可以是 22 + 25c) 56，可以是 28 + 283. a) 3, 8 = 38 或 83b) 4, 5 = 45 或 54c) 6, 7 = 67 或 76题目三：1. 四个圆圈2. a) 25，偶数是无b) 38，偶数是38c) 41，偶数是无3. a) 17，个位数是 7，十位数是 1b) 39，个位数是 9，十位数是 3c) 52，个位数是 2，十位数是 5题目四：1. a) 12，17，25，39b) 14，23，48，56c) 19，28，32，452. a) 42，35，21，18b) 53，47，29，12c) 64，39，27，163. a) 17 < 25b) 39 < 48c) 51 < 63。

中班数字分解练习题一、数字分解基础练习1. 请将数字5分解成两个数的和。

2. 请将数字8分解成两个不同的数的和。

3. 请将数字10分解成三个数的和。

4. 请将数字7分解成一个单数和一个双数的和。

5. 请将数字12分解成两个偶数的和。

二、数字分解进阶练习1. 请将数字15分解成三个不同的奇数的和。

2. 请将数字18分解成两个偶数和一个奇数的和。

3. 请将数字20分解成四个数的和，其中三个数为偶数。

4. 请将数字9分解成两个相同的数的和。

5. 请将数字16分解成四个不同的数的和。

三、数字分解应用练习1. 小明有10个糖果，他想分给两个朋友，请写出所有可能的分糖果方式。

2. 小红有8个苹果，她想分给三个小朋友，请写出所有可能的分苹果方式。

3. 小华有12个球，他想分给四个同学，请写出所有可能的分球方式。

4. 请将数字13分解成两个质数的和。

5. 请将数字17分解成一个质数和一个合数的和。

四、数字分解挑战练习1. 请将数字21分解成三个质数的和。

2. 请将数字24分解成四个不同的偶数的和。

3. 请将数字25分解成五个不同的奇数的和。

4. 请将数字30分解成三个不同的数的和，且这三个数的乘积为180。

5. 请将数字11分解成两个质数的和，且这两个质数的差为2。

五、数字分解逻辑推理练习1. 如果数字6可以分解成两个数的和，其中一个数是3，那么另一个数是多少？2. 数字12可以分解成两个数的和，如果其中一个数是5，那么另一个数是奇数还是偶数？3. 请找出所有将数字14分解成两个数的和的方法，其中一个数是质数。

4. 数字20可以分解成一个偶数和一个奇数的和，请写出所有可能的组合。

5. 如果数字18可以分解成三个数的和，且这三个数都不相同，请给出一种分解方法。

六、数字分解创意练习1. 请用数字分解的方式，设计一个加法游戏，使得最终的和为20。

2. 尝试用数字分解的方法，将数字22表示为三个连续整数的和。

3. 请用数字分解的方式，将数字16表示为四个数的乘积。