函数幅频特性曲线

实验十二 幅频特性和相频特性一、实验目的：研究ＲＣ串、并联电路的频率特性。

二、实验原理及电路图 1、实验原理电路的频域特性反映了电路对于不同的频率输入时，其正弦稳态响应的性质，一般用电路的网络函数()H j ω表示。

当电路的网络函数为输出电压与输入电压之比时，又称为电压传输特性。

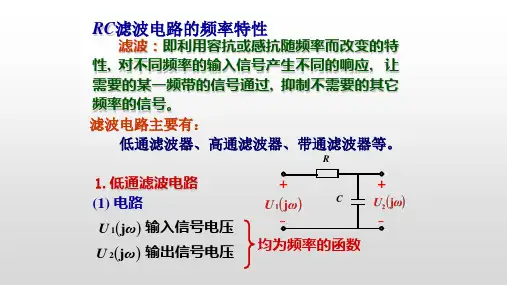
即：()21U H j U ω=1）低通电路U 2图1-1 低通滤波电路 图1-2 低通滤波电路幅频特性 简单的RC 滤波电路如图4.3.1所示。

当输入为1U ，输出为2U 时，构成的是低通滤波电路。

因为：112111U U U j C j RCR j Cωωω=⨯=++所以：()()()2111U H j H j U j RC ωωϕωω===∠+()H j ω=()H j ω是幅频特性，低通电路的幅频特性如图4.3.2所示，在1RCω=时，()0.707H j ω==，即210.707U U =，通常2U 降低到10.707U 时的角频率称为截止频率，记为0ω。

2）高通电路2图2-1 高通滤波电路 图2-2 高通滤波电路的幅频特性12111U j RCU R U j RCR j C ωωω=⨯=⨯+⎛⎫+ ⎪⎝⎭所以：()()()211U j RC H j H j U jRC ωωωϕω===∠+其中()H j ω传输特性的幅频特性。

电路的截止频率01RC ω= 高通电路的幅频特性如4.3.4所示 当0ωω<<时，即低频时()1H j RC ωω=<<当0ωω>>时，即高频时，()1H j ω=。

3）研究RC 串、并联电路的频率特性：Aff 31图15-2f0ϕ︒90︒-90iu ou +--+RR CC图 15-1)1j(31)j (iｏRC RC UUN ωωω-+==其中幅频特性为：22io)1(31)(RC RC U U A ωωω-+==相频特性为：31arctg)(o RCRC i ωωϕϕωϕ--=-=幅频特性和相频特性曲线如图15－2所示，幅频特性呈带通特性。

1、频率响应法
•基本思想是把系统中的信号分解为多种不同频率的正弦信号，这些信号经过控制系统时，会以一定的规律产生幅值和相位的变化，通过分析这些
变化规律就能得出关于系统运动的性能指标。

•由于幅值和相位的变化称频率特性函数可以绘制在图形上，因此该方法非常直观。

另外，可以用实验法建立系统的模型，也可以据开环频率特性分析闭环系统的特性。

该方法具有很高的工程价值，深受工程技术人员欢迎。

6 频率响应分析法2
2、频率特性的图示方法
•为了直观地分析系统的特性，通常把幅频和相频特性以图形的形式表示出来：
1.幅相频率特性（奈氏图）
2.对数频率特性（Bode图）
3.对数幅相特性（尼氏图）
6 频率响应分析法5
2.1 幅相频率特性图
•极坐标图：奈奎斯特(Nyquist)图，幅相特性图，当频率连续变化时，频率特性函数在复平面的运动轨迹。

G(jω)=x(ω)+ j y(ω)
ω：0→+∞
6 频率响应分析法6。

绘制开环对数幅频特性曲线
在控制系统的分析与设计中，开环传递函数是一个重要的概念。

开环传递函数可以反映系统的频率响应特性，为系统的调节与控制提供重要的依据。

本文将以某系统的开环传递函数为例，介绍如何绘制开环对数幅频特性曲线。

开环传递函数是指系统的输出与输入之间的函数关系。

在频率域中，它可以表示为H(jω)，其中ω 是角频率。

对数幅频特性曲线是将开环传递函数的幅值以对数形式绘制的曲线，表示系统在不同频率下的幅值响应。

绘制对数幅频特性曲线的步骤如下：
计算开环传递函数的幅值：H(jω) = |H(jω)|
设定横坐标的范围和刻度，并按照要求选择合适的频率单位。

将开环传递函数的幅值用对数形式表示，即y = log |H(jω)|。

绘制曲线，并观察系统在不同频率下的幅值响应。

绘制完成后，我们就可以通过观察对数幅频特性曲线来了解系统的频率响应特性。

例如，当频率单位为赫兹时，如果对数幅频特性曲线呈现出典型的高通特性，即随着频率的增大，幅值也随之增大，那么这意味着系统在高频时更加灵敏。

如果对数幅频特性曲线呈现出典
型的低通特性，即随着频率的增大，幅值减小，那么这意味着系统在低频时更加稳定。

绘制开环对数幅频特性曲线是了解系统频率响应特性的重要方法。

通过观察对数幅频特性曲线，我们可以了解系统在不同频率下的幅值响应，为系统的调节与控制提供重要的依据。

实验四 二阶开环及闭环系统的频率特性曲线（北京理工大学 自动化学院 班级： 姓名： 学号：）摘要：自动控制中有两个曲线是研究的重点，它们分别是波特图和奈奎斯特曲线，本实验将根据如是电路图有计算机绘制以上两种图，并研究相关参数。

关键词：开环、闭环、波特图、奈奎斯特曲线。

一、 实验目的1. 了解和掌握Ⅰ型二阶闭环系统中的对数幅频特性L （ω）和相频特性，实频特性Re(ω)和虚频特性Im(ω)的计算。

2. 了解和掌握欠阻尼Ⅰ型二阶闭环系统中的自然频率ωn 、阻尼比ξ对谐振频率ωr 和谐振峰值L(ωr)的影响及ωr 和L(ωr) 的计算。

3. 了解阻尼比ξ对开环参数幅值穿越频率ωc 和相位裕度的影响及幅值穿越频率ωc 和相位裕度的计算。

4. 了解和掌握Ⅰ型二阶闭环系统对数幅频曲线、相频曲线和幅相曲线的构造及绘制方法。

二、 实验过程被测系统结构所示被测系统传函：()()()()1()()C s G s s R s G s H s φ==+ 以角频率ω为参数的闭环系统对数幅频特性和相频特性为：()20lg |()|, ()()L j j ωφωφωφω==∠自然频率为n ω=阻尼比为ξ=谐振频率为r ωω=谐振峰值为()r L ω=二阶闭环系统模拟电路的各环节参数：积分环节的积分时间常数11i T R C =⨯=1s ，惯性环节的惯性常数32T R C =⨯=0.1s ，开环增益 3/K R R =。

设K=25（R=4K Ω）， ωn=15.81rad/s ， ξ=0.316.计算得ωr=14.14rad/s ，L （ωr ） =4.44dB 。

二阶闭环系统频率特性测试电路如 图1所示。

图1 二阶闭环系统频率特性测试电路测试结束后（约10min），将显示被测系统的闭环对数幅频、相频特性曲线（bode图）和幅相曲线（奈奎斯特图），分别如下图3、图四所示：图3图4三、实验结果表 1 不同参数系统的谐振频率和谐振峰值开环增益K 惯性常数T积分常数iT谐振频率/(1rad s-⋅) 谐振峰值/dBL计算值测量值计算值测量值25 0.1114.143 14.00 4.443 4.03 0.2 10.604 10.50 7.198 6.67 0.3 8.818 8.00 8.878 7.7720 0.1 0.5 18.708 19.20 6.301 6.09 0.2四、思考题1.说明在实际应用中，开环和闭环的不同特性。

由系统函数怎么求幅频和相频全文共四篇示例，供读者参考第一篇示例：系统函数是描述傅里叶变换频域特性的重要概念，在信号处理和控制系统领域有着广泛的应用。

系统函数通常表示为H(ω)，其中ω为频率，H(ω)描述了输入信号在系统中的传递特性，即输出信号与输入信号之间的关系。

在频域分析中，系统函数的求取是非常重要的步骤，可以通过系统函数求取幅频和相频响应。

求取系统函数的一种基本方法是通过系统的传递函数，传递函数表示系统的输出与输入之间的关系。

传递函数可以表示为H(s)，其中s 为复变量。

借助拉普拉斯变换，可以将系统的微分方程转换为传递函数形式。

传递函数可以通过系统参数和结构来确定，通过传递函数可以求取系统函数H(ω)。

系统函数H(ω)一般可以表示为复数形式，即H(ω) =|H(ω)|e^(jφ)，其中|H(ω)|为幅频响应，φ为相频响应。

幅频响应描述了系统对不同频率信号的增益或衰减程度，相频响应描述了系统对不同频率信号的相位延迟。

在实际计算中，可以通过频率响应曲线来求取系统函数H(ω)的幅频和相频响应。

通过对系统的输入信号进行傅里叶变换，得到输入信号的频谱，再通过传递函数H(s)和输出信号的频谱的卷积运算，得到输出信号的频谱。

通过对比输入信号和输出信号的频谱，可以求取系统函数H(ω)的幅频和相频响应。

另一种方法是通过估计系统的单位脉冲响应来求取系统函数H(ω)的的幅频和相频响应。

单位脉冲响应是系统对单位脉冲信号的响应，可以通过单位脉冲信号的冲激响应函数和系统函数H(ω)之间的卷积运算来求取系统函数的幅频和相频响应。

单位脉冲响应法通常用于线性时不变系统的分析。

在数字信号处理中，可以通过离散系统的差分方程和Z变换来求取系统函数H(ω)的幅频和相频响应。

通过将差分方程转换为系统函数的差分方程表示形式，再通过Z变换得到系统的传递函数H(z)，进而求取系统函数H(ω)的幅频和相频响应。

通过系统函数求取幅频和相频响应是信号处理和控制系统分析的重要步骤。

matlab幅频特性曲线函数
在Matlab中,可以使用freqz函数生成幅频特性曲线。

freqz函数的语法如下：
[H,f] = freqz(b,a,N,Fs)
其中,b和a是数字滤波器的分子和分母系数,N是频率响应曲线上的点数,Fs是采样频率。

例如,下面的代码将生成一个低通Butterworth滤波器的幅频特性曲线：
```matlab
fs = 1000; % 采样频率
fc = 100; % 截止频率
N = 1000; % 绘制点数
[b,a] = butter(6, 2*fc/fs); % 生成Butterworth低通滤波器系数
[H,f] = freqz(b, a, N, fs); % 计算频率响应
plot(f, abs(H)); % 绘制幅频特性曲线
```
上述代码中,首先定义了采样频率fs、截止频率fc和绘制点数N,然后使用butter函数生成Butterworth低通滤波器的系数,最后调用freqz函数计算滤波器的频率响应,并使用plot函数绘制幅频特性曲线。

值得注意的是,freqz函数返回的频率向量f是单位为赫兹（Hz）的,因此在绘制幅频特性曲线的时候,需要将f转换为角频率。

例如,下面的代码将在横轴上绘制角频率：
```matlab
plot(f*2*pi/fs, abs(H));
```。

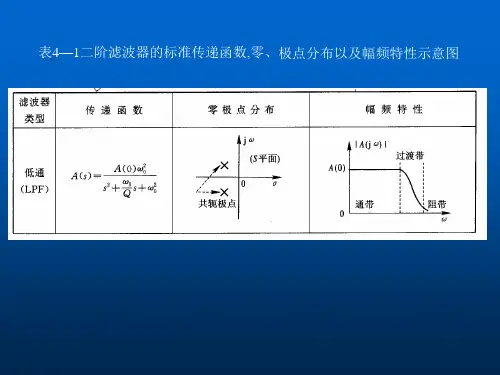
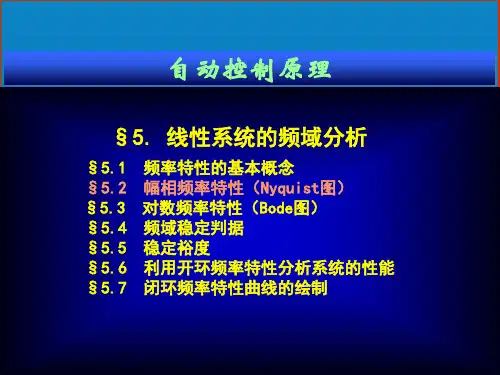
第五章频率特性1．本章的教学要求1) 掌握频率特性的基本概念、性质及求取方法；2) 掌握典型环节及系统的频率特性图一奈奎斯特(Nyquist)图的绘制方法；3) 掌握典型环节及系统的对数频率特性图一波德图(Bode)图的绘制方法；4) 使学生掌握频率特性的实验测定法。

5) 使学生掌握奈奎斯特( N yq u i st )稳定性判据应用；6) 掌握对数频率稳定性判据( Bode 判据)应用；7) 掌握相对稳定性的基本概念，相位裕量Y、幅值裕量K g定义、计算、在Nyquist 图与Bode 图上的表示。

2．本章讲授的重点本章讲授的重点是掌握频率特性的基本概念、求取方法；奈奎斯特(Nyquist) 图的绘制方法；波德图(Bode)图的绘制方法；利用频率特性分析控制系统。

3．本章的教学安排本课程预计讲授14 个学时第一讲5.1 频率特性1．主要内容：1) 频率响应和频率特性2) 频率特性的求取方法3) 频率特性的表示方法2．讲授方法及讲授重点：本讲首先给出频率响应定义，用图说明线性系统稳态响应曲线的特点，由此引出幅频特性、相频特性的概念，然后给出频率特性的定义及数学表达式，利用图及公式说明幅频特性、相频特性、实频特性、虚频特性的关系。

在介绍频率特性的求取方法时，首先说明频率特性一般有三种求法：利用定义求取、根据系统的传递函数来求取、通过实验测得。

在此主要说明和推导根据系统的传递函数来求取的方法, 第三种方法后面介绍。

在介绍频率特性的表示方法时，首先说明频率特性的表示方法主要有如下几种：幅频特性和相频特性图、幅相频率特性图、对数频率特性图、对数幅相频率特性图、实频特性图和虚频特性图，分别简单介绍各自特点，然后强调本章重点介绍幅相频率特性(Nyquist) 图和对数频率特性(Bode) 图。

3．教学手段：Powerpoint 课件与黑板讲授相结合。

4．注意事项：在讲授本讲时，频率特性概念比较抽象，同学不好理解，但此概念在本门课中又非常重要，可以联系实际举几个简单例子说明此概念。

HUNAN UNIVERSITY电路实验综合训练报告学生姓名蔡德宏学生学号201408010128专业班级计科1401班指导老师汪原起止时间2015年12月16日——2015年12月19日一、 实验题目实验十二 幅频特性和相频特性 二、 实验摘要（关键信息）实验十二1、测量RC 串联电路组成低通滤波器的幅频特性和相频特性（元件参数：R=1K Ω，C=0.1uF ，输入信号：Vpp=3V 、f=100Hz~15KHz 正弦波。

测量10组不同频率下的Vpp ，作幅频特性曲线和相频特性曲线）。

2、测量RC 串联电路组成高通滤波器的幅频特性和相频特性（电路参数和要求同上）。

3、测量RC 串并联（文氏电桥）电路频率特性曲线和相频特性曲线。

实验十三1、测量R 、C 、L 阻抗频率特性（电路中用100Ω作保护电阻，分别测量R 、C 、L 在不同频率下的Vpp ，输入信号Vpp=3V 、f=100Hz~100KHz 的正弦波，元件参数：R=1K 、C=0.1uF 、L=20mH ），取10组数据，作幅频特性曲线。

2、搭接R 、L 、C 串联电路，通过观测Ui （t ）和UR(t)波形，找出谐振频率。

将电阻换成电位器，测量不同Q 值的谐振频率。

三、 实验环境（仪器用品）函数信号发生器（DG1022U ），示波器(DSO-X 2012A),电位器（BOHENG3296-w104），3只电阻（保护100Ω，实验1K Ω），电容器(0.1µF)，电感（20mH ），面包板，Multisim 10.0（画电路图），导线若干。

四、 实验原理和电路1、当在RC 和RL 及RLC 串联电路中加上交变电源，并不断改变电源频率时，电路的端口电压U 和电阻U 两端电压也随之发生规律性改变。

1）RC 串联电路的稳态特性有以上公式可知，随频率的增加，I,增加，减小。

当ω很小时2πψ→，电源电压主要降落在电容上，此时电容作为响应为低通滤波器；反之，0→ψ，电压主要将在电阻上，电阻作为响应称为高通滤波器。

几何法画全通系统幅频相频曲线在本文中，我们将深入探讨几何法画全通系统幅频相频曲线的方法和原理。

通过对该主题的深度和广度评估，我们将详细介绍几何法画全通系统幅频相频曲线的步骤和重要概念，以便更全面地理解这一内容。

一、几何法画全通系统幅频相频曲线的基本概念1. 全通系统的定义和概念在进行几何法绘制全通系统幅频相频曲线之前，首先需要了解全通系统的定义和概念。

全通系统是指在一定频率范围内，将输入信号的幅度和相位均传递给输出信号的系统。

全通系统具有独特的频率特性，需要通过幅频相频曲线来表示其传递特性。

2. 幅频相频曲线的重要性和应用幅频相频曲线是描述全通系统频率特性的重要工具，它能够直观地展现系统的幅度响应和相位响应随频率变化的情况。

在信号处理、通信系统等领域，幅频相频曲线具有广泛的应用，对系统性能评估和设计优化起着关键作用。

二、几何法画全通系统幅频相频曲线的步骤1. 确定系统传递函数首先需要根据具体的全通系统，确定其传递函数。

传递函数是描述系统输入与输出之间关系的数学表达式，是绘制幅频相频曲线的基础。

2. 利用几何法绘制幅频相频曲线通过几何法，可以利用传递函数的零点和极点，按照一定的规则和方法，绘制全通系统的幅频相频曲线。

在绘制过程中，需要注意选择合适的频率范围，以及对幅度和相位响应的理解和把握。

三、总结和回顾性内容通过本文的介绍，我们详细了解了几何法画全通系统幅频相频曲线的基本概念和步骤。

全通系统作为一种重要的信号处理系统，在工程应用中具有广泛的意义。

通过深入学习和理解几何法绘制幅频相频曲线的原理，我们能够更好地掌握全通系统的频率特性，从而更好地应用于实际工程中。

个人观点和理解：对于全通系统幅频相频曲线的绘制，我认为几何法是一种直观、形象且易于理解的方法。

通过几何法，可以清晰地看到系统的频率特性，有助于工程师们深入理解全通系统的工作原理和性能特点。

几何法也为工程实践提供了便利，使工程师们能够更好地设计和优化全通系统，满足各种实际需求。

1-5-1 绘制下列传递函数的对数幅频渐进特性曲线：（1）)18)(12(2)(++=s s s G ；解：①确定各交接频率ωi ，i ＝1,2。

惯性环节：ω1＝1/2 －20db/dec 惯性环节：ω2＝1/8 －20db/dec 最小交接频率：ωmin ＝ω2＝1/8②绘制低频段（ω＜ωmin ）渐进特性曲线。

Q υ＝0∴低频渐进斜率k ＝0db/dec又Q La(0.1)＝20lg2－20*0*lg0.1＝6.02db ∴曲线过（0.1，6.02）点③绘制频段（ω≥ωmin ）渐进特性曲线。

ωmin ≤ω＜ω1 k ＝－20db/decω≥ω1 k ＝－40db/dec ④系统开环对数幅频渐进特性曲线如下图：（2）)110)(1(200)(2++=s s s s G ；解：①确定各交接频率ωi ，i ＝1,2。

惯性环节：ω1＝1 －20db/dec惯性环节：ω2＝0.1 －20db/dec 最小交接频率：ωmin ＝ω2＝0.1②绘制低频段（ω＜ωmin ）渐进特性曲线。

Q υ＝2∴低频渐进斜率k ＝－40db/dec又Q La(1)＝20lg200－20*2*lg1＝20lg200＝46.02db∴曲线过（1，46.02）点③绘制频段（ω≥ωmin ）渐进特性曲线。

ωmin ≤ω＜ω1 k ＝－60db/decω≥ω1 k ＝－80db/dec ④系统开环对数幅频渐进特性曲线如下图：（3）)12)(1()11.0(8)(2++++=s s s s ss G ；解：①确定各交接频率ωi ，i ＝1,2,3。

一阶微分环节：ω1＝0.1 20db/dec惯性环节： ω2＝2 －20db/dec 振荡环节： ω3＝1 －40db/dec最小交接频率：ωmin ＝ω1＝0.1②绘制低频段（ω＜ωmin ）渐进特性曲线。

Q υ＝1∴低频渐进斜率k ＝－20db/dec又Q La(1)＝20lg8－0＝20lg8＝18.06db∴曲线过（1，18.06）点③绘制频段（ω≥ωmin ）渐进特性曲线。

1：已知x(t)=1，试用MATLAB 分析其幅频特性曲线。

解：因为x(t)=1是连续非周期信号，其对应的频谱是非周期连续的，对于连续的信号计算机不能直接加以处理，因而，需要将其先离散化，再利用离散傅里叶变换（DFT ）对其进行分析实现其近似计算。

对连续时间信号x(t)可以分解成x(t)=u(t)+u(-t-1)，通过采取不同的采样间隔来分析其频谱。

(a)对x(t)离散化的采样间隔取R=0.005，对F(W)取N=7000，图像如图a ； (b)对x(t)离散化的采样间隔取R=0.01，对F(W)取N=30，图像如图b ； (c)对x(t)离散化的采样间隔取R=0.01，对F(W)取N=7000，图像如图c 。

针对(a)情况的程序如下：R=0.005;t=-5:R:5;f=Heaviside(t)+Heaviside(-t); W1=2*pi*2;N=7000;k=0:N;W=k*W1/N; F=f*exp(-j*t'*W)*R; F=real(F);W=[-fliplr(W),W(2:7001)];F=[fliplr(F),F(2:7001)]; subplot(2,1,1);plot(t,f); xlabel('t');ylabel('x(t)'); title('x(t)函数的图像'); subplot(2,1,2);plot(W,F); xlabel('w');ylabel('F(w)');title('x(t)函数的傅里叶变换F(w)');图a R=0.005，N=7000图b R=0.01，N=30图c R=0.01，N=7000(a)和(c)作对比，时域采样间隔不同。

理论上采样间隔越小，谱分析越接近实际的谱线（在0处是一冲激），由于分辨率区别不是很大，仿真结果视觉效果基本一致。

(b)和(c)作对比，频域采样间隔不同。