等腰直角三角形的旋转

等腰直角三角形等腰直角三角形是指一个三角形的两条边相等，并且其中一个角度为90度。

它是几何学中的常见图形，具有一些独特的性质和特点。

下面将从不同的角度来探究等腰直角三角形的性质和应用。

首先，我们可以从等腰直角三角形的定义开始讨论。

等腰直角三角形由两条长度相等的边和一个90度的直角所构成。

根据直角三角形的性质，直角的两边相互垂直。

而等腰直角三角形的两条边又相等，因此我们可以得出结论：在等腰直角三角形中，直角的两边相互垂直且相等。

其次，等腰直角三角形还满足勾股定理。

勾股定理是指直角三角形中，直角边的平方等于斜边两边的平方和。

由于等腰直角三角形的两个直角边相等，那么我们可以得出：等腰直角三角形的直角边的平方等于等腰直角三角形斜边的平方的一半。

这一性质可以方便地用于解决一些与等腰直角三角形有关的问题。

在几何学中，等腰直角三角形的性质具有广泛的应用。

首先，等腰直角三角形被广泛应用于建筑和工程中的测量和布局。

在建筑设计中，往往需要根据一些特定的角度和尺寸来进行设计，而等腰直角三角形正好满足这些要求。

例如，在设计房屋的墙面、地面和天花板时，常常需要考虑到直角和相等的边。

等腰直角三角形的性质可以帮助我们准确地测量和布局，确保建筑物的结构和比例符合要求。

此外，等腰直角三角形还在数学中有着重要的地位。

它是许多其他几何形状的基础，例如正方形和长方形。

等腰直角三角形的性质可以帮助我们理解和推导这些几何形状的性质和定理。

例如，我们可以通过将一个等腰直角三角形分成两个直角三角形，来证明正方形的对角线相等。

这种推理和证明方法在数学中起着重要的作用，有助于培养逻辑思维和推理能力。

此外，等腰直角三角形还有一些有趣的性质。

例如，等腰直角三角形的两个直角边的长度不一定是整数，也可能是无理数。

这一性质在数学中有着重要的地位，与勾股定理和平方根的概念有关。

等腰直角三角形还可以通过平移和旋转等变换产生其他形状，例如正方形和正五边形。

这种变换性质在几何学中起着重要的作用，有助于研究和理解不同形状之间的关系。

等边三⾓形、等腰直⾓三⾓形之间的旋转问题（精华）等边三⾓形、等腰直⾓三⾓形之间的旋转问题（精华）1、图（1）中，C点为线段AB上⼀点，△ACM，△CBN是等边三⾓形，AN与BM相等吗？说明理由；如图（2）C点为线段AB上⼀点，等边三⾓形ACM和等边三⾓形CBN在AB的异侧，此时AN与BM 相等吗？说明理由；如图（3）C点为线段AB外⼀点，△ACM，△CBN是等边三⾓形，AN与BM相等吗？说明理由．2、如图（1）所⽰，点C为线段AB上⼀点，△ACM、△CBN是等边三⾓形，直线AN、MC交于点E，直线BM、CN交于点F．（1）求证：AN=MB；（2）将△ACM绕点C按逆时针⽅向旋转90°，其他条件不变，在图（2）中补出符合要求的图形，并判断（1）题中的结论是否依然成⽴，说明理由．3、如图，已知△ABC是等边三⾓形，E是AC延长线上⼀点，选择⼀点D，使得△CDE是等边三⾓形，如果M是线段AD的中点，N是线段BE的中点，求证：△CMN是等边三⾓形．（根据△ACD≌△BCE，得出AD=BE，AM=BN；⼜△AMC≌△BNC，可得CM=CN，∠ACM=∠BCN，证明∠NCM=∠ACB=60°即可证明△CMN是等边三⾓形；）1、（锦州）如图A，△ABC和△CEF是两个⼤⼩不等的等边三⾓形，且有⼀个公共顶点C，连接AF 和BE．（1）线段AF和BE 有怎样的⼤⼩关系?请证明你的结论；（2）将图A中的△CEF绕点C旋转⼀定的⾓度，得到图B，（1）中的结论还成⽴吗?作出判断并说明理由；（3）若将图A中的△ABC 绕点C旋转⼀定的⾓度，请你画⼭⼀个变换后的图形C（草图即可），（1）中的结论还成⽴吗?作出判断不必说明理由；（4）根据以上证明、说理、画图，归纳你的发现．（3）此⼩题图形不惟⼀，如图第（1）中的结论仍成⽴．（4）根据以上证明、说理、画图，归纳如下：如图A，⼤⼩不等的等边三⾓形ABC和等边三⾓形CEF有且仅有⼀个公共顶点C，则以点C 为旋转中⼼，任意旋转其中⼀个三⾓形，都有AF=BE．2、如图，ADC ?和BCE ?都是等边三⾓形，ο30=∠ABC ，试说明：222BC AB BD +=（综合全等和勾股定理）3、△DAC, △EBC 均是等边三⾓形，AE,BD 分别与CD,CE 交于点M,N, 求证：（1）AE=BD (2)CM=CN (3) △CMN 为等边三⾓形（4）MN ∥BC4、已知：如图1，点C 为线段AB 上⼀点，△ACM ，△CBN 都是等边三⾓形，AN 交MC 于点E ，BM 交CN 于点F ． (1)求证：AN=BM ； (2)求证：△CEF 为等边三⾓形；(3)将△ACM 绕点C 按逆时针⽅向旋转90 O ，其他条件不变，在图2中补出符合要求的图形，并判断第（1）、（2）两⼩题的结论是否仍然成⽴（不要求证明）．5、如图所⽰，已知△ABC 和△BDE 都是等边三⾓形。

旋转试题篇：抓基本图形，看变化接着上一篇旋转，这篇选取其中一个特例---等腰直角三角形进行讲解。

如图，△ABC和三角形ADE为等腰直角三角形，△ABC固定不动，△ADE绕顶点A顺时针旋转。

不难想象，△ADE的顶点旋转轨迹如图乙所示：D、E始终在在以点A为圆心、AD长为半径的圆上，且长度不变。

图甲图乙在旋转的过程中，我们发现，△ADE的位置可以大致分为三种情况：情况①：一边在△ABC内一边在△ABC外，如图1所示：情况②：一边在△ABC上，如图2所示：情况③：两边都在△ABC外，如图3所示：图1图2图3这三种情况，几何题中，是很常见的，且贯穿整个初中。

请看题：一、对接情况①的常考题。

【题1】⑴问题发现：如图⑴，△ACB和△DCE均为等边三角形，点A,D,E在同一直线上，连接BE。

填空，∠AEB的度数为；线段AD,BE之间的数量关系为；⑵拓展探究如图⑵，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A,D,E在同一直线上，CM为△DCE中DE边上的高，连接BE。

请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由。

【题2】如图，已知等腰直角三角形ABC，点P是斜边BC上一点（不与B，C重合），PE是△ABP的外接圆⊙O的直径．（1）求证：△APE是等腰直角三角形；（2）若⊙O的直径为2，求PC2+PB2的值．二、对接情况②的常考题。

【题3】在△ABC中，AB=BC，∠ABC=90°，F为AB延长线上的一点，点E在BC上，且AE=CF；⑴求证：Rt△ABE≌Rt△CBF;⑵若∠CAE=30°，求∠ACF的度数。

【题4】如图所示，H是△ABC的高AD,BE的交点，且DH=DC，则下列结论：①BD=AD；②BC=AC；③BH=AC；④CE=CD中，正确的有。

三、对接情况③的常考题。

【题5】如图①，已知△ABC，以△ABC的边AB、AC为边，分别向外作等腰直角△ABD和等腰直角△ACE，连接CD、BE、DE。

一个等腰直角三角形中的旋转全等1、（2007年成都）已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连结DH与BE相交于点G。

(!)求证：BF=AC；(2)求证：CE=12 BF；(3)CE与BC的大小关系如何？试证明你的结论。

2、在△ABC中，AD⊥BC, BE⊥AC, D、E为垂足，AD与BE交与点H，BD=AD。

求证：BH=AC。

3、（2006年辽宁沈阳）.如图1，在正方形ABCD中，点E、F分别为边BC、CD的中点，AF、DE 相交于点G，则可得结论：①AF=DE；②AF⊥DE.(不需要证明)。

(1)如图2，若点E、F不是正方形ABCD的边BC、CD的中点，但满足CE=DF.则上面的结论①、②是否仍然成立？(请直接回答“成立”或“不成立”)(2)如图3，若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上，且CE=DF，此时上面的结论①、②是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由.4、如图，△ABC中，∠ACB＝90°，AC＝BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD ⊥BC交CF的延长线于D．求证：（1）AE＝CD；（2）若AC＝12 cm，求BD的长．5、如图所示，△ABC是等腰直角三角形，∠ACB＝90°，AD是BC边上的中线，过C作AD的垂线，交AB 于点E，交AD于点F，求证：∠ADC＝∠BDE．6、在直角三角形ABC 中，∠BAC=90°，AB=AC，点D、E 是直线AC 上的两个动点，且AD=EC，AM⊥BD，垂足为M，AM 的延长线交BC 于N，直线BD 直线NE 相交于点F，试判断三角形DEF的形状，并加以证明。

7、如图，在等腰Rt△ABC中，∠C＝90°，D是斜边上AB上任一点，AE⊥CD于E，BF⊥CD交CD的延长线于F，CH⊥AB于H点，交AE于G．求证：BD＝CG．8、如图（1），在Rt△ABC中，∠BAC=90°,AB=AC,点D、E是直线AC上的两个动点，且AD=CE，AM⊥BD 垂足为M，延长AM交BD于N，直线BD交直线NE于F。

中考数学压轴题分析：等腰直⾓三⾓形与动点轨迹问题本⽂内容选⾃2021年郴州中考数学⼏何压轴题。

题⽬以等腰直⾓三⾓形的旋转为背景，涉及动点轨迹问题，以及等腰三⾓形的存在性问题。

题⽬难度⼀般，不过问法⽐较典型，值得研究。

【中考真题】（2021·郴州）如图1，在等腰直⾓三⾓形中，，点，分别为，的中点，为线段上⼀动点（不与点，重合），将线段绕点逆时针⽅向旋转得到，连接，．（1）证明：；（2）如图2，连接，，交于点．①证明：在点的运动过程中，总有；②若，当的长度为多少时为等腰三⾓形？【分析】（1）由旋转的性质得到边⾓等量关系，再根据SAS证明全等即可。

（2）①由图2可以发现△AEH≌△AFG，由于∠HAG=90°，若要证明∠HFG=90°，只需得到四边形AHFG对⾓互补即可。

由于全等可以得到∠AHE=∠AGF，结论易得。

②当△AGQ为等腰三⾓形时，需要进⾏分类讨论。

需要分3种情况，但是由于点H在线段EF上运动，且不与点E、F重合，那么只需分为两种情况讨论即可。

即类型⼀：当AQ=GQ时，∠AQG=90°。

还有类型⼆：当AG=GQ时，∠GAQ=∠GQA=75°。

【答案】（1）证明：如图1，由旋转得：，，，，，；（2）①证明：如图2，在等腰直⾓三⾓形中，，，点，分别为，的中点，是的中位线，，，，，，，，，，，；②分两种情况：如图3，时，，，，，，，，，，，四边形是正⽅形，，，，当的长度为时，为等腰三⾓形；如图4，当时，，，，，，当的长度为2时，为等腰三⾓形；综上，当的长度为或2时，为等腰三⾓形．。

等腰直角三角形旋转问题的分类探析
等腰直角三角形旋转可以分为内旋转和外旋转这两种类型。

内旋转是指三角形以坐标原点为中心点，把三角形以某一角为基准，以顺时针或者逆时针
方向旋转，这种旋转属于位置之内不改变三角形的形状以及三个边的长度。

外旋转是指三角形不以坐标原点为中心点，而是将三角形的顶点向外或者向内三角形旋转，形成新的三角形。

这种方式可以改变三角形的形状，改变三个边的长度。

两种旋转方式会产生不同的解法。

因为长方形旋转中有三角形和它的对边，那么可以推导
出对应的三角形的边长。

这就是内旋转的解决方案。

外旋转的解决方案则更为复杂，因为
在旋转之后，三角形的形状和边长都发生了改变，需要先把改变后的三角形按照已有信息
重新拟合并进行外旋转解决方案，从而确定新三角形的顶点坐标。

从上面可以看出，等腰直角三角形旋转分为内旋转和外旋转两种类型，其中内旋转需要利
用已有信息，推导出三角形的边长；而外旋转需要把改变后的三角形按照已有信息重新拟
合并进行外旋转，从而确定新三角形的顶点坐标。

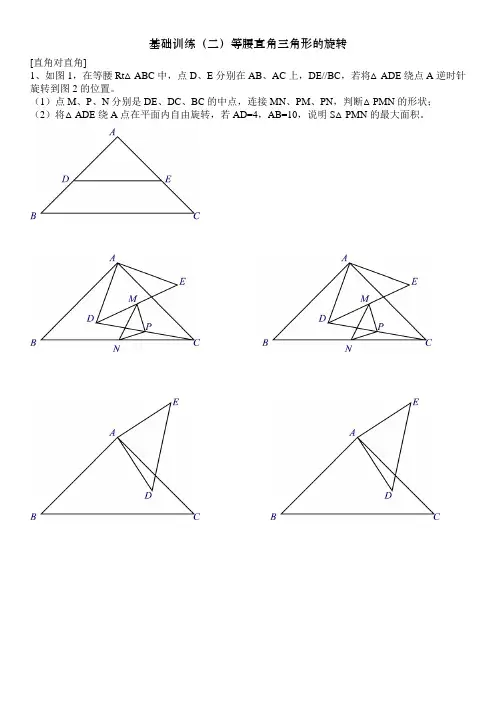
基础训练（二）等腰直角三角形的旋转[直角对直角]1、如图1，在等腰Rt△ABC中，点D、E分别在AB、AC上，DE//BC，若将△ADE绕点A逆时针旋转到图2的位置。

（1）点M、P、N分别是DE、DC、BC的中点，连接MN、PM、PN，判断△PMN的形状；（2）将△ADE绕A点在平面内自由旋转，若AD=4，AB=10，说明S△PMN的最大面积。

2、在Rt△ABC中，∠A=90°，∠B=45°，AC=4，D、E分别为AB、AC的中点。

若Rt△ADE绕A 点逆时针旋转，得到△ADE，如图1，设旋转角为α（0<α<180°），记BD与CE交于P。

（1）探求BD、CE的数量关系和位置关系；（2）如图2，CE=2时，求α；[锐角对锐角]1、已知等腰直角三角形△ABC与△DEC中，CE=DE，AB=AC，∠CED=∠CAB=90°。

（1）将△DCE绕C点旋转至如图1位置，N是BD中点，试探求EN与AN的关系并证明；（2）如图2，M是CD的中点，BE交AM于F，求AM与BE的数量关系。

2、等腰直角三角形△ABC与△AEF中，∠ACB=∠AEF=90°，连接EC、BF，点D为BF中点，连接CD。

（1）如图1，当点E落在AB边上时，探求线段EC与CD的数量关系，并证明；（2）将△AEF绕点A顺时针旋转至图2位置，探求线段EC与CD的数量关系，并证明。

如图1，△ABC与△DCE均为等腰Rt△，∠BAC=∠DCE=90°，点O为DE中点，连AD，以AB、AD为邻边作平行四边形ABFD，连AF。

（1）当D在线段AC上时，如图1，判断线段AF与AO的数量关系和位置关系；（2）若AB=4，CE=2，在图1的基础上，将△CED绕C点继续逆时针旋转到某一位置如图2，此时平行四边形ABFD 为菱形，求AF的长度。

如图，AB垂直平分CD于O，AB=BC，E是BC延长线上一点，F为DB延长线上一点，连接AE、AF，∠EAF=∠EBF。

D F，(1)设F点的坐标是(x，y)，求x、y之间的关系;( 2) 求线段DF 的最小值．( 3) 求 F 点经过的路径的长．图6 图7七、反思解题改善教学高效课堂常见于课堂容量大，教师分析、讲解高位切入、云端行走，把学生的质疑、分析、修改、反思寄希望于课下或者同一节课辗转题目之间时的时间缝隙，这样的做法恰恰忽视了数学“逻辑关联、前后一致”的本质，久而久之，学生的深层次的逻辑思维能力、逻辑严谨性没有培养起来，解题总是停留在刻意模仿的阶段( 形式运算阶段) ，与“培养学生走上社会所需要的各种能力”的数学教育理念大相径庭．通过研究以上变式题目使笔者深深体会到欲通过一道“孤立”的难题培养学生的各方面的能力不可小觑，教师的引导要脚踏实地，一步一个脚印，帮助学生按照知识源、方法论与解题需求关联性的远近程度排列并串联起来，方是题目解法的自然生成，也能够体现题目在培育人的逻辑思维完善性、严谨性等方面的重要价值．此外，教学时可详尽剖析各知识源的异同点和使用条件、特征与范围，以提高学生的辨析与应用能力［1］．总之，尊重教育教学规律、尊重学生的数学现实、尊重数学学科的特点，步步为营、环环相扣才能够释放出解题的精彩，流露出切实的学生本位，让学生获得对于他生命成长有意义的东西．参考文献:［1］刘华为．从教“怎样做”到教“怎样想”［J］．中学数学教学参考:中旬，2016(6):26 －28．［1．山东省淄博市周村区王村中学(255300)2．山东省淄博市周村区第三中学(255300)］双等腰直角三角形旋转定值问题探究■熊猛摘要: 等腰直角三角形是特殊的等腰三角形( 有一个角是直角) ，也是特殊的直角三角形( 等腰) ，因此等腰直角三角形具有等腰三角形和直角三角形的所有性质( 如三线合一、勾股定理、直角三角形斜边中线定理等) ．旋转问题中的定值问题的解决，一般思路是从特殊到一般，化动为静．本文对双等腰直角三角形中的旋转定值问题进行探究，以期读者通过本专题的思考，2D E2．图1 图2学会抓住基本图形及基本数量关系解决问题．关键词: 双等腰直角三角形; 旋转; 定值旋转问题中有一个非常经典的数学问题:等腰直角△A B C中，D为B C的中点，E 为A B边上一动点，∠E D F=90°，交A C于点F．我们可以得出很多结论，比如:①A E =C F;②D E =D F;③C F2+B E2=解决这个问题的策略很简单，连结AD，证明△A D E ≌△C D F，上面的结论很容易得出．对这个问题，我们可以做如下的简单变化．变式1:等腰直角△A B C中，D为B C的中点，△EDF 是以点D 为顶点的等腰直角三角形，连结BE、A F，△E D F绕点D旋转过程中，B E 和A F有何关系?实质上通过A D，证明△BD E ≌△A D F，很容易得作者简介: 熊猛( 1972 －) ，男，四川巴中人，中学高级教师，主要从事初中数学教学研究槡 槡槡图3 图4 出问题结论: 相等且互相垂直． 如果我们再做如下变化呢?变式 2: △A B C 与 △E F G 是等腰直角三角形，D 为斜边 B C 、 GF 的中点， 连 结 AF 、CE ， 问 △EFG 绕点D 旋转过程中，A F 与图9 图10 形，G 为 A C 、D E 的中点，连结 C D 、B F ，问 C D 与 B F 有何关系?本题同样可以根据上述分析问题的方式，可以联想到解决该问题的关键与 BG 、FG 这两条连线有关，事实上，两等边三角形两条中线与边的高之间有如下关CE 有何关系?解决这个问题，似乎难度就图5 系: B G = 3 C G ，F G = 3 D G ，从而B GCG = FG DG = 槡3 ， 而 上来了，作图准确的情况下，很容易看出 AF 与CE 的关系是相等且互相垂直． 当然，我们在解决这个问题时， 我们可以分两个步骤思考:步骤 1: 特殊情况( 存在好些种特殊情形)∠AGD = ∠FGD = 90°，图11 图12 则∠A G D + ∠B G D = ∠F G D + ∠B G D ，即 ∠B G F= ∠C G D ，所以 △B G F ∽ △C G D ，图6 图7 第二步: 对这些特殊情形的 所以BF CD= B G= 3 ． 若证 B F ⊥ C D ，只需延长C D CG分析，我们可以看出上述两种情形都与 AD 、DE 相关，因此一般情形下，我们连结 AD 、DE ，就很容易发现△A D F ≌ △C D E ． 从而可 证得结论: AF 与 CE 的关系是相 图8 等且互相垂直．我们再对变式 2 进行变式:变式3: △A B C 与 △E F G 是等腰直角三角形，D 为斜边 B C 、G F 的中点，连结 A E 、C G ，问 △E F G 绕点 D 旋转过程中，A E 与 C G 有何关系? 对这个问题的变式，我想大家很容易就可以分析出 △A D E ≌ △C D G ，从而推出结论． 再将变式 2 中的 “等腰直角三角形”改为“等边三角形”，就可以改变成如下的问题:变式 4: 如图 11，△A B C 与 △D E F 均为等边三角交 B F 于点 M ，通过相似，可有 ∠G B F = ∠G C D ，加上一对对顶角，从而 ∠B MC = ∠B G C ，则B F ⊥CD ． 我们还可对顶点的位置做如下变式:变式5: 如图13，△A B C 与△A D E 是等腰直角三角形，连结 BD ，C E ，判断 BD 与C E 的关系．图13 图14 分析: 很容易证明到: △A DB ≌ △A E C ，则 BD = C E ，∠A DB = ∠A C E ，因此∠ABC + ∠BCE + ∠ACE = ∠ABC + ∠BCE + ∠A DB = 90°，从而BD ⊥ C E ． 我们还可以发现，双等腰直角三角形问题与斜边·6·上的中线有关联，因此我们又可以有如下的变式．变式6:如图15，△A B C与△A D E 是等腰直角三角形，F、G分别为E D、B C的中点，试判断C E 和F G的数量关系．看是不是更容易了．变式8:如图19，已知△A B C和△A D E 都是等腰直角三角形，A为它们的公共直角顶点，把△A D E 绕点A 顺时针旋转α角( 0 ＜α＜90°)，点M 是BE 的中点，连分析: 如图16，ACAG= AEAF= 槡2 ，结A M、C D，判断A M与C D的关系．∠EAF = ∠CAG = 45°，所以∠CAE = ∠FAG，所以△CAE ∽ △FAG所以CEFG= AEAF= 槡2 ．图19 图20分析: 本题是一道难度颇大的问题，但在变式5中，已经得到BD =CE 这个结论，可以给我们启发，作B C、C D中点，连结M G、N G，则根据中位线定理，易得MG = NG，且MG ⊥ NG，从而容易得到△AMG ≌图15 图16如果将一等腰直角三角形的顶点绕一锐角顶点变换，可做如下变化．变式7:如图17，△A B C与△D C E 是等腰直角三角形，F、G分别为E D、B C的中点，连结A E，F G．若A C= 2C E，若A E =3，求F G的长．图17 图18分析:连结C F，根据以上题目的分析，很容易想到:△CNG，实际上是△AMG 绕点G 旋转了90°得到△C N G，因此A M=C N= 1 C D，垂直关系也很容易得2出了．到这里:我们再来总结回顾双直角三角形绕点旋转问题，一方面，主要用到以下等腰三角形的重要结论: ① 两条直角边相等; ② 斜边上的中线等于斜边的一半; ③ 三线合一; ④ 等腰直角三角形三边比例为1 ∶ 1∶ 槡3 ; 另一方面，解决双等腰直角旋转问题中定值问题，先从特殊到一般，关键是动中求静，灵活运用有关数学知识解决问题．第三，在解题过程中要善于总结，抓住基本图形及基本数量关系解决同类问题．参考文献:AC =CE 而=C G=2，∠A C G=∠E C F=45°，从CF［1］吕小文．双等腰直角三角形”模型的探究与应用［J］．学苑教育，2015(9):45．［2］吴国庆．例谈旋转中的双等腰直角三角形［J］．△A C E ∽△G C F，因此A E =A C=槡2 ，所以F G=中小学数学:初中版，2016(7 －8):66 －67．槡2 AE =3 槡2 ．GF CG［广东省深圳市龙岗中学( 518116) ］2 2事实上:如图，△A B C与△D C E 是等腰直角三角形，F、G分别为E D、B C的中点，连结A E，F G．则一定会有: AEFG= 槡2 ．到这里，我们再来解决一道综合性更大的问题，看·7·槡2 C G槡2 C F。

中考数学图形旋转难？用5个模型就能搞定旋转的定义在平面内，将一个图形绕一个定点沿某个方向转动一定的角度，这样的图形变换称为旋转，这个定点叫旋转中心，转动的角度叫旋转角。

旋转变换不改变图形的形状和大小通过旋转，图形上的每一点都绕旋转中心沿相同的方向转动同样大小的角度旋转变换前后的图形有下列性质:(1)对应点到旋转中心的距离相等，(2)对应点与旋转中心的连线所成的角等于旋转角;(3)对应线段相等，对应线段的夹角等于旋转角，对应线段的垂直平分线都经过旋转中心。

常见的几种模型旋转类型题目举例1、正三角形类型在正ΔABC中，P为ΔABC内一点，将ΔABP绕A点按逆时针方向旋转60°，使得AB与AC重合。

经过这样旋转变化，将图（1-1-a）中的PA、PB、PC三条线段集中于图（1-1-b）中的一个ΔP'CP 中，此时ΔP'AP也为正三角形。

例1如图（1-1），设P是等边ΔABC内的一点，PA=3，PB=4，PC=5，∠APB的度数是________.2、正方形类型在正方形ABCD中，P为正方形ABCD内一点，将ΔABP绕B点按顺时针方向旋转90°，使得BA与BC重合。

经过旋转变化，将图（2-1-a）中的PA、PB、PC三条线段集中于图（2-1-b）中的ΔCPP'中，此时ΔBPP'为等腰直角三角形。

例2如图（2-1），P是正方形ABCD内一点，点P到正方形的三个顶点A、B、C的距离分别为PA=1，PB=2，PC=3。

求正方形ABCD面积。

3、等腰直角三角形类型在等腰直角三角形ΔABC中，∠C=90°,P为ΔABC内一点，将ΔAPC绕C点按逆时针方向旋转90°，使得AC与BC重合。

经过这样旋转变化，在图（3-1-b）中的一个ΔP'CP为等腰直角三角形。

例3如图，在ΔABC中，∠ACB=90°，BC=AC，P为ΔABC内一点，且PA=3，PB=1，PC=2。