矩阵8

8阶离散余弦变换矩阵。

离散余弦变换（DCT）是一种常用的信号处理技术，广泛应用于图像和视频压缩、音频编码和解码等领域。

它通过将信号分解成一系列正弦基函数的加权和，实现信号在频域的表示和处理。

8阶离散余弦变换矩阵是一个8×8的矩阵，用于将8×8的图像块转换为频域表示。

这个矩阵是由一组正弦基函数构成，每个基函数在空域上是离散的，但在频域上是连续的。

通过对图像块进行离散余弦变换，可以得到图像块在频域上的系数，这些系数可以用于图像压缩和其他信号处理任务。

离散余弦变换的过程可以简单概括为以下几个步骤：
1. 将图像块进行预处理，例如减去均值或进行颜色转换等操作。

2. 将预处理后的图像块分成8×8的小块。

3. 对每个小块进行离散余弦变换，得到小块在频域上的系数。

4. 将频域系数进行量化，即将系数的精度降低，以减小数据量。

5. 对量化后的系数进行编码，以便于储存或传输。

离散余弦变换的主要优点是能够将图像数据在频域上进行压缩，使得图像可以更高效地储存和传输。

同时，它还具有一定的抗噪性能，可以减小图像信号受到噪声干扰的影响。

然而，离散余弦变换也有一些局限性。

它不能很好地处理图像中的边缘和纹理等高频信息，容易导致图像出现锯齿状的伪影。

为了克服这些问题，人们提出了一些改进的离散余弦变换方法，如离散小波变换等。

离散余弦变换作为一种常用的信号处理技术，在图像和视频编码等领域具有重要的应用价值。

通过合理地利用离散余弦变换，我们可以实现对图像和视频数据的高效处理和传输，为多媒体技术的发展做出贡献。

在有限元分析中，应变矩阵是一个重要的概念，用于描述物体在受力后形状和尺寸的变化。

对于一个八节点六面体单元，应变矩阵的构建通常基于节点坐标和节点位移。

假设我们有一个六面体单元，其8个节点分别为N1到N8。

每个节点有三个自由度：x、y和z方向上的位移。

假设每个节点的位移分别为u、v和w。

首先，我们需要定义一个参考应变矩阵B。

对于一个六面体单元，B可以表示为：
B = [B1 B2 B3]
其中，B1、B2和B3是参考应变矩阵的三个子矩阵：
B1 = [0 0 0 0 0 0 0 0]
B2 = [0 0 0 0 0 0 0 0]
B3 = [0 0 0 0 0 0 0 0]
然后，我们可以根据节点的位移来更新B：
B1 = [∂u/∂x ∂u/∂y ∂u/∂z u/x u/y u/z u/x² u/y²]
B2 = [∂v/∂x ∂v/∂y ∂v/∂z v/x v/y v/z v/x² v/y²]
B3 = [∂w/∂x ∂w/∂y ∂w/∂z w/x w/y w/z w/x² w/y²]
其中，偏导数表示节点位移对坐标的偏导数，而其他项则基于偏导数和节点位移计算得出。

最后，我们可以将B与刚度矩阵K相乘，以得到节点力：
F = KB
注意，这只是一种常见的有限元分析方法，并且实际情况可能因具体的应用和需求而有所不同。

建议查阅相关文献或咨询专业人士以获取更准确的信息。

第八章 λ—矩阵一 内容概述 1 基本概念 1)λ— 矩阵 设p 是一个数域，λ是一个文字，则称以数域P 上λ的多项式作为元素的矩阵为λ—矩阵，记为 A （λ）,B(λ)等。

2)λ—矩阵的运算：加法，减法，乘法，数乘和转置等，伴随矩阵，行列式，λ—矩阵的秩。

可逆λ—矩阵，λ—矩阵的初等变换，λ—矩阵的等价。

3)行列式因子：设m*n 的 —矩阵A(λ)的秩为r ，对于正整数k,1≤k ≤r 在A(λ)中所有k 级子式的首项系数为1的最大公因式称为 A(λ) 的K 级行列式因子。

记为D K (λ). 4)—矩阵的标准形，不变因子()()()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛0...0...21x r x x d d d r ≥1,d i (λ)(i=1,2….r )是首项系数为1的多项式且d i (λ)|d 1+i (λ)(i=1,2,…r -1)称为A(λ) 的标准形。

d 1(λ),d 2(λ),…d r (λ)称为A(λ) 的不变因子。

5)行列式因子与不变因子的关系：D K (λ)=d 1(λ)…d k (λ)k=1,2,…r. d 1(λ)=D 1(λ)d k (λ)=()()λλ1-K K D D K=2,3…r6)初等因子，设 A 与 n*n 矩阵，把A 的每个次数大于0不变因子分解成互不相同的一次因式之方幂的乘积，所有这些一次因式的方幂（相同的按出现的次数计算）称为A 的初等因子。

A 的初等因子和不变因子相互唯一决定。

7）若当标准形⎪⎪⎪⎪⎪⎭⎫⎝⎛S J J J ...21 J i 为若当块 2. 矩阵等价的充分必要条件：设A ()λ与B ()λ都是s ⨯n 的λ--矩阵 则A ()λ≅B ()λ 〈=〉P ()λA ()λQ ()λ=B ()λ其中P ()λ和Q ()λ都是可逆矩阵A ()λ与B ()λ有相同的标准形 〈=〉A ()λ 与B ()λ有相同的行列式因子 〈=〉A ()λ与B ()λ有相同的不变因子3．矩阵相似的充分必要条件： 设A,B 都是n 阶方阵则 〈=〉λE-A ≅λE-B〈=〉A 与B 有相同的初等因子 〈=〉A 与B 有相同的不变因子〈=〉λE-A 与λE-B 有相同的标准形4矩阵A 与对角矩阵相似的充分必要条件： （1） 有个线性无关的特征向量 （2） 初等因子全是一次的 （3） 最小多项式无重根5如何求矩阵A 的若当标准形。

第八章 矩阵特征值计算1 特征值性质和估计工程实践中有许多种振动问题，如桥梁或建筑物的振动，机械机件的振动，飞机机翼的颤动等，这些问题的求解常常归纳为求矩阵的特征值问题。

另外，一些稳定分析问题及相关问题也可以转化为求矩阵特征值与特征向量的问题。

1.1 特征值问题及性质设矩阵n n ⨯∈A R （或n n ⨯C ），特征值问题是：求C λ∈和非零向量n R ∈x ，使λ=Ax x (1.1)其中x 是矩阵A 属于特征值λ的特征向量。

A 的全体特征值组成的集合记为sp()A 。

求A 的特征值问题(1.1)等价于求A 的特征方程()det()0p I λλ=-=A (1.2)的根。

因为一般不能通过有限次运算准确求解()0p λ=的根，所以特征值问题的数值方法只能是迭代法。

反之，有时为了求多项式111()n n n n q a a a λλλλ--=++++的零点，可以把()q λ看成矩阵123101010n a a a a ----⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦的特征多项式（除(1)n -因子不计）。

这是一个Hessenberg 矩阵，可用QR 方法求特征值，从而求出代数方程()0q λ=的根。

矩阵特征值和特征向量的计算问题可分为两类：一类是求矩阵A 的全部特征值及其对应的向量；另一类是求部分特征值（一个或几个、按模最大或最小）及其对应的特征向量。

本章介绍部分特征值和特征向量的幂法、内积法；求实对称矩阵全部特征值的雅可比法、Given 方法和Householder 方法；求任意矩阵全部特征值的QR 算法。

在第5章已给出特征值的一些重要性质，下面再补充一些基本性质。

定理1 设n n R ⨯∈A ，则(1) 设λ为A 的特征值，则λμ-为μ-A I 的特征值；(2) 设12,,,n λλλ是A 的特征值，()p x 是一多项式，则矩阵()p A 的特征值是12(),(),,()n p p p λλλ。

8阶矩阵以至特征方程求初等因子与不变因子在线性代数中，矩阵是一个非常重要的概念，而其特征方程、初等因子和不变因子又是矩阵理论中的重要内容。

而针对8阶矩阵以及通过特征方程求初等因子与不变因子的问题，我们需要对矩阵、特征值和初等因子有深入的认识。

1. 矩阵的基本概念我们需要了解矩阵的基本概念。

矩阵是一个由数字排成的矩形数组，其中的数字称为矩阵的元素。

而8阶矩阵则是指有8行8列的矩阵。

矩阵在线性代数、概率统计和计算机图形学等领域有着广泛的应用，因此深入理解矩阵的性质是非常重要的。

2. 特征值与特征向量接下来，我们将介绍特征值与特征向量的概念。

对于一个n阶矩阵A，如果存在一个n维非零向量x和一个标量λ使得Ax=λx成立，那么λ称为矩阵A的特征值，而x称为相应于特征值λ的特征向量。

通过求解特征值和特征向量，我们可以对矩阵的性质有更深入的理解。

3. 特征方程的求解特征方程是求解特征值的一种重要方法。

对于n阶矩阵A，其特征方程为|A-λI|=0，其中I为n阶单位矩阵，λ为特征值。

通过解特征方程，我们可以求得矩阵的特征值，进而求得其特征向量，从而对矩阵进行更深入的分析。

4. 初等因子与不变因子我们将介绍初等因子与不变因子的概念。

对于一个n阶矩阵A，如果λ为其特征值，而m为其重数，那么(λI-A)^m的不变因子即为λ的初等因子。

初等因子与不变因子是矩阵理论中非常重要的概念，其求解对于矩阵的性质分析有着重要的作用。

在深入了解了矩阵的基本概念、特征值与特征向量以及特征方程的求解之后，我们可以更好地求解初等因子与不变因子的问题，进而对矩阵的性质有更全面的理解和分析。

总结回顾本文通过介绍矩阵的基本概念、特征值与特征向量以及特征方程的求解，探讨了求解初等因子与不变因子的方法。

通过深入的讨论和分析，我们可以更好地理解并应用矩阵理论，对于相关问题有更深入的认识和掌握。

个人观点与理解在我看来，矩阵理论是非常重要且深奥的数学分支之一。

yeren矩阵8进8出切换器使用说明摘要：1.概述2.功能与特点3.使用方法4.注意事项5.结束语正文：一、概述yeren 矩阵8 进8 出切换器是一款高性能的矩阵切换设备，适用于各种音视频信号的切换和分配。

它具有8 路输入和8 路输出，支持多种信号格式，可广泛应用于会议室、教学系统、家庭影音、监控系统等领域。

二、功能与特点1.高性能：yeren 矩阵8 进8 出切换器采用高品质的芯片和先进的工艺制造，具备出色的信号传输性能和稳定性。

2.广泛兼容：该切换器支持多种信号格式，如VGA、HDMI、DVI、Audio 等，满足不同应用场景的需求。

3.灵活切换：用户可以通过遥控器、面板按键或者RS-485 控制信号的切换，操作简单便捷。

4.智能保护：设备具备智能检测和保护功能，能够自动检测信号并进行相应的保护，确保设备运行安全可靠。

三、使用方法1.连接线路：根据需要将输入设备（如电脑、摄像机等）连接到切换器的输入端口，将输出设备（如投影仪、监视器等）连接到切换器的输出端口。

2.启动设备：分别开启输入设备和输出设备，确保它们处于正常工作状态。

3.操控切换：使用遥控器、面板按键或者RS-485 控制设备进行信号切换，实现不同信号之间的自由切换。

4.调整参数：如需调整信号的显示效果，可进入设备的菜单界面进行相关参数的设置。

四、注意事项1.在使用过程中，请勿将设备暴露在潮湿、高温或者强磁场环境中，以免影响设备的正常运行。

2.在进行连接时，请确保各接口的连接正确无误，避免因接错线导致的设备损坏。

3.如遇到问题，请勿自行拆卸设备，以免造成不必要的损坏。

建议联系专业技术人员进行处理。

五、结束语yeren 矩阵8 进8 出切换器凭借其优异的性能、广泛的兼容性、灵活的切换方式以及智能保护功能，成为了音视频信号切换设备的理想选择。

第八章 λ-矩阵本章主要介绍λ-矩阵及其性质，并用这些性质证明若当标准形的主要定理。

§1 λ-矩阵如果一个矩阵的元素是λ的多项式，即][λP 的元素，这个矩阵就称为λ-矩阵。

为了与λ-矩阵相区别，我们把以数域P 中的数为元素的矩阵称为数字矩阵。

由于数域中的数也是][λP 中的元素，所以在λ-矩阵中包括以数为元素的矩阵，即数字矩阵为λ-矩阵的一个特殊情形。

同样可以定义一个λ-矩阵的行列式，既然有行列式，也就有λ-矩阵的子式的概念。

利用这个概念。

我们有定义1 如果λ-矩阵)(λA 中有一个r )1(≥r 级子狮不为零。

而所有1+r 级子式（如果有的话）全为零，则称)(λA 的秩为r ，零矩阵的秩规定为零。

定义2 一个n n ⨯的λ-矩阵)(λA 称为可逆的，如果有一个n n ⨯的λ-矩阵)(λB 使)(λA )(λB =)(λB )(λA =E （1） 这里E 是n 级单位矩阵。

适合（1）的矩阵)(λB （它是唯一的）称为)(λA 的逆矩阵，记为)(1λ-A关于λ-矩阵可逆的条件有定理1 一个n n ⨯的λ-矩阵)(λA 是可逆的充分必要条件为行列式|)(|λA 是一个非零的数。

§2 λ-矩阵在初等变换下的标准形λ-矩阵也有初等变换。

定义3 下面的三种变换叫做λ-矩阵的初等变换：（1）矩阵的两行（列）互换位置；（2）矩阵的某一行（列）乘以非零的常数c ；（3）矩阵的某一行（列）加另一行（列）的)(λΦ倍，)(λΦ是一个多项式。

初等变换都是可逆的，并且有))(())((),,(),(111---==c i p c i p j i p j i p ,))(,())(,(1ϕφ-=-j i p j i p 。

为了写起来方便起见，我们采用以下的记号：],[j i 代表j i ,行（列）互换位置；)]([c i 代表用非零的数c 去乘i 行（列）；)]([φj i +代表把j 行（列）的)(λφ倍加到i 行（列）。

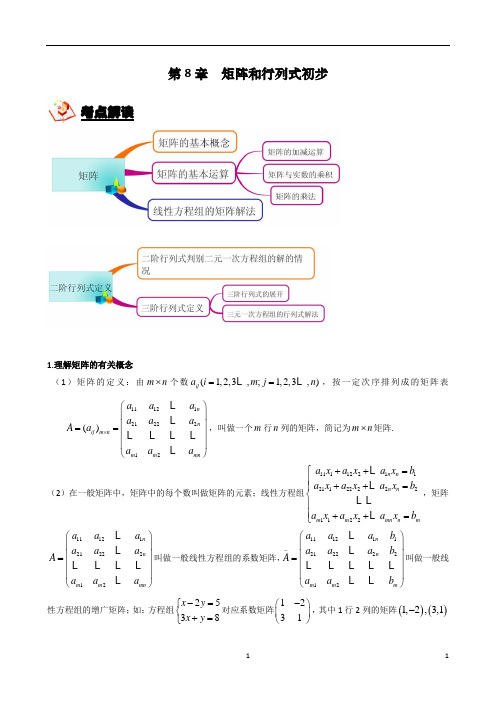
第8章矩阵和行列式初步考点解读1.理解矩阵的有关概念（1）矩阵的定义：由m n⨯个数(1,2,3,;1,2,3,)ija i m j n==L L，按一定次序排列成的矩阵表111212122212()nnij m nm m mna a aa a aA aa a a⨯⎛⎫⎪⎪==⎪⎪⎝⎭LLL L L LL，叫做一个m行n列的矩阵，简记为m n⨯矩阵.（2）在一般矩阵中，矩阵中的每个数叫做矩阵的元素；线性方程组11112211211222221122n nn nm m mn n ma x a x a x ba x a x a x ba x a x a x b++=⎧⎪++=⎪⎨⎪⎪++=⎩LLL LL，矩阵A=111212122212nnm m mna a aa a aa a a⎛⎫⎪⎪⎪⎪⎝⎭LLL L L LL叫做一般线性方程组的系数矩阵，A-=11121121222212nnm m ma a a ba a a ba a b⎛⎫⎪⎪⎪⎪⎝⎭LLL L L L LL L叫做一般线性方程组的增广矩阵；如：方程组2538x yx y-=⎧⎨+=⎩对应系数矩阵1231-⎛⎫⎪⎝⎭，其中1行2列的矩阵()()1,2,3,1-叫做系数矩阵的两个行向量；2行1列的矩阵12,31-⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭叫做系数矩阵的列向量；（3）当矩阵的行数与列数相等时，该矩阵称为方矩阵，简称方阵；我们把主对角线元素为1、其余元素均为零的方矩阵，如1001⎛⎫⎪⎝⎭，叫做单位矩阵.2.矩阵的运算及其性质（1）矩阵的加法，若111212122212()n n ij m nm m mn a a a a a a A a a a a ⨯⎛⎫⎪ ⎪== ⎪⎪⎝⎭L L L L L L L，111212122212()n n ij m n m m mn b b b b b b B b b b b ⨯⎛⎫ ⎪⎪== ⎪ ⎪⎝⎭LL L LL L L，则C A B =+=111112121121212222221122n n n n m m m m mn mna b a b a b a b a b a b a b a b a b +++++++++L LL L L L L.（2）矩阵的加法满足性质: 交换律,结合律.（3）数与矩阵乘法定义：以数k 乘矩阵()ij A a =的每个元素所得的矩阵()ij ka 叫做数k 与矩阵A 相乘的积，记作kA ； （4）设矩阵111211121112212221222122,,a a b b c c A B C a a b b c c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.如果它们元素间的关系可以用下列等式表示：1122(1,2;1,2)ij i j i j c a b a b i j =+==，则C 叫做矩阵A 和矩阵B 的积，记作C =AB（5）矩阵A 的初等变换，指的是对A 实施如下变换：3．行列式的有关概念与性质（1）初中代数中，二元线性方程组111222,a x b y c a x b y c +=⎧⎨+=⎩当12210a b a b -≠时，二元线性方程组有唯一解：1221122112211221c b c b x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩，为了方便记忆，引入定义a c b d =ad bc -，a c b d 叫做二阶行列式， ad bc -叫做二阶行列式的展开式；设1122a b D a b =，1122x c b D c b =，1122y a c D a c =，则方程组的唯一解可表示为：xy D x D D y D⎧=⎪⎪⎨⎪=⎪⎩. （i ）0D ≠，方程组有唯一解；（ii ）0D =：①x y D D 、中至少有一个不为零，方程组无解； ②0x y D D ==，方程组有无穷多解.（3）三阶行列式的两种展开方法：①按对角线展开.123123123a b c b c a c a b=++321123132a b c b a c a b c---②按一行（或一列）展开.111222333a b ca b ca b c=123231312321213132a b c a b c a b c a b c a b c a b c++---123321322312332()()()a b c b c b a c a c c a b a b=-+-+-(4)把三阶行列式某元素所在的行和列划去，剩下的元素组成的二阶行列式，叫做这个元素的余子式；如果用,i j分别表示某个元素所在的行数和列数，那么这个元素的余子式．补充与提高：行列式运算性质：①把行列式的某一行的所有元素乘以一个数k，等于用k乘以这个行列式；②行列式中某一行所有元素的公因子可以提到行列式记号的外边；③如果行列式中某一行的元素全为0，那么这个行列式的值为0；④交换行列式的任意两行，行列式的绝对值不变，符号相反；⑤如果行列式有两行的对应元素相同，那么这个行列式的值为0；⑥如果行列式有两行的对应元素成比例，那么这个行列式的值为0；⑦如果行列式的某一行的元素都是二项式，那么这个行列式等于把这些二项式各取一项组成相应的行，而其余行不变的两个行列式的和；例如：111222222333a b ca ab bc ca b c'''+++=111222333a b ca b ca b c+111222333a b ca b ca b c'''.注意：红线上三元素的乘积均为正，蓝线上三元素的乘积均为负.乘以(1)i j+-所得的式子，叫做这个元素的代数余子式.（5）三阶行列式D 等于它的任意一行（或列）的所有元素分别和它们的代数余子式的乘积的和.例如：111222333a b c D a b c a b c ==222222a A b B c C ++.(6)三元线性方程组111122223333a x b y c z d a x b y c z d a x b y c z d ++=⎧⎪++=⎨⎪++=⎩，对应系数行列式111222333a b c D a b c a b c =,111222333x d b c D d b c d b c =，111222333y a d c D a d c a d c =，111222333z a b d D a b d a b d =.①当0D ≠时，方程组有唯一解x y z D x D D y D D z D ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩；②当0=0x y D D D =且，时，方程组有无穷多解；③当0x y D D D =且，不全为0时，方程组无解.(7)①三角形的面积公式: △ABC 的三个顶点坐标分别为112233(,),(,),(,)A x y B x y C x y ，则ABC S =△11223311121x y x y x y .②同一平面上A B C 、、三点共线的充要条件为112233111x y x y x y =0.8.1矩阵的概念例题精讲【例1】写出下列线性方程组的系数矩阵和增广矩阵：（1）3560437x y x y ++=⎧⎨=-⎩（2）214625x z y z x y z -=⎧⎪+=⎨⎪-+=⎩一个元素的代数余子式通常用这个元素相应的大写字母并附加相同的下标来表示【参考答案】（1）35356,43437-⎛⎫⎛⎫ ⎪ ⎪---⎝⎭⎝⎭ （2）1021021014,01462112115--⎛⎫⎛⎫⎪ ⎪⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭8.2矩阵的运算例题精讲【例1】已知矩阵 3 0-2 1A ⎛⎫= ⎪⎝⎭，矩阵-2 1 2 2B ⎛⎫= ⎪⎝⎭，求矩阵X ，使其满足B X A =-32．【参考答案】813320⎛⎫-⎪ ⎪ ⎪-⎝⎭【例2】已知下列矩阵⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛--=3110146,602413,591732C B A ，计算： （1）A(B+C) (2)(B+C)A (3)BA+CA (4)从（1）（2）（3）的计算结果你能得出什么结论？ 【参考答案】（1）1198245⎛⎫ ⎪⎝⎭ （2）151842234610131133---⎛⎫ ⎪-- ⎪ ⎪---⎝⎭ （3）151842234610131133---⎛⎫ ⎪-- ⎪ ⎪---⎝⎭（4）(B+C)A= BA+CA8.3二阶行列式例题精讲【例1】展开并化简下列行列式： （1）3423- （2）245lg 2lg - 【参考答案】（1）17- （2）2lg 24lg5+【例2】判断m 取什么值时，下列关于x,y 的线性方程组（1）有唯一解？（2）无解？（3）有无穷解？⎪⎩⎪⎨⎧=+-+-=--1)1()1(1)5(22y m x m y m x【参考答案】221(5)(1)(2)(3)1(1)m D m m m m m --==++-+-+221(5)2(1)(2)1(1)x m D m m m ---==-+-+11211y D m m -==++（1）1,2,3m ≠--时，方程组有唯一解； （2）13m =-或 方程组无解； （3）2m =-方程组有无穷解．8.4三阶行列式例题精讲【例1】按要求计算下列行列式（1）直接化简计算行列式D=412101423--的值； （2）按照第一行展开； （3）按照第一列展开． 【参考答案】（1）19D = （2）011110324142421D --=-+（3）01242431214141D ---=-+-【例2】通过对课本知识的学习，我们知道，对于三元一次方程组⎪⎩⎪⎨⎧=++=++=++333322221111dz c y b x a d z c y b x a d z c y b x a ，其中x ，y ，z是未知数，系数)3,2,1(=i c b a i i i 、、不全为零，当系数行列式D=0时，方程组无解或有无穷多解． 以下是几位同学在D =0的条件下，类比二元一次方程组的解的情况，对三元一次方程组的解的情况的一些探索结论：结论一：当D=0，且0===z y x D D D 时，方程组有无穷多解 结论二：当D=0，且都z y x D D D ,,不为零时，方程组有无穷多解 结论三：当D=0，且0===z y x D D D 时，方程组无解．可惜的是这些结论都不正确，下面分别给出了一些反例，现在请你分析一下，这些给出的方程组分别是哪个错误结论的反例，并说出你的理由．（A ）⎪⎩⎪⎨⎧=++=++=++232132032z y x z y x z y x （B ）⎪⎩⎪⎨⎧=+=++=+0420202y x z y x y x （C ）⎪⎩⎪⎨⎧=++=++-=+230212z y x z y x y x【参考答案】 （A ）x y z D D D D ====而方程组无解，是结论一的反例． （B ）x y z D D D D ====而方程组无穷多解，是结论三的反例． （C ）0125x y z D D D D ====- 而方程无解，是结论二的反例．过关演练2020年一模汇编——矩阵、行列式一、填空题【宝山2】已知5124=--λλ，则=λ . 【答案】3【解析】由行列式的运算得：524=---)()(λλ，即3=λ【杨浦2】 关于x ，y 的方程组2130x y x y -=⎧⎨+=⎩的增广矩阵为【答案】211130-⎛⎫⎪⎝⎭【解析】根据增广矩阵的含义，所以是211130-⎛⎫⎪⎝⎭【长宁，嘉定，金山3】行列式12 31-的值为_______.【答案】7【解析】行列式的化简，12 31-=711--32=⨯⨯）（【浦东4】若关于y x 、的方程组为12x y x y +=⎧⎨-=⎩，则该方程组的增广矩阵为____________．【答案】111112⎛⎫⎪-⎝⎭【解析】矩阵行列式定义【松江6】若关于x y 、的二元一次方程组42mx y m x my m+=+⎧⎨+=⎩无解，则实数m =【答案】2- 【解析】令24401m D m m==-=，2m ∴=±；令22420x m D m m mm+==-=，得0m =或2；令22201y m m D m m m+==--=，得2m =或1-；因为方程组无解，0D ∴=，x D 、y D 不同时为0，2m ∴=-二、选择题【黄浦13】方程2153x x=的解集是（ ） 【A 】{2} 【B 】{2,2}- 【C 】{1,1}- 【D 】{i,i}- 【答案】B【解析】2235,2x x -==±，解集是{2,2}-2020届高三数学一轮复习典型题专项训练6、（2019届嘉定长宁区高三二模）若线性方程组的增广矩阵为2012m n ⎛⎫⎪⎝⎭，则m n +=7、（2019届普陀区高三二模）行列式中第2行第1列元素的代数余子式的值为﹣10，则k＝ ．8、（2019届徐汇区高三二模）函数cos2sin ()3cos x xf x x-=在区间(0,]2π上的最小值为9、（宝山区2018高三上期末）关于x y ，的二元一次方程组x y x y 341310+=⎧⎨-=⎩1、（2019届黄浦区高三二模）行列式1247的值为 2、（2019届闵行松江区高三二模）若x 、y 的方程组10240x my x y n +-=⎧⎨-+=⎩有无穷多组解，则11m n 的值为3、（2019届浦东新区高三二模）若行列式128012x -=，则x =4、（2019届杨浦区高三二模）函数arcsin 211xx y =-的值域是5、（2019届宝山区高三二模）方程sec 301sin x x=的解集为__________的增广矩阵为 （ ）（A ）3411310-⎛⎫⎪-⎝⎭ （B ）3411310⎛⎫ ⎪--⎝⎭ （C ）3411310⎛⎫⎪-⎝⎭ （D ）3411310⎛⎫ ⎪⎝⎭10、（奉贤区2018高三上期末）关于x 、y 的二元一次方程组的增广矩阵是⎪⎪⎭⎫⎝⎛222111c b a c b a ，则方程组存在唯一解的条件是（ ）．A ．⎪⎪⎭⎫⎝⎛21a a 与⎪⎪⎭⎫ ⎝⎛21b b 平行 B ．⎪⎪⎭⎫ ⎝⎛21a a 与⎪⎪⎭⎫ ⎝⎛21c c 不平行 C ．⎪⎪⎭⎫ ⎝⎛21a a 与⎪⎪⎭⎫⎝⎛21b b 不平行 D ．⎪⎪⎭⎫ ⎝⎛21b b 与⎪⎪⎭⎫ ⎝⎛21c c 不平行 11、（杨浦区2018高三上期末）已知一个关于x 、y 的二元一次方程组的增广矩阵是112012-⎛⎫⎪⎝⎭，则x y += 12、（虹口区2019届高三一模）若复数sin i 1cos iz θθ-=（i 为虚数单位），则||z 的最大值为 13、（宝山区2019届高三上期末（一模））关于,x y 的二元一次方程组的增广矩阵为12-3015⎛⎫⎪⎝⎭，则x y += ．14、（奉贤区2019届高三上期末（一模））下列以行列式表达的结果中，与sin()αβ-相等的是（ ）A.sin sin cos cos αβαβ- B.cos sin sin cos βαβα C. sin sin cos cos αβαβ D. cos sin sin cos ααββ-15、（黄浦区2019届高三上期末（一模））已知三阶行列式123456789，元素8的余子式的值与代数余子式的值之和为16、（闵行区2019届高三上期末（一模））方程110322x =-的解为17、（浦东新区2019届高三上期末（一模））不等式2log 1021x >的解为18、（松江区2019届高三上期末（一模））若增广矩阵为1112m m m m +⎛⎫⎪⎝⎭的线性方程组无解，则实数m 的值为19、（徐汇区2019届高三上期末（一模））若数列{}n a 的通项公式为*2()111n na n N n n=∈+，则lim n n a →∞=___________.20、（杨浦区2019届高三上期末（一模））在行列式274434651xx--中，第3行第2列的元素的代数余子式记作()f x ，则1()y f x =+的零点是参考答案： 二、行列式1、－12、33、34、14[,]22ππ-+ 5、,3x x k k Z ππ⎧⎫=-+∈⎨⎬⎩⎭6、37、－148、9、C 10、ｃ 11、－16012、1213、－8 14、C 15、0 16、2log 5x = 17、(4,)+∞ 18、－1 19、－1 20、－1。

矩阵基本性质标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]矩阵的基本性质矩阵A的第A第A列的元素为A AA。

我们A A或（A）表A×A的单位矩阵。

1.矩阵的加减法（1）A=A±A,对应元素相加减（2）矩阵加减法满足的运算法则a.交换律：A+A=A+Ab.结合律：(A+A)+A=A+（A+A）c.A+A=Ad.A−A=A2.矩阵的数乘（1）A=A A，各元素均乘以常数（2）矩阵数乘满足的运算法则a.数对矩阵的分配律：A(A+A)=A A+A Ab.矩阵对数的分配律：(A+A)A=A A+A Ac.结合律：(AA)A=A(A A)d.A?A=A3.矩阵的乘法（1）A=A A×A A A×A，左行右列对应元素相乘后求和为C的第A行第A列的元素（2）矩阵乘法满足的运算法则a.对于一般矩阵不满足交换律，只有两个方正满足且有AA=AA=Ab.分配律：A(A+A)=AA+AAc.结合律：(AA)A=A(AA)d.数乘结合律：A(AA)=A(A A)4.矩阵的转置A A, (A A)AA=A AA（1）矩阵的幂：A1=A,A2=AA,…,A A+1=A(A A)（2）矩阵乘法满足的运算法则a. (A A)A=Ab. (A+A)A=A A+A Ac. (A A)A=A(A A)d. (AA)A=A A A A5.对称矩阵：A A=A即a AA=a AA；反对称矩阵：A A=−A即a AA=−a AA （1）设A,A为（反）对称矩阵，则A±A仍是（反）对称矩阵。

（2）设A,A为对称矩阵，则AA或AA仍是对称矩阵的充要条件AA=AA。

（3）设A 为（反）对称矩阵，则A A ，A A 也是（反）对称矩阵。

（4）对任意矩阵A ，则A ≡12(A +A A ),A ≡12(A +A A )分别是对称矩阵和反对称矩阵且A =A +A .（5）(A A )A =A6. Hermite 矩阵：A A =A 即a AA =a AA ̅̅̅̅̅̅̅；反Hermite 矩阵，A A =−A即a AA =−a AA ̅̅̅̅̅̅̅ a.A A =(A ̅)Ab. (A +A )A =A A +A Ac. (A A )A =A ̅̅̅(A A )d. (AA )A =A A A Ae. (A A )A =Af. (A A )−A =(A −A )A （当A矩阵可逆时）7.正交矩阵：若A A A =A A A =A ,则A ,(A )∈A A ×A 是正交矩阵（1）A −A =A A ∈A A ×A（2）det A =±1（3）AA , AA ∈A A ×A8.酉矩阵：若A A A =A A A =A ,则A ,(A )∈A A ×A 是酉矩阵（1）A −A =A A ∈A A ×A（2）|det A |=1（3）AA , AA ∈A A ×A（4）A A ∈A A ×A9.正规矩阵：若A A A =A A A ,则A 是正规矩阵；若A A A =AA A ,则A 是实正规矩阵10.矩阵的迹和行列式（1）AA (A )=∑A AA A A =A =∑A A A A =A 为矩阵A 的迹；|A |或det (A )为行列式（2）AA (AA )=AA (AA )；注：矩阵乘法不满足交换律（3）AA (AAA )=AA (AAA )=AA (AAA )（4）A =AAA , A 为酉矩阵，则AA (A )=AA (A )（5）|A A +AA A |=|A A +A A A |（6）|A A +AA A |=|A A +A A A |（7）|A A |=|A |（8）|A A |=A A |A |（9）|AA |=|A ||A |（10）det (A +AA )=det (A +AA )（11）|A |=∏A A A A =A（12）A =log [det (A A +AAA ∗)], A =A A A A ，则 A =∑log (1+A AA A )A A =1其中A A 为AA ∗奇异分解值的特征值11.矩阵的伴随矩阵A ∗（1）设A ={A AA }由行列式|A |的代数余子式A AA 所构成的矩阵（2）AA ∗=A ∗A =|A |A12.矩阵的逆（逆矩阵是唯一的）（1）A 的逆矩阵记作A −A , AA −A =A −A A =A ;（2）|A |≠0（A 为非奇矩阵）时，A −A =A|A |A ∗（3）|A |≠0且A ≠0，则(A A )−A =1A A −A（4）由AAA −A A −A =A ，得(AA )−A =A −A A −A（5）(A A )−A =(A −A )A（6）若|A |≠0，|A −A |=A|A |（7）若A 是非奇上（下）三角矩阵，则A −A 也上（下）三角矩阵（8）A −A =(A −A )A（9）(A −A +A A A −A A )−A A A A −A =AA A (AAA A +A )−A（10）(A +AA )−A A =A (A +AA )−A（11）Woodbury 恒等式 :(A +AA −A A )−A =A −A −A −A A (A +AA −A A )−A AA −A（12）A −A =A ∧−1A A12.对角矩阵，矩阵A 为对称矩阵，A 正交矩阵，则A −A AA =AAAA(A A ,A A )为对角矩阵或A −A AA =A A AA =AAAA (A A ,A A )=∧，则A =A ∧A A =∑A A A A A A A A A =A ; A −A =A ∧−1A A =∑1A AA A A A AA A =A 13.矩阵的导数（1）A (AA )=A A A +A A A（2）A (A −A )=−A −A A A A −A（3）A AA |A |=AA (A −A A A )（4）A AA AA (AA )=A AA（5）A AA (AA )=A A（6）A AA (A A A )=A（7）A AA (A )=A（8）A AA (AAA A )=A (A +A A )AA|A|=(A−A)A （9）A。

int8 矩阵乘法矩阵乘法是线性代数中的基本运算之一，它可以帮助我们解决许多实际问题。

在本文中，我们将以人类的视角，用朴实的语言来描述int8矩阵乘法的过程和意义。

矩阵乘法是将两个矩阵相乘得到一个新的矩阵的运算。

我们先来看一下什么是int8矩阵。

int8是一种数据类型，表示一个8位的整数，范围从-128到127。

矩阵是由一组按照特定排列方式排列的数所组成的二维数组。

当我们将两个int8矩阵相乘时，我们将按照一定的规则对矩阵中的元素进行运算，最终得到一个新的int8矩阵。

在矩阵乘法中，两个矩阵的乘积的行数等于第一个矩阵的行数，列数等于第二个矩阵的列数。

假设我们有一个3行2列的矩阵A和一个2行4列的矩阵B，它们的乘积C将会是一个3行4列的矩阵。

矩阵C中的每个元素都是通过对矩阵A的一行和矩阵B的一列进行一系列乘法和求和运算得到的。

为了更好地理解矩阵乘法的过程，让我们以一个具体的例子来说明。

假设我们有一个2行2列的矩阵A和一个2行2列的矩阵B，它们的乘积C将会是一个2行2列的矩阵。

我们可以按照以下步骤进行计算：我们将矩阵A的第一行和矩阵B的第一列对应元素相乘，并将结果相加。

这样我们得到了C的第一个元素。

然后，我们将矩阵A的第一行和矩阵B的第二列对应元素相乘，并将结果相加。

这样我们得到了C的第二个元素。

接下来，我们将矩阵A的第二行和矩阵B的第一列对应元素相乘，并将结果相加。

这样我们得到了C的第三个元素。

我们将矩阵A的第二行和矩阵B的第二列对应元素相乘，并将结果相加。

这样我们得到了C的第四个元素。

通过这样的计算，我们就得到了矩阵C。

这个过程可能看起来有些繁琐，但是它可以帮助我们解决许多实际问题。

例如，在计算机图形学中，矩阵乘法可以用来进行坐标转换和变换矩阵的组合。

总的来说，int8矩阵乘法是一种基本的线性代数运算，它可以帮助我们解决许多实际问题。

通过对矩阵中的元素进行一系列乘法和求和运算，我们可以得到一个新的int8矩阵。