河南省宝丰县杨庄镇八年级数学下册1.3线段的垂直平分线导学案1(无答案)(新版)北师大版

课题：1.3 线段的垂直平分线班级: 姓名: 小组: 评价:【学习目标】1.证明线段垂直平分线的性质定理和判定定理．2.能够证明三角形三边垂直平分线交于一点。

3.能够利用尺规作已知线段的垂直平分线和已知底边及底边上的高作出等腰三角形。

【重点难点】重点：证明线段垂直平分线的性质定理和判定定理难点：证明三线共点【导学流程】一、基础感知：1.线段的垂直平分线性质定理：线段垂直平分线上的到的。

2.线段的垂直平分线的判定定理：到的的，在这条线段的。

二、深入学习3.已知：如右图，直线MN⊥AB，垂足是C，且AC=BC，P是MN上的点．求证：P A=PB．证明：∵∴∵∴∴数学语言表述：∵∴4. 已知：如图，在△ABC 中，AB = AC，O 是△ABC 内一点，且 OB = OC.求证：直线 AO 垂直平分线段BC。

．问题记录5.用尺规作出下列三角形三边的垂直平分线，你发现什么结论？归纳： （称作三角形的外心）6. 在锐角三角形ABC 中，∠B AC =50°，AC 、BC 的垂直平分线交于点O ，则∠1__∠2，∠3____∠4，∠5____∠6，∠2+∠3=______°，∠1+∠4=______°，∠5+∠6=______°，∠BOC =___ _°三、迁移应用7.三角形的外心的性质：三角形三条边的垂直平分线交于一点 ，并且这一点到三个顶点的距离相等. 已知：求证：证明：8. 已知一个等腰三角形的底边及底边上的高，求作这个等腰三角形．已知：线段a、h求作：△ABC，使AB=AC，BC=a，高AD=h作法：四、当堂检测：1.如图，在△ABC中，∠C = 90°，DE是ABBD = ；若∠B = 40°，则∠BAC =°，∠DAB =∠DAC = °。

若AC= 4， BC = 5，则△ACD的周长为。

2.如图，D为BC边上一点，且BC=BD+AD，则AD__________DC，点D在__________的垂直平分线上。

线段的垂直均分线一、问题引入：1.什么是线段的垂直均分线？2.你会画线段的垂直均分线？3.“线段的垂直均分线上的点到这条线段的两个端点的距离相等”你能证明这一结论吗？二、基础训练：议一议：写出“线段的垂直均分线上的点到这条线段的两个端点的距离相等”这一命题的抗命题？它是真命题吗？假如是，请证明，并与伙伴沟通.做一做：阅读P25 做一做，而后用尺规作出右图已知线段AB的垂直均分线CD，并说明为何CD是线段 AB的垂直均分线？A B反省：怎样用尺规作图确立已知线段的中点？三、例题展现：例：如图在△ ABC 中， AD是∠ BAC均分线 ,AD 的垂直均分线分别交 AB.BC延伸线于 F.E求证：（ 1）∠ EA D=∠EDA ;（2）DF∥AC（3）∠ EAC=∠B四、讲堂检测 :1.已知：线段 AB 及一点 P，PA=PB，则点 P 在上 .2.已知：如图，∠ BAC =1200, AB=AC,AC的垂直均分线交BC于 D则∠ ADC=.3.第 1 题第 4 题第 5题△ABC中，∠ A=500， AB=AC，AB的垂直均分线交 AC于 D则∠ DBC的度数.4.△ABC中， DE.FG 分别是边 AB.AC 垂直均分线，则∠B∠BAE，∠C∠GAF，若∠ BAC=1260，则∠ EAG=.5.如图，△ ABC 中， AB=AC=17，BC=16，DE垂直均分 AB，则△ BCD的周长是.6.有特大城市 A 及两个小城市 B.C，这三个城市共建一个污水办理厂，使得该厂到 B.C 两城市的距离相等，且使 A 市到厂的管线最短，试确立污水办理厂的地点 .中考真题：已知：如图，DE是△ ABC的 AB 边的垂直均分线，分别交AB.BC 于 D.E， AE均分∠BAC，若∠ B=3 00，求∠C。

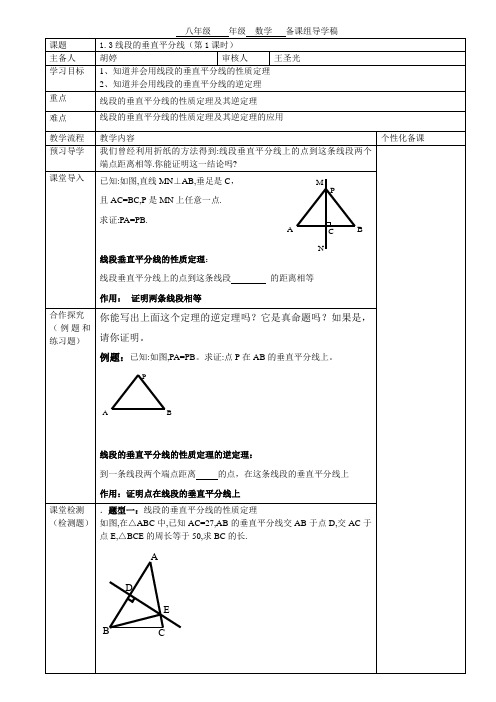
1.3 线段的垂直平分线第1课时线段的垂直平分线的性质和判定1.会证明线段的垂直平分线的性质定理及判定定理。

2.能运用线段的额垂直平分线的性质定理及判定定理进行相关的证明与计算。

阅读教材P22-23习题之前的内容，学生独立完成下列问题：1．CD是线段AB的垂直平分线， E为垂足，点P是直线CD上的任意一点，则 AE = BE PA = PB , CD ⊥ AB ，∠ AEC =∠ BEC 。

2．线段垂直平分线上的点到线段两端的距离相等 ; 到一条线段的两个端点距离相等的点，在这条线段的垂直平分线上上。

3．已知，如图，EF是线段AB的垂直平分线，M是EF上的一点，若MA=6,则MB= 6 ,若∠AMF=200，则∠BMF= 30°。

4．在△ABC中，∠A=400, ∠C=660，DE是线段AB的垂直平分线，垂足是D,DE交AC于E，则∠EBC的度数是 34°。

活动1 小组讨论例1、已知：如图，直线l⊥AB，垂足为C，且AC＝BC，D是直线l上的任意一点．求证：DA＝DB．证明：∵直线l⊥AB，∴∠DCA＝∠DCB＝90°.∵AC＝BC，DC＝DC，∴△DCA≌△DCB(SAS)．∴DA＝DB(全等三角形的对应边相等)．归纳：线段垂直平分线上点到这条线段两个端点的距离___相等_______。

推理格式:∵PC⊥AB，AC=_BC___(点P在线段AB的垂直平分线MN上),∴ PA =PB例2. 你能写出上述定理的逆命题吗？它是真命题吗？如果是，请你加以证明．解：逆命题：到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．是真命题．已知：如图，线段AB，PA＝PB.求证：点P在线段AB的垂直平分线上．证明：取线段AB的中点C，作直线PC.∴AC＝BC.在△PAC和△PBC中，PA＝PB，AC＝BC，PC＝PC，∴△PAC≌△PBC(SSS)．∴∠PCA＝∠PCB＝90°，即PC⊥AB.又C是线段AB的中点，∴PC是线段AB的垂直平分线，即点P在线段AB的垂直平分线上．归纳： 到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．活动2 跟踪训练1．如图所示，在△ABC 中，AB 的垂直平分线交B C 于点E ，若AE=23，则B 、E 两点间的距离是（ B ） A 43 B 23 C 3 D213（第1题） （第2题） （第3题）2．MN 是线段AB 的垂直平分线，垂足是D, 点P 是MN 上的一点，若AB=10cm,则BD= 5 cm ，若PA=10cm,则PB= 10 cm,PD= 5 cm.3．如图，Rt △ABC 中，∠B=900 ，AB=3cm,AC=5cm,将△ABC 折叠，使点C 与A 重合，得折痕DE,则△ABE 的周长是__7_____cm.4．如图所示，在△ABC 中,∠C=90°,AB 的垂直平分线交AC 于点D,垂足为E,若∠A=30°,CD=2.（1）求∠BDC 的度数 （2）求BD 的长解:（1）∠BDC=60°；（2）BD=4活动3 课堂小结1、线段垂直平分线上的__点__到这条线段两个端点的距离__相等_______。

1.3线段的垂直平分线
导学目标: 证明线段垂直平分线的性质定理，探索并证明线段垂直平分线的判定定理，进一步发展推理能力．
重点：证明线段垂直平分线的性质定理难点：证明线段垂直平分线的判定定理.
导学过程
导学过程
导学后反一，课前展示：
利用尺规作三角形三条边的垂直平分线，当作完此题时你发现了什么？
二，自主学习合作探究
1、怎样证明你的发现呢？
※2、证明“三线共点”的基本思路是：其中两直线必交于一点，那么只要证第三条直线过这个交点
或者说这个点在第三条直线上即可．
3、怎么知道这个交点在第三边的垂直平分线上呢？
已知：在△ABC中，设AB、BC的垂直平分线交于点P，连接AP，BP，CP．
求证：P点在AC的垂直平分线上．
证明：
4、从证明三角形三边的垂直平分线交于一点，你还能得出什么结论？
三，简单运用，巩固练习
1．分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线，说明交点分别在什么位置．
2．已知：△ABC中，AB＝A C，AD是BC边上的中线，AB的垂直平分线交AD于O．
思求证：OA＝OB＝OC．
3，问题探究：
（1）已知三角形的一条边及这条边上的高，你能作出这个三角形吗？，作出的三角形有多少个？已
知：三角形的一条边a和这边上的高h．
求作：△A BC，使BC＝a，BC边上的高为h．
（2）已知底边及底边上的高，求作等腰三角形．这样的等腰三角形你能做出多少个？
已知：线段a、h．
求作：△ABC，使AB＝AC，BC＝a，高AD＝h．
教学反思：。

杨庄一中八年级数学导学案主备课题第三节线段的垂直平分线（一）学习目标1、能够证明线段垂直平分线的性质定理、判定定理及其相关结论。

2能够利用尺规作已知线段的垂直平分线。

学习重难点重点：线段的垂直平分线性质与逆定理及其的应用。

难点：线段的垂直平分线的逆定理的理解和证明。

旧知识链接1、段的垂直平分线：垂直且____一条线段的直线是这条线段的垂直平分线。

2、线段垂直平分线上的____到这条线段两个端点的距离__________。

问题探究3、阅读教材：第3节《线段的垂直平分线》二、教材精读4、已知：如图，直线MN⊥AB，垂足是C，且AC=BC，P是M N上的任意一点。

求证：PA=PB。

证明：∵MN⊥AB，∴∠PCA=_______=90°∵在△PC和△PCB中，∴△PCA≌△PCB（）∴PA=PB（全等三角形的对应边相等）归纳：线段垂直平分线上的____到这条线段两个端点的距离__________。

推理格式:∵PC⊥AB，AC=____(点P在线段AB的垂直平分线MN上), ∴ =PB5、这个定理的逆命题：到线段两个端点的距离相等的点，_________________________,它是___命题。

如果是真命题请证明。

已知：如图，AB=AC求证：点A在线段BC的垂直平分线上证明：（提示：利用等腰三角形三线合一）CBAED ABC达 标 测试归纳：定理：到一条线段两个端点距离____ 的点，在这条线段的_________线上。

推理格式：∵AB = AC ，∴____点在线段BC 的 __。

模块二 合作探究6、已知：线段AB 求作：线段AB 的垂直平分线CD 。

解：作图如下：作法：（1）分别以点A 、B 为圆心， 以大于12AB 的长为半径作弧， 两弧相交于点C 、D（2）作直线CD 。

即直线CD 就是线段AB 的垂直平分线。

归纳：因为直线CD 与线段AB 的交点就是AB 的中点， 所以我们也用这种方法作线段的_____________。

数学导学稿一、课前自主思考：习题1．6的第1题：利用尺规作三角形三条边的垂直平分线，当作完此题时你发现了什么?二、探究活动：（一）师生探究，合作交流证明：三角形三边的垂直平分线交于一点.已知：在△ABC 中，设AB 、BC 的垂直平分线交于点O. 求证：O 点在AC 的垂直平分线上．三角形三边的垂直平分线的性质定理：三角形三边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等。

牛刀小试：1．分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线，说明交点分别在什么位置.2．已知：△ABC 中，AB=AC ，AD 是BC 边一上的中线，AB 的垂直平分线交AD 于O 求证：OA=OB=OC ．（二）小组交流，合作解决１.问题：(1)已知三角形的一条边及这条边上的高，你能作出三角形吗?如果能，能作几个?所作出的三角形都全等吗?已知：三角形的一条边a 和这边上的高h求作：△ABC ，使BC=a ，BC 边上的高为h1A DCBA a h( )1A D C BAah1A DC BA ah(2)已知等腰三角形的底边，你能用尺规作出等腰三角形吗?如果能，能作几个?所作出的三角形都全等吗?(3)已知等腰三角形的底边及底边上的高，你能用尺规作出等腰三角形吗?能作几个?（三）独立思考，解决问题已知底边及底边上的高，求作等腰三角形． 已知：线段a 、h三、课堂小结：1.通过今天的学习，同学们有何收获？还有那些疑惑？2.你认为老师上课过程中还有那些需要注意或改进的地方？3.预习时候的疑难解决了吗？四、自我检测：1.三角形三边的垂直平分线交于一点，这点叫三角形的 ，并且这点到三个顶点的距离_________.2.如果三角形三条边的中垂线的交点在三角形的外部，那么，这个三角形是 ， 如果三角形三条边的中垂线的交点在三角形的内部，那么，这个三角形是 ，如果三角形三条边的中垂线的交点在三角形的一条边上，那么，这个三角形是 ， 3.在△ABC 中，边AB 、BC 、AC 的垂直平分线相交于P ，则PA 、PB 、PC 的大小关系是 .4.若△ABC 的边BC 的垂直平分线经过顶点A ，与BC 相交于点D,且AB ＝2AD ，则△ABC 中必有一个内角的度数为（ ）A.45ºB.60ºC.90ºD.120º 5.△ABC 中，∠C=90°，AB 的垂直平分线交AB 于E ，交BC 于点D ，若CD ∶BD=1∶2，BC=6cm ，则点D 到点A 的距离为（ ）A.1.5cmB.3cmC.2cmD.4cm6.如图，在△ABC 中，∠B =115°，AC 边的垂直平分线DE 与AB 边交于点D ，且∠ACD ：∠BCD =5 ：3，则∠ACB = EDCAB6题图 7题图7.如图，在△ABC 中，AB 的垂直平分线MN 交AB 于D 点，交AC 于E 点，且AC=15cm ， △BCE 的周长等于25cm ， ○1求BC 的长？○2若∠A=36°；并且AB=AC.求证：BC=BE.（即△BCE 是等腰三角形） a hCAENMBD五、课后反思：。