数学北师大版九年级下册22.1.2 二次函数y=ax2的图象和性质

22.1.2 二次函数y ＝a x 2的图象和性质1.二次函数y ＝ax 2的图象（1）画二次函数y ＝x 2的图象. 列表：在图22－1－10的平面直角坐标系里画出二次函数y ＝x 的图象.在平面直角坐标系中描点，然后用光滑的曲线顺次连接各点，便得到了二次函数的图象，我们把这样的图象叫做 ，抛物线有一条对称轴，对称轴与抛物线的交点叫做抛物线的 .（2）在上面的平面直角坐标系里画出二次函数y ＝－x 2的图象. 2.二次函数y ＝ax 2图象的性质二次函数y ＝x 2图象的特点：（1）抛物线的开口向 （填“下”或“上”）；（2）图象是中心对称图形还是轴对称图形？ ；对称轴是 。

（3）当x ＜0时，曲线自左向右 （填“下降”或“上升”），即y 值随x 值的增大而 （填“增大”或“减小”）； （4）当x ＞0时，曲线自左向右 （填“下降”或“上升”），即y 值随x 值的增大 而 （填“增大”或“减小”）； （5）图象在x 轴的 （填“上方”或“下方”）； （6）顶点是抛物线上位置最 （填“高”或“低”）的点，y 有最 （填“大”或“小”）值，顶点坐标是 。

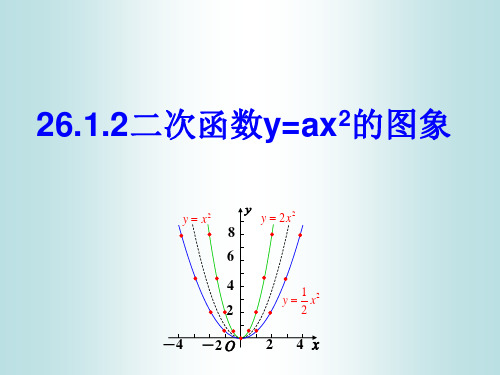
思考：类似地，你能得出二次函数y ＝－x 2图象的特点吗？► ；探究问题一画二次函数y＝ax2的图象例1在同一平面直角坐标系中，分别画出二次函数y＝x2，y＝12x2，y＝2x2的图象，并比较三个图象的相同点与不同点.相同点：①顶点相同，其坐标都为（0，0）.②对称轴相同，都为y轴③开口方向相同，它们的开口方向都向上.不同点：开口大小不同.(1)二次函数y=ax2的图象是一条抛物线(2)抛物线y=ax2的对称轴是y 轴.顶点时原点.a>0时，抛物线开口向上，顶点时抛物形的最低点.a<0时，抛物线开口向下，顶点时抛物形的最高点. (3)|a|越大，抛物线y==ax2的开口越小课堂小结1.本节所学知识：①二次函数y=ax2的图象的画法 .②二次函数y=ax2的图象特征及其性质.一般地， 抛物线 y = ax 2 的对称轴是 y 轴， 顶点是原点． 当 a ＞0 时， 抛物线开口向上，顶点是抛物线的最低点； 当 a ＜0 时， 抛物线开口向下，顶点是抛物线的最高点． 对于抛物线 y = ax 2 ，｜a ｜越大，抛物线的开口越小．如果 a ＞0，当 x ＜0 时，y 随 x 的增大而减小，当 x ＞0 时，y 随 x 的增大而增大；如果 a ＜0，当 x ＜0 时，y 随 x 的增大而增大，当 x ＞0 时，y 随 x 的增大而减小．一、选择题1.关于二次函数y ＝x 2的图象，下列说法错误的是（ ）A.它的形状是一条抛物线B.它的开口向上，且关于y 轴对称C.它的顶点是抛物线的最高点D.它的顶点在原点处，坐标为（0，0） 2.[毕节中考] 抛物线y ＝2x 2，y ＝－2x 2，y ＝12x 2的共同性质是（ ）A .开口向上B .对称轴是y 轴C .都有最高点D .y 随x 的增大而增大3.如图22－1－14所示，根据图象提供的信息，下列结论正确的是（ ）A .a 1>a 2>a 3>a 4B .a 1<a 2<a 3<a 4C .a 4>a 1>a 2>a 3D .a 2>a 3>a 1>a 44.[宁夏中考] 已知a ≠0，在同一平面直角坐标系中，函数y ＝ax 与y ＝ax 2的图象有可能是（ ）二、填空题5.抛物线y ＝10x 2的开口方向是 ，顶点坐标是 ，对称轴是 ；抛物线y ＝－25x 2的开口方向是 ，顶点坐标是 ，对称轴是 Ｗ.6.已知抛物线y ＝－2x 2经过点（1，y 1）和（2，y 2），则y 1与y 2的大小关系是 Ｗ.7.如图22－1－16所示，图中抛物线是某个二次函数的图象，则此二次函数的解析式为 ，根据图象知，当x ＝ 时，y 的值最大.22.1.3 二次函数y ＝ax 2＋k 的图像和性质二次函数y ＝ax 2＋k 的图象与性质在同一平面直角坐标系中，分别画出二次函数y ＝x 2，y ＝x 2＋1，y ＝x 2－1，的图象，并 比较三个图象的相同点与不同点.归纳：（1）抛物线y ＝x 2＋1：开口向 ，对称轴是 轴，顶点为 . （2）抛物线y ＝x 2－1：开口向 ，对称轴是 轴，顶点为 . 2.抛物线y ＝x 2＋1，y ＝x 2－1与抛物线y ＝x 2的关系：抛物线y ＝x 2抛物线y ＝x 2＋1；抛物线y ＝x 2 抛物线y ＝x 2－1.y ＝ax 2 y ＝ax 2＋k （k ＞0）. y ＝ax 2 y ＝ax 2－k （k ＞0）. 口诀：上加下减.例1 抛物线y ＝ax 2＋k 与y ＝－5x 2的形状、开口方向都相同，且其顶点坐标是（0，3），则其解析式为 ，它是由抛物线y ＝－5x 2向 平移 个单位长度得到的.例2如图22－1－23所示，隧道的截面由抛物线AED 和矩形ABCD 构成，矩形的长BC 为8 m ，宽AB 为2 m .以BC 所在的直线为x 轴，线段BC 的垂直平分线为y 轴，建立平面直角坐标系，y 轴是抛物线的对称轴，顶点E 到坐标原点O 的距离为6 m .（1）求抛物线的解析式；（2）如果该隧道内设双行道，现有一辆货运卡车高4.2 m ，宽2.4 m ，这辆货运卡车能否通过该隧道？ 通过计算说明理由.一、选择题1.下列函数中，图象形状、开口方向相同的是（ ）①y ＝－x 2；②y ＝－2x 2；③y ＝12x 2－1；④y ＝x 2＋2；⑤y ＝－2x 2＋3.A.①④B.②⑤C.②③⑤D.①②⑤2.抛物线y ＝2x 2－5的顶点坐标为（ ）A.（2，5）B.（－2，5）C.（0，－5）D.（0，5）3.[上海中考] 如果将抛物线y ＝x 2＋2向下平移1个单位长度，那么所得新抛物线的解析式是（ ） A .y ＝（x －1）2＋2 B .y ＝（x ＋1）2＋2 C .y ＝x 2＋1 D .y ＝x 2＋34.当a ＜0时，二次函数y ＝ax 2＋a 的图象经过的象限是（ ）A .第三、四象限B .第一、二象限C .第二、三、四象限D .第一、二、三象限5.对于二次函数y ＝－13x 2＋2，当x 为x 1和x 2时，对应的函数值分别为y 1和y 2.若x 1>x 2>0，则y 1与y 2的大小关系是（ ）A .y 1>y 2B .y 1<y 2C .y 1＝y 2D .无法比较7.抛物线y ＝x 2－4与x 轴交于B ，C 两点，顶点为A ，则△ABC 的面积是（ ） A .16 B .8 C .4 D .2二、填空题8.（1）抛物线y ＝－12x 2－1的开口方向是 ，顶点坐标是（ ， ），对称轴是 ，当x>0时，函数值y 随x 的增大而 ；当x<0时，函数值y 随x 的增大而 ；抛物线y ＝－12x 2－1可由抛物线y ＝－12x 2向 平移 个单位长度得到；9.若抛物线y ＝ax 2－1经过点（4，31），则a ＝ ，在这个函数图象上该点关于对称轴对称的点为 .10. 将二次函数y ＝2x 2－1的图象沿y 轴向上平移2个单位长度，所得图象对应的函数解析式为.三、解答题11.若抛物线y＝ax2＋k经过点A（－3，2），B（0，－1），求该抛物线的解析式.12.二次函数y＝－12x2＋k的图象经过点D⎝⎛⎭⎫－3，92，与x轴交于A，B两点，且点A在点B的左侧.（1）求k的值；（2）求A，B两点的坐标.13.已知抛物线y＝12x2，把它向下平移，得到的抛物线与x轴交于A，B两点，与y轴交于点C.若△ABC是直角三角形，则原抛物线应向下平移几个单位长度？14.某水渠的横截面呈抛物线，水面的宽度为AB（单位：米），现以AB所在直线为x轴，以抛物线的对称轴为y轴建立如图22－1－27所示的平面直角坐标系，设坐标原点为O.已知AB＝8米，抛物线的解析式为y＝ax2－4.（1）求a的值；（2）点C（－1，m）是抛物线上一点，点C关于原点O的对称点为点D，连接CD，BC，BD，求△BCD的面积.22.1.3 .1 二次函数y＝a(x-h)2的图象和性质问题：在同一平面直角坐标系中，画出二次函数y ＝－12x 2 、 y ＝－12()x ＋12和y ＝－12()x －12的图象。

二次函数y=ax2的图像和性质教案篇一：22.1.2二次函数y=ax2图像与性质教案2123篇二：《二次函数y=ax 的图象和性质》参考教案22.1.2二次函数y?ax2的图象和性质教学目标1．知识与技能能够用描点法作出函数y=ax2的图象，并根据图象认识和理解其性质2．过程与方法经历探索二次函数y=ax2的图象和性质的过程，体会数形结合的思想和方法.3．情感、态度与价值观在初步建立二次函数表达式与图象之间的联系中，体会数形结合与转化，体会数学内在的美感．教学重点难点1．重点函数y=ax2的图象的画法，了解抛物线的含义，理解函数y=ax2的图象与性质．2．难点用描点的方法准确地画出函数y=ax2的图象，掌握其性质特征．教与学互动设计（一）创设情境导入新课导语一回忆一次函数和反比例函数的定义，图象特征，思考二次函数的图象又有何特征呢？导语二展示（用课件或幻灯片）具有抛物线的实例让大家欣赏，议一议这与二次函数有何联系呢？导语三用红色的乒乓球作投篮动作，观察乒乓球的运动路线，思考运动路线有何规律？怎样用数学规律来描述呢？（二）合作交流解读探究1．函数y=ax2的图象画法及相关名称【探究l】画y=x2的图象学生动手实践、尝试画y=x2的图象教师分析，画图像的一般步骤：列表→描点→连线教师在学生完成图象后，在黑板上示范性画出y=x2的图象，如图22-1-1.【共同探究】次函数图像有何特征？特征如下：①形状是开口向上的抛物线②图象关于y轴对称③由最低点，没有最高点.结合图象介绍下列名称：①顶点；②对称轴；③开口及开口方向.图22-1-1图22-1-22．函数y=ax2的图象特征及其性质【探究2】在同一坐标系中，画出y=12x，y=2x2的图象.2学生自己完成此题.教师做个别指导，在学生（大部分）完成后，教师可示范性地画出两函数的图象.如图22-1-2比较图中三个抛物线的异同.相同点：①顶点相同，其坐标都为（0，0）.②对称轴相同，都为y 轴③开口方向相同，它们的开口方向都向上.不同点：开口大小不同.【练一练】画函数y=-x2，y=-施过程）比较函数y=-x2，y=-12x，y=-2x2的图象.找出它们的异同点.212x，y=-2x2的图象.（分析：仿照探究1的实2相同点：①形状都是抛物线.②顶点相同，其坐标都为（0，0）.③对称轴相同，都为y轴④开口方向相同，它们的开口方向都向下.不同点：开口大小不同.【归纳】y=ax2的图象特征：(1)二次函数y=ax2的图象是一条抛物线(2)抛物线y=ax2的对称轴是y轴.顶点时原点.a>0时，抛物线开口向上，顶点时抛物形的最低点.a(3)|a|越大，抛物线y==ax2的开口越小（三）应用迁移巩固提高类型之一如何画好二次函数的图象【点拨】画二次函数图象一般是按以下三个步骤进行.①列表、取值；②描点；③连线但初学者对三个步骤，易犯下列错误，注意避免. 【易错点1】表格中，取值过多或过少.画函数y=ax2图象,取对应值时，一般5组或7组有代表性的对应值即可.．．．【易错点2】连线不是光滑曲线，有的用折线，有的画的过渡不自然，不象抛物线.例1下图是甲、乙、丙三人画得二次函数y=2x2的图象.请你帮助修改.解：图甲中有两个错误的地方.①连线不能用直尺作线段，图象中相邻两点时用光滑曲线连接.②抛物线开口应向上无限延伸，不能到两端点为止.修改见图甲中虚线.图乙中有一个错误，其中有一个点（1，-2）的位置画错.（或表格中对应值算错）修改见图乙中虚线.图丙种错误是x的值都是非负数，没有负数，导致出现其图象只是抛物线的一半，没有对称性.修改见图丙中虚线.【点评】此三类错误是初学者应注意的三个方面，以后的练习中，应提醒大家注意.类型之二函数y=ax2的图象特征的应用例2（1）填空：函数y?()2的图象是，顶点坐标是，对称轴是，开口方向是. 1（2）函数y=x2，y=x2，y=-2x2图象如图所示，请指出三条抛物线的名称.2解：（1）y?()2可化为y=2x2.它的图象是抛物线，顶点坐标为（0，0），对称轴为y轴，开口方向向上.【点评】解析式需化为一般式，再根据图象特征解答，避免发生错误.(2)根据抛物线y=ax2中，a的值的作用来判断，最上面的抛物线为y=x2，中间的为y=12x，x轴下方的为y=-2x22【点评】抛物线y=ax2中a>0时，开口向上.a（四）总结反思拓展升华【总结】1.本节所学知识：①二次函数y=ax2的图象的画法.②二次函数y=ax2的图象特征及其性质.2.本节所用的方法：实践比较法【反思】函数y=ax2与y=-ax2的图象之间有何关系？（它们关于x 轴对称）【拓展】已知函数y=ax2经过(1,2).（1）求a的值.（2）当x(2)根据函数y=2x2知x【点评】①通常用待定系数法函数y=ax2中只有一个待定系数a,故知道其图象上一点坐标或x，y的一组对应值就可求出解析式.②结合图象知：x（五）当堂检测反馈1.抛物线y=4x2中的开口方向是向上，顶点坐标是（0，0），对称轴是y轴.抛物线y=-对称轴是y轴.2.二次函数y=ax2与y=2x2，开口大小，形状一样，开口方向相反，则a=2.【分析】a与-2互为相反数13.在同一坐标系中：①y=x2，②y=-x2，③y=2x2这三个函数图象开口最大212x的开口方向是向下，顶点坐标是（0，0），4的是①y?12x2，开口向下的是②y=-x21解：∵||2∵函数y=-x2中，二次项系数为-114.二次函数y=2x2，y=-2x2，y=x22点（0，0）；②对称轴相同，都是y轴.5．已知抛物线的顶点在原点，对称轴是y轴，且经过(-3,2).求此抛物线的解析式，并指出x>0时，y随x的变化情况.解：设此抛物线的解析式为y=ax2,∵此抛物线过点（-3，2），∴2=a·(-3)2,。

北师大版九年级下册数学第 5 讲《二次函数y=ax2(a≠0)的图象与性质》知识点梳理【学习目标】1.经历探索二次函数y=ax2 和y=ax2＋c 的图象的作法和性质的过程，进一步获得将表格、表达式、图象三者联系起来的经验．2.会作出y=ax2 和y=ax2＋c 的图象，并能比较它们与y=x2 的异同，理解a 与c 对二次函数图象的影响．3.能说出y=ax2＋c 与y=ax2 图象的开口方向、对称轴和顶点坐标．4.体会二次函数是某些实际问题的数学模型．【要点梳理】要点一、二次函数y=ax2（a≠0）的图象与性质1.二次函数y=a x2(a≠0)的图象二次函数y=ax2的图象（如图），是一条关于y 轴对称的曲线，这样的曲线叫做抛物线.抛物线y=ax2（a≠0）的对称轴是y 轴，它的顶点是坐标原点.当a＞0 时，抛物线的开口向上，顶点是它的最低点；当a＜0 时，抛物线的开口向下，顶点是它的最高点.2.二次函数y=a x2(a≠0)的图象的画法——描点法描点法画图的基本步骤：列表、描点、连线.（1）列表：选择自变量取值范围内的一些适当的x 的值，求出相应的y 值，填入表中.（自变量x 的值写在第一行，其值从左到右，从小到大.）（2）描点：以表中每对x 和y 的值为坐标，在坐标平面内准确描出相应的点.一般地，点取的越多，图象就越准确.（3）连线：按照自变量的值由小到大的顺序，把所描的点用平滑的曲线连结起来.要点诠释：（1）用描点法画二次函数y=ax2（a≠0）的图象时，应在顶点的左、右两侧对称地选取自变量x 的值，然后计算出对应的y 值.（2）二次函数y=ax2(a≠0)的图象，是轴对称图形，对称轴是y 轴．y=ax2(a≠0)是最简单的二次函数.（3）画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.3.二次函数y=a x2(a≠0)的图象的性质二次函数y=ax2（a≠0）的图象的性质，见下表：要点诠释：顶点决定抛物线的位置.几个不同的二次函数，如果二次项系数a相同，那么抛物线的开口方向、开口大小完全相同，只是顶点的位置不同. │a│相同，抛物线的开口大小、形状相同.│a│越大，开口越小，图象两边越靠近y 轴，│a│越小，开口越大，图象两边越靠近x 轴.要点二、二次函数y=a x2+c(a≠0)的图象与性质1.二次函数y=a x2+c(a≠0)的图象（1）a 0yy = ax 2+ c (c > 0)c Oxyy = ax 2 + c (c < 0) Oc x（2） a < 0yc OxyOcx2.二次函数 y =a x 2+c (a ≠0)的图象的性质y = ax 2 + c (c > 0)y = ax 2 + c (关c < 0于) 二 次 函 数y = ax 2 + c (a ≠ 0) 的性质，主要从抛物线的开口方向、顶点、对称轴、函数值的增减性以及函数的最大值或最小值等方面来研究．下面结合图象，将其性质列表归纳如下：函数y= ax 2 + c (a > 0, c > 0)y = ax 2 + c (a < 0, c > 0)图象开口方向 向上 向下 顶点坐标 (0，c) (0，c) 对称轴y 轴y 轴函数变化当 x > 0 时，y 随 x 的增大而增大； 当 x < 0 时，y 随 x 的增大而减小.当 x > 0 时，y 随 x 的增大而减小； 当 x < 0 时，y 随 x 的增大而增大.最大（小）当x = 0 时，y最小值=c当x = 0 时，y最大值=c 值【典型例题】类型一、二次函数y=ax2（a≠0）的图象与性质1．(2014 秋•青海校级月考）二次函数y=ax2与直线y=2x﹣1 的图象交于点P（1，m）（1）求a，m 的值；（2）写出二次函数的表达式，并指出x取何值时该表达式y随x的增大而增大？（3）写出该抛物线的顶点坐标和对称轴．【思路点拨】（1）把点P（1，m）分别代入二次函数y=ax2与直线y=2x﹣1 即可求出未知数的值；（2）把a 代入二次函数y=ax2与即可求出二次函数表达式；根据二次函数的对称轴及增减性判断出x 的取值．（3）根据二次函数的性质直接写出即可．【答案与解析】解：（1）点P（1，m）在y=2x﹣1 的图象上∴m=2×1﹣1=1 代入y=ax2∴a=1（2）二次函数表达式：y=x2因为函数y=x2的开口向上，对称轴为y 轴，当x＞0 时，y 随x 的增大而增大；（3）y=x2的顶点坐标为（0，0），对称轴为y 轴．【总结升华】本题考查了用待定系数法求函数解析式的方法，及二次函数的增减性．举一反三：【变式1】二次函数y =ax2与y =-2x2的形状相同，开口大小一样，开口方向相反，则a=．【答案】2.【变式2】（2015•山西模拟）抛物线y=﹣x2不具有的性质是（）．A.开口向上B. 对称轴是y 轴C. 在对称轴的左侧，y 随x 的增大而增大D. 最高点是原点【答案】A.2.已知y=(m+1)x m2+m 是二次函数且其图象开口向上,求m 的值和函数解析式.【思路点拨】根据二次函数的定义以及函数y=ax2（a≠0）的图象性质来解答.【答案与解析】⎩⎧m 2 + m = 2由题意， ⎨m +1＞0 ，解得 m=1，∴二次函数的解析式为：y= 2x 2 .【总结升华】本题中二次函数还应该有 m+1≠0 的限制条件，但当 m +1＞0 时，一定存在 m+1≠0，所以就不再考虑了.类型二、二次函数 y =a x 2+c (a ≠0)的图象与性质3. 求下列抛物线的解析式：（1） 与抛物线 y = - 1 x 2+ 3 形状相同，开口方向相反，顶点坐标是（0，-5）的抛物线； 2（2） 顶点为（0，1），经过点（3，-2）并且关于 y 轴对称的抛物线．【思路点拨】抛物线形状相同则| a | 相同，再由开口方向可确定 a 的符号，由顶点坐标可确定 c 的值，从而确定抛物线的解析式 y = ax 2 + c ．【答案与解析】（1） 由于待求抛物线 y = -1x 2 + 3 21形状相同，开口方向相反，可知二次项系数为 ， 2又顶点坐标是（0，-5），故常数项 k = -5 ，所以所求抛物线为 y = 1x 2 - 5 ．2（2） 因为抛物线的顶点为（0，1），所以其解析式可设为 y = ax 2 +1 ，又∵该抛物线过点（3，-2），∴ 9a +1 = -2 ，解得 a = - 1．3∴所求抛物线为 y = - 1x 2 +1．3【总结升华】本题考察函数 y = ax 2 + c (a ≠ 0) 的基本性质，并考察待定系数法求简单函数的解析式.4. 在同一直角坐标系中，画出 y = -x 2 和 y = -x 2 +1的图象，并根据图象回答下列问题．(1)抛物线y =-x2+1向平移个单位得到抛物线y =-x2；(2)抛物线y =-x2+1开口方向是，对称轴为，顶点坐标为；(3)抛物线y =-x2+1，当x时，随x 的增大而减小；当x时，函数y 有最值，其最值是．【思路点拨】利用描点法画出函数图象，根据图象进行解答.【答案与解析】函数y =-x2与y =-x2+1的图象如图所示：(1)下；l ；(2)向下；y 轴；(0，1)；(3)＞0；＝0；大；大； 1.【总结升华】本例题把函数y =-x2+1与函数y =-x2的图象放在同一直角坐标系中进行对比，易得出二次函数y =ax2+c(a ≠ 0) 与y =ax2 (a ≠ 0) 的图象形状相同，只是位置上下平移的结论．y =ax2+c(a ≠ 0) 可以看作是把y =ax2 (a ≠ 0) 的图象向上(k > 0) 或向下(k < 0) 平移| k | 个单位得到的．举一反三：【变式】函数y = 3x2可以由y = 3x2-1 怎样平移得到？【答案】向上平移1 个单位.。

22.1.2二次函数y=ax2的图象和性质课前预习1.二次函数y=ax2的图象是一条，对称轴是轴，顶点坐标是.当a>0时，抛物线开口，在对称轴的左侧，y随x的增大而，在对称轴的右侧，y随x的增大而，此时抛物线有最点，即当x=0时，y取得最值；当a<0时，抛物线开口，在对称轴的左侧y随x的增大而，在对称轴的右侧，y随x的增大而，此时抛物线有最点，即当x=0时，y取得最值.|a|越大，抛物线的开口越小，|a|相等说明抛物线的开口大小相同.课堂练习知识点1 二次函数y=ax2的图象1.填写下列抛物线的开口方向、对称轴、顶点坐标以及最值.2.某同学画二次函数y=ax2的图象时，列下列表格：（1）将表格中的空格补全；（2）这个二次函数的解析式为；（3）在平面直角坐标系中画出二次函数的图象.知识点2 二次函数y=ax2的性质3.已知二次函数y=（m-2）x2的图象开口向上，则m的取值范围是.4.下列各点在二次函数y=-2x2图象上的是（）A.（-1，2）B.（-1，-2）C.（-2，-4）D.（-2，4）5.关于函数y=x2的图象，下列说法错误的是（）A.它的图象是一条抛物线B.它的开口向上，且关于y轴对称C.它的顶点是抛物线的最高点D.它的顶点在原点处，坐标为（0，0）课时作业1.与二次函数y=x2开口大小相同，方向相反的二次函数是.2.二次函数y=-0.2x2的图象是一条开口向的抛物线，对称轴是，顶点坐标为.当x= 时，函数有最值；当x 0时，y随x的增大而减小.3.关于函数y=3x2的性质，下列说法正确的是（）A.无论x为任何实数，y的值总为正B.当x值增大时，y的值也增大C.它的图象关于y轴对称D.它的图象在第一、第三象限内4.已知A（-1，y₁），B（-2，y₂）都在二次函数y=x2上，则y₁，y₂之间的大小关系是（）A.y₁>y₂B.y₁=y₂C.y₁<y₂D.不能确定5.二次函数y=ax2（a＞0）的图象经过点（3，4），则其图象一定经过点（）A.（3，-4）B.（-3，-4）C.（-3，4）D.（4，3）6. 如图，当ab＞0时，函数y=ax2与函数y=bx+a的大致图象是（）7.二次函数y=2x2，y=-2x2，y=1x2的共同性质是（）2A.开口向上B.对称轴是y轴C.都有最高点D.y随x的增大而增大8.已知函数y=（m+2）226m mx+-是关于x的二次函数.（1）求m的值；（2）当m为何值时，函数图象的顶点为最低点？（3）当m为何值时，函数图象的顶点为最高点？x2；③y=-x2；9.在同一个平面直角坐标系中，画出下列函数的图象：①y=x2；②y=12④y=-1x2.2从图象上对比，说出解析式中二次项系数a对抛物线的形状有什么影响？10.如图，A，B为抛物线y=x2上的两点，且AB∥x轴，与y轴交于点C，以点O为圆心，OC为半径画圆，若2.11.函数y=ax2（a≠0）的图象与直线y=2x-3交于点（1，b）.（1）求a和b的值；（2）x在什么范围时，二次函数y=ax2中的y随x的增大而增大？（3）求抛物线y=ax2与直线y=-2的两个交点及顶点所围成的三角形的面积.。