南京、淮安市2013届高三模拟考试(南京二模、淮安三模)

南京、淮安市2013届高三模拟考试（南京二模、淮安三模）数学2013．3参考公式：锥体的体积公式为13V Sh =，其中S 是锥体的底面面积，h 是锥体的高． 一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应位置．．．．．．．上．1．已知集合A={2a ,3}，B={2,3}．若A B={1,2,3}，则实数a 的值为____． 2．函数()sin cos f x x x =的最小正周期是__________． 3．若复数12miz i-=+(i 是虚数单位)是纯虚数，则实数m 的值为____． 4．盒子中有大小相同的3只白球、2只黑球，若从中随机地摸出两只球，则两只球颜色相同的概率是______．5．根据2012年初我国发布的《环境空气质量指数AQI 技术规定（试行）》，AQI 共分为六级：(0,50]为优，(50,100]为良，(100,150]为轻度污染，(150,200]为中度污染，(200,300]为重度污染，300以上为严重污染．2012年12月1日出版的《A 市早报》对A 市2012年11月份中30天的AQI 进行了统计，频率分布直方图如图所示，根据频率分布直方图，可以看出A 市该月环境空气质量优、良的总天数为____．6．右图是一个算法流程图，其输出的n 的值是_____．7．已知圆锥的侧面展开图是一个半径为3cm ，圆心角为23π的扇形，则此圆锥的高为___cm ．8．在平面直角坐标系xOy 中，设过原点的直线l 与圆C ：22(3)(1)4x y -+-=交于M 、N 两点，若MN 23≥，则直线l 的斜率k 的取值范围是______． 9．设数列{n a }是公差不为0的等差数列，Sn为其前n 项和，若22221234a a a a +=+，55S =，则7a 的值为_____．10．若函数()f x 为定义在R 上的奇函数，当0x >时，1()23x f x -=-，则不等式()1f x >的解集为______________．11．在ABC ∆中，已知AB=2，BC=3，60ABC ∠=︒，BD ⊥AC ，D 为垂足，则BD BC ⋅的值为____．12．关于x 的不等式(21)ln 0ax x -≥对任意(0,)x ∈+∞恒成立，则实数a 的值为_____．13．在平面直角坐标系xOy 中，已知双曲线C ：22143x y -=．设过点M(0,1)的直线l 与双曲线C 交于A 、B 两点，若2AM MB =，则直线l 的斜率为_____．14．已知数列{n a }的通项公式为72n a n =+，数列{n b }的通项公式为2n b n =．若将数列{n a }，{n b }中相同的项按从小到大的顺序排列后看作数列{n c }，则9c 的值为_____． 二、解答题：本大题共6小题，共90分．15．（本小题满分14分）在ABC ∆中，已知角A ，B ，C 所对的边分别为,,a b c ，且cos 2cos C a cB b-=， （1）求B ； （2）若tan()74A π+=，求cos C 的值．16，（本小题满分14分）如图，在四棱锥P-ABCD 中，底面ABCD 是直角梯形，AD//BC ，PB ⊥平面ABCD ，CD ⊥BD ，PB=AB=AD=1，点E 在线段PA 上，且满足PE=2EA ．（1）求三棱锥E-BAD 的体积； （2）求证：PC//平面BDE ．17．（本小题满分16分）如图，某广场中间有一块扇形绿地OAB ，其中O 为扇形所在圆的圆心，60AOB ∠=︒，广场管理部门欲在绿地上修建观光小路：在AB 上选一点C ，过C 修建与OB 平行的小路CD ，与OA 平行的小路CE ，问C 应选在何处，才能使得修建的道路CD 与CE 的总长最大，并说明理由．18．（本小题满分16分）已知数列{}n a 的各项都为正数，且对任意*n N ∈，都有212n n n a a a k ++=+(k 为常数)．（1）若221()k a a =-，求证：123,,a a a 成等差数列；（2）若k=0，且245,,a a a 成等差数列，求21a a 的值； （3）已知12,a a ab ==(,a b 为常数)，是否存在常数λ，使得21n n n a a a λ+++=对任意*n N ∈都成立？若存在．求出λ；若不存在，说明理由．19．（本小题满分16分）在平面直角坐标系xOy 中，椭圆C ：22221(0)x y a b a b+=>>过点(,),(3,1)22a aA B ． （1）求椭圆C 的方程；（2）已知点00(,)P x y 在椭圆C 上，F 为椭圆的左焦点，直线l 的方程为00360x x y y +-=．①求证：直线l 与椭圆C 有唯一的公共点；②若点F 关于直线l 的对称点为Q ，求证：当点P 在椭圆C 上运动时，直线PQ 恒过定点，并求出此定点的坐标．20．（本小题满分16分）设函数2()(2)ln f x x a x a x =---．（1）求函数()f x 的单调区间；（2）若函数有两个零点，求满足条件的最小正整数a 的值；（3）若方程()f x c =有两个不相等的实数根12,x x ，求证：12()02x x f +'>．。

南京、淮安市2013届高三模拟考试（南京二模、淮安三模）历史试题2013．03本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，共120分。

考试用时100分钟。

注意事项：答题前，考生务必将学校、姓名、班级、学号写在答题卡的密封线内。

选择题答案按要求填涂在答题卡上；非选择题的答案写在答题卡上对应题目的答案空格内，答案写在试卷上无效。

考试结束后，交回答题卡。

第I卷（选择题，共60分）一、选择题：本大题共20小题，每小题3分，共计60分。

在每小题列出的四个选项中，只有一项是最符合题目要求的。

1．张鸣在《中华帝国：制度的断想》中写道：“在诸侯争雄的春秋时代，封建制原来赖以存在的基础……宗法制被打破，各个政治实体在竞争中，表现出了过于强烈的以自我为中心的倾向，同一宗法血亲系统内的争夺和厮杀自然不可避免。

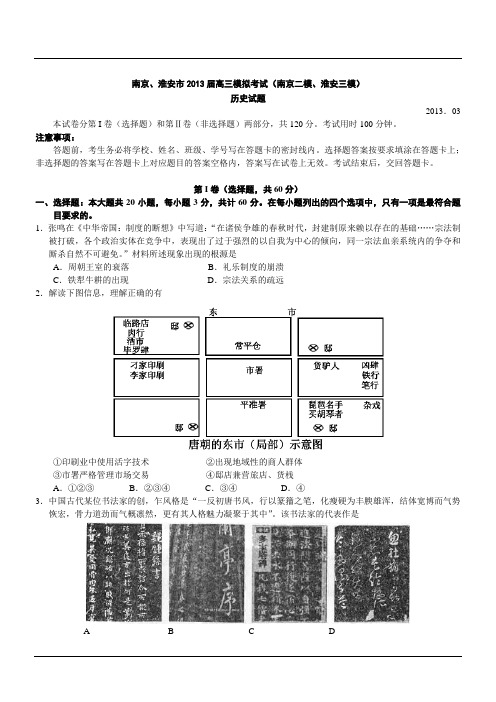
”材料所述现象出现的根源是A．周朝王室的衰落B．礼乐制度的崩溃C．铁犁牛耕的出现D．宗法关系的疏远2．解读下图信息，理解正确的有①印刷业中使用活字技术②出现地域性的商人群体③市署严格管理市场交易④邸店兼营旅店、货栈A．①②③B．②③④C．③④D．④3．中国古代某位书法家的创，乍风格是“一反初唐书风，行以篆籀之笔，化瘦硬为丰腴雄浑，结体宽博而气势恢宏，骨力道劲而气概凛然，更有其人格魅力凝聚于其中”。

该书法家的代表作是A B C D4．元代行省的设置，无视历来与划界密切相关的几条最重要的山川边界——秦岭、淮河、南岭、太行山等的存在，陕西行省越过秦岭而有汉中盆地，江西行省跨过南岭而有广东，江浙行省从江南平原逶迤直到福建山地。

统治者这么划分的主要意图是A．便于中央直接管理B．实行民族分化政策C．推行汉蒙二元统治D．防止出现地方割据5．“广州等五港口英商，或不时来往，但不可妄到乡间任意游行，更不可远入内地贸易。

……倘有英人违背此条禁约，擅到内地远游者，不论系何品级，即听该地方民人捉拿，交英国管事官依情处罪，但该民人等不得擅自殴打伤害，致伤和好。

江苏省2014届一轮复习数学试题选编23：椭圆（学生版）填空题1 ．（2013江苏高考数学）在平面直角坐标系xOy 中,椭圆C 的标准方程为)0,0(12222>>=+b a by a x ,右焦点为F ,右准线为l ,短轴的一个端点为B ,设原点到直线BF 的距离为1d ,F 到l 的距离为2d ,若126d d =,则椭圆C 的离心率为_______.2 ．（江苏省盐城市2013届高三年级第二次模拟考试数学试卷）椭圆12222=+by a x (0>>b a )的左焦点为F,直线m x =与椭圆相交于A,B 两点,若FAB ∆的周长最大时,FAB ∆的面积为ab ,则椭圆的离心率为________.3 ．（2009高考(江苏)）如图，在平面直角坐标系xoy 中，1212,,,A A B B 为椭圆22221(0)x y a b a b+=>>的四个顶点，F 为其右焦点，直线12A B 与直线1B F 相交于点T ，线段OT 与椭圆的交点M 恰为线段OT 的中点，则该椭圆的离心率为_____★_____.4 ．（南京市、盐城市2013届高三年级第一次模拟考试数学试题）已知1F 、2F 分别是椭圆14822=+y x 的左、右焦点, 点P 是椭圆上的任意一点, 则121||PF PF PF -的取值范围是 .5 ．（江苏省南京市四区县2013届高三12月联考数学试题 ）设椭圆C :)0(12222>>=+b a by a x 的左、右焦点分别为12,F F ,上顶点为A ,过点A 与2AF 垂直的直线交x 轴负半轴于点Q ,且02221=+Q F F F .则椭圆C 的离心率为___________6 ．（江苏省扬州市2013届高三下学期5月考前适应性考试数学（理）试题）在平面直角坐标系xOy中,已知点A是椭圆221259x y+=上的一个动点,点P在线段OA的延长线上,且72OA OP⋅=,则点P横坐标的最大值为______.7 ．（扬州市2012-2013学年度第一学期期末检测高三数学试题）已知椭圆22221(0) x ya ba b+=>>的离心率e=,A、B是椭圆的左、右顶点,P是椭圆上不同于A、B的一点,直线PA、PB斜倾角分别为α、β,则cos()cos()αβαβ-+=____.解答题8．（扬州市2012-2013学年度第一学期期末检测高三数学试题）如图,已知椭圆1E方程为22221(0)x ya ba b+=>>,圆2E方程为222x y a+=,过椭圆的左顶点A作斜率为1k直线1l与椭圆1E和圆2E分别相交于B、C.(Ⅰ)若11k=时,B恰好为线段AC的中点,试求椭圆1E的离心率e;(Ⅱ)若椭圆1E的离心率e=12,2F为椭圆的右焦点,当2||||2BA BF a+=时,求1k的值;(Ⅲ)设D为圆2E上不同于A的一点,直线AD的斜率为2k,当2122k bk a=时,试问直线BD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.9 ．（江苏省连云港市2013届高三上学期摸底考试（数学）（选修物理））已知椭圆的中心为原点O,一个焦点为F0),以原点为圆心的圆O与直线y x=+,过原点的直线l与椭圆交于A,B 两点,与圆O 交于C,D 两点. (1)求椭圆和圆O 的方程;(2)线段CD 恰好被椭圆三等分,求直线l 的方程.10．（2012-2013学年度苏锡常镇四市高三教学情况调研（二）数学试题）如图,设A ,B 分别为椭圆2222:1(0)x y E a b a b+=>>的右顶点和上顶点,过原点O 作直线交线段AB 于点M (异于点A ,B ),交椭圆于C ,D 两点(点C 在第一象限内),ABC ∆和ABD ∆的面积分别为1S 与2S . (1)若M 是线段AB 的中点,直线OM 的方程为13y x =,求椭圆的离心率; (2)当点M 在线段AB 上运动时,求12S S 的最大值.11．（南通市2013届高三第一次调研测试数学试卷）已知左焦点为F(-1,0)的椭圆过点E过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.(1)求椭圆的标准方程;(2)若P为线段AB的中点,求k1;(3)若k1+k2=1,求证直线MN恒过定点,并求出定点坐标.12．（江苏省淮安市2013届高三上学期第一次调研测试数学试题）已知椭圆的离心率,一条准线方程为⑴求椭圆的方程;⑵设为椭圆上的两个动点,为坐标原点,且.①当直线的倾斜角为时,求的面积;②是否存在以原点为圆心的定圆,使得该定圆始终与直线相切?若存在,请求出该定圆方程;若不存在,请说明理由.13．（江苏省徐州市2013届高三期中模拟数学试题）如图,在平面直角坐标系xoy 中,点A 为椭圆222199x y +=的右顶点, 点(1,0)D ,点,P B 在椭圆上, BP DA =. (1)求直线BD 的方程;(2)求直线BD 被过,,P A B 三点的圆C 截得的弦长;(3)是否存在分别以,PB PA 为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.14．（苏北三市（徐州、淮安、宿迁）2013届高三第二次调研考试数学试卷）如图,在平面直角坐标系xOy 中,椭圆)0(1:2222>>=+b a b y a x E 的焦距为2,且过点)26,2(. (1) 求椭圆E 的方程; (2) 若点A ,B 分别是椭圆E 的左、右顶点,直线l 经过点B 且垂直于x 轴,点P 是椭圆上异于A ,B 的任意一点,直线AP 交l 于点.M(ⅰ)设直线OM 的斜率为,1k 直线BP 的斜率为2k ,求证:21k k 为定值; (ⅱ)设过点M 垂直于PB 的直线为m . 求证:直线m 过定点,并求出定点的坐标.15．（苏北老四所县中2013届高三新学期调研考试）已知椭圆的中心为坐标原点O ，椭圆短半轴长为1，动点(2,)M t (0)t > 在直线2(a x a c=为长半轴，c 为半焦距）上。

南京、淮安市2013届高三模拟考试（南京二模、淮安三模）生物 2013．03本试卷分为选择题和非选择题两部分，共120分。

考试用时100分钟。

注意事项：答题前，考生务必将学校、姓名、班级、学号写在答题卡的密封线内。

选择题答案按要求填涂在答题卡上；非选择题的答案写在答题卡上对应题目的答案空格内，答案写在试卷上无效。

考试结束后，交回答题卡。

第Ⅰ卷(选择题共55分)一、单项选择题：本题包括20小题，每小题2分，共40分。

每小题只有一个选项最符合题意。

1．下列关于细胞内有机物的叙述中，正确的是A．植物细胞内的蔗糖和麦芽糖的水解产物都是葡萄糖B．细胞核中的核酸只含脱氧核糖，细胞质中的核酸只含核糖C．腺嘌呤核苷(腺苷)是构成ATP、RNA和DNA的基本组成单位D．蛋白质分子中肽链的盘曲和折叠被打开时，其特定功能会发生改变2．细胞呼吸原理广泛应用于生产实践中。

下表中有关措施与对应的目的不恰当的是选项应用措施目的A种子贮存晒干降低自由水含量，降低细胞呼吸B乳酸菌制作酸奶先通气，后密封加快乳酸菌繁殖，有利于乳酸发酵C水果保鲜低温降低酶的活性，降低细胞呼吸D栽种庄稼疏松土壤促进根有氧呼吸，利于吸收矿质离子3．培养某哺乳动物胚胎干细胞，测量出其细胞周期中各时期长度为：G1期(DNA合成准备期)10h、S期(DNA复制期)8h、G2期(纺锤丝形成准备期)4h，分裂期(M期)2h。

细胞中DNA相对含量和细胞数的关系如下图所示。

若在培养液中加入DNA聚合酶抑制剂培养30h，再更换到不含DNA聚合酶抑制剂的培养液中培养4h。

下列有关培养结果的图示中，细胞中的DNA相对量和细胞数的关系最相符的是4．图1是细胞膜亚显微结构及物质跨膜运输示意图，其中离子通道是一种通道蛋白，通道蛋白是横跨质膜的亲水性通道，允许适当大小的离子顺浓度梯度通过。

图2表示磷脂在细胞膜内外两侧分布的百分比。

据图分析不合理的是A．离子通过离子通道进出细胞时不需要消耗ATPB．若图1为癌细胞的细胞膜，则物质丁比正常细胞少C．图1中丁的存在决定了细胞膜具有选择透过性D．两图都可说明细胞膜的成分在膜上的分布是不对称的5．科学家将4个关键基因植入已分化的体细胞中并表达，使这个细胞成为具有类似干细胞功能的诱导多能干细胞(iPS细胞)。

江苏省徐州市2013届高三质量抽测试卷(2012年9月)数 学 I参考公式：棱锥的体积V ＝13Sh ，其中S 为底面积，h 为高．一、填空题:本大题共14小题,每小题5分,共70分．请把答案填写在答题纸相应位置上． 1． 已知集合A ＝{1,3}，B ＝{1,2,m }，若A ⊆B ，则实数m ＝ ▲ ．2． 若(1－2i)i ＝a ＋b i （a ，b ∈R ，i 为虚数单位），则ab ＝ ▲ ．3． 某工厂生产A ，B ，C 三种不同型号的产品，产品数量之比依次为2:3:5，现用分层抽样方法抽出一个容量为n 的样本，样本中A 种型号的产品有16件，那么此样本的容量n ＝ ▲ ． 4． 在大小相同的4个小球中，2个是红球，2个是白球，若从中随机抽取2个球，则所抽取的球中至少有一个 红球的概率是 ▲ ．5． 已知某算法的流程图如图所示，则程序运行结束时输出的结果为 ▲ ．6． 已知π2cos()23α-=，则cos α＝ ▲ ．7． 已知一个正六棱锥的高为10cm ，底面边长为6cm ，则这个正六棱锥的体积为 ▲ cm 3．8． 已知各项均为正数的等比数列{a n }的前n 项和为S n ，若a 3＝18，S 3＝26，则{a n }的公比q ＝ ▲ ．9． 已知实数x ，y 满足2,2,03,x y x y y +⎧⎪-⎨⎪⎩≥≤≤≤则2z x y =-的最大值是 ▲ ．10．在曲线331y x x =-+的所有切线中，斜率最小的切线的方程为 ▲ ． 11．已知直线y ＝a 与函数()2x f x =及函数()32x g x =⋅的图象分别相交于A ,B 两点，(第5题图)则A ,B 两点之间的距离为 ▲ ．12．已知二次函数2()41f x ax x c =-++的值域是[1,＋∞)，则1a ＋9c 的最小值是 ▲ ． 13．如图，A ，B 是半径为1的圆O 上两点，且∠AOB ＝π3．若点C 是圆O 上任意一点， 则→OA ▪→BC 的取值范围为 ▲ ． 14．已知a ，b ，c 是正实数，且abc ＋a ＋c ＝b ，设222223111p a b c =-++++，则p 的最大值为 ▲ ． 二、解答题：本大题共6小题，共90分．请在答．题卡指定区域．．．．．．内作答，解答时应写出文 字说明、证明过程或演算步骤． 15．（本小题满分14分）在△ABC 中，角A ,B ,C 的对边分别为a ,b ,c ，已知cos cos cos cos a C b C c B c A -=-， 且C ＝120°． （1）求角A ；（2）若a ＝2，求c ． 16．（本小题满分14分）如图，在四棱锥P ‐ABCD 中，四边形ABCD 为正方形，PA ⊥平面ABCD ，E 为PD 的中点．求证：（1）PB ∥平面AEC ；（2）平面PCD ⊥平面PAD ．17．（本小题满分14分）在一个矩形体育馆的一角MAN 内（如图所示），用长为a 的围栏设置一个运动器材储 存区域，已知B 是墙角线AM 上的一点，C 是墙角线AN 上的一点． （1）若BC ＝a ＝10，求储存区域三角形ABC 面积的最大值；C(第13题图)PA BC D E(第16题图)（2）若AB ＝AC ＝10，在折线MBCN 内选一点D ，使DB ＋DC ＝a ＝20，求储存区域四边形DBAC 面积的最大值．18．（本小题满分16分）已知椭圆E ：22221(0)x y a b a b +=>>的左顶点为A ，左、右焦点分别为F 1、F 2，且圆C ：22360x y y +--=过A ，F 2两点．（1）求椭圆E 的方程；（2）设直线PF 2的倾斜角为α，直线PF 1的倾斜角为β，当β－α＝2π3时，证明：点P 在一定圆上．19．（本小题满分16分）已知函数22()ln ()a f x x a x a x=+-∈R ．（1）讨论函数()y f x =的单调区间；（2）设2()24ln2g x x bx =-+-，当a ＝1时，若对任意的x 1，x 2∈[1,e]（e 是自然对数的底数），12()()f x g x ≥，求实数b 的取值范围．B(第17题图)20．（本小题满分16分）设()2012()k k k f n c c n c n c n k =+++⋅⋅⋅+∈N ，其中012,,,,k c c c c ⋅⋅⋅为非零常数， 数列{a n }的首项a 1＝1，前n 项和为S n ，对于任意的正整数n ，a n ＋S n ＝()k f n ． （1）若k ＝0，求证：数列{a n }是等比数列；（2）试确定所有的自然数k ，使得数列{a n }能成等差数列．附加题21．（选做题）本题包括A 、B 、C 、D 四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分，解答时应写出文字说明、证明过程或演算步骤。

诗歌鉴赏之思想情感（第二课时）学习目标：1.掌握常见题材诗的思想感情。

2.准确理解和分析古诗词中的思想感情，做到不拔高，不贴乱贴标签。

3.把握思想感情题的设题方法及答题要点。

课前预习1、(常州2013届高三第一学期期末考试)阅读下面这首宋词，回答后面的问题。

卖花声张舜民楼上久踟躇。

地远身孤。

拟将憔悴吊三闾。

自是长安日下影，流落江湖。

烂醉且消除。

不醉何如。

又看暝色满平芜。

试问寒沙新到雁，应有来书。

问题：“试问寒沙新到雁，应有来书”包含了诗人怎样的期盼？（3分）2、(盐城市2013届高三年级摸底考试)阅读下面这首诗歌，然后回答问题。

初发扬子⑴寄元大校书［唐］韦应物凄凄去亲爱，泛泛入烟雾。

归棹洛阳人，残钟广陵树。

今朝此为别，何处还相遇。

世事波上舟，沿洄⑵安得住。

【注释】（1）扬子：指扬子津，在长江北岸，近瓜州。

（2）沿洄：分别指顺流和回旋的水流。

问题：三、四两联寄寓了诗人什么样的感慨？（3分）3、(苏州市2013届高三教学调研测试)阅读下面这首宋诗，然后回答问题。

巴丘书事陈与义三分书里识巴丘，临老避胡初一游。

晚木声酣洞庭野，晴天影抱岳阳楼。

四年风露侵游子，十月江湖吐乱洲。

未必上流须鲁肃，腐儒空白九分头。

问题：结合全诗的内容，说说诗歌表达了诗人哪些情感。

（3分）课堂活动过程活动一：展示交流自主预习题1、2、3活动二：讨论归纳方法技巧活动三：当堂训练1、（扬州2013届高三第一学期期末考试）阅读下面这首宋诗，然后回答问题。

西塍废圃周密吟蛩鸣蜩引兴长，玉簪花落野塘香。

园翁莫把秋荷折，留与游鱼盖夕阳。

问题：诗歌表达了作者怎样的情感？(2分)2、（2013年苏锡常镇四市高三二模）阅读下面这首唐诗，然后回答问题。

酬李穆见寄刘长卿孤舟相访至天涯，万转云山路更赊。

欲扫柴门迎远客，青苔黄叶满贫家。

问题：三、四两句蕴含了怎样的感情？请作简要分析。

（6分）3、（2013届南京二模、淮安三模）阅读下面这首宋词，然后回答问题。

南京、淮安市2013届高三模拟考试（南京二模、淮安三模）物 理 试 题第I 卷（选择题 共 31分）说明：1．本试卷满分120分，考试时间100分钟。

2．本试卷分为第Ⅰ卷和第Ⅱ卷，所有题目一律在答题纸上相应位置规范作答。

第Ⅰ卷（选择题，共31分）一、单项选择题：本题共5小题，每小题3分，共计15分。

每小题只有一个选项符合题意。

1．如图所示，某同学斜向上抛出一小石块，忽略空气阻力。

下列关于小石块在空中运动的过程中，加速度a 随时间t 变化的图象中，正确的是2．如图所示，处于真空中的正方体存在着电荷量为＋q 或－q 的点电荷，点电荷位置图中已标明，则a 、b 两点电场强度和电势均相同的图是+q -qab+q+q+q+q-qab ababABCD3．如图所示，A 、B 为平行板电容器的金属板，G 为静电计。

开始时开关S 闭合，静电计指针张开一定角度。

为了使指针张开角度增大一些，应该采取的措施是 A ．断开开关S 后，将A 、B 两极板分开一些 B ．断开开关S 后，将A 、B 两极板靠近一些 C ．保持开关S 闭合，将A 、B 两极板靠近一些 D ．保持开关S 闭合，将R 上的滑片向右移动tta ttOOOOaaaABCDA BRS G4．已知通电长直导线周围某点的磁感应强度rIkB，即磁感应强度B 与导线中的电流I 成正比、与该点到导线的距离r 成反比。

如图所示，两根平行长直导线相距为R ，通以大小、方向均相同的电流。

规定磁场方向垂直纸面向里为正，在0-R 区间内磁感应强度B 随x 变化的图线可能是rOBRR 2rOBRR 2rOB RR 2rOB RR 2A B C D5．如图（甲）所示，两段等长细线串接着两个质量相等的小球a 、b ，悬挂于 O 点。

现在两个小球上分别加上水平方向的外力，其中作用在 b 球上的力大小为 F 、作用在 a 球上的力大小为 2F ，则此装置平衡时的位置可能如图（乙）中的哪幅图OOOOOabABCD（甲）（乙）aaa abbbbFFF F2F2F2F2F二、多项选择题：本题共4小题，每小题4分，共计16分。

2023-2024学年江苏省南京市、盐城市高三（第三次）模拟考试物理试卷一、单选题：本大题共11小题，共44分。

1.关于光学现象下列说法正确的是()A.水中紫光的传播速度比红光大B.光从空气射入玻璃时可能发生全反射C.在岸边观察前方水中的一条鱼，鱼的实际深度比看到的要浅D.分别用蓝光和红光在同一装置上做双缝干涉实验，用红光时得到的条纹间距更宽2.如图所示，虚线a、b、c为电场中的三条等差等势线，实线为一带电的粒子仅在静电力作用下通过该区域时的运动轨迹，P、R、Q是这条轨迹上的三点，由此可知()A.带电粒子在P点时的加速度小于在Q点时的加速度B.P点的电势一定高于Q点的电势C.带电粒子在R点时的电势能大于Q点时的电势能D.带电粒子在P点时的动能大于在Q点时的动能3.在医学上，放射性同位素锶制成表面敷贴器，可贴于体表治疗神经性皮炎等疾病。

锶会发生衰变，其衰变产物中有钇的同位素，半衰期为年。

下列说法正确的是()A.该衰变过程质量守恒B.的比结合能比衰变产物中钇的同位素的比结合能大C.衰变所释放的电子是原子核内的中子转变为质子时所产生的D.的原子核经过年后还剩余4.如图所示，竖直平面内的光滑金属细圆环半径为R，质量为m的带孔小球穿于环上，一长为R的轻杆一端固定于球上，另一端通过光滑的铰链连接于圆环最低点，重力加速度为g。

当圆环以角速度绕竖直直径转动时，轻杆对小球的作用力大小和方向为()A.2mg，沿杆向上B.2mg，沿杆向下C.，沿杆向上D.，沿杆向下5.A、B两颗卫星在同一平面内沿同一方向绕地球做匀速圆周运动，它们之间的距离随时间变化的关系如图所示。

已知地球的半径为r，卫星A的线速度大于卫星B的线速度，若不考虑A、B之间的万有引力，则卫星A、B绕地球运行的周期分别为()A.，B.，C.，D.，6.如图所示，理想变压器的原线圈与电阻串联后接入正弦式交流电。

变压器原、副线圈的面数比。

电路中定值电阻、、、的阻值相同，交流电压表为理想电压表。

江苏省2014届一轮复习数学试题选编27：概率（学生版）填空题1 ．（南京市、盐城市2013届高三年级第一次模拟考试数学试题）袋中装有2个红球, 2个白球, 除颜色外其余均相同, 现从中任意摸出2个小球, 则摸出的两球颜色不同的概率为 .2 ．（江苏省徐州市2013届高三考前模拟数学试题）在集合{|,1,2,,10}6n M x x n π===中任取一个元素,所取元素恰好满足方程1cos 2x =的概率是________. 3 ．（南京市、淮安市2013届高三第二次模拟考试数学试卷）盒子中有大小相同的3只白球、2只黑球,若从中随机地摸出两只球,则两只球颜色相同的概率是______.4 ．（江苏省盐城市2013届高三年级第二次模拟考试数学试卷）现有在外观上没有区别的5件产品,其中3件合格,2件不合格,从中任意抽检2件,则一件合格,另一件不合格的概率为________.5 ．（2011年高考（江苏卷））从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是______6 ．（常州市2013届高三教学期末调研测试数学试题）已知某拍卖行组织拍卖的10幅名画中,有2幅是膺品.某人在这次拍卖中随机买入了一幅画,则此人买入的这幅画是膺品的事件的概率为______.7 ．（2012年江苏理）现有10个数,它们能构成一个以1为首项,3-为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是____.8 ．（苏州市2012-2013学年度第一学期高三期末考试数学试卷）有5个数成公差不为零的等差数列,这5个数的和为15,若从这5个数中随机抽取一个数,则它小于3的概率是_______.9 ．（江苏省连云港市2013届高三上学期摸底考试（数学）（选修物理））在4次独立重复试验中,随机事件A 恰好发生l 次的概率不大于其恰好发生两次的概率,则事件A 在一次试验中发生的概率p 的取值范围是___________________.10．（徐州、宿迁市2013届高三年级第三次模拟考试数学试卷）已知数字发生器每次等可能地输出数字1或2中的一个数字,则连续输出的4个数字之和能被3整除的概率是___.11．（2009高考(江苏)）现有5根竹竿，它们的长度（单位：m ）分别为2.5，2.6，2.7，2.8，2.9，若从中一次随机抽取2根竹竿，则它们的长度恰好相差0.3m 的概率为___★___.12．（江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题）如图,ABCD 是4⨯5的方格纸,向此四边形ABCD 内抛撒一粒豆子,则豆子恰好落在阴影部分内的概率为_______________13．（江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题）正四面体的四个面上分别写有数字0,1,2,3,把两个这样的四面体抛在桌面上,则露在外面的6个数字恰好是2,0,1,3,0,3的概率为________.14．（江苏省徐州市2013届高三上学期模底考试数学试题）在大小相同的4个小球中,2个是红球,2个是白球,若从中随机抽取2个球,则所抽取的球中至少有一个红球的概率是________.15．（江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷）从集合{}1 2 3 4 5 6 7 8 9，，，，，，，，中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为______.16．（江苏省连云港市2013届高三上学期摸底考试（数学）（选修物理））已知一组抛物线2y ax bx c =++,其中a 为1、3、5、7中任取的一个数,b 为2、4、6、8中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线12x =交点处的切线相互平行的概率是_________________.17．（江苏省苏南四校2013届高三12月月考试数学试题）一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)骰子四个面上分别标有1,2,3,4这四个数字,抛掷这颗正四面体骰子,观察抛掷后能看到的数字.若连续抛掷两次,两次朝下面上的数字之积大于6的概率是______.18．（2013江苏高考数学）现在某类病毒记作n m Y X ,其中正整数m ,n (7≤m ,9≤n )可以任意选取,则n m ，都取到奇数的概率为____________.19．（苏北三市（徐州、淮安、宿迁）2013届高三第二次调研考试数学试卷）从0,1,2,3这四个数字中一次随机取两个数字,若用这两个数字组成无重复数字的两位数,则所得两位数为偶数的概率是_____.20．（江苏省2013届高三高考压轴数学试题）从集合{-1,1,2,3}中随机选取一个数记为m,从集合{-1,1,2}中随机选取一个数记为n,则方程22x ym n+=1表示双曲线的概率为________.21．（江苏省扬州市2013届高三下学期5月考前适应性考试数学（理）试题）已知某一组数据8,9,11,12,x,若这组数据的平均数为10,则其方差为______.若以连续掷两次骰子得到的点数nm,分别作为点P的横、纵坐标,则点P在直线4x y+=上的概率为______.22．（连云港市2012-2013学年度第一学期高三期末考试数学试卷）在数字1、2、3、4四个数中,任取两个不同的数,其和大于积的概率是___.23．（江苏省淮安市2013届高三上学期第一次调研测试数学试题）连续抛掷一个骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具)两次,则出现向上点数之和大于9的概率是___________.24．（江苏省南京市四区县2013届高三12月联考数学试题）若将一颗质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具),先后抛掷两次,则出现向上的点数之和为6的概率是____25．（江苏省盐城市2013届高三10月摸底考试数学试题）已知甲、乙、丙三人在3天节日中值班,每人值班1天,那么甲排在乙前面值班的概率是________.26．（江苏省徐州市2013届高三期中模拟数学试题）在闭区间 [-1,1]上任取两个实数,则它们的和不大于1的概率是_______________.27．（江苏省南京市2013届高三9月学情调研试题（数学）WORD版）有3个兴趣小组,甲､乙两位同学各参加其中一个小组,且他们参加各个兴趣小组是等可能的,则甲､乙两位同学参加同一个兴趣小组的概率为_______.28．（苏州市第一中学2013届高三“三模”数学试卷及解答）有一个容量为66的样本,数据的分组[1.5,3.5)[3.5,5.5)[5.5,7.5)[7.5,9.5)[9.5,11.5)频数 6 14 16 20 10 根据样本的频率分布估计,数据落在[5.5,9.5)的概率约是________.29．（扬州市2012-2013学年度第一学期期末检测高三数学试题）先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x,y,则x y 2=的概率为_____.30．（2013江苏高考数学）抽样统计甲、乙两位设计运动员的5此训练成绩(单位:环),结果如下:31．（江苏省2013届高三高考模拟卷（二）（数学） ）在一个袋子中装有分别标注数字1,2,3,4的四个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为5的概率是_______.32．（2012-2013学年度苏锡常镇四市高三教学情况调研（二）数学试题）在不等式组031y x x y x ⎧⎪≤⎪<≤⎨⎪⎪>⎩所表示的平面区域内所有的格点(横、纵坐标均为整数的点称为格点)中任取3个点,则该3点恰能成为一个三角形的三个顶点的概率为______.33．（江苏省南通市、泰州市、扬州市、宿迁市2013届高三第二次调研（3月）测试数学试题）设数列{a n }满足：()()*3118220()n n n n a a a a a n ++=---=∈N ，，则a 1的值大于20的概率为 ▲ ．34．（2010年高考（江苏））盒子中有大小相同的3只小球,1只黑球,若从中随机地摸出两只球,两只球颜色不同的概率是____35．（南京市、盐城市2013届高三第三次模拟考试数学试卷）在一个盒子中有分别标有数字1,2,3,4,5的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之积为偶数的概率是________.36．（苏北老四所县中2013届高三新学期调研考试）当A ，B ∈{1，2，3}时，在构成的不同直线Ax －By ＝0中，任取一条，其倾斜角小于45︒的概率是___________37．（江苏省无锡市2013届高三上学期期中考试数学试题）某学校有两个食堂,甲,乙,丙三名学生各自随机选择其中的一个食堂用餐,则他们在同一个食堂用餐的概率为___________.解答题38．（2010年高考（江苏））某厂生产甲、乙两种产品,生产甲产品一等品80%,二等品20%;生产乙产品,一等品90%,二等品10%.生产一件甲产品,如果是一等品可获利4万元,若是二等品则要亏损1万元;生产一件乙产品,如果是一等品可获利6万元,若是二等品则要亏损2万元.设生产各种产品相互独立(1)记x(单位:万元)为生产1件甲产品和件乙产品可获得的总利润,求x 的分布列 (2)求生产4件甲产品所获得的利润不少于10万元的概率39．（2012年江苏理）设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,0ξ=;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,1ξ=. (1)求概率(0)P ξ=;(2)求ξ的分布列,并求其数学期望()E ξ.40．（江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题）(1)山水城市镇江有“三山”——金山、焦山、北固山,一位游客游览这三个景点的概率都是0.5,且该游客是否游览这三个景点相互独立,用ξ表示这位游客游览的景点数和没有游览的景点数差的绝对值,求ξ的分布列和数学期望;(2)某城市有n (n 为奇数,3n ≥)个景点,一位游客游览每个景点的概率都是0.5,且该游客是否游览这n 个景点相互独立,用ξ表示这位游客游览的景点数和没有游览的景点数差的绝对值,求ξ的分布列和数学期望.41．（苏北老四所县中2013届高三新学期调研考试）如图，已知面积为1的正三角形ABC 三边的中点分别为D 、E 、F ，从A ，B,C,D ，E ，F 六个点中任取三个不同的点，所构成的三角形的面积为X （三点共线时，规定X=0）（1）求1()2P X ≥；（2）求E （X ）42．（苏州市2012-2013学年度第一学期高三期末考试数学试卷）设10件同类型的零件中有2CB件不合格品,从所有零件中依次不放回地取出3件,以X表示取出的3件中不合格品的件数.(1)求“第一次取得正品且第二次取得次品”的概率;E X.(2)求X的概率分布和数学期望()43．（江苏省南京市2013届高三9月学情调研试题（数学）WORD版）在一个盒子中有大小一样的7个球,球上分别标有数字1,1,2,2,2,3,3.现从盒子中同时摸出3个球,设随机变量X为摸出的3个球上的数字和.(1)求概率P(X≥7);(2)求X的概率分布列,并求其数学期望E(X).2013届高三学情调研卷44．（江苏省扬州市2013届高三下学期5月考前适应性考试数学（理）试题）某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成.(1)求出甲考生正确完成题数的概率分布列,并计算数学期望; (2)若考生乙每题正确完成的概率都是23,且每题正确完成与否互不影响.试从至少正确完成2题的概率分析比较两位考生的实验操作能力.45．（江苏省无锡市2013届高三上学期期末考试数学试卷）某银行的一个营业窗口可办理四类业务,假设顾客办理业务所需的时间互相独立,且都是整数分钟,经统计以往100位顾客办理业务所需的时间(t),结果如下:注:银行工作人员在办理两项业务时的间隔时间忽略不计,并将频率视为概率. (Ⅰ)求银行工作人员恰好在第6分钟开始办理第三位顾客的业务的概率;(Ⅱ)用X 表示至第4分钟末已办理完业务的顾客人数,求X 的分布列及数学期望.46．（2009高考(江苏)）对于正整数n ≥2，用n T 表示关于x 的一元二次方程220xax b ++=有实数根的有序数组(,)a b 的组数，其中{},1,2,,a b n ∈（a 和b 可以相等）；对于随机选取的{},1,2,,a b n ∈（a 和b 可以相等），记n P 为关于x 的一元二次方程220x ax b ++=有实数根的概率。

苏北三市（徐州、淮安、宿迁）2013届高三第二次调研考试数学Ⅰ参考公式：球的表面积为24R S π=，其中R 表示球的半径。

一、填空题：本大题共14题，每小题5分，共70分.请把答案填写在答题纸相．．．．应位置上．．．．.．1.已知全集},3,2,1,0{=U 集合},3,2,1{},1,0{==B A 则=B A C U )( ▲ .2.已知i 是虚数单位，实数b a ,满足,10))(43(i bi a i =++则=-b a 43 ▲ .3.一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画出了如图所示的频率分布直方图，现要从这10000人中再用分层抽样的方法抽出100人作进一步调查，则月收入在)3000,2500[（元）内应抽出 ▲ 人.4.如图是一个算法的流程图，若输入n 的值是10，则输出S 的值是 ▲ .5.若一个长方体的长、宽、高分别为3、2、1，则它的外接球的表面积是 ▲ .6.从0，1，2，3这四个数字中一次随机取两个数字，若用这两个数字组成无重复数字的两位数，则所得两位数为偶数的概率是 ▲ .注 意 事 项 考生在答题前认真阅读本注意事项及各题答题要求 1. 本试卷共4页，均为非选择题（第1题～第20题，共20题）。

本试卷满分160分，考试时间为120分钟。

考试结束后，请将本试卷和答题卡一并交回。

2. 答题前，请您务必将自己的姓名、考试号用0.5毫米黑色墨水的签字笔填写在试卷及答题纸上的规定位置。

3. 作答试题，必须用0.5毫米的黑色墨水的签字笔在答题卡上的指定位置作答，在其它位置作答一律无效。

4. 如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗。

（第3题图）1000 1500 2000 2500 3000 4000 3500 月收入（元）频率/组距0.00010.0002 0.0004 0.0005 0.0003 开始 输入n0←S2<n（第4题图结束n S S +←1-←n n输出S7.已知等比数列}{n a 的前n 项和为n S ，若62,256382-==S a a a a ，则1a 的值是▲ . 8.已知双曲线)0,0(12222>>=-b a by ax 的右焦点为,F 若以F 为圆心的圆05622=+-+x y x 与此双曲线的渐近线相切，则该双曲线的离心率为▲ .9.由命题“02,2≤++∈∃m x x R x ”是假命题，求得实数m 的取值范围是),(+∞a ，则实数a 的值是 ▲ .10.已知实数y x ,满足约束条件⎪⎩⎪⎨⎧≤+++≥≥0,12,0k y x x y x （k 为常数），若目标函数y x z +=2的最大值是311，则实数k 的值是 ▲ . 11.已知函数⎪⎩⎪⎨⎧∈-∈=]3,1(,2329]1,0[,3)(x x x x f x ，当]1,0[∈t 时，]1,0[))((∈t f f ，则实数t 的取值范围是 ▲ .12.已知角ϕ的终边经过点)1,1(-P ，点),(),,(2211y x B y x A 是函数)0)(sin()(>+=ωϕωx x f 图象上的任意两点，若2)()(21=-x f x f 时，21x x -的最小值为3π，则)2(πf 的值是 ▲ .13.若对满足条件)0,0(3>>=++y x xy y x 的任意y x ,，01)()(2≥++-+y x a y x 恒成立，则实数a 的取值范围是 ▲ .14.如图，在等腰三角形ABC 中，已知F E A AC AB ,,120,1︒===分别是边AC AB ,上的点，且,,AC n AF AB m AE ==其中),1,0(,∈n m 若BC EF ,的中点分别为,,N M 且,14=+n m 则MN 的最小值是 ▲ .二、解答题：本大题共6小题，共计90分，请在答题纸指定的区域内作答．．．．．．．．．．．，解ABMNE CF第14题图答题应写出文字说明、证明过程或演算步骤. 15.（本小题满分14分）在△ABC ，已知.sin sin 3)sin sin )(sin sin sin (sin C B A C B C B A =-+++ （1） 求角A 值；（2） 求C B cos sin 3-的最大值.16.（本小题满分14分）如图，在四棱柱1111D C B A ABCD -中，已知平面⊥C C AA 11平面,A B C D 且3===CA BC AB ,1==CD AD .（1） 求证：;1AA BD ⊥（2） 若E 为棱BC 的中点，求证：//AE 平面11D D CC .17.（本小题满分14分）如图，两座建筑物CD AB ,的底部都在同一个水平面上，且均与水平面垂直，它们的高度分别是9cm 和15cm ，从建筑物AB 的顶部A 看建筑物CD 的视角︒=∠45CAD . (1) 求BC 的长度；(2) 在线段BC 上取一点(P 点P 与点C B ,不重合），从点P 看这两座建筑物的视角分别为,,βα=∠=∠DPC APB 问点P 在何处时，βα+最小？1AE CD BA1D1B1C 第16题ADβ α18.（本小题满分16分）如图，在平面直角坐标系xOy 中，椭圆)0(1:2222>>=+b a by ax E 的焦距为2，且过点)26,2(. （1） 求椭圆E 的方程；（2） 若点A ，B 分别是椭圆E 的左、右顶点，直线l 经过点B 且垂直于x 轴，点P 是椭圆上异于A ，B 的任意一点，直线AP 交l 于点.M （ⅰ）设直线OM 的斜率为,1k 直线BP 的斜率为2k ，求证：21k k 为定值；（ⅱ）设过点M 垂直于PB 的直线为m . 求证：直线m 过定点，并求出定点的坐标.19. （本小题满分16分）已知函数).1,0(ln )(2≠>-+=a a a x x a x f x （1） 求函数)(x f 在点))0(,0(f 处的切线方程； （2） 求函数)(x f 单调区间；（3） 若存在]1,1[,21-∈x x ，使得e e x f x f (1)()(21-≥-是自然对数的底数），求ABMPOlxym实数a 的取值范围.20. （本小题满分16分）已知,0,0<>b a 且,0≠+b a 令,,11b b a a ==且对任意正整数k ，当0≥+k k b a 时，;43,412111k k k k k b b b a a =-=++当0<+k k b a 时，.43,214111k k k k k a a b a b =+-=++ （1） 求数列}{n n b a +的通项公式；（2） 若对任意的正整数n ，0<+n n b a 恒成立，问是否存在b a ,使得}{n b 为等比数列？若存在，求出b a ,满足的条件；若不存在，说明理由；（3） 若对任意的正整数,0,<+n n b a n 且,43122+=n n b b 求数列}{n b 的通项公式.徐州市2012–––2013学年度高三第一次质量检测数学Ⅱ（附加题）21.【选做题】本题包括A 、B 、C 、D 四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分.解答题应写出文字说明、证明过程或演算步骤.A[选修4—1 ：几何证明选讲]（本小题满分10分）如图，AB 是⊙O 的一条切线，切点为,B 直线ADE ,CGE CFD ,都是⊙O 的割线，已知.AB AC =求证：AC FG //B. [选修4—2 ：矩阵与变换]（本小题满分10分）若圆1:22=+y x C 在矩阵)0,0(00>>⎥⎦⎤⎢⎣⎡=b a b a A 对应的变换下变成椭圆,134:22=+y x E 求矩阵A 的逆矩阵1-A .E G BADFOC第21—A 题图C. [选修4—4 ：坐标系与参数方程]（本小题满分10分）在平面直角坐标系xOy 中，圆C 的参数方程为θθθ(sin 22,cos 22⎪⎪⎩⎪⎪⎨⎧+-=+-=r y r x 为参数,)0>r ,以O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为,1)4sin(=+πθρ若圆C 上的点到直线l 的最大距离为3，求r 的值.D. [选修4—5 ：不等式选讲]（本小题满分10分） 已知实数z y x ,,满足,2=++z y x 求22232z y x ++的最小值.【必做题】第22题、第23题，每题10分，共计20分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)如图,已知抛物线x y C 4:2=的焦点为,F 过F 的直线l 与抛物线C 交于),(),0)(,(22111y x B y y x A >两点,T 为抛物线的准线与x 轴的交点.(1) 若,1=⋅TB TA 求直线l 的斜率； (2) 求ATF ∠的最大值.23.（本小题满分10分）已知数列}{n a 满足),(12121*21N n na a a n n n ∈+-=+且.31=a（1） 计算432,,a a a 的值，由此猜想数列}{n a 的通项公式，并给出证明；TAFBO yx第22题图（2） 求证：当2≥n 时，.4n nnn a ≥徐州市2012—2013学年度高三第一次质量检测数学Ⅰ试题参考答案与评分标准一、填空题1．{2,3} 2．0 3．25 4．54 5．6π 6．597．2- 8．355 9．1 10．3- 11．37[log ,1]3 12．22- 13．37(,]6-∞ 14．77 二、解答题15．⑴因为(sin sin sin )(sin sin sin )3sin sin A B C B C A B C +++-=，由正弦定理，得()a b c b c a bc+++-=，…………………………………………2分所以222b c a bc +-=，所以2221cos 22b c a A bc +-==，………………………………4分因为(A ∈π，所以3A π=．…………………………………………………………6分 ⑵ 由3A π=，得23B C π+=，所以3sin cos B C -23sin cos()3B B π=--133sin (cos sin )22B B B =--+sin()6B π=+，……………………………………10分因为203B π<<，所以666B ππ5π<<+，……………………………………………12分当62B ππ=+，即3B π=时，3sin cos B C -的最大值为1． ……………………14分16．⑴在四边形ABCD 中，因为BA BC =，DA DC =，所以BD AC ⊥，……………2分又平面11AAC C ⊥平面ABCD ，且平面11AAC C平面ABCD AC =， BD ⊂平面ABCD ，所以BD ⊥平面11AA C C ，………………………………………4分又因为1AA ⊂平面11AA C C ，所以1BD AA ⊥．………………………………………7分⑵在三角形ABC 中，因为AB AC =，且E 为BC 中点，所以BC AE ⊥，………9分又因为在四边形ABCD 中，3AB BC CA ===，1DA DC ==， 所以60ACB ∠=︒，30ACD ∠=︒，所以BC DC ⊥，所以AE DC ，…………12分因为DC ⊂平面11D DCC ，AE ⊄平面11D DCC ，所以AE 平面11D DCC ．…14分17．⑴作AE ⊥CD ，垂足为E ，则9CE =，6DE =，设BC x =，则tan tan tan tan()1tan tan CAE DAECAD CAE DAE CAE DAE∠∠∠=∠∠=-∠⨯∠++ (2)分961961x x x x==-⋅+，化简得215540x x --=，解之得，18x =或3x =-（舍） 答：BC的长度为1．………………………………………………………………6分 ⑵设BP t =，则18(018)CP t t =-<<，2291516266(27)18tan()9151813518135118t t t t t t t t t tαβ-===-----⋅-++++++． (8)分设227()18135t f t t t =--++，222542723()(18135)t t f t t t -⨯'=-++，令()0f t '=，因为018t <<，得15627t =-，当(0,15627)t ∈-时，()0f t '<，()f t 是减函数；当(15627,18)t ∈- 时，()0f t '>，()f t 是增函数，所以，当15627t =-时，()f t 取得最小值，即tan()αβ+取得最小值，………12分因为2181350t t --<+恒成立，所以()0f t <，所以tan()0αβ<+，(,)2αβπ∈π+， 因为tan y x =在(,)2ππ上是增函数，所以当15627t =-时，αβ+取得最小值． 答：当BP 为(15627)m -时，αβ+取得最小值． ……………………………14分18．⑴由题意得22c = ，所以1c =，又222312a b =+，…………………………………2分消去a 可得，422530b b --=，解得23b =或212b =-（舍去），则24a =， 所以椭圆E的方程为22143x y +=．……………………………………………………4分 ⑵（ⅰ）设111(,)(0)P x y y ≠，0(2,)M y ，则012y k =，1212y k x =-，因为,,A P B 三点共线，所以10142y y x =+， 所以，20111221142(2)2(4)y y y k k x x ==--，8分因为11(,)P x y 在椭圆上，所以22113(4)4y x =-，故211221432(4)2y k k x ==--为定值．10分（ⅱ）直线BP 的斜率为1212y k x =-，直线m 的斜率为112m x k y -=, 则直线m 的方程为1012(2)x y y x y --=-，…………………………………………12分111101111222(2)4(2)2x x x y y x y x y y y x ---=-+=-++2211111122(4)4(2)x x y x y x y --+=++2211111122(4)123(2)x x x x y x y --+-=++=111122x x x y y --+=112(1)x x y -+， 所以直线m过定点(-． ………………………………………………………16分19．⑴因为函数2()ln (0,1)x f x a x x a a a =->≠+，所以()ln 2ln x f x a a x a '=-+，(0)0f '=，…………………………………………2分又因为(0)1f =，所以函数()f x 在点(0,(0))f 处的切线方程为1y =． …………4分⑵由⑴，()ln 2ln 2(1)ln x x f x a a x a x a a '=-=-++． 因为当0,1a a >≠时，总有()f x '在R 上是增函数， ………………………………8分又(0)0f '=，所以不等式()0f x '>的解集为(0,)∞+， 故函数()f x 的单调增区间为(0∞+．………………………………………………10分⑶因为存在12,[1,1]x x ∈-，使得12()()e 1f x f x --≥成立， 而当[1,1]x ∈-时，12max min ()()()()f x f x f x f x --≤， 所以只要max min ()()e 1f x f x --≥即可．……………………………………………12分又因为x ，()f x '，()f x 的变化情况如下表所示：x(,0)-∞0 (0,)∞+ ()f x '-+()f x减函数 极小值 增函数所以()f x 在[1,0]-上是减函数，在[0,1]上是增函数，所以当[1,1]x ∈-时，()f x的最小值()()min 01f x f ==，()f x 的最大值()max f x 为()1f -和()1f 中的最大值．因为11(1)(1)(1ln )(1ln )2ln f f a a a a a aa --=--=--+++，令1()2ln (0)g a a a a a=-->，因为22121()1(1)0g a a a a '=-=->+，所以1()2ln g a a a a=--在()0,a ∈+∞上是增函数．而(1)0g =，故当1a >时，()0g a >，即(1)(1)f f >-；当01a <<时，()0g a <，即(1)(1)f f <-．………………………………………14分所以，当1a >时，(1)(0)e 1f f --≥，即ln e 1a a --≥，函数ln y a a =-在(1,)a ∈+∞上是增函数，解得e a ≥；当01a <<时，(1)(0)e 1f f ---≥，即1ln e 1a a +-≥，函数1ln y a a =+在(0,1)a ∈上是减函数，解得10ea <≤． 综上可知，所求a的取值范围为1(0,][e,)ea ∈∞+．………………………………16分20．⑴当0n n a b +≥时，11124n n n a a b +=- 且134n n b b +=，所以111131()2442n n n n n n n a b a b b a b +++=-+=+， (2)分又当0n n a b +<时，11142n n n b a b +=-+且134n n a a +=，113111()4422n n n n n n n a b a a b a b +++=-+=+， (4)分因此，数列{}n n b a +是以b a +为首项，12为公比的等比数列， 所以，n n b a +11()2n a b -⎛⎫=+ ⎪⎝⎭．………………………………………………………5分⑵因为0n n a b +<，所以n n a a 431=+，所以134n n a a -⎛⎫= ⎪⎝⎭，11()2n n n b a b a -⎛⎫=+- ⎪⎝⎭1113()24n n a b a --⎛⎫⎛⎫=+- ⎪⎪⎝⎭⎝⎭， (8)分假设存在a ，b ，使得{}n b 能构成等比数列，则1b b =，224b a b -=，34516b ab -=， 故2245()()416b a b ab --=，化简得0=+b a ，与题中0a b +≠矛盾， 故不存在a，b使得{}n b 为等比数列． ……………………………………………10分⑶因为0n n a b <+且12243+=n n b b ，所以121222141--+-=n n n b a b所以1243+n b 21212121211113142444n n n n n a b a b b -----=-+=-+-所以2131()()44n n n n b b a b +----=-+，……………………………………………12分 由⑴知，2221211()2n n n a b a b ---⎛⎫+=+ ⎪⎝⎭，所以222121132n n n a b b b -+-+⎛⎫-=- ⎪⎝⎭)()(321213112----+-+=n n n b b b b b b246241111132222n a b b -⎡⎤+⎛⎫⎛⎫⎛⎫⎛⎫=-+++++⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦11114()141139414n n a b a b b b --⎡⎤⎛⎫-⎢⎥⎪⎡⎤++⎛⎫⎝⎭⎢⎥=-=--⎢⎥ ⎪⎢⎥⎝⎭⎢⎥⎣⎦-⎢⎥⎣⎦，…………………………………13分22133()114434nn n a b b b b +⎡⎤+⎛⎫==--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦，………………………………………………14分所以，1224()11,943()1-1,434n n na b b n b a b b n -⎧⎡⎤+⎛⎫⎪⎢⎥-- ⎪⎪⎢⎥⎝⎭⎪⎣⎦=⎨⎡⎤⎪+⎛⎫⎢⎥⎪- ⎪⎢⎥⎝⎭⎪⎣⎦⎩．为奇数时,为偶数时…………………………………16分徐州市2012—2013学年度高三第一次质量检测数学Ⅱ试题参考答案与评分标准21．A ．因为AB 为切线，AE 为割线，所以2AB AD AE =⋅，又因为AC AB =，所以2AD AE AC ⋅=．……………………………………………4分所以AD ACAC AE=，又因为EAC DAC ∠=∠，所以ADC △∽ACE △， 所以ADC ACE ∠=∠，又因为ADC EGF ∠=∠，所以EGF ACE ∠=∠，所以G．………………………………………………………………………10分B ．设点(,)P x y 为圆C ：221x y +=上任意一点，经过矩阵A 变换后对应点为(,)P x y '''，则00a x ax x b y by y '⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦，所以,x ax y by '=⎧⎨'=⎩．…………………………………………2分因为点(,)P x y '''在椭圆E ：22143x y =+上，所以2222143a xb y =+，………………4分又圆方程为221x y +=，故221,41,3a b ⎧=⎪⎪⎨⎪=⎪⎩，即224,3,a b ⎧=⎪⎨=⎪⎩，又0a >，0b >，所以2a =，3b =．所以2003⎡⎤=⎢⎥⎣⎦A ，……………………………………………………………………6分 所以1102303-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A ．…………………………………………………………………10分 C ．因为圆C 的参数方程为2cos ,22sin 2x r y r θθ⎧=-+⎪⎪⎨⎪=-+⎪⎩（θ为参数，0r >），消去参数得，()22222022x y r r ⎛⎫⎛⎫+++=> ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，所以圆心22,22C ⎛⎫-- ⎪ ⎪⎝⎭，半径为r ，……3分因为直线l 的极坐标方程为sin()14ρθπ+=，化为普通方程为2x y +=，………6分圆心C 到直线2x y +=的距离为2222222d ---==，……………………8分又因为圆C 上的点到直线l 的最大距离为3，即3d r +=，所以321r =-=．…10分D ．由柯西不等式，222222211()(2)(3)()()123x y z x y z ⎡⎤⎡⎤++++⋅++⎢⎥⎣⎦⎣⎦≤， (5)分因为2x y z =++，所以222242311x y z ++≥， 当且仅当2311123x y z ==，即6412,,111111x y z ===时，等号成立， 所以223x y z ++的最小值为2411．…………………………………………………10分 22．⑴因为抛物线24y x =焦点为()1,0F ，(1,0)T -．当l x ⊥轴时，(1,2)A ，(1,2)B -，此时0TA TB =，与1T AT B =矛盾，……………2分所以设直线l 的方程为(1)y k x =-，代入24y x =，得2222(24)0k x k x k -=++，则212224k x x k=++，121x x =， ①所以2212121616y y x x ==，所以124y y =-，②…4分因为1TA TB =，所以1212(1)(1)1x x y y =+++，将①②代入并整理得，24k =， 所以2k =±.………………………………………………………………………………6分⑵因为10y >，所以11211tan 114y y ATF y x ∠==++111114y y =+≤，当且仅当1114y y =，即12y =时，取等，所以4ATF π∠≤，所以ATF ∠的最大值为4π.……………………10分23．⑴24a =，35a =，46a =，猜想：*2()n a n n =∈+N ．……………………………2分①当1n =时，13a =，结论成立；②假设当*(1,)n k k k =∈N ≥时，结论成立，即2k a k =+，则当1n k =+时，22111111=(2)(+2)+1=+3=(+1)+22222k k k a a ka k k k k k +=-+-+， 即当1n k =+时，结论也成立，由①②得，数列{}n a 的通项公式为*2()n a n n =∈+N ．5分⑵原不等式等价于2(1)4n n+≥． 证明：显然，当2n =时，等号成立；当2n >时，01222222(1)C C C ()C ()n n n n nn n n nn n +=++++012233222C C C ()C ()n n n n n n n+++≥ 0122222>C C C ()54n n nn n n++=->， 综上所述，当2n ≥时，4nn n a n ≥．…………………………………………………10分。