伯努利方程推导

简述伯努利方程
伯努利方程是流体力学中的一个重要方程，描述了沿流体流动方向的速度变化和压力变化之间的关系。

伯努利方程是基于质量守恒和能量守恒原理推导而来的。

根据伯努利方程，对于稳定、不可压缩的流体，沿着流动方向的速度增加时，压力会降低；反之，速度减小时，压力会增加。

这个关系可以通过以下的数学表达式来表示：
P + 1/2ρv^2 + ρgh = constant
其中，P 是流体的压力，ρ是流体的密度，v 是流体的速度，g 是重力加速度，h 是流体的高度。

这个方程可以被解释为，在沿流动方向的某点，流体的总能量（包括压力能、动能和位能）保持不变。

伯努利方程的应用非常广泛。

例如，在管道中流动的液体，根据伯努利方程可以计算出某一点的压力变化和速度变化。

这对于设计水厂、油管道以及飞行器的气动特性等都非常有用。

然而，需要注意的是，伯努利方程仅适用于理想的、不可压缩的流体，并且在计算过程中需要满足一定的假设条件，如忽略粘性、摩擦等因素。

对于可压缩流体或涡流等特殊情况，伯努利方程可能不再适用。

总之，伯努利方程是流体力学中的基本方程之一，描述了流体流动中速度和压力之间的关系。

具有广泛的应用价值，但在具体应用时需要结合特定情况进行合理使用和解读。

根据流体运动方程P F dt V d ∙∇+=ρ1上式两端同时乘以速度矢量()V P V F V dt d ∙∙∇+∙=⎪⎪⎭⎫ ⎝⎛ρ122右端第二项展开——()()V P V P V F V dtd ∙∇∙-∙∙∇+∙=⎪⎪⎭⎫ ⎝⎛ρρ1122利用广义牛顿粘性假设张量P ，得出单位质量流体微团的动能方程()E V div p V P div VF V dt d -+∙+∙=⎪⎪⎭⎫ ⎝⎛ ρρ122右第三项是膨胀以及收缩在压力作用下引起的能量转化项（膨胀：动能增加<--内能减少） 右第四项是粘性耗散项：动能减少-->内能增加热流量方程：用能量方程减去动能方程 反映内能变化率的热流量方程()()dtdq V P div V F V T c dt d +∙+∙=+ ρυ12/2()E V div pV P div V F V dtd -+∙+∙=⎪⎪⎭⎫ ⎝⎛ ρρ122得到()()E V div p T c dt d dt dq dt dq E V div p T c dt d-+=++-= ρρυυ / 对于理想流体，热流量方程简化为： ()V d i v p T c dt ddt dq ρυ+=这就是通常在大气科学中所用的“热力学第一定律”的形式。

由动能方程推导伯努利方程：对于理想流体，动能方程简化为：()V div pV P div V F V dt d ρρ+∙+∙=⎪⎪⎭⎫ ⎝⎛122无热流量项。

又因为()V pdiv p V z pw y pv x pu V P div -∇∙-=⎥⎦⎤⎢⎣⎡++-=∙∂∂∂∂∂∂)()()(故最终理想流体的动能方程可以写成：p V V F V dtd∇⋅-∙=⎪⎪⎭⎫ ⎝⎛ρ22【理想流体动能的变化，仅仅是由质量力和压力梯度力对流体微团作功造成的，而与热能不发生任何转换。

】假设质量力是有势力，且质量力位势为Φ，即满足：Φ-∇=F考虑Φ为一定常场，则有：dt d V V F Φ-=Φ∇∙-=∙理想流方程体动能方程p VV F V dt d ∇⋅-∙=⎪⎪⎭⎫ ⎝⎛ρ22假设质量力是有势力，是定常场p V V dtd∇⋅-=⎪⎪⎭⎫ ⎝⎛Φ+ρ22由定常条件：p V p V t pdt dp ∇⋅-=∇⋅-∂∂-=- -->dt dpV dt d ρ122-=⎪⎪⎭⎫ ⎝⎛Φ+ 不可压缩条件0d dt ρ=-->⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛Φ+ρp dt dV dt d 22-->022=⎪⎪⎭⎫ ⎝⎛+Φ+ρp V dtd等式右端括号内部分的个体变化为零，也即：const pV =+Φ+ρ22定常运动:流体运动的迹线和流线是重合,于是沿流体运动的流线也有const pV =+Φ+ρ22例：求水从容器壁小孔中流出时的速率。

欧拉-伯努利方程
欧拉-伯努利方程是流体力学中的一种重要方程，描述了流体在不可压缩、定常、理想流动条件下沿流线的行为。

它是基于质量守恒和动量守恒原理推导而来的。

欧拉-伯努利方程可以表示为：
P + 1/2ρv²+ ρgh = 常数
其中：P是流体的压力，ρ是流体的密度，v是流体的速度，g是重力加速度，h是流体的高度。

这个方程的意义是，沿着流体的流线，在没有外力做功的情况下，流体的总能量保持不变。

方程左边的三项分别代表了流体的压力能、动能和重力势能。

欧拉-伯努利方程在流体力学中有广泛的应用，例如可以用来解释飞机的升力产生、水流的速度和压力分布、水泵和风扇的工作原理等。

它为理解和分析流体力学问题提供了重要的工具和方法。

需要注意的是，欧拉-伯努利方程是一种基于一些假设条件的简化模型，在特定的情况下有效，但也有其适用范围和限制。

伯努利方程公式介绍在物理学和工程学中，伯努利方程是描述流体在不同位置之间的速度、静压力和动压力之间关系的基本方程。

它是基于质量守恒和能量守恒的原理推导出来的。

伯努利方程广泛应用于流体力学、飞行器设计、液压系统等领域。

公式伯努利方程的数学表达式如下所示：P + (1/2)ρv^2 + ρgh = constant其中：•P 表示流体在某一点的静压力（单位为帕斯卡）；•ρ 表示流体的密度（单位为千克/立方米）；•v 表示流体在某一点的速度（单位为米/秒）；•g 表示重力加速度（单位为米/秒^2）；•h 表示流体在某一点的高度（单位为米）。

解释伯努利方程可以解释为流体在不同位置之间能量的转化。

方程的左边分别表示流体在某一点的静压力、动压力和重力势能的总和，而右边表示这些能量在流体运动过程中保持不变。

在没有外力作用的情况下，伯努利方程说明了流体在不同位置之间速度、压力和高度之间的相互关系。

应用伯努利方程在实际应用中具有广泛的意义。

下面是一些常见的应用场景：管道流动在管道流动中，伯努利方程可以用来计算流体在不同位置之间的压力变化情况。

通过测量流体的速度和压力，可以利用伯努利方程来推算出管道中的流速、管道的截面积等重要参数。

飞行器设计在飞行器设计中，伯努利方程可以帮助工程师计算飞机的升力和阻力。

通过将飞机的速度、空气密度和升力系数代入伯努利方程，可以确定飞机的升力和阻力大小，从而优化飞行器的设计。

液压系统在液压系统中，伯努利方程可以用来推算液体在管道中的压力变化。

通过测量流体的速度和压力，可以利用伯努利方程来优化液压系统的性能，例如提高液压系统的效率和减少压力损失。

总结伯努利方程是描述流体运动中速度、压力和高度之间关系的重要公式。

它通过质量守恒和能量守恒的原理，揭示了流体在不同位置之间能量的转化和平衡。

伯努利方程在物理学和工程学中具有广泛的应用，是研究流体力学和优化系统设计的基础工具。

通过深入理解和应用伯努利方程，可以对流体运动和力学系统进行准确的分析和预测。

伯努利方程原理伯努利方程原理是流体力学中的重要定律，描述了流体在沿流动方向不受外力作用时的行为。

它是基于质量守恒、动量守恒和能量守恒的基本原理而推导出来的。

我们来了解一下伯努利方程的基本概念。

伯努利方程是描述流体在沿流动方向上速度变化时，压力、速度和高度之间的关系。

它的数学表达形式为：P + 1/2ρv^2 + ρgh = 常数其中，P表示压力，ρ表示流体的密度，v表示流体的速度，g表示重力加速度，h表示流体的高度。

这个方程表明，在不受外力作用的情况下，当流体速度增大时，压力会减小；当流体速度减小时，压力会增大。

伯努利方程原理的推导基于三个基本原理：质量守恒、动量守恒和能量守恒。

质量守恒原理指的是在流体运动过程中，单位时间内通过任意截面的流体质量保持不变。

这意味着如果流体速度增大，流体密度会减小；如果流体速度减小，流体密度会增大。

动量守恒原理表明在流体运动过程中，单位时间内通过任意截面的动量保持不变。

根据牛顿第二定律，动量等于质量乘以速度，因此当流体速度增大时，流体的动量也会增大；当流体速度减小时，流体的动量也会减小。

能量守恒原理指的是在流体运动过程中，单位时间内通过任意截面的能量保持不变。

根据能量转化的原理，当流体速度增大时，其动能增加，而静压能减小；当流体速度减小时，其动能减小，而静压能增加。

基于以上三个原理，我们可以推导出伯努利方程。

在流体静止的情况下，即流体速度为零时，伯努利方程可以简化为：P + ρgh = 常数这个方程表示了在不同高度处流体的压力之间的关系，即流体的压力随着高度的增加而增加。

总结一下，伯努利方程原理是基于质量守恒、动量守恒和能量守恒的基本原理推导出来的。

它描述了流体在沿流动方向不受外力作用时的行为，即流体速度的增大导致压力的减小，流体速度的减小导致压力的增大。

伯努利方程的应用非常广泛，例如在飞机的升力产生、水管的流量控制等领域都有重要的应用。

了解伯努利方程原理可以帮助我们更好地理解和应用流体力学知识。

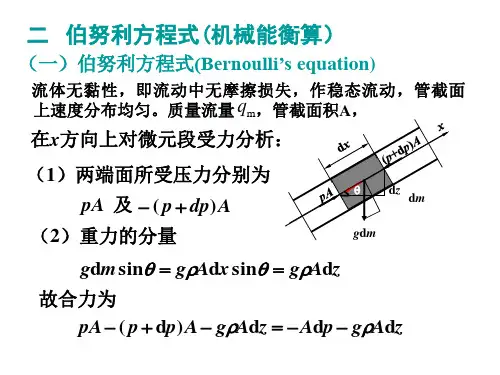
第四章 伯努利方程4.1 伯努利方程4.1.1 理想流体沿流线的伯努利方程1. 伯努利方程的推导将欧拉运动微分方程式积分可以得到流体的压力分布规律，但只能在特殊的条件下，不可能在任何的情况下都可求得其解，故我们需对流场作出如下假设：（1）理想流体（2）定常流动（3）质量力有势（4）不可压缩流体（5）沿流线积分在定常流动的条件下，理想流体的运动微分方程（欧拉运动微分方程）可以写成 ⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂=∂∂-z v v y v v x v v z p f z v v y v v x v v y p f z v v y v v x v v x p f z z z y z x z y z y y y x y x z x y x x x ρρρ111 (4.1) 将这个方程沿流线积分，如图4.1所示，可得到伯努利方程。

为此，将式(4.1)的第一式乘以x d 得x zv v x y v v x x v v x x p x f x z x y x x x d d d d 1d ∂∂+∂∂+∂∂=∂∂-ρ （1） 按照流线方程 zy x v z v y v x d d d == 将有，y v x v x y d d =，z v x v x z d d =故式（1）可写成x x x x x x x x x v v z zv v y y v v x x v v x x p x f d d d d d 1d =∂∂+∂∂+∂∂=∂∂-ρ （2） 式(4.1)的另外两式分别乘y d 、z d 后，作类似的代换，可得y y y v v y yp y f d d 1d =∂∂-ρ （3）z z z v v z zp z f d d 1d =∂∂-ρ （4） 将式（2）、（3）和式（4）相加，得 z z y y x x z y x v v v v v v z zp y y p x x p z f y f x f d d d )d d d (1d d d ++=∂∂+∂∂+∂∂-++ρ （5） p 的全微分可以表示为 dz zp dy y p dx x p dp ∂∂+∂∂+∂∂= 质量力有势，则必存在势函数U ，满足y f y f x f z zU y y U x x U U y y x d d d d d d d ++=∂∂+∂∂+∂∂=而 2/d d d d 2v v v v v v v z z y y x x =++式中等号右端的v 为平均速度。

伯努利方程的推导主要基于能量守恒与转化定律在流体力学中的应用。

以下是推导过程：考虑理想流体在重力场中的一维定常流动，在微元流管中取一流体微元进行分析。

根据欧拉方程（即无粘流体的Navier-Stokes方程），可以得到流体微元的运动微分方程。

对该微分方程进行积分，得到沿流线的伯努利积分。

假设质量力只为重力，可以得到一般形式的伯努利积分，即(V^2/2 + ∫dp/ρ + gz = C(ψ))，其中(C(ψ)) 为随流线不同而不同的伯努利常数。

请注意，上述推导过程中忽略了流体的粘性和热传导效应，因此在实际应用中可能需要进行修正。

此外，对于不同的流动条件和边界条件，伯努利方程的具体形式也可能有所不同。

伯努利方程的应用伯努利方程对于流动体系除了掌握体系的对于流动体系，除了掌握体系的物料衡算关系以外，还必须找出体系各种形式能量之间的转换关系系各种形式能量之间的转换关系。

伯努利(Bernoulli)方程：描述了流体流动过程中各种形式能量之间的转换关系，是流体在定常流动情。

是热力学第一Daniel Bernoulli ，1700-1782况下的能量衡算式是热力学第定律对流体流动过程的具体描述。

流动系统的能量流动系统的能量：流动系统的能量流动系统的能量：(3) 动能：流体以一定的速度运动时便具有一定的动能，大时所需要的功小等于流体从静止加速到流速v时所需要的功。

(4) 静压能：流体进入划定体积时需要对抗压力所做的功。

流体进入划定体积时需要对抗压力所做的功若质量为m的流体体积为，某截面处的静压强为p，截面面积为A，则将质量为m的流体压入划定体积的功为：则将质量为的流体压入划定体积的功为质量为能量还可以通过其他外界条件与流动系统进行交换，包括：：流体通过换热器吸热或放热Q e吸热时为正，放热时为负。

：泵等流体输送机械向系统做功W em 的流体交换热量=m Q e流体接受外功为正流体对外作功为负作功为负的流体所接受的功= mW e以截面两边同除以m单位质量流体稳定流动过程的总能量衡算式，流动系统的力学第一定律表达式系统内能变化系统内能变化：是单位质量流体从截面1-1到截面是单位质量流体从截面1-1到截面2-2流体通过环境直接获得的热量，Q e(1)流体通过环境直接获得的热量流体流动时需克服阻力做功，因而消耗机械能转化为热量，若流体等温流动，这部分热量则散失到系统外部。

设单位流体因克服阻力而损失的，则则不可压缩流体ρ=const=0无外加功W e=0理想流体，Σhf伯努力方程努力方程的有关伯努力方程的讨论(1)伯努力方程的适用条件：不可压缩的理想流体做定常流动而无外功输入的情况，选取截面符合缓变流条件。

单位质量流体在任一截面上所具有的势能、动能和静压能之和是一常数。

流体力学流速计算公式一、伯努利方程推导流速公式（理想不可压缩流体定常流动）1. 伯努利方程。

- 对于理想不可压缩流体作定常流动时，在同一条流线上有p+(1)/(2)ρ v^2+ρ gh = C（p是流体压强，ρ是流体密度，v是流速，h是高度，C是常量）。

- 假设水平流动（h_1 = h_2），则方程变为p_1+(1)/(2)ρ v_1^2=p_2+(1)/(2)ρ v_2^2。

- 由此可推导出流速公式v_2=√(v_1^2)+(2(p_1 - p_2))/(ρ)。

2. 适用条件。

- 理想流体（无粘性），实际流体在粘性较小时可近似使用。

- 不可压缩流体，像水在大多数情况下可视为不可压缩流体，气体在低速流动时也可近似为不可压缩流体。

- 定常流动，即流场中各点的流速等物理量不随时间变化。

3. 示例。

- 已知水管中某点1处的压强p_1 = 2×10^5Pa，流速v_1 = 1m/s，另一点2处的压强p_2 = 1.5×10^5Pa，水的密度ρ = 1000kg/m^3。

- 根据v_2=√(v_1^2)+(2(p_1 - p_2))/(ρ)，将数值代入可得：- v_2=√(1^2)+frac{2×(2×10^{5-1.5×10^5)}{1000}}- 先计算括号内的值：2×(2×10^5-1.5×10^5)=2×5×10^4=10^5。

- 则v_2=√(1 + 100)= √(101)≈10.05m/s。

二、连续性方程推导流速公式（不可压缩流体定常流动）1. 连续性方程。

- 对于不可压缩流体的定常流动，有S_1v_1 = S_2v_2（S_1、S_2分别是流管中两个截面的面积，v_1、v_2是相应截面处的流速）。

- 由此可推导出流速公式v_2=(S_1)/(S_2)v_1。

2. 适用条件。

- 不可压缩流体，如液体或低速流动的气体。

关于伯努利方程的理论推导
《伯努利方程》，又称《伯努利假设》，是20世纪著名数学家Andrey Kolmogorov提出的一种概率论模型。

伯努利方程（Bernoulli Equation）表示一个有限的概率分布，它描述了一个变量的取值依赖于另外一个变量取值所产生的不同情况之间的关系。

它是概率论中最基础而重要的概念，广泛用于统计学、机器学习、金融数学以及一些实际应用场景。

伯努利方程的公式表示为：
P（X=x）=p^x (1-p)^（1-X）
其中，X为事件的发生与否，取值为0或1；p为在某种条件下某事件发生的概率。

伯努利方程的推导如下：
当X取值为1时，事件发生，其发生概率为p，即P（X=1）=p；
当X取值为0时，事件不发生，其发生概率为1-p，即P（X=0）=1-p；
以上两式相乘可得：
P（X=1）P（X=0）=P（X=1）（1-p）=p（1-p）
根据概率乘法定律，把X取值为0或1的两种情况统一表示，可得如下公式：
P（X=x）=p^x (1-p)^（1-x）
如此，便完成了伯努利方程的推导。

伯努利方程的概念广泛应用于实际，如经济统计学中经常使用它
来表示经济变量的概率分布，在信息论中，可以把它用来衡量某个信息源的信息熵，在机器学习中，用它来表示决策树以及逻辑回归算法，而且在金融数学中，还可以使用它来模拟股市中的收益概率分布。

伯努利模型的推导及应用，即实现了统计学与概率论的完美结合。

总之，伯努利方程（Bernoulli Equation）是一种有限的概率分布模型，它比较简单，易于理解，而且应用广泛，因而在统计学、信息论、机器学习以及金融数学等领域均有着重要的应用。

化工原理伯努利方程
伯努利方程是描述流体在运动过程中能量守恒的基本原理之一。

根据伯努利方程，流体在稳态条件下沿着流线的总能量保持不变，即由速度势、静压力和流动压力组成的总能量在流体运动过程中保持恒定。

具体而言，伯努利方程可以写作：
P + 0.5ρv^2 + ρgh = 常数
其中，P是流体的静压力，ρ是流体的密度，v是流体的速度，g是重力加速度，h是流体的高度。

伯努利方程的原理可以通过下面的推导来理解。

考虑一个流经管道的流体元素，在单位时间内，流体元素穿过任意两个横截面之间的流体量是相等的。

由于质量守恒，流体密度是恒定的，所以这一流体元素在不同横截面位置上的体积速度亦是相等的。

根据动量定理，单位时间内流体元素受到的外力和单位时间内动量的改变量之间存在关系。

在伯努利方程中，流体受到的外力可以分为静压力和流动压力两部分。

静压力即为流体在静止不动时的压力，而流动压力则是流体在运动过程中产生的额外压力。

由于单位时间内流体元素的动量改变量为0，所以伯努
利方程成立。

根据伯努利方程，我们可以得到一些重要的结论。

首先，当流体的速度增加时，流体的静压力会下降，即压力和速度之间存在负相关关系。

其次，当流体的速度增加时，流体的动能也会
增加，即速度和动能之间存在正相关关系。

最后，当流体高度增加时，流体的静压力也会增加。

总之，伯努利方程是描述流体运动过程中能量守恒的重要原理，对于分析和理解流体力学问题具有重要意义。

伯努利方程详细推导
伯努利方程描述了流体在不可压缩、无粘性和稳定流动情况下的性质。

它可以用来描述流体在不同位置上的压力、速度和高度之间的关系。

伯努利方程可以用以下方式推导：
考虑在流体中沿流线选取两点A和B，应用动能定理和能量守恒定律，可以得到伯努利方程。

动能定理：单位质量的流体在速度为v时的动能为1/2 * v^2。

能量守恒定律：在无外力做功的情况下，流体的总机械能保持不变，即压力能、动能和势能之和保持不变。

根据上述原理，可以得到伯努利方程的推导过程：
首先，考虑点A和点B处的流体元。

根据动能定理，流体的动能可以表示为1/2 * ρ* v^2，其中ρ为流体密度，v为流体的速度。

根据能量守恒定律，在点A和点B处，流体的总机械能保持不变，即：
P_A + 1/2 * ρ* v_A^2 + ρ* g * h_A = P_B + 1/2 * ρ* v_B^2 + ρ* g * h_B
其中，P为压力，g为重力加速度，h为高度。

这个方程描述了压力能、动能和势能之和在两个点上的平衡关系。

假设流体是不可压缩的，可以得到ρ* v_A^2 = ρ* v_B^2，因此动能项可以简化。

最终，经过简化后的伯努利方程可以表示为：
P_A + 1/2 * ρ* v_A^2 + ρ* g * h_A = P_B + 1/2 * ρ* v_B^2 + ρ* g * h_B
这就是伯努利方程，描述了流体在两点之间的压力、速度和高度之间的关系。

伯努利方程伯努利方程就是能量守衡定律在流动液体中的表现形式。

(动能定理)1、理想液体的运动微分方程在微小流束上，取截面积为dA，长为ds的微元体，现研究理想液体定常流动条件下在重力场中沿流线运动时其力的平衡关系。

微元体的所受的重力为-ρgdAds，压力作用在两端面上的力为微元体在定常流动下的加速度为微元体的力平衡方程为上式简化后可得p，z，u只是s的函数，进一步简化得上式即为重力场中，理想液体沿流线作定常流动时的运动方程，即欧拉运动方程。

2、理想液体的伯努利方程沿流线对欧拉运动方程积分得上式两边同除以g 得以上两式即为理想液体作定常流动的伯努利方程。

伯努利方程推导简图物理意义：第一项为单位重量液体的压力能称为比压能（p/ρg ）；第二项为单位重量液体的动能称为比动能（u2/2g ）；第三项为单位重量液体的位能称为比位能（z）。

由于上述三种能量都具有长度单位，故又分别称为压力水头、速度水头和位置水头。

三者之间可以互相转换，但总和（H，称为总水头）为一定值。

3．实际液体流束的伯努利方程实际液体都具有粘性，因此液体在流动时还需克服由于粘性所引起的摩擦阻力，这必然要消耗能量，设因粘性二消耗的能量为hw'，则实际液体微小流束的伯努利方程为4．实际液体总流的伯努利方程将微小流束扩大到总流，由于在通流截面上速度u是一个变量，若用平均流速代替，则必然引起动能偏差，故必须引入动能修正系数。

于是实际液体总流的伯努利方程为式中hw---由液体粘性引起的能量损失；α1，α2---动能修正系数，一般在紊流时取α＝1，层流时取α＝2。

5．伯努利方程应用举例例1 侧壁孔口流出速度条件: p1和p2 ，h为高，以小孔中心线为基准。

例2 文丘利流量计例3 液压泵的最大吸油高度例4 试运用连续性方程和伯努利方程分析变截面水平管道各处的压力情况.条件:A1>A2>A3 比较:流速和压力的大小四、动量方程液体作用在固体壁面上的力，用动量定理来求解比较方便。

伯努利方程的一个简单推导方法
伯努利方程推导：
1、伯努利方程（Bernoulli equation）理想正压流体在有势彻体力作用下作定常运动时，运动方程（即欧拉方程）沿流线积分而得到的表达运动流体机械能守恒的方程。

因著名的瑞士科学家D.伯努利于1738年提出而得名。

2、对于重力场中的不可压缩均质流体，方程为p+ρgz+(1/2)*ρv^2=C 式中p、ρ、v分别为流体的压强、密度和速度；z 为铅垂高度；g为重力加速度。

上式各项分别表示单位体积流体的压力能p、重力势能ρg z和动能(1/2)*ρv ^2，在沿流线运动过程中，总和保持不变，即总能量守恒。

但各流线之间总能量（即上式中的常量值）可能不同。

对于气体，可忽略重力，方程简化为p+(1/2)*ρv ^2＝常量(p0)，各项分别称为静压、动压和总压。

显然，流动中速度增大，压强就减小；速度减小，压强就增大；速度降为零，压强就达到最大(理论上应等于总压)。

飞机机翼产生举力，就在于下翼面速度低而压强大，上翼面速度高而压强小，因而合力向上。