计量经济学(多元回归分析推断)

计量经济学多元回归分析案例引言计量经济学是运用数理统计和经济学方法研究经济现象的一门学科。

在实际研究中，多元回归分析是一种常用的方法。

本文将通过一个实际案例来介绍计量经济学中的多元回归分析方法和应用。

研究背景单因素回归分析在计量经济学中，单因素回归分析是最基本的方法之一。

它通过确定一个因变量和一个自变量之间的关系，来解释因变量的变化。

然而，在现实世界中，经济现象往往受到多个因素的影响，因此需要使用多元回归分析来更全面地解释经济现象的变化。

问题陈述本研究的问题是探究某个城市的房价与多个因素之间的关系。

具体来说，我们感兴趣的因变量是房价，自变量包括房屋面积、地理位置、周边设施等。

我们希望通过建立一个多元回归模型来解释房价的变化，并分析不同因素对房价的影响程度。

数据收集为了进行多元回归分析，我们需要收集相关的数据。

在本案例中，我们采集了以下数据：1.房价：通过不同的房地产网站获取该城市的房屋销售数据，包括每个房屋的售价信息。

2.房屋面积：通过购房广告或房产中介提供的信息收集每个房屋的面积数据。

3.地理位置：通过经纬度或邮政编码信息获取每个房屋的地理位置信息。

4.周边设施：通过地图应用或开放的公共数据接口获取每个房屋周边设施（如学校、医院、商场等）的数量和距离信息。

数据预处理在进行多元回归分析前，我们需要对收集到的数据进行预处理。

缺失值处理在数据收集过程中，可能会出现数据缺失的情况。

对于缺失的数据，我们可以选择删除相应的样本，或者通过插补方法进行填充。

在本案例中，我们选择使用均值填充的方法。

数据转换由于多元回归模型要求变量之间具有线性关系，因此我们需要对非数值型数据进行转换。

在本案例中，地理位置可以通过编码转换为数值型变量。

模型建立在进行多元回归分析时，我们需要选择适当的模型来描述因变量和自变量之间的关系。

在本案例中，我们选择使用普通最小二乘法（OLS）来估计回归模型的参数。

模型表达式我们将房价作为因变量（Y），房屋面积、地理位置和周边设施作为自变量（X）。

伍德⾥奇《计量经济学导论》（第6版）复习笔记和课后习题详解-多元回归分析：推断【圣才出品】第4章多元回归分析：推断4.1复习笔记考点⼀：OLS估计量的抽样分布★★★1．假定MLR.6（正态性）假定总体误差项u独⽴于所有解释变量，且服从均值为零和⽅差为σ2的正态分布，即：u～Normal（0，σ2）。

对于横截⾯回归中的应⽤来说，假定MLR.1～MLR.6被称为经典线性模型假定。

假定下对应的模型称为经典线性模型（CLM）。

2．⽤中⼼极限定理（CLT）在样本量较⼤时，u近似服从于正态分布。

正态分布的近似效果取决于u中包含多少因素以及因素分布的差异。

但是CLT的前提假定是所有不可观测的因素都以独⽴可加的⽅式影响Y。

当u是关于不可观测因素的⼀个复杂函数时，CLT论证可能并不适⽤。

3．OLS估计量的正态抽样分布定理4.1（正态抽样分布）：在CLM假定MLR.1～MLR.6下，以⾃变量的样本值为条件，有：∧βj～Normal（βj，Var（∧βj））。

将正态分布函数标准化可得：（∧βj－βj）/sd（∧βj）～Normal（0，1）。

注：∧β1，∧β2，…，∧βk的任何线性组合也都符合正态分布，且∧βj的任何⼀个⼦集也都具有⼀个联合正态分布。

考点⼆：单个总体参数检验：t检验★★★★1．总体回归函数总体模型的形式为：y＝β0＋β1x1＋…＋βk x k＋u。

假定该模型满⾜CLM假定，βj的OLS 量是⽆偏的。

2．定理4.2：标准化估计量的t分布在CLM假定MLR.1～MLR.6下，（∧βj－βj）/se（∧βj）～t n－k－1，其中，k＋1是总体模型中未知参数的个数（即k个斜率参数和截距β0）。

t统计量服从t分布⽽不是标准正态分布的原因是se（∧βj）中的常数σ已经被随机变量∧σ所取代。

t统计量的计算公式可写成标准正态随机变量（∧βj－βj）/sd（∧βj）与∧σ2/σ2的平⽅根之⽐，可以证明⼆者是独⽴的；⽽且（n－k－1）∧σ2/σ2～χ2n－k－1。

计量经济学：多元回归分析推断引言多元回归分析是计量经济学中常用的一种分析方法，用于探究多个自变量对一个因变量的影响关系。

本文将介绍多元回归分析的基本概念和原理，并且解释如何使用多元回归分析进行推断。

多元回归模型多元回归模型可以表示为：multivariate_regression_model其中，Y是因变量，表示我们想要解释的变量；X1, X2, …, Xk是自变量，表示对因变量有可能影响的变量；β0, β1, β2, …, βk是回归系数，表示自变量对因变量的影响程度；ε是误差项，表示我们未能观测到的其他影响因素。

多元回归模型的目标是通过估计回归系数，来解释因变量与自变量之间的关系，并且用这个模型进行推断。

多元回归模型的估计多元回归模型的估计可以使用最小二乘法进行。

最小二乘法的基本思想是，通过最小化因变量Y与预测值Y_hat之间的平方差，来求解回归系数的估计值。

最小二乘法估计的求解过程，可以用矩阵表示如下：multivariate_regression_estimation其中，X是自变量的矩阵，Y是因变量的向量，X T表示X的转置，(-1)表示矩阵的逆运算。

多元回归的推断多元回归模型的估计结果可以用于进行推断。

对回归系数进行假设检验，可以判断自变量对因变量是否有显著影响。

常用的假设检验有以下几种：1. 假设检验回归系数是否等于零：用于判断自变量是否对因变量有显著影响。

2. 假设检验回归系数是否等于某个特定值：用于判断自变量对因变量的影响是否等于某个理论值。

3. 假设检验多个回归系数是否同时等于零：用于判断自变量组合的整体影响是否显著。

假设检验的结果通常使用P值进行解释。

如果P值小于预先设定的显著性水平（通常为0.05），则拒绝原假设，认为回归系数是显著不等于零的。

多元回归的解释力度除了进行推断以外，多元回归模型还可以用于解释因变量的变异程度。

通过计算决定系数（R-squared），可以评估自变量对因变量的解释力度。

第7章含有定性信息的多元回归分析：二值(或虚拟)变量在前面几章中，我们的多元回归模型中的因变量和自变量都具有定量的含义。

就像小时工资率、受教育年数、大学平均成绩、空气污染量、企业销售水平和被拘捕次数等。

在每种情况下，变量的大小都传递了有用的信息。

在经验研究中，我们还必须在回归模型中考虑定性因素。

一个人的性别或种族、一个企业所属的产业（制造业、零售业等）和一个城市在美国所处的地理位置（南、北、西等）都可以被认为是定性因素。

本章的绝大部分内容都在探讨定性自变量。

我们在第7.1节介绍了描述定性信息之后，又在第7.2、7.3和7.4节中说明了，如何在多元回归模型中很容易地包含定性的解释变量。

这几节几乎涵盖了定性自变量用于横截面数据回归分析的所有流行方法。

我们在第7.5节讨论了定性因变量的一种特殊情况，即二值因变量。

这种情形下的多元回归模型具有一个有趣的含义，并被称为线性概率模型。

尽管有些计量经济学家对线性概率模型多有中伤，但其简洁性还是使之在许多经验研究中有用武之地。

虽然我们在第7.5节将指出其缺陷，但在经验研究中，这些缺陷常常都是次要的。

7.1 对定性信息的描述定性信息通常以二值信息的形式出现：一个人是男还是女；一个人有还是没有一台个人计算机；一家企业向其一类特定的雇员提供还是不提供退休金方案；一个州实行或不实行死刑。

在所有这些例子中，有关信息可通过定义一个二值变量(binary variable)或一个0-1变量来刻画。

在计量经济学中，对二值变量最常见的称呼是虚拟变量(dummy variable)，尽管这个名称并不是特别形象。

在定义一个虚拟变量时，我们必须决定赋予哪个事件的值为1和哪个事件的值为0。

比如，在一项对个人工资决定的研究中，我们可能定义female 为一个虚拟变量，并对女性取值1，而对男性取值0。

这种情形中的变量名称就是取值1的事件。

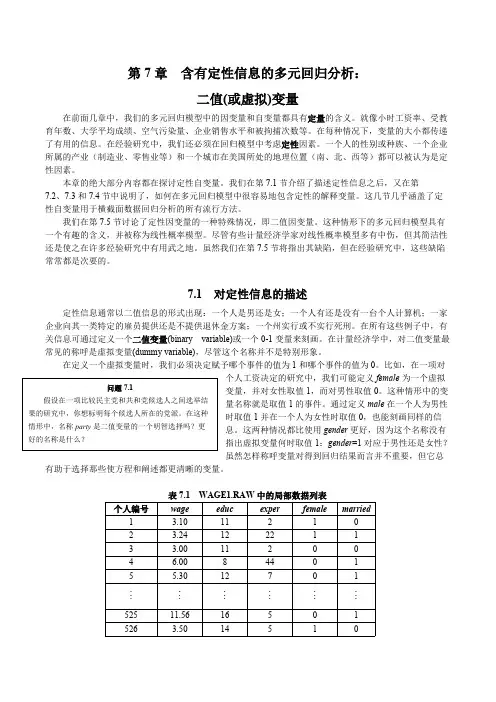
通过定义male 在一个人为男性时取值1并在一个人为女性时取值0，也能刻画同样的信息。

计量经济学复习要点第1章 绪论数据类型：截面、时间序列、面板用数据度量因果效应，其他条件不变的概念 习题：C1、C2第2章 简单线性回归回归分析的基本概念，常用术语现代意义的回归是一个被解释变量对若干个解释变量依存关系的研究，回归的实质是由固定的解释变量去估计被解释变量的平均值。

简单线性回归模型是只有一个解释变量的线性回归模型。

回归中的四个重要概念1. 总体回归模型（Population Regression Model ，PRM)t t t u x y ++=10ββ--代表了总体变量间的真实关系。

2. 总体回归函数（Population Regression Function ，PRF ）t t x y E 10)(ββ+=--代表了总体变量间的依存规律。

3. 样本回归函数（Sample Regression Function ，SRF ）tt t e x y ++=10ˆˆββ--代表了样本显示的变量关系。

4. 样本回归模型（Sample Regression Model ，SRM ）tt x y 10ˆˆˆββ+=---代表了样本显示的变量依存规律。

总体回归模型与样本回归模型的主要区别是：①描述的对象不同。

总体回归模型描述总体中变量y 与x 的相互关系，而样本回归模型描述所关的样本中变量y 与x 的相互关系。

②建立模型的依据不同。

总体回归模型是依据总体全部观测资料建立的，样本回归模型是依据样本观测资料建立的。

③模型性质不同。

总体回归模型不是随机模型，而样本回归模型是一个随机模型，它随样本的改变而改变。

总体回归模型与样本回归模型的联系是：样本回归模型是总体回归模型的一个估计式，之所以建立样本回归模型，目的是用来估计总体回归模型。

线性回归的含义线性：被解释变量是关于参数的线性函数（可以不是解释变量的线性函数） 线性回归模型的基本假设简单线性回归的基本假定：对模型和变量的假定、对随机扰动项u 的假定（零均值假定、同方差假定、无自相关假定、随机扰动与解释变量不相关假定、正态性假定） 普通最小二乘法（原理、推导）最小二乘法估计参数的原则是以“残差平方和最小”。

多元回归计量统计学
多元回归是计量统计学中的一种重要方法，用于分析多个自变量对因变量的影响。

它可以帮助我们理解多个变量之间的关系，并通过建立回归方程来预测因变量的值。

下面我将以人类的视角来叙述多元回归的相关内容。

在多元回归中，我们通常会面对一个研究问题，比如我们想知道什么因素会影响一个人的收入水平。

为了回答这个问题，我们需要收集相关的数据，比如个人的年龄、教育水平、工作经验等作为自变量，以及个人的收入作为因变量。

通过收集大量的数据，我们可以建立一个多元回归模型，通过分析自变量与因变量之间的关系来预测个人的收入水平。

在建立模型时，我们需要考虑到每个自变量对因变量的影响，并确定它们之间的权重。

为了确保模型的准确性，我们还需要进行模型评估和检验。

常见的方法包括计算模型的拟合优度和残差分析。

拟合优度可以告诉我们模型对数据的拟合程度，而残差分析可以帮助我们检查模型是否存在偏差或异常值。

除了预测个人收入水平外，多元回归还可以用于解释变量之间的关系。

通过观察回归系数的符号和大小，我们可以判断不同自变量对因变量的影响力。

这有助于我们理解变量之间的相互作用，并为决
策提供依据。

需要注意的是，多元回归只能提供相关关系，而不能确定因果关系。

因此，在解释结果时，我们需要谨慎地分析数据，并避免误导性的解释。

多元回归是计量统计学中一种重要的分析方法，可以帮助我们理解变量之间的关系，并预测因变量的值。

通过合理地选择自变量和建立适当的模型，我们可以得到准确的预测结果，并为决策提供支持。

希望通过本文的描述，读者能够更好地理解多元回归的概念和应用。

计量经济学复习要点参考教材：伍德里奇 《计量经济学导论》 第1章 绪论数据类型：截面、时间序列、面板用数据度量因果效应，其他条件不变的概念习题：C1、C2 第2章 简单线性回归回归分析的基本概念，常用术语现代意义的回归是一个被解释变量对若干个解释变量依存关系的研究，回归的实质是由固定的解释变量去估计被解释变量的平均值。

简单线性回归模型是只有一个解释变量的线性回归模型。

回归中的四个重要概念1. 总体回归模型（Population Regression Model ，PRM)t t t u x y ++=10ββ--代表了总体变量间的真实关系。

2. 总体回归函数（Population Regression Function ，PRF ）t t x y E 10)(ββ+=--代表了总体变量间的依存规律。

3. 样本回归函数（Sample Regression Function ，SRF ）tt t e x y ++=10ˆˆββ--代表了样本显示的变量关系。

4. 样本回归模型（Sample Regression Model ，SRM ）tt x y 10ˆˆˆββ+=---代表了样本显示的变量依存规律。

总体回归模型与样本回归模型的主要区别是：①描述的对象不同。

总体回归模型描述总体中变量y 与x 的相互关系，而样本回归模型描述所关的样本中变量y 与x 的相互关系。

②建立模型的依据不同。

总体回归模型是依据总体全部观测资料建立的，样本回归模型是依据样本观测资料建立的。

③模型性质不同。

总体回归模型不是随机模型，而样本回归模型是一个随机模型，它随样本的改变而改变。

总体回归模型与样本回归模型的联系是：样本回归模型是总体回归模型的一个估计式，之所以建立样本回归模型，目的是用来估计总体回归模型。

线性回归的含义线性：被解释变量是关于参数的线性函数（可以不是解释变量的线性函数）线性回归模型的基本假设简单线性回归的基本假定：对模型和变量的假定、对随机扰动项u 的假定（零均值假定、同方差假定、无自相关假定、随机扰动与解释变量不相关假定、正态性假定）普通最小二乘法（原理、推导）最小二乘法估计参数的原则是以“残差平方和最小”。

多元线性回归模型实验报告计量经济学多元线性回归模型是一种比较常见的经济学建模方法，其可用于对多个自变量和一个因变量之间的关系进行分析和预测。

在本次实验中，我们将使用一个包含多个自变量的数据集，对其进行多元线性回归分析，并对分析结果进行解释。

数据集介绍本次实验使用的数据集来自于UCI Machine Learning Repository，数据集包含有关汽车试验的多个自变量和一个连续因变量。

数据集中包含了204条记录，其中每条记录包含了一辆汽车的14个属性，分别是：MPG（燃油效率），气缸数（Cylinders）、排量（Displacement）、马力（Horsepower）、重量（Weight）、加速度（Acceleration）、模型年（Model Year）、产地（Origin）等。

模型建立在进行多元线性回归分析之前，我们首先需要对数据进行预处理。

为了确保数据的可用性，我们需要先检查数据是否存在缺失值和异常值。

如果有，需要进行相应的处理，以确保因变量和自变量之间的关系受到了正确地分析。

在对数据进行预处理之后，我们可以使用Python中的statsmodels包来对数据进行多元线性回归分析。

具体建模过程如下：```import statsmodels.api as sm# 准备自变量和因变量数据X = data[['Cylinders', 'Displacement', 'Horsepower', 'Weight', 'Acceleration', 'Model Year', 'Origin']]y = data['MPG']# 添加常数项X = sm.add_constant(X)# 拟合线性回归模型model = sm.OLS(y, X).fit()# 输出模型摘要print(model.summary())```在上述代码中，我们首先通过data[['Cylinders', 'Displacement', 'Horsepower', 'Weight', 'Acceleration', 'Model Year', 'Origin']]选择了所有自变量列，用于进行多元线性回归分析；然后，我们又通过`sm.add_constant(X)`，向自变量数据中添加了一列全为1的常数项，用于对截距进行建模；最后，我们使用`sm.OLS(y, X).fit()`来拟合线性回归模型，并使用`model.summary()`输出模型摘要。

伍德里奇《计量经济学导论》（第5版）笔记和课后习题详解第4章多元回归分析：推断4.1复习笔记一、OLS 估计量的抽样分布1．假定MLR.6（正态性）总体误差u 独立于解释变量12 k x x x ，，…，，而且服从均值为零和方差为2σ的正态分布：()2Normal 0 u σ～，。

2．经典线性模型就横截面回归中的应用而言，从假定MLR.1～MLR.6这六个假定被称为经典线性模型假定。

将这六个假定下的模型称为经典线性模型（CLM）。

在CLM 假定下，OLS 估计量01ˆˆˆ kβββ，，…，比在高斯—马尔可夫假定下具有更强的效率性质。

可以证明，OLS 估计量是最小方差无偏估计，即在所有的无偏估计中，OLS 具有最小的方差。

总结CLM 总体假定的一种简洁方法是：()201122|Normal k k y x x x x ββββσ++++～…，误差项的正态性导致OLS 估计量的正态抽样分布。

3．用中心极限定理去推导u 的分布的缺陷（1）虽然u 是影响y 而又观测不到的众多因素之和，且各因素可能各有极为不同的总体分布，但中心极限定理（CLT）在这些情形下仍成立。

正态近似的效果取决于u 中有多少因素，以及u 中包含因素分布的差异。

（2）更严重的问题是，正态近似假定所有不可观测因素都以独立而可加的方式影响着Y。

因此如果u 是不可观测因素的一个复杂函数，那么CLT 论证并不真正适用。

4．误差项的正态性导致OLS 估计量的正态抽样分布定理4.1：正态抽样分布在CLM 假定MLR.1～MLR.6下，以自变量的样本值为条件，有：()ˆˆ~Normal Var j j j βββ⎡⎤⎣⎦，因此()()()ˆˆ/sd ~Normal 0 1j j j βββ-，注：除ˆj β服从正态分布外，01ˆˆˆ k βββ，，…，的任何线性组合也都是正态分布，而且ˆjβ的任何一个子集也都具有一个联合正态分布。

二、检验对单个总体参数的假设：t 检验1．总体回归函数总体模型可写作：11o k k y x x uβββ=++⋯++假定它满足CLM 假定，OLS 得到j β的无偏估计量。