高数下册知识网络图
- 格式:docx
- 大小:320.57 KB
- 文档页数:8

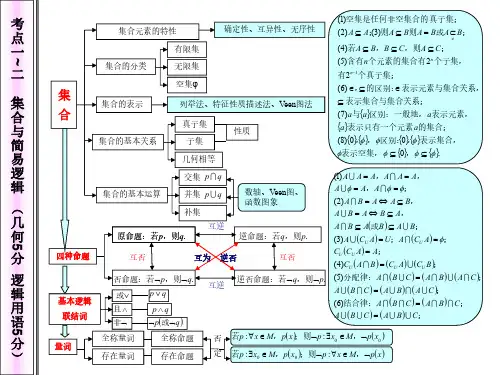
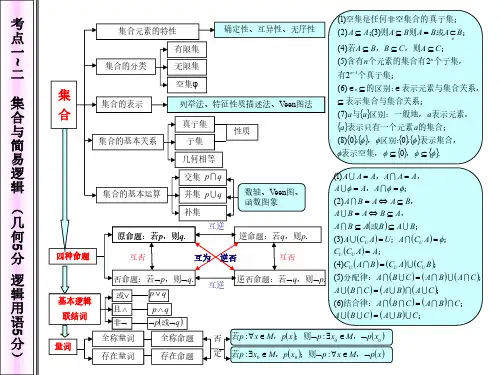
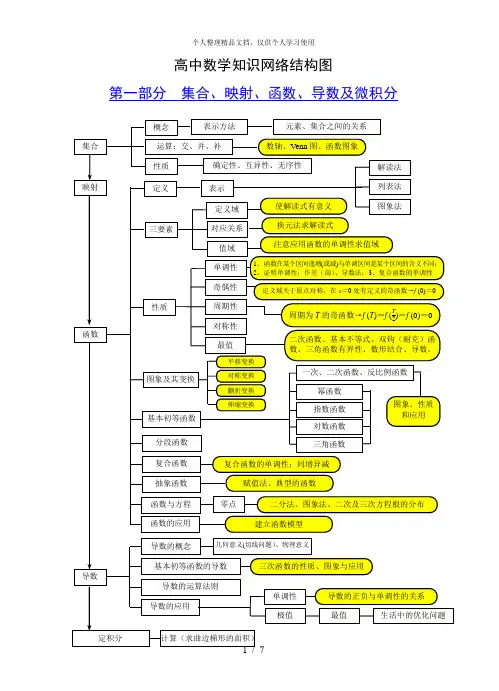
高中数学知识网络结构图第一部分 集合、映射、函数、导数及微积分集合映射概念元素、集合之间的关系 运算:交、并、补 数轴、Venn 图、函数图象性质确定性、互异性、无序性 定义表示 解读法 列表法三要素图象法定义域对应关系值域 性质奇偶性周期性 对称性 单调性 定义域关于原点对称,在x =0处有定义的奇函数→f (0)=01、函数在某个区间递增(或减)与单调区间是某个区间的含义不同;2、证明单调性:作差(商)、导数法;3、复合函数的单调性 最值二次函数、基本不等式、双钩(耐克)函数、三角函数有界性、数形结合、导数。
幂函数 对数函数 三角函数基本初等函数抽象函数 复合函数 赋值法、典型的函数函数与方程 二分法、图象法、二次及三次方程根的分布 零点函数的应用 建立函数模型使解读式有意义 导数函数基本初等函数的导数导数的概念导数的运算法则导数的应用表示方法 换元法求解读式分段函数 几何意义(切线问题)、物理意义单调性导数的正负与单调性的关系生活中的优化问题定积分计算(求曲边梯形的面积)注意应用函数的单调性求值域周期为T 的奇函数→f (T )=f (T2)=f (0)=0 复合函数的单调性:同增异减三次函数的性质、图象与应用一次、二次函数、反比例函数指数函数图象、性质 和应用平移变换对称变换 翻折变换 伸缩变换图象及其变换最值极值第二部分 三角函数与平面向量角的概念 任意角的三角函数的定义 三角函数 弧度制 弧长公式、扇形面积公式三角函数线同角三角函数的关系 诱导公式 和角、差角公式 二倍角公式公式的变形、逆用、“1”的替换 化简、求值、证明(恒等变形)三角函数 的 图 象定义域奇偶性 单调性 周期性 最值对称轴(正切函数除外)经过函数图象的最高(或低)点且垂直x 轴的直线,对称中心是正余弦函数图象的零点,正切函数的对称中心为(k π2,0)(k ∈Z )。
正弦函数y =sin x= 余弦函数y =cos x 正切函数y =tan x y =A sin(ωx +ϕ)+b①图象可由正弦曲线经过平移、伸缩得到,但要注意先平移后伸缩与先伸缩后平移不同;②图象也可以用五点作图法;③用整体代换求单调区间(注意ω的符号); ④最小正周期T =2π| ω |;⑤对称轴x =(2k +1)π-2ϕ2ω,对称中心为(k π-ϕω,b )(k ∈Z )。

高中数学知识点思维导图
----21张图理清高中数学知识结构
目录
一、集合与简易逻辑 (1)
二、函数与基本初等函数 (2)
三、导数及其应用 (3)
四、三角函数 (4)
五、解三角形与平面向量 (5)
六、数列 (6)
七、不等式 (7)
八、三视图与空间位置关系 (8)
九、立体几何 (9)
十、空间向量与立体几何 (10)
十一、直线的方程 (11)
十二、圆的方程 (12)
十三、直线系、圆系、直线与圆锥曲线关系 (13)
十四、圆锥曲线 (14)
十五、椭圆的定义与几何性质 (15)
十六、双曲线的定义与几何性质 (16)
十七、抛物线的定义与几何性质 (17)
十八、计数原理、二项式定理、推理与证明 (18)
十九、概率与统计 (20)
二十、复数 (21)
二十一、算法 (22)
一、集合与简易逻辑
二、函数与基本初等函数
三、导数及其应用
四、三角函数
五、解三角形与平面向量
六、数列
七、不等式
八、三视图与空间位置关系
九、立体几何
十、空间向量与立体几何
十一、直线的方程
十二、圆的方程
十三、直线系、圆系、直线与圆锥曲线关系
十四、圆锥曲线
十五、椭圆的定义与几何性质
十八、计数原理、二项式定理、推理与证明
十九、概率与统计
二十、复数
二十一、算法。



大一下高数知识点思维导图大一下学期高等数学是大部分理工科学生需要学习的一门重要课程。
为了更好地复习和掌握高数的知识点,下面将以思维导图的形式,系统地总结大一下学期高等数学的重点知识点。
1. 函数与极限在函数与极限这一部分,我们需要掌握函数的定义和性质,如增减性、奇偶性、周期性等。
同时,也要了解极限的定义、性质和计算方法,例如极限存在准则、夹逼定理等。
除此之外,还要熟练掌握一些常见函数的极限,如幂函数、指数函数、对数函数、三角函数等的极限运算。
2. 导数与微分导数与微分是高等数学的重要基础知识,需要掌握导数的定义、性质和计算方法。
特别是常见函数的导数,如幂函数、指数函数、对数函数、三角函数等的导数计算。
此外,还需了解一阶导数与二阶导数的关系、隐函数的求导、高阶导数等相关内容。
3. 微分中值定理与应用在微分中值定理与应用部分,掌握拉格朗日中值定理、柯西中值定理以及罗尔定理,并能灵活运用这些中值定理解决实际问题。
此外,还需了解泰勒展开式的概念和计算方法,以及利用泰勒展开逼近函数值的相关知识。
4. 不定积分与定积分不定积分与定积分是高等数学的核心内容之一,需要掌握不定积分的定义、性质和基本的计算方法。
特别是基本的不定积分公式、换元积分法和分部积分法的运用。
对于定积分,要熟悉定积分的定义、性质和基本的计算方法,掌握定积分的几何意义和物理应用,如求面积、求弧长、求体积等。
5. 微分方程微分方程是高等数学的重要应用部分,需要掌握常微分方程的基本概念、分类和一阶微分方程的解法。
特别是常见的一阶线性微分方程、二阶线性齐次微分方程和二阶线性非齐次微分方程的解法。
此外,还需了解高阶微分方程和常系数线性微分方程的解法。
总结起来,大一下学期高等数学的重点知识点可以归纳为函数与极限、导数与微分、微分中值定理与应用、不定积分与定积分以及微分方程。
通过对这些知识点的系统学习和复习,能够帮助我们更好地掌握高数的基础知识,为后续学习打下坚实的基础。
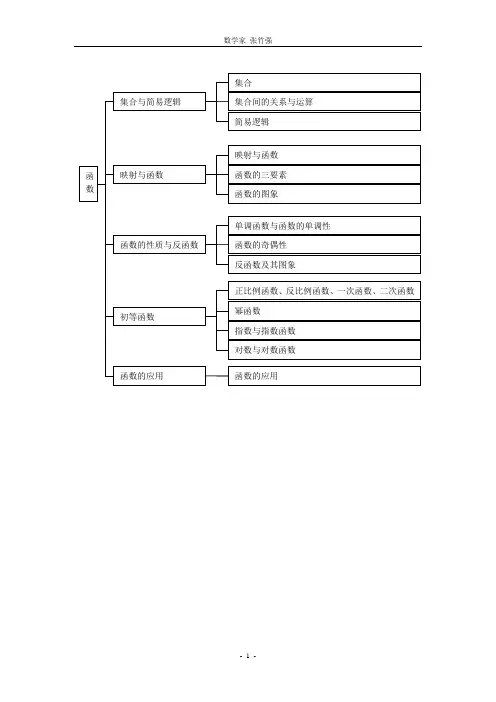
;;=⇔⊆=⇔⊆=⇔⊆A B B A B A B A A B A B I A Bn-个A中元素有n个,则A的子集共有2n个,真子集有21集合间的运算数形结合解集合问题2n R a +∈则2n n a n a ++≥不等式的最值问题不等式、三角函数和三角形的结合平均值不等式2nnn a a n++≥当且仅当柯西不等式221nii a =≤⋅∑当且仅当2,,)a n 时取等号1111221n j n j n n n a b a b a b a b a b a b ++≤++≤+++,n Z 是∀0≠时,当且仅当0)时左等号成立②,,n x 是区间1122)()()()n n n n q x q f x q f x q f x ++≤+++1,,,1nn i i q R q +=∈=∑)。
上凸函数不等号转向.B ,通常作差比较A 分析综合法1}n ma+仍是等比数列,其公比为)lim n n a ++=sin sin αβtan tan 1tan tan α±三角形中的三角函数关系式2(AB x =两个非零向量垂直的充要条件的坐标表示,则a ⊥b 分2PP 所成比为两向量的夹角公式的坐标表示的夹角的余弦夹角公式11222221231cos ||||a b a b a ba b a b a a a b ++⋅⋅==⋅++两点间的距离2212()(x x y y =-+-空间向量的直角坐标运算律若123(,,a a a a =,12(,,b b b b =则①112233(,,a b a b a b a +=++,11(a b a b -=-123(,,)()a a a R λλλλλ=∈,1122a b a b a b ⋅=++②112233//,,a ba ab a b λλλ⇔===,110a b a b a ⊥⇔+③若111(,,)A x y z 则2(AB x =-模长公式若123(,,a a a a =2212||a a a a a =⋅=+空间的向量空间向量的运算,,(OB OA AB a b BA OA OB a b OP a λλ=+=+=-=-=运算律:⑴加法交换律:a b b a +=+⑵加法结合律:⑶数乘分配律:b a b a λλλ+=+)(空间向量的加减与数乘OB OA AB =+=a +b , AB OB OA =-,,(OP λ=a 空间向量的加减与数乘运算律⑴加法交换律:a + b = + a ⑵加法结合律:(a + b ) + c =⑶数乘分配律:λ(a + b )λa +λb .空间共面向量定理及推论平行六面体空间向量的夹角 向量的数乘积||||cos ,a b a b a b ⋅=⋅⋅<>空间向量数乘积的性质①||cos ,a ea a e ⋅=<>.②0ab a b ⊥⇔⋅=.③2||a a a =⋅.空间向量数量积运算律()()()a b a b a b λλλ⋅=⋅=⋅②a b b a ⋅=⋅(交换律) ③()a b c a b a c ⋅+=⋅+⋅(分配律)④e ⋅a = a ⋅e =|a |cos ,a e a ⊥b ⇔ a ⋅b = 0⑥当a 与b 同向时,a ⋅b = |a ||b |;当a 与b 反向时,特别的a ⋅a = |a |2或||a a a =⋅⑦cos ,||||a ba b a b ⋅=⑧|a ⋅b |∈,则lBααβ=且l,则A、B、C。

高三下数学知识点梳理图在高中数学学科中,高三下学期是学习的重要阶段。
在这个阶段,学生们不仅要夯实基础知识,还要学习更加复杂和深入的数学概念和技巧。
为了帮助同学们更好地梳理数学知识点,下面我将结合图表的形式,系统地呈现高三下学期数学知识点的概览。
一、函数与方程1. 基本函数常见的基本函数包括线性函数、指数函数、对数函数、幂函数、三角函数等。
学生们应该熟练掌握它们的定义、特征以及基本性质。
2. 函数的图像与性质了解函数的图像和性质是解题的关键。
通过观察和分析函数的图像,可以确定函数的增减性、极值点、拐点等重要特征。
3. 方程与不等式掌握一元一次方程、一元二次方程的求解方法,并能熟练运用二次方程的根与系数的关系。
此外,还需掌握一元一次不等式、一元二次不等式的求解方法。
二、解析几何1. 平面几何掌握平面直角坐标系、曲线的方程与性质、直线与圆的方程与性质、判定图形相似和全等的方法等。
2. 空间几何熟悉空间坐标系以及空间几何体的性质和特征,如点、线、面、体以及它们的投影与旋转等。
三、数列与数学归纳法1. 数列的定义与表示理解数列的定义与表示方法,并能判断数列的等差、等比等特性。
2. 数列的通项公式与递推关系熟练推导数列的通项公式和递推关系,运用这些公式解决数列的各类问题。
四、概率与统计1. 概率了解基本概率理论,并能运用概率模型计算事件发生的可能性。
2. 统计掌握常见的统计概念和方法,如样本与总体、频率分布、统计图表、均值与标准差等。
五、三角函数与三角恒等式1. 三角函数的定义与性质熟悉常见的三角函数及其定义,掌握它们的特性和图像,能够利用基本性质求解三角方程与不等式。
2. 三角恒等式的运用掌握三角恒等式的基本概念与运用方法,并能运用它们解决相关问题,如证明题、三角方程的解等。
六、导数与微分1. 导数的概念与性质理解导数的定义与几何意义,熟练运用导数的基本性质,如导数的四则运算、常用函数的导数等。
2. 微分与应用问题理解微分的定义,能够应用微分解决函数的极值、最值、曲线的凸凹性等问题。

高二下数学知识点结构图数学是一门科学,也是一门艺术。
而在高二下学期,学生们将进一步学习数学的各个知识点,掌握更加深入的数学原理和应用。
为了帮助大家更好地理解和掌握高二下学期的数学知识,我将为大家呈现一个详细的高二下数学知识点结构图。
1. 数与式1.1 实数与实数运算1.2 一元一次方程与不等式1.3 二次根式与一元二次方程1.4 指数与对数1.5 复数2. 函数2.1 小初函数概念2.2 一元二次函数2.3 幂函数与指数函数2.4 对数函数与指数方程2.5 三角函数2.6 函数的运算与初等函数的复合3. 数列与数学归纳法3.1 等差数列与等比数列3.2 递归与通项公式3.3 数列的求和3.4 极限与无穷等4. 三角函数4.1 三角函数的定义与性质4.2 三角函数的图像与性质4.3 三角函数的公式与变换4.4 三角函数的解法与证明5. 三角恒等变换与反三角函数5.1 三角恒等变换5.2 反三角函数的概念与性质5.3 反三角函数的图像与性质5.4 反三角函数的应用6. 二次函数6.1 二次函数的定义与性质6.2 二次函数的图像与性质6.3 二次函数的极值与最值6.4 判断某种情况下二次函数与其它函数的关系 6.5 二次函数的应用7. 三角方程与不等式7.1 三角方程的解法7.2 三角方程的应用7.3 三角不等式的解法7.4 三角不等式的应用8. 统计与概率8.1 描述统计与统计图8.2 随机事件与概率8.3 离散型随机变量与分布律8.4 随机变量的期望与方差8.5 离散型随机变量的分布函数与分布图8.6 二项分布与正态分布以上是高二下学期数学知识点的结构图。
这个结构图按照知识点的不同进行了分类和层次划分,帮助我们更好地了解各个知识点的关系和重要性。
在学习数学时,我们可以根据这个结构图来进行有针对性的学习和复习,从而更加高效地掌握数学知识。
总结起来,高二下学期的数学知识点包括数与式、函数、数列与数学归纳法、三角函数、三角恒等变换与反三角函数、二次函数、三角方程与不等式以及统计与概率。
第八章 总结向量代数定义 定义与运算的几何表达 在直角坐标系下的表示向量有大小、有方向. 记作a 或ABa (,,)x y z x y z a i a j a k a a a =++=,,x x y y z z a prj a a prj a a prj a ===模向量a 的模记作aa 222x y z a a a =++和差c a b =+ c a b =-=+c a b {},,=±±±x x y y z z a b a b a b单位向量 0a ≠,则a a e a= a e 222(,,)=++x y z x y z a a a a a a方向余弦 设a 与,,x y z 轴的夹角分别为αβγ,,,则方向余弦分别为cos αβγ,cos ,coscos y x z a a a aaaαβγ===,cos ,coscos a e αβγ=(,cos ,cos ) 222cos 1αβγ+=+cos cos点乘(数量积)θcos b a b a =⋅,θ为向量a 与b 的夹角zz yyxx b a b a b a ++=⋅b a 叉乘(向量积) b a c ⨯= θsin b a c = θ为向量a 与b 的夹角 向量c 与a ,b 都垂直 zyxz y xb b b a a a k j ib a =⨯ 定理与公式垂直 0a b a b ⊥⇔⋅= 0x x y y z z a b a b a b a b ⊥⇔++=平行//0a b a b ⇔⨯=//y zx x y za a a ab b b b ⇔==交角余弦两向量夹角余弦ba ba ⋅=θcos 222222cos x x y y z zx y z x y z a b a b a b a a a b b b θ++=++⋅++投影向量a 在非零向量b 上的投影cos()b a bprj a a a b b∧⋅== 222x x y y z zb x y za b a b a b prj a b b b ++=++空间曲面 ∑:0),,(=z y x F法向量000000000((,,),(,,),(,,))x y z n F x y z F x y z F x y z = 切平“面”方程:000000000000(,,)()(,,)()(,,)()0x x x F x y z x x F x y z y y F x y z z z -+-+-=法“线“方程:),,(),,(),,(000000000000z y x F z z z y x F y y z y x F x x z y x -=-=- ),(y x f z = 0000((,),(,),1)x y n f x y f x y =--或0000((,),(,),1)x y n f x y f x y =-切平“面”方程:0)())(,())(,(0000000=---+-z z y y y x f x x y x f y x法“线“方程:1),(),(0000000--=-=-z z y x f y y y x f x x y x 第十章 总结重积分 积分类型计算方法典型例题二重积分()σd ,⎰⎰=Dy x f I平面薄片的质量质量=面密度⨯面积(1) 利用直角坐标系X —型 ⎰⎰⎰⎰=Dbax x dy y x f dx dxdy y x f )()(21),(),(φφY —型⎰⎰⎰⎰=dcy y Ddx y x f dy dxdy y x f )()(21),(),(ϕϕP141—例1、例3(2)利用极坐标系 使用原则(1) 积分区域的边界曲线易于用极坐标方程表示( 含圆弧,直线段 );(2) 被积函数用极坐标变量表示较简单( 含22()x y α+,α为实数 )21()()(cos ,sin )(cos ,sin )Df d d d f d βϕθαϕθρθρθρρθθρθρθρρ=⎰⎰⎰⎰02θπ≤≤ 0θπ≤≤ 2πθπ≤≤P147—例5(3)利用积分区域的对称性与被积函数的奇偶性 当D 关于y 轴对称时,(关于x 轴对称时,有类似结论) P141—例2应用该性质更方第十一章总结所有类型的积分:○1定义:四步法——分割、代替、求和、取极限;○2性质:对积分的范围具有可加性,具有线性性;○3对坐标的积分,积分区域对称与被积函数的奇偶性。
第十二章总结无穷级数常数项级数傅立叶级数幂级数一般项级数正项级数用收敛定义,nns∞→lim存在常数项级数的基本性质常数项级数的基本性质○若级数收敛,各项同乘同一常数仍收敛.○两个收敛级数的和差仍收敛.注:一敛、一散之和必发散;两散和、差必发散.○去掉、加上或改变级数有限项,不改变其收敛性.○若级数收敛,则对这级数的项任意加括号后所成的级数仍收敛,且其和不变。
推论:如果加括号后所成的级数发散,则原来级数也发散.注:收敛级数去括号后未必收敛.○(必要条件)如果级数收敛,则0lim=→nnu莱布尼茨判别法若1+≥nnuu且0lim=∞→nnu,则∑∞=--11)1(nnn u收敛nu∑和nv∑都是正项级数,且nnvu≤.若nv∑收敛,则nu∑也收敛;若nu∑发散,则nv∑也发散.比较判别法比较判别法的极限形式nu∑和nv∑都是正项级数,且lvunnn=∞→lim,则○1若+∞<<l0,nu∑与nv∑同敛或同散;○2若0=l,nv∑收敛,nu∑也收敛;○3如果+∞=l,nv∑发散,nu∑也发散。
比值判别法根值判别法nu∑是正项级数,ρ=+∞→nnn uu1lim,ρ=∞→nnnulim,则1<ρ时收敛;1>ρ(ρ=+∞)时发散;1=ρ时可能收敛也可能发散.收敛性和函数展成幂级数nnnxa∑∞=0,ρ=+∞→nnn aa1lim,1,0;,0;0,.R R Rρρρρ=≠=+∞===+∞缺项级数用比值审敛法求收敛半径)(xs的性质○在收敛域I上连续;○在收敛域),(RR-内可导,且可逐项求导;○和函数)(xs在收敛域I上可积分,且可逐项积分.(R不变,收敛域可能变化).直接展开:泰勒级数间接展开:六个常用展开式11(11)1nnx xx∞==-<<-∑11()!x nne x xn∞==-∞<<+∞∑22TT lπ==∑∞=++=10)sincos(2)(nnnnxbnxaaxf⎰-=πππdxxfa)(1⎰-=πππnxdxxfancos)(1⎰-=πππnxdxxfbnsin)(1收敛定理x是连续点,收敛于)(xf;x是间断点,收敛于)]()([21+-+xfxf周期延拓)(xf为奇函数,正弦级数,奇延拓;)(xf为偶函数,余弦级数、偶延拓.交错级数。