第3章 控制对象的特性

第三章控制对象的动态特性习题与参考解答3-1 什么是自衡特性？具有自衡特性被控过程的系统框图有什么特点？1）在扰动作用破坏其平衡工况后，被控过程在没有外部干预的情况下自动恢复平衡的特性，称为自衡特性。

2）被控过程输出对扰动存在负反馈。

3-2 什么是单容过程和多容过程？1）单容：只有一个储蓄容量。

2）多容：有一个以上储蓄容量。

3-3 什么是控制通道和扰动通道(干扰通道)?对于不同的通道，对象的特性参数(K、T、τ)对控制有什么不同的影响?对于一个被控对象来说，输入量是扰动量和操纵变量，而输出是被控变量。

由对象的输入变量至输出变量的信号联系称为通道。

操纵变量至被控变量的信号联系称为控制通道；扰动量至被控变量的信号联系称为扰动通道。

一般来说，对于不同的通道，对象的特性参数(K、T、τ)对控制作用的影响是不同的。

对于控制通道：放大系数K大，操纵变量的变化对被控变量的影响就大，即控制作用对扰动的补偿能力强，余差也小；放大系数K小，控制作用的影响不显著，被控变量的变化缓慢。

但K太大，会使控制作用对被控变量的影响过强，使系统的稳定性下降。

在相同的控制作用下，时间常数T大，则被控变量的变化比较缓慢，此时对象比较平稳，容易进行控制，但过渡过程时间较长；若时间常数T小，则被控变量变化速度快，不易控制。

时间常数太大或太小，在控制上都将存在一定困难，因此，需根据实际情况适中考虑。

滞后时间τ的存在，使得控制作用总是落后于被控变量的变化，造成被控变量的最大偏差增大，控制质量下降。

因此，应尽量减小滞后时间τ。

对于扰动通道：放大系数K大对控制不利，因为，当扰动频繁出现且幅度较大时，被控变量的波动就会很大，使得最大偏差增大；而放大系数K小，既使扰动较大，对被控变量仍然不会产生多大影响。

时间常数T大，扰动作用比较平缓，被控变量变化较平稳，对象较易控制。

纯滞后的存在，相当于将扰动推迟τ0时间才进入系统，并不影响控制系统的品质；而容量滞后的存在，则将使阶跃扰动的影响趋于缓和，被控变量的变化相应也缓和些，因此，对系统是有利的。

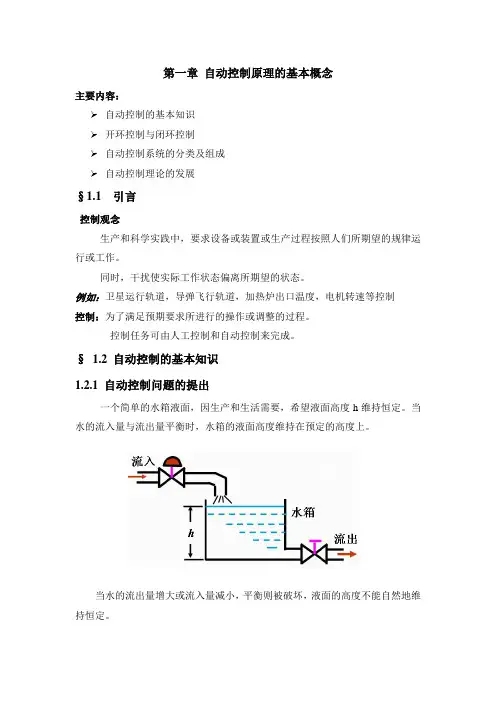
第一章自动控制原理的基本概念主要内容：自动控制的基本知识开环控制与闭环控制自动控制系统的分类及组成自动控制理论的发展§1.1 引言控制观念生产和科学实践中，要求设备或装置或生产过程按照人们所期望的规律运行或工作。

同时，干扰使实际工作状态偏离所期望的状态。

例如：卫星运行轨道，导弹飞行轨道，加热炉出口温度，电机转速等控制控制：为了满足预期要求所进行的操作或调整的过程。

控制任务可由人工控制和自动控制来完成。

§ 1.2 自动控制的基本知识1.2.1 自动控制问题的提出一个简单的水箱液面，因生产和生活需要，希望液面高度h维持恒定。

当水的流入量与流出量平衡时，水箱的液面高度维持在预定的高度上。

当水的流出量增大或流入量减小，平衡则被破坏，液面的高度不能自然地维持恒定。

所谓控制就是强制性地改变某些物理量(如上例中的进水量)，而使另外某些特定的物理量（如液面高度h）维持在某种特定的标准上。

人工控制的例子。

这种人为地强制性地改变进水量，而使液面高度维持恒定的过程，即是人工控制过程。

1.2.2 自动控制的定义及基本职能元件1. 自动控制的定义自动控制就是在没有人直接参与的情况下，利用控制器使被控对象(或过程)的某些物理量(或状态)自动地按预先给定的规律去运行。

当出水与进水的平衡被破坏时，水箱水位下降(或上升)，出现偏差。

这偏差由浮子检测出来，自动控制器在偏差的作用下，控制阀门开大(或关小)，对偏差进行修正，从而保持液面高度不变。

2. 自动控制的基本职能元件自动控制的实现,实际上是由自动控制装置来代替人的基本功能，从而实现自动控制的。

画出以上人工控制与动控制的功能方框图进行对照。

比较两图可以看出，自动控制实现人工控制的功能，存在必不可少的三种代替人的职能的基本元件：测量元件与变送器（代替眼睛）自动控制器（代替大脑）执行元件（代替肌肉、手）这些基本元件与被控对象相连接，一起构成一个自动控制系统。

下图是典型控制系统方框图。

第三章线性系统的时域分析控制系统的时域响应取决于系统本身的参数和结构，还与系统的初始状态以及输入信号的形式有关。

一、典型输入信号常用的典型输入信号：阶跃函数、斜坡函数（等速度函数）、抛物线函数（等加速度函数）、脉冲函数及正弦函数。

1.阶跃函数（1）阶跃函数表达式幅值为1的阶跃函数称为单位阶跃函数，表达式为常记为1（t），其拉普拉斯变换（2）阶跃信号额图形2.斜坡函数（1）斜坡函数的表达式其拉普拉斯变换为当A=1时，称为单位斜坡函数。

（2）斜坡函数的图形3.抛物线函数（1）抛物线函数的表达式当A=1/2时，称为单位抛物线函数。

抛物线函数的拉普拉斯变换为（2）抛物线函数的图形4.脉冲函数（1）脉冲函数表达式当A=1时，记为。

令，则称为单位脉冲函数。

（2）单位脉冲函数的拉普拉斯变换为（3）特性单位脉冲传递函数是单位阶跃函数对时间的导数，而单位阶跃函数则是单位脉冲函数对时间的积分。

5.正弦函数在实际中，有的控制系统，其输入信号常用正弦函数来描述，可以求得系统的频率响应。

二、线性定常系统的时域响应1.时域分析（1）定义时域分析就是分析系统的时间响应，也就是分析描述其运动的微分方程的解。

（2）微分方程单变量线性定常系统的常微分方程如下所示2.解的结构（1）由于各项系数都是常数，可判断其解必然存在并且唯一。

（2）从线性微分方程理论可知，其通解是由它的任一个特解与其对应的齐次微分方程通解之和所组成，即（3）为了求解高阶常微分方程，还可利用拉普拉斯变换方法，由此得到时域响应为（4）单位阶跃响应与单位脉冲响应①系统的单位脉冲响应是单位阶跃响应的导数；②系统的脉冲响应中只有暂态分量，而稳态分量总是零，也就是说不存在与输入相对应的稳态响应。

所以，系统的脉冲响应更能直观地反映系统的暂态性能。

三、控制系统时域响应的性能指标1.暂态性能常用性能指标通常有：最大超调量、上升时间、峰值时间和调整时间。

（1）最大超调量：在暂态响应期间超过终值c（∞）的最大偏离量，即（2）峰值时间：最大超调量发生的时间（从t=0开始计时）。

第三章 直升机的增稳与控制增稳系统直升机作为控制对象与固定翼飞机相比有更复杂的动力学。

除了应考虑机体的六自由度运动以外，还必需考虑旋翼及尾桨相对于机身的旋转，以及桨叶相对于挥舞铰的运动。

这些决定了直升机具有较差的稳定性与操纵性。

早期的直升机由于执行任务比较简单，性能要求也比较低，直升机的不稳定运动模态发散周期比较长，驾驶员可以对这种不稳定的发散模态进行不断的人工修正。

随着直升机性能不断提高，以及执行的任务越来越复杂，特别是武装直升机不仅要执行反潜，对地攻击，对空射击，而且要完成超低空贴地飞行，进行地形跟随与地形回避机动，还需要抵御阵风扰动等，再加上直升机固有的不稳定性，仅依靠人工操纵已十分困难，所以与固定翼飞机相比，更需采用增稳系统（SAS ）、控制增稳系统（CSAS ）或自动飞行控制系统（AFCS ），并不断引入主动控制技术，向着电传操纵（FBW ）及光传操纵方向发展。

本章将论述在人工操纵状态下的各工作通道的增稳及控制增稳系统基本工作原理、典型结构及设计方法。

为便于论述工作原理、便于设计和仿真，本章首先构建了以结构图形式给出的直升机四通道线性动力学模型。

3.1 直升机结构图形式的数学模型为了便于分析增稳系统基本工作原理，需理解直升机动力学方程各气动导数物理含义，列出不计纵侧向之间气动耦合的如下纵向和侧向线性化增量运动动力学方程，其中纵向运动可由式（2-56），（2-57）导出u u u u u ue c u w q e c uX u X w X X q X X θδδθδδ∆=∆+∆+∆-∆+∆+∆ （3-1） w w w w w we c u w q e c w Z u Z w Z Z q Z Z θδδθδδ∆=∆+∆+∆-∆+∆+∆ （3-2） q q q q q q e c u w q e c q M u M w M M q M M θδδθδδ∆=∆+∆+∆-∆+∆+∆ （3-3）由式（2-58），（2-59），（2-60）可导出侧向运动方程v v v v v v v a r v p r a r vY v Y Y Y p Y r Y Y φψδδφψδδ∆=∆+∆+∆-∆-∆+∆+∆ （3-4） p p p p p p p a r v p r a r p L v L L L p L r L L φψδδφψδδ∆=∆+∆+∆-∆-∆+∆+∆ （3-5） r r r r r r r a r v p r a r r N v N N N p N r N N φψδδφψδδ∆=∆+∆+∆-∆-∆+∆+∆ （3-6）上述6个方程的物理含义十分清楚，方程（3-1）、（3-2）、（3-4）是力的方程。

自动控制原理(孟华)第3章习题解答自动控制原理(孟华)的习题答案。

3.1.已知系统的单位阶跃响应为c(t) 1 0.2e 60t 1.2e 10t试求：（1）系统的闭环传递函数Φ(s)=？(2) 阻尼比ζ=？无自然振荡频率ωn=？解：（1）由c(t)得系统的单位脉冲响应为g(t) 12e 60t 12e 10t (t 0)(s) L[g(t)] 12__12 2 s 10s 60s 70s 6002n（2）与标准(s) 2对比得：2s 2 n nn 600 24.5，702 6001.4293.2.设图3.36 (a)所示系统的单位阶跃响应如图3.36 (b)所示。

试确定系统参数K1,K2和a。

(a) (b)图3.36 习题3.2图解：系统的传递函数为K12 nK1K2s(s a)W(s) K2 2 K2 2K1s as K1s 2 n n1s(s a)又由图可知：超调量Mp4 3133峰值时间tp 0.1 s自动控制原理(孟华)的习题答案。

代入得2n K1 1 21e30.1 2 n K K2解得：ln32；0.33，n10 2233.3，K1 n 1108.89，a 2 n 2 0.33 33.3 21.98，K2 K 3。

3.3. 给定典型二阶系统的设计性能指标：超调量p 5%，调节时间ts 3s，峰值时间tp 1s，试确定系统极点配置的区域，以获得预期的响应特性。

解：设该二阶系统的开环传递函数为2nG sss 2 n 20.05 p e33 则满足上述设计性能指标：ts nt 1 p2n得：0.69，n 1 n2由上述各不等式得系统极点配置的区域如下图阴影部分所示：自动控制原理(孟华)的习题答案。

3.4.设一系统如图3.37所示。

(a)求闭环传递函数C(s)/R(s)，并在S平面上画出零极点分布图；(b)当r(t)为单位阶跃函数时，求c(t)并做出c(t)与t的关系曲线。

图3.37 习题3.4图解：(a)系统框图化简之后有C(s)2 s2 R(s)s 0.5s 2.252 s(s35j)(s j)22z1 2,s1,2零极点分布图如下：35j 2自动控制原理(孟华)的习题答案。