数型结合处理甲烷的正四面体结构
- 格式:doc
- 大小:29.50 KB
- 文档页数:1



运用数形结合巧解化学题目数形结合是一种将数学与几何形状相结合的方法,通过图形的具体形态和性质来解决数学问题。
在化学学科中,数形结合也有很大的应用价值。
下面将通过举两个例子来介绍数形结合在化学题目中的巧妙应用。
例一:求解气体分子速度分布的平均速度在热力学中,气体分子的速度分布可通过麦克斯韦速度分布定律描述。
该定律告诉我们,气体分子的速度与温度呈正比,而与分子量呈反比。
求解气体分子速度分布的平均速度的问题也经常出现。
麦克斯韦速度分布定律公式为:f(v) = 4π(v^2) * (m / 2πkT)^(3/2) * exp(-(mv^2) / 2kT)f(v)表示速度为v的分子所占的百分比,m表示分子的质量,k表示玻尔兹曼常数,T 表示温度。
现求解气体分子速度分布的平均速度。
我们可以将麦克斯韦速度分布定律的公式与数形结合,构造一个半径为v的球体,球体的体积表示速度为v的分子所占的百分比,球体的体积与速度v满足的关系为:V = 4/3 * π * v^3根据麦克斯韦速度分布定律,速度为v的分子所占的百分比为f(v),故速度分布的平均速度v_avg可以表示为:v_avg = ∫(v * f(v) * dV)将球体的体积表达式代入,可得:v_avg = ∫(v * f(v) * (4/3 * π * v^3) * dv)通过对上式进行求解,可以求得气体分子速度分布的平均速度。
例二:计算化学平衡常数在化学反应中,平衡常数是用来描述反应物和生成物浓度之间平衡比例的定量指标。
对于一个反应式aA + bB ⇄ cC + dD,平衡常数Kc定义为反应物和生成物浓度的乘积之比的绝对值:Kc = ([C]^c * [D]^d) / ([A]^a * [B]^b)[C]表示C的浓度,[A]表示A的浓度,[B]表示B的浓度,[D]表示D的浓度。
当我们计算化学平衡常数时,可以将化学反应平衡的各个物质浓度用图形表示出来,并利用数形结合的思想解决问题。

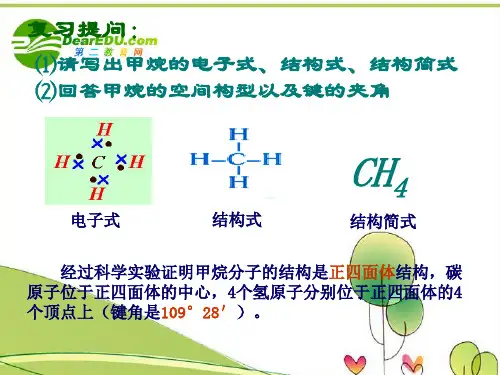

第 一 节 甲烷1、 使学生了解甲烷的结构式和甲烷的正四面体结构。
2、 使学生掌握甲烷的化学性质,实验室制法和收集方法。
3、 使学生了解取代反应。
4、 培养学生观察、分析实验现象,形成规律性认识,并应用概念认识新事物的思维能力。
甲烷的实验室制法,甲烷的化学性质,取代反应。
甲烷的分子结构、甲烷的取代反应。
实验5——1、实验5——2用品二课时 自学——辅导法[引 言]1、什么是有机物?定义:含碳元素的化合物(碳氢化合物及其衍生物)称为有机化合物。
简称有机物(注意:CO 、CO 2、H 2CO 3及碳盐例外,它们称为无机物)。
2、有机物与人类的关系。
3、人类早期、和现在取得有机物的手段。
[阅 读]P115页上[提 问]1、有机物和无机物的种类比较(多少)2、为什么有机物的种类繁多?3、组成有机物的元素。
4、那类有机物叫烃?最简单的烃是什么?[简 述]有机物的特点:①有机物种类繁多,结构复杂。
②大多数有机物难溶于水而易溶于汽油、酒精、苯等有机溶剂。
③绝大多数有机物受热易分解,而且容易燃烧。
④绝大多数有机物是非电解质,不易导电,熔点低。
⑤有机物所起的化学反应比较复杂,一般比较慢,并且还常伴随有副反应发生。
[板 书] 第一节 甲 烷一、甲烷的分子结构[阅 读]P115页——116页上要求掌握:⑴甲烷的分子式⑵甲烷的电子式⑶甲烷的结构式⑷甲烷的分子结构示意图[展示甲烷的球辊模型和比例模型]加深对甲烷的正四面体结构的认识。
CH4分子中1个C与4个H形成一个四面体,C在正四面体中心,4个H在正四面体的4个顶点。
①键角:109°28 ˊ正四面体②键长:C-H键键长:1.09×10-10m③键能:413 KJ·mol-1但由于有机物的立体结构式书写起来比较费事,为方便起见,一般采用平面的结构式。
[板书]甲烷的物理性质⑴无色、无味气体⑵在标准状况下,ρ=0.717g·L-1⑶极难溶于水[板书]二、甲烷的实验室制法1、原料:无水CH3COONa和干燥的碱石灰(NaOH和CaO)。

有机物分子中原子的共面共线问题衡南二中胡必爱有机分子中原子的共面共线是中学有机化学教学的一个难点。
此类题目的解题思维方法如下:原子共面共线问题思维的基础:甲烷的正四面体结构;乙烯、苯、萘、蒽的平面结构;乙炔的直线结构。
1.甲烷的正四面体结构在甲烷分子中,一个碳原子和任意两个氢原子可确定一个平面,其余两个氢原子分别位于平面的两侧,即甲烷分子中有且只有三原子共面(称为三角形规则).当甲烷分子中某氢原子被其他原子或原子团取代时,该代替原子的共面问题,可将它看作是原来氢原子位置。
其结构式可写成如图2所示。
左侧甲基和②C构成“甲烷分子。
此分子中⑤H,①C,②C构成三角形。
中间亚甲基和①C,③C构成“甲烷"分子。
此分子中①C,②C,③C构成三角形,同理②C,③C,④H构成三角形,即丙烷分子中最多两个碳原子(①C,②C,③C)三个氢原子(④H,⑤H)五原子可能共面。
2.乙稀的平面结构乙烯分子中的所有原子都在同一平面内,键角为120°。
当乙烯分子中某氢原子被其他原子或原子团取代时,则代替该氢原子的原子一定在乙烯的平面内。
其结构式可写成如图4所示。
三个氢原子(①②③)和三个碳原子(④⑤⑥)六原子一定共面。
根据三角形规则[⑤C,⑥C,⑦H构成三角形]。
⑦H也可能在这个平面上.至少6个原子(6个碳原子),至多10个原子[6个碳原子和4个氢原子(每个甲基可提供一个氢原子)]共面。
3.苯的平面结构苯分子所有原子在同一平面内,键角为120°。
当苯分子中的一个氢原子被其他原子或原子团取代时,代替该氢原子的原子一定在苯分子所在平面内.甲苯中的7个碳原子(苯环上的6个碳原子和甲基上的一个碳原子),5个氢原子(苯环上的5个氢原子)这12个原子一定共面。
此外甲基上1个氢原子(①H,②C,③C构成三角形)也可以转到这个平面上,其余两个氢原子分布在平面两侧。
故甲苯分子中最多有可能是13个原子共面.同理可分析萘分子中10个碳原子,8个氢原子18原子共面和蒽分子中14个碳原子,10个氢原子,共24个原子共面问题。

第65节甲烷有机化合物中,有一大类物质仅由碳、氢两种元素组成,这类物质叫做烃。
甲烷是烃类中最简单的物质甲烷又叫沼气,也叫坑气。
其原因是池沼的底部和煤矿的坑道所产生的气体的主要成分是甲烷。
这些甲烷是在隔绝空气的情况下,由植物残体经某些微生物发酵的作用而生成的。
在天然气中,甲烷的体积分数为80%~97%。
农村中建沼气池可以解决部分农家使用燃料问题,同时也有利于改善农村环境卫生。
甲烷是没有颜色、没有气味的气体。
在标准状况下,密度为0.717g/L,甲烷极难溶于水,易燃烧。
一、甲烷分子的结构在前面的学习中我们已经知道甲烷的分子式是CH4.经过大量科学实验证明,甲烷分子中的一个碳原子和四个氢原子不在同一个平面上,而是形成了一个如图13-9所示的正四面体的立体结构:请运用学过的知识分析1个碳原子和4个氢原子是怎样结合成如此美妙的正四面体结构的分子的?哪些事实可以证明甲烷分子具有正四面体结构?写出甲烷分子的电子式和结构式二、甲烷的制法和性质先将无水醋酸钠和碱石灰按1:3质量比充分混合后,迅速装进试管中,用酒精灯加热。
并用排水集气法把甲烷收集到试管中。
观察甲烷的颜色并闻它的气味。
在实验室中,可用无水醋酸钠和碱石灰混合加热制备CH4.反应的化学方程式如下:在通常情况下,甲烷是比较稳定的物质,它与强酸、强碱或强氧化剂等一般不发生化学反应。
但是,甲烷的稳定性是相对的,在一定条件下,也会发生某些反应1.取代反应取一支大试管,用排饱和食盐水的方法收集4体积Cl2和1体积CH4,再把装有混合气体的试管放在盛有饱和食盐水的水槽中,光照,观察反应的现象,见图13-11。
在室温下,甲烷和氯气的混合气体可以在黑暗中长期保存而不起任何反应。
但混合物在紫外光照射下就会发生反应,黄绿色的C2会逐渐减少。
反应的化学方程式可表示如下(为了理解反应发生的情况,用结构式代替分子式):有机物分子中的某些原子或原子团被其他原子或原子团代替的反应叫做取代反应。

甲烷的空间构型甲烷(CH4)是一种无色、无臭的气体,由一个碳原子和四个氢原子组成。
甲烷是最简单的烷烃,也是天然气的主要成分之一。
甲烷的空间构型指的是分子中碳和氢原子之间的排列方式和几何结构。
本文将详细介绍甲烷的空间构型及其相关性质。
甲烷的空间构型可以用分子构型图来表示。
甲烷的分子式为CH4,碳原子位于中心,四个氢原子分别连接在碳原子的四个顶点上。
这种构型又被称为正四面体构型。
在正四面体构型中,碳原子与四个氢原子之间的键角都为109.5°。
甲烷分子的构型是由原子之间的共价键连接决定的。
碳原子有四个价电子,氢原子有一个价电子。
碳原子通过与四个氢原子形成共价键来实现其八个价电子的稳定配置。
每个碳-氢键都是共用一对电子,形成共价键。
甲烷的空间构型是通过碳-氢键的长度和键角来描述的。
甲烷分子的空间构型对其化学性质具有重要影响。
由于甲烷分子的空间构型稳定且紧凑,它具有低沸点、低密度和高燃烧热等性质。
甲烷是一种非极性分子,不溶于水。
由于其氢原子比碳原子电负性更低,使得碳和氢原子之间的键呈现等电子分布,不产生电荷偏离。
这导致甲烷分子没有极性,分子中的正负电荷分布均匀。
甲烷的空间构型也对其化学反应的进行起到重要作用。
例如,在燃烧反应中,甲烷与氧气反应生成二氧化碳和水。
这是一种高温反应,燃烧过程中,甲烷分子中的碳-氢键被断裂,产生新的碳-氧和氢-氧键。
空间构型的稳定性使得甲烷能够有效地与氧气反应,并释放出大量的能量。
总结起来,甲烷的空间构型是一个由一个碳原子和四个氢原子组成的正四面体构型。
空间构型的稳定性使甲烷具有一系列特性,如低沸点、低密度和高燃烧热等。
甲烷是一种非极性分子,不溶于水。
空间构型也对甲烷的化学反应起到重要的影响。
通过分析甲烷的空间构型,可以更好地理解其性质和参与的化学反应。

证明甲烷是正四面体结构的事实甲烷,即化学式为CH4的分子,是一种简单的有机化合物。
它由一个碳原子和四个氢原子组成,四个氢原子均连接在碳原子上,形成一个四面体结构。
下面将从分子结构、键角和化学性质等方面来证明甲烷是正四面体结构的事实。
我们来看甲烷的分子结构。
甲烷的分子中有一个碳原子和四个氢原子。
碳原子与每个氢原子之间通过共价键相连。
共价键的形成是由于碳原子的四个价电子和氢原子的一个价电子之间的共享。
由于碳原子形成四个共价键,每个氢原子都与碳原子相连,甲烷分子的结构呈正四面体。
我们来分析甲烷分子中的键角。
键角是指两个相邻原子和其中一个氢原子之间的夹角。
在甲烷分子中,碳原子与四个氢原子之间的键角均相等。
根据实验测定,甲烷分子中的C-H键角约为109.5度。
正四面体的内角为109.47度,非常接近甲烷分子中的键角。
这进一步证明了甲烷是正四面体结构的事实。
甲烷的化学性质也支持它是正四面体结构。
由于甲烷分子中的四个氢原子位置相对等,因此它具有旋转对称性。
这种旋转对称性使甲烷分子在化学反应中具有特殊的稳定性。
甲烷与氧气反应时,氧气会优先与甲烷分子中的碳原子发生反应,而不是与氢原子发生反应。
这是因为甲烷分子中的四个氢原子位置相对等,氧气无法选择性地与其中的一个氢原子发生反应。
这种化学性质与正四面体的对称性一致,进一步证明了甲烷是正四面体结构的事实。
甲烷是正四面体结构的事实可以通过分子结构、键角和化学性质等方面来证明。
甲烷分子中的四个氢原子均连接在碳原子上,形成一个四面体结构。
碳原子与氢原子之间的键角约为109.5度,非常接近正四面体的内角。
甲烷分子具有旋转对称性,使其在化学反应中具有特殊的稳定性。
这些事实明确地表明甲烷是正四面体结构的。

景德镇市2025届高三第一次质检试题数学(答案在最后)命题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分,考试时间120分钟。
第I 卷(选择题)一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}|20A x x =∈-≤≤Z ,{}2|230B x x x =--≤,则A B ⋂=()A.[2,1]--B.[1,3]-C.{2,3}-D.{1,0}-2.已知1i2iz +=+(i 为虚数单位),则z 在复平面内对应的点在第()象限A.一B.二C.三D.四3.已知(2,0)a =,(1,1)b = ,则|2|a b - 的值为()A.1B.2C.3D.44.已知2sin cos 3αα+=-,则sin 2α=()A.518-B.518C.59-D.595.过点(0,1)A 且与曲线3()21f x x x =+-相切的直线方程是()A.51y x =+ B.21y x =+ C.1y x =+ D.21y x =-+6.函数2()sin 3f x x x π=-的零点个数是()A.5B.6C.7D.87.函数()f x 的定义域为R ,(21)f x +是奇函数,当1x >时()12()log 21x f x -=-,则()0f x ≥的解集是()A.[0,1)[2,)⋃+∞B.[0,1][2,)⋃+∞ C.(,0)[2,)-∞⋃+∞ D.(,0][2,)-∞⋃+∞8.甲烷是最简单的有机化合物,其分子式为4CH ,它是由四个氢原子和一个碳原子构成,甲烷在自然界分布很广,是天然气、沼气、煤矿坑道气及可燃冰的主要成分之一.甲烷分子是正四面体空间构型,如图,四个氢原子分别位于正四面体的顶点ABCD 处,碳原子位于正四面体的中心O 处.若正四面体ABCD 的棱长为1,则平面OAB 和平面OCD 位于正四面体内部的交线长度为()A.22B.33C.63D.1二、选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.下列说法正确的是()A.函数()cos 22f x x ππ⎛⎫=-⎪⎝⎭为偶函数,且最小正周期为4B.若(1,1)a = ,2a b ⋅=,则b 往a 2C.P 是抛物线22y x =上一点,(1,0)A ,则PA 的最小值为1D.已知两直线1:210l mx y +-=与2:(1)10l x m y +-+=,则“2m =”是“1l ,2l 互相平行”的充分不必要条件10.在高三一次大型联考中,物理方向共有35万人参加,其中男生有20万人.现为了了解该次考试的数学成绩,用分层随机抽样的方法从中抽取350人,其中m 名男生的数学平均成绩为77分,n 名女生的数学平均成绩为70分.已知35万人的数学成绩~(,16)X N μ,μ近似为样本均值,则下列正确的是()参考数据:若()2~,X N μσ,则()0.6826P X μσμσ-<<+≈,(22)0.9544P X μσμσ-<<+≈,(33)0.9974P X μσμσ-<<+≈A.200m =B.总体是35万人C.样本均值为73.5D.估计该次联考中物理方向数学成绩低于66分的约有7980人11.已知A ,B 分别为双曲线22221(0,0)x y a b a b-=>>的左、右顶点,离心率为e ,()00,P x y 为双曲线上位于第一象限内任意一点,设PAB α∠=,PBA β∠=,PAB △的面积为S ,则下列说法正确的是()A.||||PA PB 的值随着0x 的增大而减小 B.tan tan αβ是定值C.2tan tan b aαβ-≤ D.若2tan()0S a αβ⋅++≥,则12e <≤第II 卷(非选择题)三、填空题:本大题共3小题,每小题5分,共15分.12.已知公比不为1的等比数列{}n a ,11a =且13a ,22a ,3a 成等差,则2025a =________.13.已知2221:210C x y ax a +--+= 与2222:(1)(1)(0)C x y r r -++=> ,若存在实数a 的值使得两圆仅有一条公切线,则r 的最小值为________.14.甲口袋装有1个黑球和2个白球,乙口袋装有2个黑球和1个白球,这些球除颜色外完全相同.第一步,从甲口袋中随机取一个球放入乙口袋;第二步,从乙口袋中随机取一个球放入甲口袋;第三步,从甲口袋中随机取出一个球并记录颜色.在第三步取出的是黑球的条件下,第一步从甲口袋中取的球是黑色的概率是________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)已知函数()sin 22)f x x x x =+-∈R .(1)求函数()f x 的单调递减区间和对称中心;(2)在ABC △中,角A ,B ,C 所对的边分别是a ,b ,c ,若()0f A =,32AB BC ⋅=- 且c =,求a .16.(15分)如图四棱锥P ABCD -,底面ABCD 是边长为1的正方形,平面PCD ⊥平面PAD ,PA AD =,PA BC ⊥.(1)求证:CD ⊥平面PAD ;(2)求二面角B PC D --的余弦值.17.(15分)已知O 为坐标原点,椭圆2222:1(0)x y a b a b Γ+=>>,12C ⎛⎫ ⎪⎝⎭是Γ上一点,离心率2e =.(1)求Γ的方程;(2)斜率为12的直线l 交Γ于A ,B 两点,P 在以AB 为直径的圆上,求OP 的最大值.18.(17分)已知函数()ln 2bf x a x x x=++,其中0a ≠.(1)已知2b =-,若()f x 在定义域内单调递增,求a 的最小值;(2)求证:存在常数m 使得()m f x f a x ⎛⎫+=⎪⎝⎭,并求出b 的值;(3)在(2)的条件下,若方程2()0f x a -=存在三个根1x ,2x ,()3123x x x x <<,且311x x e +<+,求a 的取值范围.19.(17分)第一组数据()12,,,n x x x ,其中12n x x x <<< ,第二组数据()121,,,,n n z z z z + ,这1n +个数互不相等,1z ,2z 分别为其中最大与第二大的数.先从第二组数据中剔除一个数(剩余数相对位置保持不变)得到一组新数据,若将该组数据中相邻两数对换位置称为一次对换,经过至少k 次对换得到最终数据()12,,,n y y y ,简记()k τ.若用直线y a bx =+拟合点列(),(1,2,,)i i i P x y i n =,相关系数niix ynxyr -=∑(1)第一组数据(3,0,2,5,9)-,第二组数据(10,8,2,5,1,4)-,若剔除10,经过()1k τ后得到(8,5,4,2,1)-拟合最佳;若剔除8,经过()2k τ得到(1,2,4,5,10)-最佳.求12k k +的值;(2)在一组互不相等的数的排列()12,,,n a a a 中,定义在i a 的右边比其小的数的个数称为i a 的逆序数.已知1a ,3a 的逆序数分别为1n -,3n -,剩余各数按相对顺序从大到小排列.若经过()k τ后将这n 个数从小到大顺序排列,求k 的所有可能取值;(3)若剔除1z 后经过至少1m 次对换()1m τ后得到拟合效果最佳,相关系数为1r .剔除2z 后经过至少2m 次对换()2m τ后得到拟合效果最佳,相关系数为2r .若120r r <,求证:12m m +为定值,并求出该定值.景德镇市2025届高三第一次质检试题数学参考答案第Ⅰ卷(选择题共58分)一、选择题:本大题共8小题,每小题5分,满分40分.1234567891011DDBCABBABCADABD1.D 【解析】{}0,1,2--=A ,[]1,3B =-,A B =I {}10,-.故选D .2.D 【解析】()()1213255i i i iz i +-++===+,∴35i z -=对应的点为31,55⎛⎫- ⎪⎝⎭在第四象限.故选D .3.B 【解析】()202,a b -=-,22a b -= .故选B .4.C 【解析】()25sin 22sin cos sin cos 19ααααα==+-=-,故选C .5.A 【解析】()232f x x '=+,点A 不在曲线上,由已知可求得切线过点()1,4--,得直线方程为,51y x =+,故选A .6.B 【解析】数形结合.故选B .7.B 【解析】∵()12+x f 是奇函数,∴()()01212=+-++x f x f ,即()x f 关于()0,1点对称.又函数()x f 的定义域为R ,故()01=f .且当1>x 时()()12log 12-=-x x f ,令()0≥x f ,即()⎩⎨⎧>≥--1012log 12x x ,解得2≥x .根据对称性可知当1<x 时,10<≤x .综上所述,()0≥x f 的解集是[][)+∞,21,0 .故选B .8.A 【解析】分别取,AB CD 的中点,E F ,不难发现平面OAB 即平面FAB ,平面OCD 即平面ECD ,∴平面OAB 和平面OCD 位于正四面体内部的交线为线段EF ,∵正四面体ABCD 的棱长为1,不难计算得出2EF =.故选A .EF二、选择题:本大题共3小题,每小题6分,满分18分.9.BC 【解析】∵πππcos sin 222x x ⎛⎫-=⎪⎝⎭,显然()f x 是奇函数,故A 错误;b 往a 方向上的投影长为2a b a ⋅=,故B 正确;设()00,P x y ,其中2002y x =,∴()22001PA x y =-+()220001211x x x =-+=+,即PA 的最小值为1,故C 正确;∵12,l l 互相平行,∴()12m m -=,解得2m =或1m =-,经检验1m =-时两直线重合,∴“2m =”为“12,l l 互相平行”的充要条件,故D 错误.故选BC .10.AD 【解析】由分层随机抽样的特征可知:2035020035m =⨯=,故A 正确;总体是35万考生的数学成绩,故B 错误;根据分层随机抽样的均值知样本均值201577703535x =⨯+⨯=74,故C 错误;∵274,16μσ==,266μσ-=,()10.954420.02282P X μσ-<-≈=,∴小于66分的人数约为3500000.02287980⨯=人,故D 正确.故选AD .11.ABD 【解析】在△PAB 中,由正弦定理可知()sin πsin sin sin PA PB ββαα-==,显然π,βα-均为锐角且随着0x 的增大分别减小与增大,即()sin π,sin βα-随着0x 的增大分别减小与增大,∴PAPB的值随着0x 的增大而减小,故A 正确;200022000tan tan PA PB y y y k k x a x a x a αβ⋅=-=-⋅=-+--,由于2200221x y a b -=,∴()2222002b y x a a =-,∴22tan tan b aαβ⋅=-为定值,故B 正确;22000000022222000000222tan tan y y x y x y x b x a x a x a y x a y a αβ-=+==⋅=⋅+---,而00y b x a <,∴2222tan tan a b bb a aαβ->⋅=,故C 错误;0012S AB y ay ==,00002222220202tan tan tan()1tan tan 1a y a b yx a a b x a x a y aαβαβαβ-+-++==-=⋅-⋅+-+,∴222220222222022tan()a y a a b S a b x a a b αβ⋅+=-=-+-+,∴2222220a b a a b-+≥+,解得a b ≥,∴1e <≤D 正确.故选ABD.第Ⅱ卷(非选择题共92分)三、填空题:本大题共3小题,每小题5分,满分15分.12.20243【解析】由题知:∵1233,2,a a a 成等差,∴21343a a a =+,又{}n a 是公比不为1的等比数列,∴243q q =+,∴3q =,20242025=3a .故答案为20243.13.2【解析】()221:1C x a y -+= ,∴()1,0C a ,半径为1,()()2222:11C x y r -++= ,∴()21,1C -,半径为r .若两圆仅有一条公切线,即两圆相内切,∴121C C r =-.由于121C C =≥,故11r -≥,2r ≥,即r 的最小值为2.14.51【解析】第一次给出黑球且第二次给出黑球且第三次给出黑球的概率为112,第一次给出黑球且第二次给出白球且第三次给出黑球的概率为0,第一次给出白球且第二次给出黑球且第三次给出黑球的概率为29,第一次给出白球且第二次给出白球且第三次给出黑球的概率为19,∴在第三步取出的是黑球的条件下,第一步从甲口袋中取的球是黑色的概率111212151299=++.故答案为51.四、解答题:本大题共5小题,满分77分.15.(本小题13分)解:(1)()33π2sin 232cos 32sin -⎪⎭⎫⎝⎛+=-+=x x x x f ,…………………………2分该函数的单调递减区间为:()Z ∈⎦⎤⎢⎣⎡++k k k 127ππ12ππ……………………………………4分令π3π2k x =+,解得()6π13-=k x ,∴函数)(x f 的对称中心坐标为()⎪⎭⎫⎝⎛--3,6π13k ,其中Z ∈k .……………………………6分(2)∵0)(=A f ,∴233π2sin =⎪⎭⎫ ⎝⎛+A ,∴3π3π2=+A 或32π,∵()π,0∈A ,∴6π=A .…………………………………………………………………………………………8分∵()223c bc AB AC AB BC AB -=-⋅=⋅,…………………………………………………9分且23-=⋅BC AB ,b c 3=,∴⎪⎩⎪⎨⎧=-=-bc c bc 323232,解得:⎩⎨⎧==31c b …………………11分由余弦定理可知,1cos 222=-+=A bc c b a .…………………………………………13分16.(本小题15分)解:(1)取PD 中点E ,连接AE ,∵PA AD =,故AE PD ⊥.∵AE PD ⊥,平面PCD ⊥平面PAD ,AE ⊂平面PAD ,∴AE ⊥平面PCD ,∴AE CD ⊥.…………………………………………………………4分又∵AD CD ⊥,∴CD ⊥平面PAD .………………………………………………………6分(2)由上可知CD PA ⊥,又PA BC ⊥,∴PA ⊥平面ABCD .…………………………………………………………………………7分如图以A 为坐标原点,AB,AD,AP 为x,y,z 轴建立空间直角坐标系.……………………8分∴()()()()()0,0,0,1,0,0,1,1,0,0,1,0,0,0,1A B C D P ,……………………………………9分设平面PBC 的法向量()1111,,n x y z = ,则110n BC y n PB x z ⎧⋅==⎪⎨⋅=-=⎪⎩,令1z =,解得()11,0,1n =.………………………………………………………………………………11分同理,平面PDC 的法向量()20,1,1n =,……………………………………………………13分∴平面PBC 与平面PDC 夹角余弦值1212121cos ,2n n n n n n ⋅==…………………………14分∵二面角B PC D --为钝角,∴二面角B PC D --的余弦值为12-. (15)分17.(本小题15分)解析:(1)由题意2231142a b c a⎧+=⎪⎪⎨⎪=⎪⎩,解得21a b c ⎧=⎪=⎨⎪=⎩,∴椭圆Γ的方程为2214x y +=.………………………………………………………………5分(2)设直线l 为12y x m =+,设()()1122,,,A x y B x y ,设AB 中点为M ,联立221214y x m x y ⎧=+⎪⎪⎨⎪+=⎪⎩⇒222220x mx m ++-=,根据韦达定理可知12212222x x m x x m +=-⎧⎪⎨=-⎪⎩,其中()()222242202m m m ∆=-->⇒<.………………………………………………8分∴,2m M m ⎛⎫-⎪⎝⎭,OM =.∴12AB x =-==,………………………10分∴(122OP OM AB m ≤+=+,…………………………………………12分令π0,2m θθ⎡⎤∈ ⎢⎥⎣⎦⎛⎫=⎪⎝⎭,∴sin )2sin )π(42m θθθ=+=+≤,等号当且仅当π4θ=,即1m =时取到,满足22m <………………………………………14分∴||OP ≤||OP.……………………………………………………15分18.(本小题17分)解:(1)依题意可知当0>x 时,()0222≥++='xx a x f 恒成立,…………………………1分即022≥++x x a ,而xx 22+的最小值为4,故04≥+a ,………………………………3分解得4-≥a ,即a 的最小值为4-.……………………………………………………………4分(2)()⎪⎭⎫ ⎝⎛+++=⎪⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++=⎪⎭⎫⎝⎛+x m x m m b m a m bx xm x m a x b x x a x m f x f 2ln 2ln 2ln ,……………………………………………………………………………………………………6分∵a x m x m m b m a =⎪⎭⎫ ⎝⎛+++2ln ,∴⎪⎩⎪⎨⎧=+=02ln mmb am a ,解得⎩⎨⎧-==e b e m 2.即当e b 2-=时,()a x e f x f =⎪⎭⎫⎝⎛+.…………………………………………………………9分(3)构造函数()()222ln 2a x e x x a a x f x g --+=-=,则方程()02=-a x f 存在三个根即函数函数()x g 存在三个零点.∵()a x e f x f =⎪⎭⎫ ⎝⎛+,∴()0=⎪⎭⎫⎝⎛+x e g x g .………………10分令e x =,得()0=e g ,于是e 为()x g 的一个零点.…………………………………11分若()x g 存在零点3x ,且e x >3,由()033=⎪⎪⎭⎫⎝⎛+x e g x g 可知,则()x g 必存在相应的零点1x ,且e x ex <=31.∴()x g 必在()+∞,e 上存在唯一零点3x .……………………………13分若()0222≥++='x e x a x g 恒成立,即02≥⎪⎭⎫ ⎝⎛++x e x a 成立,解得e a 4-≥,此时()x g 在()+∞,e 上单调递增,无零点;………………………………………………………………14分若e a 4-<,则()04<+='e a e g ,且()()043>--=''xe ax x g ,∴()x g '在()+∞e 上单调递增,故()x g '在()+∞,e 上存在零点0x ,当()0,x e x ∈时,()0<'x g ,()x g 单调递减,当()+∞∈,0x x 时,()0>'x g ,()x g 单调递增.……………………………………………15分∵113+<+e x x ,即133+<+e x ex ,解得e x <3,………………………………………16分∴()()03=>x g e g ,即e a 44->.综上所述,a 的取值范围是()e e 4,44--.…………………………………………………17分19.(本小题17分)解:(1)第一次将()4,1,5,2,8-对换得到()1,2,4,5,8-,∴31=k .…………………………2分第二次将()4,1,5,2,10-对换得到()10,5,4,2,1-,∴72=k .故1021=+k k .…………………………………………………………………………………4分(2)∵1a 的逆序数分别为1-n ,∴1a 必为这n 个数中的最大数.3a 的逆序数分别为3-n ,则3a 可能是这n 个数中第二大或者第三大的数.………………5分若3a 是第二大的数,先将1a 对换到末位需要1-n 次对换,再将3a 对换到倒数第二位需要3-n 次对换,而后将其余各数对换到相应位置分别需要0,1,,2,3 --n n 次对换,则222--=n n k ;…………………………………………………………………………………6分若3a 是第三大的数,则2a 只能是第二大的数,同理1a 需要对换1-n 次,2a 需要对换2-n 次,3a 需要对换3-n 次,…,∴22n n k -=.……………………………………………………8分综上所述,222--=n n k 或22nn k -=.……………………………………………………9分(3)先证明排序不等式,不妨假设n n b b b a a a <<<<<< 2121,,n k k k ,,21是n ,21,,的一个排列,{}n j i ,,2,1, ∈∀,不妨假设j i >,则()()ni j n j i k n k j k i k k k n k j k i k k b a b a b a b a b a b a b a b a b a ba ++++++-++++++ 21212121()()j i k k j i b b a a --=,于是()()n i j n j i k n k j k i k k k n k j k i k k b a b a b a b a b a b a b a b a b a ba ++++++>++++++ 21212121成立的充要条件为j i k k >,于是经过若干次对换后得:∑∑∑===-+<<ni i i n i k i ni in i b a b a ba i 1111.……………………………………………………………………………………………………12分假设()n y y y ,,,21 经过若干次对换后得到()n y y y ''',,,21,其中n y y y '<<'<' 21,则∑∑∑===-+'<<'ni i i n i i i ni in iy x y x y x 1111.∵∑∑∑===---=ni ini ini iiyn yxn xyx n yx r 1221221,其中∑∑==--ni ini iy n yxn x122122与y x n 均为正常数,要使得拟合效果最佳,则1→r .∵021<r r ,不妨假设0,021<>r r ,则1,121-→→r r .……………………………………………………………………………………………………13分设()13,,,+n n z z z 的所有逆序数之和为q ,反之,正序数之和为p ,由于这1-n 个数互不相等,则21-=+n C q p .∵剔除1z 后要使得拟合效果最佳且11→r ,即∑=ni iiyx 1尽可能大,则应将()132,,,,+n n z z z z 按从小到大的顺序排列.将()13,,,+n n z z z 中的数按大数优先对换的原则,则将该组数按从小到大的顺序排列共需q 次对换,再将2z 排最前面有1-n 次对换,故q n m +-=11.………………………………14分∵剔除2z 后要使得拟合效果最佳且12-→r ,即∑=ni iiyx 1尽可能小,则应将()131,,,,+n n z z z z 按从大到小的顺序排列.而()13,,,+n n z z z 中的数按小数优先对换的原则,则将该组数按从大到小的顺序排列共需要p 次对换,1z 位置不变,故p m =2.……………………………………………………15分∴21122121nn Cn q p n m m n -=+-=++-=+-.…………………………………………16分若0,021><r r ,同理可得2221nn m m -=+.综上所述,2221nn m m -=+为定值.………………………………………………………17分。
甲烷四面体结构嘿,朋友!想象一下这样一个场景,在一个阳光明媚的周末午后,你走进了一间化学实验室。
实验室里,各种瓶瓶罐罐整齐地排列着,墙壁上挂满了化学元素周期表和复杂的化学结构图。
在这当中,有一个神奇的家伙正等着你去揭开它神秘的面纱,那就是甲烷。
说起甲烷,咱们得先聊聊它那独特的四面体结构。
你瞧,甲烷分子中的碳原子就像是一个小小的国王,被四个氢原子臣民紧紧围绕着。
这四个氢原子可听话了,它们均匀地分布在碳原子的四周,构成了一个完美的四面体。
这就好像是一个正四面体的帐篷,碳原子稳稳地坐在帐篷的中心,而氢原子则像是固定帐篷的四个角。
这时候,实验室里的老师走了过来,他笑着对你说:“孩子,你能想象吗?如果把这个四面体结构放大无数倍,那可就是一个超级稳定的空间结构。
” 你眨眨眼睛,心里充满了好奇。
老师接着解释道:“你看,这四个氢原子和碳原子之间的距离相等,角度也相同,这使得它们之间的作用力达到了一种完美的平衡。
这难道不神奇吗?” 你不禁点了点头,仿佛看到了这个小小的四面体在微观世界里稳定地存在着。
想象一下,如果这四个氢原子分布不均匀,或者角度不对,那会怎样?就好像是四个人抬着一个轿子,如果有人用力不均,轿子就会倾斜,甚至摔倒。
而甲烷的四面体结构,可不会出现这样的情况。
再类比一下我们的生活,一个稳定和谐的家庭,是不是就像甲烷的四面体结构?每个家庭成员都在自己的位置上,发挥着应有的作用,相互之间的关系平衡而稳定。
你可能会问,研究这个甲烷四面体结构有啥用呢?用处可大啦!了解了它,我们就能更好地理解有机化学中的许多反应,开发出更多有用的化学产品。
这就像是掌握了一把神奇的钥匙,可以打开无数知识和应用的大门。
所以说,甲烷的四面体结构可不是一个简单的几何形状,它是微观世界里的奇妙杰作,是化学世界里的稳定基石。
怎么样,是不是对这个小小的四面体结构刮目相看啦?。
甲烷乙烯乙炔的空间构型甲烷、乙烯和乙炔,这三个家伙在化学界可是颇有名气的哦。
想象一下,甲烷就像是个温和的小绵羊,性格温顺,四周飘着淡淡的气味,常常在厨房里陪伴我们,没事就跟碳原子、氢原子聊聊天。
它的分子结构是个简单的四面体,像个立体的宝石,真是可爱。
你知道吗?甲烷的每个氢原子都跟碳原子紧紧相拥,形成了一个稳定的小家庭,彼此依赖,真是羡煞旁人。
接下来是乙烯,嘿,这家伙可有点儿不一样了。
它的性格就像个活泼的小青年,比较喜欢“玩”些新花样。
乙烯的结构是个平面,这就让它更加灵活,像个跳舞的小精灵。
它的双键就像是它的招牌动作,给人一种时刻准备好要出奇招的感觉。
想象一下,乙烯在化学反应中就像个迅猛的赛车,谁要是敢跟它赛跑,估计得小心翼翼,免得被甩在身后。
它的每个分子都能和其他分子快速地打成一片,反应速度可谓快如闪电。
乙炔就登场了,这小子简直就是个狂野的艺术家,生活在火焰与激情中。
乙炔的结构有点特殊,它的线性形状就像是一根闪闪发光的火把,随时准备燃烧。
乙炔的三键就像是它的摇滚精神,给人一种无畏无惧的感觉。
别看它的外表冷静,内心可是火热得很,随时都能引发一场大爆炸。
乙炔的这份特立独行,仿佛是在告诉大家,生活得疯狂一点才有意思。
说到这三种物质的空间构型,其实就像是不同性格的小伙伴们聚在一起,气氛也不尽相同。
甲烷那种稳重踏实的感觉,让人觉得特别安心。
乙烯则像个朋友,永远给你带来新鲜感,活力满满。
而乙炔,呵,这家伙让人又爱又恨,充满了惊喜和危险,就像是一场刺激的冒险。
生活中,这三种物质就像是一场华丽的舞会,各自展示着不同的风采。
从化学的角度看,甲烷、乙烯和乙炔的空间构型其实反映了它们的反应特性。
甲烷的稳定性让它在化学反应中不容易被打扰,仿佛是在告诉我们,稳扎稳打才是王道。
而乙烯那种双键的灵活性,让它在化学反应中如鱼得水,反应速度杠杠的,真是令人赞叹。
至于乙炔,虽然它的反应活性极高,但却也让人感到不安,毕竟火焰的热情往往伴随着潜在的危险。
甲烷学习两误区甲烷是最简单的烃,也是第一个我们全面学习的有机物。
今后对其他有机物的学习都是建立在对甲烷认识的基础上。
作为初学者,不可避免会对它的有关知识产生一些误解,以下重点剖析两误区。
误区一误认为和是两种物质。
二氯甲烷的结构式有以上两种写法,相当多的同学认为这两种写法表示的是两种物质。
同学们产生此错误认识的主要原因是对甲烷的正四面体构型认识不清或是缺乏一定的空间想像力。
如图1所示:甲烷空间构型是正四面体结构,其中的氢原子连接起来正好构成一个正四面体。
如果将其中的两个氢原子用氯原子取代即形成二氯甲烷,如图2所示。
其实,题目所示两种结构式的写法可以看成是从不同的角度观察同一个模型所看到的平面图像。
显然,题目所示的两种结构式表示同种物质,或者说,二氯甲烷没有同分异构体。
这一事实也证明甲烷的空间构型是四面体结构。
误区之二CH4与Cl2物质的量之比为1∶1时,有机产物只有CH3Cl 。
甲烷与氯气的光取代反应如下所示:某些同学认为当CH4与Cl2物质的量之比为1∶1时,有机产物只有CH3Cl,而没有CH2Cl2等其他氯代产物;或者当CH4与Cl2物质的量比为1∶2时,有机产物只有CH2Cl2,而没有其他氯代产物……以上理解是错误的!这种理解往往是因为某些已往知识的负面影响造成的。
比如CO2与NaOH溶液反应时,当二者物质的量之比为1∶2时,产物是Na2CO3和H2O;当二者物质的量之比为1∶1时,产物是NaHCO3。
相关反应为:CO2+2NaOH==Na2CO3+H2O;CO2+NaOH==NaHCO3。
与无机反应有很大的不同,物质的量之比为1∶1的甲烷与氯气在反应中很难停留在一氯甲烷阶段。
当一氯甲烷生成后,一氯甲烷会继续与氯气反应生成二氯甲烷、三氯甲烷等,最后的有机产物往往是四种氯代甲烷的混合物。