下载文档原格式
摘要如今全民大爱篮球运动，投球的命中率是一场比赛输赢的关键所在，能否投入篮筐与投球时运动员所处的位置、投球时的角度和投球时的出手速度有很大关系，该论文主要以罚球为出发点，排除了运动员因运动而造成的各种不利因素，讨论其罚球时球心与篮筐中心距离，球心所处高度以及投球速度之间的变化对球入篮的影响。
把其简化成物理学上的上抛运动，对其水平上用匀速运动讨论起运动规律，在垂直方向以初速度为投球时的速度v，加速度为g做均减速运动讨论其运动规律。
综合求解出其运动轨迹，利用导数意义，求出所需高度，速度等变量的最值，得出以下结论和规律，在标准的篮球场上，当运动员出手速度和出手角度均随着出手高度增加而减小，但当出手高度一定时，出手速度越大则球入筐时的入射角度也越大，速度一定时，出手高度越大，出手角度应越大，但是随着速度的增加，高度对出手角度的影响变小，说明取决出手角度的变化对出手速度更为敏感。
在出手高度为1.8~2.1m之间时，出手速度一般要大于8m/s。
入射角度一般需要大于33.1。
分析出手角度和出手速度的最大偏差，得出速度越大，出手角度的允许偏差越小，而出手速度的允许偏差越大，且对出手角度的要求比对出手速度的要求严格;出手速度一定时，出手高度越大，出手角度的允许偏差越小，出手速度的允许偏差越大。
关键词：投篮，出手高度，出手速度，入射角度问题提出在激烈的篮球比赛中，提高投篮命中率对于获胜无疑起着决定作用，而出手角度和出手速度是决定投篮能否命中的两个关键因素。
这里讨论比赛中最简单、但对于胜负也常常是很重要的一种投篮方式——罚球。
我们建立数学模型研究以下数学问题：1)先不考虑篮球和篮框的大小，把它们的中心看成质点，只是简单的讨论球心命中框心的条件。
对不同的出手高度h和出手速度v，确定所对应的不同的出手角度α时所对应的不同篮框的入射角度β；2)考虑篮球和篮框的大小，讨论球心命中框心且球入框的条件。
检查上面得到的出手角度α和篮框的入射角度β是否符合这个条件；3)为了使球入框，球心不一定要命中框心，可以偏前或偏后(这里暂不考虑偏左或偏右)，只要球能入框就成，讨论保证球入框的条件下，出手角度允许的最大偏差，和出手速度允许的最大偏差；4)考虑在空气阻力的影响条件下，讨论球心命中框心的条件；1问题的分析与模型的建立1.1模型假设①、假设球出手后不考虑自身的旋转；②、不考虑篮球碰篮板；③、不考虑空气阻力对篮球的影响时；符号假定d 篮球直径D 篮框直径L 罚球点和篮框中心的水平距离H 篮框中心的高度h 篮球运动员的出手高度v 篮球运动员投篮出手速度按照标准尺寸，L=4.6m，H=3.05m，d=24.6cm，D=45cm1.2、问题的分析与模型的建立①问题1)的分析与模型的建立不考虑篮球和篮框的大小的简单情况，相当于将球视为质点（球心）的斜抛运动。
投篮命中率的数学模型摘要随着篮球运动的普与，篮球比赛中紧X、激烈的气氛和更加具有攻击性的防守等因素导致投篮命中率大大降低。
根据研究显示，影响投篮命中率有两个关键因素：出手角度和出手速度。
本文主要运用运动力学的知识，建立有效的篮球投射模型, 从篮球投射时球的出手角度、出手速度、出手高度和篮球球心与篮框中心的水平距离、篮球入射角之间的关系入手，分析各种因素对投篮命中率的影响，并作适当的假设，在合理估计出手点与篮框中心距离并保持出手速度稳定的情况下, 确定投篮的最优出手角度和最优出手速度，得出一个既能使投篮时不过多消耗体力又能提高投篮命中率的结论。
首先，本文将三角函数、导数、微分等数学知识与运动学、力学等物理知识相互结合，在罚球投篮这一具体问题的相应具体情境下对此进展了深入分析。
其次，本文建立了与之相关的数学模型，通过不同投篮情况的图表分析归纳出对应的公式，在多重公式的累加条件下最后整理得到满足要求的最终条件X围，得出模型的结果。
在求解过程中，本文使用了MathType数学软件对所用的数学符号作了系统的整理，借此列出了各组公式，同时给出了详细的计算与分析过程，并得出最终结果。
本文在第一问中所设定的不考虑球出手后自身的旋转与球碰篮板或篮框的情况，即在只针对空心球的情况下又限制变量，分别讨论篮框大小、篮球大小、空气阻力与出手角度和速度的最大偏差这四个不同变量下命中率受到的的影响，给出公式，计算出结果。
最终，本文探讨出提高罚球命中率的方法是控制投篮时的出手角度和出手速度，使之分别限制在一定的X围内。
出手角度和速度的过高或过低都会使罚球命中率不能保持在较高水平。
在第二问中本文针对篮球擦板后进篮的情况，假定篮球在碰撞过程中没有能量损耗的理想情况，讨论出了分别在限制区边线距篮框中心30度、45度、90度〔罚球线〕位置上这三种不同情境下出手角度、出手速度与投篮的命中率之间的关系。
当运动员所站的位置改变时，即投篮出手点到篮框的距离改变时，出手角度和出手速度的增加或减少都影响了投篮的命中率。
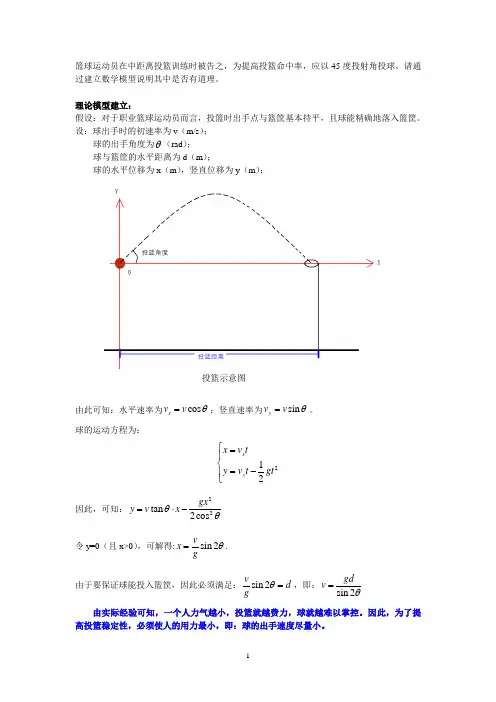
篮球运动员在中距离投篮训练时被告之，为提高投篮命中率，应以45度投射角投球。
请通过建立数学模型说明其中是否有道理。
理论模型建立：假设：对于职业篮球运动员而言，投篮时出手点与篮筐基本持平，且球能精确地落入篮筐。
设：球出手时的初速率为v （m/s ）；球的出手角度为θ（rad ）； 球与篮筐的水平距离为d （m ）； 球的水平位移为x （m ），竖直位移为y （m ）；投篮示意图由此可知：水平速率为cos x v v θ=；竖直速率为sin y v v θ=。
球的运动方程为：212x y x v ty v t gt ⎧=⎪⎨=-⎪⎩ 因此，可知：22tan 2cos gx y v x θθ=⋅-令y=0（且x>0），可解得:sin 2vx gθ=. 由于要保证球能投入篮筐，因此必须满足：sin 2v d g θ=，即：sin 2gd v θ= 由实际经验可知，一个人力气越小，投篮就越费力，球就越难以掌控。
因此，为了提高投篮稳定性，必须使人的用力最小，即：球的出手速度尽量小。
因此，整个问题就归结为如下优化模型：2min ()..02f v s t θπθ=≤<因此，原问题就等价于如下优化模型：21min sin 2..02f s t θπθ=≤<容易求得，问题的解为：4πθ=最优。
结论：当投篮角度为45度时，篮球落入篮筐时的状态是最稳定的，因此，以45度角投篮时，可以提高投篮命中率。
改进：一般化的投篮模型一般情形：球员身高较矮，投篮时球的出手点与篮筐的垂直距离为h （m ），求这种一般情形下运动员的最优投篮角度。
投篮示意图一、投篮模型的建立：由之前的讨论可知，篮球的运动方程如下：22tan 2cos gx y v x θθ=⋅- 由于当篮球的水平位移达到投篮距离d 时，篮球必须入筐，因此抛物线过（d ，h ）点。
由此可知球出手时的速率为：222cos sin 2h gd v d θθ+= ----------------------（*）利用一开始时的结论，为了使投篮尽量稳定，就等价于确定如下优化问题的解：2min ()..02f v s t θπθ=≤<其中：222cos ()sin 2h gd v d θθθ+=二、理论模型的计算： 令d=3.5（m ），g=9.8（m/s^2）；结论：从计算结果可以看出，只要高度差小于2米，最优投篮角度都差不多在45°左右。
摘 要本文针对投篮问题进行研究，根据物理运动学原理分析投篮方式的关键因素及特点，建立层次模型对增加观赏度和个人表现力进行分析。
问题一要求分析罚球、两分球及三分球投篮方式的特点及各自提高命中率的关键因素，并为投篮训练和竞赛策略提供建议。
在篮球投射出去时是做斜抛运动，结合运动学原理来分析三种投篮方式。
投射罚球和两分球时距离较近，则忽略空气阻力的影响，得到运动轨迹方程如下：222tan 2cos gy x x v αα=⋅- 对于关键因素和特点可用篮球飞行过程中的运行区域的面积表示命中率，在选手最小速度运球的情况下对几个变量求偏导数，根据系数大小找出前两个关键因素，其中对于三分球采用入射角度限制的方法进行分析，得出以下结论：二分球的特点是定点投篮，关键因素有出手高度、出手速度、出手角度度；罚球的特点是投射距离固定，关键因素有出手速度和出手角度；三分球的特点是选择跳投的方式，关键因素有出手速度、出手角度和投篮距离。
综合对三种投篮方式的分析，建议队员投射前应适当的调整投射距离的位置和出手角度这主要跟平时的训练有关，在训练时尽可能的控制手腕力量，加强对力量控制方面的练习。
问题二要求分析新规定能否增加篮球竞赛的观赏程度以及体现球员的个人表现力。
分析规则修改前后的数据找出影响观赏度和个人表现力的重要指标，利用层次分析法确定权重，找出影响的最主要指标，为了提高指标体系的可靠性，利用模糊综合评价模型进行进一步的完善，得知助攻、失误和个人能力是决定增加观赏度和提高个人表现力的关键因素。
关键词 命中率 控制变量 运动学 AHP -模糊综合评价模型一、问题背景与重述1.1问题背景投篮是在比赛中，队员运用各种专门、合理的动作将球投进对方球篮的方法。
投篮是篮球运动中一项关键性技术，是唯一的得分手段。
进攻队运用各种技术、战术的目的，都是为了创造更多更好的投篮机会并力求投中得分；防守队积极防御都是为了阻挠对方投篮得分。
随着篮球运动的发展，运动员身高、身体素质及技术水平的提高，促使投篮技术不断发展：出手部位由低到高，出手速度由慢到快，投篮方式越来越多，命中率不断提高。
摘要如今全民大爱篮球运动，投球的命中率是一场比赛输赢的关键所在，能否投入篮筐与投球时运动员所处的位置、投球时的角度和投球时的出手速度有很大关系，该论文主要以罚球为出发点,排除了运动员因运动而造成的各种不利因素，讨论其罚球时球心与篮筐中心距离，球心所处高度以及投球速度之间的变化对球入篮的影响。
把其简化成物理学上的上抛运动，对其水平上用匀速运动讨论起运动规律，在垂直方向以初速度为投球时的速度v,加速度为g做均减速运动讨论其运动规律。
综合求解出其运动轨迹，利用导数意义,求出所需高度,速度等变量的最值,得出以下结论和规律，在标准的篮球场上，当运动员出手速度和出手角度均随着出手高度增加而减小,但当出手高度一定时，出手速度越大则球入筐时的入射角度也越大，速度一定时，出手高度越大，出手角度应越大，但是随着速度的增加，高度对出手角度的影响变小，说明取决出手角度的变化对出手速度更为敏感。
在出手高度为1.8～2.1m之间时，出手速度一般要大于8m/s。
入射角度一般需要大于33.1。
分析出手角度和出手速度的最大偏差，得出速度越大，出手角度的允许偏差越小,而出手速度的允许偏差越大，且对出手角度的要求比对出手速度的要求严格；出手速度一定时,出手高度越大，出手角度的允许偏差越小，出手速度的允许偏差越大。
关键词：投篮，出手高度,出手速度，入射角度问题提出在激烈的篮球比赛中,提高投篮命中率对于获胜无疑起着决定作用，而出手角度和出手速度是决定投篮能否命中的两个关键因素。
这里讨论比赛中最简单、但对于胜负也常常是很重要的一种投篮方式-—罚球.我们建立数学模型研究以下数学问题：1)先不考虑篮球和篮框的大小,把它们的中心看成质点,只是简单的讨论球心命中框心的条件.对不同的出手高度h和出手速度v，确定所对应的不同的出手角度α时所对应的不同篮框的入射角度β；2)考虑篮球和篮框的大小，讨论球心命中框心且球入框的条件。
检查上面得到的出手角度α和篮框的入射角度β是否符合这个条件；3)为了使球入框，球心不一定要命中框心，可以偏前或偏后(这里暂不考虑偏左或偏右)，只要球能入框就成，讨论保证球入框的条件下，出手角度允许的最大偏差,和出手速度允许的最大偏差；4)考虑在空气阻力的影响条件下,讨论球心命中框心的条件；1问题的分析与模型的建立1.1模型假设①、假设球出手后不考虑自身的旋转；②、不考虑篮球碰篮板;③、不考虑空气阻力对篮球的影响时；符号假定d 篮球直径D 篮框直径L 罚球点和篮框中心的水平距离H 篮框中心的高度h 篮球运动员的出手高度v 篮球运动员投篮出手速度按照标准尺寸，L=4.6m，H=3.05m，d=24。
摘要如今全民大爱篮球运动，投球的命中率是一场比赛输赢的关键所在，能否投入篮筐与投球时运动员所处的位置、投球时的角度和投球时的出手速度有很大关系，该论文主要以罚球为出发点，排除了运动员因运动而造成的各种不利因素，讨论其罚球时球心与篮筐中心距离，球心所处高度以及投球速度之间的变化对球入篮的影响。
把其简化成物理学上的上抛运动，对其水平上用匀速运动讨论起运动规律，在垂直方向以初速度为投球时的速度v，加速度为g做均减速运动讨论其运动规律。
综合求解出其运动轨迹，利用导数意义，求出所需高度，速度等变量的最值，得出以下结论和规律，在标准的篮球场上，当运动员出手速度和出手角度均随着出手高度增加而减小，但当出手高度一定时，出手速度越大则球入筐时的入射角度也越大，速度一定时，出手高度越大，出手角度应越大，但是随着速度的增加，高度对出手角度的影响变小，说明取决出手角度的变化对出手速度更为敏感。
在出手高度为1.8~2.1m之间时，出手速度一般要大于8m/s。
入射角度一般需要大于33.1。
分析出手角度和出手速度的最大偏差，得出速度越大，出手角度的允许偏差越小，而出手速度的允许偏差越大，且对出手角度的要求比对出手速度的要求严格;出手速度一定时，出手高度越大，出手角度的允许偏差越小，出手速度的允许偏差越大。
关键词：投篮，出手高度，出手速度，入射角度问题提出在激烈的篮球比赛中，提高投篮命中率对于获胜无疑起着决定作用，而出手角度和出手速度是决定投篮能否命中的两个关键因素。
这里讨论比赛中最简单、但对于胜负也常常是很重要的一种投篮方式——罚球。
我们建立数学模型研究以下数学问题：1)先不考虑篮球和篮框的大小，把它们的中心看成质点，只是简单的讨论球心命中框心的条件。
对不同的出手高度h和出手速度v，确定所对应的不同的出手角度α时所对应的不同篮框的入射角度β；2)考虑篮球和篮框的大小，讨论球心命中框心且球入框的条件。
检查上面得到的出手角度α和篮框的入射角度β是否符合这个条件；3)为了使球入框，球心不一定要命中框心，可以偏前或偏后(这里暂不考虑偏左或偏右)，只要球能入框就成，讨论保证球入框的条件下，出手角度允许的最大偏差，和出手速度允许的最大偏差；4)考虑在空气阻力的影响条件下，讨论球心命中框心的条件；1问题的分析与模型的建立1.1 模型假设①、假设球出手后不考虑自身的旋转；②、不考虑篮球碰篮板；③、不考虑空气阻力对篮球的影响时；符号假定d 篮球直径D 篮框直径L 罚球点和篮框中心的水平距离H 篮框中心的高度h 篮球运动员的出手高度v 篮球运动员投篮出手速度按照标准尺寸，L=4.6m，H=3.05m，d=24.6cm，D=45cm1.2、问题的分析与模型的建立①问题1)的分析与模型的建立不考虑篮球和篮框的大小的简单情况，相当于将球视为质点（球心）的斜抛运动。
数学建模投篮命中率的数学模型Document number【SA80SAB-SAA9SYT-SAATC-SA6UT-SA18】投篮命中率的数学模型摘要随着篮球运动的普及，篮球比赛中紧张、激烈的气氛和更加具有攻击性的防守等因素导致投篮命中率大大降低。
根据研究显示，影响投篮命中率有两个关键因素：出手角度和出手速度。
本文主要运用运动力学的知识，建立有效的篮球投射模型, 从篮球投射时球的出手角度、出手速度、出手高度和篮球球心与篮框中心的水平距离、篮球入射角之间的关系入手，分析各种因素对投篮命中率的影响，并作适当的假设，在合理估计出手点与篮框中心距离并保持出手速度稳定的情况下, 确定投篮的最佳出手角度和最佳出手速度，得出一个既能使投篮时不过多耗费体力又能提高投篮命中率的结论。
首先，本文将三角函数、导数、微分等数学知识及运动学、力学等物理知识相互结合，在罚球投篮这一具体问题的相应具体情境下对此进行了深入分析。
其次，本文建立了与之相关的数学模型，通过不同投篮情况的图表分析归纳出对应的公式，在多重公式的累加条件下最后整理得到满足要求的最终条件范围，得出模型的结果。
在求解过程中，本文使用了MathType数学软件对所用的数学符号作了系统的整理，借此列出了各组公式，同时给出了详细的计算及分析过程，并得出最终结果。
本文在第一问中所设定的不考虑球出手后自身的旋转及球碰篮板或篮框的情况，即在只针对空心球的情况下又限制变量，分别讨论篮框大小、篮球大小、空气阻力及出手角度和速度的最大偏差这四个不同变量下命中率受到的的影响，给出公式，计算出结果。
最终，本文探讨出提高罚球命中率的方法是控制投篮时的出手角度和出手速度，使之分别限制在一定的范围内。
出手角度和速度的过高或过低都会使罚球命中率不能保持在较高水平。
在第二问中本文针对篮球擦板后进篮的情况，假定篮球在碰撞过程中没有能量损耗的理想情况，讨论出了分别在限制区边线距篮框中心30度、45度、90度（罚球线）位置上这三种不同情境下出手角度、出手速度与投篮的命中率之间的关系。
摘要如今全民大爱篮球运动，投球的命中率是一场比赛输赢的关键所在，能否投入篮筐与投球时运动员所处的位置、投球时的角度和投球时的出手速度有很大关系，该论文主要以罚球为出发点，排除了运动员因运动而造成的各种不利因素，讨论其罚球时球心与篮筐中心距离，球心所处高度以及投球速度之间的变化对球入篮的影响。
把其简化成物理学上的上抛运动，对其水平上用匀速运动讨论起运动规律，在垂直方向以初速度为投球时的速度v，加速度为g做均减速运动讨论其运动规律。
综合求解出其运动轨迹，利用导数意义，求出所需高度，速度等变量的最值，得出以下结论和规律，在标准的篮球场上，当运动员出手速度和出手角度均随着出手高度增加而减小，但当出手高度一定时，出手速度越大则球入筐时的入射角度也越大，速度一定时，出手高度越大，出手角度应越大，但是随着速度的增加，高度对出手角度的影响变小，说明取决出手角度的变化对出手速度更为敏感。
在出手高度为1.8~2.1m之间时，出手速度一般要大于8m/s。
入射角度一般需要大于33.1。
分析出手角度和出手速度的最大偏差，得出速度越大，出手角度的允许偏差越小，而出手速度的允许偏差越大，且对出手角度的要求比对出手速度的要求严格;出手速度一定时，出手高度越大，出手角度的允许偏差越小，出手速度的允许偏差越大。
关键词：投篮，出手高度，出手速度，入射角度问题提出在激烈的篮球比赛中，提高投篮命中率对于获胜无疑起着决定作用，而出手角度和出手速度是决定投篮能否命中的两个关键因素。
这里讨论比赛中最简单、但对于胜负也常常是很重要的一种投篮方式——罚球。
我们建立数学模型研究以下数学问题：1)先不考虑篮球和篮框的大小，把它们的中心看成质点，只是简单的讨论球心命中框心的条件。
对不同的出手高度h和出手速度v，确定所对应的不同的出手角度α时所对应的不同篮框的入射角度β；2)考虑篮球和篮框的大小，讨论球心命中框心且球入框的条件。
检查上面得到的出手角度α和篮框的入射角度β是否符合这个条件；3)为了使球入框，球心不一定要命中框心，可以偏前或偏后(这里暂不考虑偏左或偏右)，只要球能入框就成，讨论保证球入框的条件下，出手角度允许的最大偏差，和出手速度允许的最大偏差；4)考虑在空气阻力的影响条件下，讨论球心命中框心的条件；1问题的分析与模型的建立1.1模型假设①、假设球出手后不考虑自身的旋转；②、不考虑篮球碰篮板；③、不考虑空气阻力对篮球的影响时；符号假定d 篮球直径D 篮框直径L 罚球点和篮框中心的水平距离H 篮框中心的高度h 篮球运动员的出手高度v 篮球运动员投篮出手速度按照标准尺寸，L=4.6m，H=3.05m，d=24.6cm，D=45cm1.2、问题的分析与模型的建立①问题1)的分析与模型的建立不考虑篮球和篮框的大小的简单情况，相当于将球视为质点（球心）的斜抛运动。
将坐标原点定在球心P，列出x(水平)方向和y（竖直）方向的运动方程，就可以得到球心的运动轨迹，于是球心命中框心的条件可以表示为出手角度与出手速度、出手高度之间的关系，以及篮框的入射角度与出手角度，由此可对不同的出手速度、出手高度，计算出手角度和入射角度。
图1.1 投篮模型由于不考虑篮球和篮筐的大小，不考虑空气阻力的影响，从未出手时的球心p 为坐标原点，x 轴为水平方向，y 轴为竖直方向，篮球在 t=0时以出手速度 v 和出手角度α投出，可视为质点(球心)的斜抛运动，其运动方程是我们熟知的()cos x t vt α=2()sin 2gt y t vt α=- (1.1)其中g 是重力加速度，由此可得到球心运动轨迹为如下抛物线：222tan 2cos gy x x v αα=- (1.2)以x=L ，y=H-h 代入上式，就得到球心命中框心的条件2tan 1v gL α⎡⎢=±⎢⎣ (1.3) 可以看出，给定出手速度v 和出手高度h ，有两个出手角度满足这个条件。
而上式有解的前提为2222102g gL H h v v ⎛⎫--+≥ ⎪⎝⎭(1.4) 可对v 求解得2v g H h ⎡≥-⎣ (1.5) 于是对于一定的高度h ，使上式等号成立的为最小出手速度v 它是h 的减函数。
由(1.3)式计算出两个出手速度角度记作1α、2α且设12αα>，可以看出1α是h 和v 的减函数球入篮筐时的入射角度β可从下式得到tan x Ldy dxβ==(1.6)这里的导数由(1.2)式计算代入后可得2()tan tan H h Lβα-=-(1.7) 于是对应于1α、2α，有1β、1β，设12ββ> ② 问题2)的分析与模型的建立：考虑篮球和篮框的大小时，篮球的直径d ，篮框的直径D 。
显然，即使球心命中球框，若入射角β太小，球会碰到框的近侧A ，不能入框。
如图所示：图1.2 球入篮时的模型由图不难得出β满足的球心应命中框心且球入框的条件。
sin dDβ>(1.8) 将d=24.6cm ，D=45.0cm 代入得 β>33.1，前面计算结果中不满足这个条件的，当然应该去掉。
③ 问题3)的分析与模型的建立：球入框时，球心可以偏离框心，偏前的最大距离为x ∆，x ∆可以从入射角β算出.根据β和球心轨迹中x 与α的关系，能够得到出手角度α允许的最大偏差x ∆，出手速度v 允许的最大偏差v ∆可以类似的处理。
球入筐时球心可以偏前(偏后与偏前一样)的最大距离为22sin D d x β∆=-(1.9)为了得到出手角度允许的最大偏差，可以在(1.3)式中以L+x ∆代替L 重新计算，但是由于x ∆中包含β，从而α也包含，所以这种方法不能解析的求出。
如果从(1.2)式出发并将y=H-h 代入，可得2tan 0222g x H h x v cos αα-+-= (1.10)对α求导并令x=L ，就有()22L v gLtan dx d gL v sin cos αααα-=- (1.11)用xα∆∆近似代替左边的导数，即可得到出手角度的偏差α∆与x ∆的如下关系 2gL -sin cos v =x 2L(-gLtan )v αααα∆∆ (1.12)由α∆和已经得到的α也容易计算相对偏差类似的，(1.10)式对v 求导并令x=L ，可得到出手速度允许的最大偏差xα∆∆ 2sin cos 2gL v v v x gLαα-∆=∆ (1.13)由(1.12)、(1.13)式的相对偏差为2tan vv v gL αα⎛⎫∆=∆- ⎪⎝⎭(1.14)2模型的求解及结果分析2.1对不同出手高度的最小出手速度和对应的出手角度使(1.5)式等号成立的v 为最小出手速度min v ，在这个速度下由(1.3)式可得相应的出手角度0α为20tan v gLα= (2.1)取出手高度 h=1.8~2.1(m)，利用公式2v g H h ⎡=-⎣求出min v ，再根据20tan v gLα=，求出α，用MATLAB 求解，代码如下：function v=fun(h); H=3.05; g=9.8; L=4.6;v=sqrt(g*[H-h+sqrt(L^2+(H-h)^2)]); fun(1.8) ans =7.6789 fun(1.9) ans =7.5985 fun(2.0) ans =7.5186 fun(2.1) ans =7.4392结果如下图所示。
表2.1对不同出手高度的最小出手速度和对应的出手角度由此得出，对应与最小出手速度是最小出手角度，他们均随着出手高度的增加而略有减小;出手速度一般不要小于8米/秒.2.2 对不同的出手速度和出手高度的出手角度和入射角度 对出手速度v=8.0~9.0(m/s)和出手高度1.8~2.1(m)，由公式2tan 1v gL α⎡⎢=⎢⎣，用MATLAB 求解1α、2α function f=fun1(v); L=4.6; H=3.05; g=9.8; h=1.8;t=v^2/(g*L)*(1+sqrt(1-2*g/v^2*(H-h+g*L^2/(2*v^2)))); f=atan(t)/pi*180; fun1(8.0) ans =62.4099用此求出所有的1α，同理可求出2αfunction f=fun1(v); L=4.6; H=3.05; g=9.8; h=1.8;t=v^2/(g*L)*(1-sqrt(1-2*g/v^2*(H-h+g*L^2/(2*v^2)))); f=atan(t)/pi*180; fun1(8.0) ans =42.7925求出所有的2α，利用所求出的α，再根据公式2()tan tan H h Lβα-=-，计算出不同的出手角度1α、2α所对应的不同的入射角度1β、2β，结果见下表2表2.2 对不同出手速度和出手高度的出手角度和入射角度根据前面计算，β应大于33.1才能保证球入框，这里的2β均小于33.1，不满足条件，所以在考虑篮球和篮框大小的实际情况下，出手角度只能是1α所对应的1β。
可以发现，速度一定时，出手高度越大，出手角度应越大，但是随着速度的增加，高度对出手角度的影响变小，这种影响在1左右；出手高度一定时，速度越大，出手角度也应越大，出手速度的影响在7~9之间。
2.3 分析出手角度和出手速度的最大偏差利用2sin cos 2(tan )gL v x L gL v αααα-∆=∆-和上面所求的的1α，计算出手角度最大偏差α∆和αα∆，再利用(13)、(14)式计算出手速度的最大偏差v ∆和vv∆，下面只将h=1.8(m)，h=2.0(m)的结果列入下表中。
表2.3 出手角度和出手速度之间的偏差关系总的看来，允许偏差都相当小。
进一步分析可知，速度越大，角度的允许偏差越小，而速度的允许偏差越大，且对角度的要求比对速度的要求严格；出手速度一定时，高度越大，出手角度的允许偏差越小，出手速度的允许偏差越大，但这时对出手角度和出手速度的要求都相对较低。
3模型的改进3.1当考虑空气阻力的影响时，出手角度有什么变化。
考虑水平方向的阻力时，应该用微分方程求解球心的运动轨迹，由于阻力很小，可作适当简化。
然后与前面类似的作各种计算。
假设只考虑水平方向的阻力，且阻力与速度成正比，设比例系数为 k 。
这时水平方向的运动由微分方程0,(0)0,(0)cos x kx x x v α+=== (3.1)其解为：1()cos kte x t v kα--= (3.2)因为阻力不大，时间t 也很小(约1秒)，所以将(3.2)式中的公式做泰勒展开后忽略二阶以上的项得到(不考虑竖直方向的阻力，故 y(t)仍与(1.1)式相同)，得到2cos ()cos 2kvt x t vt αα=-2()sin 2gt y t v t α=-(3.3)在不考虑篮球和篮筐大小时，球心命中框心的条件由方程组2cos cos 02kvt vt L αα--=2sin ()02gt vt H h α---= (3.4)同理于模型1)，2) 的求解，即可求出对不同出手速度和出手高度的出手角度和入射角度。
