基于模糊控制的速度跟踪控制问题(C语言以及MATLAB仿真实现)

静止背景下的多目标追踪随着计算机技术以及智能汽车行业的发展，多目标的检测与追踪的实用性与研究价值逐渐提高。

在计算机视觉的三层结构中，目标跟踪属于中间层，是其他高层任务，例如动作识别以及行为分析等的基础。

其主要应用可包括视频监控，检测异常行为人机交互，对复杂场景中目标交互的识别与处理，以及虚拟现实及医学图像。

目标跟踪又包括单目标跟踪和多目标跟踪。

单目标跟踪可以通过目标的表观建模或者运动建模，以处理光照、形变、遮挡等问题，而多目标跟踪问题则更加复杂，除了单目标跟踪回遇到的问题外，还需要目标间的关联匹配。

另外在多目标跟踪任务中经常会碰到 目标的频繁遮挡、轨迹开始终止时刻未知、目标太小、表观相似、目标间交互、低帧率等等问题。

静止背景下的多目标追踪可分为两步来实现，第一步是在视频文件的每帧中检测出移动的目标，第二步是将检测到的目标与跟踪轨迹实时匹配。

在本次实验中，利用混合高斯模型进行背景减除，使用形态学操作消除噪声，通过卡尔曼滤波预测目标位置，最后利用匈牙利算法进行匹配，实现静止背景下的多目标追踪。

1 实验原理1.1 混合高斯模型单高斯模型是利用高维高斯分布概率来进行模式分类：11()exp[(x )(x )]2T x N C μσμ-=--- 其中μ用训练样本均值代替，σ用样本方差代替，X 为d 维的样本向量。

通过高斯概率公式就可以得出类别C 属于正（负）样本的概率。

而混合高斯模型就是数据从多个高斯分布中产生，每个GMM 由k 个单高斯分布线性叠加而成。

相当于对各个高斯分布进行加权，权系数越大，那么这个数据属于这个高斯分布的可能性越大。

(x)(k)*p(x |k)P p =∑利用混合高斯模型(GMM)可以进行背景减除，将前后景分离，得到移动的目标。

对每个像素点建立由k 个单高斯模型线性叠加而成的模型，在这些混合高斯背景模型中，认为像素之间的颜色信息互不相关，对各像素点的处理都是相互独立的。

单个像素点在t 时刻服从混合高斯分布概率密度函数：,,,1(x )(x ,,)kt i t t i t i t i p w ημτ==∑其中k 为分布模式总数，,,(x ,,)t i t i t ημτ为t 时刻第i 个高斯分布，,i t μ为其均值，,i t τ为其协方差矩阵。

利用Matlab进行模糊逻辑和模糊控制的基本原理Matlab是一种强大的数学计算软件，广泛应用于各个领域的工程和科学研究。

在现实生活中，我们经常会遇到一些模糊不清、不确定的情况，而模糊逻辑和模糊控制正是用来处理这些模糊问题的有效工具。

本文将介绍利用Matlab进行模糊逻辑和模糊控制的基本原理，并通过一些具体案例来说明其在实际应用中的价值。

首先，我们需要了解模糊逻辑和模糊控制的基本概念和原理。

模糊逻辑是Lotfi Zadeh教授于1965年提出的一种处理模糊信息的形式化逻辑系统。

与传统的布尔逻辑只有两个取值（真和假）不同，模糊逻辑引入了模糊概念，可以处理多个取值范围内的逻辑判断。

其基本原理是将模糊的语言描述转化为数学上的模糊集合，然后通过模糊运算进行推理和决策。

在Matlab中，可以使用Fuzzy Logic Toolbox工具箱来进行模糊逻辑的建模和模拟。

该工具箱提供了一系列的函数和工具，可以帮助我们创建模糊逻辑系统、定义模糊集合和模糊规则，并进行输入输出的模糊化和去模糊化运算。

一个典型的模糊逻辑系统包括三个主要组成部分：模糊集合、模糊规则和模糊推理。

模糊集合用于描述模糊化的输入和输出变量，可以是三角形、梯形、高斯等形状。

模糊规则定义了模糊逻辑系统的推理过程，通常由一系列的if-then规则组成，如“如果温度较低，则输出加热”，其中“温度较低”和“加热”为模糊集合的标签。

模糊推理根据输入变量的模糊值和模糊规则，计算出输出变量的模糊值。

为了更好地理解模糊逻辑的原理和应用，我们以一个简单的案例来说明。

假设我们需要设计一个自动化灯光控制系统，使得灯光的亮度能够根据环境光线的强弱自动调节。

首先，我们需要收集一些实际的数据来建立模糊逻辑系统。

通过传感器测量到的环境光强度作为输入变量，设定的亮度值作为输出变量。

在Matlab中，可以使用Fuzzy Logic Designer来创建一个模糊逻辑系统。

首先，我们需要定义输入和输出变量，以及它们的模糊集合。

模糊自适应整定PID控制matlab仿真程序(刘金锟-先进PID控制及其MATLAB仿真)2这个例子的程序百度文库里有很多版本，但我下了很多都有错误，运行不了。

以下程序我一字一字的敲出来的，已经成功运行，绝对无误。

仿真实例，被控对象为p G (s)=ss s 1047035.8752350023++ 采样时间为1ms ，采用模糊PID 控制进行阶跃响应，在第300个采样时间时控制器输出加1.0的干扰，相应的运行结果如图1~13所示。

仿真程序如下：将以下程序保存为fuzzypid.m 文件，即可得到仿真结果。

%fuzzy tunning PID controlclear all ;clear all ;a=newfis('fuzzpid');a=addvar(a,'input','e',[-3,3]); %parameter ea=addmf(a,'input',1,'NB','zmf',[-3,-1]);a=addmf(a,'input',1,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);a=addmf(a,'input',1,'PM','trimf',[0,2,3]);a=addmf(a,'input',1,'PB','smf',[1,3]);a=addvar(a,'input','ec',[-3,3]); %parameter eca=addmf(a,'input',2,'NB','zmf',[-3,-1]);a=addmf(a,'input',2,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',2,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',2,'Z','trimf',[-2,0,2]);a=addmf(a,'input',2,'PS','trimf',[-1,1,3]);a=addmf(a,'input',2,'PM','trimf',[0,2,3]);a=addmf(a,'input',2,'PB','smf',[1,3]);a=addvar(a,'output','kp',[-0.3,0.3]); %parameter kpa=addmf(a,'output',1,'NB','zmf',[-0.3,-0.1]);a=addmf(a,'output',1,'NM','trimf',[-0.3,-0.2,0]);a=addmf(a,'output',1,'NS','trimf',[-0.3,-0.1,0.1]);a=addmf(a,'output',1,'Z','trimf',[-0.2,0,0.2]);a=addmf(a,'output',1,'PS','trimf',[-0.1,0.1,0.3]);a=addmf(a,'output',1,'PM','trimf',[0,0.2,0.3]);a=addmf(a,'output',1,'PB','smf',[0.1,0.3]);a=addvar(a,'output','ki',[-0.06,0.06]); %parameter ki a=addmf(a,'output',2,'NB','zmf',[-0.06,-0.02]);a=addmf(a,'output',2,'NM','trimf',[-0.06,-0.04,0]);a=addmf(a,'output',2,'NS','trimf',[-0.06,-0.02,0.02]); a=addmf(a,'output',2,'Z','trimf',[-0.04,0,0.04]);a=addmf(a,'output',2,'PS','trimf',[-0.02,0.02,0.06]);a=addmf(a,'output',2,'PM','trimf',[0,0.04,0.06]);a=addmf(a,'output',2,'PB','smf',[0.02,0.06]);a=addvar(a,'output','kd',[-3,3]); %parameter kda=addmf(a,'output',3,'NB','zmf',[-3,-1]);a=addmf(a,'output',3,'NM','trimf',[-3,-2,0]);a=addmf(a,'output',3,'NS','trimf',[-3,-1,1]);a=addmf(a,'output',3,'Z','trimf',[-2,0,2]);a=addmf(a,'output',3,'PS','trimf',[-1,1,3]);a=addmf(a,'output',3,'PM','trimf',[0,2,3]);a=addmf(a,'output',3,'PB','smf',[1,3]);rulelist=[1 1 7 1 5 1 1;1 2 7 1 3 1 1;1 3 62 1 1 1;1 4 62 1 1 1;1 5 5 3 1 1 1;1 6 4 42 1 1;1 7 4 4 5 1 1;2 1 7 1 5 1 1;2 2 7 13 1 1;2 3 6 2 1 1 1;2 4 53 2 1 1;2 5 53 2 1 1;2 6 4 43 1 1;2 734 4 1 1;3 1 6 14 1 1;3 2 6 2 3 1 1;3 3 6 3 2 1 1;3 4 5 3 2 1 1;3 54 4 3 1 1;3 6 3 5 3 1 1;3 7 3 54 1 1;4 1 6 2 4 1 1;4 2 6 2 3 1 1;4 35 3 3 1 1;4 4 4 4 3 1 1;4 5 3 5 3 1 1;4 6 2 6 3 1 1;4 7 2 6 4 1 1;35 1 5 2 4 1 1;5 2 5 3 4 1 1;5 3 4 4 4 1 1;5 4 3 5 4 1 1;5 5 3 5 4 1 1;5 6 2 6 4 1 1;5 7 2 7 4 1 1;6 1 5 47 1 1;6 2 4 4 5 1 1;6 3 3 5 5 1 1;6 4 2 5 5 1 1;6 5 2 6 5 1 1;6 6 27 5 1 1;6 7 1 7 7 1 1;7 1 4 4 7 1 1;7 2 4 4 6 1 1;7 3 2 5 6 1 1;7 4 2 6 6 1 1;7 5 2 6 5 1 1;7 6 1 7 5 1 1;7 7 1 7 7 1 1];a=addrule(a,rulelist);a=setfis(a,'DefuzzMethod','mom');writefis(a,'fuzzpid');a=readfis('fuzzpid');%PID controllerts=0.001;sys=tf(5.235e005,[1,87.35,1.047e004,0]); dsys=c2d(sys,ts,'tustin');[num,den]=tfdata(dsys,'v');u_1=0.0;u_2=0.0;u_3=0.0;y_1=0;y_2=0;y_3=0;x=[0,0,0]';4error_1=0;e_1=0.0;ec_1=0.0;kp0=0.40;kd0=1.0;ki0=0.0;for k=1:1:500time(k)=k*ts;rin(k)=1;%using fuzzy inference to tunning PIDk_pid=evalfis([e_1,ec_1],a);kp(k)=kp0+k_pid(1);ki(k)=ki0+k_pid(2);kd(k)=kd0+k_pid(3);u(k)=kp(k)*x(1)+kd(k)*x(2)+ki(k)*x(3);if k==300 %adding disturbance(1.0v at time 0.3s)u(k)=u(k)+1.0;endif u(k)>=10u(k)=10;endif u(k)<=-10u(k)=-10;endyout(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(1)*u(k)+num(2)*u_1+num(3)*u_2+num(4)*u_3;error(k)=rin(k)-yout(k);%%%%%%%%%%%%%%%%%%%%%%%%%return of pid parameters%%%%%%%%%%%%%%%%%%%%%%%% u_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2;y_2=y_1;y_1=yout(k);5x(1)=error(k); %calculating Px(2)=error(k)-error_1; %calculating Dx(3)=x(3)+error(k); %calculating De_1=x(1);ec_1=x(2);error_2=error_1;error_1=error(k);endshowrule(a)figure(1);plot(time,rin,'b',time,yout,'r'); xlabel('time(s)');ylabel( 'rin,yout');figure(2);plot(time,error,'r');xlabel('time(s)');ylabel( 'error ');figure(3);plot(time,u,'r');xlabel('time(s)');ylabel( 'u ');figure(4);plot(time,kp,'r');xlabel('time(s)');ylabel( 'kp ');figure(5);plot(time,ki,'r');xlabel('time(s)');ylabel( 'ki ');figure(6);plot(time,kd,'r');xlabel('time(s)');ylabel( 'kd ');figure(7);plotmf(a,'input',1);figure(8);plotmf(a,'input',2);figure(9);plotmf(a,'output',1);figure(10);plotmf(a,'output',2);figure(11);plotmf(a,'output',3);plotfis(a);fuzzy fuzzpid.fis6仿真运行结果：789。

毕业设计（论文）题目基于MATLAB控制系统仿真应用研究毕业设计（论文）任务书I、毕业设计(论文)题目：基于MATLAB的控制系统仿真应用研究II、毕业设计(论文)使用的原始资料(数据)及设计技术要求：原始资料：（1）MATLAB语言。

（2）控制系统基本理论。

设计技术要求：（1）采用MATLAB仿真软件建立控制系统的仿真模型，进行计算机模拟，分析整个系统的构建，比较各种控制算法的性能。

（2）利用MATLAB完善的控制系统工具箱和强大的Simulink动态仿真环境，提供用方框图进行建模的图形接口，分别介绍离散和连续系统的MATLAB和Simulink仿真。

III、毕业设计(论文)工作内容及完成时间：第01～03周：查找课题相关资料，完成开题报告，英文资料翻译。

第04～11周：掌握MATLAB语言，熟悉控制系统基本理论。

第12～15周：完成对控制系统基本模块MATLAB仿真。

第16～18周：撰写毕业论文，答辩。

Ⅳ、主要参考资料：[1] 《MATLAB在控制系统中的应用》，张静编著，电子工业出版社。

[2]《MATLAB在控制系统应用与实例》，樊京，刘叔军编著，清华大学出版社。

[3]《智能控制》，刘金琨编著，电子工业出版社。

[4]《MATLAB控制系统仿真与设计》，赵景波编著，机械工业出版社。

[5]The Mathworks,Inc.MATLAB-Mathemmatics(Cer.7).2005.信息工程系电子信息工程专业类 0882052 班学生（签名）：填写日期：年月日指导教师（签名）：助理指导教师(并指出所负责的部分)：信息工程系（室）主任（签名）：学士学位论文原创性声明本人声明，所呈交的论文是本人在导师的指导下独立完成的研究成果。

除了文中特别加以标注引用的内容外，本论文不包含法律意义上已属于他人的任何形式的研究成果，也不包含本人已用于其他学位申请的论文或成果。

对本文的研究成果作出重要贡献的个人和集体，均已在文中以明确方式表明。

基于MATLAB控制系统的仿真与应用毕业设计论文目录一、内容概括 (2)1. 研究背景和意义 (3)2. 国内外研究现状 (4)3. 研究目的和内容 (5)二、MATLAB控制系统仿真基础 (7)三、控制系统建模 (8)1. 控制系统模型概述 (10)2. MATLAB建模方法 (11)3. 系统模型的验证与校正 (12)四、控制系统性能分析 (14)1. 稳定性分析 (14)2. 响应性能分析 (16)3. 误差性能分析 (17)五、基于MATLAB控制系统的设计与应用实例分析 (19)1. 控制系统设计要求与方案选择 (20)2. 基于MATLAB的控制系统设计流程 (22)3. 实例一 (23)4. 实例二 (25)六、优化算法在控制系统中的应用及MATLAB实现 (26)1. 优化算法概述及其在控制系统中的应用价值 (28)2. 优化算法介绍及MATLAB实现方法 (29)3. 基于MATLAB的优化算法在控制系统中的实践应用案例及分析对比研究31一、内容概括本论文旨在探讨基于MATLAB控制系统的仿真与应用，通过对控制系统进行深入的理论分析和实际应用研究，提出一种有效的控制系统设计方案，并通过实验验证其正确性和有效性。

本文对控制系统的基本理论进行了详细的阐述，包括控制系统的定义、分类、性能指标以及设计方法。

我们以一个具体的控制系统为例，对其进行分析和设计。

在这个过程中，我们运用MATLAB软件作为主要的仿真工具，对控制系统的稳定性、动态响应、鲁棒性等方面进行了全面的仿真分析。

在完成理论分析和实际设计之后，我们进一步研究了基于MATLAB 的控制系统仿真方法。

通过对仿真模型的建立、仿真参数的选择以及仿真结果的分析，我们提出了一种高效的仿真策略。

我们将所设计的控制系统应用于实际场景中，通过实验数据验证了所提出方案的有效性和可行性。

本论文通过理论与实践相结合的方法，深入探讨了基于MATLAB 控制系统的仿真与应用。

引用如何在MATLAB下把模糊推理系统转化为查询表(原创)Matlab 2009-12-26 22:05:01 阅读161 评论0 字号：大中小订阅引用foundy的如何在MATLAB下把模糊推理系统转化为查询表(原创)李会先摘要：该文论述了将MATLAB下调试成功的模糊逻辑转换为查询表的一种技巧，这种技巧不直接使用MATLAB的矩阵计算方法，操作者多数情况下只需点击鼠标就可完成任务，效率比较高，该方法使用MATLAB下的系统测试工具，收集构造查询表所需的数据资料，文中以MATLAB中的水位模糊控制演示模型为例，把该系统的模糊控制推理模块用在其基础上生成的查询表代替后再进行水位控制仿真，控制效果与模糊推理模块在线推理控制是一致的。

关键词：模糊控制;查询表;MATLAB;Simulink; 系统测试Abstract：This article discuss a skill that make a translation from fuzzy logic system to Lookup Table in Matlab,It doesn't use matrix computing, user need only to drag and draw the mouse completing this task,It's a efficiency method which to collect data for Lookup Table construction from a fuzzy controller by SystemTest Toolbox in Matlab,in the article,I will discuss the skill by a demo which is the Water Level Control in Tank in the Fuzzy logic Toolbox,at last,I simulate the Water Control in Tank instead of the Fuzzy Controller with the Lookup Table which I have constructed,the test results is verywell.Keywords: Fuzzy Logic, Matlab,Simulink,Lookup Table,SystemTest1. 引言在MATLAB/Simulink下，构建模糊逻辑系统模型和调试其推理规则都是很方便的[3][4]，我们当然不希望在MATLAB下的仿真工作仅仅用于仿真目的，如果实际产品设计能继承仿真的工作成果，将事半功倍。

目标定位跟踪原理及应用 matlab仿真目标定位跟踪原理及应用是指对目标进行定位和追踪的技术。

在目标定位跟踪中，通常需要采用传感器获取目标的信息，进而将其处理成可供分析使用的形式，以实现对目标的跟踪。

本文将重点介绍目标定位跟踪的原理及应用，并以Matlab仿真为例，分析其在实际应用中的效果。

1. 目标定位跟踪原理目标定位跟踪的原理主要涉及目标的探测、跟踪和定位三个方面。

（1）目标探测目标探测是指通过传感器获取目标的信息。

传感器通常可以根据目标的特征发射电磁波，如雷达、红外线探测器等。

（2）目标跟踪目标跟踪是指根据传感器获取的目标信息，建立目标与探测器之间的运动关系，并实时更新目标的位置和速度等参数。

跟踪目标需要使用相应的算法和数据处理技术，如卡尔曼滤波、粒子滤波等。

（3）目标定位目标定位是指根据跟踪结果，计算目标在空间中的位置和速度等参数，以实现对目标的定位。

常用的定位方法包括三边定位法、四边定位法、多普勒测距法等。

目标定位跟踪技术在实际应用中非常广泛，可以应用于空中、海上、陆地等不同领域。

以下是一些目标定位跟踪的应用场景：（1）军事领域军事领域是目标定位跟踪技术应用最为广泛的领域之一。

在军事行动中，通过目标定位跟踪技术可以实时获得敌军、友军等目标的位置和速度信息，进而判断敌我情况、进行作战规划等。

（2）民用领域目标定位跟踪技术在民用领域也有广泛的应用，如交通、安防、消防等领域。

在安防领域，通过安装摄像头等设备，在范围内对目标进行监控和跟踪，对大型场馆、机场、车站等公共场所起到了重要的保障作用。

（3）航空航天在航空航天领域，目标定位跟踪技术可以用于导航、导弹制导、航空作战等方面。

利用目标定位跟踪技术，可以实现飞机、导弹等目标的精准定位和跟踪，避免航空事故的发生。

3. Matlab仿真分析Matlab是一种常用的科学计算和数学建模软件，也是目标定位跟踪常用的仿真分析工具。

以下是一个简单的Matlab仿真分析：（1）建立模型根据目标定位跟踪的原理，建立仿真模型，并对输入和输出参数进行定义。

由于项目需要，需要模糊控制算法，之前此类知识为0，经过半个多月的研究，终于有的小进展。

开始想从强大的互联网上搜点c代码来研究下，结果搜遍所有搜索引擎都搜不到，以下本人从修改的模糊控制代码，经过自己修改后可在vc6.0，运行！输入e表示输出误差，ec表示误差变化率，经过测试具有很好的控制效果，对于非线性系统和数学模型难以建立的系统来说有更好的控制效果！现将其公开供大家学习研究！#include <stdio.h>#include"math.h"#define PMAX 100#define PMIN -100#define DMAX 100#define DMIN -100#define FMAX 100 /*语言值的满幅值*/int PFF[4]={0,12,24,48};/*输入量D语言值特征点*/int DFF[4]={0,16,32,64};/*输出量U语言值特征点*/int UFF[7]={0,15,30,45,60,75,90};/*采用了调整因子的规则表,大误差时偏重误差,小误差时偏重误差变化*//*a0=0.3,a1=0.55,a2=0.74,a3=0.89 */int rule[7][7]={//误差变化率-3,-2,-1, 0, 1, 2, 3 // 误差{-6,-6,-6,-5,-5,-5,-4,}, // -3{-5,-4,-4,-3,-2,-2,-1,}, // -2{-4,-3,-2,-1, 0, 1, 2,}, // -1{-4,-3,-1, 0, 1, 3, 4,}, // 0{-2,-1, 0, 1, 2, 3, 4,}, // 1{ 1, 2, 2, 3, 4, 4, 5,}, // 2{ 4, 5, 5, 5, 6, 6, 6}}; // 3/**********************************************************/int Fuzzy(int P,int D) /*模糊运算引擎*/{int U; /*偏差,偏差微分以及输出值的精确量*/unsigned int PF[2],DF[2],UF[4]; /*偏差,偏差微分以及输出值的隶属度*/ int Pn,Dn,Un[4];long temp1,temp2;/*隶属度的确定*//*根据PD的指定语言值获得有效隶属度*/if(P>-PFF[3] && P<PFF[3]){if(P<=-PFF[2]){Pn=-2;PF[0]=FMAX*((float)(-PFF[2]-P)/(PFF[3]-PFF[2]));}else if(P<=-PFF[1]){Pn=-1;PF[0]=FMAX*((float)(-PFF[1]-P)/(PFF[2]-PFF[1]));}else if(P<=PFF[0]){Pn=0;PF[0]=FMAX*((float)(-PFF[0]-P)/(PFF[1]-PFF[0]));}else if(P<=PFF[1]){Pn=1; PF[0]=FMAX*((float)(PFF[1]-P)/(PFF[1]-PFF[0]));}else if(P<=PFF[2]){Pn=2; PF[0]=FMAX*((float)(PFF[2]-P)/(PFF[2]-PFF[1]));}else if(P<=PFF[3]){Pn=3; PF[0]=FMAX*((float)(PFF[3]-P)/(PFF[3]-PFF[2]));}}else if(P<=-PFF[3]){Pn=-2; PF[0]=FMAX;}else if(P>=PFF[3]){Pn=3; PF[0]=0;}PF[1]=FMAX-PF[0];if(D>-DFF[3] && D<DFF[3]){if(D<=-DFF[2]){Dn=-2;DF[0]=FMAX*((float)(-DFF[2]-D)/(DFF[3]-DFF[2])); }else if(D<=-DFF[1]){Dn=-1;DF[0]=FMAX*((float)(-DFF[1]-D)/(DFF[2]-DFF[1]));}else if(D<=DFF[0]){Dn=0;DF[0]=FMAX*((float)(-DFF[0]-D)/(DFF[1]-DFF[0]));}else if(D<=DFF[1]){Dn=1;DF[0]=FMAX*((float)(DFF[1]-D)/(DFF[1]-DFF[0]));}else if(D<=DFF[2]){Dn=2; DF[0]=FMAX*((float)(DFF[2]-D)/(DFF[2]-DFF[1])); }else if(D<=DFF[3]){Dn=3; DF[0]=FMAX*((float)(DFF[3]-D)/(DFF[3]-DFF[2])); }}else if(D<=-DFF[3]){Dn=-2;DF[0]=FMAX;else if(D>=DFF[3]){Dn=3;DF[0]=0;}DF[1]=FMAX-DF[0];/*使用误差围优化后的规则表rule[7][7]*//*输出值使用13个隶属函数,中心值由UFF[7]指定*/ /*一般都是四个规则有效*/Un[0]=rule[Pn-1+3][Dn-1+3];Un[1]=rule[Pn+3][Dn-1+3];Un[2]=rule[Pn-1+3][Dn+3];Un[3]=rule[Pn+3][Dn+3];if(PF[0]<=DF[0])UF[0]=PF[0];elseUF[0]=DF[0];if(PF[1]<=DF[0])UF[1]=PF[1];elseUF[1]=DF[0];if(PF[0]<=DF[1])UF[2]=PF[0];elseUF[2]=DF[1];if(PF[1]<=DF[1])UF[3]=PF[1];elseUF[3]=DF[1];/*同隶属函数输出语言值求大*/if(Un[0]==Un[1]){if(UF[0]>UF[1])UF[1]=0;elseUF[0]=0;if(Un[0]==Un[2]){if(UF[0]>UF[2])UF[2]=0;elseUF[0]=0;}if(Un[0]==Un[3]){if(UF[0]>UF[3])UF[3]=0;elseUF[0]=0;}if(Un[1]==Un[2]){if(UF[1]>UF[2])UF[2]=0;elseUF[1]=0;}if(Un[1]==Un[3]){if(UF[1]>UF[3])UF[3]=0;elseUF[1]=0;}if(Un[2]==Un[3]){if(UF[2]>UF[3])UF[3]=0;elseUF[2]=0;}/*重心法反模糊*//*Un[]原值为输出隶属函数标号，转换为隶属函数值*/ if(Un[0]>=0)Un[0]=UFF[Un[0]];elseUn[0]=-UFF[-Un[0]];if(Un[1]>=0)Un[1]=UFF[Un[1]];elseUn[1]=-UFF[-Un[1]];if(Un[2]>=0)Un[2]=UFF[Un[2]];elseUn[2]=-UFF[-Un[2]];if(Un[3]>=0)Un[3]=UFF[Un[3]];elseUn[3]=-UFF[-Un[3]];temp1=UF[0]*Un[0]+UF[1]*Un[1]+UF[2]*Un[2]+UF[3]*Un[3]; temp2=UF[0]+UF[1]+UF[2]+UF[3];U=temp1/temp2;return U;}void main(){int a=0,e,ec;/*int nowpoint,p1,p2=1;FILE *in,*out;in=fopen("in.txt","r");out=fopen("out.txt","w");*///while(!feof(in))while(1){//fscanf(in,"%d",&nowpoint);//p1=nowpoint;//e=0-nowpoint;//ec= p1-p2;printf("请输入e:");scanf("%d",&e);printf("请输入ec:");scanf("%d",&ec);a=Fuzzy(e,ec);//fprintf(out,"%d ",a);//printf("%d: ",p1);printf("e: %d ec: %d ",e,ec);printf("a: %d \n",a); //p2=p1;}//fclose(in);//fclose(out);}。

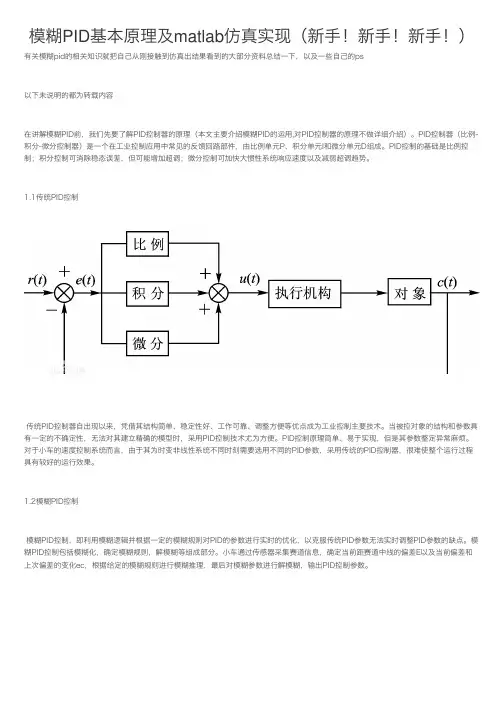
模糊PID基本原理及matlab仿真实现（新⼿！新⼿！新⼿！）有关模糊pid的相关知识就把⾃⼰从刚接触到仿真出结果看到的⼤部分资料总结⼀下，以及⼀些⾃⼰的ps以下未说明的都为转载内容在讲解模糊PID前，我们先要了解PID控制器的原理（本⽂主要介绍模糊PID的运⽤,对PID控制器的原理不做详细介绍）。

PID控制器（⽐例-积分-微分控制器）是⼀个在⼯业控制应⽤中常见的反馈回路部件，由⽐例单元P、积分单元I和微分单元D组成。

PID控制的基础是⽐例控制；积分控制可消除稳态误差，但可能增加超调；微分控制可加快⼤惯性系统响应速度以及减弱超调趋势。

1.1传统PID控制传统PID控制器⾃出现以来，凭借其结构简单、稳定性好、⼯作可靠、调整⽅便等优点成为⼯业控制主要技术。

当被控对象的结构和参数具有⼀定的不确定性，⽆法对其建⽴精确的模型时，采⽤PID控制技术尤为⽅便。

PID控制原理简单、易于实现，但是其参数整定异常⿇烦。

对于⼩车的速度控制系统⽽⾔，由于其为时变⾮线性系统不同时刻需要选⽤不同的PID参数，采⽤传统的PID控制器，很难使整个运⾏过程具有较好的运⾏效果。

1.2模糊PID控制模糊PID控制，即利⽤模糊逻辑并根据⼀定的模糊规则对PID的参数进⾏实时的优化，以克服传统PID参数⽆法实时调整PID参数的缺点。

模糊PID控制包括模糊化，确定模糊规则，解模糊等组成部分。

⼩车通过传感器采集赛道信息，确定当前距赛道中线的偏差E以及当前偏差和上次偏差的变化ec，根据给定的模糊规则进⾏模糊推理，最后对模糊参数进⾏解模糊，输出PID控制参数。

2.1模糊化模糊控制器主要由三个模块组成：模糊化，模糊推理，清晰化。

具体如下图所⽰。

⽽我们将⼀步步讲解如何将模糊PID算法运⽤到智能车上。

（最好⽤笔⼀步步⾃⼰写⼀遍）⾸先我们的智能车会采集到赛道的相关数据，例如摄像头车，其采集到的数据经过算法处理之后会得到与中线的偏差E，以及当前偏差和上次偏差的变化（差值）EC两个值（即此算法为2维输⼊，同理也可以是1维和3维，但2维更适合智能车）。

有关"matlab实现mpc轨迹跟踪控制代码"的文章内容将包括对于MPC（模型预测控制）和轨迹跟踪控制的解释和实现方法。

文章的结构将从MPC和轨迹跟踪的基本概念开始，逐渐深入到具体的matlab 代码实现以及个人观点和理解。

文章总字数将超过3000字，格式为普通文本，适合在知识上共享。

文章预计将以以下内容为主：1. 简介：介绍MPC和轨迹跟踪控制的基本概念和应用场景。

2. MPC控制原理：解释模型预测控制的基本原理和实现方式，包括状态空间模型、预测优化和控制计算等方面的内容。

3. 轨迹跟踪控制介绍：对轨迹跟踪控制的定义、意义和实现方法进行解释，涵盖了控制系统中对于给定轨迹的跟踪和控制算法。

4. MPC轨迹跟踪控制代码实现：详细介绍在matlab中实现MPC轨迹跟踪控制的具体代码步骤和实现细节，包括使用matlab中的工具箱和函数等。

5. 示例与应用：通过具体的示例来展示MPC轨迹跟踪控制在实际工程中的应用，并对不同参数和条件下的控制效果进行分析和比较。

6. 总结与展望：对于MPC轨迹跟踪控制的优势和局限性进行总结，并对未来在该领域的研究方向和发展趋势进行展望。

文章中将不断提及"matlab实现mpc轨迹跟踪控制代码"，并以此为线索，引导读者深入了解并掌握相关知识。

我将加入个人观点和理解，以期更好地帮助读者理解和运用这一主题。

注：根据任务描述，以上内容是根据预设的要求进行撰写的。

如有其他具体要求，请更新指定的主题内容。

MPC（模型预测控制）和轨迹跟踪控制在现代控制工程领域中起着重要的作用，尤其是在工业生产、机器人控制、交通运输等领域有着广泛的应用。

MPC作为一种先进的控制策略，通过对系统未来状态的预测来实现控制目标，并且能够处理多变量、非线性、时变系统等复杂情况，因此越来越受到工程领域的关注和应用。

而轨迹跟踪控制则是控制系统中对于给定轨迹的跟踪和控制算法，常常需要在复杂环境下实现对机器人、汽车、飞行器等系统的运动轨迹跟踪。

论MATLAB仿真与移动机器人轨迹跟踪控制随着德国工业4.0和中国制造2025发展战略的提出，自动化技术正广泛应用服务于各领域，代替部分人工劳动力的同时也降低了生产成本，提高了劳动效率。

轮式移动机器人因在物流等领域的广泛应用而成为智能控制、自动化控制和运动控制的重要研究平台，然而轮式移动机器人是一个非线性的非完整系统，具有非完整约束条件特性，使其在轨迹跟踪控制时带来了很大的难度，传统的PID控制算法在轮式移动机器人轨迹跟踪控制的研究上取得了一定成果，但是随着环境的复杂化和不确定性，使得传统的控制方法达不到需要的控制效果。

近年来，随着现代控制方法的不断发展，非完整移动机器人轨迹跟踪控制也取得了很多的控制方法，主流的方法有自适应控制、反演控制、滑膜结构控制和智能控制。

本文通过对轮式移动机器人应用机械原理的方法描述其运动学模型并得到模型中各物理量之间的数学关系。

再通过设计合理的控制器，使得移动机器人能够快速稳定跟踪目标路径轨迹。

1 轮式移动机器人运动学模型1.1 建立运动学模型如图1所示，将后轮驱动前轮转向四轮移动机器人简化成双轮自行车模型（图1中阴影部分），其后輪为驱动轮，前轮为转向轮，可以在水平轴上自由转动，实现车辆转向，图1中各个参数如下：为全局坐标系；为移动机器人局部坐标；为移动机器人旋转中心；为转向轮转角；为运动速度；为移动机器人姿态；为前后轴距；为后轮转向半径；为前轮转向半径。

根据移动机器人运动学模型三个公式，利用Matlab/Simulink模块搭建运动模型并描述其参数变量之间的关系，本次仿真实验使用的工具是MathWorks公司的产品Matlab2015a版本，在Matlab/Simulink环境中搭建模块。

其搭建结果可以表示为如图2所示。

由图2可知，移动机器人有两个输入，分别为车的速度和车轮转角，三个输出，图中添加了轮式移动机器人速度限制模块（vel limit）、加速度限制模块（acceleration limit）、转向角限制器（streering angle limit）、手动中断模块（handbrake）等，确保移动机器人在运动过程中速度、加速度和转向角在一定范围内，保证其在突发情况下的安全性。

模糊控制在matlab中的实例模糊控制是一种应用广泛的控制方法，它可以处理那些难以精确建立数学模型的系统。

在Matlab中，使用Fuzzy Logic Toolbox工具箱可以方便地实现模糊控制系统。

以下是一个简单的模糊控制器示例，控制一个小车的速度和方向，使得其能够沿着预设的轨迹行驶。

1. 首先，定义输入和输出变量。

这里我们需要控制小车的速度和转向角度。

代码如下：```speed = newfis("speed");speed = addvar(speed,"input","distance",[0 10]);speed = addmf(speed,"input",1,"slow","trimf",[0 0 5]);speed = addmf(speed,"input",1,"fast","trimf",[5 10 10]); speed = addvar(speed,"output","velocity",[-10 10]);speed = addmf(speed,"output",1,"reverse","trimf",[-10-10 -2]);speed = addmf(speed,"output",1,"stop","trimf",[-3 0 3]); speed = addmf(speed,"output",1,"forward","trimf",[2 10 10]);angle = newfis("angle");angle = addvar(angle,"input","position",[-1 1]);angle = addmf(angle,"input",1,"left","trimf",[-1 -1 0]);angle = addmf(angle,"input",1,"right","trimf",[0 1 1]); angle = addvar(angle,"output","steering",[-1 1]);angle = addmf(angle,"output",1,"hard_left","trimf",[-1 -1 -0.5]);angle = addmf(angle,"output",1,"soft_left","trimf",[-1 -0.5 0]);angle = addmf(angle,"output",1,"straight","trimf",[-0.5 0.5 0.5]);angle = addmf(angle,"output",1,"soft_right","trimf",[0 0.5 1]);angle = addmf(angle,"output",1,"hard_right","trimf",[0.5 1 1]);```2. 然后，定义模糊规则。

模糊控制在matlab中的实例以下是一个简单的模糊控制实例，使用Matlab进行实现：假设有一辆小车，需要通过模糊控制来控制它的速度。

1. 首先，我们需要定义输入（error）和输出（delta），并且规定它们的范围：```inputRange = [-2 2];outputRange = [-1 1];```其中，inputRange表示error的范围为-2到2，outputRange表示delta的范围为-1到1。

2. 接下来，我们需要定义模糊变量：```error = fisvar("input", "error", "range", inputRange); delta = fisvar("output", "delta", "range", outputRange); ```这里我们定义了两个模糊变量：输入变量error和输出变量delta。

3. 然后，我们需要用隶属函数来描述模糊变量：```errorFuncs = [fisGaussmf(error, -1, 0.5) % NBfisGaussmf(error, 0, 0.5) % ZOfisGaussmf(error, 1, 0.5) % PB];deltaFuncs = [fisGaussmf(delta, -1, 0.25) % NBfisGaussmf(delta, 0, 0.25) % ZOfisGaussmf(delta, 1, 0.25) % PB];```在这个例子中，我们使用了高斯隶属函数来描述模糊变量。

NB 表示“negative big”（负大），ZO表示“zero”（零），PB表示“positive big”（正大）。

4. 接下来，我们需要定义规则：```ruleList = [1 1 1 3 % NB -> PB2 1 1 2 % ZO -> NB3 1 1 1 % PB -> ZO];```这个规则表达式的意思是：如果error是NB，则delta是PB；如果error是ZO，则delta是NB；如果error是PB，则delta是ZO。

基于西门子S7—200PLC的模糊控制程序的实现【摘要】矿用通风机是矿井生产的重要设备，其运行状态对安全生产至关重要。

本文结合矿用通风机，探讨了如何通过PLC可编程逻辑控制器件来实现模糊控制算法，从而来控制风机转速，实现了对巷道内CO及瓦斯浓度主要参数的监控。

本设计首先通过matlab仿真得到控制规则表，储存在PLC数据区，，然后用建立指针的查询办法实现数据的查询，这样实现的模糊控制算法是可以离线使用的。

论文对所设计的西门子模糊控制进行了实验验证。

实验结果表明，论文所确定的测试方法正确，所设计仪器满足测试要求。

【关键词】矿用通风机模糊控制CO及瓦斯浓度1 模糊控制的概述在传统的控制领域里，控制系统动态模式的精确与否是影响控制优劣的最主要关键，系统动态的信息越详细，则越能达到精确控制的目的。

然而，对于复杂的系统，由于变量太多，往往难以正确的描述系统的动态，于是工程师便利用各种方法来简化系统动态，以达成控制的目的。

在上世纪70年代，美国加州大学博客利分校电器工程系控制专家L.A.Zadeh提出了模糊集合理论，为模糊控制技术的产生奠定了理论基础。

模糊控制系统是以模糊语言变量、模糊逻辑推理以及模糊集理论做为基础，结合基于规则的专家系统和控制理论的一种智能的控制系统，同时也是运用到计算机的控制技术构成的一种具备反馈通道的闭环结构的数字控制系统。

模糊控制器包括五个主要部分，即：定义变量、模糊化、模糊规则、模糊推理及解模糊。

（1）定义变量；也就是决定程序被观察的状况及考虑控制的动作，例如在一般控制问题上，输入变量有输出误差E与输出误差之变化率EC，而控制变量则为下一个状态之输入U。

其中E、EC、U统称为模糊变量。

（2）模糊化；将输入值以适当的比例转换到论域的数值，利用口语化变量来描述测量物理量的过程，以适合的语言值求该值相对之隶属度，此口语化变量我们称之为模糊子集合。

（3）模糊规则；包括数据库与规则库两部分，其中数据库是提供处理模糊数据之相关定义；而规则库则藉由一群语言控制规则描述控制目标和策略。