关联矩阵 回路矩阵 割集矩阵

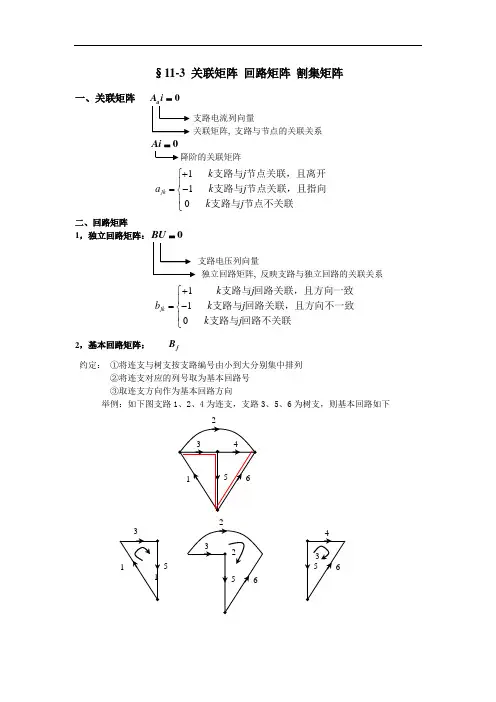
§11-3 关联矩阵 回路矩阵 割集矩阵一、关联矩阵 0Ai =支路电流列向量关联矩阵, 支路与节点的关联关系降阶的关联矩阵11jk k j a k j k j +⎧⎪=-⎨⎪⎩支路与节点关联，且离开支路与节点关联，且指向支路与节点不关联 二、回路矩阵1，独立回路矩阵： 支路电压列向量独立回路矩阵, 反映支路与独立回路的关联关系11jk k j b k j k j +⎧⎪=-⎨⎪⎩支路与回路关联，且方向一致支路与回路关联，且方向不一致支路与回路不关联 2，基本回路矩阵： f B 约定： ①将连支与树支按支路编号由小到大分别集中排列②将连支对应的列号取为基本回路号③取连支方向作为基本回路方向举例：如下图支路1、2、4为连支，支路3、5、6为树支，则基本回路如下5 31243561001100101111001011f t t B B ⎡⎤⎢⎥=---=⎡⎤⎣⎦⎢⎥⎢⎥--⎣⎦标准形式 三、割集矩阵1，独立割集矩阵1123213463156:0: 0:0Q i i i Q i i i i Q i i i -++=-++=-+=1234561110001011010100011i i i i i i ⎡⎤⎢⎥⎢⎥-⎡⎤⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦0Qi =支路电流列向量独立割集矩阵,反映支路与独立割集的关联关系1,1,0kj k j q k j k j +⎧⎪=-⎨⎪⎩支路与割集关联且方向一致支路与割集关联且方向不一致支路与割集不关联2，基本割集矩阵 f Q约定： ①将树支与连支按支路编号由小到大分别集中排列②将树支对应的列号称为基本割集号③取树支方向作为基本割集方向Q举例：如下图支路1、2、4为连支，支路3、5、6为树支，则基本割集如下，基本割集矩阵为3 5 6 1 2 41001100101111001011f tt Q Q -⎡⎤⎢⎥=-=⎡⎤⎣⎦⎢⎥⎢⎥⎣⎦标准形式 比较该例割集矩阵与前例的基本回路矩阵，可以看出对于同一个有向图，选取同一棵树，当连支分块和树支反映中，各支路左右顺序不变时，则有：T l t Q B =-事实上，该关系式可以得到证明，详见书中§11-4 。

关联矩阵、回路矩阵和割集矩阵的关系对于同一个电路，若各支路，节点的编号及方向均相同时，其列写出的关联矩阵，回路矩阵和割集矩阵之间存在着一定的联系。

对于图7-5-1所示的有向图，选支路1、2、3为树支，作单树支割集如图所示，则可写出其基本回路矩阵与基本割集矩阵如下：图 7-5-1用左乘，可得：即有：（7-5-1）由矩阵性质可得另一形式为：（7-5-2）此二式反映了相同编号的网络中，基本割集矩阵与基本回路矩阵之间的关系。

对于式7-5-1的一般证明可简略描述如下：令，则D中任一元素为，下标j表示第j条单连支回路，k表示第k个割集，而则表示把第j回路中i支路元素与第k割集中i支路元素相乘。

显然，若i支路不是同时包含在j回路与k割集中，则其乘积必为零。

而同时包含在j回路与k割集中的支路条数必为偶数。

因为若移去k割集的所有支路，则电路分为独立的两部分。

若闭合回路跨越两部分电路，显然其连接两部分的支路条数（包含在k割集中）必为偶数条。

例如对于图7-5-1所示的网络，同时包含在割集1与回路1（由支路4组成的单连支回路）中的支路为4与1。

对于成对出现在回路和割集中的支路，如果二条支路方向与回路一致，（此时对应行中二个元素同号），则该二条支路与割集方向必一正一反（此时对应行中二个元素异号），则的值必为零。

反之，若二条支路方向与回路方向一正一反，则相对于割集方向必同号，其乘积亦为零。

可见矩阵D中元素均为零，从而可推出式（7-5-1）。

若网络支路编号严格按先树支后连支编排，则式（7-5-1）可写为：即有：（7-5-3）式中，表示由树支组成的回路矩阵子矩阵；表示由连支组成的割集矩阵子矩阵。

对于图7-5-1的电路，若设节点4为参考节点，写出它的关联矩阵为：用A左乘，得：即有：（7-5-4）或（7-5-5）实际上若选择割集只包围一个节点，且割集方向离开节点，则这样组成的割集即为关联矩阵A，即是说关联矩阵无非是割集矩阵的一种形式。

矩阵论在电路分析中的应用摘要: 随着科学技术的迅速发展，古典的线性代数知识已不能满足现代科技的需要，矩阵理论与方法已成为现代科技领域必不可少的工具。

诸如数值分析、优化理论、微分方程、概率统计、控制论、力学、电子学、网络等学科领域都与矩阵理论有着密切的联系，甚至在经济管理、金融、保险、社会科学等领域，矩阵理论与方法也有着十分重要的应用。

当今电子计算机及计算技术的迅速发展为矩阵理论的应用开辟了更广阔的前景。

本文以电路分析为例，讲解矩阵论的重要作用。

关键词: 矩阵论；电路分析Application of matrix theory in circuit analysisAbstract: With the rapid development of science and technology, classical linear algebra knowledge can no longer meet the needs of modern science and technology. Matrix theory and methods have become essential tools in modern science and technology. Disciplinary fields such as numerical analysis, optimization theory, differential equations, probability statistics, cybernetics, mechanics, electronics, and networks are all closely related to matrix theory. Even in thefields of economic management, finance, insurance, social sciences, matrix theory also has very important applications. The rapid development of today's electronic computers and computing technologies has opened up a wider prospect for the application of matrix theory. This article uses circuit analysis as an example to explain the important role of matrix theory.Key words: Matrix theory; circuit analysis在电路分析中，对于一个有n个节点，b条支路的电路图，每条支路的电压和电流均为未知，共有2b个未知量。

第15章电路方程的矩阵形式●本章重点1、了解图有关的概念；2、掌握与图的描述有关的三个矩阵；3、基本回路与基本割集的选择；4、状态方程的列写方法。

●本章难点1、复杂电路建立状态方程。

●教学方法本章主要讲述了图论中的基本概念、三个重要矩阵（关联矩阵、回路矩阵和割集矩阵）及由此导出的KCL、KVL矩阵方程，最后，讲述了列写电路的状态方程的两种方法，即直观法和系统法。

对重点内容，课堂上不仅要把概念讲解透彻，并通过讲例题加以分析，课下布置一定的作业，使学生加深对内容的理解并牢固掌握。

本章讲授共用4课时。

对回路电流方程、节点电压方程、割集电压方程和列表方程等内容以自学为主。

●授课内容15.1割集一、图的概念1，图(线图)：线段（支路）与点（节点）的集合。

2，有向图：标出支路电压，电流参考方向的图。

3，连通图：任意两个节点间至少存在一条由支路构成的路径。

4，子图：若图G1中所有支路和节点都属于图G，就把G1称为G的子图。

二、树、基本回路、割集(a) (b) (c)(d) (e) (f)1、树1）定义：在连通图G中，把所有的节点连通起来，但不包含任一闭合路径的部分线图称为一棵树。

①含所有节点，②不具有回路，③连通的，④为G的子图。

电路的图G如图(a)所示，图(b)为图G的一棵树，图(c)不是图G的树（未含所有节点）；图(d)不是图G的树（出现了回路）；图(e)不是图G的树（不是连通图）；图(f)不是图G的树（不是图G的子图）。

2）树支：属于一棵树的支路称为该树的数支。

树支数＝n－1＝独立节点数3）连支：不属于一棵树的支路称为该树的连支。

连支数＝b-(n-1)=独立回路数。

连支的集合称为余树、补树2、基本回路：在图G中选取一棵树后，由一条连支及相应的树支所构成的回路称为该树的基本回路(单连支回路)。

1）基本回路数=连支数。

2）基本回路的KVL方程相互独立。

3）不同的树对应于不同的基本回路。

3、割集：图G中所有被切割支路的集合同时满足下列两个条件时称为割集。

第十五章电路方程的矩阵形式重点：1.关联矩阵；2. 结点电压方程的矩阵形式；3. 状态方程。

难点：电路状态方程列写的直观法和系统法。

§ 15.1 图的矩阵表示1. 有向图的关联矩阵2.电路的图是电路拓扑结构的抽象描述。

若图中每一支路都赋予一个参考方向，它成为有向图。

有向图的拓扑性质可以用关联矩阵、回路矩阵和割集矩阵描述 3. 关联矩阵是用结点与支路的关系描述有向图的拓扑性质。

4. 回路矩阵是用回路与支路的关系描述有向图的拓扑性质。

5. 割集矩阵是用割集与支路的关系描述有向图的拓扑性质。

6. 本节仅介绍关联矩阵以及用它表示的基尔霍夫定律的矩阵形式。

7.一条支路连接某两个结点，则称该支路与这两个结点相关联。

支路与结点的关联性质可以用关联矩阵描述。

设有向图的结点数为 n ,支路数为b ,且所有结点与支路均加以编号。

于是，该有向图的关联矩阵为一个 」阶的矩阵，用 表示。

它的每一行对应一个结点，每一列对应一条支路，它的任一元素 定义如下：8.，表示支路 k 与结点j 关联并且它的方向背离结点9.-1 一，表示支路k 与结点j 关联并且它指向结点； 10.n:A，表示支路k 与结点j 无关联。

对于图 15.1 所示的有向图，它的关联矩阵是1 23 45 61'-I -1 0 1 0 0A=2 0 0 1 -1-1 D 3 41 0 0 0+1 +4 0 +1 -1 0图 15.1J-的每一列元素之和为零。

关联矩阵丄的特点:①每一列只有两个非零元素，一个是+1，—个是-1，如果把 的任一行划去，剩下的矩阵用 亠』表示，并称为降阶关联矩阵（今后主要用这种降阶关联矩阵， 所以往往略去“降阶”二字） ，被划去的行对应的结点可以当作参 考结点。

例如，若以结点4为参考结点，把上式中'3-的第4行划去，得 A0 0-1 0+1 -+1的第3行划去，得 A0 01-1 0 0 -1或一个-1 ，每一个这样的列必对应于与参考结从而画岀有向图。