当前位置：文档之家 › 微积分基本定理PPT优秀课件

微积分基本定理PPT优秀课件

  • 格式：ppt
  • 大小：339.00 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

微积分基本公式PPT课件

微积分基本公式PPT课件
xa a
x
( x a) f ( x) f (t)dt
证 F ( x)
a
(x a)2
x
只要证明 ( x a) f ( x) f (t)dt 0 即可. a
令 g( x) ( x a) f ( x)
x
f (t)dt ,
a
则 g( x) f ( x) ( x a) f ( x) f ( x)
原函数.
该定理告诉我们, 连续函数一定有原函数.
6
变限积分函数的求导：
d x f (t)dt f ( x) ，
dx a
d
b
f (t)dt
d
x f (t)dt f ( x) ，
dx x
dx b
设(x) 在[a, b]上可导,则
d
(x)
f (t)dt f [( x)]( x) .
dx a
证 设 Φ( x) x f (t)dt ，则 (x) f (t)dt Φ[( x)]，
a
a
所以
d
(x)
f (t)dt Φ[ ( x)] ( x) f [( x)]( x) .
dx a
7
更一般地，设 ( x) ， ( x) 在[a, b] 上可导,则
d (x)
f (t)dt
dx ( x)
§6.3 微积分基本定理
用定义求定积分实际上是行不通 的,下面介绍计算定积分的方法
原函数存在定理 牛顿-莱布尼茨公式
1
原函数存在定理
定理6.3 设函数f ( x)在[a, b]上连续, 则变上限积分
x
Φ( x) a f (t)dt
在[a, b]上可导, 且
Φ( x) d
x

《微积分的基本定理》课件

《微积分的基本定理》课件

物理
在物理学科中，该定理可以用来 解决各种物理量如质量、速度、 力等的积分问题，例如计算物体 的动量、动能等。
工程
在工程领域，该定理可以用来解 决各种实际问题的积分计算，例 如计算电路中的电流、求解流体 动力学中的压力分布等。
02 定理的证明
定理证明的思路
明确问题
首先，我们需要明确微积分的基本定理是关于什 么的，以及它要解决的问题是什么。
难点2
如何利用积分运算法则简化每个小部分的积 分。
关键点1
理解定积分的定义和性质，以及它们在证明 定理中的作用。
关键点2
掌握导数的定义和性质，以及它们在推导原 函数值增量中的应用。
03 定理的推论和扩 展
推论一：积分中值定理
总结词
积分中值定理是微积分中的一个重要定理，它表明在闭区间上连续的函数一定存在至少一个点，使得该函数在此 点的值为该区间上函数积分的平均值。
详细描述
积分中值定理是微积分中的一个基本定理，它表明如果一个函数在闭区间上连续，那么在这个区间内一定存在至 少一个点，使得该函数在这一点处的值等于该函数在整个区间上的平均值。这个定理在解决一些微积分问题时非 常有用，因为它可以帮助我们找到函数在某个点处的值，而不需要计算整个区间的积分。
推论二：洛必达法则
个定积分的值就是曲边梯形的面积。
应用实例二：求解不定积分
总结词
微积分的基本定理是求解不定积分的关 键工具。
VS
详细描述
不定积分是微分学的逆运算，其求解过程 需要用到微积分的基本定理。根据基本定 理，不定积分∫f(x)dx = F(x) + C，其中 F(x)是f(x)的一个原函数，C是常数。通过 基本定理，我们可以找到一个函数F(x)， 使得F'(x) = f(x)。这样，我们就可以求解 不定积分了。

高等数学《微积分基本定理》课件

高等数学《微积分基本定理》课件
5.3 微积分基本定理
5.3.1 积分上限函数及其导数 5.3.2 微积分的基本定理
5.3.1 积分上限函数及其导数
1、 问题的提出
在变速直线运动中,) v(t)
物体在时间间隔
内经过的路程为 T2v(t)dt T1
另一方面这段路程可表示为 s(T2 ) s(T1 )
又由
～
b0
,得 c1 2
故a 1
例4.
证明
只要证
在
内为单调递增函数 .
F ( x) 0
证:
x
x
f (x)0
f (t)dt
x
f (x)0 t
f (t)dt
x 0
f
(t )d t
2
x
f
(
x
)
(
0
x
t
)
f (t)dt
x
0
f
(t )d t
2
0
例 5 设 f ( x)在[0,1]上连续，且 f ( x) 1.证明
b a
f
( x)dx
F
(
x
)
b a
F (b)
F (a)
★ 微积分基本定理
牛顿——莱布尼兹公式
b
a f ( x)dx
f ( )(b a) F ( )(b a) F(b) F(a)
积分中值定理
微分中值定理
通常把这一公式又叫微积分基本定理
例1 求
2 (2cos x sin x 1)dx.
所以f ( x)在[a, b]上连续
定理 2 如果 f ( x)在[a, b]上连续，则积分上限的函
数( x)
x
a
f

微积分的基本定理PPT课件

微积分的基本定理PPT课件

所以F( x) 0即原方程在[0,1]上只有一个解.
第11页/共30页
定理2（原函数存在定理）
如果 f ( x)在[a,b]上连续，则积分上限的函
数( x)
x
a
f
(t )dt 就是
f
( x) 在[a,b] 上的一个
原函数.
定理的重要意义：
（1）肯定了连续函数的原函数是存在的. （2）初步揭示了积分学中的定积分与原函数之间的联系.
第12页/共30页
三、牛顿—莱布尼茨公式
定理 3（微积分基本公式）
如果F ( x) 是连续函数 f ( x) 在区间[a,b] 上
的一个原函数，则ab f ( x)dx F (b) F (a).
证 已知F( x)是 f ( x)的一个原函数，
又
( x)
x
a
f (t )dt 也是 f ( x) 的一个原函数,
三、 1、2 5 ； 2、 ； 3、 1 ； 4、4.
8
3
4
第28页/共30页
四、1、0；
2、1 . 10
六、 5 , 0. 33
0 , x 0
七、( x)
1 2
(1
cos
x)
,
0
x
.
1 , x
第29页/共30页
感谢您的欣赏
第30页/共30页
原式
1
2xdx
2
5dx 6.
0
1
o 12x
第16页/共30页
例6 求 2 max{x, x2 }dx. 2
y
解
由图形可知
y x2
f ( x) max{x, x2 }
y x

( 人教A版)微积分基本定理课件 (共38张PPT)

( 人教A版)微积分基本定理课件 (共38张PPT)

2
2
答案：D
3．设 f(x)＝x22－，x0，≤1x<≤x≤1，2，
则2f(x)dx 等于________． 0
解析：2f(x)dx＝1x2dx＋2(2－x)dx
0
0
1
＝x3310 ＋(2x－x22)21
＝13＋[(2×2－222)－(2－12)]＝56.
答案：56
探究一 计算简单函数的定积分
[自主梳理]
如果 f(x)是区间[a，b]上的 连续 函数，并且 F′(x) 内容 ＝ f(x)，那么bf(x)dx＝ F(b)－F(a)
a
符号
bf(x)dx＝F(x)ba ＝ F(b)－F(a)
a
二、定积分和曲边梯形面积的关系 设曲边梯形在 x 轴上方的面积为 S 上，x 轴下方的面积为 S 下，则 1．当曲边梯形的面积在 x 轴上方时，如图(1)， 则bf(x)dx＝ S 上．
(7)baxdx＝lnaxaba (a>0 且 a≠1)． a
1．计算下列定积分．
(1)1(x3－2x)dx； 0
(2)
2 0
(x＋cos
x)dx；
(3
解析：(1)∵(14x4－x2)′＝x3－2x，
∴1(x3－2x)dx＝(14x4－x2)10 ＝－34. 0
2．(1)若
f(x)＝x2 cos
x≤0 x－1
x>0
2．常见函数的定积分公式： (1)bCdx＝Cxba (C 为常数)．
a
(2)abxndx＝n＋1 1xn＋1ba (n≠－1)． (3)bsin xdx＝－cos xba .
a
(4)bcos xdx＝sin xba . a
(5)b1xdx＝ln xba (b>a>0)． a

《微积分学基本定理》课件

《微积分学基本定理》课件

解决微分方程
通过微积分学基本定理，我们可以将复杂的微分方 程转化为易于处理的积分方程，从而找到微分方程 的解。
分析函数的极值
利用微积分学基本定理，可以分析函数的极 值条件，这对于优化问题、经济模型等实际 问题具有重要意义。
在实数理论中的应用
实数完备性
微积分学基本定理在实数理论中发挥了关键作用，它证明了实数系 的完备性，为实数理论的发展奠定了基础。
PART 02
微积分学基本定理的表述
REPORTING
定理的数学表达
总结词
简洁明了地表达了微积分学基本定理的数学形式。
详细描述
微积分学基本定理通常用积分形式和微分形式两种方式表达。积分形式表述为 ：∫(f(x))dx = F(b) - F(a)，其中∫代表积分，f(x)是待积分的函数，F(x)是f(x)的 原函数；微分形式表述为：∫(dy/dx) dx = y。
详细描述
02 习题一主要考察学生对微积分学基本定理的基础概念
理解，包括定理的表述、公式记忆以及简单应用。
解答
03
通过解析和证明，帮助学生深入理解微积分学基本定
理，并掌握其应用方法。
习题二及解答
总结词：复杂应用
详细描述：习题二涉及微积分学基本定理的复杂应用，包括多步骤推导、 不同定理的综合运用等，旨在提高学生的解题能力和思维灵活性。
揭示函数性质
通过应用微积分学基本定理，我 们可以研究函数的积分与函数的 性质之间的关系，从而深入了解 函数的特性。
证明积分不等式
利用微积分学基本定理，可以证 明各种积分不等式，这些不等式 在数学分析和实际问题中都有广 泛的应用。
在微分学中的应用
导数的定义
微积分学基本定理实际上给出了导数的定义 ，它描述了函数值随自变量变化的规律，是 研究函数局部行为的关键。

《微积分基本定理》课件

《微积分基本定理》课件

证明方法三：使用不定积分和定积分的性质
总结词
利用不定积分和定积分的性质来证明微积分基本定理 。
详细描述
首先，我们知道不定积分的定义是$int f(x) dx = F(x) + C$，其中$F(x)$是$f(x)$的一个原函数，$C$是常 数。然后，根据定积分的性质，我们知道 $int_{a}^{b} f(x) dx = F(b) - F(a)$。因此，我们可以 将微积分基本定理的结论表示为$int_{a}^{b} f(x) dx = lim_{Delta x to 0} sum_{i=1}^{n} f(xi_i) Delta x$ ，其中$xi_i$是每个小区间的中点，$Delta x$是每个 小区间的宽度。最后，我们利用不定积分的定义和极 限的性质来证明这个结论。
我们可以将积分看作是计算曲线下方的面积。对于一个给 定的函数，我们可以在坐标系中画出其图像。然后，将积 分区间分成若干个小区间，每个小区间的宽度为$Delta x$ ，高度为$f(x)$。因此，每个小矩形的高度与宽度的乘积 即为该小区间的面积。所有小矩形的面积之和即为整个曲 线下方的面积，即函数的积分值。
广义微积分基本定理的应用
广义微积分基本定理在数学分析和实变函数等领域中有 着重要的应用，例如在证明某些积分的收敛性和求解某 些特殊类型的积分等。
THANKS
感谢观看
微积分基本定理是微积分学中的核心定理，它建立了函数积分与导数之间 的联系，为解决各种问题提供了重要的方法和思路。
微积分基本定理的背景
微积分基本定理的起源可以追溯到17世纪，当 时科学家们开始研究如何求解各种物理问题， 如速度、加速度、面积和体积等。
牛顿和莱布尼茨等科学家在研究这些问题时， 发现了微积分基本定理，从而为解决这些问题 提供了重要的方法和工具。

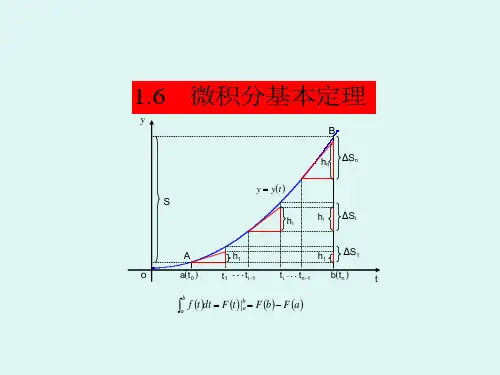
微积分基本定理PPT课件

微积分基本定理PPT课件

的斜率等于y' ti1 ,于是
Si hi tan DPC t
y' ti1 t.
A
o
at0
B
hn ΔSn
y yt
D
P t
hi C
hi ΔSi
h1
h1 ΔS1
t1
ti1
ti tn1 btn
t
图1.6 2
结合图1.6 1,可得物体总位移
n
n
n
n
S ΔSi hi v ti1 Δt s' ti1 Δt.
t1
ti1
ti tn1
btn
t
显然,物体的位移S是函数y yt在t b处与t a 处的函数值之差,即S yb ya. ①
另一方面,我们还可以利用定积分 ,由yt来求位移S.
y B
hn ΔSn
y yt
S
hi
hi ΔSi
A
h1
h1
ΔS1
o
at0
t1
ti1
ti tn1
btn
1.6 微积分基本定理
y B
hn ΔSn
y yt
S
hi
hi ΔSi
A
h1
h1
ΔS1
o
at0
t1
ti1
ti tn1
btn
t
b
a
f
t dt
F t|ba
F
b
F
a
我们发现,虽然被积函数 f x x3比较简单,但直接
用定积分的定义计算 1 x3dx的值却比较麻烦. 0
再例如 2 1dx,也不方便直接用定义计 算 .
t
用分点a t0 t1 ti1 ti tn b将区间

微积分学基本定理(精)ppt课件

微积分学基本定理(精)ppt课件
a bf(x)d xF (x)|b aF (b )F (a )
证明: 已 知 F ( x ) 是 f ( x ) 的 一 个 原 函 数 ，
又 (x)a xf(t)d也 t是 f(x)的 一 个 原 函 数 ,
x
F (x) (x)Caf(t)d tC x[a,b]
x
F(x)a f(t)d tC
微积分学基本定理 与定积分的计算
一 变限积分与原函数的存在性
1 变限积分的概念 定义
， 设 f( x ) 在 [ a ,b ] 上则 可 ( x ) x f 积 ( t) d ,x t[ a ,b ] a
定 义 了 一 个 以x为 积自 分变 上量 限 ，的 称函 为数 变
限的定积，分 或积分上限.函数
b
b
af(x)g(x)d xg(b)f(x)d;x (6)
2) 推论 设函 f在 数 [a,b]上可 ,若 积 g为单调 , 函
则[a,b],使得
b
b
af(x )g (x )d x g (a )af(x )d x g (b )f(x )d;x
证明: 若 g为增,令 函 h(x) 数 g(x)g(a)则 , h为非 、 增函 , 由 数定 9.1(i1 理 )i , [a,b]使 , 得
1 et2dt
lim
x0
cosx
x2
sinxeco2sx
lim
x0
2x
1. 2e
3 积分第二中值定理
1) 定理9.11 设函f数 在[a,b]上可，积
(i)若函 g在 [a,数 b]上,且 减 g(x)0,则 [a,b]使 , 得
b
af(x)g(x)d xg(a)af(x)d;x (5)

微积分基本定理_图文_图文

微积分基本定理_图文_图文
微积分基本定理_图文_图文.ppt
【课标要求】 1．了解微积分基本定理的内容与含义． 2．会利用微积分基本定理求函数的定积分． 【核心扫描】 1．用微积分基本定理求函数的定积分是本课的重点． 2．对微积分基本定理的考查常以选择、填空题的形式出现．
1．微积分基本定理
自学导引
连续
f(x)
F(b)－F(a)

(1)用微积分基本定理求定积分的步骤： ①求f(x)的一个原函数F(x)； ②计算F(b)－F(a)． (2)注意事项： ①有时需先化简，再求积分； ②f(x)的原函数有无穷多个，如F(x)＋c，计算时，一般只写一个最 简单的，不再加任意常数c.
【变式1】 求下列定积分：
求较复杂函数的定积分的方法： (1)掌握基本初等函数的导数以及导数的运算法则，正确求解被积 函数的原函数，当原函数不易求时，可将被积函数适当变形后求 解，具体方法是能化简的化简，不能化简的变为幂函数、正、余 函数、指数、对数函数与常数的和与差． (2)精确定位积分区间，分清积分下限与积分上限．
定积分的应用体现了积分与函数的内在联系，可以通过 积分构造新的函数，进而对这一函数进行性质、最值等方面的考 查，解题过程中注意体会转化思想的应用．
【题后反思】 (1)求分段函数的定积分时，可利用积分性质将其表 示为几段积分和的形式； (2)带绝对值的解析式，先根据绝对值的意义找到分界点，去掉绝 对值号，化为分段函数； (3)含有字母参数的绝对值问题要注意分类讨论．
2．被积函数为分段函数或绝对值函数时的正确处理方式 分段函数和绝对值函数积分时要分段去积和去掉绝对值符
号去积．处理这类积分一定要弄清分段临界点，同时对于定积分 的性质，必须熟记在心．
题型一 求简单函数的定积分 【例1】 计算下列定积分
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
微积分基本定理
深大师院二附校唐丽
一、教材分析 ⒈ 地位、作用：
欧洲数学家们冲出了古希腊人“严格证明” 的圣殿，以直观推断的思维方式，创立了被恩 格斯誉为“人类精神的最高胜利”的微积分学， 微积分基本定理正是它的核心！
2．教学重点、难点分析： 重点： 通过探究变速直线运动物体的速
度与位移的关系，发现微积分基本定理的雏 形，进而把结论一般化,是这节课的重点.
li
i
通过讨论发现山高
hi li sini
那么把所有 h i 累加起来
不正好就是山的高度吗？
n
hi
i 1
以研究这小段山高为例： 问题1能否）把一小段的山高近似地看作一个直角三角形呢？ 问题2 假设是直角三角形，那么斜边如何构造呢？ 问题3 在这个直角三角形种哪些量是已知或可求的？
微积分基本定 就是勾股定
的切线，由导数的几何意义可知： AD的斜率就是tan∠DAC，所以
=
hi tanDACt
h i ta n D A C t s'(ti 1 ) t
另一方面曲线S在左端点A处的切线就是s ( t i ，1 )
引进导数．
⒉近似代替：当 t 很小时，我们可以认为 Si hi
教学过程：
⒈引题——追根溯源：
公元3世纪诞生的刘徽著名的“割圆术”
割之弥细，所失越 割之又割少，．以至于 则与圆不周可合割体，而无
所失矣．
教学过程：
⒉情景设置：
①首先让学生回顾计算
1
0
x
3
dx
的过程：
= （分割、近似代替、求和、取极限）
lim 1 x 3 dx
ni f( )x
0
n n i1
⒈分割： a t 0 t 1 t i 1 t i t n b 等分成n个小区间 [ t 0 , t1 ] , [t1,t2], , [ti1,ti], , [tn1,tn ]
可用线段ＡＤ来近似代替曲边 AB，得到直角三角形ACD，AD
正是曲线s s(t) 在左端点A处
nபைடு நூலகம்
和式难求．
=
li m n 1 i n i 1 11
④当被积函数是 1 如何求呢？
x
4
,
x5
,
1 x3
lim(1 )
n 2 3
n
寻求新方法
⒊探究——问题模型：
如图，一个作变速直线运动的物体的运动规律
是= s s(t) 由导数的概念可知，它在任意时刻t的速
度是 v(t)s(t) 。设这个物体在时间段a,b内的位
⒋教学方法和手段： 尽管已是高中学生，但抽象的概念依然
令学生望而生畏，因此着眼于个别实例的研 究，强调来龙去脉，淡化证明过程。学生既 不用面对极限、无穷项求和、导数、积分综 合难题的证明，又不失为良好的推导微积分 基本定理的过程。
二、学情分析：
⒈ 根据函数曲线图学生不难看出位移差
ss(b)s(a)
能力目标： 让学生能够体会微积分运动变化地思维 方式和初等数学中静态的思维方式的区别， 并且培养学生在探索过程中善于变通的思想， 敢于挑战陈规的精神!
情感目标： A 揭示寻求计算定积分新方法的必要性, 激发学生的求知欲。 B 体会“以直代曲”——临渊羡鱼，不如退 而结网的思想。 C 感受用近似无限接近精确的方法。
难点：进一步引导学生应用定积分的基 本思想来探究问题，同时利用导数的意义作 为桥梁来转化被积函数是这节课的难点。
⒊教学目标分析： 知识目标：使学生经历定理的发现过程，直
观了解微积分基本定理的含义和几何意义，并理 解导数与定积分的互逆关系；通过计算两个简单 的定积分，使学生体会微积分基本定理的优越性， 理解微积分在数学史上举足轻重的地位。
s(t)v(t)
n ba
=
slim n i1
n v(ti1)
让学生观察，这不正是速度函数 v ( t ) 的定积分吗？
（引入定积分得到左边雏形）
b
s a v(t)dt.
（建立导数与积分的关系）sa bv(t)d ta bs'(t)d ts(b ) s(a )
归纳小结：③式表明，速度函数v ( t )在区间[a，b] 上的定积分等于位移函数s ( t ) 在区间[a，b]的右端
⒉由于学生刚学习了导数，知道导数的几何 意义即为切线的斜率,路程对时间的导数即为 速度 s(t)v(t)
二、学情分析：
⒊ 上一节中刚学习了“汽车行驶的路程”，学
生明白路程的计算实际上是一个求定积分的过程， 即对 v(t) 的定积分。
⒋ 让学生再一次感受小区间不断细分对近似程度 的影响，如何通过逐步逼近而求出定积分。
移为S，你能分别用 v (t ) ，s (t ) 表示Ｓ吗？
观察图象得到物体的位移s，即
ss(b)s(a)
分析:
下面我们讨论如何用速度函数v(t)来表示位 移s，因为在上一节“汽车行驶的路程”中，学 生知道了位移就是对速度函数v(t)的定积分，在 此学生肯定会联想到只要知道了v(t), 不就解决了 吗？但是题目已知的只是路程函数s(t), 因此接 下来的关键在于建立v(t)与s(t)的关系。下面分8 个步骤来讨论：
n
n
n
⒊求和：
S Si hi s'(ti1)t.
i1
i1
i1
n
⒋取极限：物体的总位移的近似值 s '( ti 1 ) t
i 1
就越接近精确值S． 即
S lit m 0i n 1s'(ti 1) tln i m i n 1b nas'(ti 1),
点处的函数值s(b)与左端点处的函数值s (a)之差． ③式是否具有一般性呢？
⒋ 水到渠成：给出微积分基本定理的一般形式。
连续函数 f(x),若 f(x)F(x)，则abf(x)dxF(b)F(a)
即牛顿——莱布尼兹公式（Newton—Leibniz Formula）
n i 3 1
lim ( )
n n i1
n
lim1(11)2 1 n 4 n 4
教学过程：
②接着动手利用定义计算 2 1 dx
lim 2 1 dx
n f (i )x
1x
n n i1
1x
lim n 1 1 i n i 1 n
③重复以上步骤学生遇到 了麻烦；引导学生分析原因：