全等三角形SSS

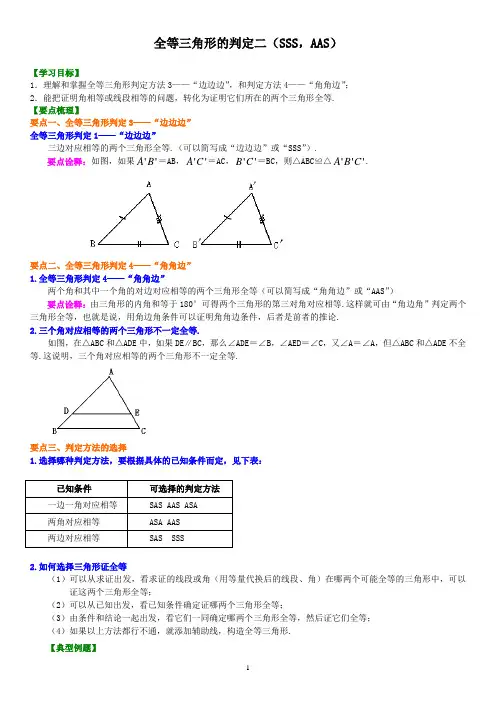
全等三角形的判定二（SSS ，AAS ）【学习目标】1．理解和掌握全等三角形判定方法3——“边边边”，和判定方法4——“角角边”；2．能把证明角相等或线段相等的问题，转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定3——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.（可以简写成“边边边”或“SSS ”）.要点诠释：如图，如果''A B ＝AB ，''A C ＝AC ，''B C ＝BC ，则△ABC ≌△'''A B C .要点二、全等三角形判定4——“角角边”1.全等三角形判定4——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等（可以简写成“角角边”或“AAS ”）要点诠释：由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等，也就是说，用角边角条件可以证明角角边条件，后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图，在△ABC 和△ADE 中，如果DE ∥BC ，那么∠ADE ＝∠B ，∠AED ＝∠C ，又∠A ＝∠A ，但△ABC 和△ADE 不全等.这说明，三个角对应相等的两个三角形不一定全等.要点三、判定方法的选择1.选择哪种判定方法，要根据具体的已知条件而定，见下表： 已知条件可选择的判定方法 一边一角对应相等SAS AAS ASA 两角对应相等ASA AAS 两边对应相等 SAS SSS2.如何选择三角形证全等（1）可以从求证出发，看求证的线段或角（用等量代换后的线段、角）在哪两个可能全等的三角形中，可以证这两个三角形全等；（2）可以从已知出发，看已知条件确定证哪两个三角形全等；（3）由条件和结论一起出发，看它们一同确定哪两个三角形全等，然后证它们全等；（4）如果以上方法都行不通，就添加辅助线，构造全等三角形.【典型例题】1、已知：如图，△RPQ 中，RP ＝RQ ，M 为PQ 的中点．求证：RM 平分∠PRQ ．【思路点拨】由中点的定义得PM ＝QM ，RM 为公共边，则可由SSS 定理证明全等.【答案与解析】证明：∵M 为PQ 的中点（已知），∴PM ＝QM在△RPM 和△RQM 中，()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边 ∴△RPM ≌△RQM （SSS ）．∴ ∠PRM ＝∠QRM （全等三角形对应角相等）．即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到，如：公共边、公共角、对顶角等条件隐含在题目或图形之中. 把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等，综合应用全等三角形的性质和判定.举一反三：【变式】已知：如图，AD ＝BC ，AC ＝BD.试证明：∠CAD ＝∠DBC.【答案】证明：连接DC ，在△ACD 与△BDC 中()AD BC AC BDCD DC ⎧=⎪=⎨⎪=⎩公共边 ∴△ACD≌△BDC（SSS ）∴∠CAD ＝∠DBC （全等三角形对应角相等）2、已知：如图，AB ⊥AE ，AD ⊥AC ，∠E ＝∠B ，DE ＝CB ．求证：AD ＝AC ．【思路点拨】要证AC ＝AD ，就是证含有这两个线段的三角形△BAC ≌△EAD.【答案与解析】证明：∵AB ⊥AE ，AD ⊥AC ，∴∠CAD ＝∠BAE ＝90°∴∠CAD ＋∠DAB ＝∠BAE ＋∠DAB ，即∠BAC ＝∠EAD在△BAC 和△EAD 中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC ≌△EAD （AAS ）∴AC ＝AD【总结升华】我们要善于把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等．举一反三：【变式】如图，AD 是△ABC 的中线，过C 、B 分别作AD 及AD 的延长线的垂线CF 、BE.求证：BE ＝CF.【答案】证明：∵AD 为△ABC 的中线∴BD ＝CD∵BE ⊥AD ，CF ⊥AD ，∴∠BED ＝∠CFD ＝90°，在△BED 和△CFD 中BED CFD BDE CDFBD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩（对顶角相等） ∴△BED ≌△CFD （AAS ）∴BE ＝CF3、如图：AB=A′B′，∠A=∠A′，若△ABC≌△A′B′C′，则还需添加的一个条件有（）种．A.1B. 2C.3D.4【思路点拨】本题要证明△ ABC≌△ A′B′C′，已知了AB=A′B′，∠A=∠ A′，可用的判别方法有ASA，AAS，及SAS，所以可添加一对角∠B=∠B′，或∠C=∠C′，或一对边AC=A′C′，分别由已知与所添的条件即可得证．【答案与解析】解：添加的条件可以为：∠B=∠B′；∠C=∠C′；AC=A′C′，共3种．若添加∠B=∠B′，证明：在△ABC和△A′B′C′中，，∴△ABC≌△A′B′C′（ASA）；若添加∠C=∠C′，证明：在△ABC和△A′B′C′中，，∴△ABC≌△A′B′C′（AAS）；若添加AC=A′C′，证明：在△ABC和△A′B′C′中，，∴△ABC≌△A′B′C′（SAS）．故选C.【总结升华】此题考查了全等三角形的判定，是一道条件开放型问题，需要由因索果，逆向推理，逐步探求使结论成立的条件，解决这类问题要注意挖掘隐含的条件，如公共角、公共边、对顶角相等，这类问题的答案往往不唯一，只有合理即可．熟练掌握全等三角形的判定方法是解本题的关键．类型三、全等三角形判定的实际应用4、“三月三，放风筝”．下图是小明制作的风筝，他根据DE ＝DF ，EH ＝FH ，不用度量，就知道∠DEH ＝∠DFH ．请你用所学的知识证明．【答案与解析】证明：在△DEH 和△DFH 中，DE DF EH FH DH DH ⎧⎪⎨⎪=⎩＝＝∴△DEH ≌△DFH(SSS)∴∠DEH ＝∠DFH ．【总结升华】证明△DEH ≌△DFH ，就可以得到∠DEH ＝∠DFH ，我们要善于从实际问题中抽离出来数学模型，这道题用“SSS ”定理就能解决问题.举一反三：【变式】雨伞的中截面如图所示，伞骨AB=AC ，支撑杆OE=OF ，AE=AB ，AF=AC ，当O 沿AD 滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD 与∠CAD 有何关系？说明理由．【答案】解：雨伞开闭过程中二者关系始终是：∠BAD=∠CAD，理由如下：∵AB=AC，AE=AB ，AF=AC ，∴AE=AF，在△AOE 与△AOF 中，，∴△AOE≌△AOF（SSS ），∴∠BAD=∠CAD．。

三边确定三角形唯一
【昨日复习】：1、能够的两个图形叫全等形。

完全重合指的是形状，大小
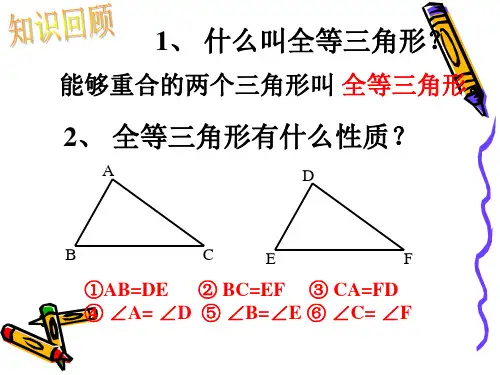
2、叫全等三角形。

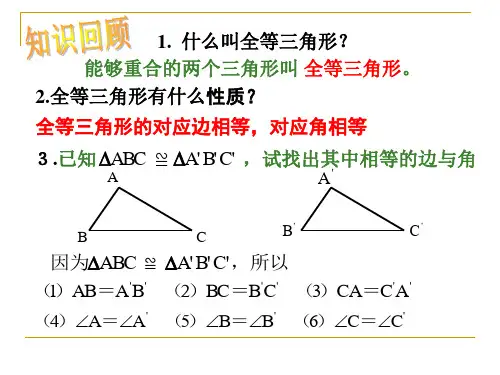
已知两三角形全等，立即应相到的：
全等三角形的对应边，对应角。

3、全等符号怎样书写？
怎样找对应边对应角？对应边所对的角必是，反之，
【把握今天】：
1、三条线段的长度满足怎样的关系才能围成三角形？你还记得吗？
三角形的任意两边之和必须。

2、请你画出长为6cm，8cm，10cm的三条线段，再画出以它们为边长的三角形。

问：每个同学画出的这样的三角形都全等吗？
3、所以可以得出结论：
三边对应相等的两个三角形全等（可简写成“边边边”或“SSS”）
4、怎样画一个三角形使得它和已知的三角形全等呢？
已知：如图，△ABC，求作△DEF，使得△ABC≌△DEF。

看来：虽然全等三角形的三条边对应相等，三个角对应相等，
但只要满足其中的部分条件就可保证三角形全等。

5、讲例：
例1，如图，△ABC是一个支撑架的一部分，AB=AC，AD是连接A与BC中点D的支柱，求证：△ABD≌△ACD。

分析：因为三边对应相等的两个三角形全等，所以可以看看它们的三条边是否对应相等。

证明：
6、怎样不用量角器，只用圆规和直尺画出已知角的平分线？（可用量角器检验）
已知：如图，∠AOB，求作：∠AOB的平分线。

作法：略
证明：。

第三讲：全等三角形的判定探索全等三角形的条件：一个条件：一个角和或者一条边两个条件：两个角、两条边、一边一角三个条件：全等三角形判定一：三边对应相等的两个三角形全等，简写为“边边边”或“SSS ”（即：两个三角形的三边分别对应相等，那么这两个三角形全等）注意：此定理说明：只要三角形三边长度确定，则三角形的形状和大小也就完全确定了。

例1：如图是一个平分角的仪器，其中AB=AD ，BC=DC ，将点A 放在角的顶点，AB 和AD 沿着角的两边放正，沿AC 画一条射线AE ，AE 就是角平分线，请说明它的道理．例2：如图，△ABC 中 AB=AC ， D 为BC 中点；求证：①△ABD ≌△ACD ；②∠BAD=∠CAD ；③AD ⊥BC例3：已知AB=DE ，AC=DF ，且BF=CE ，求证∠A=∠DD CB A例4：如图，AC与BD交于点O，AD=CB，E、F是BD上两点，且AE=CF，DE=BF.请推导下列结论：(1)∠D=∠B；(2)AE∥CF．例5：如图，已知AB=CD，AC=BD，求证：∠A=∠D例6：在四边形ABCD中,AB=CD,AD=BC,求证：∠A=∠C由：以上两题，你想到了什么？全等三角形判定二：两角和它们的夹边对应相等的两个三角形全等，简写成“角边角”或“ASA”推论：两角和其中一个角的对边对应相等的两个三角形全等，简写成“角角边”或“AAS”ASA:例1：如图：已知BD＝CE，∠B＝∠C，△ABD与△ACE全等吗？为什么？ADE例2：如图，AB=DC ，∠A=∠D ．试说明：∠1=∠2例3：已知：如图，∠DAB=∠CAB ，∠DBE=∠CBE 。

求证：AC=AD.例4：如图，已知：AE=CE ，∠A=∠C ，∠BED=∠AEC ，且点B 在线段CD 上，求证：∠EBD=∠D例5：（2012•顺义区二模）已知：如图，E ，F 在BC 上，且AE ∥DF ，AB ∥CD ，AB=CD ．求证：BF=CE ．例6：．（2013•舟山）如图，△ABC 与△DCB 中，AC 与BD 交于点E ，且∠A=∠D ，AB=DC ．（1）求证：△ABE ≌DCE ；（2）当∠AEB=50°，求∠EBC 的度数？A B CD O 1 2AAS:例1：（2013•玉林改编）如图，点E在线段BC上，∠B=∠AEB，∠1=∠2，∠C=∠D．求证：△ABC≌△AED．例2：（2012•湘西州）如图，AC与BD相交于点O，AO=DO，∠B=∠C．求证：△ABO≌△DCO．例3：（2012•衡阳）如图，AF=DC，BC∥EF，请只补充一个条件，使得△ABC≌△DEF，并说明理由．例4：（2012•河源）如图，已知AB=CD，∠B=∠C，AC和BD相交于点O，E是AD的中点，连接OE．（1）求证：△AOB≌△DOC；（2）求∠AEO的度数．例5：（2011•泉州）如图，已知点E，C在线段BF上，BE=CF，AB∥DE，∠A=∠D．求证：△ABC≌△DEF．例6：（2013•珠海）如图，已知，EC=AC，∠BCE=∠DCA，∠A=∠E；求证：BC=DC．例7：如图，在△ABC中，∠B=2∠C,AD是△ABC的角平分线，∠1=∠C,求证AC=AB+BD巩固练习：1.（2008•永春县）已知：如图，∠A=∠DCF，F是AC的中点．求证：△AEF≌△CDF．2.如图, AB∥CD, AD、BC交于O点, EF过点O分别交AB、CD于E、F，且AE=DF,求证：O是EF的中点3.如图，∠ABC=∠DCB，∠ACB=∠DCB，试说明△ABC≌△DCB.4.（2005•镇江）如图①，∠ABC=∠DCB，请补充一个条件，使△ABC≌△DCB；并证明。

全等三角形判定的三种类型1.SSS判定（边边边）SSS判定是指当两个三角形的三条边分别相等时，它们是全等三角形。

例如，对于两个三角形ABC和DEF，如果AB=DE，BC=EF，AC=DF，则可以通过SSS判定断定三角形ABC和DEF是全等的。

SSS判定的原理是，边长相等可以确保两个三角形的相应边之间的角度也是相等的，根据三角形角度之和为180°的性质，可以推导出它们的角度也是相等的，进而判断三角形全等。

2.SAS判定（边角边）SAS判定是指当两个三角形的两边和夹角分别相等时，它们是全等三角形。

例如，对于两个三角形ABC和DEF，如果AB=DE，∠BAC=∠EDF，BC=EF，则可以通过SAS判定判断三角形ABC和DEF是全等的。

SAS判定的原理是，两个三角形的一边和与这边相邻的两个角相等时，可以确保这两个三角形的三个边都相等，从而判断它们全等。

3.ASA判定（角边角）ASA判定是指当两个三角形的两角和边分别相等时，它们是全等三角形。

例如，对于两个三角形ABC和DEF，如果∠BAC=∠EDF，∠ABC=∠DEF，AC=DF，则可以通过ASA判定判断三角形ABC和DEF是全等的。

ASA判定的原理是，两个三角形的两个角和这两个角所夹的边相等时，可以确保这两个三角形的第三个角也相等，从而判断它们全等。

此外，还有两种特殊情况的判定方法：4.直角全等判定如果两个直角三角形的三个边分别相等，那么它们一定是全等的。

这是因为直角三角形的两个直角以及第三个角也是相等的。

5.等腰全等判定如果两个三角形都为等腰三角形，并且有一个角相等，那么它们一定是全等的。

这是因为等腰三角形的两个底角和底边相等，所以只需要一个额外的角相等即可推断两个等腰三角形全等。

综上所述，全等三角形的判定可以通过SSS、SAS、ASA以及两种特殊情况的判定方法来进行。

这些判定方法不仅可以帮助我们判断三角形的全等性质，而且在数学推导和证明过程中也有重要的应用。

全等三角形SSS在初中数学的几何世界里，全等三角形是一个非常重要的概念，而其中的“SSS”（边边边）判定定理更是基础且关键的一部分。

今天，咱们就来好好聊聊这个“SSS”。

首先，咱们得明白啥是全等三角形。

简单说，就是两个三角形的形状和大小完全一样，放在一起能够完全重合。

那怎么判断两个三角形是不是全等呢？这就轮到“SSS”登场啦。

“SSS”指的是，如果两个三角形的三条边分别对应相等，那么这两个三角形就是全等的。

为啥三条边相等就能判定全等呢？咱们来琢磨琢磨。

想象一下，咱给定了三条确定长度的线段，要拼成一个三角形。

是不是只有一种拼法？因为三角形的三条边长度确定了，它的形状和大小也就固定下来了。

所以，如果两个三角形的三条边都对应相等，那就意味着它们的形状和大小都完全相同，必然是全等的。

比如说，有一个三角形的三条边分别是 3 厘米、4 厘米和 5 厘米。

另一个三角形也有三条边，长度同样是 3 厘米、4 厘米和 5 厘米。

那这两个三角形就是全等的。

在实际解题中，“SSS”判定定理可是大有用处。

比如，给咱两个三角形，告诉咱三条边的长度分别相等，那咱们就可以毫不犹豫地说这两个三角形全等。

再举个例子，在一个几何图形里，已知三角形ABC 和三角形DEF，AB ＝ DE，BC ＝ EF，AC ＝ DF，那就可以得出三角形 ABC 全等于三角形 DEF。

然后，根据全等三角形的性质，对应角也相等。

这就能帮咱们解决很多角度或者线段长度的问题。

而且，“SSS”判定定理还能和其他判定定理（比如 SAS、ASA 等）一起配合使用，让咱们更轻松地解决复杂的几何难题。

学习“SSS”判定定理的时候，大家可得多做些练习题，加深理解和记忆。

比如说，给出两个三角形的三条边长度，让判断是否全等；或者已知两个三角形全等，给出其中一些边的长度，求另一些边的长度。

总之，全等三角形的“SSS”判定定理虽然看起来简单，但其作用可不容小觑。

掌握好了它，咱们在几何的海洋里就能更加游刃有余。

11.2 三角形全等的判定第1课时 三角形全等的判定（SSS ）【要点归纳】1．三角形全等的判定（1） 如果两个三角形满足三条边对应相等，三个角对应相等，那么它们全等。

（2） 如果两个三角形满足三边三角六个条件中的一个或者两个对应相等，那么不能保证三角形全等。

（3） 两个三角形全等至少需要三个条件对应相等。

2.三角形全等的“SSS ”判定方法 三边对应相等的两个三角形全等（可以简写成“边边边”或者“SSS ”）【题型归类】类型一：利用“SSS ”证明三角形全等例1. 如图11-2-1。

已知AB=AC ，AE=AD ，BD=CE ，求证:△AEB ≌△ADC.【点拨】此题考查三角形全等条件SSS 的应用.在确定的两个三角形中找全等的条件是证明三角形全等的常用方法.要证明△AEB ≌△ADC,已经具备了两个条件AB=AC ，AE=AD.第三个条件BE=CD 需要由BD=CE 得出.【证明】∵BD=CE,∴BD －ED=CE －ED,即BE=CD,在△AEB 和△ADC 中, AB AC AE AD BE CD =⎧⎪=⎨⎪=⎩∴△AEB ≌△ADC （SSS ）类型二：利用三角形全等证明线段（或者角）相等，直线平行例2.如图11-2-2所示，AB=CD ，AE=DF ，CE=BF ，判断EC 与BF 的数量和位置关系，说明理由。

【点拨】此题综合考查全等三角形的判定和性质。

要说明E C ∥BF ，只要∠ACE=∠DBF ，进而考虑证明△AEC ≌△DFB 。

【解】 E C ∥BF ，E C=BF 。

理由：∵AB=CD ，∴AB ＋BC=CD ＋BC ， 即AC=DB在△ACE 和△DBFC 中AE=DF,AC DB,,EC BF ⎧⎪=⎨⎪=⎩∴△ACE ≌△DBFC （SSS ）∴∠ACE=∠DBF ，E C=BF 。

∴E C ∥BF 。

【易错示例】【例】如图11-2-3所示，在△ABC 和△EFD ，AD=FC ，AB=FE ，BC=DE 。

引言：全等三角形是指在几何学中，具有相同边长和相等内角的两个三角形。

全等三角形的判定是三角形重要的基本理论之一。

在本文中，我们将继续探讨全等三角形的判定方法，并重点讨论sss（两边和夹角对）条件下的判定方法。

概述：全等三角形的判定方法有多种，包括sss、asa、sas、saa等条件。

在前文中，我们已经介绍了sss（两边和夹角对）条件下全等三角形的判定方法，本文将进一步深入探讨并展示具体的例子。

正文内容：一、sss条件下全等三角形的判定方法1.根据sss条件判定两个三角形的三条边相等，即边AB=边DE、边AC=边DF、边BC=边EF。

2.根据sss条件判定两个三角形的夹角相等，即∠BAC=∠EDF、∠ABC=∠EFD、∠ACB=∠DFE。

3.若满足边边边对应相等和夹角夹角夹相等，则可判定两个三角形全等。

4.示例：已知三角形ABC和DEF，满足边AB=边DE、边AC=边DF、边BC=边EF，且∠BAC=∠EDF、∠ABC=∠EFD、∠ACB=∠DFE，可以判定三角形ABC与DEF全等。

二、sss条件判定的注意事项1.注意边边边对应相等的顺序，即需要确保对应的边顺序相同，如边AB=边DE，不能判定边AC=边DF。

2.注意夹角夹角夹相等的顺序，即需要确保对应的夹角顺序相同，如∠BAC=∠EDF，不能判定∠BCA=∠DFE。

三、sss条件下全等三角形的实际应用1.在实际问题中，sss条件往往能够提供便利的判定，尤其适用于已知两个三角形的边长和其中一个内角的情况。

2.示例：在电路板制作中，若已知一个三角形的边长和一个内角，通过sss条件可以很方便地判定另一个三角形是否全等，从而保证电路板的制作精度。

四、sss条件判定的局限性和改进方法1.sss条件只适用于已知所有三条边和它们对应的夹角的情况，若条件不足，则无法判定全等。

五、总结全等三角形的判定是三角形学习中的重要内容之一，sss（两边和夹角对）条件提供了一种方便快捷的判定方法。

全等三角形的四种判定方法
1.SSS判定法（边-边-边）：
SSS判定法是通过比较两个三角形的边长来判断它们是否全等。

当三
个边的长度完全相等时，两个三角形就是全等的。

这是最直观的方法，也
是最易判定的方法之一
2.SAS判定法（边-角-边）：
SAS判定法是通过比较两个三角形的边长和夹角来判断它们是否全等。

当两个三角形的一对相邻边和它们之间的夹角相等时，这两个三角形就是
全等的。

3.ASA判定法（角-边-角）：
ASA判定法是通过比较两个三角形的两个角度和它们之间的夹边来判
断它们是否全等。

当两个三角形的两个角度和它们之间的夹边相等时，这
两个三角形就是全等的。

4.AAS判定法（角-角-边）：
AAS判定法是通过比较两个三角形的两个角度和一个非夹角边来判断
它们是否全等。

当两个三角形的两个角度和一个非夹角边相等时，这两个
三角形就是全等的。

这些判定方法都基于三角形的重要性质：对于两个全等的三角形，它
们的对应边长相等，对应角度相等。

因此，通过比较两个三角形的边长和
角度可以判断它们是否全等。

在实际应用中，这些判定方法可以用来解决各种问题，比如计算三角形的面积、寻找相似三角形等。

此外，全等三角形的概念也是其他几何学概念的基础，比如正方形和正五边形都是全等三角形的特殊情况。

综上所述，全等三角形的判定方法有四种：SSS、SAS、ASA和AAS。

通过比较边长和角度的相等性可以确定两个三角形是否全等。

这些方法在解决几何问题中非常有用，并且为其他几何学概念的理解提供了基础。