分数除法单元知识点的归纳与整理
- 格式:docx
- 大小:8.12 KB
- 文档页数:2

分数除法主要知识点总结分数除法是数学中的一个重要概念,它是指将一个分数除以另一个分数,得到一个新的分数的过程。
在进行分数除法运算时,需要掌握一些基本的知识点和技巧。
下面将对分数除法的主要知识点进行总结。
1. 分数与除法的基本概念分数是表示一个整体被分成若干等份中的一份的数,分数由分子和分母组成。
分母表示整体被分成的份数,分子表示其中的若干等份中的一份。
例如,1/2表示一个整体被平均分成2份中的一份。
除法是一种数学操作,用来求两个数的商的运算。
在分数除法中,我们要求的是将一个分数除以另一个分数,得到一个新的分数。
2. 分数除法的运算规则在进行分数除法运算时,有一些基本的运算规则需要遵循。
下面是分数除法的运算规则:(1)将除数的倒数作为分母在进行分数除法运算时,需要将除数的倒数作为分母。
例如,要计算2/3除以1/4,需要先将除数1/4的倒数4/1作为分母,然后将分子2/3乘以分母的倒数4/1,得到8/3。
(2)将除数的倒数乘以被除数进行分数除法运算时,需要将除数的倒数乘以被除数,得到商的分子。
例如,2/3除以1/4,除数1/4的倒数是4/1,将4/1乘以被除数2/3,得到8/3,即商的分子。
(3)化简在得到商的分子后,需要对分子和分母进行化简,使得分数的分子和分母没有公因数。
例如,8/3可以化简为2 2/3。
3. 分数除法的解题方法在解题时,可以根据分数除法的运算规则来进行计算。
下面以一个例题来说明分数除法的解题方法:例题:计算2/3÷1/4。
解题步骤:(1)将除数的倒数作为分母:1/4的倒数是4/1。
(2)将除数的倒数乘以被除数:4/1×2/3=8/3。
(3)化简:8/3=2 2/3。
所以,2/3÷1/4=2 2/3。
4. 分数除法的应用分数除法在日常生活和实际问题中有很多应用。
例如,购买食材时需要按照食谱的要求计算不同比例的配料,这就需要运用分数除法来计算。
另外,在做手工制作或者烹饪时,也需要按照分数比例来计算原料的用量。

《分数除法》知识清单一、分数除法的意义分数除法是分数乘法的逆运算。
分数除法的意义与整数除法的意义相同,都是已知两个因数的积与其中一个因数,求另一个因数的运算。
例如:$\frac{2}{3} \div \frac{1}{2}$表示已知两个因数的积是$\frac{2}{3}$,其中一个因数是$\frac{1}{2}$,求另一个因数是多少。
二、分数除法的计算法则1、分数除以整数分数除以整数(0 除外),等于分数乘以这个整数的倒数。
例如:$\frac{3}{8} \div 3 =\frac{3}{8} \times \frac{1}{3} =\frac{1}{8}$2、一个数除以分数一个数除以分数,等于这个数乘以分数的倒数。
例如:$2 \div \frac{3}{4} = 2 \times \frac{4}{3} =\frac{8}{3}$在计算分数除法时,要先将除法转化为乘法,然后按照分数乘法的计算方法进行计算。
三、分数除法中的倒数1、倒数的定义乘积是 1 的两个数互为倒数。
例如:$\frac{2}{3}$和$\frac{3}{2}$互为倒数,因为$\frac{2}{3} \times \frac{3}{2} = 1$。
2、求倒数的方法(1)求分数的倒数:将分子分母调换位置。
例如:$\frac{5}{7}$的倒数是$\frac{7}{5}$。
(2)求整数的倒数(0 除外):把整数看作分母是 1 的分数,再调换分子分母的位置。
例如:5 的倒数是$\frac{1}{5}$。
(3)求小数的倒数:先把小数化成分数,再求分数的倒数。
例如:025 =$\frac{1}{4}$,所以 025 的倒数是 4 。
3、 1 的倒数是 1,0 没有倒数。
四、分数除法的应用1、已知一个数的几分之几是多少,求这个数这类问题可以用方程来解决,设这个数为 x ,根据分数乘法的意义列出方程。
例如:一个数的$\frac{2}{3}$是 12 ,求这个数。

分数除法知识点总结整理一、分数的除法规则1. 分数的除法运算规则分数的除法运算规则是将一个分数除以另一个分数,得到一个新的分数。
当进行分数相除时,我们需要将除数倒数,然后将被除数乘以倒数得到商。
具体来说,如果要计算两个分数的商,可以将分数化为通分形式,然后将除数的分母和被除数的分子相乘,得到分子,再将除数的分子和被除数的分母相乘,得到分母,最后将得到的分子和分母化为最简分数形式,即为所得的商。
2. 分数的除数和被除数在进行分数除法运算时,除数表示将分子分成几份,而被除数表示每份的数量。
除数和被除数的关系是除数除以被除数等于商。
例如,如果除数为2/3,被除数为4/5,那么2/3÷ 4/5 的意思是将4/5分成2/3份,每份的数量是多少?3. 分数的倒数在分数除法中,要先将除数倒数,即将除数的分子和分母互换位置。
例如,要求4/5的倒数,可以通过将4/5的分子和分母互换位置得到5/4,即4/5的倒数是5/4。
二、分数除法的计算步骤1. 分数除法的计算步骤分数除法的计算步骤包括以下几个步骤:1)将除数倒数;2)将被除数乘以倒数得到商;3)将得到的商化为最简分数形式。
2. 分数除法的示例以1/2 ÷ 1/3为例,首先将除数1/3倒数得到3/1,然后将被除数1/2乘以倒数3/1得到3/2,最后将3/2化为最简分数形式得到1 1/2,即1/2 ÷ 1/3 = 1 1/2。
三、分数除法的应用1. 分数除法的应用范围分数除法的应用范围非常广泛,可以用于解决各种实际问题,例如在日常生活和工作中,我们经常需要进行分数的除法运算,计算出几个分数的商,来帮助我们解决一些实际问题。
分数除法的实际问题可以包括以下几种类型:1)分配问题:将一定数量的物品按照一定比例分配给不同的人,需要进行分数的除法运算;2)时间问题:计算一段时间内的工作量,需要进行分数的除法运算;3)距离问题:计算两个地点之间的距离,需要进行分数的除法运算。

第三单元 《分数除法》一、倒数1.倒数的意义:乘积是1的两个数互为倒数。
这两个数可以是分数、小数、整数。
倒数是两个数的关系,它们互相依存,不能单独存在。
单独一个数不能称为倒数。
(必须说清谁是谁的倒数)2.判断两个数是否互为倒数的方法是:一要看两个数的乘积是不是1。
二要看相乘的两个数的分子和分母是否颠倒了位置。
例如:a ×b =1则a 、b 互为倒数。
3.找一个数的倒数的方法:①找分数的倒数:交换分子、分母的位置。
(a b 的倒数是ba )②找整数的倒数:找一个整数的倒数,先把整数看成分母是1的分数, 再交换分子和分母的位置(即整数1)。
③找带分数的倒数:先把带分数化成假分数,再交换分子和分母的位置。
④找小数的倒数:先把小数化成分数再求倒数。
4.特殊数的倒数:①1的倒数是它本身1,因为1×1=1②0没有倒数,因为任何数乘0积都是0,且0不能作分母。
真分数的倒数是假分数,真分数的倒数大于1,也大于它本身。
假分数的倒数小于或等于1;带分数的倒数小于1。
二、分数除法的意义:分数除法的意义:分数除法的意义与整数除法的意义相同,都是已知两个因数的积与其中一个因数,求另一个因数的运算。
例如:52÷4表示已知两个数的积是52 与其中一个因数4,求另一个因数是多少。
还表示把52平均分成4份,每份是多少。
二、分数除法的计算法则1.分数除以整数的计算方法:分数除以整数(0除外),等于分数乘这个整数的倒数(除法转化乘法)。
2.整数除以分数,可以转化为整数乘这个分数的倒数。
3.分数除以分数,可以转化为分数乘这个分数的倒数。
4.一个数除以一个不等于0的数,等于乘这个数的倒数(除法转化乘法)。
即甲数除以乙数(0除外),等于甲数乘乙数的倒数。
除法转化成乘法时,被除数一定不能变,“÷”号变成“×”号,除数变成它的倒数。
5.被除数不为0,商与被除数的比较①除以大于1的数,商小于被除数;②除以小于1的数,商大于被除数;③除以等于1的数,商等于被除数。
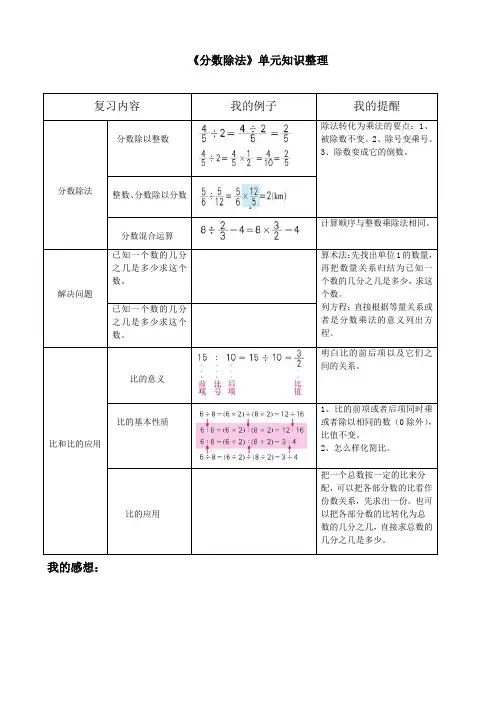
《分数除法》单元知识整理我的感想:复习内容我的例子我的提醒分数除法分数除以整数除法转化为乘法的要点:1、被除数不变。
2、除号变乘号。
3、除数娈成它的倒数。
整数、分数除以分数分数混合运算计算顺序与整数乘除法相同。
解决问题已知一个数的几分之几是多少求这个数。
算术法:先找出单位1的数量,再把数量关系归结为已知一个数的几分之几是多少,求这个数。
列方程:直接根据等量关系或者是分数乘法的意义列出方程。
已知一个数的几分之几是多少求这个数。
比和比的应用比的意义明白比的前后项以及它们之间的关系。
比的基本性质1、比的前项或者后项同时乘或者除以相同的数(0除外),比值不变。
2、怎么样化简比。
比的应用把一个总数按一定的比来分配,可以把各部分数的比看作份数关系,先求出一份。
也可以把各部分数的比转化为总数的几分之几,直接求总数的几分之几是多少。
《分数除法》评研题班别__________姓名__________ 一、想一想,填一填。
1、120的2/3是();甲数的3/4是240,甲数是()。
2、把2/7×1/4=1/14 改写成除法算式是()。
3、1/2里面有()个1/10;3吨的2/3是()吨。
4、5.6∶4.2化成最简单的整数比是(),比值是()。
5、()∶()=0.75 = 12÷()=()/326、5/12÷1/8 =()×()=()7、一个比的比值是2/3,如果这个比的前项是10,那么后项是()。
8、女生人数是男生人数的3/5,女生人数与男生人数的比是(),男生占全班人数的( )/( )。
二、请你来当小裁判。
1、两个分数相除,商一定大于被除数。
()2、5厘米∶20米=5÷20=1/4()三、用心选一选。
(将正确答案的序号填在括号里)1、a是b的1/4,b就是a的()。
A、4倍B1/4、C、3/42、“乙的7/11相当于甲”,应该把()看作单位“1”。
A、甲B、乙C、无法确定3、1克盐放入100克水中,盐与盐水的比是()。

分数除法知识点总结分数除法是初中数学中的重要知识点,它是我们进行分数运算和解题的基础。
在学习分数除法时,我们需要了解一些关键概念和技巧,下面就让我们来进行总结和归纳。
一、什么是分数除法在分数除法中,被除数是一个分数,除数也是一个分数。
我们的目标是找到一个数,使得被除数与这个数的乘积等于除数。
具体而言,分数除法可以表示为:被除数 ÷除数 = 商(也是一个分数)。
二、分数除法的基本原理分数除法的基本原理是借助于乘法来实现。
为了简化计算,我们首先将除数倒置(即将除数的分子和分母互换),然后将乘法转化为分数的乘法。
这样一来,我们只需要将被除数与倒置后的除数相乘即可求出商。
三、分数除法的步骤分数除法的步骤如下:1. 将除数倒置,即将除数的分子和分母互换;2. 将被除数与倒置后的除数进行乘法运算;3. 化简所得分数,即将乘积的分子和分母约分,使其为最简形式。
四、分数除法的特殊情况有时候在分数除法中会遇到一些特殊情况,我们需要注意处理。
1. 除数为0时,分数除法是没有意义的,因为任何数除以0都是无穷大或无解;2. 除数和被除数都是整数时,可以将它们转化为分数再进行运算,例如将1转化为1/1;3. 结果是整数时,可以将其直接写成整数形式,而无需写成分数形式。
五、分数除法的练习方法要熟练掌握分数除法,多做一些练习是非常重要的。
可以通过以下方法进行练习:1. 利用电子教辅软件或在线学习平台,选择一些分数除法题目进行练习;2. 每天划分一定时间进行分数除法的练习,例如每天做5到10道题目;3. 注意整理和总结自己在练习中出现的错误,以便后续及时纠正。
总之,分数除法是我们在初中数学中必须掌握的基础知识点。
通过理解分数除法的基本原理和步骤,我们能够轻松解决各类分数除法问题。
通过大量的练习,我们可以提高自己的计算能力和解题水平。
希望本文对大家有所帮助!。

分数除法知识点总结分数除法是数学中的一个重要概念,它涉及到分数的运算和简化。
在学习分数除法时,我们需要理解以下几个知识点:1.分数的定义:分数是由一个有限整数和一个非零整数构成的数,其中非零整数称为分母,有限整数称为分子。
一般形式为a/b,其中a是分子,b是分母。
分子表示分数的份数,分母表示一个整体被分成了几等份。
2.分数除法基本概念:分数除法是指将一个分数除以另一个分数,得到一个新的分数或一个整数作为商的过程。
分数除法的基本概念是建立在整除的基础上,即分子整除分母。
3.分数除法的步骤:(1)将除数的分子与被除数的分子相乘,得到新的分数的分子。
(2)将除数的分母与被除数的分母相乘,得到新的分数的分母。
(3)对新的分数进行简化,即将分子和分母同时除以它们的最大公因数,得到最简分数。
4.约分:在分数除法中,约分是非常重要的一步,它可以使得分数的分子和分母都较小,便于计算和比较。
约分的基本原则是找到分子和分母的最大公因数,然后将分子和分母同时除以最大公因数得到的商即为约分后的分数。
5.分数除法的特殊情况:(1)分子为零的情况:如果被除数的分子为零,则无论除数的分子和分母是多少,商都为零。
(2)分母为零的情况:分母为零的分数是没有意义的,因为任何数除以零都是没有意义的。
6.分数除法的计算规则:(1)如果两个分数都是带分数,可以先将它们转化为假分数,然后再进行分数除法的计算。
(2)如果一个分数是带分数,另一个分数是真分数,可以先将两个分数都转化为假分数,然后再进行分数除法的计算。
(3)如果两个分数都是真分数,可以直接进行分数除法的计算。
(4)如果分子和分母都可以被一个相同的非零整数整除,则可以直接进行约分。
总结起来,分数除法是指将一个分数除以另一个分数,得到一个新的分数或一个整数作为商的过程。
在进行分数除法的计算时,我们需要将分子和分母分别相乘,然后对新的分数进行约分,得到最简分数。
此外,分数除法还涉及到分数的转化和约分的步骤。

苏教版数学六年级上册第三单元《分数除法》知识点整理(重点归纳)第三单元:分数除法1、计算方法分数除法的法则为:甲数除以乙数(不为0)等于甲数乘以乙数的倒数。
因此,计算分数除法时,可以遵循“一变、二倒、三算、四验”的步骤。
对于分数连除或乘除混合计算,可以从左向右依次计算,但一般是遇到除以一个数,把它改写成乘这个数的倒数来计算,即转化成分数的连乘来计算。
需要注意的是,只能把除号后面的数改写成它的倒数,其他数字不能改写。
2、已知一个数的几分之几是多少,求这个数。
例如,一条裤子的价钱是45元,是上衣单价的8分之5,求上衣的单价。
解决这个问题需要将上衣的单价看成单位1,平均分成8份,裤子的价钱是其中的5份。
因此,可以得出数量关系式:上衣的单价×5/8=裤子的价钱。
解答时,可以采用两种方法,一种是设上衣的单价是x元,然后通过方程来解,另一种是逆向思考,用裤子的单价除以5/8得到上衣的单价。
3、分数乘除法应用题的比较举例说明,XXX家养了20只公鸡,母鸡占公鸡的4/5,求母鸡的只数。
可以得出数量关系式:公鸡的只数×5/4=母鸡的只数。
解答时,可以直接用单位“1”的量×分率=分率所对应的量,即20×5/4=16只母鸡。
另一个例子是,XXX家养了20只公鸡,公鸡占母鸡的4/5,求母鸡的只数。
此时,数量关系式为:母鸡的只数×4/5=公鸡的只数。
解答时,可以设母鸡有x只,然后通过方程或比较量÷对应的分率求出单位“1”的量,即20÷4/5=25只母鸡。
4、认识比比指的是两个数相除,也称为两个数的比。
比与分数、除法的关系为:a:b=a÷b=(b≠0)。
比的前项除以后项得到的商称为比值,可以是整数、分数或小数,不带单位名称。
比的前项和后项同时乘或除以一个相同的数(除外),比值不变。
最简整数比是指比的前项和后项是互质数,即除了1以外没有其他公因数。

分数除法六年级知识点总结分数是六年级数学中的重要概念之一,而分数除法更是在学习阶段中必不可少的一部分。
下面对分数除法的相关知识点进行总结,帮助同学们更好地理解和掌握这个概念。
1. 分数的除法定义分数的除法是指将一个分数除以另一个分数,其结果仍然是一个分数。
例如,1/2÷1/4=2,表示1/2被1/4除等于2。
2. 分数除法的原则在进行分数除法运算时,有以下几个原则需要遵守:a. 除以一个数等于乘以这个数的倒数:a/b÷c/d = a/b × d/c。
b. 分数除法的结果也是一个分数。
3. 分数除法的步骤进行分数除法运算时,可以按照以下步骤进行:a. 将除法转化为乘法:将除法变为分数相乘的形式。
即a/b÷c/d 转化为 a/b × d/c。
b. 化简分数:将分数化简到最简形式。
如果分子和分母有公因数,可以进行约简操作。
c. 乘法运算:对分数进行乘法运算。
分子与分子相乘,分母与分母相乘。
d. 化简结果:将乘法得到的结果化简到最简形式。
4. 分数除法的例题讲解例题1:计算1/2÷1/3。
解答:按照分数除法的步骤,将除法转化为乘法:1/2÷1/3 = 1/2 × 3/1 = 3/2。
结果3/2是一个真分数,可以进一步化简得到1 1/2。
例题2:计算3/4÷2/5。
解答:按照分数除法的步骤,将除法转化为乘法:3/4÷2/5 = 3/4 × 5/2 = 15/8。
结果15/8是一个假分数,可以进一步化简得到1 7/8。
例题3:计算2/5÷4/3。
解答:按照分数除法的步骤,将除法转化为乘法:2/5÷4/3 =2/5 × 3/4 = 6/20。
结果6/20可以进一步化简得到3/10。
5. 注意事项在进行分数除法运算时,需要注意以下几点:a. 分母不能为零:分母为零的分数是没有意义的,因此在进行分数除法运算时,要确保除数的分母不为零。

第三单元《分数除法》知识点1.分数除法计算(1)分数除法的意义和分数除以整数:整数除法的意义:已知两个因数的积与其中一个因数,求另一个因数的运算。
分数除法的意义与整数除法的意义相同,都是已知两个因数的积与其中一个因数,求另一个因数的运算。
分数除以整数的计算方法:把一个数平均分成整数份,求其中的几份就是求这个数的几分之几是多少。
分数除以整数(0除外)的计算方法:(1)用分子和整数相除的商做分子,分母不变。
(2)分数除以整数,等于分数乘这个整数的倒数。
一个数除以分数的计算方法:一个数除以分数,等于这个数乘分数的倒数。
分数除法的统一计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数。
商与被除数的大小关系:一个数(0除外)除以小于1的数,商大于被除数,除以1,商等于被除数,除以大于1的数,商小于被除数。
0除以任何数商都为0.(1)两个真分数相除,商一定大于被除数。
(2)一个数除以假分数,商一定小于等于被除数。
(3)分数除法的混合运算除加、除减混合运算,如果没有括号,先算除法,后算加减。
分数连除,可以分步转化为乘法计算,也可以一次都转化为乘法再计算,能约分的要约分。
不含括号的分数混合运算的运算顺序:在一个分数混合运算的算式里,如果只含有同一级运算,按照从左到右的顺序计算;如果含有两级运算,先算第二级运算,再算第一级运算。
含有括号的分数混和运算的运算顺序:在一个分数混合运算的算式里,如果既有小括号又有中括号,要先算小括号里面的,再算中括号里面的。
整数的运算定律在分数混和运算中的运用:在进行分数的混和运算中,可以利用加法、减法、乘法、除法的运算定律或运算性质,使计算简便。
2.解决问题已知一个数的几分之几是多少,求这个数的应用题解法列方程解题的关键:找出题中数量间的等量关系。
用算术法解除法应用题的关键:找准已知数量对应的单位“1”的几分之几。
解简单的“已知一个数的几分之几是多少,求这个数”的解题方法:方程解法:(1)找出单位“1”,设未知量为x;(2)找出题中的数量关系式;(3)列出方程。

六年级数学第三单元知识点总结:分数除法一、分数除法1、分数除法的意义:乘法:因数× 因数 = 积除法:积÷ 一个因数 = 另一个因数分数除法与整数除法的意义相同,表示已知两个因数的积和其中一个因数,求另一个因数的运算。
2、分数除法的计算法则:除以一个不为0的数,等于乘这个数的倒数。
规律(分数除法比较大小时):(1)当除数大于1,商小于被除数;(2)当除数小于1(不等于0),商大于被除数;(3)当除数等于1,商等于被除数。
“[ ]”叫做中括号。
一个算式里,如果既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的.二、分数除法解决问题(求单位“1”的量(用除法):已知单位“1”的几分之几是多少,求单位“1”的量。
)1、数量关系式和分数乘法解决问题中的关系式相同:(1)分率前是“的":单位“1"的量×分率=分率对应量(2)分率前是“多或少”的意思: 单位“1"的量×(1分率)=分率对应量2、解法:(建议:最好用方程解答)(1)方程:根据数量关系式设未知量为X,用方程解答。
(2)算术(用除法): 分率对应量÷对应分率 = 单位“1"的量3、求一个数是另一个数的几分之几:就一个数÷另一个数4、求一个数比另一个数多(少)几分之几: 两个数的相差量÷单位“1"的量或:① 求多几分之几:大数÷小数– 1② 求少几分之几: 1 –小数÷大数三、比和比的应用(一)、比的意义1、比的意义:两个数相除又叫做两个数的比。
2、在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比的前项除以后项所得的商,叫做比值。
例如 15 :10 = 15÷10=3/2(比值通常用分数表示,也可以用小数或整数表示) ∶∶ ∶ ∶前项比号后项比值3、比可以表示两个相同量的关系,即倍数关系。
六年级第三单元 分数除法知识点整理分数除法1、分数除法的意义:乘法: 因数 × 因数 = 积 除法: 积 ÷ 一个因数 = 另一个因数分数除法与整数除法的意义相同,表示已知两个因数的积和其中一个因数,求另一个因数的运算。
例如:98÷32表示已知两个因数的积是98,其中一个因数是32,求另一个因数是多少。
2、分数除法计算法则:除以一个不为0的数,等于乘这个数的倒数。
(甲数除以乙数(0除外),等于乘乙数的倒数) 例如:98÷32=98×233、除法规律(分数除法比较大小时):(1)、当除数大于1,商小于被除数;(2)、当除数小于1(不等于0),商大于被除数;(3)、当除数等于1,商等于被除数。
4、 “[]”叫做中括号。
一个算式里,如果既有小括号,又有中括号,要先算小括号里面的, 再算中括号里面的。
二、分数除法解决问题 (未知单位“1”的量(用除法):已知单位“1”的几分之几是多少,求单位“1”的量。
)1、数量关系式和分数乘法解决问题中的关系式相同:(1)分率前是“的”: 单位“1”的量×分率=分率对应量(2)分率前是“多或少”的意思: 单位“1”的量×(1±分率)=分率对应量2、解法:(建议:最好用方程解答)(1)方程: 根据数量关系式设未知量为X,用方程解答。
(2)算术(用除法): 对应量÷对应分率 = 单位“1”的量3、求一个数是另一个数的几分之几: 比较量÷单位“1”的量=分率4、求一个数比另一个数多(少)几分之几:两个数的相差量÷单位“1”的量=多(少)的分率或:① 求多几分之几:大数÷小数 – 1② 求少几分之几: 1 - 小数÷大数三、工程问题用“1”表示工作总量,用工作时间1表示工作效率,用工作总量÷工作效率求出工作时间。
数量关系:工作效率×工作时间=工作总量工作总量÷工作时间=工作效率 工作总量÷工作效率=工作时间。
最新版六年级数学上册第三单元分数除法1.分数除法计算(1)分数除法的意义和分数除以整数整数除法的意义:已知两个因数的积与其中一个因数,求另一个因数的运算。
已知两个因数的积与其中一个因数,求另一个因数,用(除法)计算。
1013103=÷的意义是:已知两个因数的积是103,其中一个因数是3,求另一个因数是多少。
分数除法的意义与整数除法的意义相同,都是已知两个因数的积与其中一个因数,求另一个因数的运算。
分数除以整数的计算方法把一个数平均分成整数份,求其中的几份就是求这个数的几分之几是多少。
分数除以整数(0除外)的计算方法:(1)用分子和整数相除的商做分子,分母不变。
(2)分数除以整数,等于分数乘这个整数的倒数。
练习: 1.填空(1)根据3565372=⨯和分数除法意义可得:=÷53356( ),=÷72356( )。
(2)把29m 长的绳子平均剪成4段,每段是29m 的( )。
(3)打字员打一份文件,打了20分钟后还剩52,平均每分钟打这份文件的( )。
2.列式计算。
(1)一个数的6倍是51,这个数是多少?(2)51的61是多少?3.看图列式计算。
811(2)一个数除以分数知识点一:一个数除以分数的计算方法:一个数除以分数,等于这个数乘分数的倒数。
知识点二:分数除法的统一计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数。
知识点三:商与被除数的大小关系:一个数(0除外)除以小于1的数,商大于被除数,除以1,商等于被除数,除以大于1的数,商小于被除数。
0除以任何数商都为0.练习:1.算一算4851625÷ 44392213÷ 1427277⨯ 210÷2.填空。
(1)32的43是( ),它和32÷( )得数相同。
(2)分数除法可以转化为( )进行计算,计算过程中,转变成乘( )的倒数。
4.判断。
(1)两个真分数相除,商大于被除数。
分数除法单元知识点的归纳与整理一、分数除法的意义:分数除法是分数乘法的逆运算,已知两个数的积与其中一个因数,求另一个因数的运算。
二、分数除法计算法则:除以一个数(0除外),等于乘上这个数的倒数。
1、被除数÷除数=被除数×除数的倒数。
2、除法转化成乘法时,被除数一定不能变,“÷”变成“×”,除数变成它的倒数。
3、分数除法算式中出现小数、带分数时要先化成分数、假分数再计算。
4、被除数与商的变化规律:①除以大于1的数,商小于被除数:a÷b=c当b>1时,c(a≠0)②除以小于1的数,商大于被除数:a÷b=c当b<1时,c>a(a≠0b≠0)③除以等于1的数,商等于被除数:a÷b=c当b=1时,c=a三、分数除法混合运算①连除:属同级运算,按照从左往右的顺序进行计算;或者先把所有除法转化成乘法再计算;或者依据“除以几个数,等于乘上这几个数的积”的简便方法计算。
加、减法为一级运算,乘、除法为二级运算。
②混合运算:没有括号的先乘、除后加、减,有括号的先算括号里面,再算括号外面。
四、比:两个数相除也叫两个数的比1、比式中,比号(∶)前面的数叫前项,比号后面的项叫做后项,比号相当于除号,比的前项除以后项的商叫做比值。
2、比表示的是两个数的关系,可以用分数表示,写成分数的形式,读作几比几。
注:区分比和比值:比值是一个数,通常用分数表示,也可以是整数、小数。
比是一个式子,表示两个数的关系,可以写成比,也可以写成分数的形式。
3、比的基本性质:比的前项和后项同时乘以或除以相同的数(0除外),比值不变。
3、化简比:化简之后结果还是一个比,不是一个数。
(1)、用比的前项和后项同时除以它们的最大公约数。
(2)、两个分数的比,用前项后项同时乘分母的最小公倍数,再按化简整数比的方法来化简。
也可以求出比值再写成比的形式。
(3)、两个小数的比,向右移动小数点的位置,也是先化成整数比。
分数除法1、分数除法的意义(1)乘法:因数*因数=积;除法:积/一个因数=另一个因数(2)分数除法与整数除法的意义相同,表示已知两个因数的积和其中一个因数,求另一个因数的运算。
例如:3/44/5表示已知两个因数的积是3/4和其中一个因数是4/5,求另一个因数的运算。
2、分数除法的计算法则除以一个不为0的数,等于乘这个数的倒数。
先约分再计算。
只有在乘号的两边或连乘时才能约分。
注:0例如:3(1(2(34(1(2除法:a(3计算结束,认真验算。
5、分数除法应用题1.观察题目中有没有分率,发现分率先找关键句。
(关键句是指含有分率的句子)?2.找单位“1”(单位“1”是指要平均分的量,一般在“比”“相当于”“是”“占”的后面)?3.分析数量关系???单位“1”的量×分率=?分率对应量例如:一批煤,运走3/5,正好是6吨,这批煤有多少吨??“3/5”是分率,找单位“1”,根据“运走3/5”就是“运走的是这批煤的3/5”把这批煤看做单位“1”;数量关系:一批煤×3/5=运走的;这批煤的吨数不知道,用方程解?解:设这批煤有X吨?3/5X=6????X=6÷3/5?X=6×5/3?X=10例如:一批煤,运走3/5,剩下6吨,这批煤有多少吨??“3/5”是分率,找单位“1”,根据“运走3/5”就是“运走的是这批煤的3/5”把这批煤看做单位“1”;数量关系:一批煤×3/5=运走的;这批煤的吨数不知道,用方程解?解:设这批煤有X吨X—3/5X=6????2/5X=6?X=6÷2/5?X=6×5/2???????》前项后项b.理解比的意义,找和要分配的量相对应的份数c.求出每份数???要分配的量÷相对应的份数=每份数?d.求要求的量???每份数×相应的份数=要求的量?e.验算例如:学校把栽260棵树的任务按4:5:4分配给六年级一二三班,六年级三个班各栽了多少棵树?? a.找要分配的量???“260棵树”?b.理解比的意义,找和要分配的量相对应的份数(因为260棵树是三个班共栽的,所以相应的份数是4+5+4=13份)?c.求出每份数要分配的量÷相对应的份数=每份数???260÷13=?20(棵)?d.求要求的量?每份数×相应的份数=要求的量?一班:20×4=?80棵?二班:20×5=100棵?三班:20×4=?80棵? e.验算?80+100+80=260棵???80:100:80=4:5:4。
分数除法总结知识点一、分数的性质1. 分数的定义:分数是指由分子和分母组成的有理数,分子表示被分成的份数,分母表示每份的数量。
2. 分数的大小比较:分数的大小比较可以通过分子和分母的比较来判断,分子大的分数大,分母大的分数小。
3. 分数的基本性质(1)相等的分数:如果两个分数的分子和分母成比例,则它们是相等的。
(2)最简分数:如果一个分数的分子和分母没有公因数,那么它就是最简分数。
(3)分数的约分和通分:约分是指将分数的分子和分母除以它们的最大公因数,使得分数变为最简分数。
通分是指使分数的分母相等,可以通过分数相乘来实现。
二、分数的除法运算规律1. 分数除法的计算:分数除法的计算规律是:先将除数取倒数,然后与被除数相乘即可得到商。
2. 分数除法的性质:分数除法也满足分数的运算性质,如交换律、结合律等。
3. 分数除法的逆运算:分数的除法运算的逆运算是分数的乘法运算。
三、分数除法的解题方法1. 分数除法的算术操作:在分数除法的运算过程中,我们需要先将除数取倒数,然后与被除数相乘,求得商。
2. 分数除法的解题步骤:解决分数除法的问题,我们需要按照以下步骤进行:(1)将除数取倒数;(2)将被除数与除数的倒数相乘,求得商。
3. 分数除法的解题技巧:在解题过程中,我们需要注意分数的约分和通分,以及分数的化简。
四、分数除法的应用1. 分数除法在生活中的应用:分数除法在生活中有着丰富的应用,比如厨房中的食材配比、药品的配比等。
2. 分数除法在数学中的应用:分数除法在数学中有着广泛的应用,比如在分数的加减乘除运算中经常涉及到分数的除法运算。
3. 分数除法在其它学科中的应用:分数除法在物理、化学、经济学等学科中都有着丰富的应用,比如在物质的比例、化学反应中物质的配比等方面。
五、分数除法的拓展1. 分数除法与整数除法的关系:分数除法可以看作是整数除法的一种拓展,它们有着类似的运算规律和解题方法。
2. 分数除法与分数乘法的关系:分数除法的逆运算是分数乘法,它们是相互联系的。
分数除法知识点总结分数除法是指两个分数相除的运算。
在分数除法中,我们需要了解以下几个知识点:1.分数除法的定义:分数除法是指将一个分数除以另一个分数的运算。
分数除法可以用以下等式表示:$\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot\frac{d}{c} = \frac{a \cdot d}{b \cdot c}$。
其中,$\frac{a}{b}$和$\frac{c}{d}$是两个分数,$a$、$b$、$c$、$d$是分子和分母。
2.分数除法的步骤:-第一步:将除法转换为乘法。
将除法问题转换为乘法问题,即将除号变成乘号。
-第二步:求解乘法问题。
将两个分数相乘,分子相乘得到新的分子,分母相乘得到新的分母。
-第三步:化简结果。
将得到的分子和分母化简,使得它们的最大公约数为13.相同分母的分数除法:当两个分数的分母相同时,可以直接将它们的分子相除得到结果的分子,分母保持不变。
即 $\frac{a}{b} \div \frac{c}{b} =\frac{a}{c}$。
例如,$\frac{2}{5} \div \frac{3}{5} = \frac{2}{3}$。
4.不同分母的分数除法:当两个分数的分母不相同时,我们需要通过求最小公倍数来找到一个相同的分母。
分数相除的步骤如下:-第一步:求两个分母的最小公倍数。
-第二步:将两个分数的分子分别乘以最小公倍数除以原来的分母,得到新的分子。
-第三步:两个新的分数的分母都为最小公倍数,将它们的分子相除得到结果的分子。
5.分数除以整数的运算:当分数除以一个整数时,将整数看作分母为1的分数,然后按照分数除法的规则进行计算。
即 $\frac{a}{b} \div c = \frac{a}{b} \div\frac{c}{1} = \frac{a}{b} \cdot \frac{1}{c} = \frac{a}{b \cdotc}$。