贝塞尔公式计算
- 格式:xlsx
- 大小:32.41 KB
- 文档页数:4
样本标准差得表示公式数学表达式:•S-标准偏差(%)•n-试样总数或测量次数,一般n值不应少于20-30个•i-物料中某成分得各次测量值,1~n;[编辑]标准偏差得使用方法•在价格变化剧烈时,该指标值通常很高。
•如果价格保持平稳,这个指标值不高。
•在价格发生剧烈得上涨/下降之前,该指标值总就是很低。
[编辑]标准偏差得计算步骤标准偏差得计算步骤就是:步骤一、(每个样本数据-样本全部数据之平均值)2。
步骤二、把步骤一所得得各个数值相加。
步骤三、把步骤二得结果除以 (n - 1)(“n”指样本数目)。
步骤四、从步骤三所得得数值之平方根就就是抽样得标准偏差。
[编辑]六个计算标准偏差得公式[1][编辑]标准偏差得理论计算公式设对真值为X得某量进行一组等精度测量, 其测得值为l1、l2、……l n。
令测得值l与该量真值X之差为真差占σ, 则有σ= l i−X1= l2−Xσ2……σn = l n−X我们定义标准偏差(也称标准差)σ为(1)由于真值X都就是不可知得, 因此真差σ占也就无法求得, 故式只有理论意义而无实用价值。
[编辑]标准偏差σ得常用估计—贝塞尔公式由于真值就是不可知得, 在实际应用中, 我们常用n次测量得算术平均值来代表真值。
理论上也证明, 随着测量次数得增多, 算术平均值最接近真值, 当时, 算术平均值就就是真值。
于就是我们用测得值l i与算术平均值之差——剩余误差(也叫残差)V i来代替真差σ , 即设一组等精度测量值为l1、l2、……l n则……通过数学推导可得真差σ与剩余误差V得关系为将上式代入式(1)有(2)式(2)就就是著名得贝塞尔公式(Bessel)。
它用于有限次测量次数时标准偏差得计算。
由于当时,,可见贝塞尔公式与σ得定义式(1)就是完全一致得。
应该指出, 在n有限时, 用贝塞尔公式所得到得就是标准偏差σ得一个估计值。
它不就是总体标准偏差σ。
因此, 我们称式(2)为标准偏差σ得常用估计。

样本标准差的表示公式数学表达式:•S—标准偏差(%)•n—试样总数或测量次数,一般n值不应少于20—30个•i—物料中某成分的各次测量值,1~n;[编辑]标准偏差的使用方法•在价格变化剧烈时,该指标值通常很高。
•如果价格保持平稳,这个指标值不高。
•在价格发生剧烈的上涨/下降之前,该指标值总是很低. [编辑]标准偏差的计算步骤标准偏差的计算步骤是:步骤一、(每个样本数据-样本全部数据之平均值)2。
步骤二、把步骤一所得的各个数值相加。
步骤三、把步骤二的结果除以 (n — 1)(“n”指样本数目)。
步骤四、从步骤三所得的数值之平方根就是抽样的标准偏差。
[编辑]六个计算标准偏差的公式[1][编辑]标准偏差的理论计算公式设对真值为X的某量进行一组等精度测量, 其测得值为l1、l2、……l n。
令测得值l与该量真值X之差为真差占σ,则有σl i−X.。
.。
文档交流1 =σ2 = l2−X……σn = l n−X我们定义标准偏差(也称标准差)σ为(1)由于真值X都是不可知的,因此真差σ占也就无法求得, 故式只有理论意义而无实用价值。
[编辑]标准偏差σ的常用估计—贝塞尔公式由于真值是不可知的,在实际应用中, 我们常用n次测量的算术平均值来代表真值。
理论上也证明, 随着测量次数的增多,算术平均值最接近真值,当时,算术平均值就是真值。
.。
.文档交流于是我们用测得值l i与算术平均值之差——剩余误差(也叫残差)V i来代替真差σ,即设一组等精度测量值为l1、l2、……l n则……通过数学推导可得真差σ与剩余误差V的关系为将上式代入式(1)有(2)式(2)就是著名的贝塞尔公式(Bessel).它用于有限次测量次数时标准偏差的计算.由于当时,,可见贝塞尔公式与σ的定义式(1)是完全一致的。
应该指出, 在n有限时, 用贝塞尔公式所得到的是标准偏差σ的一个估计值。
它不是总体标准偏差σ。
因此, 我们称式(2)为标准偏差σ的常用估计。


样本标准差的表示公式数学表达式:•S—标准偏差(%)•n—试样总数或测量次数,一般n值不应少于20—30个•i—物料中某成分的各次测量值,1~n;[编辑]标准偏差的使用方法•在价格变化剧烈时,该指标值通常很高。
•如果价格保持平稳,这个指标值不高。
•在价格发生剧烈的上涨/下降之前,该指标值总是很低. [编辑]标准偏差的计算步骤标准偏差的计算步骤是:步骤一、(每个样本数据-样本全部数据之平均值)2。
步骤二、把步骤一所得的各个数值相加。
步骤三、把步骤二的结果除以 (n — 1)(“n”指样本数目)。
步骤四、从步骤三所得的数值之平方根就是抽样的标准偏差。
[编辑]六个计算标准偏差的公式[1][编辑]标准偏差的理论计算公式设对真值为X的某量进行一组等精度测量, 其测得值为l1、l2、……l n。
令测得值l与该量真值X之差为真差占σ,则有σl i−X.。
.。
文档交流1 =σ2 = l2−X……σn = l n−X我们定义标准偏差(也称标准差)σ为(1)由于真值X都是不可知的,因此真差σ占也就无法求得, 故式只有理论意义而无实用价值。
[编辑]标准偏差σ的常用估计—贝塞尔公式由于真值是不可知的,在实际应用中, 我们常用n次测量的算术平均值来代表真值。
理论上也证明, 随着测量次数的增多,算术平均值最接近真值,当时,算术平均值就是真值。
.。
.文档交流于是我们用测得值l i与算术平均值之差——剩余误差(也叫残差)V i来代替真差σ,即设一组等精度测量值为l1、l2、……l n则……通过数学推导可得真差σ与剩余误差V的关系为将上式代入式(1)有(2)式(2)就是著名的贝塞尔公式(Bessel).它用于有限次测量次数时标准偏差的计算.由于当时,,可见贝塞尔公式与σ的定义式(1)是完全一致的。
应该指出, 在n有限时, 用贝塞尔公式所得到的是标准偏差σ的一个估计值。
它不是总体标准偏差σ。
因此, 我们称式(2)为标准偏差σ的常用估计。
![[最新]贝塞尔公式](https://uimg.taocdn.com/85bcc8566c85ec3a87c2c5ec.webp)
[最新]贝塞尔公式样本标准差的表示公式数学表达式:, S-标准偏差(%), n-试样总数或测量次数,一般n值不应少于20-30个, i-物料中某成分的各次测量值,1,n; [编辑]标准偏差的使用方法, 在价格变化剧烈时,该指标值通常很高。
, 如果价格保持平稳,这个指标值不高。
, 在价格发生剧烈的上涨/下降之前,该指标值总是很低。
[编辑]标准偏差的计算步骤标准偏差的计算步骤是:2 步骤一、(每个样本数据 , 样本全部数据之平均值)。
步骤二、把步骤一所得的各个数值相加。
步骤三、把步骤二的结果除以 (n - 1)(“n”指样本数目)。
步骤四、从步骤三所得的数值之平方根就是抽样的标准偏差。
[编辑][1]六个计算标准偏差的公式 [编辑]标准偏差的理论计算公式设对真值为X的某量进行一组等精度测量, 其测得值为l、l、……l。
令12n测得值l与该量真值X之差为真差占σ, 则有σ = l ? X 1iσ = l ? X 22……σ = l ? X nn我们定义标准偏差(也称标准差)σ为(1)由于真值X都是不可知的, 因此真差σ占也就无法求得, 故式只有理论意义而无实用价值。
[编辑]标准偏差σ的常用估计—贝塞尔公式由于真值是不可知的, 在实际应用中, 我们常用n次测量的算术平均值来代表真值。
理论上也证明, 随着测量次数的增多, 算术平均值最接近真值, 当时, 算术平均值就是真值。
于是我们用测得值l与算术平均值之差——剩余误差(也叫残差)V来代ii替真差σ , 即设一组等精度测量值为l、l、……l 12n则……通过数学推导可得真差σ与剩余误差V的关系为将上式代入式(1)有(2)式(2)就是著名的贝塞尔公式(Bessel)。
它用于有限次测量次数时标准偏差的计算。
由于当时,,可见贝塞尔公式与σ的定义式(1)是完全一致的。
应该指出, 在n有限时, 用贝塞尔公式所得到的是标准偏差σ的一个估计值。
它不是总体标准偏差σ。
因此, 我们称式(2)为标准偏差σ的常用估计。

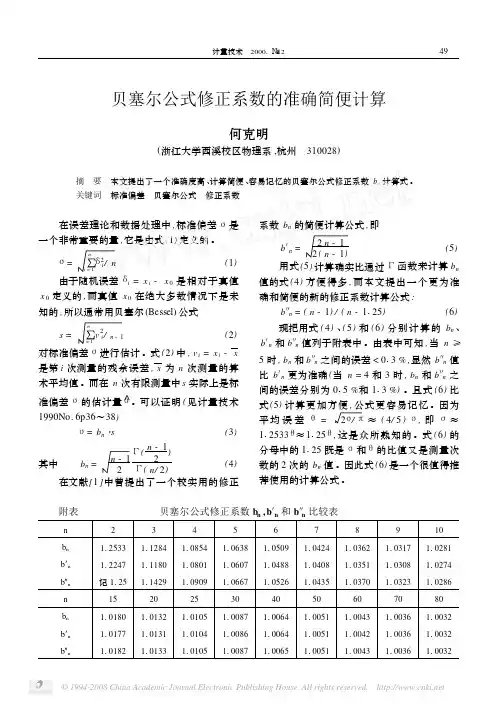
C.贝塞尔函数的有关公式贝塞尔方程的持解B p(z)为(柱)贝塞尔函数。
有第一类柱贝塞尔函数J p(z)p为整数n时,J-n=(-1)n J n;p不为整数时,J p与J-p线性无关。
第二类柱贝塞尔函数N p(z)(柱诺依曼函数)n为整数时N-n=(-1)n N n。
第三类柱贝塞尔函数H p(z) (柱汉开尔函数):第一类柱汉开尔函数H p(1)(z)= J p(z)+j N p(z)第二类柱汉开尔函数H p(2)(z)= J p(z)-j N p(z)大宗量z小宗量z 0,为欧拉常数见微波与光电子学中的电磁理论p668J n(z)的母函数和有关公式函数e z(t/2-1/2t)称为第一类贝塞尔函数的母函数,或称生成函数,若将此函数在t=0附近展开成罗朗级数,可得到在上式中作代换,令t=e j ,t= je j 等,可得又可得如z=x为实数贝塞尔函数的加法公式J n(z)的零点 niJ’n(z)的零点γni半整数阶贝塞尔函数J n+1/2(z)的零点χnpJ'n+1/2(z)的零点χ'npD.朗斯基行列式及其它关系式E.修正贝塞尔函数有关公式贝塞尔方程中用(j z)代换z,得到修正的贝塞尔方程方程的两个线性无关的解为I p(z)=j-p J p(j z).称为第一类修正的柱贝塞尔函数。
K p(z)=(π/2)j p+1H p(1)(j z).称为第二类修正的柱贝塞尔函数。
大宗量z小宗量z 0(0210)《古代散文》复习思考题一、填空题1.甲骨卜辞、和《易经》中的卦、爻辞是我国古代散文的萌芽。
2.深于比兴、,是先秦散文的突出特点。
3.《》长于描写外交辞令。
4.《国语》的突出特点是长于。
5.“兼爱”、“非攻”是思想的核心。
6.先秦诸子中,善养“浩然之气”。
7.先秦诸子中,提出了“言不尽意”、“得意忘言”的观点。
8.荀子的《》是我国最早以“赋”名篇的作品。
9.《鵩鸟赋》是的骚体赋。
10.枚乘的《》标志着散体赋的正式形成。

贝塞尔公式详细推导过程《贝塞尔公式的详细推导过程》引言:贝塞尔公式是数学中一种重要且广泛应用的公式,它的推导过程相对较复杂、细致,但却十分精彩。
在本文中,我们将详细介绍贝塞尔公式的推导过程,让读者对这一公式有更深入的理解。
一、贝塞尔公式的定义:贝塞尔公式是一种用连分数表示的数学公式,其一般形式为:J_n(x) = \frac{1}{\pi}\int_{0}^{\pi} \cos(n\theta - x\sin\theta)d\theta其中,J_n(x) 表示第n阶贝塞尔函数,x 是实数,\theta 表示角度,\pi 表示圆周率。
二、推导过程:1. 首先,我们从欧拉公式 e^ix = \cos(x) + i\sin(x) 出发,将其展开得到:e^{ix} = \cos(x) + i\sin(x)2. 接下来,我们将展开中的i\sin(x) 转化为两个实数的乘积。
我们知道,正弦函数的定义式为:\sin(x) = \frac{e^{ix} - e^{-ix}}{2i}代入之前的展开式,得到:i\sin(x) = \frac{e^{ix} - e^{-ix}}{2}3. 现在,我们用这个展开式来推导贝塞尔公式。
我们首先将贝塞尔函数展开成幂级数形式:J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k}4. 接下来,我们将展开式中的 e^{ix} 替换为 \cos(x) + i\sin(x):J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k} \left(\cos(x) + i\sin(x)\right)5. 然后,我们将正弦函数用欧拉公式展开为两个指数函数的乘积:J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k} \left(\cos(x) + i\frac{e^{ix} - e^{-ix}}{2}\right)6. 继续推导,我们可以将指数函数的乘积展开为两项之差:J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k} \left(\cos(x) + \frac{i e^{ix}}{2} - \frac{i e^{-ix}}{2}\right)7. 现在,我们可以将展开式中的 i 消去:J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k} \left(\cos(x) + \frac{e^{ix} - e^{-ix}}{2}\right)8. 之后,我们可以将展开式进行拆分,分别对两项进行求和,并利用复数的性质对其中的复数部分进行化简:J_n(x) = \left(\frac{x}{2}\right)^n \left(\sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k}\cos(x) + \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k}\frac{e^{ix} - e^{-ix}}{2}\right)9. 最后,我们可以将两个求和式进行整理,将其中的复数部分转化为积分形式:J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k}\cos(x) + \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k}\frac{1}{\pi}\int_{0}^{\pi} \cos(n\theta -x\sin\theta)d\theta10. 将整理后的展开式中的求和式转化为连分数形式,即可得到贝塞尔公式:J_n(x) = \frac{1}{\pi}\int_{0}^{\pi} \cos(n\theta - x\sin\theta)d\theta结论:通过上述推导过程,我们可以将贝塞尔公式从指数函数的展开式推导得到,将其转化为连分数形式。

贝塞尔公式是一个用于计算标准偏差的公式,特别是在有限次测量次数时的标准偏差计算中非常常见。
这个公式的推导是基于真差与剩余误差(也叫残差)之间的关系。
在对某一真值X进行等精度测量时,设测得值为l1、l2、……ln,其算术平均值为X'。
此时,我们可以定义真差σ为测得值li与该量真值X之差,即σ=li−X。
然后我们用剩余误差Vi来代替真差σ,即Vi = li−X'。
通过数学推导,可以得到真差σ与剩余误差V的关系式。
将上式代入标准偏差的计算公式,就可以得到贝塞尔公式。
这个公式的应用十分广泛,例如在一组测量次数较多的情况下,可以用样本方差来估计总体方差,进而计算总体标准差。

贝塞尔曲线长度计算贝塞尔曲线是常用于计算机图形学和设计中的一种曲线。
作为矢量图形设计和制作中的基本要素,贝塞尔曲线被广泛应用于包括平面设计、工业设计、建筑设计、动画制作、游戏开发等领域。
贝塞尔曲线的长度计算是这一领域中非常重要的一个问题。
因为贝塞尔曲线不像直线那样是可以直观地测量长度的,所以需要采用特定的方法来计算贝塞尔曲线的长度。
首先需要了解的是,计算贝塞尔曲线长度的方法与贝塞尔曲线的控制点个数有关。
通常情况下,我们所使用的贝塞尔曲线是二次贝塞尔曲线或三次贝塞尔曲线。
对于二次贝塞尔曲线,计算长度的方法是比较简单的。
我们可以通过逐步拆分曲线段,并计算曲线段长度的方法来计算整条曲线的长度。
具体计算公式为:L ≈ ∑k=1n-1√(xk+1-xk)²+(yk+1-yk)²其中,n为曲线段的数量,xk和yk分别是曲线段起点和终点的横纵坐标。
对于三次贝塞尔曲线,计算长度的方法则略有不同。
由于三次贝塞尔曲线存在两个控制点,所以需要先将曲线拆分成若干条二次贝塞尔曲线,再分别计算曲线段长度并相加得到整条曲线的长度。
具体计算公式为:L ≈ ∑k=1n√(xk+1-xk)²+(yk+1-yk)²其中,n为二次贝塞尔曲线段的数量,xk和yk分别是曲线段起点和终点的横纵坐标。
需要注意的是,上述公式只是计算长度的近似值,因为贝塞尔曲线通常是一个连续的曲线,实际测量长度时会存在一定的误差。
但是这种方法仍然被广泛应用于各种设计领域,并获得了一定的实用效果。
除了上述计算贝塞尔曲线长度的方法外,还可以使用计算机辅助设计软件来自动计算贝塞尔曲线的长度。
例如,在Adobe Illustrator 中,可以直接通过选择曲线并查看信息面板来获取曲线的长度和其他信息。
在AutoCAD中,也有相应的命令可以帮助我们计算贝塞尔曲线的长度。
总之,计算贝塞尔曲线长度是一项非常重要的工作,对于各种设计领域都具有重要作用。

wps贝塞尔公式WPS(金山办公)是一款办公软件套装,包含WPS表格(类似Excel)、WPS文字(类似Word)和WPS演示(类似PPT)。
在WPS表格中,可以使用贝塞尔公式来计算贝塞尔函数值。
贝塞尔函数是一类在计算机图形学和工程计算中广泛应用的函数,用于描述曲线的形状。
贝塞尔公式可以根据给定的控制点计算出贝塞尔曲线上的点。
在WPS表格中,可以使用BESSELI 和BESSELY函数来计算贝塞尔函数值。
BESSELI函数计算贝塞尔函数值(也称为Weber函数或Neumann函数),其语法如下:BESSELI(X, N)其中,X是计算函数的值,N是函数的阶数。
BESSELY函数计算贝塞尔函数值(也称为Weber函数或Neumann函数),其语法如下:BESSELY(X, N)其中,X是计算函数的值,N是函数的阶数。
在WPS表格中,可以使用贝塞尔公式来计算贝塞尔曲线上的点,从而绘制出贝塞尔曲线。
具体步骤如下:1. 输入控制点:在表格中输入贝塞尔曲线的控制点,例如A1、B1、C1等。
2. 计算贝塞尔函数值:使用BESSELI或BESSELY函数计算贝塞尔函数值,例如在D1单元格输入=BESSELI(A1, 2),在E1单元格输入=BESSELY(B1, 2),在F1单元格输入=BESSELY(C1,2)。
3. 绘制贝塞尔曲线:使用绘图工具,在图表中绘制出贝塞尔曲线。
在WPS表格中,可以通过“插入”菜单选择“图表”,然后选择合适的图表类型(例如折线图),将计算出的贝塞尔函数值和对应的X值作为数据源,绘制出贝塞尔曲线。
最后,请注意,贝塞尔公式在WPS表格中的具体实现可能因版本和功能更新而有所不同。
在使用过程中,请参考WPS表格的官方文档和帮助中心获取更详细的信息。
贝塞尔公式
贝塞尔公式,又名分段函数法,是1800年由法国数学家拉普拉斯贝塞尔(Raphael de la Pierre)发明的一种数学工具,在数学、计算机科学和制图等领域有广泛的应用。
基本思想是一些变化相对缓慢的函数,经过变换之后,可以把复杂的函数分解成一系列的相对简单的子函数,再通过特殊的算法,把这些子函数加以组合,使复杂函数有更高的准确度。
贝塞尔公式的基本原理是,在多边形的边界内,用多边形的每条边建立一个分段函数,这种函数有两个功能:其一是最多可以接受多边形的边数来作为分段函数的参数;其二是可以根据贝塞尔曲线边缘上不同位置上上下文规律,来调节分段函数的形状。
贝塞尔公式的运用范围涉及多次数学变换,包括但不限于:
一、几何变换:包括坐标变换,参数变换以及变型几何变换等;
二、代数变换:包括一般的线性变换、二次曲面等变换;
三、拟合变换:对一组数据进行拟合,使用贝塞尔公式来计算,得到相应拟合曲线;
四、曲线变换:把曲线变换成贝塞尔曲线,以便精确描述曲线形状;
五、计算机图形学:将贝塞尔曲线应用于计算机图形学中,可以生成更加精细的图像;
此外,贝塞尔公式还可以应用于投影和地理信息系统,用于定义投影器的特征参数,以便在大地投影中取得较高的准确度。
根据贝塞
尔公式的定义,数学平面上的点可以被映射到空间中,因此用于3D
绘图的技术也能用贝塞尔公式来实现。
贝塞尔公式的应用极其广泛,从拟合曲线到制造更加精细的图像,从改善绘图精度到把数据映射到三维空间中,都可以利用这一数学工具。
贝塞尔公式不仅能够帮助人们实现复杂的数学变换,还能大大提高运算的准确度。
bezier曲线表达式贝塞尔曲线是一种光滑的曲线,它由一系列的控制点来定义。
它可以用于各种各样的应用,包括计算机图形学、动画和物理模拟等。
贝塞尔曲线最常见的形式是二次和三次贝塞尔曲线。
二次贝塞尔曲线由三个点来定义:起始点、控制点和终止点。
这三个点的位置决定了曲线的形状。
三次贝塞尔曲线由四个点来定义:起始点、两个控制点和终止点。
通过调整这些点的位置,可以创建各种不同形状的曲线。
一般来说,二次贝塞尔曲线可以用以下的形式来表示:P(t) = (1 - t)² * P₀ + 2 * t * (1 - t) * P₁ + t² * P₂其中,P(t)是曲线上的点,t的取值范围是0到1,P₀、P₁和P₂分别是起始点、控制点和终止点。
三次贝塞尔曲线的表达式稍微复杂一些:P(t) = (1 - t)³ * P₀ + 3 * t * (1 - t)² * P₁ + 3 * t² * (1 - t) * P₂ + t³ * P₃其中,P(t)是曲线上的点,t的取值范围是0到1,P₀、P₁、P₂和P₃分别是起始点、两个控制点和终止点。
贝塞尔曲线的特点之一是它具有良好的局部控制性。
这意味着通过调整控制点的位置,我们可以在曲线的局部区域内改变曲线的形状,而不会影响其他区域。
这使得贝塞尔曲线在图形设计中非常有用,因为我们可以通过少量的控制点来创建复杂的曲线形状。
另一个重要的特性是贝塞尔曲线可以近似任何形状。
通过增加控制点的数量,我们可以逼近任何形状,从简单的直线到复杂的曲线。
这使得贝塞尔曲线在计算机图形学和动画中非常有用,因为它们可以用来创建各种各样的图形效果和动画效果。
贝塞尔曲线的计算和渲染算法有多种不同的实现方式。
一种常见的方法是使用递归二分法来计算曲线上的点。
具体来说,我们可以从起始点和终止点开始,然后通过将曲线分成两半并计算中间点来逐步逼近想要的曲线形状。
样本标准差得表示公式数学表达式:•S-标准偏差(%)•n-试样总数或测量次数,一般n值不应少于20-30个•i-物料中某成分得各次测量值,1~n;[编辑]标准偏差得使用方法•在价格变化剧烈时,该指标值通常很高。
•如果价格保持平稳,这个指标值不高。
•在价格发生剧烈得上涨/下降之前,该指标值总就是很低。
[编辑]标准偏差得计算步骤标准偏差得计算步骤就是:步骤一、(每个样本数据-样本全部数据之平均值)2。
步骤二、把步骤一所得得各个数值相加。
步骤三、把步骤二得结果除以 (n - 1)(“n”指样本数目)。
步骤四、从步骤三所得得数值之平方根就就是抽样得标准偏差。
[编辑]六个计算标准偏差得公式[1][编辑]标准偏差得理论计算公式设对真值为X得某量进行一组等精度测量, 其测得值为l1、l2、……l n。
令测得值l与该量真值X之差为真差占σ, 则有σ= l i−X1= l2−Xσ2……σn = l n−X我们定义标准偏差(也称标准差)σ为(1)由于真值X都就是不可知得, 因此真差σ占也就无法求得, 故式只有理论意义而无实用价值。
[编辑]标准偏差σ得常用估计—贝塞尔公式由于真值就是不可知得, 在实际应用中, 我们常用n次测量得算术平均值来代表真值。
理论上也证明, 随着测量次数得增多, 算术平均值最接近真值, 当时, 算术平均值就就是真值。
于就是我们用测得值l i与算术平均值之差——剩余误差(也叫残差)V i来代替真差σ , 即设一组等精度测量值为l1、l2、……l n则……通过数学推导可得真差σ与剩余误差V得关系为将上式代入式(1)有(2)式(2)就就是著名得贝塞尔公式(Bessel)。
它用于有限次测量次数时标准偏差得计算。
由于当时,,可见贝塞尔公式与σ得定义式(1)就是完全一致得。
应该指出, 在n有限时, 用贝塞尔公式所得到得就是标准偏差σ得一个估计值。
它不就是总体标准偏差σ。
因此, 我们称式(2)为标准偏差σ得常用估计。
样本标准差的表示公式数学表达式:∙S-标准偏差(%)∙n-试样总数或测量次数,一般n值不应少于20-30个∙i-物料中某成分的各次测量值,1~n;[编辑]标准偏差的使用方法∙在价格变化剧烈时,该指标值通常很高。
∙如果价格保持平稳,这个指标值不高。
∙在价格发生剧烈的上涨/下降之前,该指标值总是很低。
[编辑]标准偏差的计算步骤标准偏差的计算步骤是:步骤一、(每个样本数据-样本全部数据之平均值)2。
步骤二、把步骤一所得的各个数值相加。
步骤三、把步骤二的结果除以 (n - 1)(“n”指样本数目)。
步骤四、从步骤三所得的数值之平方根就是抽样的标准偏差。
[编辑]六个计算标准偏差的公式[1][编辑]标准偏差的理论计算公式设对真值为X的某量进行一组等精度测量, 其测得值为l1、l2、……l n。
令测得值l与该量真值X之差为真差占σ, 则有σ1 = l i−X σ2 = l2−X……σn = l n−X我们定义标准偏差(也称标准差)σ为(1)由于真值X都是不可知的, 因此真差σ占也就无法求得, 故式只有理论意义而无实用价值。
[编辑]标准偏差σ的常用估计—贝塞尔公式由于真值是不可知的, 在实际应用中, 我们常用n次测量的算术平均值来代表真值。
理论上也证明, 随着测量次数的增多, 算术平均值最接近真值, 当时, 算术平均值就是真值。
于是我们用测得值l i与算术平均值之差——剩余误差(也叫残差)V i来代替真差σ , 即设一组等精度测量值为l1、l2、……l n则……通过数学推导可得真差σ与剩余误差V的关系为将上式代入式(1)有(2)式(2)就是著名的贝塞尔公式(Bessel)。
它用于有限次测量次数时标准偏差的计算。
由于当时,,可见贝塞尔公式与σ的定义式(1)是完全一致的。
应该指出, 在n有限时, 用贝塞尔公式所得到的是标准偏差σ的一个估计值。
它不是总体标准偏差σ。
因此, 我们称式(2)为标准偏差σ的常用估计。
为了强调这一点, 我们将σ的估计值用“S ”表示。
实验标准(偏)差——贝塞尔公式
(2011-08-08 12:57:13)
对同一被测量X作n次测量,表征每次测量结果分散性的
量s(xi)可按下式算出:
式中xi为第i次测量的结果; 为所考虑的n次测量结果的算术平均值;称为残差。
上式称作贝塞尔公式,它描述了各个测量值的分散度。
有时将s(xi)称作单次测量结果的标准偏差,或称为实验标准差。
自由度?
在方差计算中,自由度为和的项数减去和的限制数,记为?。
在重复条件下对被测量做n次独立测量,其样本方差
式中vi为残差。
所以在方差的计算式中,和的项数即为残差vi的个数n。
而且残差之和为零,即??i=0 是限制条件,故限制数为1,因此可得自由度?=n-1。