高中数学阶段质量检测(三)统计案例北师大选修2-3

第三章单元质量评估时限：120分钟满分：150分第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的)1．散点图在回归分析过程中的作用是(D)A．查找个体个数B．比较个体数据大小关系C．探究个体分类D．粗略判断变量是否线性相关解析：由于散点图是由解释变量和预报变量绘制的图形，所以它可以粗略判断变量间是否具有线性相关关系，故选D.2．变量x，y的5组数据的散点图如图所示，去掉哪个点对应的数据后，剩下的4组数据的线性相关性最强(A)A．E B．CC．D D．A解析：E偏离得最多，故选A.3．对有线性相关关系的两个变量建立的回归直线方程y＝a＋bx中，回归系数b(A) A．可以小于0 B．只能大于0C．能等于0 D．只能小于0解析：若b＝0，则相关系数r＝0，此时不具有线性相关关系，但b可以大于0也可以小于0.4．对两个变量y与x进行回归分析，分别选择不同的模型，它们的相关系数r如下，其中拟合效果最好的模型是(A)A．模型Ⅰ：相关系数r为0.96B．模型Ⅱ：相关系数r为－0.81C．模型Ⅲ：相关系数r为－0.53D．模型Ⅳ：相关系数r为0.35解析：|r|越大，拟合效果越好，故选A.5．下列说法不正确的是(D)A．回归分析中，R2的值越大，说明残差平方和越小B．若一组观测值(x1，y1)，(x2，y2)，…，(x n，y n)满足y i＝bx i＋a＋e i(i＝1,2，…，n)，若e i恒为0，则R2＝1C．回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法D．画残差图时，纵坐标为残差，横坐标一定是编号解析：画残差图时，纵坐标为残差，横坐标可以是编号，也可以是原始数据，也可以是数据估计值，D不正确，故选D.6．一位母亲记录了儿子3～9岁的身高，数据如表．由此建立的身高与年龄的回归模型为y＝7.19x＋73.93.用这个模型预测这个孩子10岁时的身高，则正确的叙述是(C)B．身高在145.83 cm以上C．身高在145.83 cm左右D．身高在145.83 cm以下解析：将x＝10代入得y＝145.83，但这种预测不一定准确，应该在这个值的左右．故选C.7．考察四个班的学生数学、物理成绩，得到列联表如下：A．34 B．20C．37 D．248．已知回归直线的斜率的估计值是1.23，样本点的中心为(4,5)，则线性回归方程是(C)A．y＝1.23x＋4 B．y＝1.23x＋5C．y＝1.23x＋0.08 D．y＝0.08x＋1.23解析：由题意知b＝1.23，直线经过中心(4,5)，则a＝0.08，所以线性回归方程为y＝1.23x ＋0.08.9．对两个变量y和x进行线性相关检验，n是观察值组数，r是相关系数，且已知：①n ＝7，r＝0.953 3；②n＝15，r＝0.301 2；③n＝17，r＝0.999 1；④n＝3，r＝0.995 0.则变量y和x具有相关关系的是(B)A．①和②B．①和③C ．②和④D ．③和④解析：②中r 太小，④中观察值组数太少．10．下表是某厂1～4月份用水量(单位：百吨)的一组数据：月份x 1 2 3 4 用水量y4.5432.5程是y ＝－0.7x ＋a ，则a 等于( C )A ．5B ．5.05C ．5.25D ．6解析：x ＝2.5，y ＝3.5，∵回归直线方程过定点(x ，y )，∴3.5＝－0.7×2.5＋a . ∴a ＝5.25.11．在一次男女生是否说谎的调查中，得到如表数据，根据表中数据可知下列结论中正确的是( D )说谎 不说谎 合计 男 6 7 13 女 8 9 17 合计141630A.B ．在此次调查中有99%的把握认为说谎与性别有关 C ．在此次调查中有90%的把握认为说谎与性别有关 D ．在此次调查中没有充分证据显示说谎与性别有关 解析：根据表中数据可求得χ2＝30×(6×9－7×8)213×17×14×16≈0.002 4，因为0.002 4<2.706，所。

【金学案】2015年春高中数学第三章统计案例（3课时）北师大版选修2-3知识点新课程标准的要求层次要求领域目标要求回归分析的基本思想及其初步应用通过典型案例的探究,进一步了解回归的基本思想、方法及初步应用在《数学》(必修3)概率统计的基础上,通过典型案例进一步介绍回归分析的基本思想、方法及其初步应用;通过典型案例介绍独立性检验的基本思想、方法及其初步应用,认识统计方法在决策中的作用独立性检验的基本思想及其初步应用在具体情境中,通过典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想、方法及初步应用1.在学习回归分析内容时,应首先回顾必修课程中的相关内容,复习如何画散点图,如何利用最小二乘法求线性回归方程,并关注本章内容和必修课程中相关内容的区别与联系.认识和体会进行相关性检验的必要性,了解如何求线性相关系数r,并能对两个随机变量进行回归分析.在此基础上,会将非线性回归问题转化为线性回归问题来解决.2.通过具体实例,了解独立性检验的基本思想,能够根据实际问题列出2×2列联表,求出χ2的值,并能根据求得的值判断两个变量是否相关.3.带着如下问题阅读教材:(1)为什么要引入线性相关系数?(2)如何将非线性回归模型转化为线性回归模型?(3)独立性检验的基本思想、方法是什么?(4)哪种类型的数据可以进行独立性检验,哪种类型的数据可进行回归分析?第1课时回归分析1.会对两个变量的相关关系进行分析、判断.2.了解回归分析的基本思想,会对两个变量的具体问题进行回归分析.3.掌握运用最小二乘法建立回归模型的基本步骤和方法.重点:熟练掌握回归分析,建立回归模型,求各相关指数的步骤.难点:如何求回归直线方程以及对相关系数r的理解和运用.我们每个人都有自己的身高和体重,那么如果把身高和体重分别作为变量,它们能够构成函数关系吗?问题1:散点图在考虑两个量的关系时,为了对变量之间的关系有一个大致的了解,人们通常将变量所对应的点描出来,这些点就组成了变量之间的一个图,通常称这种图为变量之间的散点图.问题2:相关关系与线性回归相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系称为相关关系.相关关系分为线性相关和非线性相关.函数关系中的两个变量间是一种确定性关系,相关关系是一种非确定性关系.线性回归:对具有相关关系的两个变量进行统计分析的一种常用方法.问题3:线性相关系数r=称为两个变量数据(x i,y i)(i=1,2,…,n)的线性相关系数.r用来刻画两个变量的线性回归效果:当r>0时,表明两个变量正相关;当r<0时,表明两个变量负相关;r的绝对值越接近于0时,表明两个变量之间越不存在线性相关关系.问题4:线性回归分析的步骤对于一组具有线性相关关系的数据:(x1,y1),(x2,y2),…,(x n,y n).(1)画散点图:看散点图是否呈条状分布.(2)求回归直线方程(最小二乘法):b=, =x i,=y i,其中(,)为样本中心点,回归直线方程必经过样本中心点(,),得a= -b ;(3)得出相关结论:回归直线方程为y=a+bx ,利用回归直线方程进行预测.“一只蝴蝶在巴西扇动翅膀,有可能会在美国的德克萨斯州引起一场龙卷风.”这就是洛伦兹1979年12月在华盛顿的“美国科学促进会”上的一次演讲中提出的“蝴蝶效应”.这次演讲给人们留下了极其深刻的印象.从此以后,所谓“蝴蝶效应”之说就不胫而走,名声远扬.“蝴蝶效应”之所以令人着迷、令人激动、发人深省,不但在于其大胆的想象力和迷人的美学色彩,而且在于其深刻的科学内涵和内在的哲学魅力.1.下列关系不属于相关关系的是().A.父母的身高与子女的身高B.人的身高与体重C.居民的收入与消费D.正方体的表面积和体积【解析】相关关系是一种非确定性关系,而D项是确定的关系,为函数关系,故选D.【答案】D2.设两个变量x与y之间具有线性相关关系,相关系数是r,回归方程为y=a+bx,那么必有().A.b与r符号相同B.a与r符号相同C.b与r符号相反D.a与r符号相反【解析】因为b与r的分母均为正,且分子相同,所以b与r同号.【答案】A3.某医院用光电比色检验尿汞时,得到尿汞含量x(毫克/升)与消化系数y的一组数据如下表:尿汞含量x 2 4 6 8 10消化系数y64 138 205 285 260若x与y具有线性相关关系,则回归直线方程是.【解析】利用公式b==26.95,a=-b=28.7,从而回归直线方程为y=26.95x+28.7.【答案】y=26.95x+28.74.某10名同学的数学、物理、语文成绩如下表:数学136 125 122 87 108 113 111 70 94 74物理107 91 92 76 93 85 82 78 78 73语文86 114 104 109 100 106 112 104 95 99试分别研究他们的数学成绩与物理成绩的关系、数学成绩与语文成绩的关系,你能发现什么规律?【解析】可求出物理成绩与数学成绩的相关系数r≈0.87>0.75,从而认为物理成绩与数学成绩之间具有很强的线性相关关系.而由语文成绩与数学成绩的相关系数|r|≈0.092远小于0.75,说明语文成绩与数学成绩不具有线性相关关系.因此,数学成绩好的同学,一般来说物理成绩也较好,它们之间的联系较紧密,而数学成绩好的同学,语文成绩可能好也可能差,它们之间的关系不大.相关关系的判断与分析有下列关系:①人的年龄与他(她)拥有的财富之间的关系;②曲线上的点与该点的坐标之间的关系;③苹果的产量与气候之间的关系;④森林中的同一种树木,其断面直径与高度之间的关系;⑤学生与他(她)的学号之间的关系.其中有相关关系的是(填写你认为正确的序号).【方法指导】根据相关关系的概念进行判断.【解析】序号关系理由①相关关系人的年龄和他(她)的财富有一定的关系,一般中年人财富多,年轻人少,少儿基本没有②函数关曲线上的点与其坐标一一对应,是确定的系③相关关系气候能影响苹果的产量④相关关系同一种树木,其断面直径和高度之间有一定的关系,但不确定⑤对应关系确定的一一对应关系【答案】①③④【小结】相关关系是一种非确定性关系,是指两个变量之间有关系,但是两者之间的关系还受其他因素的影响,只是影响大小的问题.回归直线过样本中心点(,)的性质的应用观察两个相关变量的如下数据:x-1 -2 -3 -4 -5 5 4 3 2 1y-0.9 -2 -3.1 -3.9 -5.1 5 4.1 2.9 2.1 0.9则两个变量间的回归直线方程为().A.y=0.5x-1B.y=xC.y=2x+0.3D.y=x+1【方法指导】根据回归直线方程y=a+bx经过样本中心点(,)可计算出结果.【解析】∵=0,=0,回归直线方程经过样本中心点(,),代入所给选项中检验,可知,只有y=x符合条件.【答案】B先判定相关性,再求回归直线方程某种图书每册的成本费y(元)与印刷册数x(千册)有关,经统计得到数据如下:x 1 2 3 5 10 20 30 50 100 200y 10.155.524.082.852.111.621.411.31.211.15检验每册书的成本费y与印刷册数的倒数之间是否有线性相关关系?如果有,求出y对x的回归方程.【方法指导】本题是非线性回归分析问题,不妨设变量u=,题意要求对u与y作相关性检验,如果它们具有线性相关关系,就可以进一步求出y对u的回归直线方程,这时,再回代u=,就得到了y对x的回归曲线方程.【解析】将上表数据列表分析如下:i 1 2 3 4 5 6 7 8 9 10x i 1 2 3 5 10 20 30 50 100 200 421y i 10.155.52 4.08 2.852.111.621.411.31.21 1.15 31.4 1 4 9 25 100 400 9002501000400053939 103.0330.4716.658.124.452.621.991.691.46 1.32 171.8x i y i 10.1511.0412.2414.2521.132.442.365 121 230 559.48∴=42.1,=1772.41,=3.14,n=10,10=1321.94,可以求得r=0.9998,由r=0.9998>0.75,因此变量y与之间具有较强的线性相关关系.∵b====-0.02,∴a=-b=3.14-(-0.02)×42.1=3.98. ∴y 与x 的回归方程为y=3.98-0.02x.[问题]当x=1时,由回归方程得y=3.96,而实际上y=10.15,为什么有这么大的偏差?上述回归方程是y 与x 的回归方程吗?[结论]因为y 与之间具有较强的线性相关关系,而y 与x 之间没有明显的线性相关关系,故应先通过变量变换(即换元),令u=,并通过对u 与y 作相关性检验,求出y 对u 的回归直线方程,最后再回代u=,得到y 对x 的回归方程.于是正确解如下:首先作变量变换,令u=,则题目所给数据变成如下表所示的数据:u i 1 0.5 0.33 0.2 0.10.05 0.03 0.02 0.01 0.005y i 10.15 5.52 4.08 2.85 2.11 1.62 1.41 1.30 1.211.15可以求得r ≈0.9998>0.75,因此变量y 与u 之间具有较强的线性相关关系,并且b ≈8.973,a=-b ≈1.125,最后回代u=可得y=+1.125.因此y 与x 的回归方程为y=+1.125.【小结】本题中y 与x 之间不具有线性相关关系,因而是非线性回归分析问题,对此类回归分析问题,应先求线性相关系数r ,利用r 来判断两个变量之间是否具有线性相关关系.当|r|>0.75时,认为有很强的线性相关关系,可以求回归直线方程,并可用求得的回归直线方程来预测变量的取值;当|r|<0.75时,认为两个变量之间线性相关关系不显著,这时求回归直线方程没有多大的实际价值,要采用变量变换(即换元法)转化为线性回归问题求解.由施肥量x 与水稻产量y 试验数据的关系,画出散点图,并指明相关性.施化肥量x15 20 25 30 35 40 45水稻产量y330 345 365 405 445 450 455【解析】散点图为:通过图像可知是正相关.已知x 、y 的取值如表所示,若从散点图分析,y 与x 线性相关,且y=0.95x+a ,求a 的值.x 0 1 2 3 4 y 2.2 4.3 4.8 4.8 6.7【解析】由表中数据得=2,=4.56,由于线性回归方程一定经过样本中心点(,),即(2,4.56),在回归直线方程y=bx+a 中,代入点(2,4.56)得a=-b=4.56-0.95×2=2.66.10名同学在高一和高二的数学成绩如下表:x74 71 72 68 76 73 67 70 65 74y76 75 71 70 76 79 65 77 62 72其中x为高一数学成绩,y为高二数学成绩.(1)y与x是否具有相关关系;(2)如果y与x具有相关关系,求回归直线方程.【解析】(1)由已知表格中的数据,利用计算器进行计算得=71,=72.3,x i y i=51467,=50520,=52541.则r==≈0.78.由0.78>0.75认为x与y之间具有线性相关关系.(2)y与x具有线性相关关系,设回归直线方程为y=a+bx,则b==≈1.22,a=-b=72.3-1.22×71=-14.32,所以y关于x的回归直线方程为y=1.22x-14.32.1.对相关系数r,下列说法正确的是().A.r越大,两变量的线性相关程度越大B.r越小,两变量的线性相关程度越大C.|r|越大,两变量的线性相关程度越大;|r|越小,两变量的线性相关程度越小D.|r|≤1,且|r|越接近1,两变量的线性相关程度越大;|r|越接近0,两变量的线性相关程度越小【解析】由两个变量的相关系数公式r=可知,相关程度的强弱与|r|和1的接近程度有关,|r|越接近1,两变量的线性相关程度越大,|r|越接近0,两变量的线性相关程度越小.【答案】D2.工人月工资y(元)关于劳动生产率x(千元)的回归方程为y=650+80x,下列说法正确的个数是().①劳动生产率为1000元,工资约为730元;②劳动生产率提高1000元,则工资约提高80元;③劳动生产率提高1000元,则工资约提高730元;④当月工资为810元,劳动生产率约为2000元.A.1B.2C.3D.4【解析】①②④正确,注意单位的一致性,故选C.【答案】C3.若预报体重y(kg)和身高x(cm)之间的线性回归方程为y=0.849x-85.712,如果要找到体重为41.638 kg的人,(填“一定”或“不一定”)在身高为150 cm的人群中.【解析】体重不仅受身高的影响,还受其他因素的影响.【答案】不一定4.某个体服装店经营某种服装,一周内获纯利润y(元)与该周每天销售这种服装的件数x之间的一组数据如下:x 3 4 5 6 7 8 9y66 69 73 81 89 90 91已知=280,=45309,x i y i=3487.(1)求,;(2)一周内获纯利润y与该周每天销售件数x之间是否线性相关?如果线性相关,求出回归直线方程.【解析】(1)=(3+4+5+6+7+8+9)=6,=(66+69+73+81+89+90+91)≈79.86.(2)根据已知=280,=45309,x i y i=3487,得相关系数r=≈0.973.由于0.973>0.75,所以纯利润y与每天销售件数x之间具有显著的线性相关关系.利用已知数据可求得回归直线方程为y=4.746x+51.386.(2013年·湖南卷)四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:①y与x负相关且y=2.347x-6.423;②y与x负相关且y=-3.476x+5.648;③y与x正相关且y=5.437x+8.493;④y与x正相关且y=-4.326x-4.578.其中一定不正确的结论的序号是().A.①②B.②③C.③④D.①④【解析】由正相关、负相关的性质可知在①中,斜率为2.347>0,不可能负相关;在④中,斜率为-4.326<0,不可能正相关,故①④一定不正确.选D.【答案】D1.下列两个变量之间的关系是相关关系的是().A.圆的面积与半径B.球的体积与半径C.角度与它的正弦值D.一个考生的数学成绩与物理成绩【解析】由题意知A表示圆的面积与半径之间的关系S=πr2;B表示球的体积与半径之间的关系V=πr2;C表示角度与它的正弦值y=sin α,以上所说的都是确定的函数关系,相关关系不是确定性的关系,故选D.【答案】D2.在对两个变量x,y进行线性回归分析时有下列步骤:①对所求出的回归方程作出解释;②收集数据(x i,y i),其中i=1,2,…,n;③求线性回归方程;④求相关系数;⑤根据所搜集的数据绘制散点图.如果根据可靠性要求能够作出变量x,y具有线性相关结论,那么在下列操作顺序中正确的是().A.①②⑤③④B.③②④⑤①C.②④③①⑤D.②⑤④③①【解析】根据线性回归分析思想可知,两个变量x,y进行线性回归分析时,应先收集数据(x i,y i),然后绘制散点图,再求相关系数和线性回归方程,最后对所求的回归方程作出解释,因此选D.【答案】D3.如图所示有5组数据,去掉后,剩下的4组数据的线性相关性更强.【解析】根据散点图判定两变量的线性相关性,样本数据点越集中在某一直线附近,这两变量的线性相关性越强,显然去掉D(3,10)后,其余各点更能集中在某一直线附近,即线性相关性更强.【答案】D(3,10)4.一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万件)之间由如下一组数据:x 1.081.121.191.281.361.481.591.681.81.871.982.07y 2.252.372.42.552.642.752.923.033.143.263.363.5(1)画出散点图;(2)检验相关系数r的显著性水平;(3)求月总成本y与月产量x之间的回归直线方程.【解析】i 1 2 3 4 5 6 7 8 9 10 11 12x i1.08 1.121.191.281.361.481.591.681.81.871.982.07y i2.25 2.372.42.552.642.752.923.033.143.263.363.5x i y i 2.432.6542.8563.2643.5904.074.6435.0905.6526.0966.6537.245=,=,=29.808,=99.2081,x i y i=54.243(1)画出散点图,如图所示.(2)r==≈0.99>0.75,这说明每月产品的总成本y(万元)与该月产量x(万件)之间存在显著的线性相关关系.(3)设回归直线方程y=bx+a,利用计算a,b,得b≈1.215, a=-b≈0.974,即回归直线方程为y=1.215x+0.974.5.设一个回归方程为y=3-5x,当变量x增加一个单位时().A.y平均增加3个单位B.y平均减小5个单位C.y平均增加5个单位D.y平均减小3个单位【解析】-5是斜率的估计值,说明x每增加一个单位,y平均减少5个单位.【答案】B6.对于一组具有线性相关关系的数据(x1,y1),(x2,y2),…,(x n,y n),其回归方程的截距为().A.a=y+bxB.a=+bC.a=y-bxD.a=-b【解析】回归直线方程中的截距即为a,由公式=b+a得a=-b,故选D.【答案】D7.许多因素都会影响贫穷,教育也许是其中之一,在研究这两个因素的关系时收集了美国50个州的成年人受过9年或更少教育的百分比(x)和收入低于官方规定的贫困线的人数占本州人数的百分比(y)的数据,建立的回归直线方程为y=0.8x+4.6,则成年人受过9年或更少教育的百分比(x)和收入低于官方的贫困线的人数占本州人数的百分比(y)之间的相关系数.(填“大于0”或“小于0”)【解析】一个地区受过9年或更少教育的百分比每增加1%,收入低于官方规定的贫困线的人数占本州人数的百分比将增加0.8%左右.【答案】大于08.假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:使用年限x2 3 4 5 6维修费用y2.23.8 5.5 6.5 7.0若由资料知y对x呈线性相关关系.试求:(1)线性回归方程y=bx+a的回归系数a,b;(2)估计使用年限为10年时的维修费用.【解析】(1)制表如下:i 1 2 3 4 5 合计x i 2 3 4 5 6 20y i2.2 3.8 5.5 6.5 7.0 25x i y i4.4 11.4 22.0 32.5 42.0 112.34 9 16 25 36 90=4,=5,=90,x i y i=112.3于是b===1.23,a=-b=5-1.23×4=0.08.(2)由(1)知回归直线方程为y=1.23x+0.08,当x=10时,y=1.23×10+0.08=12.3+0.08=12.38,即估计使用10年时的维修费用是12.38万元.9.若y与x之间的一组数据如下:x0 1 2 3 4y 1 3 5 5 6则拟合这5对数据的回归直线一定经过的点是.【解析】根据回归直线y=bx+a一定过样本中心点(,),且==2,==4,知点(2,4)一定在回归直线上.【答案】(2,4)10.某工业部门进行一项研究,分析该部门的产量与生产费用之间的关系,从这个工业部门内随机抽选了10个企业作样本,有如下资料:产量x(千件) 费用y(千元)40 150 42 140 48 160 55 170 65 150产量x(千件) 费用y(千元)79 16288 185100 165120 190140 185完成下列要求:(1)计算x与y的相关系数;(2)这两个变量之间是否线性相关?若线性相关,求回归直线方程y=bx+a.【解析】(1)制表如下:i x i y i x i y i1 40 150 1600 22500 60002 42 140 1764 19600 58803 48 160 2304 25600 76804 55 170 3025 28900 93505 65 150 4225 22500 97506 79 162 6241 26244 127987 88 185 7744 34225 162808 100 165 10000 27225 165009 120 190 14400 36100 2280010 140 185 19600 34225 25900合计777 1657 70903 277119 132938==77.7,==165.7,=70903,=277119,x i y i=132938r=≈0.808.即x与y的相关系数r≈0.808.(2)因为r>0.75.所以x与y之间具有很强的线性相关关系.则b=≈0.398,a=165.7-×77.7b≈134.8,所以回归直线方程为y=0.398x+134.8.第2课时回归分析的应用1.根据线性回归方程,对相关结论进行预测.2.理解从散点图进行非线性回归分析的意义,掌握如何将非线性回归问题转化为线性回归问题的方法.3.了解在解决实际问题的过程中寻找更好的模型的方法.重点:根据线性回归方程,对相关结论进行预测,探究非线性模型通过变换转化为线性回归模型的方法.难点:了解常用函数的图像特点,选择不同的模型建模,并通过相关指数对不同的模型进行比较.有关法律规定:香烟盒上必须印上“吸烟有害健康”的警示语,那么吸烟和健康之间有因果关系吗?每一个吸烟者的健康问题都是由吸烟引起的吗?你认为“健康问题不一定是由吸烟引起的,所以可以吸烟”的说法对吗?要回答这个问题,我们先来一起学习本节的知识吧!问题1: 刻画回归方程的拟合效果相关系数r=用来刻画数组(x i,y i)中两个变量的线性回归效果,当|r| >0.75时,我们认为数组(x i,y i) 中两个变量有很强的线性相关关系;当|r| <0.75时,则认为两个变量之间线性相关关系不显著.问题2:在回归分析中,通过模型计算预测变量的值时,应注意的问题.(1)回归方程只适用于我们所研究的样本的总体;(2)我们所建立的回归方程一般都有时间性;(3)样本取值的范围会影响回归方程的适用范围;(4)不能期望回归方程得到的预测值就是预测变量的精确值.问题3:几种能转化为线性回归模型的非线性回归模型(1)幂函数曲线y=ax b作变换u=ln y,v=ln x,c=ln a,得线性函数u=c+bv .(2)指数曲线y=a e bx作变换u=ln y,c=ln a,得线性函数u=c+bx .(3)倒指数曲线y=a作变换u=ln y,c=ln a,v=,得线性函数u=c+bv .(4)对数曲线y=a+b ln x作变换u=y,v=ln x,得线性函数u=a+bv .问题4:非线性回归问题进行回归分析的方法(1)若问题中已给出经验公式,这时可以将解释变量进行交换(换元),将变量的非线性关系转化为线性关系,将问题化为线性回归分析问题来解决.(2)若问题中没有给出经验公式,需要我们画出已知数据的散点图,通过与各种函数(如指数函数、对数函数、幂函数等)的图像作比较,选择一种与这些散点拟合得最好的函数,然后采用适当的变量交换,将问题化为线性回归分析问题来解决.从以下几个方面认识相关关系:(1)相关关系与函数关系不同.函数关系中的两个变量间是一种确定性关系;相关关系是一种非确定性关系.(2)函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.相关关系在现实生活中大量存在,从某种意义上讲,函数关系是一种理想的关系模型,而相关关系是一种更为一般的情况.因此研究相关关系,不仅可以使我们处理更为广泛的数学应用问题,还可以使我们对函数关系的认识上升到一个新的高度.一般情况下,在尚未断定两个变量之间是否具有线性相关关系的情况下,应先进行相关性检验,在确认其具有线性相关关系后,再求其回归直线方程;由部分数据得到的回归直线,可以对两个变量间的线性相关关系进行估计,这实际上是将非确定性的相关关系问题转化成确定性的函数关系问题进行研究.由于回归直线将部分观测值所反映的规律性进行了延伸,它在情况预测、资料补充等方面有着广泛的应用.1.下列两个变量之间的关系不是函数关系的是().A.角度和它的余弦值B.正方形的边长和面积C.正n边形的边数和各内角度数之和D.人的年龄和身高【解析】函数关系就是一种变量之间的确定性的关系,A,B,C三项都是函数关系,它们的函数表达式分别为f(θ)=cos θ,g(a)=a2,h(n)=nπ-2π.D项不是函数关系,对于年龄确定的人群,仍可以有不同的身高,故选D.【答案】D2.为了表示n个点与相应直线在整体上接近程度,我们常用()表示.A.(y i-y)B.(y i-)C.(y i-y)2D.(y i-)2【解析】由回归直线方程y=a+bx,可知y为一个量的估计量,而y i为它的实际值,在最小二乘法中[y i-(a+bx)]2,即(y i-y)2,故选C.【答案】C3.在一次实验中,测得(x,y)的四组值分别是A(1,2),B(2,3),C(3,4),D(4,5),则y与x之间的回归直线方程为.【解析】因为A,B,C,D四点都在直线y=x+1上,故填y=x+1.【答案】y=x+14.1907年一项关于16艘轮船的研究中,船的吨位区间位于192吨到3246吨,船员的人数从5人到32人,船员的人数关于船的吨位的回归分析得到如下结果:船员人数=9.1+0.006×吨位.(1)假定两艘轮船吨位相差1000吨,船员平均人数相差多少?(2)估计最小的船的船员数和最大的船的船员数.【解析】(1)船员平均人数之差=0.006×吨位之差=0.006×1000=6,即船员平均相差6人.(2)9.1+0.006×192=10.252,估计最小的船的船员数为10.9.1+0.006×3246=28.576,估计最大的船的船员数为28.利用公式,确定回归直线方程某5名学生的数学和化学成绩如下表:学生A B C D E学科数学成绩(x) 88 76 73 66 63化学成绩(y) 78 65 71 64 61(1)画出散点图;(2)求化学成绩(y)对数学成绩(x)的回归直线方程.【方法指导】熟记公式,根据表格计算公式中所需的各种数据.【解析】(1)散点图(略).(2)=73.2,=67.8,x i y i=25054,=27174,所以b==≈0.625.a=-b=67.8-0.625×73.2=22.05.所以y对x的回归直线方程为y=0.625x+22.05.【小结】利用公式求解时应注意以下几点:①求b时应先求出,,x i y i,,再由a=-b求a的值,并写出回归直线方程.②线性回归方程中的截距a和斜率b都是通过样本估计而来,存在着误差,这种误差可能导致预测结果的偏差.③回归直线方程y=a+bx中的b表示x增加1个单位时y的变化量为b,而a是不随x的变化而变化的量.④可以利用回归直线方程y=a+bx预测在x取某一个值时,y的估计值.根据回归直线方程,对结果进行分析或预测从某大学中随机选取 8 名女大学生,其身高和体重数据如下表:编号 1 2 3 4 5 6 7 8身高/cm 165 165 157 170 175 165 155 170体重/kg 48 57 50 54 64 61 43 59求根据女大学生的身高预测体重的回归方程,并预测一名身高为 172 cm 的女大学生的体重.【方法指导】可以计算出r≈0.798>0.75.这表明体重与身高有较强的线性相关关系,从而可以建立身高和体重的线性回归方程,根据身高和体重的线性回归方程,由身高预测体重.【解析】由于问题中要求根据身高预测体重,因此选取身高为自变量x ,体重为因变量y.作出散点图(如图).从图中可以看出,样本点呈条状分布,身高和体重有较强的线性相关关系,因此可以用线性回归方程来近似刻画它们之间的关系,根据公式,可以得到b≈0.848,a≈-85.712.于是得到回归方程y=0.848x-85.712.因此,对于身高172 cm 的女大学生,由回归方程可以预测其体重为y=0.848×172-85.712=60.144 kg.【小结】解析中b=0.848是斜率的估计值,说明身高x每增加1个单位时,体重y就增加0.848 kg,这表明体重与身高具有正的线性相关关系.尽管身高172 cm的女大学生的体重不一定是60.144 kg,但一般可以认为她的体重接近60.144 kg.可线性化的非线性回归问题一只红铃虫的产卵数y和温度x之间的7组观测数据列于下表:温度x/℃21 23 25 27 29 32 35产卵数y/7 11 21 24 66 115 325个试建立y与x之间的回归方程,并预测温度为28 ℃时产卵数目.【方法指导】作出散点图(或根据已知的散点图)分析欲采用较为恰当的拟合曲线,用换元法转化成线性关系再进行回归分析.【解析】选择变量,画散点图.在散点图中,根据已有的函数知识,可以发现样本点分布在某一条指数函数曲线y=c1的周围,其中c1和c2是待定参数.即问题变为如何估计待定参数c1和c2.我们可以通过对数变换把指数关系变为线性关系.令z=ln y,则变换后样本点应该分布在直线z=bx+a(a=ln c1 ,b=c2)的周围.这样,就可以利用线性回归模型来建立y 和x之间的非线性回归方程了.由已知表的数据可以得到变换后的样本数据表(下表):x21 23 25 27 29 32 35z1.946 3.398 3.045 3.178 4.190 4.745 5.784下图给出了表中数据的散点图.从图中可以看出,变换后的样本点分布在一条直线附近,因此可以用线性回归方程来拟合.由表中的数据得到线性回归方程z=0.242x-2.884.相关系数r≈0.953.因此红铃虫的产卵数对温度的非线性回归方程为y=e0.242x-2.884.当x=28 ℃时,y≈49.预测当气温为28 ℃时,产卵数为49个.综上所述,在本题中指数函数模型比一元线性模型、二次函数模型有更好的拟合效果.【小结】对于给定的样本点(x1,y1),(x2,y2),…,(x n,y n),其中a和b都是未知参数.应先根据散点图或利用相关系数r判断两变量间是否存在线性相关关系,若两变量线性相关性显著,采用例1的方法进行线性回归分析;若两变量线性相关性不显著,则可采用例2的方法和步骤进行拟合效果分析.在某种产品表面进行腐蚀线实验,得到腐蚀深度y与腐蚀时间t之间对应的一组数据:时间t(s) 5 10 15 20 30 40 50 60 70 90 120深度6 10 10 13 16 17 19 23 25 29 46y(μm)试求腐蚀深度y对时间t的回归直线方程.【解析】经计算可得相关系数r≈0.982>0.75,所以可以认为y与t之间有较强的线性相关关系.≈46.36,≈19.45,=36750,=5422,t i y i=13910.b==≈0.3.a=-b=19.45-0.3×46.36≈5.542.故所求的回归直线方程为y=0.3t+5.542.一机器可以按各种不同的速度运转,其生产物件有一些会有缺点,每小时生产有缺点物件的多少随机器运转速度而变化,用x表示转速(单位:转/秒),用y表示每小时生产的有缺点物件个数,现观测得到(x,y)的4组观测值为(8,5),(12,8),(14,9),(16,11).。

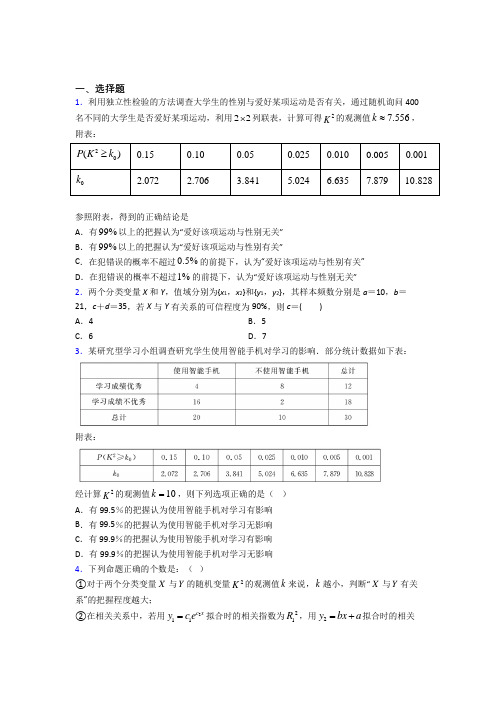
一、选择题1．利用独立性检验的方法调查大学生的性别与爱好某项运动是否有关，通过随机询问400名不同的大学生是否爱好某项运动，利用22⨯列联表，计算可得2K 的观测值7.556k ≈，附表：20()P K k ≥0.15 0.100.050.025 0.010 0.005 0.001 0k 2.0722.7063.8415.0246.6357.87910.828参照附表，得到的正确结论是A ．有99%以上的把握认为“爱好该项运动与性别无关”B ．有99%以上的把握认为“爱好该项运动与性别有关”C ．在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别有关”D ．在犯错误的概率不超过1%的前提下，认为“爱好该项运动与性别无关”2．两个分类变量X 和Y ，值域分别为{x 1，x 2}和{y 1，y 2}，其样本频数分别是a ＝10，b ＝21，c ＋d ＝35，若X 与Y 有关系的可信程度为90%，则c ＝( ) A ．4 B ．5 C ．6D ．73．某研究型学习小组调查研究学生使用智能手机对学习的影响．部分统计数据如下表：附表：经计算2K 的观测值10k =，则下列选项正确的是（ ） A ．有99.5％的把握认为使用智能手机对学习有影响 B ．有99.5％的把握认为使用智能手机对学习无影响 C ．有99.9％的把握认为使用智能手机对学习有影响 D ．有99.9％的把握认为使用智能手机对学习无影响 4．下列命题正确的个数是：（ ）①对于两个分类变量X 与Y 的随机变量2K 的观测值k 来说，k 越小，判断“X 与Y 有关系”的把握程度越大；②在相关关系中，若用211c x y c e =拟合时的相关指数为21R ，用2y bx a =+拟合时的相关指数为22R ，且2212R R >，则1y 的拟合效果好；③利用计算机产生0~1之间的均匀随机数a ，则事件“310a ->”发生的概率为23； ④“0,0a b >>”是“2b aa b+≥”的充分不必要条件 A ．1B ．2C ．3D ．45．给出下列说法：①用()()221211ˆni i i n i i i y y R y y ==-=--∑∑刻画回归效果，当2R 越大时，模型的拟合效果越差，反之则越好；②归纳推理是由特殊到一般的推理，而演绎推移则是由一般到特殊的推理；③综合法证明数学问题是“由因索果”，分析法证明数学问题是“执果索因”；④设有一个回归方程ˆ35yx =+，变量x 增加1个单位时，y 平均增加5个单位；⑤线性回归方程ˆˆˆy bx a =+必过点(),x y .其中错误的个数有（ ）A ．0个B ．1个C ．2个D ．3个6．某班主任对全班50名学生进行了作业量的调查，数据如表：若推断“学生的性别与认为作业量大有关”，则这种推断犯错误的概率不超过（ ）附：()()()()()22n ad bc K a b c d a c b d -=++++A ．0.01B ．0.025C ．0.10D ．0.057．某研究型学习小组调查研究学生使用智能手机对学习的影响，部分统计数据如下表：使用智能手机 不使用智能手机 总计 学习成绩优秀 4 8 12 学习成绩不优秀 16 2 18 总计201030计算得K 2＝10，则下列选项正确的是( ) A ．有99.5%的把握认为使用智能手机对学习有影响B．有99.5%的把握认为使用智能手机对学习无影响C．在犯错误的概率不超过0.1%的前提下，认为使用智能手机对学习有影响D．在犯错误的概率不超过1%的前提下，认为使用智能手机对学习无影响8．为考察数学成绩与物理成绩的关系,在高二随机抽取了300名学生,得到下面的列联表:现判断数学成绩与物理成绩有关系,则犯错误的概率不超过()A．0.005 B．0.01 C．0.02 D．0.059．春节期间，“厉行节约，反对浪费”之风悄然吹开，某市通过随机询问100名性别不同的居民是否能做到“光盘”，得到如下的列联表：由此表得到的正确结论是()A．在犯错误的概率不超过0．01的前提下，认为“该市居民能否做到‘光盘’与性别有关”B．在犯错误的概率不超过0．01的前提下，认为“该市居民能否做到‘光盘’与性别无关”C．在犯错误的概率不超过0．1的前提下，认为“该市居民能否做到‘光盘’与性别有关”D．在犯错误的概率不超过0．1的前提下，认为“该市居民能否做到‘光盘’与性别无关”10．以下四个命题中：①在回归分析中，可用相关指数R2的值判断拟合的效果，R2越大，模型的拟合效果越好；②两个随机变量的线性相关性越强，相关系数的绝对值越接近1；③若数据x1，x2，x3，…，x n的方差为1，则2x1,2x2,2x3，…，2x n的方差为2；④对分类变量x与y的随机变量K2的观测值k来说，k越小，判断“x与y有关系”的把握程度越大．其中真命题的个数为()A．1 B．2C．3 D．411．利用独立性检验来考虑两个分类变量X和Y是否有关系时，通过查阅临界值表来确定推断“X与Y有关系”的可信度，如果k＞5.024，那么就推断“X和Y有关系”，这种推断犯错误的概率不超过（）A ．0.25B ．0.75C ．0.025D ．0.97512．某工厂为了调查工人文化程度与月收入的关系，随机抽取了部分工人，得到如下列表：由上表中数据计算得2K =()21051030204555503075⨯⨯-⨯⨯⨯⨯≈6.109，请根据下表，估计有多大把握认为“文化程度与月收入有关系”（ ）A ．1％B ．99％C ．2.5％D ．97.5％二、填空题13．在一次独立试验中，有200人按性别和是否色弱分类如下表（单位：人）男 女 正常 73 117 色弱73你能在犯错误的概率不超过_____的前提下认为“是否色弱与性别有关”？14．利用独立性检验考察两个分类变量X 与Y 是否有关系时，若K2的观测值k=6.132，则有__________的把握认为“X 与Y 有关系”． P（K2≥k0） 0.05 0.025 0.010 0.005 k03.8415.0246.6357.87915．已知的取值如表所示：若与呈线性相关，且回归方程为，则等于 ．2 3 454616．下列4个命题：①为了了解800名学生对学校某项教改试验的意见，打算从中抽取一个容量为40的样本，考虑用系统抽样，则分段的间隔为40；②四边形ABCD 为长方形，2AB =，1BC =，O 为AB 中点，在长方形ABCD 内随机取一点P ，取得的P 点到O 的距离大于1的概率为12π-； ③把函数3sin 23y x π⎛⎫=+⎪⎝⎭的图象向右平移6π个单位，可得到3sin 2y x =的图象； ④已知回归直线的斜率的估计值为1.23，样本点的中心为()4,5，则回归直线方程为1.230.08y x =+.其中正确的命题有__________．(填上所有正确命题的编号)17．4月16日摩拜单车进驻大连市旅顺口区，绿色出行引领时尚，旅顺口区进行了“经常使用共享单车与年龄关系”的调查，得下列22⨯列联表：年轻人 非年轻人 合计 经常使用单车用户 100 20 120 不常使用单车用户 60 20 80 合计16040200则得到的2χ=__________．(小数点后保留一位) (附：()()()()()22χ-=++++n ad bc a b c d a c b d )18．已知下列命题：①从匀速传递的产品生产流水线上，质检员每30分钟从生产流水线中抽取一件产品进行某项指标检测，这样的抽样方法是系统抽样；②两个变量的线性相关程度越强，则相关系数的值越接近于1；③两个分类变量X 与Y 的观测值2k ，若2k 越小，则说明“X 与Y 有关系”的把握程度越大；④随机变量X ～(0,1)N ，则(1)2(1)1P X P X <=<-. 其中为真命题的是__________． 19．给出下列四个结论：(1)相关系数r 的取值范围是1r <；(2)用相关系数r 来刻画回归效果，r 的值越大，说明模型的拟合效果越差；(3)一个袋子里装有大小相同的5个白球和5个黑球，从中任取4个，则其中所含白球个数的期望是2；(4) 一个篮球运动员投篮一次得3分的概率为a ，得2分的概率为b ，不得分的概率为c ,且(),,0,1a b c ∈，已知他投篮一次得分的数学期望为2，则213a b+的最小值为163.其中正确结论的序号为______________.20．2018年春季，世界各地相继出现流感疫情，这已经成为全球性的公共卫生问题.为了考察某种流感疫苗的效果，某实验室随机抽取100只健康小鼠进行试验，得到如下列联表：感染 未感染 总计 注射 10 40 50 未注射 20 30 50 总计3070100参照附表，在犯错误的概率最多不超过____的前提下，可认为“注射疫苗”与“感染流感”有关系．（参考公式：()()()()()22n ad bc K a b c d a c b d -=++++.） 20()P K k ≥ 0.100.05 0.025 0.010 0.005 0.001 0k 2.7063.8415.0246.6357.87910.828三、解答题21．我国新型冠状病毒肺炎疫情期间，以网络购物和网上服务所代表的新兴消费展现出了强大的生命力，新兴消费将成为我国消费增长的新动能.某市为了了解本地居民在2020年2月至3月两个月网络购物消费情况，在网上随机对1000人做了问卷调查，得如表频数分布表：（1）作出这些数据的频率分布直方图，并估计本市居民此期间网络购物的消费平均值； （2）在调查问卷中有一项是填写本人年龄，为研究网购金额和网购人年龄的关系，以网购金额是否超过4000元为标准进行分层抽样，从上述1000人中抽取200人，得到如表列联表，请将表补充完整并根据列联表判断，在此期间是否有95%的把握认为网购金额与网购人年龄有关.参考公式和数据：()()()()()22n ad bcKa b c d a c b d-=++++.（其中n a b c d=+++为样本容量）22．2020年3月，因为新冠肺炎疫情的影响，我市全体学生只能在网上在线学习，为了研究学生在线学习情况，市教研院数学学科随机从市区各高中学校抽取120名学生对线上教学情况进行调查（其中，男生与女生的人数之比为3：1），结果发现：男生中有40名对于线上教学满意，女生中有10名表示对于线上教学不满意.（1）请完成如表2×2列联表，并回答能否有95%的把握认为对“线上教学是否满意与性别有关”；态度性别满意不满意合计男生女生合计120（2）采用分层抽样的方法，从被调查的对线上教学满意的学生中，抽取6名学生，再从这6名学生中抽取2名学生，作线上学习的经验介绍，求所选取的2名学生性别不同的概率.附：参考公式及临界值表()()()()()22n ad bcKa b c d a c b d-=++++，其中n a b c d=+++23．新冠肺炎疫情防控时期，各级各类学校纷纷组织师生开展了“停课不停学”活动，为了解班级线上学习情况，某位班主任老师进行了有关调查研究.（1）从班级随机选出5名同学，对比研究了线上学习前后两次数学考试成绩，如下表：参考公式：在线性回归方程y bx a=+，()()()() 1122211n ni i i ii in ni ii ix x y y x y nx ybx x x n x ====---==--∑∑∑∑，a y bx=-（2）针对全班45名同学（25名女生，20名男生）的线上学习满意度调查中，女姓满意率为80%，男生满意率为75%，填写下面列联表，判断能否在犯错误概率不超过0.01的前提下，认为线上学习满意度与学生性别有关？参考公式和数据：()()()()()2n ad bcxa b c d a c b d-=++++，()20.0500.0100.0013.8416.63510.828P x kk≥24．某足球运动员进行射门训练，若打进球门算成功，否则算失败.已知某天该球员射门成功次数与射门距离的统计数据如下：（1）请问是否有90%的把握认为该球员射门成功与射门距离是否超过30米有关？参考公式及数据：22(),()()()()n ad bc K n a b c d a b c d a c b d -==+++++++.（2）当该球员距离球门30米射门时，设射门角（射门点与球场底线中点的连线和底线所成的锐角或直角）为([0,])2πθθ∈，其射门成功率为2+3()cos sin 4f θθθθθ=+⋅-，求该球员射门成功率最高时射门角θ的值.25．某大学读书协会为了解本校大学生网上阅读与传统纸质阅读的情况，调查了该大学1000名大学生(男、女各占一半)，就偏向网上阅读和偏向传统纸质阅读的情况做了调查记录.记录显示，偏向网上阅读的男大学生比偏向传统纸质阅读的男大学生多300人，这1000名大学生中，偏向传统纸质阅读的大学生共有400人. （1）根据题意，完成下列2×2列联表；（2）根据列联表，判断能否有99.9%的把握认为该大学的大学生的阅读方式与性别有关，说明你的理由.附： 22(-)()()()()n ad bc K a b c d a c b d =++++(n=a+b+c+d ).26．2016年欧洲杯将于2016年6月10日到7月10日在法国举行．为了使得赛会有序进行，欧足联在全球范围内选聘了30名志愿者（其中男性16名，女性14名）．调查发现，男性中有10人会英语，女性中有6人会英语． （1）根据以上数据完成以下2×2列联表：并回答能否在犯错的概率不超过0.10的前提下认为性别与会英语有关？参考公式：22()()()()()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++参考数据：（2）会英语的6名女性志愿者中曾有4人在法国工作过，若从会英语的6名女性志愿者中随机抽取2人做导游，则抽出的2人都在法国工作过的概率是多少？【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】根据2K 的观测值7.556k ≈，对照表中数据，即可得到相应的结论． 【详解】根据2K 的观测值7.556k ≈，对照表中数据得出有0.01的几率说明这两个变量之间的关系是不可信的，即有10.0199%-=的把握说明两个变量之间有关系，故选B ． 【点睛】本题主要考查独立性检验的应用，独立性检验的一般步骤：（1）根据样本数据制成22⨯列联表；（2）根据公式计算2K 的观测值k ；（3）查表比较k 与临界值的大小关系，作统计判断．（注意：在实际问题中，独立性检验的结论也仅仅是一种数学关系，得到的结论也可能犯错误）2．B解析：B 【解析】【分析】根据22⨯列联表，以及独立检验随机变量的临界值参考表,计算2K 对应的值，验证24,5,6,7,c K =是否恰好满足即可【详解】列22⨯列联表可知：()22661030521 3.024 2.70615513135K ⨯⨯-⨯=≈>⨯⨯⨯，所以5c =时，X 与Y 有关系的可信程度为90%，而其余的值4,6,7c c c ===皆不满足,故选B ． 【点睛】独立性检验的一般步骤：（1）根据样本数据制成22⨯列联表；（2）根据公式()()()()()22n ad bc K a b a d a c b d -=++++计算2K 的值；(3) 查表比较2K 与临界值的大小关系，作统计判断.（注意：在实际问题中，独立性检验的结论也仅仅是一种数学关系，得到的结论也可能犯错误.）3．A解析：A 【解析】 【分析】由题意结合2K 的观测值k 由独立性检验的数学思想给出正确的结论即可. 【详解】由于2K 的观测值10k =7.879>,其对应的值0.0050.5%=，据此结合独立性检验的思想可知：有99.5％的把握认为使用智能手机对学习有影响. 本题选择A 选项. 【点睛】独立性检验得出的结论是带有概率性质的，只能说结论成立的概率有多大，而不能完全肯定一个结论，因此才出现了临界值表，在分析问题时一定要注意这点，不可对某个问题下确定性结论，否则就可能对统计计算的结果作出错误的解释．4．C解析：C 【解析】分析：根据独立性检验的性质可判断①；根据回归分析的基本原理可判断②；根据几何概型概率公式可判断③； 根据不等式的性质可判断④.详解：①对于两个分类变量X 与Y 的随机变量2K 的观测值k 来说，k 越小，判断“X 与Y 有关系”的把握程度越小，①错误；②在相关关系中，若用211c x y c e =拟合时的相关指数为21R ，用2y bx a =+拟合时的相关指数为22R ，且2212R R >，则1y 的拟合效果好，②正确；③利用计算机产生0~1之间的均匀随机数a ，则事件“310a ->”发生的概率为1123103-=-，正确； ④“0,0a b >>”可得到“2b a a b +≥”， “2b aa b+≥”时“0,0a b >>”不一定成立，所以“0,0a b >>”是“2b aa b+≥”的充分不必要条件，正确，即正确命题的个数是3，故选C. 点睛：本题主要通过对多个命题真假的判断，主要综合独立性检验、回归分析、几何概型概率公式、不等式的性质，属于中档题.这种题型综合性较强，也是高考的命题热点，同学们往往因为某一处知识点掌握不好而导致“全盘皆输”，因此做这类题目更要细心、多读题，尽量挖掘出题目中的隐含条件，另外，要注意从简单的自己已经掌握的知识点入手，然后集中精力突破较难的命题.5．B解析：B 【解析】分析：①可由相关指数的概念判断;②③由推理,综合法和反证法的概念判断；④和⑤由线性回归分析判断即可.详解：①相关指数2R 越大,则相关性越强,模型的拟合效果越好.错误;② 归纳推理是由特殊到一般的推理,而演绎推理是由一般到特殊的推理,由归纳推理与演绎推理的概念可知正确.③综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”,由概念可知正确. ④由回归方程的系数意义知，当变量x 增加1个单位时，y 平均增加5个单位，正确；⑤线性回归方程ˆˆˆy bx a =+必过样本中心点(),x y ，正确.故选B.点睛：本题是一道综合性考题，即考查了推理与证明的原理，又考查了利用2R 判断模型拟合程度，同时还考查了线性回归分析的相关概念，属于中档题.6．B解析：B分析：根据表格中所给数据，代入公式()()()()()22n ad bcKa b c d a c b d-=++++，求出观测值，把所求的观测值同临界值进行比较，从而可得结果.详解：根据表中数据得到()22501815895.059 5.02427232426K⨯⨯-⨯=≈>⨯⨯⨯，所以，若推断“学生的性别与认为作业量大有关”，则这种推断犯错误的概率不超过0.025，故选B.点睛：本题主要考查独立性检验的应用，解题的关键是正确求出这组数据的观测值，计算过程一定要细心，避免出现计算错误，属于基础题.7．A解析：A【解析】因为7.879＜K2＜10.828，所以有99.5%的把握认为使用智能手机对学习有影响．故选A.8．D解析：D【解析】因为K2的观测值k=2300(371433585) 12217872228⨯-⨯⨯⨯⨯≈4.514>3.841,所以在犯错误的概率不超过0.05的前提下认为数学成绩与物理成绩有关系. 选D. 9．C解析：C【解析】由2×2列联表得到a＝45，b＝10，c＝30，d＝15．则a＋b＝55，c＋d＝45，a＋c＝75，b＋d＝25，ad＝675，bc＝300，n＝100．所以K2的观测值k＝2100675-30055457525⨯⨯⨯（）≈3．030．因为2．706<3．030<3．841．选C.点睛：根据卡方公式求K2，再与参考数据比较，最后作出判断.10．B解析：B【解析】由题意得，若数据x1，x2，x3，…，x n的方差为1，则2x1,2x2,2x3，…，2x n的方差为4，所以③不正确；对分类变量x与y的随机变量K2的观测值k来说，k越小，判断“x与y 有关系”的把握程度越小，所以④不正确．其中①、②是正确的，故选B.11．C解析：C【解析】∵P（k＞5.024）＝0.025，故在犯错误的概率不超过0.025的条件下，认为“X和Y考点：独立性检验.12．D解析：D 【解析】 试题由题根据二列联表得出；2K =()21051030204555503075⨯⨯-⨯⨯⨯⨯≈6.109，对应参考值得 2 5.024K >，则有10.0250.975-=，即有97.5%的把握认为文化程度与月收入有关系。

阶段质量检测(三)统计案例[考试时间：分钟试卷总分：分]第Ⅰ卷(选择题)一、选择题(本大题共小题，每小题分，共分．在每小题给出的四个选项中，只有一项是符合题目要求的)．(全国新课标)在一组样本数据(，)，(，)，…，(，)(≥，，，…，不全相等)的散点图中，若所有样本点(，)(＝，…，)都在直线＝＋上，则这组样本数据的样本相关系数为( )．－．．．已知与之间的一组数据：则与的线性回归方程＝＋必过点( )．() ．()．() ．()．下列现象的相关程度最高的是( )．某商店的职工人数与商品销售额之间的相关系数为．流通费用率与商业利润之间的相关系数为－．商品销售额与商业利润之间的相关系数为．商品销售额与流通费用率之间的相关系数为－．已知某车间加工零件的个数与所花费时间()之间的线性回归方程为＝＋，则加工个零件大约需要( )．．．．．设两个变量和之间具有线性相关关系，它们的相关系数是，关于的回归直线的斜率是，纵轴上的截距是，那么必有( )．与的符号相同．与的符号相同．与的符号相反．与的符号相反．以下关于线性回归的判断，正确的个数是( )①若散点图中的所有点都在一条直线附近，则这条直线的方程为回归方程②散点图中的绝大多数点都线性相关，个别特殊点不影响线性回归，如图中的，，点③已知线性回归方程为＝－＋，则＝时，的估计值为④线性回归方程的意义是它反映了样本整体的变化趋势．．．．．某考察团对全国大城市的职工人均工资水平(千元)与居民人均消费水平(千元)进行统计调查，与具有相关关系，回归方程为＝＋.若某城市居民人均消费水平为千元，估计该城市人均消费额占人均工资收入的百分比为( )．．．．．两个相关变量满足如下关系：则两变量的回归方程为( )．＝＋．＝－．＝＋．＝＋.若线性回归方程中的回归系数＝时，则相关系数为( )．＝．＝－．＝．无法确定．某工厂为预测某种产品的回收率，需要研究它和原料有效成分含量之间的相关关系，现取了组观察值．计算知＝，＝，＝，＝，则对的线性回归方程是( )．＝＋．＝－＋．＝＋．＝－答题栏第Ⅱ卷(非选择题)二、填空题(本大题共小题，每小题分，共分，请把正确的答案填在题中的横线上)．为了判断高中三年级学生选修文科是否与性别有关，现随机抽取名学生，得到如下×列联表：。

高中数学第三章统计案例单元测评北师大版选修2-3编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第三章统计案例单元测评北师大版选修2-3）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第三章统计案例单元测评北师大版选修2-3的全部内容。

《统计案例》测评（时间90分钟，满分100分）一、选择题（本大题共12小题，每小题4分,共48分） 1.下面变量之间的关系是函数关系的是A 。

已知二次函数y=ax 2+bx+c,其中a 、c 是已知常数，取b 为自变量，因变量是这个函数的判别式Δ=b 2—4acB.光照时间和果树亩产量C.降雪量和交通事故发生率D.每亩施用肥料量和粮食亩产量答案：A 解析：B 、C 、D 是相关关系，A 是确定性关系,即函数关系。

2.设有一个回归方程为y=3—5x,变量x 增加一个单位时A 。

y 平均增加3个单位B 。

y 平均减少5个单位 C.y 平均增加5个单位 D.y 平均减少3个单位答案：B 解析：斜率b=—5的意义是：变量x 增加1个单位时,y 平均增加-5个单位,即y 平均减少5个单位。

3。

若回归直线方程中的回归系数b=0时，则相关系数为A.r=1 B 。

r=—1 C 。

r=0 D.无法确定 答案：C解析：当b=0时，即∑∑==--ni ini ii xn xy x n yx 1221=⇒∑=ni i i y x 1—n x y =0，∴r=∑∑∑===---ni i ni i ni ii yn y xn x yx n yx 1221221=0.4。

在一个2×2列联表中，由其数据计算得χ2=13.097,则其两个变量间有关系的可能性为 A 。

第三章 统计案例综合测试题一、选择题(本大题共12小题，每小题5分，共60分．每小题中只有一项符合题目要求) 1．在对两个变量x, y 进行线性回归分析时有下列步骤：①对所求出的回归直线方程作出解释；②收集数据(x i ，y i )，i ＝1，2，…，n ；③求线性回归方程；④求相关系数；⑤根据所搜集的数据绘制散点图．若根据可靠性要求能够作出变量x ，y 具有线性相关结论，则下列操作顺序正确的是( ) A ．①②⑤③④ B ．③②④⑤① C ．②④③①⑤ D ．②⑤④③①答案 D解析 由对两个变量进行回归分析的步骤，知选D.2．为了考查两个变量x 和y 之间的线性相关性，甲、乙两位同学各自独立地做了10次和15次试验，并且利用线性回归方法，求得回归直线分别为l 1和l 2，已知两个人在试验中发现对变量x 的观测数据的平均值都是s ，对变量y 的观测数据的平均值都是t ，那么下列说法正确的是( ) A ．l 1和l 2有交点(s ，t) B ．l 1与l 2相交，但交点不一定是(s ，t) C ．l 1与l 2必定平行 D ．l 1与l 2必定重合 答案 A解析 由回归直线定义知选A.3．实验测得四组(x ，y)的值为(1，2)，(2，3)，(3，4)，(4，5)，则y 与x 之间的回归直线方程为( ) A ．y ∧＝x ＋1 B ．y ∧＝x ＋2 C ．y ∧＝2x ＋1 D ．y ∧＝x －1答案 A解析 求出样本中心(x ，y)代入选项检验知选A.4．(2014·重庆)已知变量x 与y 正相关，且由观测数据算得样本平均数x ＝3，y ＝3.5，则由该观测数据算得的线性回归方程可能是( ) A ．y ∧＝0.4x ＋2.3 B ．y ∧＝2x －2.4 C ．y ∧＝－2x ＋9.5 D ．y ∧＝－0.3x ＋4.4 答案 A解析 利用正相关和样本点的中心在回归直线上对选项进行排除．因为变量x 和y 正相关，则回归直线的斜率为正，故可以排除选项C 和D.因为样本点的中心在回归直线上，把点(3，3.5)的坐标分别代入选项A 和B 中的直线方程进行检验，可以排除B ，故选A.5．(2014·湖北)根据如下样本数据x 3 4 5 6 7 8 y4.02.5－0.50.5－2.0－3.0得到的回归方程为y ＝b x ＋a ，则( ) A ．a ∧>0，b ∧>0 B ．a ∧>0，b ∧<0 C ．a ∧<0，b ∧>0 D ．a ∧<0，b ∧<0答案 B解析 用样本数据中的x ，y 分别当作点的横、纵坐标，在平面直角坐标系xOy 中作出散点图，由图可知b<0，a>0.故选B. 6．下面是一个2×2列联表y 1 y 2 总计 x 1 a 21 73 x 2 2 25 27 总计b46100其中a 、b 处填的值分别为( A ．52 54 B ．54 52 C ．94 146 D ．146 94答案 A解析 由a ＋21＝73，得a ＝52，a ＋2＝b ，得b ＝54.故选A. 7．设有一个回归方程为y ∧＝3－5x ，则变量x 增加一个单位时( ) A ．y 平均增加3个单位 B ．y 平均减少5个单位 C ．y 平均增加5个单位 D ．y 平均减少3个单位 答案 B解析 ∵－5是斜率的估计值，说明x 每增加一个单位时，y 平均减少5个单位．故选B. 8．在一个2×2列联表中，由其数据计算得K 2＝13.097，则其两个变量间有关系的可能性为( ) A ．99% B ．95% C ．90% D ．无关系答案 A解析 ∵如果K 2的估计值k>10.828时，就有99.9%的把握认为“x 与y 有关系”．故选A. 9．两个相关变量满足如下关系：x 10 15 20 25 30 y1 0031 0051 0101 0111 014A. y ∧＝0.56x ＋997.4 B. y ∧＝0.63x －231.2 B. y ∧＝50.2x ＋501.4 D. y ∧＝60.4x ＋400.7答案 A解析 利用公式b ∧＝＝0.56，a ∧＝y －－b ∧x ＝997.4.∴回归直线方程为y ∧＝0.56x ＋997.4.故选A. 10.线性回归方程y ∧＝b ∧x ＋a ∧必过（ ） A.（0，0） B.（x ，0） C.（0，y ） D.（x ，y ）答案 D解析 回归直线方程一定过样本点的中心（x ，y ）.故选D.11.在回归分析中，代表了数据点和它在回归直线上相应位置的差异的是（ ） A.总偏差平方和 B.残差平方和 C.回归平方和 D.相关指数R 2答案 B解析 y i －y ∧＝e ∧i ，∑ni ＝1e ∧ i 2为残差平方和.故选B. 12.如果根据性别与是否爱好运动的列联表得到K 2≈3.852>3.841，所以判断性别与运动有关，那么这种判断犯错的可能性不超过（ ） A.2.5% B.0.5% C.1% D.5%答案 D解析 ∵P（K 2≥3.841）≈0.05，故“判断性别与运动有关”出错的可能性为5%. 二、填空题（本大题共4小题，每小题5分，共20分，把答案填在题中横线上） 13.在一项打鼾与患心脏病的调查中，共调查了1 671人，经过计算得K 2＝27.63，根据这一数据分析，我们有理由认为打鼾与患心脏病是 的（有关，无关）. 答案 有关解析 K 2>10.828就有99.9%的理由认为两个量是有关的.14.在研究硝酸钠的可溶性程度时，观测它在不同温度的水中的溶解度，得观测结果如下：,温度（x ） 0 10 20 50 70 溶解度（y ）66.776.085.0112.3128.0由此得到回归直线的斜率是 . 答案 0.880 9解析 把表中的数据代入公式b ∧=≈0.880 9.15.用身高（cm ）预报体重（kg ）满足y ∧＝0.849x －85.712，若要找到41.638 kg 的人，________是在150 cm 的人群中．(填“一定”、“不一定”) 答案 不一定解析 因为统计的方法是可能犯错误的，利用线性回归方程预报变量的值不是精确值，但一般认为实际测量值应在预报值左右．16．某高校教“统计初步”课程的教师随机调查了选该课程的一些学生的情况，具体数据如下表：非统计专业统计专业 男 14 11 女718为了判断主修统计的数据，得到K 2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ）＝50×（14×18－11×7）225×25×21×29≈4.023.因为 4.023>3.841，所以判定主修统计专业与性别有关系，那么这种判断出错的可能性为________． 答案 5%解析 ∵查临界值表，得P(K 2≥3.841)＝0.05，故这种判断出错的可能性为5%. 三、解答题(本大题共7小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(10分)某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：零件的个数x(个) 2 3 4 5 加工的时间y(小时)2.53.04.04.5(1)(2)求出y 关于x 的线性回归方程y ∧＝b ∧x ＋a ∧，并在坐标系中画出回归直线； (3)试预测加工10个零件需要多少时间？解析 （1）散点图如下图：,（2）由表中数据得：∑4i ＝1x i y i ＝52.5，x －＝3.5，y －＝3.5，∑4i ＝1x i 2＝54，∴b ∧＝0.7，a ∧＝1.05，∴y ∧＝0.7x ＋1.05.,回归直线如图中所示.（3）将x ＝10代入回归直线方程，,得y ∧＝0.7×10＋1.05＝8.05（小时）. ∴预测加工10个零件需要8.05小时.18.（12分）某企业的某种产品产量与单位成本数据如下：月份 1 2 3 4 5 6 产量（千件） 2 3 4 3 4 5 单位成本（元）737271736968（1）试确定回归直线；（2）指出产量每增加1 000件时，单位成本下降多少？（3）假定产量为6 000件时，单位成本是多少？单位成本为70元时，产量应为多少件？ 解析 （1）设x 表示每月产量（单位：千件），y 表示单位成本（单位：元）作散点图.由图知y 与x 间呈线性相关关系，设线性回归方程为y ∧＝b ∧x ＋a ∧由公式可求得b ∧＝－1.818，a ∧＝77.363. ∴线性回归方程为y ∧＝－1.818x ＋77.363.（2）由线性回归方程知，每增加1 000件产量，单位成本下降1.818元. （3）当x ＝6 000时，y ＝－1.818×6＋77.363＝66.455（元）， 当y ＝70时，70＝－1.818x ＋77.363，得x ＝4.05（千件）.19.（12分）某地最近十年粮食需求量逐年上升，下表是部分统计数据：年份 2002 2004 2006 2008 2010 需求量（万吨）236246257276286（1）利用所给数据求年需求量与年份之间的回归直线方程y ∧＝bx+a ； (2)利用(1)中所求出的直线方程预测该地2012年的粮食需求量．解析 (1)由所给数据看出，年需求量与年份之间是近似直线上升，下面来求回归直线方程．为此对数据预处理如下：年份－2006 －4 －2 0 2 4 需求量－257－21－111929对预处理后的数据，容易算得x ＝0，y ＝3.2.b ＝（－4）×（－21）＋（－2）×（－11）＋2×19＋4×2942＋22＋22＋42＝26040＝6.5， a ＝y －－b x －＝3.2.由上述计算结果，知所求回归直线方程为y ∧－257＝b(x －2 006)＋a ＝6.5(x －2 006)＋3.2， 即y ∧＝6.5(x －2 006)＋260.2.①(2)利用直线方程①，可预测2012年的粮食需求量为6．5×(2 012－2 006)＋260.2＝6.5×6＋260.2＝299.2(万吨)≈300(万吨)．20．(12分)某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查，统计数据如下表所示：积极参加 班级工作 不太主动参 加班级工作合计 学习积极性高 18 7 25 学习积极性一般6 19 25 合计242650(1)到不太主动参加班级工作且学习积极性一般的学生的概率是多少？(2)试运用独立性检验的思想方法分析：学生的学习积极性与对待班级工作的态度是否有关？并说明理由．解析 (1)积极参加班级工作的学生有24名，总人数为50名，概率为2450＝1225.不太主动参加班级工作且学习积极性一般的学生有19名，概率为1950.(2)K 2＝50×（18×19－6×7）225×25×24×26≈11.5.∵K 2>10.828，∴有99.9%的把握认为学习积极性与对待班级工作的态度有关系．21．(12分)某运动队研制了一种有助于运动员在大运动量的训练后快速恢复体力的口服制剂，为了实验新药的效果而抽取若干名运动员来实验，所得资料如下：性别药恢复效果男运动员女运动员未用 用 未用 用 有效(恢复得好) 60 120 45 180 无效(恢复得差)45 45 60 255 总计105165105435解析 对男运动员K 2＝270×（60×45－45×120）2105×165×180×90≈7.013>6.635，有99%的把握认定药剂对男运动员有效．对女运动员K 2＝540×（45×255－60×180）2105×435×225×315≈0.076<2.706，没有充足的证据显示药剂与女运动员体力恢复有关系．因此该药对男运动员药效较好． 22．(12分)第17届亚运会于2014年9月19日至10月4日在韩国仁川进行，为了搞好接待工作，组委会招募了16名男志愿者和14名女志愿者，调查发现，男、女志愿者中分别有10人和6人喜爱运动，其余人不喜爱运动． (1)根据以上数据完成以下2×2列联表：喜爱运动 不喜爱运动总计 男 10 16 女 6 14 总计30(2)动有关？(3)如果从喜欢运动的女志愿者中(其中恰有4人会外语)，抽取2名负责翻译工作，那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少？参考公式：K 2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ），其中n ＝a ＋b ＋c ＋d.参考数据：P(K 2≥k 0)0.40 0.25 0.10 0.010 k 00.7081.3232.7066.635解析 (1)喜爱运动 不喜爱运动总计 男 10 6 16 女 6 8 14 总计161430(2)K 2＝30×（10×8－6×6）2（10＋6）（6＋8）（10＋6）（6＋8）≈1.1 575<2.706.因此，在犯错误的概率不超过0.10的前提下不能判断喜爱运动与性别有关． (3)喜欢运动的女志愿者有6人，设喜欢运动的女志愿者分别为A 、B 、C 、D 、E 、F ，其中A 、B 、C 、D 会外语，则从这6人中任取2人有AB ，AC ，AD ，AE ，AF ，BC ，BD ，BE ，BF ，CD ，CE ，CF ，DE ，DF ，EF ，共15种取法，其中两人都不会外语的只有EF 这1种取法．故抽出的志愿者中至少有1人能胜任翻译工作的概率是P ＝1－115＝1415.。

一、选择题1．某商场为了了解不同厂家生产的散装面包的月销售量y （千克）与售价x （元/千克）之间的关系，随机统计了某几个月的月销售量与当月各散装面包的售价，相关数据如下表：由表中数据算出线性回归方程为 3.1ˆˆyx a =-+，则样本在()18180，处的残差为（ ） A ．0B ．1.4C ．2D ．2.12．下列说法中错误的是（ ）A ．先把高二年级的2000名学生编号：1到2000，再从编号为1到50的学生中随机抽取1名学生，其编号为m ，然后抽取编号为50m +，100m +，150m +，……的学生，这种抽样方法是系统抽样法.B ．一组数据的方差为2s ，平均数为x ，将这组数据的每一个数都乘以2，所得的一组新数据的方差和平均数为24s ，2x .C ．若两个随机变量的线性相关性越强，则相关系数r 的值越接近于1.D ．若一组数据1，a ，3的平均数是2，则该组数据的方差是23. 3．利用独立性检验的方法调查大学生的性别与爱好某项运动是否有关，通过随机询问400名不同的大学生是否爱好某项运动，利用22⨯列联表，计算可得2K 的观测值7.556k ≈，附表：参照附表，得到的正确结论是A ．有99%以上的把握认为“爱好该项运动与性别无关”B ．有99%以上的把握认为“爱好该项运动与性别有关”C ．在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别有关”D ．在犯错误的概率不超过1%的前提下，认为“爱好该项运动与性别无关”4．为了解高中生对电视台某节目的态度，在某中学随机调查了110名学生，根据得到的联表算得2K 的观测值 5.278k ≈． 附表：参照附表，得到的正确结论是 （ ）A ．在犯错误的概率不超过1%的前提下，认为“喜欢该节目与性别有关”B ．在犯错误的概率不超过1%的前提下，认为“喜欢该节目与性别无关”C ．有97.5%以上的把握认为“喜欢该节目与性别有关”D ．有97.5%以上的把握认为“喜欢该节目与性别无关”5．某商品销售量y （件）与销售价格x （元/件）负相关，则其回归方程可能是A ．10200ˆyx =-+ B ．10200ˆyx =+ C ．10200ˆyx =-- D ．10200ˆyx =- 6．两个分类变量X 和Y ，值域分别为{x 1，x 2}和{y 1，y 2}，其样本频数分别是a ＝10，b ＝21，c ＋d ＝35，若X 与Y 有关系的可信程度为90%，则c ＝( ) A ．4 B ．5 C ．6D ．77．设导弹发射的事故率为0.01，若发射10次，其出事故的次数为ξ，则下列结论正确的是 （ ） A ．0.1E ξ=B ．•01D ξ=C ．10()0.01?0.99k k P k ξ-==D ．1010()0.99?0.01kkkP k C ξ-==8．某市政府调查市民收入与旅游欲望时，采用独立性检验法抽取3 000人，计算发现k 2＝6．023，则根据这一数据查阅下表，市政府断言市民收入增减与旅游欲望有关系的把握是( )A ．90%B ．95%C ．97．5%D ．99．5%9．某班主任对全班50名学生进行了作业量的调查，数据如下表：合计 26 24 50若推断“学生的性别与认为作业量大有关”，则这种推断犯错误的概率不超过( )附：()()()()()22n ad bc K a b c d a c b d -=++++ P(K 2>k 0) 0.15 0.10 0.05 0.025 0.01 0.001 k 02.0722.7063.8415.0246.63510.828A ．0.01B ．0.025C ．0.10D ．0.0510．如表为某公司员工工作年限x （年）与平均月薪y （千元）对照表．已知y 关于x 的线性回归方程为0.70.35y x =+，则下列结论错误的是（ ） x 3 4 5 6 y2.5t44.5A ．回归直线一定过点（4.5，3.5）B ．工作年限与平均月薪呈正相关C ．t 的取值是3.5D ．工作年限每增加1年，工资平均提高700元11．下列命题中：①线性回归方程y bx a =+必过点(),x y ；②在回归方程35y x =-中，当变量增加一个单位时，y 平均增加5个单位； ③在回归分析中，相关指数2R 为0.80的模型比相关指数2R 为0.98的模型拟合的效果要好；④在回归直线0.58ˆyx =-中，变量2x =时，变量y 的值一定是-7． 其中假命题的个数是 ( ) A ．1B ．2C ．3D ．412．下列说法：①将一组数据中的每个数据都乘以同一个非零常数a 后，标准差也变为原来的a 倍； ②设有一个回归方程35y x =-，变量x 增加1个单位时，y 平均减少5个单位； ③线性相关系数r 越大，两个变量的线性相关性越强；反之，线性相关性越弱；④在某项测量中，测量结果ξ服从正态分布()()21,0N σσ>，若ξ位于区域()0,1的概率为0.4，则ξ位于区域()1,+∞内的概率为0.6⑤利用统计量2χ来判断“两个事件,X Y 的关系”时，算出的2χ值越大，判断“X 与Y 有关”的把握就越大其中正确的个数是 A ．1B ．2C ．3D ．4二、填空题13．如图所示是世界20个地区受教育程度的人口百分比与人均收入的散点图，样本点基本集中在一个条型区域，因此两个变量呈线性相关关系．利用散点图中的数据建立的回归方程为ˆ 3.19388.193yx =+，若受教育的人口百分比相差10%，则其人均收入相差_________．14．对相关系数r ，①r 越大，线性相关程度越大； ②r 越小，线性相关程度越大；③|r|越大，线性相关程度越小，|r|越接近0，线性相关程度越大； ④|r|≤1且|r|越接近1，线性相关程度越大，|r|越接近0，线性相关程度越小 以上说法中，正确说法的序号是__________．15．如果根据性别与是否爱好运动的列联表得到K 2≈3．852＞3．841，则判断性别与是否爱好运动有关，那么这种判断犯错的可能性不超过________． 16．某班主任对全班50名学生作了一次调查，所得数据如表：认为作业多认为作业不多总计喜欢玩电脑游戏18927不喜欢玩电脑游戏81523总计262450由表中数据计算得到K 2的观测值k≈5.059，于是________（填“能”或“不能”）在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关．17．已知方程是根据女大学生的身高预报她的体重的回归方程，其中x的单位是cm ，的单位是kg ，那么针对某个体(160，53)的残差是________．18．下列命题中，正确的命题有__________．①回归直线ˆˆˆy bx a =+恒过样本点的中心(),x y ，且至少过一个样本点；②将一组数据的每个数据都加一个相同的常数后，方差不变；③用相关指数2R 来刻面回归效果；表示预报变量对解释变量变化的贡献率，越接近于1，说明模型的拟合效果越好；④若分类变量X 和Y 的随机变量2K 的观测值K 越大，则“X 与Y 相关”的可信程度越小；⑤.对于自变量x 和因变量y ，当x 取值一定时，y 的取值具有一定的随机性，x ，y 间的这种非确定关系叫做函数关系；⑥．残差图中残差点比较均匀的地落在水平的带状区域中，说明选用的模型比较合适； ⑦.两个模型中残差平方和越小的模型拟合的效果越好. 19．给出下列四个结论：(1)相关系数r 的取值范围是1r <；(2)用相关系数r 来刻画回归效果，r 的值越大，说明模型的拟合效果越差；(3)一个袋子里装有大小相同的5个白球和5个黑球，从中任取4个，则其中所含白球个数的期望是2；(4) 一个篮球运动员投篮一次得3分的概率为a ，得2分的概率为b ，不得分的概率为c ,且(),,0,1a b c ∈，已知他投篮一次得分的数学期望为2，则213a b+的最小值为163.其中正确结论的序号为______________.20．2018年春季，世界各地相继出现流感疫情，这已经成为全球性的公共卫生问题.为了考察某种流感疫苗的效果，某实验室随机抽取100只健康小鼠进行试验，得到如下列联表：感染 未感染 总计 注射 10 40 50 未注射 20 30 50 总计3070100关系．（参考公式：()()()()()22n ad bc K a b c d a c b d -=++++.） 20()P K k ≥ 0.100.05 0.025 0.010 0.005 0.001三、解答题21．某共享单车经营企业欲向甲巿投放单车，为制定适宜的经营策略﹐该企业首先在已投放单车的乙市进行单车使用情况调查.调查过程分随机问卷﹑整理分析及开座谈会三个阶段.在随机问卷阶段，A ，B 两个调查小组分赴全市不同区域发放问卷并及时收回﹔在整理分析阶段，两个调查小组从所获取的有效问卷中，针对15岁至45岁的人群，按比例随机抽取了300份，进行了数据统计，具体情况如下表：参考公式：()()()()()2n ad bc K a b c d a c b d -=++++，其中n a b c d =+++.参考数据：样本，再用分层抽样的方法将“年龄达到35岁”的被抽个体数分配到“经常使用单车”和“偶尔使用单车”中去.①求这60人中“年龄达到35岁且偶尔使用单车”的人数﹔②为听取对发展共享单车的建议，调查组专门组织所抽取的"年龄达到35岁且偶尔使用单车的人员召开座谈会，会后共有3份礼品赠送给其中3人，每人1份(其余人员仅赠送骑行优惠券).已知参加座谈会的人员中有且只有4人来自A 组，求A 组这4人中得到礼品的人数X 的分布列和数学期望；（2）从统计数据可直观得出“是否经常使用共享单车与年龄有关”的结论.在用独立性检验的方法说明该结论成立时，为使犯错误的概率尽可能小，当年龄设定为25岁时，根据已有数据，完成下列2×2列联表(单位：人)，并判断是否在犯错误的概率不超过1%的前提下有把握认为“经常使用共享单车与年龄有关”？22．为考察某种药物预防禽流感的效果，进行动物家禽试验，调查了100个样本，统计结果为：服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本．（1）根据所给样本数据画出22⨯列联表；（2）请问能有多大把握认为药物有效？附公式：()()()()()22=n ad bc K a b c d a c b d -++++．23．新高考，取消文理科，实行“33+”，成绩由语文、数学、外语统一高考 成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况，随机调查50人（把年龄在[)15,45称为中青年，年龄在[)45,75称为中老年），并把调查结果制成下表：（1）分别估计中青年和中老年对新高考了解的概率；（2）请根据上表完成下面22⨯列联表，是否有95%的把握判断对新高考的了解与年龄（中青年、中老年）有关？附：()()()()()22n ad bcKa b c d a c b d-=++++.24．十九大以来，某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求，带领广大农村地区人民群众脱贫奔小康，经过不懈的努力奋斗拼搏，新农村建设取得了巨大进步，农民年收入也逐年增加．为了实现2020年脱贫的工作计划，该地扶贫办随机收集了以下50位农民的统计数据，以此研究脱贫攻坚的效果是否与农民的受教育的发展状况有关：（1）根据列联表运用独立性检验的思想方法分析：能否有99%的把握认为“脱贫攻坚的效果与农民的受教育的发展状况有关”，并说明理由；（2）现用分层抽样的方法在全部受过教育的农民中随机抽取5位农民作为代表，再从这5位农民代表中任选2位继续调查，求这2位农民代表中至少有1位脱贫攻坚效果明显的概率．参考附表：参考公式：()()()()()22n ad bcKa b a c b d c d+=++++，其中n a b c d=+++．25．新冠状病毒严重威胁着人们的身体健康，我国某医疗机构为了调查新冠状病毒对我国公民的感染程度，选了某小区的100位居民调查结果统计如下：（1）根据已知数据，把表格数据填写完整；（2）能否在犯错误的概率不超过5%的前提下认为感染新冠状病与不同年龄有关？（3）已知在被调查的年龄大于50岁的感染者中有5名女性，其中2位是女教师，现从这5名女性中随机抽取3人，求至多有1位教师的概率．附：()()()()()22n ad bcKa b c d a c b d-=++++，n a b c d=+++.26．电视传媒公司为了解某地区电视观众对某类体育节目的收视情况，随机抽取100名观众进行调查，将日均收看体育节目时间不低于40分钟的观众称为“体育迷”，数据统计如下表：（1）是否有99%的把握认为“体育迷”与性别有关？（2）该体育类节目为了提升收视率，规定“体育迷”每天奖励积分2分，“非体育迷”每天奖励积分1分，积分累计一定数量可以用积分换购自己喜爱的物品.用表中的样本频率作为概率的估计值.某日3名观众来领取积分，记此3人当日的积分总和为随机变量ξ，求ξ的分布列和数学期望.附：()()()()()22n ad bc a b c d a c b d χ-=++++，其中n a b c d =+++.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】根据表中的数据求出(),x y ，利用回归直线方程经过样本中心点(),x y 求出ˆa ，把18x = 代入回归直线方程求出ˆy，利用残差的定义ˆy y -即可求解. 【详解】由表格得(),x y 为()24,160 ，又回归直线方程 3.1ˆˆyx a =-+经过样本中心点(),x y ， 所以160 3.124ˆa=-⨯+，解得ˆ234.4a =， 所以回归直线方程为 3.123.4ˆ4yx =-+， 把18x = 代入回归直线方程可得，ˆ178.6y=， 故样本在()18180， 处的残差为180178.6 1.4-=. 故选：B 【点睛】本题考查回归直线方程经过样本中心点和利用回归直线方程求某点处的残差；考查运算求解能力；熟练掌握回归直线方程经过样本中心点和残差的定义是求解本题的关键；属于中档题.2．C解析：C 【分析】根据题意，对选项中的命题进行分析，判断真假性即可． 【详解】对于A ，根据抽样方法特征是数据多，抽样间隔相等，是系统抽样，所以A 正确； 对于B ，一组数据的方差为2s ，平均数为x ，将这组数据的每一个数都乘以2，所得的一组新数据的方差和平均数为24s ，2x ，所以B 正确；对于C ，两个随机变量的线性相关性越强，则相关系数||r 的值越接近于1，所以C 错误；对于D ，一组数据1、a 、3的平均数是2，所以2a =；所以该组数据的方差是222212[(12)(22)(32)]33s =⨯-+-+-=，所以D 正确．故选：C ． 【点睛】本题主要考查抽样和统计，考查方差和平均数的计算，考查两个随机变量的相关性，意在考查学生对这些知识的理解掌握水平3．B解析：B 【分析】根据2K 的观测值7.556k ≈，对照表中数据，即可得到相应的结论． 【详解】根据2K 的观测值7.556k ≈，对照表中数据得出有0.01的几率说明这两个变量之间的关系是不可信的，即有10.0199%-=的把握说明两个变量之间有关系，故选B ． 【点睛】本题主要考查独立性检验的应用，独立性检验的一般步骤：（1）根据样本数据制成22⨯列联表；（2）根据公式计算2K 的观测值k ；（3）查表比较k 与临界值的大小关系，作统计判断．（注意：在实际问题中，独立性检验的结论也仅仅是一种数学关系，得到的结论也可能犯错误）4．C解析：C 【分析】因为5.278 6.635<，根据附表中的数据，即可得到判断的结论，得到答案． 【详解】因为5.278 6.635<，所以不能在犯错误的概率不超过1%的前提下，认为“喜欢该节目与性别有关”；又5.278 5.024>，所以有97.5%以上的把握认为“喜欢该节目与性别有关”，故选C ． 【点睛】本题主要考查独立性检验的应用，独立性检验的一般步骤：（1）根据样本数据制成22⨯列联表；（2）根据公式计算2K 的观测值k ；（3）查表比较k 与临界值的大小关系，作统计判断．（注意：在实际问题中，独立性检验的结论也仅仅是一种数学关系，得到的结论也可能犯错误）5．A解析：A 【解析】试题分析：因为商品销售量x 与销售价格ˆy负相关，所以排除B ，D 选项， 将0x =代入10200ˆyx =--可得2000ˆy =-<，不符合实际．故A 正确． 考点：线性回归方程．【方法点睛】本题主要考查线性回归方程，属容易题．线性回归方程ˆˆˆy bx a =+当ˆ0b<时ˆ,x y 负相关；当ˆ0b >时ˆ,x y 正相关． 6．B解析：B 【解析】 【分析】根据22⨯列联表，以及独立检验随机变量的临界值参考表,计算2K 对应的值，验证24,5,6,7,c K =是否恰好满足即可【详解】列22⨯列联表可知：()22661030521 3.024 2.70615513135K ⨯⨯-⨯=≈>⨯⨯⨯，所以5c =时，X 与Y 有关系的可信程度为90%，而其余的值4,6,7c c c ===皆不满足,故选B ． 【点睛】独立性检验的一般步骤：（1）根据样本数据制成22⨯列联表；（2）根据公式()()()()()22n ad bc K a b a d a c b d -=++++计算2K 的值；(3) 查表比较2K 与临界值的大小关系，作统计判断.（注意：在实际问题中，独立性检验的结论也仅仅是一种数学关系，得到的结论也可能犯错误.）7．A解析：A【解析】【分析】由题意知本题是在相同的条件下发生的试验，发射的事故率都为0.01，实验的结果只有发生和不发生两种结果，故本题符合独立重复试验，由独立重复试验的期望公式得到结果.【详解】由题意知本题是在相同的条件下发生的试验，发射的事故率都为0.01，故本题符合独立重复试验，即ξ～(10,0.01)B.∴100.010.1Eξ=⨯=故选A．【点睛】解决离散型随机变量分布列和期望问题时，主要依据概率的有关概念和运算，同时还要注意题目中离散型随机变量服从什么分布，若服从特殊的分布则运算要简单的多．8．C解析：C【详解】∵2 6.023 5.024K=>∴可断言市民收入增减与旅游欲望有关的把握为97.5%.故选C.点睛：本题主要考查独立性检验的实际应用.独立性检验的一般步骤：（1）根据样本数据制成22⨯列联表；（2）根据公式22()()()()()n ad bcKa b c d a c b d-=++++，计算出2K的值；（3）查表比较2K与临界值的大小关系，作统计判断.9．B解析：B【解析】K2＝≈5.059>5.024，因为P(K2>5.024)＝0.025，所以这种推断犯错误的概率不超过0.025.选B10．C解析：C【解析】由已知中的数据可得：34564.54x+++==，2.54 4.51144t ty++++==，∵数据中心点(),x y 一定在回归直线上，∴110.7 4.50.354t+=⨯+解得3t =，故C 错误；故11 3.54t+=， 回归直线一定过点（4.53.5，），ABD 正确；故选C ． 11．C解析：C 【解析】对于①，线性回归方程 ˆˆˆybx a =+必过点)x y （，，满足回归直线的性质，所以①正确；对于②，在回归方程ˆ35y x =-中，当变量x 增加一个单位时，y 平均减少5个单位，不是增加5个单位；所以②不正确；对于③，在回归分析中，相关指数2R 为0.80的模型比相关指数2R 为0.98的模型拟合的效果要好，该判断恰好相反；所以③不正确；对于④，在回归直线0.58ˆy x =-中，变量2x =时，变量y 的值一定是-7．不是一定为7，而是可能是7，也可能在7附近，所以④不正确；故选C.12．B解析：B 【解析】逐一考查所给的说法：①将一组数据中的每个数据都乘以同一个非零常数a 倍，原说法错误；②设有一个回归方程35y x =-，变量x 增加1个单位时，y 平均减少5个单位，原说法正确；③线性相关系数r 的绝对值越大，两个变量的线性相关性越强；反之，线性相关性越弱，原说法错误；④在某项测量中，测量结果ξ服从正态分布()()21,0N σσ>，若ξ位于区域()0,1的概率为0.4，则ξ位于区域()1,+∞内的概率为0.5，原说法错误；⑤利用统计量2χ来判断“两个事件,X Y 的关系”时，算出的2χ值越大，判断“X 与Y 有关”的把握就越大，原说法正确. 本题选择B 选项.二、填空题13．93美元【分析】设所受教育百分比分别为且利用回归方程计算即可【详解】设所受教育百分比分别为且根据回归方程为收入相差大约为：即受教育的人口百分比相差则其人均收入相差约美元故答案为：3193美元【点睛】解析：93美元 【分析】设所受教育百分比分别为%,%a b ，且10a b -=，利用回归方程计算即可． 【详解】设所受教育百分比分别为%,%a b ，且10a b -= 根据回归方程为 3.19388.193y x ∧=+， 收入相差大约为：()3.19388.193 3.19388.193 3.1931031.93a b ⨯+-⨯+=⨯=，即受教育的人口百分比相差10%，则其人均收入相差约31.93美元． 故答案为：31.93美元． 【点睛】本题考查了线性回归方程的应用问题，属于中档题．14．④【解析】两个变量之间的相关系数r 的绝对值越接近于1表示两个变量的线性相关性越强r 的绝对值非常接近于0时表示两个变量之间几乎不存在线性相关故答案为④解析：④ 【解析】两个变量之间的相关系数，r 的绝对值越接近于1，表示两个变量的线性相关性越强，r 的绝对值非常接近于0时，表示两个变量之间几乎不存在线性相关．故答案为④．15．【解析】∵P(K2≥3841)≈005∴判断性别与是否爱好运动有关出错的可能性不超过5点睛：根据卡方公式计算再与参考数据比较就可确定可能性 解析：5%【解析】∵P (K 2≥3．841)≈0．05．∴判断性别与是否爱好运动有关，出错的可能性不超过5%． 点睛：根据卡方公式计算2K ，再与参考数据比较，就可确定可能性.16．不能【解析】查表知若要在犯错误的概率不超过001的前提下认为喜欢玩电脑游戏与认为作业多有关则临界值k0＝6635本题中k≈5059＜6635所以不能在犯错误的概率不超过001的前提下认为喜欢玩电脑游解析：不能 【解析】查表知若要在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关，则临界值k 0＝6.635.本题中，k≈5.059＜6.635，所以不能在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关． 考点：独立性检验.17．【解析】将x ＝160代入得所以残差考点：线性回归方程残差 解析：【解析】将x ＝160代入，得，所以残差考点：线性回归方程，残差.18．②⑥⑦【解析】①回归直线恒过样本点的中心可以不过任何一个样本点；②将一组数据中的每个数据都加上同一个常数后根据方差公式可知方差恒不变；③用相关指数来刻面回归效果；表示预报变量对解释变量变化的贡献率越解析：②⑥⑦ 【解析】①回归直线ˆˆˆy bx a =+恒过样本点的中心(),x y ，可以不过任何一个样本点；②将一组数据中的每个数据都加上同一个常数后，根据方差公式可知方差恒不变； ③用相关指数2R 来刻面回归效果；表示预报变量对解释变量变化的贡献率，越接近于0，说明模型的拟合效果越好；④若分类变量X 和Y 的随机变量2K 的观测值K 越大，则“X 与Y 相关”的可信程度越大；⑤.对于自变量x 和因变量y ，当x 取值一定时，y 的取值具有一定的随机性，x ，y 间的这种非确定关系叫做相关关系；⑥．残差图中残差点比较均匀的地落在水平的带状区域中，说明选用的模型比较合适； ⑦.两个模型中残差平方和越小的模型拟合的效果越好. 故答案为：②⑥⑦19．(3)(4)【解析】分析：（1）相关系数的范围；（2）由相关指数r 的含有知|r|的值越大说明模型的拟合效果越好；（3）离散型随机变量的期望；（4）根据期望公式得到3a+2b=2进而利用均值不等式求最解析：(3)(4) 【解析】分析：（1）相关系数的范围；（2）由相关指数r 的含有知，|r|的值越大，说明模型的拟合效果越好；（3）离散型随机变量的期望；（4）根据期望公式得到3a+2b=2，进而利用均值不等式求最值.详解：（1）相关系数r 的取值范围是1r ≤，故（1）错误；（2）用相关指数r 来刻画回归效果，|r|的值越大，说明模型的拟合效果越好，故（2）错误；（3）含零个白球的概率为5210，含一个白球的概率为50210，含二个白球的概率为100210，含三个白球的概率为50210，含四个白球的概率为5210，白球个数的期望为：550100505012342210210210210210⨯+⨯+⨯+⨯+⨯=，故（3）正确；（4）∵3a+2b+0•c=2，a ，b ，c ∈（0，1），∴213a b +=（213a b +）•12（3a+2b ）=12（6+4b a +a b +23）≥12（203 =12（203+4）=163（当且仅当a=2b ，即a=12，b=14时取“=”），故（4）正确． 其中正确结论的序号为：（3）（4）． 故答案为（3）（4）．点睛：本题考查相关系数的有关概念，考查离散型随机变量的期望及概率统计与基本不等式的综合应用，属于中档题．20．05【详解】分析：直接利用独立性检验公式计算即得解详解：由题得所以犯错误的概率最多不超过005的前提下可认为注射疫苗与感染流感有关系故答案为005点睛：本题主要考查独立性检验和的计算意在考查学生对这解析：05 【详解】分析：直接利用独立性检验2K 公式计算即得解.详解：由题得22100(10302040)100 4.762 3.8413070505021K ⨯-⨯==≈>⨯⨯⨯,所以犯错误的概率最多不超过0.05的前提下，可认为“注射疫苗”与“感染流感”有关系． 故答案为0.05.点睛：本题主要考查独立性检验和2K 的计算，意在考查学生对这些知识的掌握水平和解决实际问题的能力.三、解答题21．（1）① 9人；②分布列答案见解析，数学期望：43；（2）列联表答案见解析，在犯错误的概率不超过1%的前提下没有把握认为“经常使用共享单车与年龄有关”. 【分析】（1）利用分层抽样，按比例计算这60人中“年龄达到35岁且偶尔使用单车”的人数﹔直接分析X 服从超几何分布，求概率，写出分布列，求出数学期望；（2）根据题意，25m =填写2×2列联表，套公式计算 3.063K ≈，对应参考值下结论. 【详解】解：（1）①从300人中抽取60人，其中“年龄达到35岁”的有1006020300⨯=人， 再将这20人用分层抽样法按"是否经常使用单车"进行名额划分，其中“年龄达到35岁且偶尔使用单车”的人数为45209100⨯=. ②A 组这4人中得到礼品的人数X 的可能取值为0，1，2，3，相应概率为：()35395042C P X C ===，()12453910121C C P X C ===， ()214539C C 52C 14P X ===，()3439C 13C 21P X ===.故其分布列为∴数学期望()0123422114213E X =⨯+⨯+⨯+⨯= （2）25m =时，按“年龄是否达到25岁”对数据进行整理，得到如下列联表()2300678711333300210049 3.06320010018012020010018012016K ⨯⨯-⨯⨯===≈⨯⨯⨯⨯⨯⨯ ∴3.063 6.635<所以在犯错误的概率不超过1%的前提下没有把握认为“经常使用共享单车与年龄有关”. 【点睛】(1) 求离散型随机变量的分布列时，要特别注意. 随机变量是否服从二项分布、超几何分布等特殊的分布；(2)独立性检验的题目直接根据题意完成完成2×2列联表,直接套公式求出K ,对照参数下结论，一般较易.22．（1）列联表见解析；（2）大概有90%把握认为药物有效． 【分析】（1）根据服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本，根据各种数据，列好表格，填好数据，得到列联表.（2）根据列联表数据，代入临界值公式，做出观测值，进行比较，即可得出结果. 【详解】（1）根据服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本，得到列联表。

一、选择题1．已知x 与y 之间的几组数据如下表：参考公式：线性回归方程y bx a =+，其中()()()121niii nii x x y y b x x ==--=-∑∑，a y bx =-；相关系数()()niix x y y r --=∑上表数据中y 的平均值为2.5，若某同学对m 赋了三个值分别为1.5，2，2.5得到三条线性回归直线方程分别为11y b x a =+，22y b x a =+，33y b x a =+，对应的相关系数分别为1r ，2r ，3r ，下列结论中错误．．的是（ ） A ．三条回归直线有共同交点 B ．相关系数中，2r 最大 C ．12b b >D ．12a a >2．下列说法错误．．的是（ ） A ．10xy ≠是5x ≠或2y ≠的充分不必要条件B ．若命题p ：x R ∀∈，210x x ++≠，则p ⌝：x R ∃∈，210x x ++=C ．已知随机变量()2~2,X N σ，且()40.84P X ≤=，则()00.16P X ≤=D ．相关系数r 越接近1，表示线性相关程度越弱． 3．已知两个统计案例如下：①为了探究患肺炎与吸烟的关系，调查了339名50岁以上的人，调查结果如下表：②为了解某地母亲与女儿身高的关系，随机测得10对母女的身高如下表：则对这些数据的处理所应用的统计方法是（ ） A ．①回归分析，②取平均值 B ．①独立性检验，②回归分析 C ．①回归分析，②独立性检验D ．①独立性检验，②取平均值4．对于独立性检验，下列说法正确的是（ ） A ．2 3.841K >时，有95%的把握说事件A 与B 无关 B ．2 6.635K >时，有99%的把握说事件A 与B 有关 C ．2 3.841K ≤时，有95%的把握说事件A 与B 有关 D ．2 6.635K >时，有99%的把握说事件A 与B 无关 5．下列命题中正确命题的个数是（1）对分类变量X 与Y 的随机变量2K 的观测值k 来说，k 越小，判断“X 与Y 有关系”的把握越大；（2）若将一组样本数据中的每个数据都加上同一个常数后，则样本的方差不变； （3）在残差图，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高； （4）设随机变量ξ服从正态分布()0,1N ； 若()1P p ξ>=，则()1102P p ξ-<<=-（ ） A ．4B ．3C ．2D ．16．对四对变量Y 和x 进行线性相关性检验,已知n 是观测值组数,r 是相关系数,且已知: ①n=7,r=0.953 3;②n=15,r=0.301 2;③n=17,r=0.499 1;④n=3,r=0.995 0,则变量Y 和x 具有线性相关关系的是( ) A ．①和② B ．①和③ C ．②和④D ．③和④7．给出下列说法：①用()()221211ˆni i i n i i i y y R y y ==-=--∑∑刻画回归效果，当2R 越大时，模型的拟合效果越差，反之则越好；②归纳推理是由特殊到一般的推理，而演绎推移则是由一般到特殊的推理；③综合法证明数学问题是“由因索果”，分析法证明数学问题是“执果索因”；④设有一个回归方程ˆ35yx =+，变量x 增加1个单位时，y 平均增加5个单位；⑤线性回归方程ˆˆˆy bx a =+必过点(),x y .其中错误的个数有（ ）A ．0个B ．1个C ．2个D ．3个8．为了普及环保知识，增强环保意识，某大学从理工类专业的A 班和文史类专业的B 班各抽取20名同学参加环保知识测试，统计得到成绩与专业的列联表：（ ）附：参考公式及数据：（1）统计量：()()()()()22n ad bcKa b c d a c b d-=++++，（n a b c d=+++）.（2）独立性检验的临界值表：则下列说法正确的是A．有95%的把握认为环保知识测试成绩与专业有关B．有95%的把握认为环保知识测试成绩与专业无关C．有99%的把握认为环保知识测试成绩与专业有关D．有99%的把握认为环保知识测试成绩与专业无关9．通过随机询问250名不同性别的高中生在购买食物时是否看营养说明书，得到如下列联表：从调查的结果分析，认为性别和读营养说明书的关系为（）附：()()()()()22n ad bc K a b c d a c b d -=++++ . A ．95%以上认为无关 B ．90%～95%认为有关 C ．95%～99.9%认为有关D ．99.9%以上认为有关10．某种产品的广告费支出x 与销售额y （单位：万元）之间有下表关系： x 2 4 5 6 8 y3040605070y 与x 的线性回归方程为 6.5175ˆ.y x =+，当广告支出5万元时，随机误差的效应（残差）为（ ） A ．40 B ．20 C ．30D ．1011．下列说法中，不正确的是A ．两个变量的任何一组观测值都能得到线性回归方程B ．在平面直角坐标系中，用描点的方法得到表示两个变量的关系的图象叫做散点图C ．线性回归方程反映了两个变量所具备的线性相关关系D ．线性相关关系可分为正相关和负相关 12．有下列数据： x123y35.9912.01下列四个函数中，模拟效果最好的为（ ） A ．B ．C ．D ．二、填空题13．对相关系数r ，①r 越大，线性相关程度越大； ②r 越小，线性相关程度越大；③|r|越大，线性相关程度越小，|r|越接近0，线性相关程度越大； ④|r|≤1且|r|越接近1，线性相关程度越大，|r|越接近0，线性相关程度越小 以上说法中，正确说法的序号是__________．14． 2.5PM 是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，下图是据某地某日早7点至晚8点甲、乙两个 2.5PM 监测点统计的数据（单位：毫克／每立方米）列出的茎叶图，则甲、乙两地浓度的方差较小的是_________．15．某单位为了了解用电量y (度)与气温x (度)之间的关系，随机统计了某4天的用电量与当天气温，并制作了如下的对照表由表中数据，得回归直线方程ˆˆˆy bx a =+，若ˆ2b=-，则ˆa =________． 16．在西非肆虐的“埃博拉病毒”的传播速度很快，这已经成为全球性的威胁，为了考查某种埃博拉病毒疫苗的效果，现随机抽取100只小鼠进行试验，得到如下列联表：附表：参照附表，在犯错误的概率不超过______（填百分比）的前提下，认为“小动物是否被感染与有没有服用疫苗有关”.17．已知方程ˆ0.8582.71yx =-是根据女大学生的身高预报她的体重的回归方程，其中x 的单位是cm ，ˆy的单位是kg ，那么针对某个体(160,53)的残差是______________． 18．给出下列结论：（1）在回归分析中，可用相关指数R 2的值判断模型的拟合效果，R 2越大，模型的拟合效果越好；（2）某工产加工的某种钢管，内径与规定的内径尺寸之差是离散型随机变量； （3）随机变量的方差和标准差都反映了随机变量的取值偏离于均值的平均程度，它们越小，则随机变量偏离于均值的平均程度越小；（4）若关于x 的不等式2x x a a -+-≥在R 上恒成立，则a 的最大值是1；（5）甲、乙两人向同一目标同时射击一次，事件A ：“甲、乙中至少一人击中目标”与事件B ：“甲，乙都没有击中目标”是相互独立事件．其中结论正确的是 ．（把所有正确结论的序号填上）19．给出下列四个结论：(1)相关系数r的取值范围是1r<；(2)用相关系数r来刻画回归效果，r的值越大，说明模型的拟合效果越差；(3)一个袋子里装有大小相同的5个白球和5个黑球，从中任取4个，则其中所含白球个数的期望是2；(4) 一个篮球运动员投篮一次得3分的概率为a，得2分的概率为b，不得分的概率为c,且(),,0,1a b c∈，已知他投篮一次得分的数学期望为2，则213a b+的最小值为163.其中正确结论的序号为______________.20．为了了解司机开车时礼让斑马线行人的情况，交警部门调查了100名机动车司机，得到以下统计数据：礼让斑马线行人不礼让斑马线行人男性司机人数4015女性司机人数2025若以2χ为统计量进行独立性检验，则2χ的值是__________.（结果保留2位小数）参考公式()11221221 21212n n n n nn n n nχ++++-=三、解答题21．我国新型冠状病毒肺炎疫情期间，以网络购物和网上服务所代表的新兴消费展现出了强大的生命力，新兴消费将成为我国消费增长的新动能.某市为了了解本地居民在2020年2月至3月两个月网络购物消费情况，在网上随机对1000人做了问卷调查，得如表频数分布表：（1）作出这些数据的频率分布直方图，并估计本市居民此期间网络购物的消费平均值；（2）在调查问卷中有一项是填写本人年龄，为研究网购金额和网购人年龄的关系，以网购金额是否超过4000元为标准进行分层抽样，从上述1000人中抽取200人，得到如表列联表，请将表补充完整并根据列联表判断，在此期间是否有95%的把握认为网购金额与网购人年龄有关.参考公式和数据：()()()()()22n ad bcKa b c d a c b d-=++++.（其中n a b c d=+++为样本容量）22．海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取100 个网箱，测量各箱水产品的产量(单位：kg)，其频率分布直方图如图：（1）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关；箱产量<50kg箱产量≥50kg合计旧养殖法新养殖法合计（2）在新养殖法养殖的网箱中，按照分层抽样的方法从箱产量少于50kg和不少于50kg的网箱中随机抽取5箱，再从中抽取3箱进行研究，这3箱中产量不少于50kg的网箱数为X，求X的分布列和数学期望.()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++ ()2P K k ≥ 0.1000.050 0.010 0.005 0.001 k 2.706 3.8416.6357.87910.82823．支付宝和微信支付是目前市场占有率较高的支付方式，某第三方调研机构对使用这两种支付方式的人数作了对比，从全国随机抽取了100个地区作为研究样本，计算了各个地区样本的使用人数，其频率分布直方图如下，（1）记A 表示事件“微信支付人数低于50千人”，估计A 的概率；（2）填写下面2╳2列联表，并根据2╳2列联表判断是否有99%的把握认为支付人数与支付方式有关；()()()()()2n ad bc K a b c d a c b d -=++++．24．在第十五次全国国民阅读调查中，某地区调查组获得一个容量为200的样本，其中城镇居民150人，农村居民50人，在这些居民中，经常阅读的城镇居民100人，农村居民24人.（1）完成上面2×2列联表，并判断是否有95%的把握认为经常阅读与居民居住地有关？ （2）从该地区居民城镇的居民中，随机抽取5位居民参加一次阅读交流活动，记这5位居民中经常阅读的人数为X ，若用样本的频率作为概率，求随机变量X 的分布列和期望.附：K 2＝2()()()()()n ad bc a b c d a c b d -++++，其中n ＝a +b +c +d .25．电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图；将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性.（1）根据已知条件完成下列联表，并判断能否在犯错误率不超过0.05的前提下认为“体育迷”与性别有关？非体育迷体育迷合计男女合计（2）将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率.附：参考公式：()()()()()22n ad bcKa b c d a c b d-=++++，n a b c d=+++.()2P K k≥0.050.01k 3.841 6.63526．为迎接2022年北京冬季奥运会，普及冬奥知识，某校开展了“冰雪答题王”冬奥知识竞赛活动．现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生，将他们的比赛成绩（满分为100分）分为6组：[40,50),[50,60),[60,70)，[70,80),[80,90),[90,100]得到如图所示的频率分布直方图．（Ⅰ）求a 的值；（Ⅱ）记A 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生，该学生的比赛成绩不低于80分”，估计A 的概率；（Ⅲ）在抽取的100名学生中，规定：比赛成绩不低于80分为“优秀”，比赛成绩低于80分为“非优秀”．请在答题卡上将22⨯列联表补充完整，并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”？参考公式及数据：22()()()()()n ad bc K a b c d a c b d -=++++，n a b c d =+++．()20P K k ≥ 0.100.05 0.025 0.010 0.005 0.001 0k 2.7063.8415.0246.6357.87910.828【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】由题意可得5m n +=，分别取m 与n 的值，由公式计算出1122123,,,,,,b a b a r r r 的值，逐一分析四个选项，即可得到答案． 【详解】由题意，1410m n +++=，即5m n +=． 若 1.5m =，则 3.5n =，此时12342.54x +++==， 2.5y =． ()()()()()()()()()()411 2.51 2.52 2.5 1.5 2.53 2.5 3.5 2.54 2.54 2.5 5.5iii x x y y =--=--+--+--+--=∑ ，()()()4222221 1.50.50.5 1.55i i x x =-=-+-++=∑ ， ()()()42222211.511 1.5 6.5i i y y =-=-+-++=∑．则1 5.51.15b ==，1 2.5 1.1 2.50.25a =-⨯=- ，1r =≈； 若2m =，则3n =，此时12342.54x +++==， 2.5y =． ()()()()()()()()()()411 2.51 2.52 2.52 2.53 2.53 2.54 2.54 2.55iii x x y y =--=--+--+--+--=∑，()4215ii x x =-=∑，()()()42222211.50.50.5 1.55i i y y =-=-+-++=∑．2515b ==，2 2.51 2.50a =-⨯=，21r ==； 若 2.5m =，则 2.5n =，此时12342.54x +++==， 2.5y =． ()()()()()()()()()()411 2.51 2.52 2.5 2.5 2.53 2.5 2.5 2.54 2.54 2.5 4.5iii x x y y =--=--+--+--+--=∑，()4215i i x x =-=∑，()()422211.5 1.5 4.5i i y y =-=-+=∑，3r ==由样本点的中心相同，故A 正确；由以上计算可得，相关系数中，2r 最大，12b b >，12a a <，故B ，C 正确，D 错误． 故选：D ． 【点睛】本题考查线性回归方程与相关系数的求法，考查计算能力，是中档题．2．D解析：D 【分析】A 选项,由“若10xy ≠,则5x ≠或2y ≠”的逆否命题判断充分性,由其否命题判断必要性；由全称命题的否定的概念判断选项B ；由正态分布的性质判断选项C ；由相关系数的概念判断选项D. 【详解】对于选项A,命题“若10xy ≠,则5x ≠或2y ≠”的逆否命题为“若5x =且2x =,则10xy =”,为真命题,而命题“若10xy =,则5x =且2x =”为假命题,所以10xy ≠是5x ≠或2y ≠的充分不必要条件,故A 正确；对于选项B,由全称命题的否定可得p ⌝:x R ∃∈,210x x ++=,故B 正确；对于选项C,由随机变量()2~2,X N σ,且()40.84P X ≤=,则()()()041410.840.16P X P X P X ≤=≥=-≤=-=,故C 正确；对于选项D,相关系数r 越接近1,表示线性相关程度越强,故D 错误, 故选:D 【点睛】本题考查充分不必要条件的判断,考查全称命题的否定,考查正态分布的概率,考查相关系数的概念,熟练掌握各知识点是解题关键.3．B解析：B 【分析】根据独立性检验和回归分析的概念，即可作出判定，得到答案． 【详解】由题意，独立性检验通常是研究两个分类变量之间是否有关系，所以①采用独立性检验， 回归分析通常是研究两个具有相关关系的变量的相关程度，②采用回归分析， 综上可知①是独立性检验，②是回归分析，故选B ． 【点睛】本题主要考查了独立性检验和回归分析的概念及其判定，其中解答中熟记独立性检验和回归分析的概念是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题．4．B解析：B 【分析】根据独立性检验中卡方的概念知，选B. 【详解】根据独立性检验中卡方的概念知,2 6.635K >时，有99%的把握说事件A 与B 有关选B. 【点睛】本题主要考查了独立性检验中卡方的概念，属于中档题.5．B解析：B 【解析】 【分析】根据独立性检验的定义可判断（1）；根据方差的性质可判断（2）；根据残差的性质可判断（3）；根据正态分布的对称性可判断（4）. 【详解】（1）对分类变量X 与Y 的随机变量2K 的观测值K 来说，K 越大，判断“X 与Y 有关系”的把握越大，故（1）错误；（2）若将一组样本数据中的每个数据都加上同一个常数后，数据的离散程度不变，则样本的方差不变，故（2）正确；（3）根据残差的定义可知，在残差图，残差点分布的带状区域的宽度越狭窄，预测值与实际值越接近，其模型拟合的精度越高，（3）正确；（4）设随机变量ξ服从正态分布()0,1N ，若()1P p ζ>=，则()1P p ζ<-=，则()1112P p ζ-<<=-，则()1102P p ζ-<<=-，故（4）正确， 故正确的命题的个数为3个，故选B. 【点睛】本题主要通过对多个命题真假的判断，主要综合考查独立性检验的定义、方差的性质、残差的性质以及正态分布的对称性，属于中档题. 这种题型综合性较强，也是高考的命题热点，同学们往往因为某一处知识点掌握不好而导致“全盘皆输”，因此做这类题目更要细心、多读题，尽量挖掘出题目中的隐含条件，另外，要注意从简单的自己已经掌握的知识点入手，然后集中精力突破较难的命题.6．B解析：B 【解析】分析：先查相关系数检验的临界值表，再判断变量Y 和x 具有线性相关关系的选项. 详解: 查相关系数检验的临界值表 ①r 0.05=0.754,r ＞r 0.05； ②r 0.05=0.514,r ＜r 0.05; ③r 0.05=0.482,r ＞r 0.05； ④r 0.05=0.997,r 0.05＞r.∴y 和x 具有线性相关关系的是①③.故答案为B.点睛：本题主要考查相关系数，意在考查学生对这些知识的掌握水平.7．B解析：B 【解析】分析：①可由相关指数的概念判断;②③由推理,综合法和反证法的概念判断；④和⑤由线性回归分析判断即可.详解：①相关指数2R 越大,则相关性越强,模型的拟合效果越好.错误;② 归纳推理是由特殊到一般的推理,而演绎推理是由一般到特殊的推理,由归纳推理与演绎推理的概念可知正确.③综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”,由概念可知正确. ④由回归方程的系数意义知，当变量x 增加1个单位时，y 平均增加5个单位，正确；⑤线性回归方程ˆˆˆy bx a =+必过样本中心点(),x y ，正确.故选B.点睛：本题是一道综合性考题，即考查了推理与证明的原理，又考查了利用2R 判断模型拟合程度，同时还考查了线性回归分析的相关概念，属于中档题.8．A【解析】分析：首先计算观测值k 0的值，然后给出结论即可. 详解：由列联表计算观测值：()2401413672804.912 3.8412119202057k ⨯⨯-⨯==≈>⨯⨯⨯， 则有95%的把握认为环保知识测试成绩与专业有关. 本题选择A 选项.点睛：本题主要考查独立性检验及其应用等知识，意在考查学生的转化能力和计算求解能力.9．D解析：D 【解析】分析：由列联表中的数据，利用公式()()()()()22n ad bc K a b c d a c b d -=++++求得2K ，与邻界值比较，即可得到结论. 详解：()222509070603021.6310.828120130150100K ⨯⨯-⨯=≈>⨯⨯⨯，∴有0099.9的把握认为性别和读营养说明书的有关.点睛：独立性检验的一般步骤：（1）根据样本数据制成22⨯列联表；（2）根据公式()()()()()22n ad bc K a b a d a c b d -=++++计算2K 的值；(3) 查表比较2K 与临界值的大小关系，作统计判断.（注意：在实际问题中，独立性检验的结论也仅仅是一种数学关系，得到的结论也可能犯错误.）10．D解析：D 【解析】∵y 与x 的线性回归方程为 6.5175ˆ.y x =+ 当5x =时，ˆ50y=． 当广告支出5万元时，由表格得：60y = 故随机误差的效应（残差）为605010.-= 故选D ．11．A解析：A 【解析】要得到线性回归方程应至少有两个变量的两组观测值，因此A 不正确．根据散点图、线性回归方程、线性相关关系的概念可得B ，C ，D 都正确．故选A ．12．A【解析】当x＝1，2，3时，分别代入求y值，离y最近的值模拟效果最好，可知A模拟效果最好．故选A.考点：非线性回归方程的选择.二、填空题13．④【解析】两个变量之间的相关系数r的绝对值越接近于1表示两个变量的线性相关性越强r的绝对值非常接近于0时表示两个变量之间几乎不存在线性相关故答案为④解析：④【解析】两个变量之间的相关系数，r的绝对值越接近于1，表示两个变量的线性相关性越强，r的绝对值非常接近于0时，表示两个变量之间几乎不存在线性相关．故答案为④．14．甲【解析】根据茎叶图中的数据可知甲地的数据都集中在006和007之间数据分布比较稳定而乙地的数据分布比较分散不如甲地数据集中故甲地的方差小故答案为甲解析：甲【解析】根据茎叶图中的数据可知，甲地的数据都集中在0.06和0.07之间，数据分布比较稳定，而乙地的数据分布比较分散，不如甲地数据集中，故甲地的方差小，故答案为甲. 15．【解析】试题分析：由题意得即样本中心点代入回归直线方程得考点：回归直线方程的应用解析：60【解析】试题分析：由题意得18131011542x++-==，24343864404y+++==，即样本中心点15(,40)2，代入回归直线方程，得15402602ˆˆa a=-⨯+⇒=.考点：回归直线方程的应用.16．％【解析】试题分析：所以在犯错误不超过％的前提下认为小动物是否被感染与有没有服用疫苗有关考点：1卡方统计量2统计；【易错点晴】本题主要考查的是统计中的卡方统计量属于容易题解题时一定要注意计算问题很多解析：％【解析】试题分析：，所以在犯错误不超过％的前提下，认为“小动物是否被感染与有没有服用疫苗有关” ． 考点：1.卡方统计量，2.统计；【易错点晴】本题主要考查的是统计中的卡方统计量，属于容易题．解题时一定要注意计算问题，很多同学列式正确计算错误，从而不能正确得到结果．另外，学生容易把答案写为％，所以一定要注意本题中的问题是什么，否则很容易出现错误．17．【解析】将代入得所以残差 解析：0.29-【解析】将160x =代入0.85 2.1ˆ87yx =-，得0.8516082.71ˆ53.29y =⨯-=，所以残差5353.ˆ290ˆ.29ey y =-=-=-． 18．（1）（3）（4）【分析】根据相关指数离散型随机变量随机变量的方差和标准差绝对值不等式和相互独立事件相关的知识对五个结论逐一分析由此得出正确结论的序号【详解】对于（1）R2越大模型的拟合效果越好结论解析：（1），（3），（4） 【分析】根据相关指数、离散型随机变量、随机变量的方差和标准差、绝对值不等式和相互独立事件相关的知识，对五个结论逐一分析，由此得出正确结论的序号. 【详解】对于（1）,R 2越大，模型的拟合效果越好，结论正确.对于（2），内径与规定的内径尺寸之差是连续型随机变量，结论错误.对于（3），根据随机变量的方差和标准差的知识可判断出结论正确.对于（4），根据绝对值不等式有22x x a a a -+-≥-≥，所以2a a -≤-或2a a -≥，前者解得1a ≤，后者无解，故a 的最大值为1，结论正确.对于（5），事件A ：“甲、乙中至少一人击中目标”与事件B ：“甲，乙都没有击中目标”是对立事件，不是相互独立事件，结论错误.综上所述，正确结论为（1），（3），（4）. 【点睛】本小题主要考查关指数、离散型随机变量、随机变量的方差和标准差、绝对值不等式和相互独立事件相关的知识，考查分析与解决问题的能力，属于基础题.19．(3)(4)【解析】分析：（1）相关系数的范围；（2）由相关指数r 的含有知|r|的值越大说明模型的拟合效果越好；（3）离散型随机变量的期望；（4）根据期望公式得到3a+2b=2进而利用均值不等式求最解析：(3)(4) 【解析】分析：（1）相关系数的范围；（2）由相关指数r 的含有知，|r|的值越大，说明模型的拟合效果越好；（3）离散型随机变量的期望；（4）根据期望公式得到3a+2b=2，进而利用均值不等式求最值.详解：（1）相关系数r 的取值范围是1r ≤，故（1）错误；（2）用相关指数r 来刻画回归效果，|r|的值越大，说明模型的拟合效果越好，故（2）错误；（3）含零个白球的概率为5210，含一个白球的概率为50210，含二个白球的概率为100210，含三个白球的概率为50210，含四个白球的概率为5210， 白球个数的期望为：550100505012342210210210210210⨯+⨯+⨯+⨯+⨯=，故（3）正确； （4）∵3a+2b+0•c=2，a ，b ，c ∈（0，1）， ∴213a b +=（213a b +）•12（3a+2b ）=12（6+4b a +a b +23）≥12（203+24b aa b ⋅） =12（203+4）=163（当且仅当a=2b ，即a=12，b=14时取“=”），故（4）正确． 其中正确结论的序号为：（3）（4）． 故答案为（3）（4）．点睛：本题考查相关系数的有关概念，考查离散型随机变量的期望及概率统计与基本不等式的综合应用，属于中档题．20．【解析】分析：根据题意填写2×2列联表计算观测值对照临界值得出结论详解：填写2×2列联表如下：根据数表计算=≈825＞7879所以有995的把握认为开车时使用手机与司机的性别有关；点睛：独立性检验的 解析：8.25【解析】分析：根据题意填写2×2列联表，计算观测值，对照临界值得出结论. 详解：填写2×2列联表，如下：根据数表，计算()()()()()22n ad bc a b c d a c b d -X =++++=()21004025201555456040⨯⨯-⨯⨯⨯⨯≈8.25＞7.879，所以有99.5%的把握认为开车时使用手机与司机的性别有关；点睛：独立性检验的一般步骤：（I ）根据样本数据制成22⨯列联表；（II ）根据公式()()()()()22n ad bc K a b a d a c b d -=++++计算2K 的值；（III ） 查表比较2K 与临界值的大小关系，作统计判断．（注意：在实际问题中，独立性检验的结论也仅仅是一种数学关系，得到的结论也可能犯错误．）三、解答题21．（1）直方图见解析，3360元；（2）列联表见解析，没有95%的把握认为网购金额与网购人年龄有关. 【分析】(1)由频数分布表计算出各组数据的纵坐标（频率除以组距），再做出频率分布直方图, 由频率分布直方图估计平均值的定义可得本市居民此期间网络购物的消费平均值; (2) 根据频数分布表中的数据可知网购金额不超过4000元的有700人，超过4000元的有300人，根据分层抽样可得网购金额不超过4000元需要抽取140人，超过4000元的需要抽取60人，再根据列联表的性质即可完成表格，再根据列联表的数据计算出2K 并与给定的参考表对照得到结论. 【详解】（1）由题可知随机对1000人做问卷调查，消费数据的组距为2000， 可求得频率分布直方图纵轴上每组的数据(频率除以组距)， 即3000.0001510002000=⨯，4000.000210002000=⨯，1800.0000910002000=⨯，600.0000310002000=⨯，则[]0,2000，(]2000,4000，(]4000,6000，(]6000,8000，(]8000,10000， 对应的的数据(频率除以组距)分别是0.00015，0.0002，0.00009，0.00003，0.00003， 从而得出频率分布直方图，由频率分布直方图估计平均值的定义，可得10000.330000.450000.1870000.0690000.0630012009004205403360x =⨯+⨯+⨯+⨯+⨯=++++=（元），故本市居民此期间网络购物的消费平均值为3360元； （2）由数据可知以网购金额不超过4000元的有2007001401000⨯=（人）， 超过4000元的有200300601000⨯=（人），可得列联表.由()()()()220075356525502.3813.8411406010010021n ad bc K a b c d a c b d -⨯⨯-⨯===≈<++++⨯⨯⨯. 故在此期间没有95%的把握认为网购金额与网购人年龄有关. 【点睛】本题第一问考查了平均数的计算、画出频率分布直方图，其中主要是计算出纵坐标的值（频率除以组距）属于常见题型，第二问主要考查完善列联表，2K 的计算，属于中档题目，解题中对计算能力要求较高.22．（1）列联表见解析，有把握；（2）分布列见解析，1.8. 【分析】（1）完成列联表求出2K ，从而有99%的把握认为箱产量与养殖方法有关．（2）推导出X 的可能取值为1，2，3，分别求出相应的概率，由此能求出X 的分布列和数学期望． 【详解】解：（1）依题意，得下表：2200(62603840)9.68 6.63510298100100K ⨯-⨯∴=≈>⨯⨯⨯，即2( 6.635)0.010P K ∴>=所以，有99%的把握认为箱产量与养殖方法有关；（2）按照分层抽样的方法从箱产量少于50kg 和不少于50kg 的网箱中随机抽取5箱,分别为2箱和3箱，从中再抽3箱，则1,2,3X =则2123353(1)10C C P X C ===，1223356(2)10C C P X C ===，0323351(3)10C C P X C ===，X 的分布列为所以，1123 1.8101010EX=⨯+⨯+⨯=【点睛】本题考查独立检验的应用，考查离散型随机变量的分布列、数学期望的求法，考查运算求解能力，属于中档题．23．（1）0.62；（2）列联表见解析，有99%的把握认为支付人数与支付方式有关．【分析】（1）由频率分布直方图可得微信支付人数低于50千人的频率；（2）根据频率分布直方图得出<50千人和≥50千人的人数，得列联表，计算出2K，比较后可得结论．【详解】（1）根据题意，由微信支付人数的频率分布直方图可得：()()0.0120.0140.0240.0340.04050.62P A=++++⨯=（2）根据题意，补全列联表可得：则有()22006266383415.705 6.63510010096104K⋅⨯-⨯=≈>⨯⨯⨯，故有99%的把握认为支付人数与支付方式有关．【点睛】本题考查频率分布直方图，考查列联表，独立性检验，计算出2K即得，本题属于基础题．24．（1）见解析；（2）分布列见解析，期望是10 3.【分析】（1）先根据题中数据完成列联表，再进行计算，判断；（2）根据题意得X服从二项分布，进而求解.【详解】（1）由题意得，。

章末质量评估(三)(时间：100分钟 满分：120分)一、选择题(每小题5分，共50分) 1．下列结论正确的是( )．①函数关系是一种确定性关系； ②相关关系是一种非确定性关系；③回归分析是对具有函数关系的两个变量进行统计分析的一种方法； ④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法． A ．①②④ B ．①②③ C ．②③④D ．①②③④ 解析 回归分析是对具有相关关系的两个变量进行统计分析的一种方法，故③不正确． 答案 A2．两个相关变量满足如下关系( )．A ．y ＝0.56x ＋997.4B ．y ＝0.63x －231.2C ．y ＝50.2x ＋501.4D ．y ＝60.4x ＋400.7解析 利用公式b ＝∑i ＝15x i y i －5x y∑i ＝15x 2i －5x 2≈0.56，a ＝y －b x ≈997.4.∴线性回归方程为y ＝0.56x ＋997.4. 答案 A3．如果有95%的把握说事件A 和B 有关系，那么具体计算出的数据( )．A ．χ2＞3.841 B ．χ2＜3.841 C ．χ2＞6.635D ．χ2＜6.635解析 由独立性判断的方法可知，如果有95%的把握，则χ2＞3.841. 答案 A4．若事件E 与F 相互独立，且P (E )＝P (F )＝14，则P (E ∩F )的值等于( )．A ．0 B.116C.14D.12解析 P (E ∩F )＝P (E )·P (F )＝14×14＝116.答案 B5．分类变量X 和Y 的列联表如下：( )．A ．ad －bc 越小，说明X 与Y 关系越弱B ．ad －bc 越大，说明X 与Y 关系越强C ．(ad －bc )2越大，说明X 与Y 关系越强 D ．(ad －bc )2越接近于0，说明X 与Y 关系越强 解析 因为χ2＝n ad －bc 2a ＋ba ＋cb ＋dc ＋d，当(ad －bc )2越大时，χ2越大，说明X 与Y 关系越强． 答案 C6．一位母亲记录了她儿子3到9岁的身高，建立了她儿子身高与年龄的回归模型y ＝73.93＋7.19x (单位：cm)，她用这个模型预测儿子10岁时的身高，则下面的叙述正确的是( )．A ．她儿子10岁时的身高一定是145.83 cmB ．她儿子10岁时的身高一定是145.83 cm 以上C ．她儿子10岁时的身高在145.83 cm 左右D ．她儿子10岁时的身高一定是145.83 cm 以下 解析 用线性回归方程预测的值不是精确值而是估计值． 答案 C7．考察人的高血压病是否与食盐摄入量有关，对某地区人群进行跟踪调查，得到以下数据：A．99% B．95% C．90% D．无充分依据解析χ2＝－2254×1 379×60×1 573≈80.155，∵80.155＞6.635，∴有99%的把握认为人的高血压病与食盐摄入量有关．答案 A8．下列说法中错误的是( )．A．如果变量x与y之间存在着线性相关关系，则我们根据实验数据得到的点(x i，y i)(i ＝1,2，…，n)将散布在某一条直线的附近B．如果两个变量x与y之间不存在线性关系，那么根据它们的一组数据(x i，y i)(i＝1,2，…，n)不能写出一个线性方程C．设x，y是具有相关关系的两个变量，且x关于y的线性回归方程为y＝bx＋a，b 叫做回归系数D．为使求出的线性回归方程有意义，可用统计假设检验的方法来判断变量y与x之间是否存在线性相关关系解析如果两个变量x、y之间不存在线性关系，仍能套用线性回归系数公式，求得b、a，从而写出一个线性方程，不过此方程不能称为线性回归方程．答案 B9．如图所示，在这5组数据中，去掉哪组数据后，剩下的4组数据的线性相关系数最大( )．A．A(1,3) B．B(2,4)C ．C (4,5)D ．D (3,10)解析 从散点图容易观察，去掉D (3,10)后，其余点大致在一条直线附近． 答案 D10．设两个独立事件A 和B 都不发生的概率为19，A 发生B 不发生的概率与B 发生A 不发生的概率相同，则事件A 发生的概率P (A )是( )．A.29B.118C.13D.23解析 ∵P (A B )＝19，即P (A )·P (B )＝19.P (A B )＝P (B A )，即P (A )·P (B )＝P (B )·P (A )， P (A )(1－P (B ))＝P (B )(1－P (A ))，P (A )＝P (B )．∴P (A )＝P (B )，又P (A )·P (B )＝19，∴P (A )＝13，∴P (A )＝23.答案 D二、填空题(每小题5分，共30分)11．已知一个线性回归方程为y ＝1.5x ＋45，x i ∈{}1，7，5，13，19，则y＝________.解析 因为x ＝15×(1＋7＋5＋13＋19)＝9，且y ＝1.5x ＋45，所以y ＝1.5×9＋45＝58.5. 答案 58.512．若由一个2×2列联表中的数据计算得χ2≈4.013，那么有________的把握认为两个变量间有关系．解析 由χ2≈4.013＞3.841，故有95%的把握认为两个变量间有关系． 答案 95%13．抛掷红、蓝两颗骰子，若已知蓝骰子的点数为3或6时，则两骰子点数之和大于8的概率为________．解析 设蓝骰子的点数为3或6时的事件为A ，两骰子点数之和大于8的事件为B . 则：P (A )＝13，P (A ∩B )＝1036＝518，∴P (B |A )＝P A ∩BP A ＝51813＝56.答案 5614．某大学在研究性别与职称(分正教授、副教授)之间是否有关系，你认为应该收集的数据是________．解析 本题研究的两个变量是性别与职称．因此收集的数据应分别是男、女正、副教授人数．答案 男正教授人数，男副教授人数，女正教授人数，女副教授人数 15．某天上午李明要参加奥运志愿者活动，为了准时起床，他用甲、乙两个闹钟叫醒自己．假设甲闹钟准时响的概率是0.80，乙闹钟准时响的概率是0.90，则两个闹钟至少有一个准时响的概率是________．解析 两个闹钟至少有一个准时响有三种情况：甲准时响而乙没准时响，其概率为0.80×(1－0.90)＝0.08；乙准时响而甲没准时响，其概率是(1－0.80)×0.90＝0.18；甲、乙都准时响，其概率为0.80×0.90＝0.72，故两个闹钟至少有一个准时响的概率为：0.08＋0.18＋0.72＝0.98. 答案 0.9816．某化工厂为预测某产品的回收率y ，需研究它和原料有效成份含量之间的相关关系，现取了8对观察值，计算得：∑i ＝18x i ＝52，∑i ＝18y i ＝228，∑i ＝18x 2i ＝478，∑i ＝18x i y i ＝1 849，则y 与x 的线性回归方程是________． 答案 y ＝11.47＋2.62x 三、解答题(每小题10分，共40分)17．假定某企业的某种产品产量与单位成本数据如下：(1)(2)指出产量每增加1 000件时，单位成本下降多少；(3)假定产量为6 000件时，单位成本是多少？单位成本为70元时，产量应为多少？解 (1)∑i ＝16x i ＝21，∑i ＝16y i ＝426，∑i ＝16x 2i ＝79，∑i ＝16y 2i ＝30 268，∑i ＝16x i y i ＝1 481，x ＝3.5，y ＝71，b ＝∑i ＝16x i y i －6x y∑i ＝16x 2i －6x 2＝1 481－6×3.5×7179－6×3.52＝－105.5＝－1.818， a ＝y －b x ＝71＋1.818×3.5＝77.363，∴回归方程为y ＝77.363－1.818x .r ＝∑i ＝16x i y i －6xy∑i ＝16x 2i －6x2∑i ＝16y 2－6i y 2＝1 481－6×3.5×7179－6×3.5230 268－6×712＝－105.5×22＝－1011＝－0.91.(2)产量每增加1 000件时单位成本下降1.818元． (3)当x ＝6时，y ＝66.455元．18．为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？ (3)根据(2)的结论，能否提出更好的调查方法来估计该地区的老年人中，需要志愿者提供帮助的老年人的比例？说明理由． 附：χ2＝a ＋bc ＋d a ＋cb ＋d解 (1)调查的500位老年人中有70位需要志愿者提供帮助，因此在该地区老年人中，需要帮助的老年人的比例的估计值为70500×100%＝14%.(2)χ2＝－2200×300×70×430≈9.967，因为9.967＞6.635，所以有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关．(3)根据(2)的结论可知，该地区的老年人是否需要志愿者提供帮助与性别有关，并且从样本数据能够看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异，因此在调查时，先确定该地区老年人中男女的比例，再把老年人分成男女两层，并且采用分层抽样方法比简单随机抽样方法更好．19．某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查，统计数据如下表所示：少？抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少？(2)试运用独立性检验的思想方法分析：学生的学习积极性与对待班级工作的态度是否有关系？说明理由．解 (1)随机抽查这个班的一名学生，有50种不同的抽查方法，由于积极参加班级工作的学生有18＋6＝24人，所以有24种不同的抽法，因此由古典概型的计算公式可得抽到积极参加班级工作的学生的概率是P 1＝2450＝1225，又因为不太主动参加班级工作且学习积极性一般的学生有19人，所以抽到不太主动参加班级工作且学习积极性一般的学生的概率是P 2＝1950.(2)由χ2统计量的计算公式得χ2＝－224×26×25×25≈11.538，由于11.538＞6.635，所以我们有99.9%的把握认为“学生的学习积极性与对待班级工作的态度有关系”．20．下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据.(1)(2)请根据上表提供的数据，用最小二乘法求出y 关于x 的线性回归方程y ＝a ＋bx ； (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？ (参考数值：3×2.5＋4×3＋5×4＋6×4.5＝66.5) 解 (1)由题设所给数据，可得散点图如图．(2)由对照数据，计算得∑i ＝14x 2i ＝86，x ＝3＋4＋5＋64＝4.5，y ＝2.5＋3＋4＋4.54＝3.5， 已知∑i ＝14x i y i ＝66.5，所以，由最小二乘法确定的回归方程的系数为b ＝∑i ＝14x i y i －4x·y∑i ＝14x 2i －4x 2＝66.5－4×4.5×3.586－4×4.52＝0.7. a ＝y －b x ＝3.5－0.7×4.5＝0.35.因此，所求的线性回归方程为y ＝0.35＋0.7x .(3)由(2)的回归方程及技改前生产100吨甲产品的生产能耗，能降低的生产能耗为90－(0.35＋0.7×100)＝19.65(吨标准煤)．。

高中数学第三章统计案例单元检测北师大版选修2-3编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第三章统计案例单元检测北师大版选修2-3）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第三章统计案例单元检测北师大版选修2-3的全部内容。

第三章统计案例单元检测(时间：45分钟满分：100分）一、选择题(每小题6分，共48分）1．下列说法正确的是（)．A．任何两个变量都具有相关关系B．球的体积与该球的半径具有相关关系C．农作物产量与施肥量之间是一种确定性关系D．某商品的生产量与该商品的价格是一种非确定性关系2．该商品的销售额与利润之间的线性相关系数是0。

78,这说明二者之间存在着( ）．A．高度相关B．中度相关C．弱度相关D．极弱相关3。

如图所示，有5组数据(x,y)，去掉哪组数据后,剩下的4组数据的线性相关系数最大（）．A．A B．B C．C D．D4．下表是某厂1～4由散点图可知，用水量y y ＝－0。

7x＋a,则a＝( ）．A．5 B．5。

05 C．5。

25 D．65．一位母亲记录了她儿子3到9岁的身高，建立了她儿子身高与年龄的回归模型y＝73。

93＋7。

19x。

她用这个模型预测儿子10岁时的身高，则下面的叙述正确的是（）．A．她儿子10岁时的身高一定是145。

83 cmB．她儿子10岁时的身高在145.83 cm以上C．她儿子10岁时的身高在145。

83 cm左右D．她儿子10岁时的身高在145。

83 cm以下6．在一个2×2列联表中，由数据计算得χ2＝13.097，则其两个变量间有关系的可能性为( )．A．99％B．95％C．90% D．无关系7．下面是调查某地区男女中学生喜欢理科的等高条形图，阴影部分表示喜欢理科的百分比，从下图可以看出（)．A ．性别与喜欢理科无关B ．女生中喜欢理科的比例为80%C ．男生比女生喜欢理科的可能性大些D ．男生不喜欢理科的比例为60%8．某科研机构为了研究中年人秃发与患心脏病是否有关，随机调查了一些中年人的情况,具体数据如表，根据表中数据则可判定秃发与患心脏病有关,那么这种判定出错的可能性为（ ).A ．0.1B ．0。