isTriangle三角形测试用例

黑盒测试三角形简介黑盒测试是一种软件测试方法，通过检查软件的输入和输出，而无需关注内部的实现细节。

本文将介绍如何进行黑盒测试，并以三角形的判定为例进行详细说明。

三角形判定规则在进行三角形测试之前，我们首先需要了解三角形的定义和判定规则。

三角形是由三条边组成的图形，它有以下几个特征： - 三边之和大于第三边 -两边之差小于第三边 - 三边的长度分别为a、b、c，其中a、b、c均大于0根据三角形的三边长度，可以将三角形分为以下几种情况： - 等边三角形：三边长度相等 - 等腰三角形：两边长度相等 - 直角三角形：有一个角为90度 - 钝角三角形：三个角均大于90度 - 锐角三角形：三个角均小于90度黑盒测试方法黑盒测试的目的是检查软件的功能是否按照预期工作，它不关心具体的代码实现，而是从输入和输出的角度出发进行测试。

下面是一些常用的黑盒测试方法：等价类划分等价类划分是一种常用的黑盒测试方法，它将测试用例分为几个等价类，每个等价类代表一个功能的特定条件。

测试用例选择一个等价类进行测试即可，通过这个等价类的测试用例可以代表整个等价类的测试结果。

在三角形判定中，我们可以将输入的三个边长分为以下几个等价类： - 有效等价类：满足三角形判定规则的三个边长组合 - 无效等价类：不满足三角形判定规则的三个边长组合边界值分析边界值分析是一种考虑输入值的边界情况的黑盒测试方法。

通常，边界值是最小输入和最大输入，以及最小输入减去或最大输入加上1的情况。

在三角形判定中，我们可以选择以下边界值进行测试： - 最小输入：三个边均为0 - 边界输入：三个边中有一个边等于1，另外两个边等于最大允许值 - 最大输入：三个边均为最大允许值错误推测法错误推测法是一种根据错误、故障和失败的经验推测可能存在的错误并进行测试的方法。

通过推测错误并进行测试，可以发现软件中可能存在的隐藏错误。

在三角形判定中，我们可以通过错误推测法选择一些可能存在的错误进行测试，例如： - 输入的边长度数据类型错误 - 输入的边长度超出了合理范围 - 输入的边长度顺序错误三角形测试用例根据上述的黑盒测试方法，我们可以选择一些测试用例进行三角形判定的测试。

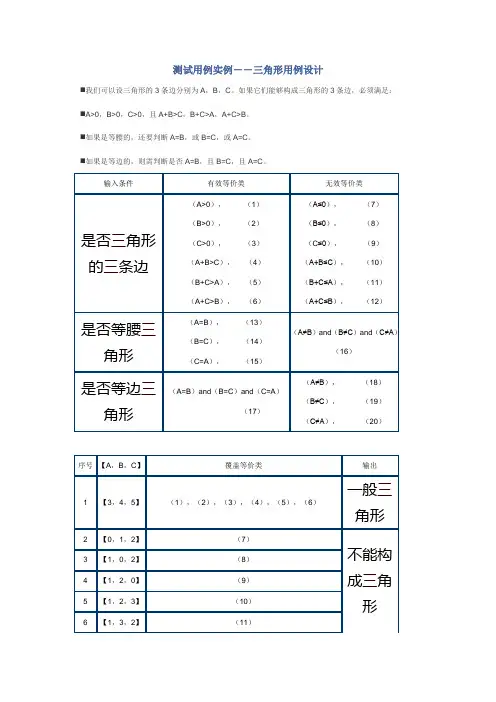
三⾓形的测试⽤例设计在三⾓形计算中，要求三⾓形的三个边长：A B C 。

1、当三边不可能构成三⾓形时提⽰错误，可构成三⾓形时计算三⾓形周长。

2、若是等腰三⾓形打印“等腰三⾓形”，若两个等腰的平⽅和等于第三边平⽅和，则打印“等腰直⾓三⾓形”。

3、若是等边三⾓形，则打印：“等边三⾓形”。

4、画出程序流程图并设计⼀个测试⽤例。

分析⼀下：1、构成三⾓形的条件：任意两边之和⼤于第三边；2、构成等腰三⾓形的条件：任意两边相等；3、构成等腰直⾓三⾓形的条件：任意两边相等，⽽且两条边的平⽅和等于第三边的平⽅和；4、构成等边三⾓形的条件：三条边都相等。

那么⽤什么样的设计⽅法进⾏测试⽤例的设计呢？⼀、等价类划分：三⾓形三条边A、B、C的数据类型不同⼆、边界值分析：由于三⾓形的边长可以是正整数或正⼩数，所以就不对长度进⾏测试，那么边界值分析就不⽤了三、因果图法：三⾓形的三条边数据输⼊组合我们再分析⼀下三⾓形的等价类：有效等价类：输⼊3个正整数或正⼩数：1、两数之和⼤于第三数，如A<B+C；B<C+A；C<A+B2、两数之和不⼤于第三数3、两数相等，如A=B或B=C或C=A4、三数相等，如A=B=C5、三数不相等，如A！=B，B！=C，C！=A⽆效等价类：1、空2、负整数3、⾮数字4、少于三个数三⾓形测试⽤例类别输⼊条件有效等价类⽆效等价类是否是三⾓形(A>0) (1)(B>0) (2)(C>0) (3)(A+B>C) (4)(B+C>A) (5)(C+A>B) (6)(A<=0) (7)(B<=0) (8)(C<=0) (9)(A+B<=C) (10)(B+C<=A) (11)(C+A<=B) (12)是否是等腰三⾓形(A=B) (13)(B=C) (14)(A!=B)and(B!=C)and(C!=A)(16)形(C=A) (15)(16)是否是等腰直⾓三⾓形(A=B)and(A2+B2=C2) (17)(B=C)and(B2+C2=A2) (18)(C=A)and(C2+A2=B2) (19)(A!=B)and(B!=C)and(C!=A) (20)是否是等边三⾓形(A=B)and(B=C)and(C=A) (21)(A!=B) (22)(B!=C) (23)(C!=A) (24)三⾓形测试⽤例：⽤最少的测试⽤例覆盖所有的有效等价类，⽽⽆效等价类每个类型都要覆盖到序号输⼊[A,B,C]覆盖等价类输出1[3,4,5](1)(2)(3)(4)(5)(6)是三⾓形2[0,1,2](7)⾮三⾓形3[1,0,2](8)⾮三⾓形4[1,2,0](9)⾮三⾓形5[1,2,3](10)⾮三⾓形6[1,3,2](11)⾮三⾓形7[3,1,2](12)⾮三⾓形8[3,3,4](1)(2)(3)(4)(5)(6)(13)等腰三⾓形9[3,4,4](1)(2)(3)(4)(5)(6)(14)等腰三⾓形10[3,4,3](1)(2)(3)(4)(5)(6)(15)等腰三⾓形11[2√2,2√2,4](1)(2)(3)(4)(5)(6)(17)等腰直⾓三⾓形12[4,2√2,2√2](1)(2)(3)(4)(5)(6)(18)等腰直⾓三⾓形13[2√2,4,2√2](1)(2)(3)(4)(5)(6)(19)等腰直⾓三⾓形14[3,4,5](1)(2)(3)(4)(5)(6)(16)(20)(22)(23)(24)是三⾓形15[3,3,3](1)(2)(3)(4)(5)(6)(16)(21)等边三⾓形16[,,,]⽆效等价类错误提⽰17[-3,4,5]⽆效等价类错误提⽰18[a,3,@]⽆效等价类错误提⽰19[3,4]⽆效等价类错误提⽰。

黑龙江大学实验报告黑龙江大学教务处测试计划（GB8567——88）1引言1.1编写目的1.掌握软件测试技术中白盒测试方法；2.掌握如何进行单元测试。

1.2背景测试程序名称：triangle（三角形形状测试）任务提出者：金虎老师开发者：用户：测试环境：WINDOWS XP ; VC++6.0说明：由于程序较小，并且只是作为了解白盒测试的小程序，因此不涉及较高的实验环境，并且测试环境和运行环境在理论上是一样的，因此不存在较大的测试差异。

1.3定义a:三角型的第一条边b:三角型的第二条边c:三角型的第三条边一般三角形：三边都不相等的三角形等腰三角形：有任意两边相等的三角形等边三角形：三边都相等的三角形不能构成三角形：因不满足需求条件而不能构成三角形1.4参考资料1．《软件测试教程》．宫云战．机械工业出版社2008年9月2．《软件测试技术》．曲朝阳．中国水利水电出版社2006年8月3．《软件测试教程》．贺平．电子工业出版社2005年6月2计划2.1软件说明2.2测试内容单元测试。

某程序规定：输入三个整数作为三边的边长构成三角形。

当此三角形为一般三角形、等腰三角形及等边三角形时，分别说明。

2.3测试（标识符）2.3.1进度安排2.3.2条件所需测试机器：机房机器，品牌为联想，基本配置为奔腾4处理器，256M内存，80M硬盘系统环境：WINDOWS XP工具环境：VC++6.0中文版参与人员2.3.3测试资料1．《软件测试教程》．宫云战．机械工业出版社2008年9月2．《软件测试技术》．曲朝阳．中国水利水电出版社2006年8月3．《软件测试教程》．贺平．电子工业出版社2005年6月2.3.4测试培训1．《软件测试教程》宫云战机械工业出版社2008年9月第三章白盒测试2．金虎老师第三张白盒测试PPT课件3测试设计说明3.1测试此项测试采用白盒测试方法来测试该功能。

3.1.1控制环形复杂度为：6基本路径集如下：路径一：1-2-9-8路径二：1-2-3-10-8路径三：1-2-3-4-11-8路径四：1-2-3-4-5-12-8 路径五：1-2-3-4-5-6-13-8 路径六：1-2-3-4-5-6-7-83.1.2输入测试用例如下：3.1.3输出3.1.4过程由于这个程序比较简单，因此没有比较繁琐的步骤以及控制命令。

软件测试与质量保证作业一、测试问题描述输入三个整数a、b、c，分别作为三角形的三条边，通过程序判断这三条边是否能构成三角形？如果能构成三角形，则判断三角形的类型（等边三角形、等腰三角形、一般三角形）。

要求输入三个整数a、b、c，必须满足以下条件：1≤a≤200；1≤b≤200；1≤c≤200。

用边界值分析法设计测试用例。

用黑盒测试方法设计测试用例。

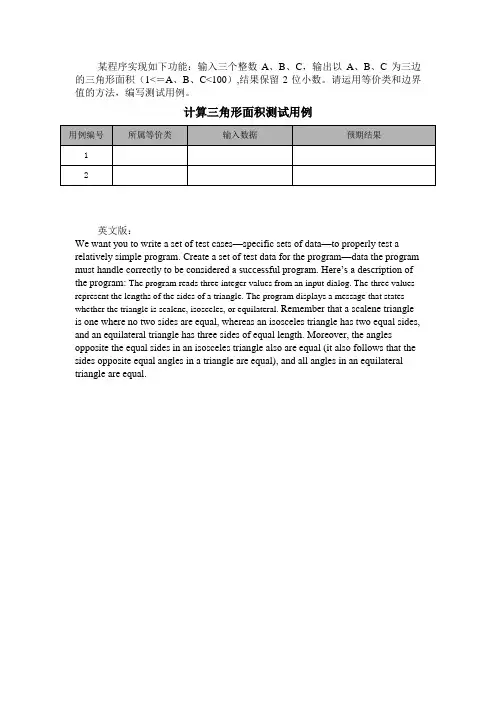
二、设计测试用例1. 用边界值测试方法设计测试用例用边界值分析法设计测试用例，按照下列步骤进行：（1）分析各变量取值边界值分析的基本思想是使用输入变量的最小值、略高于最小值、正常值、略低于最大值和最大值设计测试用例。

因此a，b，c的边界取值是：1，2，100，199，200。

（2）测试用例数有n个变量的程序，其边界值分析会产生4n+1个测试用例。

这里有3个变量，因此会产生13个测试用例。

（3）设计测试用例用边界值分析法设计测试用例就是使一个变量取边界值（分别取最小值、略高于最小值、正常值、略低于最大值和最大值），其余变量取正常值，然后对每个变量重复进行。

本例用边界值分析法设计的测试用例见表1-1。

表1-1 三角形问题的测试用例测试用例输入数据预期输出a b c1 100 100 1 等腰三角形2 100 100 2 等腰三角形3 100 100 100 等边三角形4 100 100 199 等腰三角形5 100 100 200 非三角形6 100 1 100 等腰三角形7 100 2 100等腰三角形8100 199 100 等腰三角形9 100200 100非三角形10 1100 100 等腰三角形11 2 100 100 等腰三角形12 199 100 100 等腰三角形13 200 100 100 非三角形2. 用等价类测试方法设计测试用例（1）首先分析题目中给出的条件和隐含的输入要求，输入条件如下：a)正整数；b)三个数；c)构成一般三角形；d)构成等腰三角形；e)构成等边三角形；f)不能构成三角形（2）根据输入条件的要求划分等价类，列出等价类表并编号，如表1-2所示。

三角形问题的等价类测试用例(总1页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--三角形问题的等价类测试用例四种可能出现的输出：非三角形、不等边三角形、等腰三角形和等边三角形可以使用这些输出标识如下所示的输出（值域）等价类：R1={〈a，b，c〉：有三条边a、b和c的等边三角形}R2={〈a，b，c〉：有三条边a、b和c的等腰三角形}R3={〈a，b，c〉：有三条边a、b和c的不等边三角形}R4={〈a，b，c〉：三条边a、b和c不构成三角形}四个弱一般等价类测试用例是：测试用例 a b c 预期输出WN1 5 5 5 等边三角形WN2 2 2 3 等腰三角形WN3 3 4 5 不等边三角形WN4 4 1 2 非三角形由于变量a、b和c没有有效区间，则强一般等价类测试用例与弱一般等价类测试用例相同。

考虑a、b和c的无效值产生的以下额外弱健壮等价类测试用例：测试用例 a b c 预期输出WR1 -1 5 5 a取值不在所允许的取值值域内WR2 5 -1 5 b取值不在所允许的取值值域内WR3 5 5 -1 c取值不在所允许的取值值域内WR4 201 5 5 a取值不在所允许的取值值域内WR5 5 201 5 b取值不在所允许的取值值域内WR6 5 5 201 c取值不在所允许的取值值域内以下是额外强健壮性等价类测试用例三维立方的一个“角”：测试用例 a b c 预期输出SR1 -1 5 5 a 取值不在所允许的取值值域内SR2 5 -1 5 b 取值不在所允许的取值值域内SR3 5 5 -1 c 取值不在所允许的取值值域内SR4 -1 -1 5 a、b取值不在所允许的取值值域内SR5 5 -1 -1 b、c取值不在所允许的取值值域内SR6 -1 5 -1 a、c取值不在所允许的取值值域内SR7 -1 -1 -1 a、b、c取值不在所允许的取值值域内。

三角形测试用例设计作者：ღ王正也ღ某程序规定："输入三个整数a、b、c分别作为三边的边长构成三角形。

通过程序判定所构成的三角形的类型，当此三角形为一般三角形、等腰三角形及等边三角形时，分别作计算… "。

用等价类划分方法为该程序进行测试用例设计。

之前面试了几个地方都问了这个题，网上找了下答案。

不懂测试理论，也不知道啥叫等级类，也不知道哪个答案更准确。

不知道为什么所有答案给出的用例里没有测试边界值，极大的值，负数，小数等等答案1：/godmap/blog/item/12ed690f14cc9c2b6059f3bc. html三角形等价类列表判定类型有效等价类无效等价类一般三角形((a>0) Λ(b>0) Λ(c>0)) Λ (a<=0 V b<=0 V c<=0) Λ(((a+b)>c) V ((a+c)>b) V ((b+c)>a)) (1) (((a+b)<=c) V ((a+c)<=b) V ((b+c)<=a)) (2)等腰三角形(1) Λ (a=b V a=c V b=c) (3) (2) V (a!=b V b!=c V a!=c) (4)等边三角形(1) Λ (a=b=c ) (5) (2) V (a!=b!=c) (6)根据上表组成的测试用例：三角形等价类测试用例ID 输入数据覆盖测试用例输出结果a b c1 3 4 5 (1) 一般三角形2 0 4 5 (2) 非(一般)三角形3 3 0 5 (2)4 3 4 0 (2)5 1 4 5 (2)6 3 8 5 (2)7 3 2 1 (2)8 3 3 5 (3) 等腰三角形9 3 4 310 3 4 411 3 4 9 (4) 非等腰三角形12 3 3 3 (5) 等边三角形13 -1 0 1 (6) 非等边三角形答案2： /?uid-275201-action-viewspace-ite mid-218955分析题目中给出和隐含的对输入条件的要求：（1）整数（2）三个数（3）非零数（4）正数（5）两边之和大于第三边（6）等腰（7）等边如果a、b 、c满足条件（ 1 ）~ （ 4 ），则输出下列四种情况之一：1)如果不满足条件（5），则程序输出为" 非三角形" 。

某程序实现如下功能：输入三个整数A、B、C，输出以A、B、C为三边的三角形面积（1<＝A、B、C<100）,结果保留2位小数。

请运用等价类和边界值的方法，编写测试用例。

计算三角形面积测试用例英文版：We want you to write a set of test cases—specific sets of data—to properly test a relatively simple program. Create a set of test data for the program—data the program must handle correctly to be considered a successful program. Here’s a description of the program: The program reads three integer values from an input dialog. The three values represent the lengths of the sides of a triangle. The program displays a message that states whether the triangle is scalene, isosceles, or equilateral. Remember that a scalene triangle is one where no two sides are equal, whereas an isosceles triangle has two equal sides, and an equilateral triangle has three sides of equal length. Moreover, the angles opposite the equal sides in an isosceles triangle also are equal (it also follows that the sides opposite equal angles in a triangle are equal), and all angles in an equilateral triangle are equal.。

三角形测试用例题目：输入三个数a、b、c分别作为三边的边长构成三角形。

通过程序判定所构成的三角形是一般三角形、等腰三角形还是等边三角形时。

用等价类划分方法为该程序设计测试用例。

三角形等价类列表判定类型有效等价类无效等价类一般三角形((a>0) Λ(b>0) Λ(c>0))Λ (a<=0 V b<=0 V c<=0) Λ(((a+b)>c) V ((a+c)>b) V ((b+c)>a)) (1) (((a+b)<=c) V ((a+c)<=b) V ((b+c)<=a)) (2)等腰三角形(1) Λ (a=b V a=c V b=c)(3)(2) V (a!=b Λ b!=c Λ a!=c) (4) 等边三角形(1) Λ (a=b=c ) (5) (2) V (a!=b!=c)(6)根据上表组成的测试用例：三角形等价类测试用例ID 输入数据覆盖测试用例输出结果a b c1 3 4 5 (1) 一般三角形2 0 4 5 (2) 非(一般)三角形3 3 0 5 (2)4 3 4 0 (2)5 1 4 5 (2)6 3 8 5 (2)7 3 2 1 (2)8 3 3 5 (3) 等腰三角形9 3 4 310 3 4 411 3 4 9 (4) 非等腰三角形12 3 3 3 (5) 等边三角形13 -1 0 1 (6) 非等边三角形三角形程序的测试用例：序号测试内容测试数据预期结果1 等边 5,5,5 4,5,5 等边2 等腰 4,4,5 5,4,4 等腰3 任意 3,4,5 任意4 非三角形 9,4,4 4,9,4 4,4,9 No5 退化三角形 8,4,4 4,8,4 4,4,8 No6 零数据 0,4,5 4,0,5 4,5,0 No7 零数据 0,0,0 No8 负数据-3,4,5 3,-4,5 3,4-5 运行出错9 负数据 -3,-4,-5 运行出错10 遗漏数据3,4 运行出错11 非整数 3.3,4,5 运行出错12 非数字符A,4,5 （类型不符）。

一．题目要求：使用c#语言编写程序，实现下面功能：输入三个数，判断能否构成三角形，如果能构成三角形，判断其为等边三角形、等腰三角形或不等边三角形。

三角形的判定方法有返回值，并对该方法进行测试。

二．源代码程序：using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace TriangleTest{class Triangle{int a,b,c;public Triangle(int a0,int b0,int c0){this.a = a0;this.b = b0;this.c = c0;}public bool IsTriangle(){if ((a + b) > c && (a + c) > b && (b + c) > a)return true;elsereturn false;}public bool IsTwoEqualTriangle(){if (IsTriangle()){if (a == b || a == c || b == c)return true;elsereturn false;}else{Console.WriteLine("It is not a triangle!");return false;}}public bool IsThreeEqualTriangle(){if (IsTriangle()){if (a == b && a == c)return true;elsereturn false;}else{Console.WriteLine("It is not a triangle!");return false;}}static void Main(string[] args){int a=0, b=0, c=0;Console.WriteLine("Please input three edges:\n");a =Convert.ToInt32(Console.ReadLine());b = Convert.ToInt32(Console.ReadLine());c = Convert.ToInt32(Console.ReadLine());Triangle tri = new Triangle(a,b,c);if (tri.IsThreeEqualTriangle())Console.WriteLine("It is a threeequal triangle!");else{if (tri.IsTwoEqualTriangle())Console.WriteLine("It is a twoequal triangle!");elseif(tri.IsTriangle())Console.WriteLine("It is a triangle!");elseConsole.WriteLine("It is not a triangle!");}Console.ReadLine();}}}三．程序运行结果：1.判断是否为三角形：2.判断是否为等腰三角形：3.判断是否为等边三角形：四．测试脚本：进行三角形单元测试时，可选择总体测试，也可以一个一个测试。

输入三角形边长判断能否组成三角形的测试用例输入三角形边长判断能否组成三角形的测试用例是一种常见的测试方法，用于测试三角形的合法性。

在这种测试中，我们需要输入三个数字作为三角形的三条边长，然后判断这三条边长是否能够组成一个合法的三角形。

在进行这种测试时，我们需要注意以下几点：1. 三角形的边长必须大于0。

如果输入的任意一条边长小于等于0，则无法组成三角形。

2. 任意两条边长之和必须大于第三条边长。

如果输入的三条边长无法满足这个条件，则无法组成三角形。

3. 如果输入的三条边长能够组成一个三角形，则需要判断这个三角形的类型。

根据三角形的三条边长的关系，三角形可以分为等边三角形、等腰三角形和普通三角形。

下面是一些常见的测试用例：1. 输入三个正整数，且这三个数能够组成一个合法的三角形。

这个测试用例可以用来测试程序在正常情况下的运行情况。

2. 输入三个正整数，其中有一个数小于等于0。

这个测试用例可以用来测试程序在输入不合法数据时的处理情况。

3. 输入三个正整数，其中任意两个数之和小于等于第三个数。

这个测试用例可以用来测试程序在输入不合法数据时的处理情况。

4. 输入三个正整数，其中两个数相等。

这个测试用例可以用来测试程序在判断等腰三角形时的准确性。

5. 输入三个正整数，其中三个数都相等。

这个测试用例可以用来测试程序在判断等边三角形时的准确性。

6. 输入三个正整数，其中两个数之和等于第三个数。

这个测试用例可以用来测试程序在输入边长相等的三角形时的准确性。

在进行这些测试时，我们需要注意输入数据的范围和类型，以及程序的输出结果是否符合预期。

如果程序能够正确地处理这些测试用例，那么就可以认为程序的功能是正确的。

总之，输入三角形边长判断能否组成三角形的测试用例是一种非常重要的测试方法，可以帮助我们测试程序的正确性和稳定性。

在进行这种测试时，我们需要注意输入数据的合法性和程序的输出结果是否符合预期，以确保程序的质量和可靠性。

三角形等价类划分法测试用例在我们的生活中，三角形可真是个有趣的小家伙。

它那三条边、一堆角，真是让人忍不住想去研究一下。

咱们今天就聊聊三角形等价类划分法。

别看这名字听起来有点复杂，其实它就像是把三角形按形状和大小分门别类。

就像你去商店挑衣服，大小合适的、颜色漂亮的，都是你的心头好。

三角形也一样，按照边的长度和角的大小，分成不同的“家族”。

我们得知道三角形有哪几种。

你可能说，三角形不就三种嘛：等边、等腰和不等边。

对！等边三角形，嘿，那三条边可真是兄弟情深，长度完全一样。

再来就是等腰，至少有两条边是“情投意合”的。

而不等边，就像那种感情复杂的关系，三条边各有各的特点，谁也不想妥协。

把这些小家伙们分类，就好比在宴会上安排座位，谁跟谁坐一块，得讲究。

我们就可以“深入探讨”这些三角形的特点了。

等边三角形就像是那种完美的生活，不管从哪个角度看，都是一模一样的，给人一种和谐的感觉。

等腰三角形有点像情侣，两边长得差不多，中间的角则代表着它们的亲密。

而不等边三角形就显得有些张扬，每一边都有自己的主张，谁也不愿意妥协。

想象一下，如果让这三种三角形来参加一场比赛，等边三角形肯定是“稳如老狗”，因为它无论怎么转，都不会变。

等腰三角形在比赛中会努力展现自己的魅力，试图吸引更多目光。

而不等边三角形呢，嘿，绝对是个搞笑角色，可能会因为奇怪的形状而吸引所有人的注意力。

这些个性让三角形的世界充满了乐趣。

怎么用这个三角形等价类划分法来测试呢？你可以想象一下，给每一种三角形设定一些规则。

比如说，等边三角形能否通过一些公式来计算面积，看看它是否符合预期。

如果算出来的面积和实际测量的完全一样，那就说明它是个“乖孩子”，完全符合要求。

等腰三角形呢，可以测试它的对称性，看看左右两边是否真的如你所愿。

而不等边三角形则更考验你，因为它的变化多端，想要确保每个角度和边都符合要求，那可得细心一些。

这个方法的好处在于，它让我们能轻松识别出三角形的特点，简直是“一目了然”。

三角形边界值测试用例哎，今天咱们聊聊三角形的边界值测试用例。

说实话，这个话题一听就让人感觉很学术，但其实可以很有趣。

想象一下，三角形就像咱们生活中的小朋友，有大小、形状各种各样。

每个小朋友都得有朋友对吧？那边界值测试就好比是我们在选朋友时要考虑的因素。

三角形有三条边，想想看，这三条边就像三位兄弟，各有各的性格。

如果一条边太短，另一条边再长一点，嘿嘿，这可就有问题了。

你总不能让小弟总是跟大哥比肩吧！这时候，咱们就得看看这三条边之间的关系，看看是不是符合三角形的标准。

记得有句话说，三角形的任意两边之和大于第三边，这就像咱们平常的朋友关系，得互相支持才行。

否则，怎么能成三角形呢？再说了，测试用例就像是玩游戏之前的准备，不能随随便便上场。

得先试试自己的角色，看看他们配不配。

比如说，给你一组边长：3、4、5。

这三条边搭在一起，嘿，居然能形成一个三角形！就像三位好朋友聚在一起，气氛特别好。

再给你一组边长：1、2、3，这组合一出来，大家就得说，“不行，这玩意儿根本没法成形！”真是让人哭笑不得。

测试用例还得覆盖各种情况。

比如边长相等的情况，嘿，这时候就像是双胞胎，根本没法分辨谁是谁。

想象一下，三个边都一样长，那这就是个等边三角形，真是太和谐了！不过，咱们也得考虑那些不太和谐的组合。

比如一边特别长，另一边特别短，这可就成了扭曲的形状，让人看着都想摇头。

在测试的过程中，我们还得记得边界值。

想想那边界值就像是我们生活中的底线。

举个例子，边长恰好是0，这就像是我们说“没朋友”一样，根本不可能有三角形。

再比如，边长正好是负数，那就更是让人无语，完全没戏。

生活中也一样，有时候界限划得太模糊，朋友之间就容易出问题。

而说到具体的边界值，比如说2、2、4，大家就得瞪大眼睛，认真考虑一下。

这组数字可不是什么普通的组合，完全不符合三角形的标准。

就像咱们交朋友得挑对的人，不然可就容易遭遇“乌龙”。

所以呀，这些测试用例真的很重要，帮助我们避免很多不必要的麻烦。

三角形问题的边界值测试用例
在使用等价类划分法对三角形问题进行测试时，边界值分析是非常重要的一步。

边界值是指数据集中最小值和最大值以及这些值的邻近值。

对于三角形问题，我们需要考虑三条边的长度，因此需要进行以下的边界值分析：等价类划分法：三角形问题边界值分析
1.三角形边界值：
三角形的边界值由其三边的长度决定。

由于三角形的性质，任意两边之和必须大于第三边，因此需要考虑以下三种情况：
最小值：三边长度都取最小值，形成无法构成三角形的情况。

最大值：三边长度都取最大值，形成等边三角形。

最小值与最大值的邻近值：三边长度分别为最小值、最大值和最小值与最大值的邻近值，这样可以覆盖所有可能的情况，包括等腰三角形、一般三角形和等边三角形。

2.非三角形边界值：
除了考虑能够构成三角形的情况，还需要考虑无法构成三角形的情况，即任意两边之和小于等于第三边的情况。

此时，需要考虑以下两种情况：两条边之和等于第三边：这种情况下，两条边可以构成一条直线，也就是退化的三角形。

两条边之和小于第三边：这种情况下，三条边无法构成三角形。

通过以上的边界值分析，我们可以设计出各种测试用例来覆盖三角形问题的各种情况，包括等腰三角形、一般三角形、等边三角形、退化的三角形以及无法构成三角形的情况。

这样可以有效地提高测试用例的覆盖率，
— 1 —
从而提高软件的质量。

— 2 —。

三角形问题测试报告————————————————————————————————作者：————————————————————————————————日期：三角形问题测试报告1、简介1.1编写目的本测试报告为三角形问题的测试报告，目的在于总结测试阶段的测试以及分析测试结果，通过测试来检测每个功能是否都能正常使用。

预期参考人员包括测试人员、开发人员和需要阅读本报告的老师。

1.2项目背景本项目为软件测试专周任务。

1.3术语边界值分析法：就是对输入或输出的边界值进行测试的一种黑盒测试方法。

通常边界值分析法是作为对等价类划分法的补充，这种情况下，其测试用例来自等价类的边界。

等价类划分：把程序的输入域划分成若干部分（子集），然后从每个部分中选取少数代表性数据作为测试用例。

每一类的代表性数据在测试中的作用等价于这一类中的其他值。

白盒测试：又称结构测试、透明盒测试、逻辑驱动测试或基于代码的测试。

白盒测试是一种测试用例设计方法，盒子指的是被测试的软件，白盒指的是盒子是可视的，你清楚盒子内部的东西以及里面是如何运作的。

"白盒"法全面了解程序内部逻辑结构、对所有逻辑路径进行测试。

"白盒"法是穷举路径测试。

在使用这一方案时，测试者必须检查程序的内部结构，从检查程序的逻辑着手，得出测试数据。

贯穿程序的独立路径数是天文数字。

黑盒测试：也称功能测试，它是通过测试来检测每个功能是否都能正常使用。

在测试中，把程序看作一个不能打开的黑盒子，在完全不考虑程序内部结构和内部特性的情况下，在程序接口进行测试，它只检查程序功能是否按照需求规格说明书的规定正常使用，程序是否能适当地接收输入数据而产生正确的输出信息。

黑盒测试着眼于程序外部结构，不考虑内部逻辑结构，主要针对软件界面和软件功能进行测试。

1.4参考资料《软件测试教程第2版》 《软件测试入门与提高》 《软件测试实例分析》2、 测试概要2.1程序流程图输入三条边a,b,c输出结果一般三角形等腰三角形(a+b>c)&&(a+c>b)&&(b+c>a)不能构成三角形(a==b&&b!=c)||(a==c&&c!=b)||(b==c&&a!=b)a==b&&a==c等边三角形(a*a+b*b==c*c)||(a*a+c*c ==b*b)||(c*c+b*b==a*a)直角三角形YNYYYNNN①⑨③②④⑥⑤⑦⑧2.2测试程序源代码using System;using System.Collections.Generic;using ponentModel;using System.Data;using System.Drawing;using System.Linq;using System.Text;using System.Windows.Forms;namespace triangle{public partial class Form1 : Form{public Form1(){InitializeComponent();}private void Form1_Load(object sender, EventArgs e){lb_result.Text = "";tb_sideA.Focus();}private void bt_test_Click(object sender, EventArgs e){try{int x = int.Parse(tb_sideA.Text);int y = int.Parse(tb_sideB.Text);int z = int.Parse(tb_sideC.Text);utils u = new utils();if (u.checkNotZero(x, y, z)){if (u.checkTriangle(x, y, z)){if (x == y && x == z && z == y){lb_result.Text = "(*^__^*) 嘻嘻这是一个等边三角形";}else if (x * x + y * y == z * z || x * x + z * z == y * y || z * z + y * y == x * x){lb_result.Text = "(*^__^*) 嘻嘻这是一个直角三角形";}else if (x == y || x == z || z == y){lb_result.Text = "(*^__^*) 嘻嘻这是一个等腰三角形";}else{lb_result.Text = "⊙﹏⊙b汗这是一个一般三角形";}}else{lb_result.Text = " ╮(╯_╰)╭这不是一个三角形";}}else{lb_result.Text = " +_+ 输入有误，请重来";}}catch { }}private void bt_clear_Click(object sender, EventArgs e){tb_sideA.Text = "";tb_sideB.Text = "";tb_sideC.Text = "";tb_sideA.Focus();}private void bt_exit_Click(object sender, EventArgs e){this.Close();this.Dispose();}}class utils{public Boolean checkTriangle(int x, int y, int z){if (x + y > z && x + z > y && z + y > x){return true;}return false;}public Boolean checkNotZero(int x, int y, int z){if (x >= 0 && x <= 100 && y >= 0 && y <= 100 && z >= 0 && z <= 100){return true;}return false;}}}2.3白盒测试语句覆盖：编号 a b c 覆盖对象期望输出实际结果1 4 4 5 ①②③等腰三角形等腰三角形2 4 4 4 ①②④⑤等边三角形等边三角形3 345 ①②④⑥⑦直角三角形直角三角形4 456 ①②④⑥⑧一般三角形直角三角形5 4 5 9 ①⑨不能构成三角形不能构成三角形判定覆盖：编号 a b c 覆盖对象期望输出实际结果1 4 4 5 ①②③等腰三角形等腰三角形2 4 4 4 ①②④⑤等边三角形等边三角形3 345 ①②④⑥⑦直角三角形直角三角形4 456 ①②④⑥⑧一般三角形一般三角形5 4 5 9 ①⑨不能构成三角形不能构成三角形条件覆盖：判定1T1_1 (a + b > c) T1_2(a + c > b) T1_3 (b + c > a)判定2T2_1 (a == b && b != c)T2_2 (a == c && c != b)T2_3 (b == c && a != b)判定3T3_1 (a == b) T3_2 (b == c)判定4T4_1 (a*a+b*b==c*c)T4_2 (a*a+c*c==b*b)T4_3 (c*c+b*b==a*a)编号 a b c 覆盖对象期望输出实际结果6 4 4 5 T1_1,T1_2, T1_3,T2_1, F2_2, F2_3等腰三角形等腰三角形7 4 5 4 T1_1,T1_2, T1_3,F2_1, T2_2, F2_3等腰三角形等腰三角形8 4 5 5 T1_1,T1_2, T1_3,F2_1, F2_2, T2_3等腰三角形等腰三角形9 4 4 4 T1_1,T1_2, T1_3,F2_1,F2_2,F2_3,T3_1,T3_2等边三角形等边三角形10 3 4 5 T1_1,T1_2, T1_3,F2_1,F2_2,F2_3,F3_1,F3_2,T4_1, F4_1, F4_1直角三角形直角三角形11 3 5 4 T1_1,T1_2, T1_3,F2_1,F2_2,F2_3,F3_1,F3_2,T4_1, F4_2, F4_3直角三角形直角三角形12 5 3 4 T1_1,T1_2, T1_3,F2_1,F2_2,F2_3,F3_1,F3_2,F4_1, T4_2, F4_3直角三角形直角三角形13 4 5 6 T1_1,T1_2, T1_3,F2_1,F2_2,F2_3 ,F3_1,F3_2,F4_1, F4_2,F4_3一般三角形一般三角形14 3 4 7 F1_1,T1_2, T1_3 不能构成三角形不能构成三角形15 3 7 4 T1_1,F1_2, T1_3 不能构成三角形不能构成三角形16 7 3 4 T1_1,T1_2, F1_3 不能构成三角形不能构成三角形2.4黑盒测试边界值分析：每条边的取值范围[0,100]编号 a b c 期望输出实际结果1 0 50 50 无效输入无效输入2 1 50 50 等腰三角形等腰三角形3 100 50 50 等腰三角形等腰三角形4 101 50 50 无效输入无效输入5 50 0 50 无效输入无效输入6 50 1 50 等腰三角形等腰三角形7 50 100 50 等腰三角形等腰三角形8 50 101 50 无效输入无效输入9 50 50 0 无效输入无效输入10 50 50 1 等腰三角形等腰三角形11 50 50 100 等腰三角形等腰三角形12 -1 50 101 无效输入无效输入13 50 50 50 等边三角形等边三角形等价类划分：输入条件有效等价类编号无效等价类编号是否构成三角形a>=1&&a<=100 1a<1 7b<1 8 b>=1&&b<=100 2c<1 9a>100 10 c>=1&&c<=100 3c>100 11c>100 12a+b>c 4 a+b<=c 13 a+c>b 5 a+c<=b 14 b+c>a 6 b+c<=a 15是否等腰三角形a==b && b!=c 16a!=b&&b!=c 19 a==c && c!=b 17b==c && a!=b 18是否等边三角形a==b && a==c 20a!=b 21b!=c 22a!=c 23是否直角三角形a*a+b*b==c*c 24 a*a+b*b!=c*c &&a*a+c*c!=b*b &&c*c+b*b!=a*a27 a*a+c*c==b*b 25c*c+b*b==a*a 26编号 a b c 覆盖等价类预期输出1 4 5 6 1,2,3,4,5,6 一般三角形2 -4 5 6 7 无效输入3 4 -5 6 8 无效输入4 45 -6 9 无效输入5 101 56 10 无效输入6 4 101 6 11 无效输入7 4 5 101 12 无效输入8 4 5 9 13 不能构成三角形9 4 13 9 14 不能构成三角形10 14 5 9 15 不能构成三角形11 4 4 6 1,2,3,4,5,6,16 等腰三角形12 4 6 4 1,2,3,4,5,6,17 等腰三角形13 4 6 6 1,2,3,4,5,6,18 等腰三角形14 4 5 6 1,2,3,4,5,6,19 一般三角形15 4 4 4 1,2,3,4,5,6,20 等边三角形16 4 5 6 1,2,3,4,5,6,21 一般三角形17 4 5 6 1,2,3,4,5,6,22 一般三角形18 4 5 6 1,2,3,4,5,6,23 一般三角形19 3 4 5 1,2,3,4,5,6,24 直角三角形20 3 5 4 1,2,3,4,5,6,25 直角三角形21 5 3 4 1,2,3,4,5,6,26 直角三角形22 4 5 6 1,2,3,4,5,6,27 一般三角形2.5测试环境与配置操作系统：windows 8.1Cpu：Intel(R) Core(TM)i7_4700HQ内存：8G3、测试结论与总结测试执行只是针对部分用户进行测试，尚有未考虑充分之处。

4.8三⾓形测试⽤例4.8 三⾓形测试⽤例基本问题：输⼊三⾓形的三条边长，判断是否能够构成⼀个三⾓形，以及是什么样⼦的三⾓形（直⾓，锐⾓，钝⾓，等边，等腰）1 如何⽤⼀个byte来表⽰各种输出情况？76543210三⾓形标记位直⾓锐⾓钝⾓等边等腰2 如果你是⼀名测试⼯程师，应该如何写测试⽤例呢？问题2的解法其中1-6是程序在正常输⼊下的功能测试7-9是测试程序在⾮法输⼊时的表现10-18是测试程序对边界附近输⼊的处理(假设1<=a,b,c<=100)⽤例id输⼊预期输出描述1(4,1,2)00000000⾮三⾓形2(5,5,5)10001011等边三⾓形3(2,2,3)10000001等腰三⾓形4(3,4,5)10010000直⾓三⾓形5(2,3,4)10000100钝⾓三⾓形6(100,99,2)10001000钝⾓三⾓形7(0,1,2)000000000值8(-1,1,2)00000000负值9(a,1,2)00000000类型错误10(50,50,1)10000001等腰三⾓形11(50,50,2)10000001等腰三⾓形12(100,100,99)10000001等腰三⾓形13(100,100,100)10001011等边三⾓形14(50,50,100)00000000⾮三⾓形15(1,1,1)10001011等边三⾓形16(1,1,2)00000000⾮三⾓形17(1,1,99)00000000⾮三⾓形18(1,1,100)00000000⾮三⾓形拓展问题：1 如果三⾓形的各个边长是浮点数，测试⽤例会有什么变化呢？边界会很复杂吧2 如果你负责测试⽂本编辑软件word的另存为Save as的功能，你能写出来多少条有条理，有组织的测试⽤例？看常⽤的⽂件类型了。