长方体和正方体棱长总和练习题教学文案

上课内容：长方体和正方体的棱长总和上课班级：五（1）班上课时间：2015年3月17日上午第一节上课教师：教学目标：1、进一步掌握长方体和正方体的特征。

2、通过学习活动，让学生掌握长方体和正方体的棱长总和的计算方法，能够正确的计算棱长总和。

3、发展学生的空间观念和知识的迁移思想。

教学重点：理解长方体和正方体棱长总和的含义。

教学难点：能正确计算长方体和正方体的棱长总和。

教学过程与方法：一、导入揭题1、复习（利用手中的长方体和正方体，说说它们各自的特征）2、质疑：用铁丝焊成一个长20厘米，宽15厘米，高10厘米的长方体框架，至少需要铁丝多少厘米？3、揭题（板书长方体的棱长总和）二、明确学习目标1.理解长方体和正方体棱长总和的含义。

2.能正确计算长方体和正方体的棱长总和。

三、引导学生学习标杆题，展示、反思、训练、点拨（标杆题）用铁丝焊成一个长20厘米，宽15厘米，高10厘米的长方体框架，至少需要铁丝多少厘米？学习活动（一）：1、观察手中的长方体，说说你是怎样理解“棱长总和”的？2、根据长方体棱的特点，想一想可以怎样计算长方体的棱长总和？跟你们组的成员说说你的想法。

3、总结归纳长方体的棱长总和计算公式。

（类比训练一）1、根据图中数据填空：长方体的长是（）厘米，宽（）厘米，高是（）厘米。

12条棱长的和是（）厘米。

2、独立完成标杆题。

学习活动（二）：1、根据长方体棱长总和的计算方法，结合正方体棱长的特点，小组内议一议正方体棱长总和的计算方法。

2、归纳正方体棱长总和的计算公式。

（类比训练二）这幅图中的正方体，12条棱长的和是（）分米。

四、拓展训练1、为迎接“五一”国际劳动节，工人叔叔要在工人俱乐部的四周装上彩灯（地面的四边不装）。

已知工人俱乐部的长90m，宽55m，高20m，工人叔叔至少需要多长的彩灯线？2、小文用48厘米的塑料管做了一个正方体框架，请问这个正方体框架的棱长是多少厘米？五、全课小结说说这节课你学到了什么？。

1.一个长方体，长5分米，宽3分米，高4分米，求它的所有棱长的和。

2.用钢筋做一个长和宽都是3.5分米，高是10厘米的长方体框架，需多少分米的钢筋？3.一个长方体的长是15厘米，宽是12厘米，棱长总和是148厘米，求它的高。

4.两根同样长的铁丝焊一个长方体和正方体，长方体长7厘米，宽5厘米，高3厘米，求正方体的棱长是多少？5.一根铁丝，如果做成一个正方体框架模型，棱长8厘米；如果改做成一个长10厘米，宽9厘米的长方体框架模型，求高是多少？6.把110厘米长的铁丝焊成一个长方体框架，长是宽的2倍，宽是高的1.5倍，求长方体的长、宽、高分别是多少厘米？7.用一根长96厘米的铁丝做成一个最大的正方体框架，这个正方体的表面积是多少平方厘米，体积是多少立方厘米？8.某车间为制作一种长4米、宽2米、高3米的长方体铁架，需要把长10米的钢筋截成符合要求的短钢筋。

做成这样的一个铁架，至少需要长10米的钢筋多少根？一、填空1.长方体或者正方体（）叫做它的表面积。

2.一个正方体的棱长是10厘米，它的表面积是（）平方厘米。

3.一个长方体长4分米，宽3分米，高2分米，它的表面积是（）平方分米。

4.正方体的棱长之和是60分米，它的表面积是（）平方分米。

5.用两个长6厘米，宽3厘米，高1厘米的长方体拼成一个表面积尽可能小的正方体，这个拼成的长方体的表面积是（）平方厘米。

二、选择题。

1.用两个棱长是1分米的正方体小木块拼成一个长方体，拼成的长方体的表面积是（）。

A.增加了B.减少了C.没有变2.如果把一个棱长是10厘米的正方体切成两个完全相同的长方体，这两个长方体的表面积之和比原来的正方体表面积（）。

A.增加了B.减少了C.没有变化3.正方体的棱长扩大2倍，它的表面积就（）。

A.扩大2倍B.扩大4倍C.扩大6倍4.大正方体的表面积是小正方体的4倍，那么大正方体的棱长之和是小正方体的（）A.2倍B.4倍C.6倍D.8倍5.把一个正方体切成大小相等的8个小正方体，8个小正方体的表面积之和（）。

长方体与正方体棱长总和及表面积一、棱长总和1、公式长方体棱长总和=（长+宽+高）×4正方体棱长总和=棱长×122、例题（1）一个长方体的长是5厘米，宽是4厘米，高是2厘米，它的棱长总和是多少厘米？（2）用角铁做一个长方体框架，这个长方体框架的长是2米，宽是1米，高是0.5米，至少要用多少米长的角铁？（3）用一条长60厘米的铁丝围成一个长方体框架，长是8厘米，宽是5厘米，高是多少厘米？（4）用一条长60厘米的铁丝围成一个正方体框架，这个框架的棱长是多少厘米？试一试：1、用一根长48厘米的木条钉成一个正方体框架，这个框架的棱长是多少厘米？2、用铁支焊接一个棱长是5厘米的正方体框架，至少要用多长的铁支？3、用80厘米长的木料钉一个长方体框架，长是10厘米，高是2厘米，宽是多少厘米？4、用52厘米长的铁丝围一个长方体框架，长是5厘米，高是宽的3倍，宽是多少厘米？二、表面积1、公式长方体表面积=（长×宽+长×高+宽×高）×2正主体表面积=棱长×棱长×62、例题（1）做一个长方体木箱，长是10分米，宽是5分米，高是3分米，至少要用多少平方分米的木板？（2）一个教室的长是8米，宽是6米，高是4米。

现在要粉刷这个教室（四周与天花板），除去门窗及黑板的面积12平方米，要粉刷多少平方米？（3）做一个棱长是6分米的正方形无盖鱼缸，需要玻璃多少平方分米？试一试：1、一个正方体柜子，棱长是 1.2米,做这个柜子至少要用多少平方米的木板？2、一个长方体的游泳池，长20米，宽18米，水深2.5米,如在四壁和底面抹水泥,求抹水泥的面积是多少平方米?3、一个房间的长6米，宽3.5米，高3米，门窗面积是8平方米。

现在要把这个房间的四壁和顶面粉刷水泥，粉刷水泥的面积是多少平方米？如果每平方米需要水泥4千克，一共要水泥多少千克？4、有一种无盖的玻璃鱼缸，长20厘米，宽15厘米，高10厘米，做这样一对鱼缸需要多少平方厘米的玻璃？5、楼房外壁用于流水的水管是长方体。

生活中的长方体和正方体——六年级数学国庆综合实践活动（2015.09）班级姓名同学们，你们注意过像右边包装箱上这样的连乘式吗？它表示这个长方体包装箱的长、宽、高分别是185毫米、150毫米和230毫米。

在一些家用电器（如冰箱、洗衣机、微波炉、电饭锅等）的背面，都会贴着一张铭牌，标示出电器的有关数据，其中就包括电器的外形尺寸和容积。

观察右边的这张电冰箱的铭牌，其中的“宽”（左右方向）其实就是长，而“深”（前后方向）就是宽。

根据铭牌中的数据，填写下面的内容：长毫米，宽毫米，高毫米，体积是立方分米（用计算器计算，得数保留整数，注意单位名称），容积是升。

请你观察家里的家用电器（如冰箱、洗衣机、微波炉等）背后的铭牌，也可以在电器的说明书中查找它的相关尺寸，填写下表（体积用计算器计算，得数保留整数，注意单位名称）：电器名称长/mm 宽/mm 高/mm 体积/dm3容积/L常见的手帕纸（下左图），一般长约8厘米，宽5.5厘米，厚2.5厘米。

厂家一般都是将10包手帕纸包装在一起进行销售，包装形式如下右图：那10包手帕纸有多少种不同的包装方式呢？请你在下面画出包装的示意图（如有困难，可以准备10包手帕纸摆一摆），并分别计算一下每种包装方式需要塑料纸多少平方厘米？（重叠部分忽略不计）示意图列式计算通过计算，我发现（）种包装最节省材料。

测算自己心脏和大脑的体积心脏和大脑是我们人体最为重要的两个器官。

你知道它们的大小吗？研究表明，人体的心脏大约和自己的右拳差不多大，而人的大脑大约是并拢双拳的大小。

看来，我们可以通过测量自己拳头的体积，了解心脏和大脑的体积。

想一想，可以用什么方法来测量自己拳头的体积，从而知道自己心脏和大脑的体积呢？（回忆一下《乌鸦喝水》的故事，是否能受到什么启发？）请你认真设计测量方法，将测量步骤写下来，并将测量过程的照片贴在下面。

计算：我心脏的体积大约是：，大脑的体积大约是：。

同学们，通过这次综合实践活动，你有什么收获？把你的想法写下来吧！。

长方体正方体圆柱圆锥知识表格正方体、长方体、圆柱、圆锥比较表格名称图形侧面展开图特点表面积公式体积公式长方体〔1〕6个面,每个面都是长方形,也可能相对的两个面是正方形。

〔2〕12条棱，相对的棱长度相等。

〔3〕有8个顶点。

长方体的表面积=（a×b＋a×c＋b×c）×2(a,b,c分别为长宽高)长方体的体积=a×b×c正方体（特殊长方体）〔1〕有6个面，每个面面积相等，形状完全相同。

〔2〕有8个顶点〔3〕有12条棱，每条棱长度相等。

正方体的表面积=a×a×6(a为棱长)正方体的体积=a×a×a圆柱（1）由两个大小相同的圆形底面和一个曲面组成。

（2）有无数条高圆柱的表面积=两个底面积＋一个侧面积（有时候加一个底面积，那就是无盖）圆柱的体积=S底×h（底面积×高）圆锥（1）由一个圆形底面和一个曲面组成圆锥的表面积=侧面积+一个地面的面积圆锥的体积=S底×h÷3（或者×三分之一，因为等底等高的时候，圆柱是圆锥的三倍）。

【长方体、正方体的棱长总和的计算】学案 学习内容：北师大版五年级下册第二单元长方体（一）中的内容。

学习目标：1、通过观察发现长方体、正方体的棱长总和的计算方法。

2、利用长方体、正方体的棱长总和的计算方法，解决一些简单的生活问题。

3、端正坐姿、规范写姿，不插嘴学会倾听，大声说话，说完整话。

教具准备：长方体、正方体各一个。

学习重点：掌握长方体和正方体的棱长总和的计算方法。

学习难点：结合实际问题，求长方体或正方体的棱长总和。

学习过程：一、我是口算小能手。

（3分钟）。

名次： 得分： 35×53= 92×43= 1211×53= 32× 41= 85×103= 52×52= 76×61 = 107×35 = 51 ×325 = 94×21=65×35= 61 ×83= 1211×74= 89×74= 127×143= 31×79= 94×27= 2120 ×51= 73×61= 107×75= 二、认真看下面的例题，掌握长方体和正方体棱长总和的计算方法。

例题：张老师制作以下的长方体和正方体框架（如下图），每个框架需要多长的铁丝？（接头处忽略不计）1、题目解析：铁丝框架是由122、A 图为长方体，长方体共有12条棱，这12条棱可分为3组，即4条长、4条宽和4条高，把4条长、4条宽和4条高相加；或用一组长、宽、高的和乘4，即可得到长方体12条棱的棱长总和。

长方体棱长总和算法一：3×4+1×4+2×4 算法二：（3+2+1）×4 =12+4+8 =6×4=24（cm ） =24（cm ） 答：长方体框架需要24厘米长的铁丝。

如果用a 表示长方体的长，用b 表示长方体的宽，用h 表示长方体的高，长方体棱长总和计算方法可以表示为4a+4b+4h ，或表示为4(a+b+h)。

6.学习活动设计一、整理与练习1.理一理（1）长方体和正方体各有哪些特征？有什么联系？【相同点（面、棱、顶点的个数），不同点（面的形状、面的大小、棱的长度）联系：用集合图表示（正方体是特殊的长方体）】（2）体积和容积的意义分别指什么？常用的体积和容积的单位有哪些？相邻体积单位间的进率是多少？体积：物体所占（ ）的大小叫物体的体积。

容积：容器所能（ ）叫容器的容积。

常用的体积（容积）单位有：立方米→（ ）→ （ ） 升 → （ ）体积（容积）相邻单位间的进率是（ ） 【帮助学生区分清楚：体积和容积的区别是二者意义不同，使用的单位有：立方米、立方分米、立方厘米，如果计量液体的体积，可以用升或毫升，但计量体积较大的液体时，也使用到立方米，例如游泳池或蓄水池的容积，一般都使用立方米。

】 （3）怎样计算长方体和正方体的表面积、体积、棱长总和？解决实际问题要注意什么？名 a a a 正方体h ba 长方体棱长和体积表面积图形和条件称2.练一练（1）长方体木箱的体积与容积比较（ ）。

①一样大 ②体积大 ③容积大 ④无法比较（2）二、基本练习1.课本P23第1题。

（1）先判断它们是正方体还是长方体？（2）估计哪个体积最大？（3）计算每个图形的体积和表面积。

体积表面积2. 课本P23第2题。

（1）认识量杯。

（2）根据量杯中水的变化，判断土豆的体积，为测量不规则物体的体积打下基础。

列式：____________________________；这个土豆的体积是（）立方厘米。

3.【帮助学生进一步熟悉长方体、正方体底面积、表面积和体积的计算方法，提高应用相关公式和方法解决问题的能力】4. 课本P24第6题。

（1）学生要能清楚的分辨并测量三个维度的棱长（长、宽、高）（2）加深对长方体、正方体展开图的认识和理解。

三、综合练习1. 一个长方体的长、宽、高分别是9厘米、6厘米、6厘米。

（1）它的棱长总和是多少?（2）从这个长方体上截下一个最大的正方体，剩下部分的体积是多少?2.一个长方体无盖的水箱，长0.8米，宽0.65米，高0.6米。

刘延革《长方体和正方体的练习课》课堂实录一、课前谈话:师：其实刚才抽奖的过程用到了数学中什么知识?你看呀,知识和我们生活中的应用分家了,对,生：可能性师：大点声说,对,可能性,或是概率,对不对?我们所学的数学知识在我们生活中的应用是不是挺广泛的?今天我们将要学习什么内容?生：长方体和正方体师：对了,有的同学看了这个题目,会有个疑问,我们上个月刚刚学过这个内容,没关系,今天我们就来上一节练习课,已学过,那正好,我们这节课来温过知新一下.老师有个疑问,在我们上个月学习的长方体和正方体的内容,我们都学习了他们什么学习内容?生：我知道了长方体和正方体都有6个面,12条棱和8个顶点师：恩,那也就是概括地说,我们认识了长方体和正方体的特征.还学了什么?生：我们还学了怎样计算表面积和体积.师：学了计算它的表面积和体积,对吧,求积的内容,还学了?生：我们还学了表示体积的体积单位师：还学了新的计量单位，体积单位和单位间的换算,对不对?我们今天就在学了这些的基础上来上一节练习课,好吗?二、练习师：请看大屏幕棱长为6，单位：分米）认识这个几何形体吗？生：正方体师：如果我们知道他的棱长之和是72分米这个信息，你觉得我们可以求出它的什么？生1：我们可以求出它的棱长是多少。

师：还能求出什么？生2：求出它的表面积和体积生3：求出它的底面积师：你们觉得要求出这几个问题，必须要知道哪个问题？生：棱长师：那怎么求出它的棱长？生：用棱长总和除以一共有12条棱师：列式是？生：72除以12师：都同意吗？那一起帮他口算一下72除以12，单位分米生：等于6分米师：单位分米我用dm表示，那我来问你们为什么除以12？生：因为正方体有12条棱，72里有12条程度相等的棱组成的，把它平均分成12份，就求出一条棱。

师：恩。

这句话其实突出了2个重要的要素，一个是正方体有12条棱，他后面又补充上来一个？生：12条棱程度是相等的师：这条重要不重要？对，这12条棱长底是相等的，所以我们才能直接除以12.对吧，那么现在我们知道了它的棱长是6分米，那接下来就可以求一求它的表面积和体积。

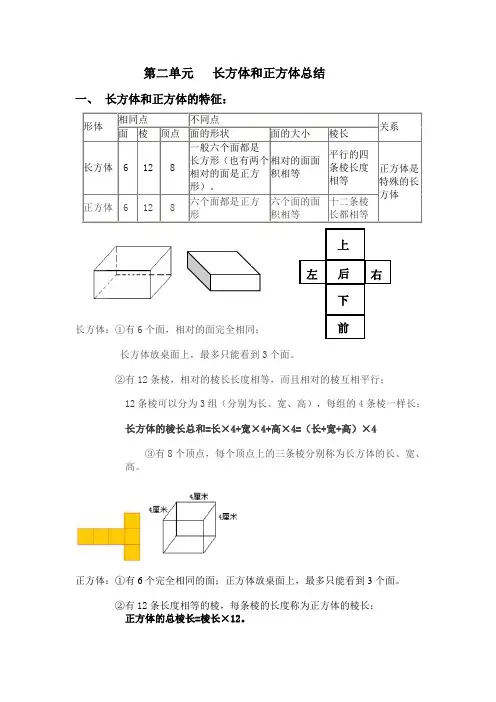
第二单元长方体和正方体总结一、长方体和正方体的特征：形体相同点不同点关系面棱顶点面的形状面的大小棱长长方体 6 12 8一般六个面都是长方形（也有两个相对的面是正方形）。

相对的面面积相等平行的四条棱长度相等正方体是特殊的长方体正方体 6 12 8六个面都是正方形六个面的面积相等十二条棱长都相等长方体：①有6个面，相对的面完全相同；长方体放桌面上，最多只能看到3个面。

②有12条棱，相对的棱长长度相等，而且相对的棱互相平行；12条棱可以分为3组（分别为长、宽、高），每组的4条棱一样长；长方体的棱长总和=长×4+宽×4+高×4=（长+宽+高）×4③有8个顶点，每个顶点上的三条棱分别称为长方体的长、宽、高。

正方体：①有6个完全相同的面；正方体放桌面上，最多只能看到3个面。

②有12条长度相等的棱，每条棱的长度称为正方体的棱长；正方体的总棱长=棱长×12。

上下左后右前③有8个顶点。

练一练：1.一个长方体长、宽、高分别是10cm、7 cm、4 cm ，这个长方体的棱长和是多少厘米？（提示：根据长方体的总棱长公式计算）2.一个长方体的棱长和是160dm，其中，长是20dm，宽是8dm，它的高是多少？从一个顶点引出的三条棱的长度总和是多少？3.将一根铁丝长720厘米做成正方体，则正方体的棱长是多少厘米？二、长方体和正方体的表面积定义：长方体或正方体6个面的总面积，叫做它的表面积。

1.法一：(1)长方体的表面积（有六个面）=长×宽×2+长×高×2+宽×高×2=（长×宽+长×高+宽×高）×2（因为长方体相对的面完全相同）法二：前、后面：长×高×2=X左、右面：长×高×2=Y上、下面：长×宽×2=Z则长方体的表面积（有六个面）= X + Y + Z2.正方体的表面积（有六个面）=棱长×棱长×6（因为正方体的六个面完全相同）在解决一些问题时，要充分考虑实际情况，想清楚要算几个面。