弧齿锥齿轮SGM法铣齿计算

浅谈弧齿锥齿轮的测量与计算摘要：弧齿锥齿轮的测量计算是齿轮测量的难点，本文简要介绍弧齿锥齿轮的优点及测量与计算关键词：弧齿锥齿轮测量计算前言圆弧线锥齿轮简称弧齿锥齿轮或弧线锥齿轮，由于弧齿锥齿轮的优点较多，近几年应用极广，特别是在钢铁企业中应用较广。

股份公司二炼钢厂拉矫机上使用的三环减速机就是这种弧齿锥齿轮，每年用量4-5台，都是从外地生产厂家进货，每台价值1.80万元，总重225kg。

折合单价80元/公斤，附加值较高。

而弧齿锥齿的测量加工是个难题，如果能将这种齿轮自己加工，将给公司带来一定的经济效益。

1.弧齿锥齿轮的优点：1.1.圆弧齿轮啮合中的诱导曲率半径很大，所以其抗点蚀能力远高于渐开线齿。

试验和使用结果表明，对于HB≦350的中速以下的圆弧齿，按工作齿面接触强度来说，其承载能力至少比渐开线齿提高0.5-1.5倍。

1.2.齿轮传动时，圆弧齿的接触区域沿齿长方向高速移动，造成有利的润滑条件，因此摩擦损耗小，效率高。

1.3.圆弧齿轮齿面间在齿高方向各点的相对润滑速度是相同的。

因此，圆弧齿轮的磨损小而且均匀，具有良好的跑合性能。

实践证明，圆弧齿的跑合过程相当短，在比较好的情况下，跑合后齿面的表面光洁度等级很高，表面状况跟挤压加工过的表面相似。

1.4.圆弧齿轮没有根切现象，故小齿的齿数可做得很少（如6～8），其最少齿数主要受轴的强度和刚度限制。

1.5.圆弧齿轮齿面间由于存在着较厚的油膜，起着缓冲的作用，因此，齿的噪音和振动较渐开线齿小。

传动平稳。

2.弧齿锥齿轮的测量与计算2.1.弧齿锥齿轮的选型：2.1.1.弧齿锥齿轮分三种即：弧齿锥齿轮（β≠0）、零度弧齿锥齿轮（β=0）、等高弧齿锥齿轮。

弧齿锥齿轮相比之下优点较多：①牙齿为弧线形，同时啮合的齿数要较直齿和零度弧齿为多，承载能力比其它两种更高。

②与零度弧齿锥齿轮相比工作平稳性更高。

噪音和振动更小。

③与等高弧齿相比更不易发生根切。

④齿有局部接触，故对安装误差和变形不敏感。

锥齿轮设计计算锥齿轮是一种广泛应用于机械传动的齿轮类型，其具有非常好的传动效率和稳定性。

在进行锥齿轮设计时需要考虑不同的因素，包括齿轮参数、齿轮材料等。

本文将就锥齿轮设计计算相关问题进行阐述。

1.锥齿轮基本参数锥齿轮的基本参数包括啮合角、齿数、齿宽、模数、齿高等。

其中啮合角和齿数是最为重要的两个参数，影响到锥齿轮的传动效率和承载能力。

一般来说，锥齿轮的啮合角应该选择在20度-30度范围之间，同时齿数一般选择在14个到38个之间。

齿宽和模数则分别影响到锥齿轮的承载能力和精度，一般来说应当根据具体的需求进行选择。

2.锥齿轮与传动比传动比指的是锥齿轮的前后轴转速比值，通常使用V表示。

在进行锥齿轮设计时需要根据实际需求计算出锥齿轮的传动比，从而确定前后轴的转速比值。

传动比可以通过公式计算出来，其中大齿轮和小齿轮的齿数分别为Z1和Z2，等效啮合角为αm，传动比可以表示为：V=(cosαm−(Z2/Z1)^2)/(cosαm+(Z2/Z1)^2)在进行计算时需要注意，传动比的取值应当落在实际需求范围之内，并且还需要满足锥齿轮传动效率、承载能力、噪声等方面的要求。

3.锥齿轮材料选取锥齿轮材料的选取非常重要，直接关系到锥齿轮的强度、耐磨性、疲劳寿命等方面。

一般来说，锥齿轮的材料应当具有良好的强度和硬度，例如钢、铸铁等材料。

同时锥齿轮的表面硬化处理可以进一步提高其耐磨性和疲劳寿命。

在进行材料选取时需要考虑实际应用条件，例如负荷、转速、温度等因素，选择适当的材料可以有效地提高锥齿轮的寿命和传动效率。

4.锥齿轮精度计算锥齿轮的精度包括整体精度、齿面精度、啮合误差等方面。

其中啮合误差对锥齿轮的传动效率影响较大，需要进行精确的计算和控制。

啮合误差包括径向误差、轴向误差、齿距误差、齿形误差等方面，需要根据具体的设计要求进行计算和控制。

一般来说，锥齿轮的啮合误差应当控制在10微米以下，以确保其传动效率和稳定性。

综上所述，锥齿轮设计计算是一个相对复杂的过程，需要考虑多个因素综合影响。

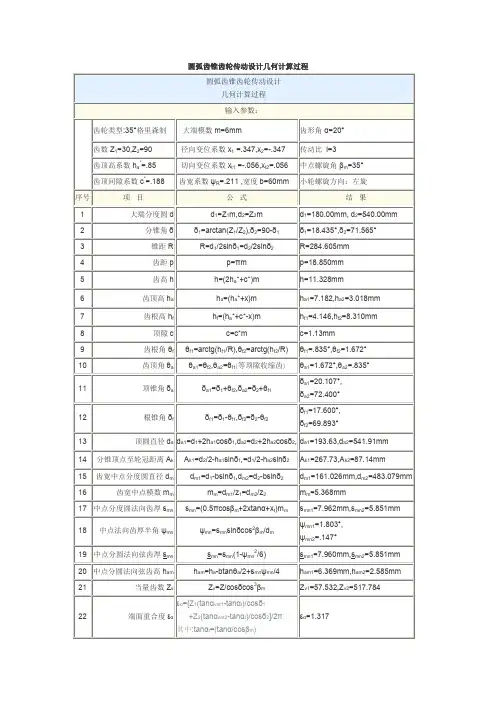
圆弧齿锥齿轮计算公式(总3页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式：1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=ar ctg(hf2/R)10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)11顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2,14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm22端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1 +Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=23齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径：求扇形弧半径扇形弧即指整个圆圈中的一部分。

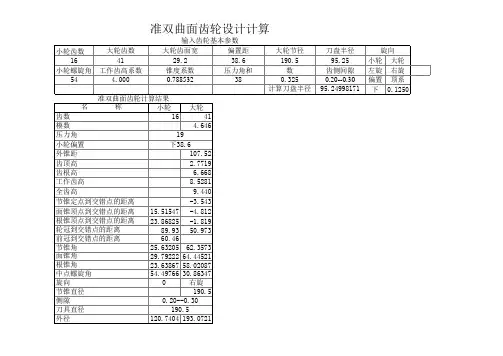
圆弧等高齿锥齿轮的切齿计算是最简单的，可以用作图法进行：一、计算大轮刀位、极角、大端小端螺旋角，垂直轮位的变化范围1.O为摇台中心，M为齿面中点，OM长度为中点锥距；2.在M点作直线，与X轴的夹角为螺旋角ps的直线；3.作与上述直线垂直的直线MO C，截MO C=r C；4.连接OO C，OO C的长就是刀位S，OO C与X轴的夹角q就是滚动中心的极角；5.以O C为中心，以r C为半径作圆弧，它就是齿线，与内端和外端分别交于M i和M o；6.连OM O、O C M O，与O C M O垂直的直线与OM O的夹角pso就是大端螺旋角。

同样可以作出小端螺旋角psi；7.如图可以量出展成M O和M i点时的极角qo和qi，加工时摇台角在qi-Δ~qo+Δ之间变化，Δ可取3~5°；8.垂直轮位展成时在r C cos（psi）~r C cos（pso）之间变化。

二、大轮加工时的轮位、床位大轮加工时的垂直轮位为0，水平轮位为0，床位由图可知X BG = -b GB G为大轮齿根高。

大轮的安装角为大轮节锥角gama。

大轮加工时的滚比R a = N C / NN C是冠轮齿数，N C = N/sinГ。

N是大轮齿数，Г是大轮节锥角。

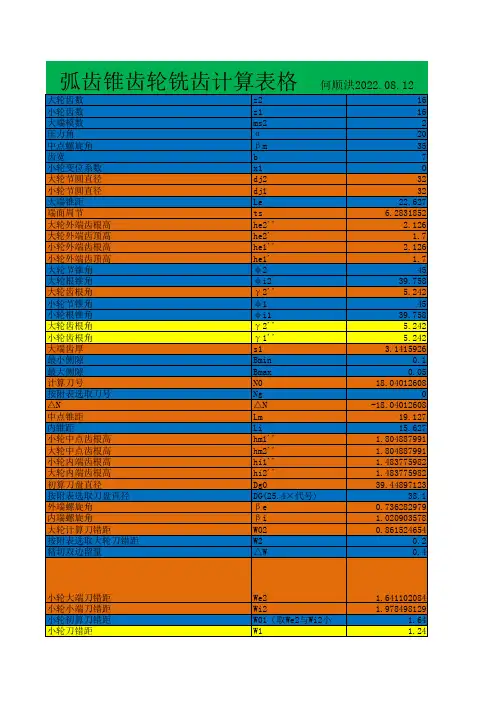
三、大轮凸面、凹面中点的螺旋角和齿长曲率半径，刀顶距为W G，那么设刀盘名义半径为r大轮内刀、即大轮凸面的成形半径为r i = r C - 0.5W G - b G tan(a)a为刀盘压力角，通常为20°。

同样可知大轮外刀，即大轮凹面的成形半径为r O = r C + 0.5W G + b G tan(a)它们当然可以用作图法求出。

大轮凸面中点的实际螺旋角可以用作图法求得：以S、A M、r i为边做三角形，由刀盘中心向X轴作垂线，夹角psi就是大轮凸面计算点的实际螺旋角。

同样可以求出大轮凹面计算点的实际螺旋角pso。

四、小轮切齿计算与大轮凸面相配的小轮凹面（用精外切刀加工）中点的压力角应该等于a，螺旋角应该等于psi，其成形半径应该比大轮凸面的成形半径大Δr，以形成曲率差，其大小与设计所要求的接触区长度有关。

圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式：1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=arctg(hf2/R) 10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2, 14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=(0.5πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1+Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=1.29723齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径：求扇形弧半径扇形弧即指整个圆圈中的一部分。

通常的已知条件是由水平线除２组成的大边和以垂直线组成的小边。

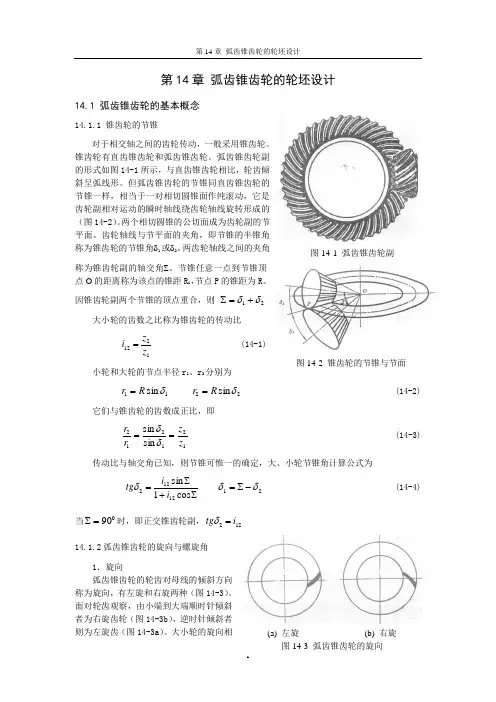
第14章 弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动，一般采用锥齿轮。

锥齿轮有直齿锥齿轮和弧齿锥齿轮。

弧齿锥齿轮副的形式如图14-1所示，与直齿锥齿轮相比，轮齿倾斜呈弧线形。

但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样，相当于一对相切圆锥面作纯滚动，它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的（图14-2）。

两个相切圆锥的公切面成为齿轮副的节平面。

齿轮轴线与节平面的夹角，即节锥的半锥角称为锥齿轮的节锥角δ1或δ2。

两齿轮轴线之间的夹角称为锥齿轮副的轴交角∑。

节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ，节点P 的锥距为R 。

因锥齿轮副两个节锥的顶点重合，则 21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(14-1) 小轮和大轮的节点半径r 1、r 2分别为11sin δR r = 22sin δR r = (14-2)它们与锥齿轮的齿数成正比，即121212sin sin z z r r ==δδ (14-3) 传动比与轴交角已知，则节锥可惟一的确定，大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑= (14-4)当090=∑时，即正交锥齿轮副，122i tg =δ 14.1.2弧齿锥齿轮的旋向与螺旋角1．旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向，有左旋和右旋两种（图14-3）。

面对轮齿观察，由小端到大端顺时针倾斜者为右旋齿轮（图14-3b ），逆时针倾斜者则为左旋齿（图14-3a ）。

大小轮的旋向相图14-2 锥齿轮的节锥与节面(a) 左旋 (b) 右旋图14-3 弧齿锥齿轮的旋向图14-1 弧齿锥齿轮副反时，才能啮合。

一般情况下，工作面为顺时针旋转的（从主动轮背后看，或正对被动轮观察），主动锥齿轮的螺旋方向为左旋，被动轮为右旋（图14-1）；工作面为逆时针旋转的，情况相反。

全工序法弧齿锥齿轮加工参数计算方法在机械制造领域，齿轮是一种非常常见的零部件，广泛应用于各种机械传动系统中。

在齿轮中，弧齿锥齿轮因其结构特点和使用场合的不同而显得尤为重要。

全工序法弧齿锥齿轮是一种加工工艺较为复杂的齿轮类型，需要考虑多个参数才能获得最佳的加工效果。

我们来了解一下什么是全工序法弧齿锥齿轮。

全工序法是指在一台机床上完成齿轮的所有加工工序，包括铣齿、车齿、滚挤等。

相较于分工序法，全工序法能够保证齿轮的几何精度和表面粗糙度，并且能够提高生产效率，因此在实际应用中得到广泛的应用。

而弧齿锥齿轮是一种齿轮的结构形式，其齿廓呈弧形。

在加工过程中，需要考虑齿轮的模数、螺旋角、齿顶间隙等参数，以确保加工出理想的弧齿锥齿轮。

在进行全工序法弧齿锥齿轮加工参数计算时，首先要确定齿轮的模数。

模数是描述齿轮齿形和尺寸的重要参数，一般根据传动比、齿数和中心距来确定。

模数的选择直接影响到齿轮的传动性能和加工成本，因此需要根据具体的使用要求来确定模数值。

要考虑弧齿锥齿轮的螺旋角。

螺旋角是指齿轮轴线上齿顶锥面与轴线的夹角，是描述螺旋齿轮齿形的重要参数。

在全工序法弧齿锥齿轮的加工过程中，螺旋角的选择直接影响到齿轮的传动效果和噪音水平。

通常情况下，螺旋角的选择要根据齿轮的使用环境和传动要求来确定，以获得最佳的传动性能。

齿顶间隙也是全工序法弧齿锥齿轮加工过程中需要考虑的重要参数之一。

齿顶间隙是指齿轮齿顶与对齿轮啮合的齿条或齿轮齿顶之间的间隙，是保证齿轮啮合顺畅的重要因素。

在加工过程中，齿顶间隙的选择需要考虑到齿轮的使用要求和加工工艺，以确保齿轮在高速、大扭矩等工况下能够正常运行。

全工序法弧齿锥齿轮加工参数计算是一个复杂而又重要的过程，需要综合考虑多个因素才能获得理想的加工效果。

在实际应用中，需要根据具体的使用情况和加工设备的性能来确定最佳的加工参数，以确保获得高质量的弧齿锥齿轮。

在我的个人观点和理解中，全工序法弧齿锥齿轮加工参数计算是一个重要而又复杂的工艺过程，需要综合考虑多个因素来进行合理的选择。

4弧齿锥齿轮的加工调整计算四弧齿锥齿轮是一种常见的齿轮类型，广泛应用于机械设备中。

在加工和调整四弧齿锥齿轮时，需要进行一系列的计算和调整，以保证齿轮的性能和运行精度。

本文将详细介绍四弧齿锥齿轮的加工调整计算。

首先，需要明确四弧齿锥齿轮的基本参数。

四弧齿锥齿轮由齿数、模数、部分齿宽系数、螺旋角等参数决定。

在加工和调整过程中，需要根据这些参数计算齿轮的各种尺寸和角度。

一、计算齿轮的齿数和模数：齿数是齿轮的重要参数之一，一般根据设计要求来确定。

模数是齿轮的副产物，是齿宽与齿数的比值。

根据齿数和模数可以计算出齿轮的模数。

齿轮的模数计算公式为：m=Z/b。

其中，m为模数，Z为齿数，b为齿宽。

二、计算齿轮的齿宽和齿高：齿宽是齿轮的另一个重要参数，一般由设计要求和工艺条件来确定。

根据齿宽和模数可以计算出齿轮的齿高。

齿轮的齿高计算公式为：h=1.25m。

其中，h为齿高、m为模数。

三、计算齿轮的分度圆半径和齿根半径：分度圆半径是齿轮最重要的参数之一，是齿轮齿槽几何形状的基准。

根据模数和齿数可以计算出齿轮的分度圆半径。

齿轮的分度圆半径计算公式为：Rm=Zm。

其中，Rm为分度圆半径，Z为齿数。

齿根半径是齿轮齿根处几何形状的基准。

根据模数可以计算出齿轮的齿根半径。

齿轮的齿根半径计算公式为：Rh=1.2m。

其中，Rh为齿根半径，m为模数。

四、计算齿轮的螺旋角和压力角：螺旋角和压力角是齿轮的重要几何参数，决定了齿轮的传动性能和运动特性。

根据设计要求和工艺条件来确定。

螺旋角的计算公式为：α=arctan(tanβ/cosγ)。

其中，α为螺旋角，β为压力角，γ为齿轮轴线与交点线之间的夹角。

压力角的计算公式为：β=10°-24°-45°(z1/z2)。

其中，β为压力角，z1为主齿轮的齿数，z2为从齿轮的齿数。

以上是四弧齿锥齿轮加工调整的一般计算方法。

在实际加工和调整过程中，还需要结合具体的工艺要求和设备精度进行一系列修正和调整。

弧齿锥齿轮测绘计算
弧齿锥齿轮是传动装置中常用的机械零部件，其主要参数的测绘计算
对于产品的质量至关重要。

测绘计算通常包含三个步骤：测量齿距、
测量基本圆的参数、计算副圆和半螺距参数。

第一步，测量齿距。

齿距是指齿轮相邻齿节圆心距离，它是齿轮的核
心参数，影响到齿轮的齿廓特性及传动整体特性，因此必须准确测量，在测量之前，要仔细检查齿轮和齿轮毂的形状和尺寸，确保使用正确
的测量工具，避免测量误差。

第二步，测量基本圆参数。

齿轮的基本尺寸参数是圆的相应参数，要
准确地测量每一个参数，如节圆的半径、圆弧的中径、角等，以保证
基本尺寸的准确性，否则可能会产生传动特性的差异。

第三步，计算副圆和半螺距参数。

副圆和半螺距是齿轮传动中互动作
用重要因素，左右面齿轮必须正确配准，因此需要准确计算副圆和半
螺距参数，确保互动特性和传动效率达到设计要求。

综上，正确测绘计算弧齿锥齿轮的参数有助于保障齿轮产品质量，使
弧齿锥齿轮传动均能达到设计要求，以实现传动效果。

第15章 弧齿锥齿轮的加工调整计算弧齿锥齿轮的切齿是按照“假想齿轮”的原理进行的，而采用的切齿方法要根据具体情况而定。

15.1 弧齿锥齿轮的切齿原理与刀号对于收缩齿弧齿锥齿轮的加工，通常采用平顶齿轮原理进行加工。

就是在切齿的过程中，假想有一个平顶齿轮与机床摇台同心，它通过机床摇台的转动而与被切齿轮做无隙的啮合。

这个假想平顶齿轮的轮齿表面，是由安装在机床摇台上的铣刀盘刀片切削刃的相对于摇台运动的轨迹表面所代替,如图15-1中所示。

在这个运动过程中，代表假想平顶齿轮轮齿的刀片切削刃就在被切齿轮的轮坯上逐渐地切出齿形。

YS2250(Y225)和Y2280等机床就是按“假想平顶齿轮”原理设计的。

在调整切齿机床的时候，必须使被切齿轮的节锥面与假想平顶齿轮的节锥面相切并做纯滚动。

而切齿时刀顶旋转平面则需和被切齿轮的根锥相切，也就是说，刀盘轴线与根锥母线垂直，而非与节锥母线垂直，如图15-2所示。

所以铣刀盘轴线与被切齿轮的节锥面倾斜了一个大小等于被切齿轮齿根角f的角度，使被切齿轮两则齿面的压力角出现了误差，这样就产生了刀号修正问题。

如图15-2，用螺旋角接近900时的情况予以说明刀号与压力角的关系。

由于在切齿时采用了“平顶产形轮”原理，工件是按照根锥角进行安装的，铣刀盘轴线垂直于根锥母线，因而和节锥母线倾斜一个齿根角f。

这样，当外切刀片与内切刀片使用图15-1弧齿锥齿轮的切齿原理摇台刀盘被加工齿轮相同的压力角时，切出来的齿轮凹面与凸面在节锥上的压力角是不相等的（”≠’）。

如果要使轮齿中点处的两侧压力角相等，就需要对刀具的两个侧刃的压力角进行修正。

修正时，外侧刃齿形角减少α∆，内侧刃增加α∆。

α∆的确定可按以下公式计算βθαsin f ≈∆ (15-1)其中β代表螺旋角。

由于大轮与小轮具有不同齿根角f，所以从严格意义上来讲，在加工大轮与小轮时，相应的切齿刀盘的刀刃修正量α∆也应不同。

按照现有的刀号制度，将α∆的单位设置为分，并规定10分为一号，则刀号的计算公式为小轮理论刀盘刀号βθβθαsin 610sin 6010c 111*1f f ==∆=(15-2a) 大轮理论刀盘刀号βθβθαsin 610sin 6010c 222*2f f ==∆= (15-2b)所以，在用双面法分别加工大轮与小轮时，应该用不同刀号的刀盘。

齿轮各部分计算公式
齿轮是一种常见的机械传动装置，由于其结构复杂，设计计算也相对繁琐。

下面将介绍齿轮各部分的计算公式，包括齿数计算、模数计算、齿廓曲线计算等。

一、齿数计算公式：
齿数是齿轮设计中最基本的参数之一、一般情况下，要求输入齿轮中心距、模数和齿数，通过计算可以得到另一个齿轮的齿数。

1.齿数计算公式：
n=（πd）/m
其中，n为齿数，d为齿轮的规定直径，m为模数。

2.齿轮中心距计算公式：
a=m(z1+z2)/2
其中，a为齿轮中心距，m为模数，z1、z2为两个齿轮的齿数。

二、模数计算公式：
模数是齿轮设计中重要的参数之一，是决定齿轮尺寸的关键。

1.模数计算公式：
m=d/z
其中，m为模数，d为齿轮的规定直径，z为齿数。

三、齿廓曲线计算公式：
齿廓曲线是描述齿轮齿形的曲线，常用的齿廓曲线有圆弧、渐开线等。

1.圆弧齿廓曲线计算公式：
y = r - (r' + r' tanα)
其中，y为齿廓偏差，r为齿轮基圆半径，r'为齿轮分度圆半径，α
为压力角。

2.渐开线齿廓曲线计算公式：
x = (r + r α) cosθ + m tanθ - m tanα
其中，x为齿廓偏差，r为齿轮基圆半径，α为压力角，θ为齿廓角。

以上仅是齿轮计算中的一部分公式，实际的齿轮设计计算还需要考虑
到材料强度、结构刚度等因素。

此外，齿轮的传动特性、工作精度也需要
在设计时进行综合考虑。

第15章 弧齿锥齿轮的加工调整计算弧齿锥齿轮的切齿是按照“假想齿轮”的原理进行的，而采用的切齿方法要根据具体情况而定。

15.1 弧齿锥齿轮的切齿原理与刀号对于收缩齿弧齿锥齿轮的加工，通常采用平顶齿轮原理进行加工。

就是在切齿的过程中，假想有一个平顶齿轮与机床摇台同心，它通过机床摇台的转动而与被切齿轮做无隙的啮合。

这个假想平顶齿轮的轮齿表面，是由安装在机床摇台上的铣刀盘刀片切削刃的相对于摇台运动的轨迹表面所代替,如图15-1中所示。

在这个运动过程中，代表假想平顶齿轮轮齿的刀片切削刃就在被切齿轮的轮坯上逐渐地切出齿形。

YS2250(Y225)和Y2280等机床就是按“假想平顶齿轮”原理设计的。

在调整切齿机床的时候，必须使被切齿轮的节锥面与假想平顶齿轮的节锥面相切并做纯滚动。

而切齿时刀顶旋转平面则需和被切齿轮的根锥相切，也就是说，刀盘轴线与根锥母线垂直，而非与节锥母线垂直，如图15-2所示。

所以铣刀盘轴线与被切齿轮的节锥面倾斜了一个大小等于被切齿轮齿根角θf 的角度，使被切齿轮两则齿面的压力角出现了误差，这样就产生了刀号修正问题。

如图15-2，用螺旋角接近900时的情况予以说明刀号与压力角的关系。

由于在切齿时采用了“平顶产形轮”原理，工件是按照根锥角进行安装的，铣刀盘轴线垂直于根锥母线，因而和节锥母线倾斜一个齿根角θf 。

这样，当外切刀片与内切刀片使用相同的压力角时，切出来的齿轮凹面与凸面在节锥上的压力角是不相等的（α”≠α’）。

如果要使轮齿中点处的两侧压力角相等，就需要对刀具的两个侧刃的压力角进行修图15-1弧齿锥齿轮的切齿原理摇台刀盘 被加工齿轮正。

修正时，外侧刃齿形角减少α∆，内侧刃增加α∆。

α∆的确定可按以下公式计算βθαsin f ≈∆ (15-1)其中β代表螺旋角。

由于大轮与小轮具有不同齿根角θf ，所以从严格意义上来讲，在加工大轮与小轮时，相应的切齿刀盘的刀刃修正量α∆也应不同。

按照现有的刀号制度，将α∆的单位设置为分，并规定10分为一号，则刀号的计算公式为小轮理论刀盘刀号βθβθαsin 610sin 6010c 111*1f f ==∆= (15-2a)大轮理论刀盘刀号βθβθαsin 610sin 6010c 222*2f f ==∆=(15-2b) 所以，在用双面法分别加工大轮与小轮时，应该用不同刀号的刀盘。

圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式：1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=arctg(hf2/R) 10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2, 14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=(0.5πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1+Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=1.29723齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径：求扇形弧半径扇形弧即指整个圆圈中的一部分。

通常的已知条件是由水平线除２组成的大边和以垂直线组成的小边。