平行圆柱体承受法向载荷时的接触应力分析
- 格式:pptx
- 大小:1.75 MB
- 文档页数:35

圆柱导轨负荷是指在圆柱形导轨系统中,由于载体的垂直力、水平力或倾斜力作用于导轨上所产生的力。
这种负荷可以分为几种不同的类型:
1. 垂直负荷:这是由于重力作用在载体上产生的力,它垂直作用于导轨表面。
2. 水平负荷:当载体受到水平方向的力(如摩擦力、推进力等)时,会在导轨上产生水平方向的负荷。
3. 径向负荷:当负荷沿着导轨的半径方向作用时,称为径向负荷。
这种负荷通常是由于外部力的直接作用或者由于旋转部件产生的离心力。
4. 轴向负荷:如果负荷沿着导轨轴线方向作用,则为轴向负荷。
这种负荷常见于直线运动系统中的轴承和导轨。
5. 复合负荷:实际应用中,导轨往往同时承受多方向的负荷,这时称为复合负荷。
为了确保系统的稳定性和耐用性,设计圆柱导轨系统时需要考虑这些负荷对导轨材料、尺寸、形状以及支撑结构的影响。
通过计算预期的最大负荷和使用适当的公差和安全系数,工程师可以设计出既能承受预期负荷又能保持低摩擦和高精度的导轨系统。
此外,润滑也是减少导轨负荷影响、延长使用寿命的关键因素之一。

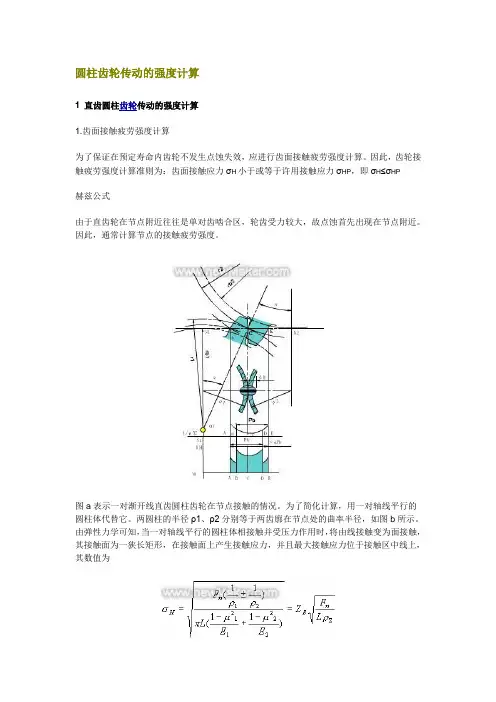
圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效,应进行齿面接触疲劳强度计算。
因此,齿轮接触疲劳强度计算准则为:齿面接触应力σH小于或等于许用接触应力σHP,即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区,轮齿受力较大,故点蚀首先出现在节点附近。
因此,通常计算节点的接触疲劳强度。
图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。
为了简化计算,用一对轴线平行的圆柱体代替它。
两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径,如图b所示。
由弹性力学可知,当一对轴线平行的圆柱体相接触并受压力作用时,将由线接触变为面接触,其接触面为一狭长矩形,在接触面上产生接触应力,并且最大接触应力位于接触区中线上,其数值为式中σH-接触应力(Mpa)Fn-法向力(N)L-接触线长度(mm)rS-综合曲率半径(mm);±-正号用于外接触,负号用于内接触ZE-材料弹性系数(),,其中E1、E2分别为两圆柱体材料的弹性模量(MPa);m1、m2分别为两圆柱体材料的泊松比。
上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同,且靠近节点的齿根处最大(图c、d)。
但为了简化计算,通常控制节点处的接触应力。
节点处的参数(1)综合曲率半径由图可知,,代入rE公式得式中:,称为齿数比。
对减速传动,u=i;对增速传动,u=1/i。
因,则有(2)计算法向力(3)接触线长度L引入重合度系数Ze,令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令,称为节点区域系数。
则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数,并将代入上式,则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径(mm);ZE-材料弹性系数(),按下表查取;注:泊松比m1=m2=0.3Z H-节点区域系数,考虑节点处轮廓曲率对接触应力的影响,可由下左图查取。

传递动力的高副机构,如摩擦轮、凸轮齿轮、链轮传动、滚动轴承、滚动螺旋等,都有接触强度问题,自然也涉及到接触应力。
在此对接触应力计算作较为全面的讨论。
两曲面的弹性体在压力作用下,相互接触时,都会产生接触应力,传递动力的高副机构在工作中往往出现的是交变应力,受交变接触应力的机器零件在一定的条件下会出现疲劳点蚀的现象,点蚀扩散到一定程度,零件就不能再用了,也就是说失效了,这样失效的形式称之为疲劳点蚀破坏,在ISO标准中是以赫兹应力公式为基础的。
本文较为集中地讨论了几种常见曲面的赫兹应力公式及常用机械零件的接触应力计算方法,便于此类零件的设计及强度验算。
1 任意两曲面体的接触应力1.1 坐标系图1所示为一曲面体的一部分,它在E点与另外一曲面体相接触,E点称为初始接触点。
取曲面在E点的法线为z轴,包括z轴可以有无限多个剖切平面,每个剖切平面与曲面相交,其交线为一条平面曲线,每条平面曲线在E点有一个曲率半径。
不同的剖切平面上的平面曲线在E点的曲率半径一般是不相等的。
这些曲率半径中,有一个最大和最小的曲率半径,称之为主曲率半径,分别用R′和R表示,这两个曲率半径所在的方向,数学上可以证明是相互垂直的。
平面曲线AEB所在的平面为yz平面,由此得出坐标轴x和y的位置。
任何相接触的曲面都可以用这种方法来确定坐标系。
由于z轴是法线方向,所以两曲面在E点接触时,z轴是相互重合的,而x1和x2之间、y1和y2之间的夹角用Φ表示(图2所示)。
图1 曲面体的坐标图2 坐标关系及接触椭圆1.2 接触应力两曲面接触并压紧,压力P沿z轴作用,在初始接触点的附近,材料发生局部的变形,靠接触点形成一个小的椭圆形平面,椭圆的长半轴a在x轴上,短半轴b在y轴上。
椭圆形接触面上各点的单位压力大小与材料的变形量有关,z轴上的变形量大,沿z轴将产生最大单位压力P0。
其余各点的单位压力P是按椭圆球规律分布的。
其方程为单位压力总压力P总=∫PdF∫d F从几何意义上讲等于半椭球的体积,故接触面上的最大单位压力P0称为接触应力σH(1)a、b的大小与二接触面的材料和几何形状有关。

接触应力计算全面讨论图1 曲面体的坐标图2 坐标关系及接触椭圆1.2 接触应力两曲面接触并压紧,压力P 沿z 轴作用,在初始接触点的附近,材料发生局部的变形,靠接触点形成一个小的椭圆形平面,椭圆的长半轴a 在x 轴上,短半轴b 在y 轴上。
椭圆形接触面上各点的单位压力大小与材料的变形量有关,z 轴上的变形量大,沿z 轴将产生最大单位压力P 0。
其余各点的单位压力P 是按椭圆球规律分布的。
其方程为单位压力总压力 P 总=∫PdF∫dF 从几何意义上讲等于半椭球的体积,故接触面上的最大单位压力P 0称为接触应力σH(1)a 、b 的大小与二接触面的材料和几何形状有关。
2 两球体的接触应力半径为R1、R2的两球体相互接触时,在压力P的作用下,形成一个半径为a的圆形接触面积即a=b(图4),由赫兹公式得式中:E1、E2为两球体材料的弹性模量;μ1、μ2为两球体材料的泊松。
图4 两球体外接触取综合曲率半径为R,则若两球体的材料均为钢时,E1=E2=E,μ1=μ2=μ=0.3,则(2)如果是两球体内接触(图5),综合曲率半径为,代入式(2)计算即可求出接触应力σH。
如果是球体与平面接触,即R2=∞,则R=R1代入式(2)计算即可。
图5 两球体内接触3 轴线平行的两圆柱体相接触时的接触应力轴线平行的两圆柱体接触时,变形前二者沿一条直线接触,压受力P 后,接触处发生了弹性变形,接触线变成宽度为2b 的矩形面(图6),接触面上的单位压力按椭圆柱规律分布。
变形最大的x 轴上压力最大,以P 0表示,接触面上其余各点的压力按半椭圆规律分布,如图7,半椭圆柱的体积等于总压力P ,故图6 两圆柱体接触图7 轴线平行的两圆柱体相接触的压力分布最大单位压力(3)由赫兹公式知代入式(3),得若两圆柱体均为钢时,E1=E2=E,μ1=μ2=0.3,取则接触应力为若为两圆柱体内接触(图8),则以代入式(4)计算。
若是圆柱体与平面接触,则R2=∞,R=R1代入式(4)计算。

一. 是非题:正确的在()中写“√”,错误的在()中写“×”1、在不改变零件静强度的条件下,加大在一定载荷下零件的弹性变形量,将会降低该零件的冲击强度。
( )2、在不改变零件静强度的条件下,加大在一定载荷下零件的弹性变形量,可提高耐冲击强度。
( )3、设计零件时,安全系数应尽可能选大些,使该零件工作更可靠与安全。
( )4、某转轴采用40钢(σS MPa =335),经校核其扭转刚度不够,可改选高强度合金结构钢40Cr ()σS MPa =785,以提高刚度。
( )5、设计某普通碳钢零件时,校核后刚度不足,采用高强度合金钢时,对提高其刚度是不起作用的。
( )6、在变应力作用下,零件的主要失效形式将是疲劳断裂,而在静应力作用下,其失效形式将是塑性变形或断裂。
( )7、只要材料的平均极限应力σlim 大于零件的平均工作应力σm ,则安全系数S 就大于1,工作是可靠的。
( )8、若材料的平均极限应力σlim 大于零件的平均工作应力σm ,则零件的安全系数不一定总是大于1。
( )9、渐开线圆柱直齿轮传动空载运转时,可以认为是处于齿面线接触状态。
( )10、渐开线圆柱直齿轮传动工作时,齿面载荷的传递是通过真实的线接触进行的。
( )11、两圆柱体相接触,其轴线互相平行,在受法向压力作用下,则两零件的接触应力不等,直径大的零件所受接触应力小。
( )12、两圆柱体相接触,其轴线互相平行,受法向压力,则两零件的接触应力相等。
( )二、选择题:把正确的选项代号填入()中1、在受轴向变载荷的紧螺栓联接中,采用柔性螺栓,是为了_____________。
A.增大变载荷下的剩余预紧力,提高联接可靠性;B.改善变载荷下的螺母支承面接触状态;C.降低应力幅σa;D.可减轻螺栓重量,节省材料。
2、已知某转轴在复合应力状态下工作,其弯矩作用与扭矩作用下的安全系数分别为Sσ=6.1,Sτ=18.5,则该转轴的实际安全系数大小为_____________________。

两表面接触应力与载荷之间关系在工程学和材料学中,负载和应力是研究物体力学性质最重要的方面之一。
在很多情况下,物体有两个表面相互接触,这时候就需要了解表面接触应力与载荷之间的关系。
第一步骤:定义两表面接触应力和载荷对于两个表面之间的接触,我们可以定义表面接触应力为两表面上相互压缩的力。
这个力是单位面积的压力,常用符号为σ。
而载荷则是作用在物体上的外力,可以是重力、压力、拉力等。
载荷通常用符号F表示,单位是牛顿或磅。
第二步骤:理解表面接触应力和载荷之间的关系当两个表面接触时,载荷会在表面上产生应力。
这个应力会在表面之间传递,直到达到适当的平衡状态。
接触应力与载荷之间的关系可以用下面的公式表示:σ = F / A其中,A是表面面积,σ是接触应力。
要理解这个公式,可以将其应用于一个简单的例子。
例如,在拖拉机车轮和地面之间的接触面上,轮径的承受载荷会被分摊到轮边缘的表面上。
若假设轮子的重量为750千克,表面接触面积为0.0015平方米,则轮边缘的接触压力将是:σ = 7500 N / 0.0015 m² = 5×10^6 Pa这个值大得惊人,但是表明了接触表面上的应力与承载的载荷是成正比关系的。
如果减少了接触面积,那么承载的载荷就会集中在更小的面积上,这最终会导致需要更高的接触应力。
第三步骤:如何影响表面接触应力表面接触应力的大小可以受到不同因素的影响。
例如,它受到物体间几何形状和表面粗糙程度的影响。
即便在表面较为光滑的情况下,也会存在微小的几何形状变化,从而导致一定程度的表面粗糙度。
此外,材料硬度也会影响表面接触应力。
硬度更高的材料可以更好地抵抗压力和剪切力,从而产生更大的表面接触应力。
最后,表面润滑也会影响表面接触应力。
例如,使用润滑剂可以减少接触力,从而减小表面接触应力。
这样,就可以减少磨损,降低噪音和稳定性问题等。
综上所述,表面接触应力与载荷之间的关系是非常重要的,并且受到多个因素的影响。




接触应力弯曲应力
接触应力和弯曲应力是在不同力学情境下描述的两种不同类型的应力。
●接触应力(Contact Stress):接触应力是指在两个物体表面相互接触的区域内的应力。
这种应力通常出现在两个固体物体表面直接接触的地方,例如在机械齿轮、轴承、齿轮传动等设备中。
接触应力的计算涉及到接触面的几何形状、力的大小和方向、材料的弹性模量等因素。
在接触应力中,关注的是两个物体之间的相互作用。
●弯曲应力(Bending Stress):弯曲应力是在物体受到外部弯曲力作用时,在横截面上产
生的应力。
这种应力通常出现在梁、悬臂、梁柱等结构中,当这些结构受到弯曲力时,横截面上的不同点承受不同的应力。
弯曲应力的计算与物体的几何形状、外部加载、材料的弹性模量和截面惯性矩等因素相关。
在弯曲应力中,关注的是物体内部不同位置的应力分布。
总体来说,接触应力和弯曲应力描述了不同应用场景下的应力状态,一个涉及到表面的相互接触,另一个涉及到结构的形变和受力。
这两种应力都是工程和材料力学中重要的概念,对于设计和分析结构和设备都具有重要意义。
摘要:通过接触力学基本知识的分类,理解和掌握;总结了关于Hertz接触理论处理两个球体的接触,球体及刚性圆柱体和弹性半空间的接触等一系列经典问题的方法;并对Hertz接触-有限元分析方法进行了简单的介绍以及讨论了Hertz理论的局限性。
最后对撞击问题进行了较为系统的分类,并给出撞击问题的实例,从简单到复杂,即从弹性,弹塑性,粘弹性做了,做了一个简单的模型,并给出了主要分析步骤和计算方法。
关键词:接触力学,Hertz理论,撞击1.基本概念的介绍 (3)1.1. 按接触物体的材料性质分类 (3)1.2. 按空间分类 (3)1.3. 按接触面的光洁度分类 (3)1.4. 按理论力学的方法分类 (4)1.5. 按接触物体的几何形状分类 (4)2. 接触力学分析方法 (4)2.1. 经典的接触力学接触问题 (4)2.2. 非经典的接触力学分析方法 (5)3.Hertz接触理论 (5)3.1. Hertz接触的一般假定: (5)3.2. 经典弹性接触问题 (5)3.3. Hertz接触-有限元分析 (11)4.撞击 (12)4.1. 碰撞 (12)4.2. 碰撞的分类 (12)4.3. 实例分析(接触力-变形模型) (13)5.收获与体会 (16)6.参考文献 (16)1.基本概念的介绍1.1. 按接触物体的材料性质分类1.1.1 弹性物体的接触这是最广泛的一类接触问题,是弹性理论的一大类专门性问题,已研究得相当成熟研究对象是弹性物体与弹性物体相接触,刚性物体与弹性物体相接触。
1.1.2 粘弹性物体的接触多研究线性粘弹性物体的接触应力和应变是线性关系但这种关系和时间、速率相关,所以是粘弹性物体它包括弹性物体和粘弹性物体的接触,刚性物体和粘弹性物体的接触。
1.1.3 塑性物体的接触主要研究材料屈服后的接触,当然是非线性的应变同应力的本构关系比较复杂包括刚性物体同塑性物体的接触、弹塑性同时存在、纯塑性等问题。
1.1.4可变形固体同液体的接触这类问题往往以流体力学为主,液体载荷影响可变形物体的应力分布有关线性弹性接触的文献最丰富,解决的问题也最多尽管如此,这类问题与弹性理论的其他专门可题有共同特性,对于它们的研究还在继续发展。
一. 是非题:正确的在()中写“√”,错误的在()中写“×”1、在不改变零件静强度的条件下,加大在一定载荷下零件的弹性变形量,将会降低该零件的冲击强度。
( )2、在不改变零件静强度的条件下,加大在一定载荷下零件的弹性变形量,可提高耐冲击强度。
( )3、设计零件时,安全系数应尽可能选大些,使该零件工作更可靠与安全。
( )4、某转轴采用40钢(σS MPa =335),经校核其扭转刚度不够,可改选高强度合金结构钢40Cr ()σS MPa =785,以提高刚度。
( )5、设计某普通碳钢零件时,校核后刚度不足,采用高强度合金钢时,对提高其刚度是不起作用的。
( )6、在变应力作用下,零件的主要失效形式将是疲劳断裂,而在静应力作用下,其失效形式将是塑性变形或断裂。
( )7、只要材料的平均极限应力σlim 大于零件的平均工作应力σm ,则安全系数S 就大于1,工作是可靠的。
( )8、若材料的平均极限应力σlim 大于零件的平均工作应力σm ,则零件的安全系数不一定总是大于1。
( )9、渐开线圆柱直齿轮传动空载运转时,可以认为是处于齿面线接触状态。
( )10、渐开线圆柱直齿轮传动工作时,齿面载荷的传递是通过真实的线接触进行的。
( )11、两圆柱体相接触,其轴线互相平行,在受法向压力作用下,则两零件的接触应力不等,直径大的零件所受接触应力小。
( )12、两圆柱体相接触,其轴线互相平行,受法向压力,则两零件的接触应力相等。
( )二、选择题:把正确的选项代号填入()中1、在受轴向变载荷的紧螺栓联接中,采用柔性螺栓,是为了_____________。
A.增大变载荷下的剩余预紧力,提高联接可靠性;B.改善变载荷下的螺母支承面接触状态;C.降低应力幅σa;D.可减轻螺栓重量,节省材料。
2、已知某转轴在复合应力状态下工作,其弯矩作用与扭矩作用下的安全系数分别为Sσ=6.1,Sτ=18.5,则该转轴的实际安全系数大小为_____________________。
第29卷第4期摩擦学学报Vo.l29No.4 2009年7月T ri b ology J u l y,2009基于H ertz理论圆柱和平面之间的滑动接触分析冯剑军,谭援强(湘潭大学机械工程学院,湖南湘潭411105)摘要:当圆柱与平面之间产生摩擦滑动接触时,基于H e rtz理论,推导了平面内应力分量的计算公式,分析了应力的分布,描述了应力分布的特点.在接触表面上,存在最大拉应力和最大压应力;最大拉应力出现在拖动边的边缘,而最大压应力发生在导向边的区域.因此,如果接触平面因拉或压应力引起失效,首先会出现在接触表面;第一型裂纹的产生及扩展首先会发生在拖动边的边缘.剪应力,主剪应力及Von-M i ses等效应力(当摩擦系数较小时)的最大值均会出现在接触体内,存在于导向边.因此,塑性滑移开始首先会发生在接触体内,然后,才扩展到接触表面.这些结论为工程应用研究提供了依据.关键词:摩擦滑动接触;等效应力;主应力;接触压力;剪切牵引力中图分类号:O31文献标识码:A文章编号:1004-0595(2009)04-0346-05滑动接触问题是接触力学的基本问题,在许多工程领域具有广泛的应用,如机械中元件之间的相互接触,计算机中磁头与磁盘的接触,电器中触头开启与闭合等,尤其是加工中刀具与工件的接触,超精密抛光加工中抛光粉颗粒与晶片间的接触等,均涉及到摩擦滑动接触问题.许多研究者对此进行了深入的研究,取得了很大的进展[1-11].对弹性体滑动接触问题的分析方法通常有2种:第一种是基于H ertz接触理论和Cou lo mb摩擦定律,其基本观点是小变形,接触面上的压力服从抛物线分布,按H ertz 接触理论确定;初始滑动时,切向力的大小和分布服从Cou lo mb摩擦定律,即为摩擦的极限状态;建立接触面上的法向变形方程时不考虑法向压力和切向力的耦合作用.这种方法计算较简单.其二是建立接触面上的法向和切向变形方程时考虑法向压力和切向力的耦合作用,需要求解奇异耦合积分方程,确定法向压力和切向力.这种方法计算较复杂.Johnson[1]介绍了滑动接触的研究方法和原理,他认为按第一种方法计算,其误差较小;同时,他介绍了采用第一种方法计算圆柱和平面之间产生滑动接触时弹性体内应力场的方法,而对接触体内应力场的分布没有作详细的分析.当圆柱和半无限平面产生弹性滑动接触时,由于材料泊松比(Piosson ratio)的作用,弹性体也会产生沿圆柱轴向的弹性滑动.如果考虑这种作用,求解将很复杂,为了简化求解,忽略轴向弹性滑动引起的切向力.Q i u a H[4]分析了一个圆柱相对于半无限平面斜滑动的情况,把剪切拖动力分解为轴向和切向两个分力,把接触区离散为有限个小区域,有效地避免了积分收敛的问题,分析表明:轴向滑动对接触面上的应力分布有影响,但是,影响较小.因此,当一个圆柱相对于半无限平面正交滑动时,可以忽略材料Poisson rati o引起的轴向弹性滑动对平面内应力分布的影响.Kogu,t E tsi o n等[5-9]认为弹-塑性滑动接触时的摩擦系数与接触压力、材料特性有关;塑性滑移开始首先会发生在接触体内部,然后才扩展到接触表面.V ijay wargi y a和Green[10]发的作用力差别较小.本文基于H ertz接触理论和Coulo mb摩擦定律,计算了平面和圆柱产生滑动接触时在半无限平面内的应力场,绘制了应力的分布曲线图,并且详细地分析了应力的分布.所获得的结果有利于准确地判断平面和圆柱产生滑动接触时塑性变形开始的区域、首先出现裂纹和裂纹扩展的位置,为研究接触体的变形和接触裂纹扩展提供依据.收稿日期:2008-11-16;修回日期:2009-04-08;联系人:谭援强,e-m a i:l Tanyq@基金项目:国家自然科学基金资助项目(50875224);教育部新世纪人才培养计划资助项目(NCET06-0708).作者简介:谭援强(1966-),男,教授,博士生导师,主要从事摩擦学和制造工艺力学的研究.1 摩擦滑动接触的计算模型无限长圆柱和无限半空间沿着垂直于圆柱轴线方向的滑动接触,如果忽略由Poisson rati o 所引起的沿着圆柱轴线方向的滑动,简称为平面和圆柱的滑动接触,可以简化为平面应变问题,其计算模型如图1所示.平面表示为体1,圆柱表示为体2.体1和体2的弹性参数分别为:E 1、E 2、T 1、T 2;体2受到向下的外载荷W 作用,如图1(a)所示,同时,体1沿着水平向右滑动,如图1(b)所示.于是,体1和体2之间产生相对运动和相互作用的分布切向摩擦力.这个分布切向摩擦力Q,分别作用在两接触体表面,方向与运动方向相反,摩擦力Q 按初始滑动时的极限摩擦状态考虑.2 摩擦滑动接触的应力分量计算式当圆柱和平面之间产生摩擦滑动接触时,平面中产生的应力场处于平面应变状态,接触产生的分布压力及切向牵引力所引起的应力可按Jonhson [1]给出的公式计算:R x =-2z PQa-ap(s)(x -s)3d s [(x -s)2+z 2]2-2PQ a-aq(s)(x -s)3d s[(x -s)2+z 2]2(1)R z=-2z 3P Q a -a p(s)d s[(x -s)+z ]-2z 2P Q a -a q(s)(x -s)d s [(x -s)2+z 2]2(2)S xz =-2z 2P Q a -ap (s)(x -s)d s [(x -s)2+z 2]2-2z P Q a-aq(s)(x -s)2d s [(x -s)2+z 2]2(3)其中:p(s)和q(s)分别为接触面上的分布接触压力和分布切向牵引力,它们分别按H ertz 理论和Coulo mb 摩擦定律确定;s 表示接触区中任意一点至接触中心的距离,x 、z 表示体1中任意一点的坐标.法向作用线载荷可表示为:P =P a 2E *4R(4)接触半宽为:a 2=4PRP E*(5)其中:R 表示圆柱的半径;E *表示等效弹性模量,1/E *=(1-T 21)E 1+(1-T 22)E 2.接触压力的分布函数为:P (s)=2P P a2(a 2-s 2)1/2-a [s [a (6)由此可知接触压力在边缘处为零.接触区中心压力为:P 0=2P P a =4Pp m =PE*P R1/2(7)P 为线载荷,假设作用在圆柱上的铅垂载荷为W ,则:P =WL,L 为圆柱轴线的长度.p m 是接触区的平均压力.当接触两体处于初始摩擦滑动状态时,Q =L p (s),L 是摩擦系数.在接触表面分布剪切牵引力Q 可以表达为:Q =q(s)=-L p 0aa 2-s 2=-q 0aa 2-s2-a [s [a (8)将分布压力(6)和分布剪切牵引力(8)分别带入到平面内的应力分量计算公式(1~3)[1],可得:R x =-p m 1+z 2+n2n 2+m2-2z +q 02x +mz(x 2-n )x (m 2+n 2)-347第4期冯剑军,等:基于H ertz 理论圆柱和平面之间的滑动接触分析2m [2x 2z 2+n 2(-1+x 2-z 2)](n 2+m 2)xz(9)R z =-p 0m 1-z 2+n2m 2+n2+q 0mz(x 2-n 2)x(m 2+n 2)(10)S xz =-p 0mz(x 2-n 2)x(m 2+n 2)+-q 0m 1-z 2+n2n 2+m2-2z(11)其中:表达式m 、n 分别为:m 2=12{[(1-x 2+z 2)2+4x 2z 2]1/2+(1-x 2+z 2)}(12)n 2=12{[(1-x 2+z 2)2+4x 2z 2]1/2-(1-x 2+z 2)}(13)在(9~13)式中:x 和z 是无量纲坐标,如果半无限平面中任意一点的坐标为(x c ,z c ),则:x =x c /a,z =z c /a.(9~11)式表示当圆柱与半无限平面产生摩擦滑动接触时在平面中应力分量的计算式.3 组合应力计算公式在平面内任意一点的应力状态可以用四个应力分量进行描述,即:R x 、R z 、S xz 以及R y.R y 是沿着圆柱轴线方向的应力,也是平面内任意一点的中间主应力,其大小根据式R y =T (R x +R z )确定.在平面中各组合应力可用应力分量表达如下:主应力可表达为:R 1=12(R x +R z )+R x -R z22+S xz 1/2(14)R 2=R y =M (R x +R z)R 3=12(R x +R z )-R x -R z22+S xz1/2(15)主剪应力为:S 1=R x -R z22+S 2xz1/2(16)Von-M ises 等效应力为:R eq =12[(R x -R y )2+(R y -R z )2+(R z -R x )2+6S 2xz ]1/2(17)通过对这些组合应力的分析,可以预测材料的变形和失效形式.4 应力的分布分析为了清楚地表达圆柱与半无限平面之间发生滑动接触时平面内应力的分布,根据上面所给出的应力计算公式,绘出了应力的分布曲线,如图2所示.在描绘图2中的(a)~(g)时,取摩擦系数L =0.3,泊松比M =0.3;而在描绘图2中的(h)时,取摩擦系数L =0.2,泊松比仍然是M =0.3.下面分析中所提到的坐标x 和z 为接触平面中点的实际坐标.F i g .2 D istri b u ti n g curves of the d i m ension less stress i n si d e the p l a ne as the f rictionally slipping contactarises bet w een a plane and a cyli n der图2 当平面和圆柱产生摩擦滑动接触时在平面中无量纲应力分布曲线348摩 擦 学 学 报第29卷为了使应力分布曲线所表示的意义具有一般性,应力和位置坐标均采用无量纲形式;上面(9)式在z= 0具有奇异性.因此,计算R x时,可以取z为一个极小量,本文取z/a=0.00001,将z的值近似看作为零,以避免这种奇异性.下面根据应力分布曲线,分析应力的变化特点.x轴向无量纲应力R x/p0相对于无量纲坐标x/ a的分布曲线如图2(a)所示.由图2(a)可知:在接触表面上,导向边(x/a<0)的R x/p0均为压应力,最大无量纲压应力出现在导向边(x/a<0),并且, |R x/p0|m ax>1,这主要是接触面上剪切牵引力作用的结果;在拖动边存在拉应力,最大无量纲拉应力发生在x/a=1处(即拖动边的边缘).在平行于接触表面的不同截面上,随着离接触表面的距离z/a的增大,x轴向无量纲应力|R x/p0|迅速减小;当z/a\ 015的横截面上,R x/p0几乎不会出现拉应力.总之,最大拉应力和最大压应力均会出现在接触表面.z轴向无量纲应力R z/p0随着无量纲坐标x/a 的变化表示在图2(b)中.图2(b)表明:在接触平面内,z轴向无量纲应力R z/p0均为压应力;在接触表面的x/a=0处,R z/p0达到最大压应力-1,而在x/ a=?1处,R z/p0=0.在平行于接触表面的截面上,随着z/a的增大,最大的无量纲压应力R z/p0逐渐减小;z轴向无量纲应力R z/p0的分布受接触面上剪切牵引力的影响较小,相对于接触中心仍然保持近似对称.这与V ijay wargi y a和G reen[10]发现的结果和与Zhupanska和U litko[11]精确计算结果基本一致.无量纲剪应力S xz/p0相对于无量纲坐标x/a的分布曲线如图2(c)所示.图2(c)表明:在接触表面上,无量纲剪应力S xz/p0的分布相对于接触中心对称;在x/a=0处,S xz/p0达到极大值.在平行于接触表面的其他横截面上均有两个极值点,极值点的位置会随着z/a的增大而向两边外移.最大剪应力不会出现在接触表面,而会存在于接触体内.因此,塑性滑移开始首先可能会发生在接触平面内.第一无量纲主应力R1/p0相对于无量纲坐标x/a 的分布如图2(d)所示.由图2(d)可知:第一无量纲主应力R1/p0不是对称分布,这是由于接触表面上剪切牵引力引起的;在拖动边存在拉应力,而在导向边均为压应力;在接触表面上,最大无量纲拉应力存在于拖动边的x/a=1处,即拖动边的边缘;而最大压应力出现在导向边-1<x/a<0的区域;在平行于接触表面的横截面上,离接触表面的距离(z/a)越大,最大拉应力和最大压应力则越小;当x/a=?2时,第一无量纲主应力R1/p0已接近于零.总之,R1/p0的最大拉应力和最大压应力,均会出现在接触表面.因此,如果接触体由第一主应力引起失效,首先可能会出现在接触表面;而第一型裂纹的产生和扩展首先可能会发生在接触表面拖动边的边缘.第三无量纲主应力R3/p0相对于无量纲坐标x/ a的分布情况如图2(e)所示.由图2(e)可知:第三无量纲主应力R3/p0分布曲线相对于接触中心不是对称分布,并且均是压应力;最大的|R3/p0|出现在接触表面-1<x/a<0的区域,而当x/a=1时,R3/ p0=0;在平行于接触表面的不同横截面上,随着z/a 的增大,最大的|R3/p0|逐渐减小,随着|x/a|的增大,|R3/p0|也会随之减小.由此可知:如果压应力的作用导致接触体失效,这种失效首先可能会出现在接触表面-1<x/a<0的区域.无量纲主剪应力S1/p0相对于无量纲坐标x/a 的分布表示在图2(f)中.从图2(f)可以看出:在接触表面的接触区,主剪应力为常量;在平行于接触表面的横截面上,无量纲主剪应力S1/p0在导向边存在极大值.总之,最大的S1/p0会出现在接触平面内部,按照T resca屈服准则,塑性开始首先会出现在接触平面内部.图2(g)、(h)表示了V on-M ises无量纲等效应力R eq/p0相对于无量纲坐标x/a的分布.由图2 (g)、(h)可知:Von-M ises无量纲等效应力R eq/p0的最大值会随着摩擦系数由小变大从接触体内移向接触表面;随着摩擦系数的增大,Von-M ises无量纲等效应力R eq/p0会增大.在接触表面上的极大值发生在x/a=0的邻近区域;在平行于接触表面的不同横截面上,随着z/a的增大,R eq/p0逐渐减小.因此,根据M ises屈服准则,当摩擦系数较小时,塑性滑移开始首先会发生在接触体内.由以上分析可知:当圆柱与平面产生滑动接触时,轴向应力、第一主应力、第三主应力的最大压应力和x轴向应力、第一主应力的最大拉应力均出现在接触表面;而剪应力,主剪应力及Von-M ises等效应力(当摩擦系数较小时)的最大值均出现在接触体内.因此,拉、压应力引起的失效均会发生在接触表面;根据T resca屈服准则、M ises屈服准则,塑性滑移开始首先会发生在接触体内,这一点与Kogut 和E tsi o n[4-8]的结论一致.5结论a.基于H ertz理论,圆柱与平面之间产生摩349第4期冯剑军,等:基于H ertz理论圆柱和平面之间的滑动接触分析擦滑动接触时平面内应力分量可以采用公式(9~11)表达.b.当圆柱与平面之间产生摩擦滑动接触时,在接触表面上存在最大拉应力和最大压力;最大拉应力出现在接触表面拖动边的边缘,而最大压应力发生在导向边.因此,如果接触体的失效是由于拉应力(或者压应力)导致的,这种失效首先可能会出现在接触表面;第一型裂纹的产生及扩展首先会发生在拖动边的边缘.c.当圆柱与平面之间产生摩擦滑动接触时,剪应力,主剪应力及Von-M ises等效应力(当摩擦系数较小时)的最大值均会出现在接触体内,并且均存在于导向边.因此,塑性滑移开始首先会发生在接触体内,然后才扩展到接触表面.参考文献:[1]Johnson K L.Con t acts Mechan ics[M].London:Camb ri dgeUn i versit y Press,1985.徐秉业,罗学富,刘信声,等译.接触力学[M<.北京:高等教育出版社,1992.[2]M i nd li n R D.Co m p li ance of elastic bodies i n con t act[J].Journ al ofApp lied M echan ics.1949,71(16):259-268. [3]M aouche N,M aitoum a m M H,Van K D.On a new m et hod ofeval uati on of the i nel astic stat e due to m ovi ng con tacts[J].W ear,1997,203-204(3):139-147.[4]Q i u aH,H ills a D A,Nowell a D,et a l.Ske w sli d i ng of anel astic cyli nder:An i nvesti gation of convecti on i n contact[J].Internati onal Journal of M echan ical Sci en ces,2008,50(2):293-298.[5]K ogu tL,E tsion I.A static fricti on model for el astic-p l asticcon t acti ng rough s urfaces[J].J ou rnal ofT ri bology,2004,126(1):35-40.[6]K ogu tL,Ets i on I.E lasti c-plas tic con tact anal ys i s of a sphereand a ri g i d fl at[J].Journal of A pp lied M echan ics,2002,69(9):657-662.[7]K ogu tL,E tsi on I.A se m i-anal yti cal s o l uti on for t h e slidingi n cep ti on of a s pheri cal con t act[J].J ou rnal ofTribol ogy,2003,125(6):499-506.[8]Chang W R,E tsion I,Bogy D B.Static fri cti on coeffi cientm odel for m et alli c rough s urfaces[J].Jou r n al of Tri bology,1988,110(1):57-63.[9]E tsi on I,Lev i nson O,H alper i n G,V arenberg M.Experi m en tali nvesti gati on of the elas tic-p lasti c con tact area and staticfri cti on of a s phere on fl at[J].J ou rnal ofT ri bology,2005,127(1):47-50.[10]V ij aywarg i ya R,Green I,A fi n ite el e m en t st udy of thedefor m ati on s,forces,s tress for m ati ons,and en ergy l oss es i nsli d i ng cyli nd ri cal con tacts[J].I n ternati onal J ou rnal of Non-L i nearM ec h an i cs,2007,42(7):914-927.[11]Zhupan s ka O I,U litko A F.Con tact w it h fri cti on of a rigi dcyli nder wit h an el asti c h alf-s pace[J].Journ al of theM echan ics and Phys i cs of Soli ds.2005,53(5):975-999.Ana l ysis of the Sli pp ing Contact Bet ween a Cyli nder anda P l ane on the Base of H ertz TheoryFENG Ji a n-j u n,T AN Yuan-qiang(School o f M echa nica l Eng i neering,Xiang t a n Universit y,Xiang t a n411105,China)Abstr act:The expressions of the stress co mponent i n the p lane(con tacti n g body)are derived as the f ricti o nally sli p p i n g contact arises bet w een a plane and a cyli n der on the basis ofH ertz theory.D istri b uti o ns of the stress i n the plane are analyzed in detai,l and the ir characteristics are presented.There exist the maxi m al tensile stress and the maxi m al co mpressive stress i n the contacting surface.The maxi m al tensile stress occurs a t the edge of the dragging si d e,and the maxi m a l co mpressive stress takes p lace at the area of t h e lead i n g si d e.There f ore,if the f a il u re i n the contact p lane is induced by the tensile or co mpressive stress,it occurs firstly i n the contacting surface;t h e first crack generati o n and propagati o n firstly take p lace at the edge of the draggi n g si d e.The maxi m ums of the shear stress,the pri n c i p al shear stress and the Von-M ises equivalent stress(when the f rictional coefficient is s m all)all occur i n si d e t h e contacting body,and they a ll exist i n the lead i n g si d e.Theref ore,The plastic slipp i n g inception firstl y takes p lace i n side the contact p lane,and then extends to the contacti n g surface.Those concl u si o ns provide a base f o r the study of the engi n eering application.K ey w ord s:f rictionally slipping contac,t equ iva lent stress,pr i n ci p al stress,contact pressure,shear tracti o nAu thor:TA N Yuan-qiang,male,bor n i n1966,Ph.D.,Pr of essor,e-m ai:l Tanyq@350摩擦学学报第29卷。
圆柱壳开孔补强的接触应力分析魏化中1,2,黄柯2,舒安庆1,2【摘要】摘要:在压力容器开孔补强的薄壳理论分析中,通常假设在补强圈与容器壳体之间没有接触,接触应力对于结构应力分布的意义和影响尚不清楚。
应用ANSYS软件对内压作用下补强圈与壳体间接触行为进行有限元分析。
考察了接触变形和接触压力,探讨了补强圈与壳体间隙变化、刚度因子以及不同直径的接管对接触行为的影响。
相对于开孔补强的薄壳理论,文中更好地预测了补强圈与容器壳体间的应力场分布,得到了一些有参考价值的结论。
【期刊名称】管道技术与设备【年(卷),期】2009(000)006【总页数】3【关键词】开孔补强;有限元;接触;间隙0 引言圆柱壳开孔补强广泛应用于石油化工、电力等各个领域。
开孔后,由于容器壁被削弱且结构的连续性遭到破坏,在壳体和接管的连接处产生很高的局部应力,该区域最薄弱,最易发生失效。
因此,采用有效的补强措施来降低接管区的应力集中,从而提高整个容器的承载能力就具有重要的工程应用价值。
多年来,在压力容器的应力分析中,一直沿用经典的薄壳理论对开孔补强结构进行分析设计。
但这样的求解过程无法预测焊接区的应力以及补强圈与壳体间接触行为[1]。
有限元技术的发展,解决了上述问题。
应用ANSYS软件对补强圈与容器壳体间的接触行为进行模拟并分析接触压力的变化规律,从而为工程优化提供依据。
1 有限元模型的建立1.1 模型结构及尺寸补强圈按工程上常用的尺寸,即外径近似为接管直径的两倍。
有限元计算模型规格如下:筒体内径500 mm;接管长度150 mm;筒体长度350 mm;接管壁厚6 mm;筒体壁厚6 mm;补强圈外径250 mm;接管内径125 mm;内压5 MPa.1.2 有限元模型由于只考虑内压作用下的应力状况,因此有限元模型可利用结构的对称性取开孔接管区的1/4建模。
采用三维实体建模,采用8节点的SOLID45单元来模拟实体结构,用面-面三维接触单元TARGET170和CONTACT173来模拟其接触行为[2]。
传递动力的高副机构,如摩擦轮、凸轮齿轮、链轮传动、滚动轴承、滚动螺旋等,都有接触强度问题,自然也涉及到接触应力。
在此对接触应力计算作较为全面的讨论。
两曲面的弹性体在压力作用下,相互接触时,都会产生接触应力,传递动力的高副机构在工作中往往出现的就是交变应力,受交变接触应力的机器零件在一定的条件下会出现疲劳点蚀的现象,点蚀扩散到一定程度,零件就不能再用了,也就就是说失效了,这样失效的形式称之为疲劳点蚀破坏,在ISO 标准中就是以赫兹应力公式为基础的。
本文较为集中地讨论了几种常见曲面的赫兹应力公式及常用机械零件的接触应力计算方法,便于此类零件的设计及强度验算。
1 任意两曲面体的接触应力1、1 坐标系图1所示为一曲面体的一部分,它在E 点与另外一曲面体相接触,E 点称为初始接触点。
取曲面在E 点的法线为z 轴,包括z 轴可以有无限多个剖切平面,每个剖切平面与曲面相交,其交线为一条平面曲线,每条平面曲线在E 点有一个曲率半径。
不同的剖切平面上的平面曲线在E 点的曲率半径一般就是不相等的。
这些曲率半径中,有一个最大与最小的曲率半径,称之为主曲率半径,分别用R′与R 表示,这两个曲率半径所在的方向,数学上可以证明就是相互垂直的。
平面曲线AEB 所在的平面为yz 平面,由此得出坐标轴x 与y 的位置。
任何相接触的曲面都可以用这种方法来确定坐标系。
由于z 轴就是法线方向,所以两曲面在E 点接触时,z 轴就是相互重合的,而x 1与x 2之间、y 1与y 2之间的夹角用Φ表示(图2所示)。
图1 曲面体的坐标图2 坐标关系及接触椭圆1、2 接触应力两曲面接触并压紧,压力P沿z轴作用,在初始接触点的附近,材料发生局部的变形,靠接触点形成一个小的椭圆形平面,椭圆的长半轴a在x轴上,短半轴b在y轴上。
椭圆形接触面上各点的单位压力大小与材料的变形量有关,z轴上的变形量大,沿z轴将产生最大单位压力P0。
其余各点的单位压力P就是按椭圆球规律分布的。