内外压容器计算2008版昆明版资料
- 格式:doc
- 大小:889.00 KB
- 文档页数:18


外压容器的设计计算外压容器是一种用于储存或输送气体、液体或粉状物料的设备,设计计算是确保容器在正常工作条件下能够承受外部压力的重要环节。
下面将从容器的负荷计算、材料选择和结构强度校核等方面进行详细介绍。
首先,容器的负荷计算是设计计算的关键步骤之一、负荷可分为静止负荷和动载荷两部分。
静止负荷包括容器本身的重量、储存物的重量以及设备上附件的负荷;动载荷包括地震力、风荷载等。
针对每个负荷的特点,需要采用相应的计算方法进行计算。
静止负荷的计算可以使用强度、稳定性和刚度等方面的计算方法,而动载荷则可以使用动力学和模态分析方法。
接下来,材料选择是外压容器设计中的另一个重要考虑因素。
一般而言,常用的材料包括钢材、不锈钢和复合材料等。
在材料选择中,需要考虑材料的强度、刚度、耐腐蚀性、可焊性、可加工性等因素。
根据容器的具体工作条件和介质特性,可以选择合适的材料。
然后,容器的结构强度校核是设计计算中最关键的一步。
容器的结构强度主要包括轴向强度、环向强度和承压壳体强度三个方面。
轴向强度是指容器在轴向受力状态下的承载能力,一般计算采用拉伸强度和挤压强度的计算方法。
环向强度是指容器在环向受力状态下的承载能力,计算时采用圈接强度和薄壁圆筒强度的计算方法。
承压壳体强度是指容器在由于外压而受到的承载能力,计算时采用塑性分析和有限元分析方法。
此外,容器的设计还需要满足相应的安全要求。
例如,容器需要满足静态不破坏条件和动态不破坏条件,防止容器发生破裂,对人身和财产造成伤害。
同时,容器还需要满足泄漏要求,确保储存物料的安全。
容器的设计还需要满足相关的法律法规和标准要求,如ASME(美国机械工程师学会)标准。
综上所述,外压容器的设计计算是确保容器在正常工作条件下能够承受外部压力的关键环节。
其中包括负荷计算、材料选择和结构强度校核等方面。
通过科学合理的设计计算,可以保证容器的安全性和可靠性,提高容器的使用寿命,为工业制造提供可靠的储存和输送设备。


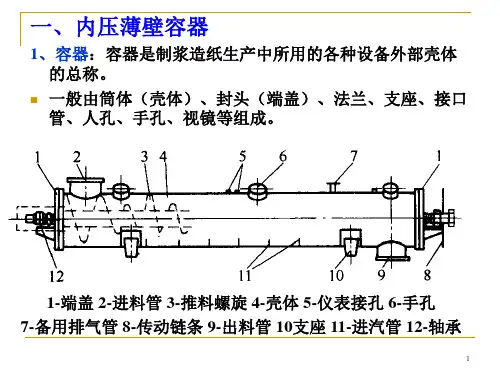

第七章 外压容器设计第一节 外压容器设计【学习目标】 掌握外压容器稳定性概念,了解加强圈设置规定;掌握外压圆筒、封头、加强圈的设计计算;掌握外压容器压力试验规定。
一、外压容器的稳定性容器在正常操作时,凡壳体外部压力高于内部者,均称为外压容器,这类容器有两种:真空容器;两个压力腔的夹套容器。
但是对于薄壁容器,承受外压作用时,往往在强度条件能够满足、应力远低于材料屈服强度的情况下,容器有可能因为不能保持自己原有的形状而出现扁塌,这种现象称为结构丧失了稳定性,即失稳。
失稳是由于外压容器刚度不足而引起的,因此,保证容器有足够的稳定性(刚度)是外压容器能够正常工作的必要条件,也是外压容器设计中首先应该考虑的问题。
按圆筒的破坏情况,外压圆筒可分为长圆筒、短圆筒和刚性圆筒三类。
长圆筒刚性最差,最易失稳,失稳时呈现两个波形。
短圆筒刚性较好,失稳时呈现两个以上的波形。
刚性圆筒具有足够的稳定性,破坏时属于强度失效。
1、临界压力外压容器由原平衡状态失去稳定性而出现扁塌时对应的压力称之为临界压力(p cr )。
影响临界压力的因素有:① 圆筒的几何尺寸δ/D (壁厚与直径的比值)、L /D (长度与直径的比值)是影响外压圆筒刚度的两个重要参数。
δ/D 的值越大,圆筒刚度越大,临界压力p cr 值也越大;L /D 的值越大,圆筒刚度越小,临界压力p cr 也越小。
② 材料的性能材料的弹性模量E 值和泊松比μ值对临界压力有直接影响,但是这两个值主要由材料的合金成分来决定,对已有材料而言无法改变,因此讨论弹性模量E 值和泊松比μ值的影响意义不大。
③ 圆筒的不圆度圆筒的不圆度会影响圆筒抵抗变形的能力,降低临界压力p cr ,因此在圆筒制造过程中要控制不圆度。
2、许用外压力与内压容器强度设计要取安全系数类似,外压容器刚度设计也要设定稳定系数,我国标准规定外压容器稳定系数m=3,故许用外压力[]3cr p p ≤。
二、外压圆筒的计算长度外压圆筒的计算长度对许用外压值影响很大。

第七章 外压容器设计第一节 外压容器设计【学习目标】 掌握外压容器稳定性概念,了解加强圈设置规定;掌握外压圆筒、封头、加强圈的设计计算;掌握外压容器压力试验规定。
一、外压容器的稳定性容器在正常操作时,凡壳体外部压力高于内部者,均称为外压容器,这类容器有两种:真空容器;两个压力腔的夹套容器。
但是对于薄壁容器,承受外压作用时,往往在强度条件能够满足、应力远低于材料屈服强度的情况下,容器有可能因为不能保持自己原有的形状而出现扁塌,这种现象称为结构丧失了稳定性,即失稳。
失稳是由于外压容器刚度不足而引起的,因此,保证容器有足够的稳定性(刚度)是外压容器能够正常工作的必要条件,也是外压容器设计中首先应该考虑的问题。
按圆筒的破坏情况,外压圆筒可分为长圆筒、短圆筒和刚性圆筒三类。
长圆筒刚性最差,最易失稳,失稳时呈现两个波形。
短圆筒刚性较好,失稳时呈现两个以上的波形。
刚性圆筒具有足够的稳定性,破坏时属于强度失效。
1、临界压力外压容器由原平衡状态失去稳定性而出现扁塌时对应的压力称之为临界压力(p cr )。
影响临界压力的因素有:① 圆筒的几何尺寸δ/D (壁厚与直径的比值)、L /D (长度与直径的比值)是影响外压圆筒刚度的两个重要参数。
δ/D 的值越大,圆筒刚度越大,临界压力p cr 值也越大;L /D 的值越大,圆筒刚度越小,临界压力p cr 也越小。
② 材料的性能材料的弹性模量E 值和泊松比μ值对临界压力有直接影响,但是这两个值主要由材料的合金成分来决定,对已有材料而言无法改变,因此讨论弹性模量E 值和泊松比μ值的影响意义不大。
③ 圆筒的不圆度圆筒的不圆度会影响圆筒抵抗变形的能力,降低临界压力p cr ,因此在圆筒制造过程中要控制不圆度。
2、许用外压力与内压容器强度设计要取安全系数类似,外压容器刚度设计也要设定稳定系数,我国标准规定外压容器稳定系数m=3,故许用外压力[]3cr p p ≤。
二、外压圆筒的计算长度外压圆筒的计算长度对许用外压值影响很大。


外压容器的设计计算外压容器是一种常见的工业设备,广泛应用于石化、化工、制药、食品等领域。
外压容器的设计计算非常重要,涉及到容器的强度、安全性、可靠性等方面。
本文将从容器设计的基本原则、压力壳体的计算、配件的设计等方面进行详细阐述。
1.容器设计的基本原则1.1强度原则:容器必须经受住内外压力和外力的作用,保证容器不发生破裂或塑性变形。
1.2稳定原则:容器的结构必须具有足够的稳定性,能够抵抗倾覆、翻滚和滑动等不稳定力矩的作用。
1.3安全原则:容器在正常操作条件下,不得发生渗漏、爆炸等危险情况,以保证人员和设备的安全。
2.压力壳体的计算压力壳体是外压容器的主要承载结构,其计算涉及到壳体的应力、应变等参数。
2.1壳体厚度计算:压力壳体的厚度应满足材料强度和设计容器的内外压力的要求,一般采用均匀厚度计算,即在整个壳体上采用相同的厚度。
2.2应力计算:根据材料的弹性模量和壳体的几何形状,可以计算出壳体在压力作用下的轴向应力和周向应力。
2.3应变计算:根据壳体的轴向应力和周向应力,可以计算出壳体的轴向应变和周向应变,以评估壳体的变形和塑性变形情况。
3.配件的设计3.1头板设计:头板的设计一般可根据受力分析,选择合适的头板形式和厚度。
常见的头板形式有平头、半球头、扁头等,其选择应根据容器的使用条件和结构要求进行合理设计。
3.2法兰设计:法兰是连接容器和管道的关键部件,其设计应满足安装、密封和维修等要求。
法兰的种类和规格应根据容器的使用要求和管道系统的设计标准进行选择。
3.3补强环设计:补强环用于增强容器的稳定性和强度,可以有效抵抗容器的扭转、屈曲和翻滚等不稳定力矩的作用。
补强环的形式和数量应根据容器的几何形状和受力情况进行优化设计。
4.其他注意事项4.1材料选择:容器的材料选择应根据容器的使用环境和要求进行合理选择,考虑到材料的强度、耐腐蚀性和可焊性等因素。
4.2焊接技术:容器的焊接工艺应满足材料的性能要求和容器的设计要求,确保焊缝的质量和可靠性。
内压薄壁容器应力测定实验实验指导书北京化工大学机电学院过程装备与控制工程系实验一、内压薄壁容器应力测定实验一、实验目的1.掌握电阻应变测量原理;2.学习电阻应变仪的使用方法,学习电阻应变片的贴片和接线技术; 3.了解封头在内压作用下的应力分布规律。
二、实验原理 1. 应力计算:薄壁压力容器主要由封头和圆筒体两个部分组成,由于各部分曲率不同,在它们的连接处曲率发生突变。
受压后,在连接处会生产边缘力系——边缘力矩和边缘剪力。
使得折边区及其两侧一定距离内的圆筒体和封头中的应力分布比较复杂,某些位置会出现较高的局部应力。
利用电阻应变测量方法可对封头和与封头相连接的部分圆筒体的应力分布进行测量。
应力测定中用电阻应变仪来测定封头各点的应变值,根据广义虎克定律换算成相应的应力值。
由于封头受力后是处于二向应力状态,在弹性范围内用广义虎克定律表示如下:经向应力:()21211μεεμσ+-=E(1-1)环向应力:()12221μεεμσ+-=E(1-2) 式中:E —材料的弹性模量μ—材料的波桑比 ε1—经向应变 ε2—环向应变。
椭圆封头上各点的应力理论计算公式如下:经向应力:()[]bb a x a s p r 2122242--=σ (1-3)环向应力:()[]()⎥⎦⎤⎢⎣⎡-----=2224421222422b a x a a bba x a s p θσ (1-4)2.电阻应变仪的基本原理:电阻应变仪将应变片电阻的微小变化,用电桥转换成电压电流的变化。
其过程为:()→∆∆→→放大器或电桥应变片I V RdR ε将()指示或纪录检流计或纪录仪放大或→∆∆I V将电阻应变片用胶水粘贴在封头外壁面上,应变片将随封头的拉伸或压缩一起变形,应变片的变形会引起应变片电阻值的变化,二者之间存在如下关系:ε⋅=∆=∆K LlK R R (1-5) 式中:ΔR/R —电阻应变片的电阻变化率ΔL/L —电阻应变片的变形率 K —电阻应变片的灵敏系数; ε—封头的应变。
内外压容器——受压元件设计一、压力容器的构成 圆筒—圆柱壳球形封头 —球壳壳体 椭圆封头(椭球壳) 以薄膜应力承载 碟封(球冠与环壳) 锥形封头(锥壳) 经典板壳结构圆平板(平盖)平板 环形板(开孔平盖) 以弯曲应力承载环(法兰环)弹性基础圆平板(管板)二、压力容器受压元件计算 1.圆筒1)应力状况:两相薄膜应力、环向应力为轴向应力的两倍。
2)壁厚计算公式:ci c ][2p D p t-=ϕσδ符号说明见GB 150。
称中径公式:适用范围,K ≤1.5,等价于p c ≤0.4[σ]f ϕ3)公式来由:内压圆筒壁厚计算公式是从圆筒与内压的静力平衡条件得出的。
设有内压圆筒如图所示(两端设封头)。
(1)圆筒受压力p c 的轴向作用: p c 在圆筒轴向产生的总轴向力:F 1=c 2i 4p D π圆筒横截面的面积:f i =πD i δ由此产生的圆筒轴向应力:σh =δδππ44i c i c2i D p D p D = 当控制σh ≤[σ]t ϕ时,则:δ1=ϕσt D p ][4i c此即按圆筒轴向应力计算的壁厚公式。
(2)圆筒受压力p c 的径向作用(见图)p c 对圆筒径向作用,在半个圆筒投影面上产生的合力(沿图中水平方向): F 2=p c ·D i ·l承受此水平合力的圆筒纵截面面积: f 2=2δl由此产生的圆筒环向应力:σθ=δδ22ic i c D p l l D p ⋅=⋅⋅ 当控制σθ≤[σ]t ϕ时,δ2=ϕσtD p ][2i c ⋅此式称为内压圆筒的内径公式。
上述计算公式认为应力是沿圆筒壁厚均匀分布的,它们对薄壁容器是适合的。
但对于具较厚壁厚的圆筒,其环向应力并不是均匀分布的。
薄壁内径公式与实际应力存在较大误差。
对厚壁圆筒中的应力情况以由弹性力学为基础推导得出的拉美公式较好地反映了其分布:由拉美公式如:厚壁筒中存在的三个方面的应力,其中只有轴向应力是沿厚度均匀布的。
内外压容器——受压元件设计一、压力容器的构成 圆筒—圆柱壳球形封头 —球壳壳体 椭圆封头(椭球壳) 以薄膜应力承载 碟封(球冠与环壳) 锥形封头(锥壳) 经典板壳结构圆平板(平盖)平板 环形板(开孔平盖) 以弯曲应力承载环(法兰环)弹性基础圆平板(管板)二、压力容器受压元件计算 1.圆筒1)应力状况:两相薄膜应力、环向应力为轴向应力的两倍。
2)壁厚计算公式:ci c ][2p D p t-=ϕσδ符号说明见GB 150。
称中径公式:适用范围,K ≤1.5,等价于p c ≤0.4[σ]f ϕ3)公式来由:内压圆筒壁厚计算公式是从圆筒与内压的静力平衡条件得出的。
设有内压圆筒如图所示(两端设封头)。
(1)圆筒受压力p c 的轴向作用: p c 在圆筒轴向产生的总轴向力:F 1=c 2i 4p D π圆筒横截面的面积:f i =πD i δ由此产生的圆筒轴向应力:σh =δδππ44i c i c2i D p D p D = 当控制σh ≤[σ]t ϕ时,则:δ1=ϕσt D p ][4i c此即按圆筒轴向应力计算的壁厚公式。
(2)圆筒受压力p c 的径向作用(见图)p c 对圆筒径向作用,在半个圆筒投影面上产生的合力(沿图中水平方向): F 2=p c ·D i ·l承受此水平合力的圆筒纵截面面积: f 2=2δl由此产生的圆筒环向应力:σθ=δδ22ic i c D p l l D p ⋅=⋅⋅ 当控制σθ≤[σ]t ϕ时,δ2=ϕσtD p ][2i c ⋅此式称为内压圆筒的内径公式。
上述计算公式认为应力是沿圆筒壁厚均匀分布的,它们对薄壁容器是适合的。
但对于具较厚壁厚的圆筒,其环向应力并不是均匀分布的。
薄壁内径公式与实际应力存在较大误差。
对厚壁圆筒中的应力情况以由弹性力学为基础推导得出的拉美公式较好地反映了其分布:由拉美公式如:厚壁筒中存在的三个方面的应力,其中只有轴向应力是沿厚度均匀布的。
内外压容器——受压元件设计中国石化工程建设公司桑如苞向全国压力容器设计同行问好!内外压容器——受压元件设计压力容器都离不开一个为建立压力所必须的承压外壳—压力壳。
内外压容器设计即是指对组成压力壳的各种元件在压力作用下的设计计算。
压力壳必须以一定方式来支承:当采用鞍式支座支承时成为卧式容器的形式,由于自重、物料等重力作用,在压力壳上(特别是支座部位)产生应力,其受力相当于一个两端外伸的简支梁,对其计算即为卧式容器标准的内容。
当采用立式支承时成为立(塔)式容器的形式,由于自重、物料重力、风载、地震等作用,在压力壳上产生应力,其受力相当于一个直立的悬臂梁,对其计算即为塔式容器标准的内容。
当压力壳做成球形以支腿支承时,即成为球罐,在自重、物料重力、风载、地震等作用下的计算即为球形储罐标准的内容。
一、压力容器的构成圆筒—圆柱壳压力作用下,以薄膜应力承载,为此整体上产生球形封头—球壳一次薄膜应力,控制值1倍许用应力。
但在相邻元件连壳体椭圆封头(椭球壳)接部位,会因变形协调产生局部薄膜应力和弯曲应力,碟封(球冠与环壳)称二次应力,控制值3倍许用应力。
典型板壳锥形封头(锥壳)结构圆平板(平盖)压力作用下,以弯曲应力承载,为此整体上产生一次弯环形板(开孔平盖)曲应力,控制值1.5倍平板许用应力。
环(法兰环)弹性基础圆平板(管板)二、压力容器受压元件计算1.圆筒1)应力状况:两相薄膜应力、环向应力为轴向应力的两倍。
2)壁厚计算公式:ci c ][2p D p t -=ϕσδ符号说明见GB 150。
称中径公式:适用范围,K ≤1.5,等价于p c ≤0.4[σ]tϕ3)公式来由:内压圆筒壁厚计算公式是从圆筒与内压的静力平衡条件得出的。
设有内压圆筒如图所示(两端设封头)。
(1)圆筒受压力p c 的轴向作用:p c 在圆筒轴向产生的总轴向力: F 1= c 2i 4p D π圆筒横截面的面积:f i =πD i δ由此产生的圆筒轴向应力:σh = δδππ44i c i c2i D p D p D =当控制σh ≤[σ]t ϕ时,则: δ1= ϕσt D p ][4ic此即按圆筒轴向应力计算的壁厚公式。
(2)圆筒受压力p c 的径向作用(见图)p c 对圆筒径向作用,在半个圆筒投影面上产生的合力(沿图中水平方向):F 2=p c ·D i ·l承受此水平合力的圆筒纵截面面积:f 2=2δl由此产生的圆筒环向应力: σθ= δδ22i c i c D p l l D p ⋅=⋅⋅当控制σθ≤[σ]t ϕ时,δ2= ϕσt D p ][2i c ⋅此式称为内压圆筒的内径公式。
上述计算公式认为应力是沿圆筒壁厚均匀分布的,它们对薄壁容器是适合的。
但对于具较厚壁厚的圆筒,其环向应力并不是均匀分布的。
薄壁内径公式与实际应力存在较大误差。
对厚壁圆筒中的应力情况以由弹性力学为基础推导得出的拉美公式较好地反映了其分布:由拉美公式:厚壁筒中存在的三个方面的应力,其中只有轴向应力是沿厚度均匀布的。
环向应力和径向应力均是非均匀分布的,且内壁处为最大值。
筒壁三向应力中,以周向应力最大,内壁处达最大值,外壁处为最小值,内外壁处的应力差值随K=D o /D i 增大而增大。
当K=1.5时,由薄壁公式按均匀分布假设计算的环向应力值比按拉美公式计算的圆筒内壁处的最大环向应力要偏低23%,存在较大的计算误差。
由于薄壁公式形式简单,计算方便、适于工程应用。
为了解决厚壁筒时薄壁公式引起的较大误差,由此采取增大计算内径,以适应增大应力计算值的要求。
为此将圆筒计算内径改为中径,即以(D i +δ)代替D i 代入薄壁内径公式中:则有:σθ= δδδδ22)(i c c c i p D p D p +=+经变形得:2σθδ-p c δ=p c D iδ(2σθ-p c )=p c ·D i当σθ控制在[σ]t ,且考虑接头系数ϕ时,即σθ取[σ]t ϕ时,则δ= cic ][2p D p t -ϕσ 此即GB 150中的内压圆筒公式,称中径公式。
当K=1.5时,按此式计算的应力与拉美公式计算的最大环向应力仅偏小3.8%。
完全满足工程设计要求。
4)公式计算应力的意义:一次总体环向薄膜应力,控制值[σ]。
5)焊接接头系数,ϕ—指纵缝接头系数。
6)二次应力:当圆筒与半球形封头、椭圆形封头连接时二次应力很小,能自动满足3[σ]的强度条件,故可不予考虑。
2.球壳1)应力状况,各向薄膜应力相等2)厚度计算式:δ=ci c ][4p D p t -ϕσ称中径公式,适用范围p c ≤0.6[σ]t ϕ等价于K ≤1.3533)公式来由同圆筒轴向应力作用情况4)计算应力的意义:一次总体、薄膜应力(环向、经向)控制值:[σ]t 。
5)焊缝接头系数:指所有拼缝接头系数(纵缝、环缝)。
注意包括球封与圆筒的连接环缝系数。
6)与圆筒的连接结构:见GB 150附录J图J1(d)、(e)、(f)。
原则:不能削薄圆筒,局部加厚球壳。
7)二次应力:当半球形封头与圆筒连接时二次应力很小,能自动满足3[σ]的强度条件,故可不予考虑。
3.椭圆封头A、内压作用下1)应力状况a.薄膜应力a)标准椭圆封头薄膜应力分布:经向应力:最大拉应力在顶点。
环向应力:最大拉应力在顶点,最大压应力在底边。
b) 变形特征:趋圆。
c) 计算对象意义:拉应力——强度计算压应力——稳定控制b.弯曲应力(与圆筒连接)a) 变形协调,形成边界力。
b) 产生二次应力c.椭圆封头的应力:薄膜应力加弯曲应力。
最大应力的发生部位、方向、组成。
d.形状系数K的意义K为封头上的最大应力与对接圆筒中的环向薄膜应力的比值,K=K分布曲线可回归成公式:K=1/6[(a/b)2+2]=1/6[2+( )2] 不同a/b的K见GB 150表7-1。
标准椭圆封头K=1。
2)计算公式δ=cic5.0][2pDKpt-ϕσ近似可理解为圆筒厚度的K倍。
3)焊缝接头系数。
环σσm axii2hD指拼缝,但不包括椭封与圆筒的连接环缝的接头系数。
4)内压稳定:a. a/b≯2.6限制条件b.防止失稳,限制封头最小有效厚度:a/b即K≤1 δmin≥0.15%D ia/b即K>1 δmin≥0.30% D iB.外压作用下:1)封头稳定计算是以薄膜应力为对象的:a.变形特征:趋扁。
b.计算对象过渡区——不存在稳定问题。
封头中心部分——“球面区”有稳定问题。
c.计算意义,按外压球壳。
当量球壳:对标准椭圆封头;当量球壳计算外半径:R o=0.9D o。
D o——封头外径。
2)对对接圆筒的影响。
外压圆筒计算长度L的意义:L为两个始终保持圆形的截面之间的距离。
椭圆封头曲面深度的1/3处可视为能保持圆形的截面,为此由两个椭圆封头与圆筒相连接的容器,该圆筒的外压计算长度L=圆筒长度+两个椭圆封头的直边段长度+两倍椭圆封头曲面深度的1/3。
3)圆筒失稳特点,a.周向失稳(外压作用)圆形截面变成波形截面,波数n从2个波至多个波。
n=2称长圆筒,n>2称短圆筒。
b.轴向失稳(轴向力及弯矩作用)塔在风弯、地震弯矩和重力载荷作用下的失稳。
轴线由直线变成波折线。
c 外压圆筒计算系数A—外压圆筒临界失稳时的周向压缩应变,与材料无关,只与结构尺寸相关(查图6—2)。
B —外压圆筒许用的周向压缩应力的2倍,与材料弹性模量有关(查图6—3至图6—10)。
d 外压圆筒许用外压的计算D 0×L ×P=2δe ×B/2×LD 0×P =δe ×B[P]=δe ×B/D 0=B/(D 0/δe)———GB150中(6—1)式。
e 外压圆筒的计算外压圆筒既有稳定问题又有压缩强度问题,但对D 0/δe ≥20的圆筒通常只有稳定问题,为此仅需按稳定进行计算,GB150中(6—1)式、(6—2)式即是。
(6—2)式是指在弹性阶段时的计算式。
对D 0/δe <20的圆筒稳定问题和压缩强度问题并存,为此需按稳定和强度分别进行计算,GB150中(6—4)式中的前一项即是按稳定计算的许用外压力,而第二项即是按压缩强度计算的许用外压力。
对D 0/δe <4的圆筒,其外压失稳都为长圆筒形式,故失稳时的临界应变A 都直接按长圆筒计算,(6—3)式即是。
4.碟形封头受力、变形特征,应力分布,稳定,控制条件与椭封相似,只不过形状系数由K (椭封)改为M 。
内容从略5.锥形封头1) 薄膜应力状态,a.计算模型:当量圆筒。
应力状况与圆筒相似,同处的环向应力等于轴向应力的两倍,但不同直径处应力不同。
b.计算公式:δ= αϕσcos 1][2c cc ⋅-p D p tD c ——计算直径。
c.计算应力的意义:一次、总体(大端)环向薄膜应力,控制值[σ]t 。
d.焊缝接头系数ϕ。
ϕ 指锥壳纵缝的接头系数。
2)弯曲应力状态(发生于与圆筒连接部位)a.变形协调,产生边界力,可引起较大边缘应力,即二次应力,需考虑。
b.锥壳端部的应力。
端部应力由薄膜应力+边缘应力组成。
大端:最大应力为纵向(轴向)拉伸薄膜应力+轴向弯曲拉伸应力组成。
小端:起控制作用的应力为环向(局部)薄膜应力。
c.大、小端厚度的确定。
a) 大端:当轴向总应力超过3[σ]t 时,(由查图7-11确定),则需另行计算厚度,称大端加强段厚度。
计算公式:δr = cic ][2p D Qp t -ϕσ 其中:Q 称应力增值系数,其中体现了边缘应力的作用,并将许用应力控制值放宽至3[σ]t 。
b) 小端:当环向局部薄膜应力超过1.1[σ]t (由查图7-13确定)时,则需另行计算厚度,称小端加强段厚度。
计算公式:δr= c ic ][2p D Qp t -ϕσ 其中:Q 也称应力增值系数,其中体现边界力作用引起的局部环向薄膜应力,并将许用应力控制值调至1.1[σ]t 。
d.加强段长度a) 锥壳大端加强段长度L1:L1= 2αδcos5.0riD与之相接的圆筒也同时加厚至δr,称圆筒加强段其最小长度L= 2r i5.0δD锥壳大端加强段长度的意义是当量圆筒在均布边界力作用下,圆筒中轴向弯曲应力的衰减长度。
b) 锥壳小端加强段长度L1L1=αδcosri sD与之相接的圆筒也同时加厚至δr,称圆筒加强段,其最小长度L=riδsD。
锥壳小端加强段长度的意义是:当量圆筒在均布边界力作用下圆筒中局部环向薄膜应力的衰减长度。
c) 锥壳大小端加强段长度比较。
略去大端与小端直径的差异,大端轴向弯曲应力的衰减长度约为小端环向薄膜应力的衰减长度的2倍(1.414倍)。
e.焊缝接头系数ϕ大端指ϕ2小端指ϕ3、ϕ4、ϕ5之小者。
应注意,锥壳加强段厚度δr计算中的ϕ与锥壳厚度δ计算中的ϕ是不同的。