线面平行典型例题.

线面平行的证明题1．如图所示，两个全等的正方形ABCD和ABEF所在平面相交于AB，M∈AC，N∈FB且AM＝FN，求证：MN∥平面BCE.2．如图，在七面体ABCDMN中，四边形ABCD是边长为2的正方形，MD⊥平面ABCD，NB⊥平面ABCD，且MD＝2，NB＝1，MB与ND交于P点，点Q在AB上，且BQ＝23 .(1)求证：QP∥平面AMD；(2)求七面体ABCDMN的体积．3．如图所示，正方体ABCD-A1B1C1D1中，直线l是平面AB1D1与下底面ABCD所在平面的交线．求证：l∥平面A1BD.4．如图，三棱柱ABC-A1B1C1，底面为正三角形，侧棱A1A⊥底面ABC，点E、F分别是棱CC1、BB1上的点，点M是线段AC上的动点，EC＝2FB.当点M在何位置时，BM∥平面AEF?答案：1、证明 过M 作MG ∥BC ，交AB 于点G ，如图所示，连接NG . ∵MG ∥BC ，BC ⊂平面BCE ，MG ⊄平面BCE ，∴MG ∥平面BCE . 又BG GA ＝CM MA ＝BNNF，∴GN ∥AF ∥BE ，同样可证明GN ∥平面BCE . 又MG ∩NG ＝G ， ∴平面MNG ∥平面BCE .又MN ⊂平面MNG ，∴MN ∥平面BCE .2、解析 (1)证明：∵MD ⊥平面ABCD ，NB ⊥平面ABCD ， ∴MD ∥NB .∴BP PM ＝NB MD ＝12.又QBQA＝232－23＝12，∴QB QA ＝BP PM . ∴在△MAB 中，QP ∥AM . 又QP ⊄平面AMD ，AM ⊂平面AMD ， ∴QP ∥平面AMD .(2)连接BD ，AC 并交于点O ，则AC ⊥BD ， 又MD ⊥平面ABCD ， ∴MD ⊥AC ，又BD ∩MD ＝D . ∴AC ⊥平面MNBD .∴AO 为四棱锥A －MNBD 的高．又S 四边形MNBD ＝12×(1＋2)×22＝32，∴V A －MNBD ＝13×32×2＝2.又V C －MNBD ＝V A －MNBD ＝2， ∴V 七面体ABCDMN ＝2V A －MNBD ＝4.3、证明 ∵平面A 1B 1C 1D 1∥平面ABCD ，且平面A 1B 1C 1D 1∩平面AB 1D 1＝B 1D 1，平面ABCD ∩平面AB 1D 1＝l ，∴l ∥B 1D 1.又B 1D 1∥BD ， ∴l ∥BD .又l ⊄平面A 1BD ，BD ⊂平面A 1BD ， ∴l ∥平面A 1BD .4、解析 法一 如图，取AE 的中点O ，连接OF ，过点O 作OM ⊥AC 于点M . ∵侧棱A 1A ⊥底面ABC ， ∴侧面A 1ACC 1⊥底面ABC ，∴OM ⊥底面ABC .又∵EC ＝2FB ，∴OM ∥FB 綉12EC ，∴四边形OMBF 为矩形， ∴BM ∥OF ，又∵OF ⊂面AEF ，BM ⊄面AEF .故BM ∥平面AEF ，此时点M 为AC 的中点．法二 如图，取EC 的中点P ，AC 的中点Q ，连接PQ 、PB 、BQ ，∴PQ∥AE.∵EC＝2FB，∴PE綉BF，PB∥EF，∴PQ∥平面AEF，PB∥平面AEF.又PQ∩PB＝P，∴平面PBQ∥平面AEF，又∵BQ⊂面PQB，∴BQ∥平面AEF.故点Q即为所求的点M，此时点M为AC的中点．。

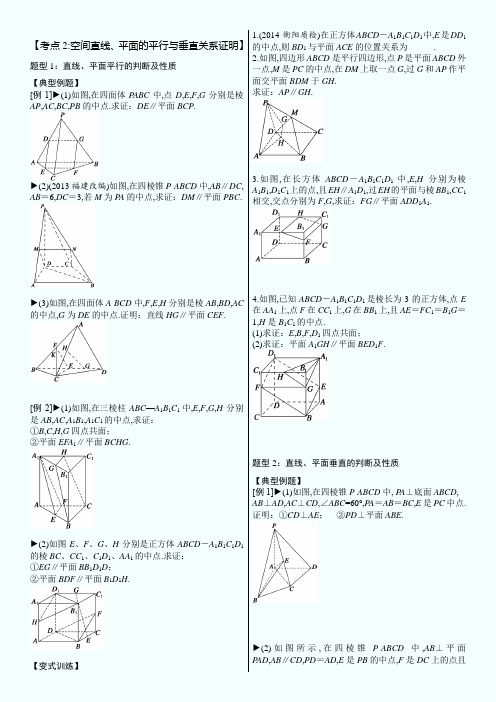
【考点2:空间直线、平面的平行与垂直关系证明】题型1：直线、平面平行的判断及性质【典型例题】[例1]►(1)如图,在四面体P ABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.求证：DE∥平面BCP .►(2)(2013福建改编)如图,在四棱锥P-ABCD中,AB∥DC, AB＝6,DC＝3,若M为P A的中点,求证：DM∥平面PBC . ►(3)如图,在四面体A-BCD中,F,E,H分别是棱AB,BD,AC 的中点,G为DE的中点.证明：直线HG∥平面CEF .[例2]►(1)如图,在三棱柱ABC—A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证：①B,C,H,G四点共面；②平面EF A1∥平面BCHG .►(2)如图E、F、G、H分别是正方体ABCD－A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证：①EG∥平面BB1D1D；②平面BDF∥平面B1D1H .【变式训练】1.(2014·衡阳质检)在正方体ABCD－A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.2.如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证：AP∥GH .3.如图,在长方体ABCD－A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证：FG∥平面ADD1A1.4.如图,已知ABCD－A1B1C1D1是棱长为3的正方体,点E 在AA1上,点F在CC1上,G在BB1上,且AE＝FC1＝B1G＝1,H是B1C1的中点.(1)求证：E,B,F,D1四点共面；(2)求证：平面A1GH∥平面BED1F .题型2：直线、平面垂直的判断及性质【典型例题】[例1]►(1)如图,在四棱锥P-ABCD中, P A⊥底面ABCD, AB⊥AD,AC⊥CD,∠ABC=60°,P A＝AB＝BC,E是PC中点. 证明：①CD⊥AE；②PD⊥平面ABE .►(2)如图所示,在四棱锥P-ABCD中,AB⊥平面P AD,AB∥CD,PD＝AD,E是PB的中点,F是DC上的点且DF＝12AB,PH为△P AD中AD边上的高.①证明：PH⊥平面ABCD；②证明：EF⊥平面P AB.[例2]►(1)[2014·辽宁文]如图所示,△ABC和△BCD所在平面互相垂直,且AB＝BC＝BD＝2,∠ABC＝∠DBC＝120°,E,F,G分别为AC,DC,AD的中点.(I)求证：EF⊥平面BCG；(II)求三棱锥D -BCG的体积.►(2)(2012·课标全国)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB＝90°,AC＝BC＝12AA1,D是棱AA1的中点.(I)证明：平面BDC1⊥平面BDC；(II)平面BDC1分此棱柱为两部分,求这两部分体积的比.►(3)(2015·大庆质检) 如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD＝DC＝BC＝1,AB＝2,AB∥DC,∠BCD＝90°.①求证：PC⊥BC；②求点A到平面PBC的距离.【变式训练】1.如图,四棱锥P—ABCD中,P A⊥底面ABCD,AB⊥AD,点E 在线段AD上,且CE∥AB. (1)求证：CE⊥平面P AD；(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD的体积.2.[2014·福建文]如图所示,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.(1)求证：CD⊥平面ABD；(2)若AB=BD=CD=1,M为AD中点,求三棱锥A -MBC的体积.3.(2015·唐山统考)如图,在三棱锥P-ABC中,P A＝PB＝AB ＝BC,∠PBC＝90°,D为AC的中点,AB⊥PD.(1)求证：平面P AB⊥平面ABC；(2)如果三棱锥P-BCD的体积为3,求P A.4.[2014·课标Ⅰ文]如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.(1)证明：B1C⊥AB；(2)若AC⊥AB1,∠CBB1＝60°,BC＝1,求三棱柱ABC-A1B1C1的高.☆题型3：直线、平面平行与垂直关系的综合【典型例题】[例1]►(1)已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题中真命题是(写出序号).①若l⊂α,m⊂α,l∥β,m∥β,则α∥β；②若l⊂α,l∥β,α∩β＝m,则l∥m；③若α∥β,l∥α,则l∥β；④若l⊥α,m∥l,α∥β,则m⊥β.►(2)(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α►(3)(2015·江西七校联考)已知直线a和平面α,β,α∩β＝l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面►(4)(2013·课标Ⅱ)已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l►(5)(2016·课标Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题：①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号) [例2]►(1)(2014·北京)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1＝AC＝2,BC＝1,E,F分别为A1C1,BC的中点.(I)求证：平面ABE⊥平面B1BCC1；(II)求证：C1F∥平面ABE；(III)求三棱锥E-ABC的体积.►(2)[2014江苏文]如图,三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知P A⊥AC,P A＝6,BC＝8,DF＝5. 求证：(I)直线P A∥平面DEF；(II)平面BDE⊥平面ABC.[例3]►(1)[2014·陕西文]四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(I)求四面体ABCD的体积；(II)证明：四边形EFGH是矩形.►(2)(2012·北京)如图1,在Rt△ABC中,∠C＝90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(I)求证：DE∥平面A1CB；(II)求证：A1F⊥BE；(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ？说明理由.【变式训练】1.(2016·浙江联考)已知a,b,c为三条不同的直线,α,β是空间两个平面,且a⊂α,b⊂β,α∩β＝c.给出下列命题：①若a与b是异面直线,则c至少与a,b中的一条相交；②若a不垂直于c,则a与b一定不垂直；③若a∥b,则必有a∥c；④若a⊥b,a⊥c,则必有α⊥β. 其中正确命题的个数是()A.0B.1C.2D.32.(2012·四川)下列命题正确的是()A.若两直线和同一平面所成的角相等,则这两条直线平行B.若一平面内有三点到另一平面的距离相等,则这两平面平行C.若一直线平行于两相交平面,则这条直线与这两平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行3.(2015·福建)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.(2016·山东济南一模)设m,n是两条不同的直线,α,β是两个不同的平面.()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α5.(2016·浙江温州联考)关于直线a,b,l及平面α,β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a ⊂α,b ⊂α,且l ⊥a ,l ⊥b ,则l ⊥αD.若a ⊥α,a ∥β,则α⊥β 6.(2015·山东二模)设m ,n 是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是( ) A.当n ⊥α时,“n ⊥β”是“α∥β”的充要条件B.当m ⊂α时,“m ⊥β”是“α⊥β”的充分不必要条件C.当m ⊂α时,“n ∥α”是“m ∥n ”的必要不充分条件D.当m ⊂α时,“n ⊥α”是“m ⊥n ”的充分不必要条件 7.(2016·浙江)已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m ∥α,n ⊥β,则( )A.m ∥lB.m ∥nC.n ⊥lD.m ⊥n 8.(2013北京)如图,四棱锥P -ABCD 中,AB ∥CD ,AB ⊥AD ,CD ＝2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD .E 和F 分别是CD 和PC 的中点.求证： (1)P A ⊥底面ABCD ； (2)BE ∥平面P AD ；(3)平面BEF ⊥平面PCD .9.[2014·山东文]如图,四棱锥P -ABCD 中,AP ⊥平面PCD , AD ∥BC ,AB ＝BC＝12AD ,E ,F 分别为线段AD ,PC 的中点. (1)求证：AP ∥平面BEF ； (2)求证：BE ⊥平面P AC .10.(2013全国Ⅱ文)如图,直三棱柱ABC －A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点.(Ⅰ)证明：BC 1∥平面A 1CD ；(Ⅱ)设AA 1=AC =CB =2,AB =22,求三棱锥C -A 1DE 的体积.11.(2013·辽宁)如图,AB 是圆O 的直径,P A 垂直圆O 所在的平面,C 是圆O 上的点. (1)求证：BC ⊥平面P AC ； (2)设Q 为P A 的中点,G 为△AOC 的重心,求证：QG ∥平面PBC .12.[2014·课标Ⅱ文]如图,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点. (1)证明：PB ∥平面AEC ；(2)设AP ＝1,AD ＝3,三棱锥P - ABD 的体积V ＝34,求A到平面PBC 的距离.13.(2015江苏)如图,在直三棱柱ABC -A 1B 1C 1中,已知AC ⊥BC ,BC ＝CC 1.设AB 1的中点为D ,B 1C ∩BC 1＝E . 求证：(1)DE ∥平面AA 1C 1C ； (2)BC 1⊥AB 1.14.(2015广东文)如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC ＝4,AB ＝6,BC ＝3. (1)证明：BC ∥平面PDA ； (2)证明：BC ⊥PD ；(3)求点C 到平面PDA 的距离.15.(2015课标Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1中,AB ＝16, BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形．(1)在图中画出这个正方形(不必说明画法和理由)； (2)求平面α把该长方体分成的两部分体积的比值．16.(2015陕西)如图,直角梯形ABCD 中,AD ∥B C,∠BAD =π2, AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点．将△ABE 沿BE 折起到如图2中△A 1BE 的位置,得到四棱锥A 1﹣BCDE ． (Ⅰ)证明：CD ⊥平面A 1OC ；(Ⅱ)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1﹣BCDE 的体积为362,求a 的值．17.(2016·课标Ⅱ文)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE ＝CF ,EF 交BD 于点H ,将△DEF 沿EF 折到△D ′EF 的位置． (1)证明：AC ⊥HD ′(2)若AB =5,AC =6,AE =54,OD ′=22,求五棱锥D ′­ABCFE 的体积．18.(2016·课标Ⅲ文)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB ＝AD ＝AC ＝3,P A ＝BC ＝4,M 为线段AD 上一点,AM ＝2MD ,N 为PC 的中点． (1)证明MN ∥平面P AB ；(2)求四面体N -BCM 的体积．19.[2017全国I 文]如图,在四棱锥P-ABCD 中,AB//CD ,且∠BAP ＝∠CDP ＝90°.(1)证明：平面PAB ⊥平面PAD ； (2)若PA =PD =AB =DC ,∠ADP ＝90°,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.20.[2017全国II 文]如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD , ∠BAD =∠ABC =90°.(1)证明：直线BC ∥平面PAD ;(2)若△PCD 面积为27,求四棱锥P-ABCD 的体积.21.[2017全国III 文]在正方体ABCD-A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A.A 1E ⊥DC 1B.A 1E ⊥BDC.A 1E ⊥BC 1D.A 1E ⊥AC22.[2017全国III 文]如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明：AC ⊥BD ；(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.。

线面平行和垂直专题练习：
1、如图，在四棱锥ABCD P -中，四边形ABCD 为正方形，P 点在平面ABCD 内的射影为A ，且AB PA =，E 为PD 中点．（1）证明：PB //平面AEC ；
2．如图所示，在棱长为a 的正方体1111ABC D A B C D -中，E ，F ，P ，Q 分别是B C ，
11C D ，1AD ，B D 的中点.
(1)求证：PQ //平面11D C C D (2)求证：EF //平面11BB D D 。

3. 如图所示，在正方体1111A B C D ABC D -中，,,,E F G H 分别是1111,,,BC C C C D A A 的中点。

求证：(1) B F ∥1HD ； (2) E G ∥平面11BB D D ； (3) 平面B D F ∥平面11B D H 。

4、如图，四面体ABCD 中，O 分别是BD
的中点，2,C A C B C D BD AB AD ======
求证：A O ⊥平面BCD ；
5、如图，已知斜三棱柱'''C B A ABC -的底面是直角三角形， 90=∠ACB ，'B 在底面上的射影D 落在BC 上，求证：⊥AC 面C C BB ''
6、如图，在四棱锥P —ABCD 中，底面ABCD 是矩形，侧棱P A 垂直于底面，E 、F 分别是AB 、PC 的中点，（1）求证 CD ⊥PD ；（2）求证 EF ∥平面PAD ；（3）当PDA ∠等于多
少度时，直线EF ⊥平面PCD ？
7、如图，已知正四棱柱1111D C B A ABCD -中，过点B 作B 1C 的垂线交侧棱CC 1于点E ，交B 1C 于点F ，求证：A 1C ⊥平面BDE ；。

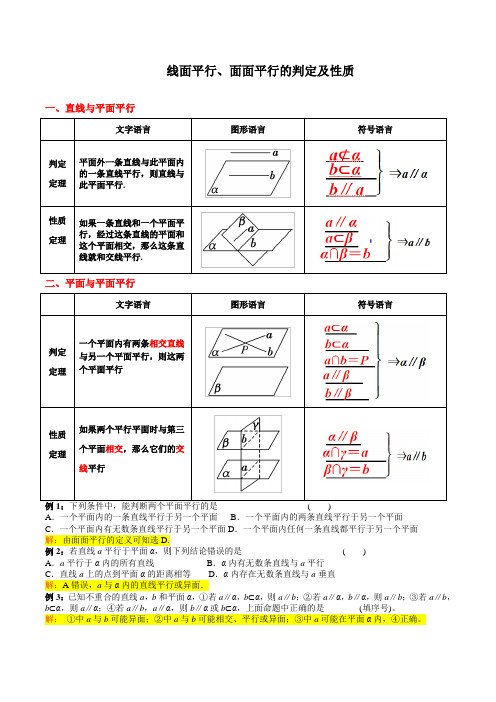
线面平行、面面平行的判定及性质一、直线与平面平行文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行，则直线与此平面平行.性质定理如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行.二、平面与平面平行文字语言图形语言符号语言判定定理一个平面内有两条相交直线与另一个平面平行，则这两个平面平行性质定理如果两个平行平面时与第三个平面相交，那么它们的交线平行A．一个平面内的一条直线平行于另一个平面B．一个平面内的两条直线平行于另一个平面C．一个平面内有无数条直线平行于另一个平面D．一个平面内任何一条直线都平行于另一个平面解：由面面平行的定义可知选D.例2：若直线a平行于平面α，则下列结论错误的是()A．a平行于α内的所有直线B．α内有无数条直线与a平行C．直线a上的点到平面α的距离相等D．α内存在无数条直线与a垂直解：A错误，a与α内的直线平行或异面．例3：已知不重合的直线a，b和平面α，①若a∥α，b⊂α，则a∥b；②若a∥α，b∥α，则a∥b；③若a∥b，b⊂α，则a∥α；④若a∥b，a∥α，则b∥α或b⊂α，上面命题中正确的是________(填序号)。

解：①中a与b可能异面；②中a与b可能相交、平行或异面；③中a可能在平面α内，④正确。

例4：已知α、β是平面，m 、n 是直线，给出下列命题：①若m ⊥α，m ⊂β，则α⊥β.②若m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β.③如果m ⊂α，n ⊄α，m 、n 是异面直线，那么n 与α相交．④若α∩β＝m ，n ∥m ，且n ⊄α，n ⊄β，则n ∥α且n ∥β其中正确命题的个数是 ( ) A ．1 B ．2 C ．3 D ．4解：对于①，由定理“如果一个平面经过另一个平面的一条垂线，那么这两个平面垂直”得知，①正确；对于②，注意到直线m ，n 可能是两条平行直线，此时平面α，β可能是相交平面，因此②不正确；对于③，满足条件的直线n 可能平行于平面α，因此③不正确；对于④，由定理“如果平面外一条直线平行于平面内一条直线，那么这条直线平行于这个平面”得知，④正确．综上所述，其中正确的命题是①④，选B.例5：已知m ，n 表示两条不同直线，α，β，γ表示不同平面，给出下列三个命题：(1)⎩⎪⎨⎪⎧ m ⊥αn ⊥α⇒m ∥n ；(2)⎩⎪⎨⎪⎧ m ⊥αm ⊥n ⇒n ∥α (3)⎩⎪⎨⎪⎧m ⊥αn ∥α⇒m ⊥n 其中真命题的个数为 ( ) A ．0 B ．1 C ．2 D ．3 解：若⎩⎪⎨⎪⎧ m ⊥α，n ⊥α，则m ∥n ，即命题(1)正确；若⎩⎪⎨⎪⎧ m ⊥α，m ⊥n ，则n ∥α或n ⊂α，即命题(2)不正确；若⎩⎪⎨⎪⎧m ⊥αn ∥α，则m ⊥n ，即命题(3)正确；综上可得，真命题共有2个．选C例6：已知m 、n 、l 1、l 2表示直线，α、β表示平面．若m ⊂α，n ⊂α，l 1⊂β，l 2⊂β，l 1∩l 2＝M ，则以下条件中，能推出α∥β的是 ( )A ．m ∥β且l 1∥αB ．m ∥β且n ∥βC ．m ∥β且n ∥l 2D ．m ∥l 1且n ∥l 2解：由定理“如果一个平面内有两条相交直线分别与另一个平面平行，那么这两个平面平行”可得，由选项D 可推知α∥β.例7：在下列条件中，可判断平面α与β平行的是（ ）.A. α、β都平行于直线lB. α内存在不共线的三点到β的距离相等C. l 、m 是α内两条直线，且l ∥β，m ∥βD. l 、m 是两条异面直线，且l ∥α，m ∥α，l ∥β，m ∥β 解：排除法，Ａ中α、β可以是相交平面；Ｂ中三点可面平面两侧；Ｃ中两直线可以不相交．故选Ｄ，也可直接证明．例8：经过平面外的两点作该平面的平行平面可以作（ ）.A. 0个B. 1个C. 0个或1个D. 1个或2个解：这两点可以是在平面同侧或两侧．选C 。

线面平行的证明方法题型归类
注意：证明线面平行的方法可分为三类：①直接法，②找中点（或作中点），③通过连接平行四边形的对角线，找中点（平行四边形的对角线互相平分）。

题型一：直接法
1、如图是正方体ABCD-A1B1C1D1，求证：BC1∥平面AB1D1
题型二：找中点（或作中点）
2、如图是四棱锥，已知BC∥AD且
1
2
BC AD
，E为中点，
求证：CE∥平面P AB
题型三：通过连接平行四边形的对角线，找中点
3、如图，在底面为平行四边形的四棱锥P-ABCD中，F为PC的中点，求证：P A∥平面FBD.
1
D
变式训练：
1、如图，在三棱柱ABC-A 1B 1C 1中，E 为AC 的中点， 求证：AB 1∥平面EBC 1.
2、如图是三棱柱ABC -A 1B 1C 1，E 为AC 的中点，求证：AB 1∥面EB C 1
3、如图，在长方体ABCD -A 1B 1C 1D 1中，E 为CC 1，求证：AC 1∥面BDE
1
1
1
1
1。

2.2 直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定1、直线和平面的位置关系一条直线和一个平面的位置关系有且只有以下三种 位置关系 直线在平面内 直线与平面相交 直线与平面平行 公共点 有无数个公共点有且只有一个公共点没有公共点 符号表示a ⊂αa ∩α=Aa||α 图形表示注：直线和平面相交或平行的情况统称为直线在平面外 2、直线和平面平行（1）定义：直线和平面没有公共点，则称此直线L 和平面α平行，记作L ||α。

（2）判定定理：如果平面外的一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。

简记为：线线平行，则线面平行.符号表示：,////a b a b a ααα⊄⊂⇒、.2.2.2 平面与平面平行的判定1、定义：没有公共点的两个平面叫做平行平面。

符号表示为：平面α、平面β，若a ∩β＝∅，则a ∥β2、判定定理：1..性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行. 简记为：线面平行，则线线平行.判定文字描述如果两个平面无公共点，责成这两个平面平行一个平面内有两条相交直线与另一个平面平行，那么这两个平面平行．如果两个平面同时垂直于一条直线，那么这两个平面垂直。

图形条件=αβ∅α,b ⊂β，α∩b ＝P α∥α，b ∥α ⇒β∥αl ⊥α l ⊥β ⇒β∥α结论//αβ //αβ //αβ符号表示：若//,,,//a a b a b αβαβ⊂=则.2.2.4 平面与平面平行的性质性质文字描述如果两个平行平面同时和第三平面相交，那么他们的交线平行 如果两个平行平面中有一个垂直于一条直线，那么另一个平面也垂直于这条直线 如果两个平面平行，那么其中一个平面内的直线平行于另一个平面 图形条件 α∥β β∩γ＝b α∩γ＝a α∥β l ⊥α α∥β a ⊂β结论a ∥bl ⊥βa ∥α1. 解题方法（1） 证明直线与平面平行的常用方法：2.利用定义，证明直线与平面没有公共点。

第24讲空间直线、平面的平行的基本概念【题型目录】题型一：直线与平面平行的基本概念题型二：直线与平面平行的轨迹问题【典型例题】题型一：直线与平面平行的基本概念【例1】直线与平面平行的充要条件是这条直线与平面内的（）A ．一条直线不相交B ．两条直线不相交C ．任意一条直线都不相交D ．无数条直线不相交【例2】如图，在长方体1111ABCD A B C D -中，M 是棱11CD 的中点，则（）A ．1//BC 平面1A BM B ．11//A B 平面BDM C ．//BM 平面1ACD D ．1//BC 平面1A MC【例3】下列四个正方体图形中，,,,,A B M N P 分别为正方体的顶点或其所在棱的中点，能得出AB //平面MNP 的图形是（）A ．B ．C ．D ．【例4】已知平面α，直线m ，n 满足m α⊄，n α⊂，则“m ∥n ”是“m ∥α”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【例5】下列命题：①一条直线与两个平行平面中的一个平面相交，必与另外一个平面相交；②如果一个平面平行于两个平行平面中的一个平面，必平行于另一个平面；③夹在两个平行平面间的平行线段相等，其中正确命题的个数是（）A ．1B ．2C ．3D ．0【例6】平面α与平面β平行的充分条件是（）A ．α内有无穷多条直线都与β平行B ．直线a α⊂，直线b β⊂，且,a b βα∥∥C ．α内的任何一条直线都与β平行D ．直线,a a αβ∥∥，且直线a 不在α内，也不在β内【例7】下列命题中正确的是（）A ．如果一条直线与一个平面平行，那么这条直线与平面内的任意一条直线平行B ．平面α内有不共线的三个点A ，B ，C 到平面β的距离相等，则αβ∥C ．b αP ，αβ∥，则b β∥D ．a αP ，a b ，b α⊄，则b αP 【例8】下列能保证直线a 与平面α平行的条件是（）A ．b α⊂，a bB ．a α⊄，b α⊂，a bC ．b α⊂､A ，B a ∈，C ，D b ∈，且AC BD ∥D ．b α⊂，c ∥α，a b ，a cP 【题型专练】1.如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 不平行的是()A ．B ．C ．D ．2.下面四个选项中一定能得出平面//α平面β的是（）A ．存在一条直线a ，//a α，//a βB ．存在一条直线a ，a α⊂，//a βC ．存在两条平行直线a ，b ，a α⊂，b β⊂，//a β，//b αD ．存在两条异面直线a ，b ，a α⊂，b β⊂，//a β，//b α3.a 、b 、l 是直线，α是平面，则下列说法正确的是（）A ．l 平行于α内的无数条直线，则//l αB ．a 不在面α，则//a αC ．若//a b ，b α⊂，则//a αD ．若//a b ，b α⊂，则a 平行于α内的无数条直线4．下列命题正确的是（）A ．若直线上有无数个点不在平面内，则直线和平面平行B ．若直线与平面相交，则直线与平面内的任意直线都是异面直线C ．若直线与平面有两个公共点，则直线在平面内D ．若直线与平面平行，则这条直线与平面内的直线平行5.正方体1111ABCD A B C D -的棱长为1，E 是AB 的中点，点F 在BC 上，则BF 等于多少时，//EF 平面11AC D A ．1B ．12C ．13D ．146.设m ，n 表示不同的直线，α，β表示不同的平面，且m ，n ⊂α．则“//αβ”是“//m β且βn//”的（）A ．充分但不必要条件B ．必要但不充分条件C ．充要条件D ．既不充分又不必要条件7.“平面α内存在无数条直线与直线l 平行”是“直线//l 平面α”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件8.如图，已知四棱柱1111ABCD A B C D -的底面为平行四边形，E ，F ，G 分别为棱1111,,AA CC C D 的中点，则下列各选项正确的是（）A ．直线1BC 与平面EFG 平行，直线1BD 与平面EFG 相交B ．直线1BC 与平面EFG 相交，直线1BD 与平面EFG 平行C ．直线1BC 、1BD 都与平面EFG 平行D ．直线1BC 、1BD 都与平面EFG 相交9.已知a ，b ，c 为三条不重合的直线，α，β，γ为三个不重合的平面其中正确的命题（）①//a c ，////b c a b ⇒；②a γ//，////b a b γ⇒；③//a c ，////c a αα⇒；④a γ//，////a ααγ⇒；⑤a α⊄，b α⊂，////a b a α⇒．A ．①⑤B ．①②C ．②④D ．③⑤10.如图，在三棱柱111ABC A B C -中，12AM MA =，12BN NB =，过MN 作一平面分别交底面三角形ABC 的边BC ，AC 于点E ，F ，则（）A ．//MF EBB ．11//A B NEC ．四边形MNEF 为平行四边形D ．四边形MNEF 为梯形11.如图所示，三棱柱ABC­A1B1C1的侧面BCC1B1是菱形，设D是A1C1上的点且A1B∥平面B1CD，则A1D∶DC1的值为________．=，则MN=___.12.如图，空间四边形ABCD中，,M N分别是△ABC和△ACD的重心，若BD m13.在直三棱柱ABC﹣A1B1C1中，D为AA1中点，点P在侧面BCC1B1上运动，当点P满足条件___________时，A1P//平面BCD(答案不唯一，填一个满足题意的条件即可)MN平面ABC 14.如图，点A，B，C，M，N为正方体的顶点或所在棱的中点，则下列各图中，不满足直线//的是（）A．B．C．D．题型二：直线与平面平行的轨迹问题【例1】在棱长为2的正方体1111ABCD A B C D -中，点M ，N 分别是棱BC ，1CC 的中点，动点P 在正方形11BCC B （包括边界）内运动.若1//PA 平面AMN ，则1PA 的最小值是（）A ．2B ．2C D 【例2】在棱长为2的正方体1111ABCD A B C D -中，,,E F G 分别为11,,AB BC C D 的中点，点P 在底面ABCD 内，若直线1D P 与平面EFG 没有公共点，则线段1D P 长的最小值是_________．P 的轨迹长度为_____________．【例3】如图，在棱长为1的正方体ABCD ﹣A 1B 1C 1D 1中，点E ，F 分别是棱BC ，CC 1的中点，P 是侧面BCC 1B 1内一点，若A 1P ∥平面AEF ，则线段A 1P 长度的取值范围是（）A ．[1]B ．[4]C ．]D ．【题型专练】1.正三棱柱111ABC A B C -的底面边长是4，侧棱长是6，M ，N 分别为1CC ，AB 的中点，若P 是侧面11BCC B 上一点，且PN 平面1AB M ，则线段PN 的最小值为（）A B C D2．正三棱柱111ABC A B C -的底面边长是4，侧棱长是6，M ，N 分别为1BB ，1CC 的中点，若点P 是三棱柱内（含棱柱的表面）的动点，MP ∥平面1AB N ，则动点P 的轨迹面积为（）A ．B ．5CD 3.如图，已知正方体ABCD A B C D ''''-，E ，F 分别为AD ，AB 的中点，点G 在上底面A B C D ''''（含边界）上运动.请补充一个恰当条件，当点G 满足___________时，有//BC '平面EFG .。

第26讲空间直线、平面的平行的判定4种常见方法【考点分析】考点一：直线与平面平行的判定：三种思路：思路一：构造中位线或线段成比例思路二：构造平行四边形思路三：证明面面平行得到线面平行【题型目录】题型一：构造中位线证明线面平行题型二：构造平行四边形证明线面平行题型三：平面与平面平行的判定题型四：面面平行证线面平行【典型例题】题型一：构造中位线证明线面平行【例1】如图，长方体1111ABCD A B C D -中，1AB AD ==，12AA =，点P 为1DD 的中点.(1)求证：直线1BD //平面PAC ；【例2】如图，在直三棱柱111ABC A B C -中，90BAC ∠=︒，12AB AC AA ===，M 为AB 的中点.(1)证明：1BC ∥平面1A CM ；【例3】如图，在长方体1111ABCD A B C D -中，底面ABCD 是边长为2的正方形，14AA =，E ，F 分别为AB ，1AC 的中点.(1)证明://EF 平面11AA D D ；【例4】正三棱柱111ABC A B C -的底面正三角形的边长为2，D 为BC 的中点，13AA =.(1)证明：1//A B 平面1ADC ；【例5】如图所示的四棱锥P ABCD -中，底面ABCD 是梯形，//AB CD ，2AD BD ==，3BDC π∠=，BC =，PD ⊥平面ABCD ，2FC PF =.（1）证明：//AP 平面BDF ；【例6】如图，在三棱锥S ABC 中，M ，N 分别为SAE △和SBC △的重心．求证：//MN 平面ABC ．【例7】如图，已知在四棱锥P -ABCD 中，PD ⊥平面ABCD ，四边形ABCD 是梯形，AB //CD ，AD ⊥DC ，CD =2AB ，PD =AD =AB ，点E 是棱PC 上一点，且CE =2PE ．证明：PA //平面BDE .【题型专练】1．如图，在四棱柱ABCD -A 1B 1C 1D 1中，底面ABCD 为平行四边形，E 为棱DD 1的中点．求证：BD 1∥平面ACE ．2．在直三棱柱111ABC A B C -中，E 是棱AB 的中点，1222AB BC BB ===，120ABC ︒∠=．(1)求证：1//BC 平面1A EC ；(2)求异面直线1AC 与1BC 所成的角的余弦值．3.如图，在直三棱柱111ABC A B C -中，已知12,,AB BC BB AB BC D ===⊥为AB 的中点.（1）求证：1BC ∥平面1ACD .4.已知正方体1111ABCD A B C D -中，P ､Q 分别为对角线BD ､1CD 上的点，且123CQ BP QD PD ==.（1）作出平面PQC 和平面11AA D D 的交线（保留作图痕迹），并求证：//PQ 平面11A D DA ；5.如图，四棱锥P ABCD -的底面是平行四边形，M 是PC 的中点，求证：//PA 平面BMD ．6．如图，在五面体P -ABCD 中，PA PB =，底面ABCD 是菱形，且60ABC ∠=︒，点M 是AB 的中点，点E 在棱PD 上，满足2DE PE =．求证：PB ∥平面EMC ．题型二：构造平行四边形证明线面平行【例1】已知P 是矩形ABCD 所在平面外一点，M ，N 分别是AB ，PC 的中点，求证：//MN 平面PAD .【例2】在如图所示的空间图形中，△ABC 是任意三角形，AE ∥CD ，且AE ＝2a ，CD ＝a ，F 为BE 的中点．求证：DF ∥平面ABC .【例3】如图，在正方体1111ABCD A B C D -中，M ，N 分别为1AB 和1CC 的中点.求证：//MN 平面ABCD .【例4】如图，在正方体1111ABCD A B C D -中，E 为1BB 的中点．（Ⅰ）求证：1//BC 平面1AD E ；【例5】在三棱柱111ABC A B C -中，AB AC ⊥，1B C ⊥平面ABC ，E 、F 分别是棱AC 、11A B 的中点.(1)设G 为11B C 的中点，求证：//EF 平面11BCC B ；【题型专练】1．如图，四棱锥P ABCD -中，底面ABCD 是平行四边形，E 、F 分别是AB 、PC 的中点．证明：//EF 平面PAD ．2．如图所示，在四棱锥P ABCD -中，底面ABCD 为平行四边形，侧面PAD 为正三角形，M 为线段PD 上一点，N 为BC 的中点.(1)当M 为PD 的中点时，求证：//MN 平面PAB .(2)当//PB 平面AMN ，求出点M 的位置，说明理由.3．在四棱锥P ABCD -中，四边形ABCD 为矩形，平面ABCD ⊥平面PAB ，点,E F 分别在线段,CB AP 上，且CE EB =，=AF FP ．求证：//EF 平面PCD .4．如图，M ，N ，K 分别是正方体1111ABCD A B C D -的棱11,,AB CD C D 的中点．求证：AN ∥平面1A MK ．题型三：平面与平面平行的判定利用判定定理证明两个平面平行的一般思路：第一步：在一个平面内找出两条相交直线.第二步：证明这两条相交直线分别平行于另一个平面.第三步：利用平面与平面平行的判定理得出结论.【例1】如图，正方体1111ABCD A B C D -中，E F 、分别为11DD CC 、的中点，求证:平面//AEC 平面1BFD .【例2】如图，在三棱柱111ABC A B C -中，E ，F ，G 分别为11B C ，11A B ，AB 的中点．(1)求证：平面11AC G ∥平面BEF ；(2)若平面11A C G BC H ⋂=，求证：H 为BC 的中点．【例3】如图所示，已知1111-ABCD A B C D 是棱长为3的正方体，点E 在1AA 上，点F 在1CC 上，G 在1BB 上，且111AE FC B G ===，H 是11B C 的中点．(1)求证：1E B F D 、、、四点共面(2)求证：平面1//AGH 平面1BED F ．【例4】如图，已知正方体1111ABCD A B C D 的棱长为1,,E F 分别是1,A D BD 的中点.(1)求证：平面1A BD 平面11CB D ；(2)求证：EF 平面11DCC D ；【题型专练】1．如图所示，在三棱柱111ABC A B C -中，E ，F ，G ，H 分别是AB ，AC ，11A B ，11A C 的中点．求证：平面1EFA ∥平面BCHG ．2．如图所示，在正方体1111A B C D ABCD -中，M ，N ，P 分别是1C C ，11B C ，11C D 的中点．求证：平面MNP ∥平面1A BD ．3．如图，在正方体1111ABCD A B C D -中，E ，F 分别为棱11,DD CC 的中点.求证：平面1//AEC 平面BDF4.在如图所示的几何体中，D 是AC 的中点，EF ∥DB ．已知G ，H ，I 分别是EC ，FB 和FC 的中点，求证：平面GHI ∥平面ABC ．题型四：面面平行证线面平行【例1】几何体E ABCD -是四棱锥，ABD △为正三角形，2BC CD ==，120BCD ∠=︒，M 为线段AE 的中点.(1)求证：//DM 平面BEC ；(2)线段EB 上是否存在一点N ，使得,,,D M N C 四点共面？若存在，请找出点N ，并证明；若不存在，并说明理由.【例2】已知三棱锥A BCD -中，△ABC ，△ACD 都是等边三角形，π2BAD ∠=，E ，F 分别为棱AB ，棱BD 的中点，G 是△BCE 的重心．(1)求异面直线CE 与BD 所成角的余弦值；(2)求证：FG 平面ADC ．【例3】如图所示的几何体中，底面ABCD 是等腰梯形，1//,60,AB CD ABC AA ∠=⊥ 平面,ABCD 11//,CC AA 且111,22CD BC AB AA ===E ，F 分别为1A D ，1CC 的中点．证明：EF ∥面ABCD ；【例4】如图，四棱台1111ABCD A B C D -中，底面ABCD 为直角梯形，//AB CD ，AB BC ⊥，1112224AB BC CD DD D C ====，P 为棱1CC 的中点，证明：//AC 平面1B DP .【例5】如图，AB 是圆柱底面圆O 的直径，点C 、F 是 AB 的两个三等分点，CD 、BE 为圆柱的母线，求证：//EF 平面OCD【题型专练】1．如图，在等腰直角三角形PAD 中，9083A AD AB B C ︒∠===，，，、分别是PA PD 、上的点，且//AD BC M N ，、分别为BP CD 、的中点，现将BCP 沿BC 折起，得到四棱锥P ABCD -，连接.MN 证明：//MN 平面PAD ；2．如图，三棱柱111ABC A B C -中，12AB AC AA ===，1160A AB A AC BAC ∠=∠=∠=︒，点M ，N 分别在1AC 和BC 上，且满足113AM AC = ，13BN BC = ，证明：MN ∥平面11ABB A 3．如图，在四棱锥P ABMN -中，PNM △是边长为2的正三角形，//AN BM ，3AN =，1BM =，22AB =，C ，D 分别是线段AB ，NP 的中点，求证：//CD 平面PBM4．如图，AD //BC 且AD ＝2BC ，AD ⊥CD ，EG //AD 且EG AD =，//CD FG 且2CD FG =，DG ⊥平面ABCD ，DA DC DG ==，若M 为CF 的中点，N 为EG 的中点，求证：MN //平面CDE ．。