倍长中线法(经典例题)

DC BA全等三角形问题中常见的辅助线——倍长中线法△ABC 中,AD 是BC 边中线方式1:直接倍长，(图1)： 延长AD 到E ，使DE =AD ，连接BE 方式2：间接倍长1) （图2）作CF ⊥AD 于F ，作BE ⊥AD 的延长线于E , 连接BE 2) （图3）延长MD 到N ，使DN =MD ，连接CD【经典例题】例1已知，如图△ABC 中，AB =5，AC =3， 则中线AD 的取值范围是_________.（提示：画出图形，倍长中线AD ，利用三角形两边之和大于第三边）例2：已知在△ABC 中，AB =AC ，D 在AB 上，E 在AC 的延长线上， DE 交BC 于F ，且DF =EF . 求证：BD =CE .（提示：方法1：过D 作DG ∥AE 交BC 于G ，证明ΔDGF ≌ΔCEFEDFC BA方法2：过E 作EG ∥AB 交BC 的延长线于G ，证明ΔEFG ≌ΔDFB方法3：过D 作DG ⊥BC 于G ，过E 作EH ⊥BC 的延长线于H ，证明ΔBDG ≌ΔECH ）例3、如图，△ABC 中，E 、F 分别在AB 、AC 上，DE ⊥DF ，D 是中点，试比较BE +CF 与EF 的大小.变式：如图，AD 为ABC ∆的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于F . 求证：EF CF BE >+（提示：方法1：在DA 上截取DG =BD ，连结EG 、FG ， 证明ΔBDE ≌ΔGDE ΔDCF ≌ΔDGF 所以BE =EG 、CF =FG 利用三角形两边之和大于第三边 方法2：倍长ED 至H ，连结CH 、FH ，证明FH =EF 、CH =BE ，利用三角形两边之和大于第三边）例4：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE =AC ，延长BE 交AC 于F ，求证：AF =EF（提示：方法1：倍长AD 至G ，连接BG ，证明ΔBDG ≌ΔCDA 三角形BEG 是等腰三角形。

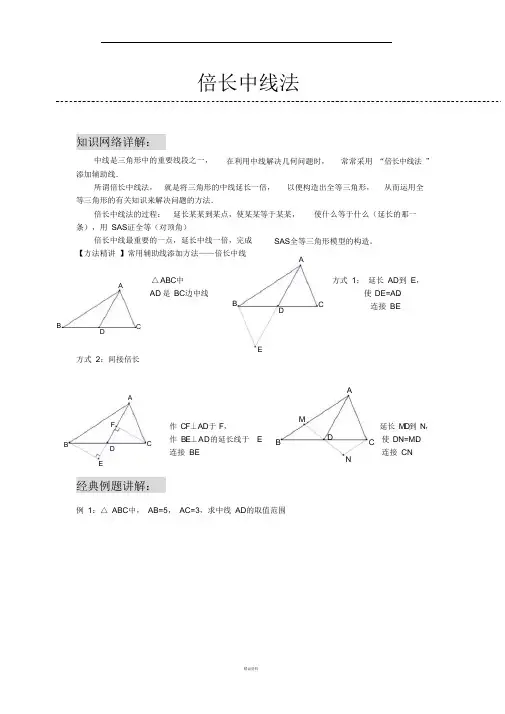
倍长中线法例 1：△ ABC 中， AB=5， AC=3，求中线 AD 的取值范围知识网络详解：中线是三角形中的重要线段之一， 添加辅助线．在利用中线解决几何问题时， 常常采用 “倍长中线法 ”所谓倍长中线法， 就是将三角形的中线延长一倍， 以便构造出全等三角形， 从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程： 延长某某到某点，使某某等于某某， 使什么等于什么（延长的那一条），用 SAS 证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成 【方法精讲 】常用辅助线添加方法——倍长中线SAS 全等三角形模型的构造。

AA△ ABC 中 AD 是 BC 边中线BDC方式 1： 延长 AD 到 E ，使 DE=AD ，连接 BEB DCE方式 2：间接倍长AAF 作 CF ⊥ AD 于 F ， MDB D C作 BE ⊥ AD 的延长线于 连接 BEE BC 延长 MD 到 N ， 使 DN=M ，D 连接 CNEN经典例题讲解：例2：已知在△ABC中，AB=AC，D 在AB上，E 在AC的延长线上，DE交BC于F，且DF=EF，求证：BD=CEADBFCE例3：已知在△ ABC中，AD是BC边上的中线， E 是AD上一点，且BE=AC，延长BE交AC于F，求证：AF=EFAFEBD C例4：已知：如图，在ABC 中，AB 交AE于点F，DF=AC.求证：AE平分BAC AC ，D、E 在BC上，且DE=EC，过D作DF // BAAFB D E C例5：已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，求证：∠C=∠BAEABCE D自检自测：1、如图，△ABC中，BD=DC=AC,E是DC的中点，求证，AD平分∠BAE.2、在四边形ABCD中，AB∥DC，E 为BC边的中点，∠BAE=∠EAF，AF 与DC的延长线相交于点F。

试探究线段AB与AF、CF之间的数量关系，并证明你的结论.ADBE CF3、如图，AD为ABC 的中线，DE平分BDA 交AB于E，DF平分ADC 交AC于F. 求证：BE CF EFAEFB CD第14 题图4、已知：如图，ABC中，C=90 ，CM AB于M，AT 平分BAC交CM于D，交BC于T，过D作DE//AB 交BC于E，求证：CT=BE.A MD BETCWelcome To Download !!!欢迎您的下载，资料仅供参考！。

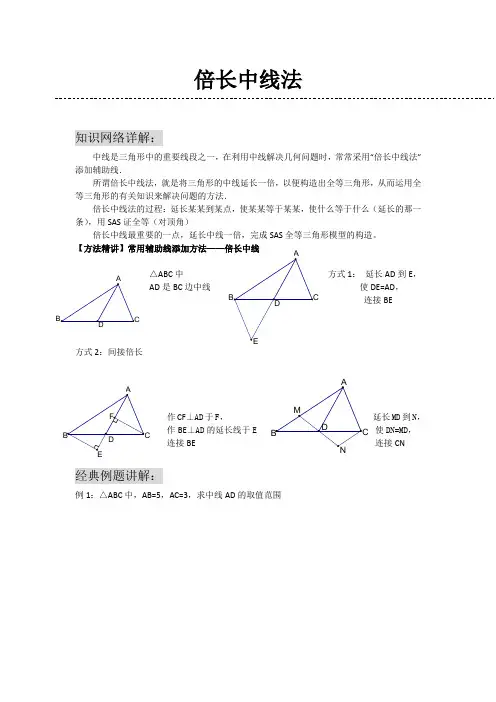
倍长中线法知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。

【方法精讲】常用辅助线添加方法——倍长中线△ABC中方式1：延长AD到E，AD是BC边中线使DE=AD，连接BE方式2：间接倍长作CF⊥AD于F，延长MD到N，作BE⊥AD的延长线于使DN=MD，连接BE 连接CN经典例题讲解：例1：△ABC中，AB=5，AC=3，求中线AD的取值范围例2：已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE例3：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF例4：已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC. 求证：AE 平分BAC ∠BABFDEC例5：已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，求证：∠C=∠BAE自检自测：1、如图，△ABC中，BD=DC=AC,E是DC的中点，求证，AD平分∠BAE.2、在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F。

试探究线段AB与AF、CF之间的数量关系，并证明你的结论.ABFEAB C3、如图，AD 为ABC ∆的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于F. 求证：EF CF BE >+4、已知：如图，∆ABC 中，∠C=90︒，CM ⊥AB 于M ，AT 平分∠BAC 交CM 于D ，交BC 于T ，过D 作DE//AB 交BC 于E ，求证：CT=BE.第 14 题图DF CBEADABCMTE。

数学倍长中线法集团档案编码：[YTTR-YTPT28-YTNTL98-UYTYNN08]倍长中线法1.如图，在正方形ABCD 中，E 为AB 边的中点，G 、F 分别为AD ，BC 边上的点，若AG=1，BF=2，∠GEF=90°，求GF 的长2.如图，CB 、CD 分别是钝角△AEC 和锐角△ABC 的中线，且AC=AB ．求证：①CE=2CD ．②CB 平分∠DCE ．3.如图已知△ABC，AD 是BC 边上的中线，分别以AB 边、AC 边为直角边各向形外作等腰直角三角形，求证EF ＝2AD.4.如图，在△ABC 中，D 是BC 边的中点，E 是AD 上一点，BE ＝AC ，BE 的延长线交AC 于点F ，求证：∠AEF=∠EAF5..如图，在△ABC 中，AD 交BC 于点D ，点E 是BC 中点，EF ∥AD 交CA 的延长线于点F ，交EF 于点G ，若BG=CF ，求证：AD 为△ABC 的角平分线.6..如图，△ABC 中，BD=DC=AC,E 是DC 的中点，求证，AD 平分∠BAE.7.：已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE9.在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

试探究线段AB 与AF 、CF 之间的数量关系，并证明你的结论10.已知：如图，ABC 中，C=90，CMAB 于M ，AT 平分BAC 交CM 于D ，交BC 于T ，过D 作DE//AB 交BC 于E ，求证：CT=BE.12.13.四边形ABCD 是矩形，将ABE 沿着直线AE 翻折，点A 落在点F 处，直线AF 与直线CD 交于点G,如图1，若E 为BC 的中点，请探究线段AB 、AG 、DG 之间的关系FEC A BD EA BC.。

八年级上册数学倍长中线典型题一、倍长中线法概述倍长中线是一种在三角形中常用的辅助线添加方法。

当遇到三角形中有中线（连接三角形一个顶点和它对边中点的线段）时，可以将中线延长一倍，构造出全等三角形，从而利用全等三角形的性质来解决问题。

二、典型例题及解析1. 已知：在△ABC中，AD是BC边上的中线，E是AD上一点，且BE = AC，延长BE交AC于F。

求证：AF = EF。

题目分析：本题有中线AD，考虑倍长中线AD来构造全等三角形。

证明：延长AD到G，使DG = AD，连接BG。

因为AD是BC边上的中线，所以BD = CD。

在△BDG和△CDA中，BD = CD（已证）∠BDG=∠CDA（对顶角相等）DG = DA（所作辅助线）所以△BDG≌△CDA(SAS)。

则BG = AC，∠G = ∠CAD。

又因为BE = AC，所以BG = BE。

所以∠G = ∠BEG。

因为∠BEG = ∠AEF（对顶角相等），∠G = ∠CAD。

所以∠AEF = ∠CAD，即AF = EF。

2. 如图，在△ABC中，AB = 5，AC = 3，则中线AD的取值范围是多少？题目分析：本题给出了三角形两边的长度，要求中线的取值范围，可通过倍长中线构造全等三角形，将已知边和中线转化到一个三角形中，利用三角形三边关系求解。

解：延长AD到E，使DE = AD，连接BE。

因为AD是中线，所以BD = CD。

在△BDE和△CDA中，BD = CD∠BDE = ∠CDADE = DA所以△BDE≌△CDA(SAS)。

则BE = AC = 3。

在△ABE中，AB BE＜AE＜AB + BE。

因为AB = 5，BE = 3，AE = 2AD。

所以5 3＜2AD＜5 + 3。

即1＜AD＜4。

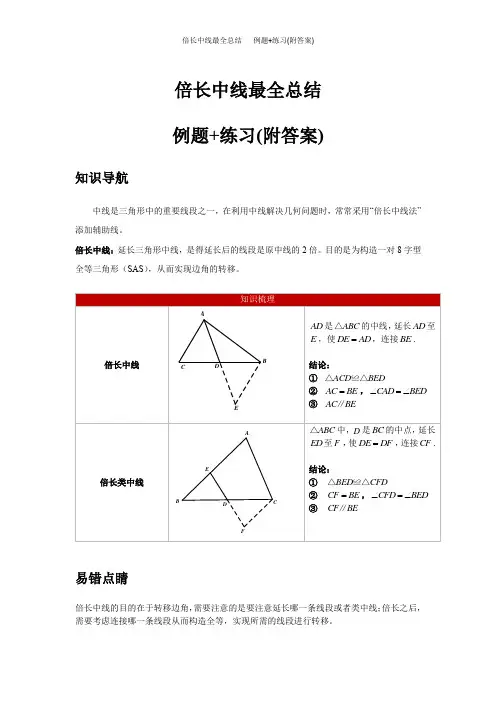
倍长中线最全总结 例题+练习(附答案)知识导航中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线。

倍长中线：延长三角形中线，是得延长后的线段是原中线的2倍。

目的是为构造一对8字型全等三角形（SAS ），从而实现边角的转移。

易错点睛倍长中线的目的在于转移边角，需要注意的是要注意延长哪一条线段或者类中线；倍长之后，需要考虑连接哪一条线段从而构造全等，实现所需的线段进行转移。

DAB C模块一 有关倍长中线的全等模型【范例】（2014秋•江汉区校级月考）如图，在ABC ∆中，AD 为中线，求证：2AB AC AD +>．【分析】延长AD 至E ，使DE AD =，构造ADC EDB ∆≅∆，再根据三角形的三边关系可得 2AB AC AD +>。

【解答】证明：由BD CD =，再延长AD 至E ，使DE AD =，D 为BC 的中点，DB CD ∴=，在ADC ∆和EDB ∆中AD DE ADC BDE DB CD =⎧⎪∠=∠⎨⎪=⎩，()ADC EDB SAS ∴∆≅∆， BE AC ∴=，在ABE ∆中，AB BE AE +>，2AB AC AD ∴+>；BB【核心考点1】倍长中线1．（2016秋•五莲县期中）如图，ABC ∆中，D 为BC 的中点． （1）求证：2AB AC AD +>；（2）若5AB =，3AC =，求AD 的取值范围．【分析】（1）再延长AD 至E ，使DE AD =，构造ADC EDB ∆≅∆，再根据三角形的三边关 系可得2AB AC AD +>；（2）直接利用三角形的三边关系：三角形两边之和大于第三边，三角形的两边差小于第三 边可得53253AD -<<+，再计算即可． 【解答】（1）证明：由BD CD =，再延长AD 至E ，使DE AD =，D 为BC 的中点，DB CD ∴=，在ADC ∆和EDB ∆中AD DEADC BDE DB CD =⎧⎪∠=∠⎨⎪=⎩，()ADC EDB SAS ∴∆≅∆， BE AC ∴=，在ABE ∆中，AB BE AE +>，2AB AC AD ∴+>；（2）5AB =，3AC =，53253AD ∴-<<+，14AD ∴<<．ABC2．如图，ABC ∆中，BD DC AC ==，E 是DC 的中点，求证：AD 平分BAE ∠．【分析】延长AE 到M ，使EM AE =，连结DM ，由SAS 证明DEM CEA ∆≅∆，得出C MDE ∠=∠，DM AC =，证出DM BD =，ADM ADB ∠=∠，由SAS 证明ADB ADM ∆≅∆，得出BAD MAD ∠=∠即可．【解答】证明：延长AE 到M ，使EM AE =，连结DM ，如图所示：E 是DC 的中点，DE CE ∴=，在DEM ∆和CEA ∆中，EM AE DEM CEADE CE =⎧⎪∠=∠⎨⎪=⎩，()DEM CEA SAS ∴∆≅∆， C MDE ∴∠=∠，DM AC =，又BD DC AC ==，DM BD ∴=，ADC CAD ∠=∠，又ADB C CAD ∠=∠+∠，ADM MDE ADC ∠=∠+∠，ADM ADB ∴∠=∠，在ADB ∆和ADM ∆中，AD AD ADB ADMBD DM =⎧⎪∠=∠⎨⎪=⎩，()ADB ADM SAS ∴∆≅∆，BAD MAD ∴∠=∠，即AD 平分BAE ∠。

倍长中线法经典例题倍长中线法是一种加法运算技巧，有效地提高了大数加法的运算复杂度，其思想是利用“倍数方法”和“中线方法”相结合，让大数加法运算变得更加容易、快捷。

今天，我们就来认真研究一下倍长中线法的经典例题，深入了解它的奥妙之处，为今后的加法运算奠定坚实的理论基础。

例题一：计算788 + 883首先，我们来看倍长中线法的思路：首先用“倍数方法”，将两个加数乘以1000，即78800 + 883000；然后，用“中线方法”，将两个乘以1000后的数放在中线上，形成一条倍长的中线，即| 7880000 | 8830000 |；最后，从右往左数，总计8位，从右往左加即可得出结果。

由于是从右往左加，所以从右边开始计算，第8位末位数相加，结果为1，但此时不进位；再加第7位，结果为8，该位也不进位；继续加第6位，结果为3，也不进位；最终结果为1671000。

即788 + 883 = 1671。

例题二：计算486 + 879先用“倍数方法”，将两个加数乘以1000，即486000 + 879000；然后，用“中线方法”，将两个乘以1000后的数放在中线上，形成一条倍长的中线，即| 4860000 | 8790000 |；最后，从右往左数，总计8位，从右往左加即可得出结果。

从右往左加，第8位末位数相加，结果为2，不进位；继续加第7位，结果为8，该位也不进位；再加第6位，结果为7，此时需要进位；最终结果为1365000。

即486 + 879 = 1365。

通过上面的两个例题，相信读者对倍长中线法的思想及操作方法已经有了一定的了解，下面我们将再来讨论一个关键概念：“倍数方法”与“中线方法”之间如何结合？其实“倍数方法”与“中线方法”之间的相互结合，就是倍长中线法的关键点所在。

前面的例题中，我们都是“倍数方法”将加数乘以1000；然后用“中线方法”将乘以1000的结果放在中线上，然后从右往左依次加数，最终得到结果。

N作 BE! AD 的延长线于倍长中线法知识网络详解:中线是三角形中的重要线段之一，在利用中线解决几何问题时, 常常采用“倍长中线法”添加辅助线.所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全 等三角形，从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程：延长某某到某点，使某某等于某某，使什么 等于什么（延长的那一条），用SAS 证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成SAS 全等三角形模 型的构造。

【方法精讲】常用辅助线添加方法倍长中线△ ABC 中式1:延长AD 到E,B --------------- ■ ------------- CDAD 是E BC使 DE=AD接BE方式2:间接倍长 AB 延长MD 到N, CE连接CN 经典例题讲解：例〔：△ ABC 中，AB=5 AC=3求中线 AD 的取值范围例2:已知在△ ABC 中，AB=AC D 在AB 上，E 在AC 的延长线上，DE 交 BC 于 F ,且 DF=EF 求证：BD=CE例3：已知在△ ABC 中 , AD 是 BC 边上的中线，E 是AD 上一点，且BE 二AC例4:已知：如图，在- ABC 中，AB = AC , DE 在 BC 上 ,且 DE 二EC 过 D 作 DF//BA 交 AE 于点 F , DF=AC.例 5：已知 CD=AB Z BDA M BAD AE 是A ABD 的中线，求证：/ C=Z BAE自检自测:1、如图，△ ABC 中 , BD=DC=AC,是 DC 的中点，求证，AD 平分/ BAE.使 DN=M ,BE延长BE 交AC 于F ,求证：AF=EF求证：AE 平分.BACDEAECCFAC2、在四边形ABCD K AB// DC E 为BC 边的中点，/ BAE K EAF AF与DC 的延长线相交于点F 。

试探究线段AB 与AF 、CF 之间的数量关 系，并证明你的结论.3、如图，AD 为 MBC 的中线，DE 平分.BDA 交AB 于E,DF 平分.AD 交 AC 于 F.求证：BE CF EF4、已知：如图， ABC 中， C=90，CM AB 于 M AT 平 分 BAC 交 CM 于 D,交 BC 于 T ，过 D 作 DE//AB 交 BC 于 E ，求证：CT=BE.ADBF。

例ABC 中，AB=5, AC=3,求中线AD 的取值范围知识网络详解:中线是三角形中的重要线段之一， 在利用中线解决几何问题时， 常常采用 倍长中线法” 添加辅助线.所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程：延长某某到某点，使某某等于某某，条）,用SAS 证全等（对顶角） 倍长中线最重要的一点，延长中线一倍，完成 经典例题讲解:使什么等于什么（延长的那一 SAS 全等三角形模型的构NE例2:已知在△ ABC 中，AB=AC D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ,且DF=EF 求证：BD=CE例3:已知在△ ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且 BE=AC 延长 BE 交AC 于F ,求证：AF=EF例4：已知：如图，在 心ABC 中，AB H AC , D 、E 在BC 上，且DE=EC 过D 作DF //BA 交 AE 于点 F , DF=AC.求证：AE 平分NBACE例 5:已知 CD=AB / BDA=/ BAD , AE 是^ ABD 的中线,2、在四边形 ABCD 中，AB// DC E 为BC 边的中点，/ BAE=/ EAF, AF 与DC 的延长线相交 于点F 。

试探究线段 AB 与AF 、CF 之间的数量关系，并证明你的结论. 求证：/ C=/BAE自检自测:1、如图，△ ABC 中，BD=DC=AC,E 是 DC 的中点，求证, AD 平分/BAE.D3、如图，AD为人ABC的中线，DE平分N BDA交AB于E, DF平分N ADC交AC于F.求证: BE+CF >EF第14题图4、已知：如图，MBC中，N C=90°, CM丄AB于M , AT平分Z BAC交CM于D,交BC于T,过D作DE//AB交BC于E,求证：CT=BE.。

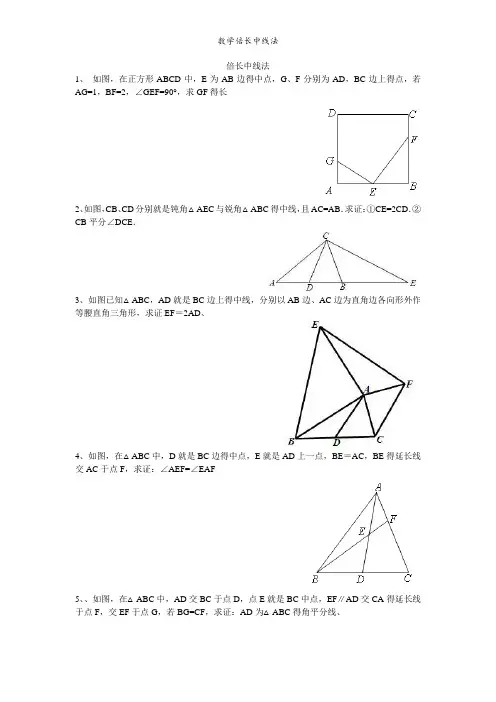
倍长中线法1、如图，在正方形ABCD中，E为AB边得中点，G、F分别为AD，BC边上得点，若AG=1，BF=2，∠GEF=90°，求GF得长2、如图，CB、CD分别就是钝角△AEC与锐角△ABC得中线，且AC=AB．求证：①CE=2CD．②CB平分∠DCE．3、如图已知△ABC，AD就是BC边上得中线，分别以AB边、AC边为直角边各向形外作等腰直角三角形，求证EF＝2AD、4、如图，在△ABC中，D就是BC边得中点，E就是AD上一点，BE＝AC，BE得延长线交AC于点F，求证：∠AEF=∠EAF5、、如图，在△ABC中，AD交BC于点D，点E就是BC中点，EF∥AD交CA得延长线于点F，交EF于点G，若BG=CF，求证：AD为△ABC得角平分线、6、、如图，△ABC 中，BD=DC=AC,E 就是DC 得中点，求证，AD 平分∠BAE 、7、：已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 得延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE9、在四边形ABCD 中，AB ∥DC ，E 为BC 边得中点，∠BAE=∠EAF ，AF 与DC 得延长线相交于点F 。

试探究线段AB 与AF 、CF 之间得数量关系，并证明您得结论 10、已知：如图， ABC 中， C=90 ，CM AB 于M ，AT 平分 BAC 交CM 于D ，交BC 于T ，过D 作DE//AB 交BC 于E ，求证：CT=BE 、12、FC AD FEABCDABCMTEGCADE第 1 题图BF DEC13、四边形ABCD就是矩形，将ABEV沿着直线AE翻折，点A落在点F处，直线AF与直线CD交于点G,如图1，若E为BC得中点，请探究线段AB、AG、DG之间得关系、GFB。

八年级数学全等三角形--倍长中线法经典例题中线是三角形中的重要线段之一。

为了解决几何问题，常常采用“倍长中线法”添加辅助线。

倍长中线法的过程是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题。

倍长中线最重要的一点是延长中线一倍，完成SAS全等三角形模型的构造。

常用的辅助线添加方法有两种：一是将中线延长到某一点，使其等于另一条边，然后连接这两个点构造全等三角形；二是通过作垂线和延长线来间接倍长中线。

例1：在△ABC中，已知AB=5，AC=3，求中线AD的取值范围。

例2：在△ABC中，已知AB=AC，D在AB上，E在AC 的延长线上，DE交BC于F，且DF=EF，求证BD=CE。

例3：在△ABC中，已知AD是BC边上的中线，E是AD上一点，且BE=AC，延长BE交AC于F，求证AF=EF。

例4：在△ABC中，已知AB≠AC，D、E在BC上，且DE=EC。

过D作DF//BA交AE于点F，DF=AC。

求证AE平分∠BAC。

例5：已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，求证∠C=∠BAE。

自检自测：1、在△ABC中，已知BD=DC=AC，E是DC的中点，求证AD平分∠BAE。

2、在四边形ABCD中，已知AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F。

试探究线段AB与AF、CF之间的数量关系，并证明你的结论。

3、在△ABC中，已知AD为中线，DE平分∠BDA交AB于E，DF平分∠ADC交AC于F。

求证BE+CF>EF。

4、在直角△ABC中，已知CM⊥XXX于M，AT平分∠BAC交CM于D，交BC于T，XXX于E。

求证CT=BE。

完整版)倍长中线法(经典例题)
倍长中线法是解决几何问题中常用的方法之一。

在利用中线解决问题时，我们可以通过添加辅助线，采用倍长中线法来构造全等三角形，从而运用全等三角形的知识来解决问题。

具体来说，倍长中线法的过程是：延长某一中线一倍，使其构造出全等三角形，然后利用全等三角形的有关知识来解决问题。

在构造全等三角形时，我们可以采用两种常用的方法：一是将中线延长到某一点，使其等于另一条中线，然后利用对顶角的SAS证明全等；二是通过间接倍长的方法，利用垂线和平行线构造出全等三角形。

倍长中线法最重要的一点是延长中线一倍，完成SAS全等三角形模型的构造。

我们可以通过经典例题来练这种方法，例如求中线的取值范围、证明BD等于CE、证明AF等于EF 等问题。

自检自测题也是巩固这种方法的好办法。

例如证明AD平分∠BAE、探究线段AB与AF、CF之间的数量关系、证明BE+CF>EF等问题都可以通过倍长中线法来解决。

倍长中线知识导航中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线。

倍长中线：延长三角形中线，是得延长后的线段是原中线的2倍。

目的是为构造一对8字型全等三角形（SAS ），从而实现边角的转移。

易错点睛倍长中线的目的在于转移边角，需要注意的是要注意延长哪一条线段或者类中线；倍长之后，需要考虑连接哪一条线段从而构造全等，实现所需的线段进行转移。

DAB C模块一 有关倍长中线的全等模型【范例】（2014秋•江汉区校级月考）如图，在ABC ∆中，AD 为中线，求证：2AB AC AD +>．【分析】延长AD 至E ，使DE AD =，构造ADC EDB ∆≅∆，再根据三角形的三边关系可得 2AB AC AD +>。

【解答】证明：由BD CD =，再延长AD 至E ，使DE AD =，D 为BC 的中点，DB CD ∴=，在ADC ∆和EDB ∆中AD DE ADC BDE DB CD =⎧⎪∠=∠⎨⎪=⎩，()ADC EDB SAS ∴∆≅∆， BE AC ∴=，在ABE ∆中，AB BE AE +>，2AB AC AD ∴+>；BB【核心考点1】倍长中线1．（2016秋•五莲县期中）如图，ABC ∆中，D 为BC 的中点． （1）求证：2AB AC AD +>；（2）若5AB =，3AC =，求AD 的取值范围．【分析】（1）再延长AD 至E ，使DE AD =，构造ADC EDB ∆≅∆，再根据三角形的三边关 系可得2AB AC AD +>；（2）直接利用三角形的三边关系：三角形两边之和大于第三边，三角形的两边差小于第三 边可得53253AD -<<+，再计算即可． 【解答】（1）证明：由BD CD =，再延长AD 至E ，使DE AD =，D 为BC 的中点，DB CD ∴=，在ADC ∆和EDB ∆中AD DEADC BDE DB CD =⎧⎪∠=∠⎨⎪=⎩，()ADC EDB SAS ∴∆≅∆， BE AC ∴=，在ABE ∆中，AB BE AE +>，2AB AC AD ∴+>；（2）5AB =，3AC =，53253AD ∴-<<+，14AD ∴<<．DABC2．如图，ABC ∆中，BD DC AC ==，E 是DC 的中点，求证：AD 平分BAE ∠．【分析】延长AE 到M ，使EM AE =，连结DM ，由SAS 证明DEM CEA ∆≅∆，得出C MDE ∠=∠，DM AC =，证出DM BD =，ADM ADB ∠=∠，由SAS 证明ADB ADM ∆≅∆，得出BAD MAD ∠=∠即可．【解答】证明：延长AE 到M ，使EM AE =，连结DM ，如图所示：E 是DC 的中点，DE CE ∴=，在DEM ∆和CEA ∆中，EM AE DEM CEADE CE =⎧⎪∠=∠⎨⎪=⎩，()DEM CEA SAS ∴∆≅∆， C MDE ∴∠=∠，DM AC =，又BD DC AC ==，DM BD ∴=，ADC CAD ∠=∠，又ADB C CAD ∠=∠+∠，ADM MDE ADC ∠=∠+∠，ADM ADB ∴∠=∠，在ADB ∆和ADM ∆中，AD AD ADB ADMBD DM =⎧⎪∠=∠⎨⎪=⎩，()ADB ADM SAS ∴∆≅∆，BAD MAD ∴∠=∠，即AD 平分BAE ∠。

倍长中线法经典例题
倍长中线法是一种数学方法，它可以用来解决一些比较复杂的数学问题。

它的思想是：在一个四边形的内部，描绘一条中线，其长度和某一边的长度保持一致，在对称的位置上将另外一条中线再次描绘出来，每条中线的长度也会和一边保持一致，以此来解决问题。

经典例题：假设有一个四边形ABCD，其中AB=2，BC=4，CD=6，问四边形ABCD的面积是多少？
首先，我们在四边形ABCD内部描绘出一条中线，使得这条中线和AB边的长度保持一致，即中线的长度也是2。

然后，在对称的位置上将另外一条中线连接出来，这条中线的长度也是2，即中线的长度也和CD边的长度保持一致。

接下来，我们将两条中线合并起来，形成一个新的四边形EFGH，由于两条中线的长度都是2，所以EF=2+2=4，GH=4+2=6，再由于EFGH四边形是对称的，所以其他两条边也是和EH，FG边的长度保持一致，即FG=4，EH=6。

最后，利用面积公式，S=（a+b）*h/2，将EFGH四边形的面积计算出来，可得：S=(4+6)*2/2=8。

所以，答案是ABCD四边形的面积是8。

倍长中线法的应用不仅仅局限于上面的例题，它也可以用来解决其他更复杂的数学问题，比如三角形、多边形等。

倍长中线法是一种非常有效的数学方法，它可以节省更多的时
间和精力，帮助数学家解决复杂的数学问题，从而拓展数学的可探索性。

(1)．倍长中线法：1、已知，如图，△ABC 中，D 是BC 中点，DE⊥DF,试判断BE ＋CF 与EF 的大小关系，并证明你的结论.【答案与解析】BE ＋CF ＞EF ；证明：延长FD 到G ，使DG ＝DF,连结BG 、EG∵D 是BC 中点∴BD＝CD又∵DE⊥DF在△EDG 和△EDF 中ED ED EDG EDF DG DF =⎧⎪∠=∠⎨⎪=⎩∴△EDG ≌△EDF （SAS ）∴EG＝EF在△FDC 与△GDB 中⎪⎩⎪⎨⎧=∠=∠=DG DF BD CD 21∴△FDC≌△GDB(SAS)∴CF＝BG∵BG＋BE ＞EG∴BE＋CF ＞EF【点评】因为D 是BC 的中点，按倍长中线法，倍长过中点的线段DF ，使DG ＝DF,证明△EDG≌△EDF ，△FDC≌△GDB，这样就把BE 、CF 与EF 线段转化到了△BEG 中，利用两边之和大于第三边可证.有中点的时候作辅助线可考虑倍长中线法（或倍长过中点的线段）.举一反三：【变式】已知：如图所示，CE 、CB 分别是△ABC 与△ADC 的中线，且∠ACB ＝∠ABC．求证：CD ＝2CE ．【答案】证明：延长CE至F使EF＝CE，连接BF．∵ EC为中线，∴ AE＝BE．在△AEC与△BEF中，,,,AE BEAEC BEF CE EF=⎧⎪∠=∠⎨⎪=⎩∴△AEC≌△BEF（SAS）．∴ AC＝BF，∠A＝∠FBE．（全等三角形对应边、角相等）又∵∠ACB＝∠ABC，∠DBC＝∠ACB＋∠A，∠FBC＝∠ABC＋∠A．∴ AC＝AB，∠DBC＝∠FBC．∴ AB＝BF．又∵ BC为△ADC的中线，∴ AB＝BD．即BF＝BD．在△FCB与△DCB中，,,,BF BDFBC DBC BC BC=⎧⎪∠=∠⎨⎪=⎩∴△FCB≌△DCB（SAS）．∴ CF＝CD．即CD＝2CE．(2)．作以角平分线为对称轴的翻折变换构造全等三角形2、已知：如图所示，在△ABC中，∠C＝2∠B，∠1＝∠2．求证：AB＝AC＋CD．【答案与解析】证明：在AB上截取AE＝AC．在△AED与△ACD中，()12()() AE ACAD AD=⎧⎪∠=∠⎨⎪=⎩已作，已知，公用边，∴△AED≌△ACD（SAS）．∴ ED＝CD．∴ ∠AED ＝∠C(全等三角形对应边、角相等)．又∵ ∠C ＝2∠B ∴∠AED ＝2∠B ．由图可知：∠AED ＝∠B ＋∠EDB ，∴ 2∠B ＝∠B ＋∠EDB ．∴ ∠B ＝∠EDB ．∴ BE ＝ED ．即BE ＝CD ．∴ AB ＝AE ＋BE ＝AC ＋CD(等量代换)．【点评】本题图形简单，结论复杂，看似无从下手，结合图形发现AB ＞AC ．故用截长补短法．在AB 上截取AE ＝AC ．这样AB 就变成了AE ＋BE ，而AE ＝AC ．只需证BE ＝CD 即可．从而把AB ＝AC ＋CD 转化为证两线段相等的问题．举一反三：【变式】如图，AD 是ABC ∆的角平分线，H ，G 分别在AC ，AB 上，且BD HD =.(1)求证：B ∠与AHD ∠互补；(2)若︒=∠+∠1802DGA B ，请探究线段AG 与线段AH 、HD 之间满足的等量关系，并加以证明.【答案】证明：（1）在AB 上取一点M, 使得AM ＝AH, 连接DM.∵ ∠CAD＝∠BAD, AD＝AD,∴ △AHD≌△AMD.∴ HD＝MD, ∠AHD＝∠AMD.∵ HD＝DB,∴ DB＝ MD.∴ ∠DMB＝∠B.∵ ∠AMD＋∠DMB ＝180︒,∴ ∠AHD＋∠B＝180︒.即 ∠B 与∠AHD 互补.（2）由（1）∠AHD＝∠AMD, HD＝MD, ∠AHD＋∠B＝180︒.∵ ∠B＋2∠DGA ＝180︒,∴ ∠AHD＝2∠DGA.∴ ∠AMD＝2∠D GM.∵ ∠AMD＝∠DGM＋∠GDM.∴ 2∠DGM＝∠DGM＋∠GDM.∴ ∠DGM＝∠GDM.∴ MD＝MG.∴ HD＝ MG.∵ AG＝ AM ＋MG,∴ AG＝ AH ＋HD.（3）.利用截长(或补短)法作构造全等三角形：3、如图所示，已知△ABC 中AB ＞AC ，AD 是∠BAC 的平分线，M 是AD 上任意一点，求M G H D C A证：MB －MC ＜AB －AC ．【答案与解析】因为AB ＞AC ，则在AB 上截取AE ＝AC ，连接ME ．在△MBE 中，MB －ME ＜BE （三角形两边之差小于第三边）．在△AMC 和△AME 中，()()()AC AE CAM EAM AM AM =⎧⎪∠=∠⎨⎪=⎩所作，角平分线的定义，公共边， ∴ △AMC ≌△AME （SAS ）．∴ MC ＝ME （全等三角形的对应边相等）．又∵ BE ＝AB －AE ，∴ BE ＝AB －AC ，∴ MB －MC ＜AB －AC ．【点评】因为AB ＞AC ，所以可在AB 上截取线段AE ＝AC ，这时BE ＝AB －AC ，如果连接EM ，在△BME 中，显然有MB －ME ＜BE ．这表明只要证明ME ＝MC ，则结论成立．充分利用角平分线的对称性，截长补短是关键.举一反三：【变式】如图，AD 是△ABC 的角平分线，AB ＞AC,求证：AB －AC ＞BD －DC【答案】证明：在AB 上截取AE ＝AC,连结DE∵AD 是△ABC 的角平分线，∴∠BAD＝∠CAD在△AED 与△ACD 中 ⎪⎩⎪⎨⎧=∠=∠=AD AD CAD BAD AC AE∴△AED≌△ADC（SAS ）∴DE＝DC在△BED 中，BE ＞BD －DC E D B A即AB －AE ＞BD －DC∴AB－AC ＞BD －DC（4）.在角的平分线上取一点向角的两边作垂线段.4、如图所示，已知E 为正方形ABCD 的边CD 的中点，点F 在BC 上，且∠DAE ＝∠FAE ．求证：AF ＝AD ＋CF ．【答案与解析】证明： 作ME ⊥AF 于M ，连接EF ．∵ 四边形ABCD 为正方形，∴ ∠C ＝∠D ＝∠EMA ＝90°．又∵ ∠DAE ＝∠FAE ，∴ AE 为∠FAD 的平分线，∴ ME ＝DE ．在Rt △AME 与Rt △ADE 中，()()AE AE DE ME =⎧⎨=⎩公用边，已证，∴ Rt △AME ≌Rt △ADE(HL)．∴ AD ＝AM(全等三角形对应边相等)．又∵ E 为CD 中点，∴ DE ＝EC ．∴ ME ＝EC ．在Rt △EMF 与Rt △ECF 中，()(ME CE EF EF =⎧⎨=⎩已证，公用边)，∴ Rt △EMF ≌Rt △ECF(HL)．∴ MF ＝FC(全等三角形对应边相等)．由图可知：AF ＝AM ＋MF ，∴ AF ＝AD ＋FC(等量代换)．【点评】与角平分线有关的辅助线： 在角两边截取相等的线段，构造全等三角形；在角的平分线上取一点向角的两边作垂线段. 四边形ABCD 为正方形，则∠D ＝90°．而∠DAE ＝∠FAE 说明AE 为∠FAD 的平分线，按常规过角平分线上的点作出到角两边的距离，而E 到AD 的距离已有，只需作E 到AF 的距离EM 即可，由角平分线性质可知ME ＝DE ．AE ＝AE ．Rt △AME 与Rt △ADE 全等有AD ＝AM ．而题中要证AF ＝AD ＋CF ．根据图知AF ＝AM ＋MF ．故只需证MF ＝FC 即可．从而把证AF ＝AD ＋CF 转化为证两条线段相等的问题．5、如图所示，在△ABC 中，AC=BC ，∠ACB=90°，D 是AC 上一点，且AE 垂直BD的延长线于E， AE=BD，求证：BD是∠ABC的平分线．【答案与解析】证明：延长AE和BC，交于点F，∵AC⊥BC，BE⊥AE，∠ADE=∠BDC（对顶角相等），∴∠EAD+∠ADE=∠CBD+∠BDC．即∠EAD=∠CBD．在Rt△ACF和Rt△BCD中．所以Rt△ACF≌Rt△BCD（ASA）．则AF=BD（全等三角形对应边相等）．∵AE=BD，∴AE=AF，即AE=EF．在Rt△BEA和Rt△BEF中，则Rt△BEA≌Rt△BEF（SAS）．所以∠ABE=∠FBE（全等三角形对应角相等），即BD是∠ABC的平分线．【点评】如果由题目已知无法直接得到三角形全等，不妨试着添加辅助线构造出三角形全等的条件，使问题得以解决．平时练习中多积累一些辅助线的添加方法.。

三角形全等之倍长中线（习题）➢例题示范例1：已知：如图，在△ABC 中，AB ≠AC ，D ，E 在BC 上，且DE =EC ，过D 作DF ∥BA 交AE 于点F ，DF =AC ．求证：AE 平分∠BAC ． 【思路分析】 读题标注：见中线，要倍长，倍长之后证全等．结合此题，DE =EC ，点E 是DC 的中点，考虑倍长，有两种考虑方法： ①考虑倍长FE ，如图所示： ②考虑倍长AE ，如图所示：A B DCE F？？G？？FECDBA （这个过程需要考虑倍长之后具体要连接哪两个点）倍长中线的目的是为了证明全等：以方法①为例，可证△DEF ≌△CEG ，由全等转移边和角，重新组织条件证明即可． 【过程书写】证明：如图，延长FE 到G ，使EG =EF ，连接CG ． 在△DEF 和△CEG 中， ∴△DEF ≌△CEG （SAS ） ∴DF =CG ，∠DFE =∠G∵DF =AC ∴CG =AC ∴∠G =∠CAE ∴∠DFE =∠CAE ∵DF ∥AB ∴∠DFE =∠BAE ∴∠BAE =∠CAE ∴AE 平分∠BAC➢ 巩固练习1.已知：如图，在△ABC 中，AB =4，AC =2，点D 为BC 边的中点，且AD 是整数，则AD =________．2.已知：如图，BD 平分∠ABC 交AC 于D ，点E 为CD 上一点，且AD =DE ，EF ∥BC 交BD 于F ． 求证：AB =EF ．3.已知：如图，在△ABC 中，AD 是BC 边上的中线，分别以AB ，AC 为直角边向外作等腰直角三角形，AB =AE ，AC =AF ，∠BAE =∠CAF =90°．求证：EF =2AD ．如图，在△ABC 中，AB >AC ，E 为BC 边的中点，AD 为∠BAC 的平分线，过E 作AD 的平行线，交AB 于F ，交CA 的延长线于G ．求证：BF =CG ．4.如图，在四边形ABCD 中，AD ∥BC ，点E 在BC 上，点F 是CD 的中点，连接AF ，EF ，AE ，若∠DAF =∠EAF ，求证：AF ⊥EF ．F E DCBAG FEDCBA➢ 思考小结1.如图，在△ABC 中，AD 平分∠BAC ，且BD =CD ． 求证：AB =AC ．比较下列两种不同的证明方法，并回答问题． 方法1：如图，延长AD 到E ，使DE =AD ，连接BE 在△BDE 和△CDA 中 ∴△BDE ≌△CDA （SAS ） ∴AC =BE ，∠E =∠2 ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC 方法2：如图，过点B 作BE ∥AC ，交AD 的延长线于点E ∵BE ∥AC ∴∠E =∠2在△BDE 和△CDA 中 ∴△BDE ≌△CDA （AAS ） ∴BE =AC∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E21ECDBA 21ECDBA∴AB=BE∴AB=AC相同点：两种方法都是通过辅助线构造全等，利用全等转移条件进而解决问题．方法1是看到中点考虑通过___________构造全等，方法2是通过平行夹中点构造全等．不同点：倍长中线的方法在证明全等时，利用的判定是________，实质是构造了一组对应边相等；利用平行夹中点证明全等时，利用的判定是_____，实质是利用平行构造了一组_____相等．2.利用“倍长中线”我们就可以证明直角三角形中非常重要的一个定理：直角三角形斜边中线等于斜边的一半．请你尝试进行证明．已知：如图，在Rt△ABC中，∠BCA=90°，CD是斜边AB的中线．求证：CD 1AB．2【参考答案】➢巩固练习1.22.证明略（提示：延长FD到点G，使得DG=DF，连接AG，证明△ADG≌△EDF，转角证明AB=EF）3.证明略（提示：延长AD到点G，使得GD=AD，连接CG，证明△ABD≌△GCD，△EAF≌△GCA）4.证明略（提示：延长FE到点H，使得EH=FE，连接CH，证明△BFE≌△CHE，转角证明BF=CG）5.证明略（提示：延长AF交BC的延长线于点G，证明△ADF≌△GCF，转角证明AF⊥EF）➢思考小结1.倍长中线SAS AAS 角2.证明略。