2017年春季学期新版青岛版九年级数学下学期5.7、二次函数的应用课件1

5.4 二次函数的图象和性质（3）
学习目标
1．会用描点法画出二次函数y=a(x-h)2+k 的图像； 2．知道抛物线y=a(x-h)2+k的对称轴与顶点坐标.
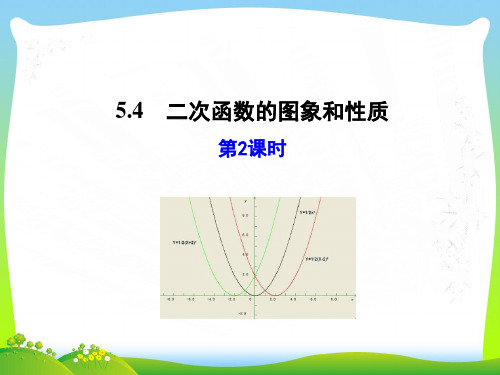
在同一坐标系中作出二次函数
y=3x²,y=3(x-1)2和y=3(x-
1)2+2的图象.
二次函数y=3x²,y=3(x-1)2和 y=3(x-1)2+2的图象有什么关
x=1
开口向上, 当x=1时y有 最小值，且 最小值= -2.
先想一想,再总结 二次函数y=a(xh)2+k的图象和性 质.
二次函数y=a(x-h)2+k的性质
几种形式的二次函数的图象之间的关系
1.判断正误: (1)二次函数y=5x2与y=-5(x+1)2+3的图象的开口大小不一样.( ) (2)在二次函数y=a(x-h)2+k中,a决定抛物线的开口方向和开口大 小,k,h决定抛物线的位置.
二次函数y=a（x-h）²+k的性质是什么？它的图 象有何特征？
特殊形式的二次函数之间，如何经过平移得到？
D√ .向左平移2个单位长度,再向下平移3个单位长度
(图象法):二次函数y=2(x-1)2+k的图象开口向上,对称轴为直线x=1,画出大致图象, 如图.
(甘肃兰州中考)抛物线y=(x-1)2-3的对称轴是
A.y轴
B.பைடு நூலகம்线x=-1
C√.直线x=1
D.直线x=-3
()
已知a,h,k为三数,且二次函数y=a(x-h)2+k在坐标平面上的图形通 过(0,5),(10,8)两点.若a<0,0<h<10,则h之值可能是 ( )

当l 取顶点的横坐标时，
这个函数有最大值.
O
5 10 15 20 25 30
因此，当l=-
2ba= -
30 =15， 2×(-1)
l
即l 是15m时，场地的面
积S最大（S=225㎡).
一般地，因为抛物线y=ax2+bx+c的顶点是最低（高）点，所以
当
时，二次函数y=ax2+bx+c有最小（大）
值.
大？
分析：先写出S与l的函数关系式，再求出使S最大的l值.
矩形场地的周长是60m，一边长为l，则另一边长为
m.场地的面积:
S=l(30-l)(0即<lS<=3-l02+).30l
请同学们画出此函数的图象
S 可以看出，这个函数的图
象是一条抛物线的一部分，
这条抛物线的顶点是函数
200
图象的最高点，也就是说， 100
∴x=2.5时，y极大值=6125
怎样确 定x的取 值范围
你能回答了吧！
由(1)(2)的讨论及现在的销售情况,你知道应该如何
定价能使利润最大了吗?
解决这类题目的一般步骤
（1）列出二次函数的解析式，并根据自变量的实际 意义，确定自变量的取值范围； （2）在自变量的取值范围内，运用公式法或通过配 方法求出二次函数的最大值或最小值.
润是__x_+_1_0__元，这种篮球每月的销售量是 500-10 个(用
x的代数式表示).
x
(2)8000元是否为每月销售篮球的最大利润?
如果是，说明理由，如果不是，要求出最大月利润,
此时篮球的售价应定为多少元?
8000元不是每月最大利润，最大月利润为9000元，此时篮

1、若将抛物线y=-2（x-2）2的图象的 顶点移到原点，则下列平移方法正确 的是（ C ） A、向上平移2个单位 B、向下平移2个单位 C、向左平移2个单位 D、向右平移2个单位
2、抛物线y=4（x-3）2的开口方向 向上 ， 对称轴是 直线x=3，顶点坐标 是 （3，0） ，抛物线是最 低 点， 当x= 3 时，y有最 小 值，其值为 0 。 抛物线与x轴交点坐标 （3，0） ，与y轴交 点坐标 （0，36）。
2
2个单位
y 1 x2 2
向右-1 平移 y 1 (x 2)2
2个-2 单位
2
顶点(－2,0)
向左平移 2个单位
顶点(0,0)
向右-3 平移 2个-4 单位
顶点(2,0)
直线x=－2
向左平移对称轴:y轴 向右平移 2个单位即直线: x=0 2个单位
直线x=2
一般地,抛物线y=a(x－h)2有如下特点:
得到，当c<0时，函数y=ax2+c的图象可由y=ax2的图
象向 下 平移 |c| 个单位得到，顶点是(0,c)，对
称轴是y轴，抛物线的开口方向由a的符号决定
y 10
9 8 7 6 5 4 3 2 1
-5 -4 -3 -2 -1 o 1 2 3 4 5 x
上加下减
(1)函数y=4x2+5的图象可由y=4x2的图象 向上 平移5 个单位得到；y=4x2-11的图象 可由 y=4x2的图象向下 平移11个单位得到。
（4）抛物线y=7x2-3的开口 上 ，对称轴是y轴 ， 顶点坐标是 (0,-3) ，在对称轴的左侧，y随x的增大 而减小，在对称轴的右侧，y随x的增大而 增大， 当x= 0 时，取得最 小 值，这个值等于 -3 。

5.4 二次函数的图象和性质
第1课时
1.知道二次函数的图象是抛物线； 2.会画y=ax2的图象，并能结合图象理解y=ax2的性 质.
思考
一次函数的图象是一条直线，反比例函数的图象 是双曲线，二次函数的图象是什么形状呢？通常怎样 画一个函数的图象？
用描点法画二次函数y=x2的图象 观察y=x2的表达式,选择适当x值,并计算 相应的y值，完成下表：
逐渐变小的有___①__④__⑤___(填题号)．
通过本课时的学习，需要我们掌握： 1.二次函数y=ax2的图象是什么？ 2.二次函数y=ax2的图象有什么性质？ 3.抛物线y=ax2 与y=-ax2有怎样的关系？
• 9、春去春又回，新桃换旧符。在那桃花盛开的地方，在这醉人芬芳的季节，愿你生活像春天一样阳光，心情像桃花一样美丽，日子像桃子一样甜蜜。 2020/12/172020/12/17Thursday, December 17, 2020
你能根据表格中的数据作出 猜想吗？
描点,连线
y
1
-4 -3 -2 -1 -1
0
1 23
4x
-2
-3
-4
y=-x2
二次函数y= -x2 的图象是抛物线.
二次函数y= -x2 的图象与y= x2 的图象关于x轴对称，
顶点都为原点，但原点是二次函数y= -x2的最高点，却是 y= x2 的最低点.
请同学们在同一坐标系内画出y= - 0.5x2,y = -2x2的图象， 并考虑这些抛物线有什么共同点和不同点.主要从以下 几个方面考虑： 1.开口方向 2.开口大小 3.对称轴 4.顶点坐标 5.有最高点还是有最低点
1.物体从某一高度落下，已知下落的高度h(m)和下落的时间 t(s)的关系式是:h=4.9t2，h是t的二次 函数，它的图象的 顶点坐标是（0，0）.

y =-1x+12
2 －4 －2
－2
－4
－6
y = - 1 x2 2
y =-1x-12
2
a＞0时，开口_向__上__, 最 低____ 点是顶点;
a＜0时，开口_向__下__, 最 _高___ 点是顶点;
2 4 对称轴是 直线x=h ， 顶点坐标
是 (h，0) 。在对称轴左侧（x<h)y随x的….
y=a(x+h)2的图象
y随x的增
大而增大
y随x的增
大而减小
画出二次函数 y=-1x+12,y=-1x-12 的图象，
2
2
并考虑它们的开口方向、对称轴和顶点．
x
··· －3 －2 －1 0 1 2 3 ···
y = - 1 x +12
2
··· －2
-1 2
0
-1 2
－2 －4.5 －8
···
y = - 1 x -12
2
··· －8 －4.5 －2
a＞0时，开口__向_上__, 最 _低___ 点是顶点;
a＜0时，开口_向__下__, 最 _高___ 点是顶点;
对称轴是 直线x=-h ， 顶点坐标是 (-h，0)
在对称轴左侧（x<-h)y随x的增大而…..
1.抛物线y=0.5(x+2)2可以由抛物线y=0.5x2 先向左 位得到.
2.已知s= –(x+1)2，当x为–1 时，s取最大 值 为0
左侧
y=ax2
a＞0 向上 y轴 a＜0 向下 y轴
a＞0 向上 y轴
y=ax2+c a＜0 向下 y轴
（0,0） （0,0）

2.已知二次函数y=-(x+1)2+3，它的图象 开口__向__下__，有最__高___点，顶点坐标 是_(_-1_，__3_)_.
03 探究新知
小明家要用60米的篱笆围成一个矩形菜园，怎样 设计才能使菜园的面积最大？最大面积是多少？

小明家要用60米的篱笆围成一个矩形菜园，怎样设计才 能使菜园的面积最大？最大面积是多少？ 解：设矩形菜园的一边长为x米，则另一边长为22y5 (15，225) （30-x）米，对应的矩形菜园面积为y平方米. 根据题意得： y=x(30-x)=-x2+30x=-(x-15)2+225.
用二次函数解决最大（小）值问题的步骤：
设出变量
变量要分清！
列出函数关系式
求解 检验结果是否符合题意
配方要谨慎！
如图，ABCD 是一块边长为2 m的正方形铁板，在边AB
上选取一点M，分别以AM和MB为边截取两块相邻的正
方形板料.当AM的长为何值时，截取的板料面积最小？
D
C
A
MB
2m
解：设AM的长为x m，则BM的长为（2-x）m，以AM和BM
∵a=-1<0，∴这个二次函数的图象开口向下， ∴顶点（15，225）是图象的最高点. ∴当x=15时，y有最大值为225.经检验，符合题意.O 15 30 x ∴当菜园的一边长为15 m时，矩形菜园面积最大， 最大面积为225 m2.
关于二次函数y=ɑx2+bx+c（ɑ≠0）的最值
最大值
-
b 2a
为边的两个正方形面积之和为y m2.
D
C
根据题意得， y=x2+(2-x)2
=2x2-4x+4
=2(x-1)2+2.

y
. 1 B．(1,2.25 ） .
AA(0,1.25) 1.25
2.25
O
Cx
用抛物线的知识解决生活中的一些实际问题的一般步骤：
建立直角坐标系
二次函数 问题求解
注意变量的取值范围
找出实际问题的答事如意
20
10
…
若日销售量 y 是销售价 x 的一次函数。 （1）求出日销售量 y（件）与销售价 x（元） 的函数关系式； （2）要使每日的销售利润最大，每件产品 的销售价应定为多少元？此时每日销售利润是 多少元？
，
分析：把实际问题转化 为平面直角坐标系里的 二次函数问题，并且把 实际问题上的数字 标 记在平面直角坐标系里。
谈一谈：你对两种不同直角坐标系的认识。
如图是某公园一圆形喷水池，水流在各方向沿形状相同的抛物线
落下，如果喷头所在处A距地面1.25米,水流路线最高处B距地面
2.25米,且距水池中心的水平距离为1米.试建立适当的坐标系,表示
该抛物线的解析式为
,如果不考虑其他因素，那
么水池的半径至少要 米，才能使喷出的水流不致落到池外。
中小学精编教育课件
5.7 二次函数的应用 第2课时
1. 二次函数y=a(x-h)2+k的图象是一条
称轴是
，顶点坐标是
.
，它的对
2 . 二次函数y=ax2+bx+c的图象是一条
，它的对称
轴是
，顶点坐标是
. 当a>0时，抛
物线开口向 ，有最 点，函数有最 值，是
；当
a<0时，抛物线开口向 ，有最 点，函数有最 值，
是
。
用抛物线的相关知识解决生活中的 一些实际问题；

成读 的书
两，
件要
事么
。旅
。行
，
身
体
和
灵
魂
总
要
东平县初中数学
我们，还在路上……
如图，ABCD是一块边长为2m的正方形铁板，在边AB上选 取一点M，分别以AM和MB为边截取两块相邻的正方形板材. 当AM的长为何值时，截取的板材面积最小？
分析：截取板材面积=正方形 AMPQ面积+正方形MBEF面积.由 已知可以构造二次函数，利用二次 函数性质解决……
D

B
1、教材51页挑战自我。 2、教材52页练习1.
（高）点，所以： 当 x b 时，
2a
二次函数y=ax2+bx+c有最小（大）值 4 ac b 2 . 4a
变式练习：用篱笆围成一个一边靠墙中间隔有一道篱笆的 的矩形菜园，已知篱笆的长度为60m，应该怎样设计才使 菜园的面积最大？最大面积是多少？
若墙的最大可利用面积为20m，那么x的取值范围？ 菜园的面积最大时，菜园的宽x等于多少？、
解函数应用题的一般步骤:
设未知数(确定自变量和函数);
找等量关系,列出函数关系式;
化简,整理成标准形式(一次函数、二次函 数等);
求自变量取值范围；
利用函数知识，求解（通常是最值问 题）；
写出答案。
有古
一人
个云
在：
路“
上读
。万
”卷
从书
古，
至行
今万
，里
学路
习。
和”
旅今
行人
都说
是：
相“
辅要
相么
You made my day!
5.7 二次函数的应用

将A、B、C三点坐标代入得：
a-b+c=6
16a+4b+c=6
9a+3b+c=2
解得：
a=1, b=-3,
c=2
所以：这个二次函数表达式为：
y ox
y=x2-3x+2
封面 例题
小组探究
1、已知二次函数对称轴为x=2，且过（3，2）、（-1,10）两点，求二次函数的表达式。
解：设y=a(x-2)2-k
2、已知二次函数极值为2，且过（3，1）、 （-1,1）两点，求二次函数的表达式。
解：设y=a(x-h)2+2
用待定系数法求函数表达式的一般步骤:
1 、设出适合的函数表达式； 2 、把已知条件代入函数表达式中，得到关于 待定系数的方程或方程组； 3、 解方程（组）求出待定系数的值； 4、 写出一般表达式。
2、已知抛物线y=a(x-h)2+k (a≠0)
若顶点坐标是（-3,4）, 则h=_-_3___,k=__4____，
代入得 y=_a_(_x_+_3_)2_+_4______
若对称轴为直线x=1，则h= _____1____
代入得y=__a_(x_-_1_)_2+_k______
课前复习
二次函数有哪几种表达式？
• 一般式：y=ax2+bx+c (a≠0) • 顶点式：y=a(x-h)2+k (a≠0)
例题选讲
例 1 已知抛物线的顶点为（－1，－6），与轴交点为
（2，3）求抛物线的表达式？
解：因为二次函数图像的顶点坐标是（－1，－6），
一般式： y=ax2+bx+c
所以，设所求的二次函数为 y=a(x＋1)2-6

例1、下列函数中，哪些是二次函数？若是, 分别指出二次项系数,一次项系数,常数项.
（1）y=3(x-1)²+1
(2)y=x+
_1_ x
(3)s=3-2t² (5)y=_x1_²-x
(4)y=(x+3)²-x² (6)v=10πr²
说明:
判断一个函数是否是二次函数, 看它是否化简 成y=ax2+bx+c（a、b、c为常数且a≠0）的形式。
1、二次函数定义:一般地, 形如y=ax²+bx+c（a， b，c是常数，a≠0）的函数叫做二次函数。
2、判断一个函数为二次函数的方法与步骤: （1）先将函数进行整理, 使其右边是含自 变量的代数式, 左边是应变量; （2）判别含自变量的代数式是否为整式; （3）判别含自变量的项的最高次数是否为2; （4）判别二次项的系数是否为0。
y 1200x 2 2400x 1200
上述三个问题中的函数解析式具有哪些共同的特征?
经化简后都具有y=ax²+bx+c 的形式．
(a，b，c是常数，a≠0
)
定义:一般地, 形如y=ax²+bx+c(a，b，c是 常数，a≠0)的函数叫做x的二次函数。其
中:a为二次项系数, b为一次项系数, c为常数 项注．意:
解：（1）a 0
(2)a 0,b 0
(3)a 0,b 0, c 0
1、下列函数中，（x,t是自变量），哪些是二 次函数？( C )
A y=ax2+bx+c
B y2=x2-4x+1
C y=x2
D y=2+ √x2+1
2、函数 y=(m-n)x2+ mx+n 是二次函数的条件 是( C ) A、m，n是常数，且m≠0 B、m，n是常数， 且n≠0 C、m，n是常数，且m≠n D、m，n为任何实