断裂力学
- 格式:docx
- 大小:3.74 MB
- 文档页数:16


材料的断裂力学分析在材料科学和工程领域中,断裂力学是一门研究材料在外力作用下如何发生破坏的学科。
通过断裂力学的分析,我们可以了解材料在正常使用条件下的破坏原因,以及如何提高材料的断裂韧性和强度。
本文将对材料的断裂力学进行详细分析。
1. 断裂力学的基本概念在了解材料的断裂力学之前,我们需要了解几个基本概念。
1.1 断裂断裂是指材料在外部应力作用下发生破坏、分离的过程。
断裂可以分为韧性断裂和脆性断裂两种类型。
韧性断裂是指材料在破坏之前会出现塑性变形,具有一定的延展性;而脆性断裂是指材料在外力作用下迅速发生破坏而不发生明显的塑性变形。
1.2 断裂韧性断裂韧性是指材料抵抗断裂破坏的能力。
一个具有高断裂韧性的材料可以在外力作用下发生一定程度的塑性变形,从而使其拉伸长度增加。
1.3 断裂强度断裂强度是指材料在破坏前能够承受的最大应力。
断裂强度可以通过拉伸实验等方式进行测定。
2. 断裂力学的分析方法断裂力学的分析方法主要有线弹性断裂力学和非线弹性断裂力学两种。
2.1 线弹性断裂力学线弹性断裂力学假设材料在破坏前的行为是线弹性的,并且材料的破坏是由于应力达到了一定的临界值所引起的。
在线弹性断裂力学中,断裂过程可以通过应力强度因子和断裂韧性来描述。
2.2 非线弹性断裂力学非线弹性断裂力学考虑了材料在破坏前的非线性行为,如塑性变形、蠕变等。
非线弹性断裂力学可以更准确地预测材料的破坏行为,但其计算复杂度较高。
3. 断裂力学的应用断裂力学在材料科学和工程中具有广泛的应用。
3.1 破坏分析通过断裂力学的分析,我们可以确定材料在受力状态下的破坏原因,从而改进材料的设计和制备工艺。
例如,在航空航天领域,对材料的断裂力学进行精确分析可以提高飞行器的安全性和可靠性。
3.2 材料评估通过断裂力学的测试和分析,我们可以评估材料的断裂韧性和强度,为材料的选择和应用提供依据。
这对于许多行业来说是至关重要的,如汽车制造、建筑工程等。
3.3 研发新材料断裂力学的理论和实验研究对于开发新的高性能材料具有重要意义。


断裂力学理论及应用研究断裂是指材料在外部加载下受到破坏产生裂纹或破片分离的物理过程,是所有材料科学中重要的研究领域之一。
断裂力学理论涉及力学、物理、化学等学科,是从宏观探讨结构构件断裂行为规律的一门学科。
本文主要从断裂力学理论的基本概念、发展历程、应用研究等方面进行探讨。
一、断裂力学理论的基本概念断裂力学理论的基本概念包括断裂韧性、应力场、应变场等。
1. 断裂韧性断裂韧性是材料断裂过程中抵抗裂纹扩展的能力。
对于材料强度越高的材料,其断裂韧性一般也越高。
一个材料的断裂韧性大小可以通过测量其断裂过程中断裂面上的裂纹扩展能量来确定。
当裂纹扩展时,其边缘会释放出能量,断裂韧性就是指在裂纹在材料中传播的过程中能够消耗这些能量的材料性质。
2. 应力场在载荷下,一个构件内的所有部分都会承受不同的应力。
应力场指的是构件内各点的应力分布状态。
应力场是描述材料内部应力状态的最基本模型。
例如,当一个材料受到拉压载荷时,其内部就会产生相应的拉伸和压缩应力。
3. 应变场应变是指材料受到外力后的形变程度,是衡量材料变形能力的重要指标。
与应力场类似,应变场指的是材料内部各点的应变状态。
例如,在机械制造过程中,材料会受到剪切应力,这会导致材料存在剪切应变。
二、断裂力学理论的发展历程断裂力学理论的发展历程可以简单划分为以下阶段:经验试验阶段、线弹性断裂力学阶段、实验与理论相结合阶段、转捩点理论阶段以及非线性断裂力学阶段。
1. 经验试验阶段经验试验阶段是断裂力学理论的雏形阶段。
在这个阶段,人们通过实验来探究材料的断裂行为,并总结出了一些经验规律。
例如,在实验中,人们发现时强度与应力之间成正比关系,这就为后来的弹性断裂力学理论的发展提供了依据。
2. 线弹性断裂力学阶段线弹性断裂力学阶段是断裂力学理论的基础阶段。
这个阶段出现了很多具有代表性的理论,例如弹性理论、能量释放率理论以及裂纹扩展跟踪技术等。
在这个阶段中,人们主要依靠线弹性理论来探究材料断裂规律。

理论与应用断裂力学断裂力学是研究材料在外部载荷作用下发生裂纹和断裂的科学,它涉及材料的断裂行为、裂纹扩展规律、断裂韧性等内容,具有广泛的理论与应用价值。
断裂力学不仅是材料科学与工程的重要组成部分,还在实际工程中起着重要的作用。
在航空航天、汽车工业、建筑工程、能源领域等各个领域,断裂力学都被广泛应用,并为材料设计与结构可靠性提供了重要的理论指导。
一、断裂力学的基本原理1. 断裂力学的基本概念断裂力学是研究材料在外部载荷作用下发生裂纹和断裂的科学。
断裂是指材料在外部力作用下发生的破坏过程,其本质是裂纹的生成、扩展和相互作用。
断裂行为受到外部载荷、裂纹形态、材料性能等多种因素的影响。
2. 裂纹力学与断裂韧性裂纹力学是断裂力学的基础理论,它描述了裂纹在材料中的行为。
裂纹尖端附近的应力场具有奇异性,裂纹尖端处的应力集中导致材料发生拉伸和剪切破坏,从而导致裂纹的扩展。
断裂韧性是衡量材料抗裂纹扩展能力的参数,它描述了材料在裂纹扩展过程中所能吸收的能量大小。
3. 断裂力学的应用范围断裂力学不仅涉及金属材料、混凝土、陶瓷材料等传统材料,还包括了纳米材料、复合材料等新型材料。
它在制造领域、材料科学、产品设计等领域都有重要的应用价值。
二、断裂力学的研究方法1. 实验方法实验是研究断裂力学的重要手段。
通过拉伸试验、冲击试验、疲劳试验等实验方法,可以获得材料的断裂行为、裂纹扩展规律、断裂韧性等重要参数。
实验结果可以验证理论模型的准确性,为理论研究提供数据支持。
2. 数值模拟方法数值模拟是断裂力学研究的重要手段之一。
有限元分析、分子动力学模拟等数值方法可以模拟材料的断裂过程,揭示裂纹扩展的规律,预测材料的断裂行为。
数值模拟方法在工程设计和材料优化中具有重要的应用价值。
3. 理论分析方法理论分析是断裂力学研究的基础。
裂纹力学理论、断裂力学理论等提供了描述裂纹扩展规律、预测裂纹扩展速率、计算断裂韧性等重要方法。
理论分析方法为工程实践提供了重要的指导,为材料设计提供了理论基础。
断裂是材料在外力作用下的分离过程,主要有脆性断裂和延性断裂延性断裂:有许多的 被称为韧窝的微型空洞组成,韧窝的形状因应力大小而定,韧窝的大小和深浅取决于第二相的数量分部以及基体塑性变形能力。
韧性断裂过程可以概括为微孔成核,微孔长大和微孔长大三个阶段。
内因 :材料本身的性质。
厚度,冶金因素。
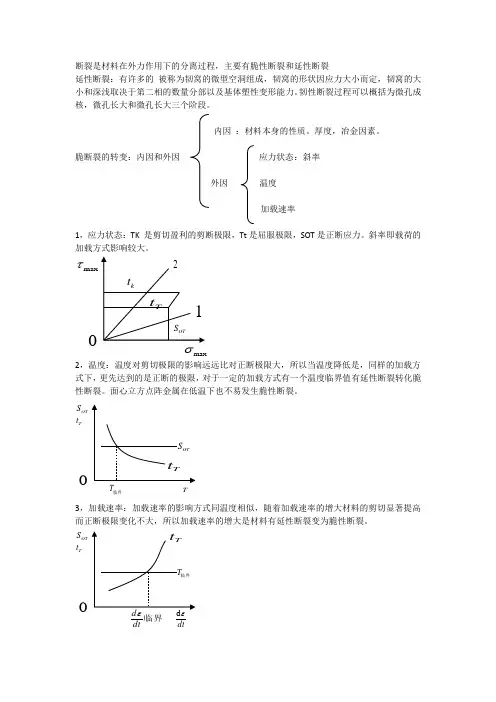
脆断裂的转变:内因和外因 应力状态:斜率 外因 温度加载速率1,应力状态:TK 是剪切盈利的剪断极限,Tt 是屈服极限,SOT 是正断应力。
斜率即载荷的加载方式影响较大。
2,温度:温度对剪切极限的影响远远比对正断极限大,所以当温度降低是,同样的加载方式下,更先达到的是正断的极限,对于一定的加载方式有一个温度临界值有延性断裂转化脆性断裂。
面心立方点阵金属在低温下也不易发生脆性断裂。
3,加载速率:加载速率的影响方式同温度相似,随着加载速率的增大材料的剪切显著提高而正断极限变化不大,所以加载速率的增大是材料有延性断裂变为脆性断裂。
O T TS t d dtεd d t临界O T TS t TT 临界maxτm axσ0断裂机制:第一类是由材料屈服为主的塑性破坏,第二类是一裂纹失稳扩展的断裂破坏。
缺陷对两类破坏都有重要影响,但是机制不同。
塑性破坏而言缺陷主要影响了结构的有效承载面积,破坏的临界条件主要有塑性极限载荷控制。
裂纹失稳扩展的断裂而言缺陷引起的局部应力应变场对结构强度起主导作用。
高强材料:断裂时,裂纹端部发生很小的的屈服:线弹性断裂力学理论。
含有裂纹的材料 延性材料:断裂时裂纹端部发生很大的屈服:弹塑性断裂力学理论。
完全塑性材料:断裂时构件整体发生均匀屈服:塑性材料断裂力学。
剩余强度:含有裂纹的结构在使用过程中任意时刻所具有的承载能力就被称为剩余强度。
所有的断裂理论的落脚点都是比较剩余强度和设计强度的大小。
能量分析:英国物理学家Griffith,在1921年首次提出了裂纹扩展时能量释放的概念。
找他的理论解释,裂纹的上下表面形成导致了应变能的释放。


材料力学中的断裂力学材料力学是研究物质在外力作用下变形、损伤和破坏行为的一门学科。
断裂力学是材料力学中的一个重要分支,研究的是材料在受到外力作用时出现破坏的现象及其规律。
断裂力学对于理解和预测材料破坏行为,具有重要的理论和实践意义,本文将就此展开讨论。
一、破坏的基本形式材料的破坏可分为两种基本形式:拉伸断裂和压缩断裂。
拉伸断裂是指在材料受到拉伸作用时,断口发生的破坏行为;压缩断裂是指在材料受到压缩作用时,断口发生的破坏行为。
除此之外,还有剪切断裂、扭转断裂、弯曲断裂等不同的破坏形式。
二、断裂力学的基本概念1.断裂应力材料在破坏前,能够承受的最大应力称为断裂应力。
断裂应力的大小与材料的强度、形状、尺寸、载荷方向等因素有关。
2.断裂韧性材料在破坏前能够吸收的最大能量称为断裂韧性。
断裂韧性的大小与材料的抗裂性能有关。
3.断裂强度材料在破坏前实际承受的最大应力称为断裂强度。
断裂强度与断裂应力的概念相似,但断裂强度是在材料实际破坏后测定得出的。
4.断裂韧度材料在破坏前能够吸收的最大能量密度称为断裂韧度。
断裂韧度与断裂韧性的概念类似。
三、断裂表征参数1.伸长率材料在破坏前拉伸变形的程度,也称为材料的变形量。
伸长率是指材料在拉伸断裂前的额定延长量比上原长度所得的比值。
2.缩颈率在材料拉伸断裂时,当材料的横截面积开始缩小,称为缩颈。
缩颈率是指材料在拉断时的截面积缩小量比上原截面积所得的比值。
3.断口形貌材料断口的形态与破坏机理有密切关系,通过观察断口形貌,可以较为直观地判断破坏机制。
四、断裂损伤机理材料的断裂破坏是一个复杂和多层次的过程,其损伤机理可以分为微观和宏观两个层次。
1.微观层次在微观层次上,材料的破坏主要是由裂纹的扩展和材料局部的塑性变形共同作用导致的。
材料的破坏前,裂纹的长度会随着载荷的增加而逐渐增加,当裂纹的长度达到一定程度时,就会出现快速扩展和破坏。
2.宏观层次在宏观层次上,材料的破坏主要是由断面剪切和拉伸引起的。


115第六章 断裂力学简介及材料典型强韧化机制§6.1 断裂的基本概念§6.1.1 断裂力学的产生和发展断裂是构件破坏的重要形式之一,影响材料断裂的因素很多,如构件的形状及尺寸,载荷的特征与分布,构件材料本身的状态及应用的环境如温度、腐蚀介质等,当然更重要的还有材料本身的强度水平。
为了防止构件的断裂或变形失效,传统的安全设计思想主要立足于外加载荷与使用材料的强度级别的选用,根据常规的强度理论,只要构件服役应力与材料的强度满足⎪⎪⎩⎪⎪⎨⎧=21m axK K s b σσσ(6- 1)则认为使用是安全的。
其中ζmax 为构建所承受的最大应力;ζ b,ζs 分别为材料的强度极限和屈服强度,K 1与K 2分别为按强度极限与按屈服强度取用的安全系数。
安全系数是一个大于1的数,其含义为扣除了材料中对强度有影响的诸因素对强度可能造成的损害作用,应当说这种考虑问题的出发点是合理的,也应当是行之有效的,因而多年来这种设计思想在工程设计中发挥了重要作用,而且还会继续发挥其重要作用。
关于断裂力学的最早理论可以追溯到1920年,为了研究玻璃、陶瓷等脆性材料的实际强度比理论强度低的原因,Griffith 提出了在固体材料中或在材料的运行过程中存在或产生裂纹的设想,计算了当裂纹存在时,板状构件中应变能的变化进而得出了一个十分重要的结果。
ζca =常数 (6- 2)其中,ζc 是断裂扩展的临界应力;a 为断裂半长度。
该理论非常成功地解释了玻璃等脆性材料的开裂现象,但应用于金属材料并不成功,又由于当时金属材料的低应力破坏事故并不突出,所以在很长一段时间内未引起人们的重视。
1949年E.Orowan 在分析了金属构件的断裂现象后对Griffith 公式提出了修正,他认为产生断裂所释放的应变能不仅能转化为表面能,也应转化为裂纹前沿的塑性应变功,而且由于塑性应变功比表面能大得多,以至于可以不考虑表面能的影响,其提出的公式为:ζca =212⎪⎭⎫⎝⎛λEU =常数 (6- 3)Orowan 公式虽然有所进步,但仍未超出经典的Griffith 公式的范围,而且同表面能一样,形变功U 也是难以测量的,因而该式仍难以实现工程上的的应用。

断裂力学
断裂力学
断裂力学是研究物质在外部应力作用下发生断裂现象的学科。
它涉及到材料力学、材料科学和工程等多个领域,对于了解材料的断裂行为以及相关工程应用具有重要意义。
在断裂力学中,力学行为可以通过弹性、塑性和粘弹性等理论来描述。
当物质承受外部应力超过其强度极限时,断裂现象就会发生。
断裂可以分为静态断裂和疲劳断裂两种形式。
静态断裂是指物质在单次应力作用下破裂,而疲劳断裂是指物质在多次应力循环作用下逐渐破裂。
断裂力学的研究内容包括断裂韧性、断裂强度、断裂机理等。
断裂韧性是材料抵抗断裂的能力,它与材料的韧性和强度有关。
断裂强度是指材料承受外部应力时的抗拆除能力。
断裂机理则是指断裂过程中发生的各种微观和宏观现象。
断裂力学的应用广泛,包括材料设计、结构工程、航空航天、汽车制造等领域。
通过研究断裂力学,可以提高材料和结构的安全性和可靠性,避免由于断裂引起的事故和损失。
总之,断裂力学是研究物质在外部应力作用下发生断裂现象的学科。
它对于了解材料的力学行为以及相关工程应用具有重要意义。
在研究断裂力学时,我们需要注意文章的逻辑清晰,流畅表达,避免包含不适宜展示的敏感词或其他不良信息,确保文章的质量和阅读体验。
断裂力学名词解释-概述说明以及解释1.引言1.1 概述在断裂力学领域,断裂现象是材料在承受外力作用下突然失效的过程。
这种突然失效可能导致严重的事故,因此研究断裂力学对于材料工程和结构设计具有重要意义。
本文将从断裂力学的基本概念入手,介绍塑性断裂和断裂韧性的相关理论和应用,并探讨其在工程领域中的实际意义。
通过深入分析断裂力学的相关名词和概念,可以更好地理解材料在断裂过程中的行为,为工程实践提供更可靠的依据。
1.2 文章结构文章结构部分内容:本文共分为引言、正文和结论三部分。
在引言部分中,将对断裂力学的概述进行介绍,解释本文的结构和目的。
正文部分将分为三个小节,分别讨论断裂力学、塑性断裂和断裂韧性的概念和相关内容。
最后在结论部分总结全文的内容并讨论其应用和未来展望。
文章结构清晰明了,有助于读者更好地理解和接受文章内容。
1.3 目的本文旨在通过对断裂力学相关名词的解释,帮助读者更深入地理解断裂力学领域的基本概念和原理。
通过对断裂力学、塑性断裂和断裂韧性等概念的深入讲解,读者可以了解不同类型的断裂行为及其在材料工程和结构设计中的重要性。
同时,通过本文的阅读,读者可以掌握相关名词的定义和内涵,为深入学习断裂力学奠定坚实基础。
通过本文的撰写,我们希望读者能够对断裂力学有一个全面而深入的理解,从而为工程实践中的断裂问题提供更有效的解决方案。
同时,我们也希望可以激发读者对断裂力学领域的兴趣,促进学术交流和探讨,推动该领域的发展和进步。
愿本文能够为读者带来启发和帮助,让我们共同探索断裂力学这一重要领域的奥秘。
2.正文2.1 断裂力学断裂力学是研究材料在外加载荷作用下如何发生裂纹和破坏的一门学科。
在工程学和材料科学领域中,断裂力学被广泛应用于预测材料的疲劳寿命、抗拉强度和韧性等参数。
断裂力学的基本原理是研究材料在受到外力作用下,裂纹会在材料内部扩展,并最终导致材料的破坏。
断裂力学中的一些重要概念包括裂纹尖端应力、裂纹尖端位移、裂纹扩展速率等。
理论与应用断裂力学断裂力学是指研究材料在机械外载作用下,如何发生破坏及其形成和扩展的科学。
断裂力学研究的对象是材料在断裂前、中、后的力学行为和损伤演变。
它是现代材料科学研究中重要的分支之一,具有广泛的理论应用价值。
本文将从理论与应用两个方面,介绍断裂力学的基本概念和发展现状。
一、理论1. 断裂力学的基本概念在强度学中,本质上我们研究的是材料最终破坏的强度,以及在材料破坏之前的稳定裂纹扩展行为。
由此,我们可以定义断裂强度和裂纹扩展强度。
并且,材料的断裂过程是在应力场下进行的,我们可以通过应力强度因子来描述应力状态下的断裂行为。
2. 断裂力学的发展现状近年来,随着计算机技术和数值模拟方法的不断发展,断裂力学从实验方法转为计算方法逐渐成为了主流。
借助高性能计算机,人们可以更准确地模拟复杂的物理过程,如图像处理、数值计算、信息处理等。
同时,人们也在从材料、构件、结构等不同层面建立对应的断裂力学体系,刻画材料的破坏机理和裂纹扩展行为,为现实应用提供可靠的理论依据。
二、应用1. 机械结构破坏分析在机械结构设计过程中,断裂力学可以帮助工程师更好地设计和优化结构,以便在使用寿命内实现最多的性能和安全。
这一流程包括确定材料强度参数、建立机械模型、检测和分析应力场、计算应力强度因子和模拟生命周期行为等。
2. 材料疲劳性能研究由于疲劳损伤在结构材料中的特殊作用,断裂力学能够有效地帮助人们更好地了解疲劳行为和裂纹扩展过程。
通过对复杂的疲劳裂纹扩展行为的数值模拟,可以确保结构的疲劳寿命至少与其设计寿命相当。
同时,材料型号和测试数据可以为工程师提供更好的信息,以更好地预测疲劳性能和生命周期。
3. 建筑结构安全评估断裂力学可以帮助我们更好地评估各种建筑结构的安全性。
结构元件的破坏状态和完整性可以通过计算应力强度因子、应力/应变超前。
实验强度和疲劳性能在结构纵向和横向上的分布。
基于断裂力学的这些分析方法,结构工程师可以更好地了解管道、桥梁、平台等建筑结构受力状态下的行为,预测结构的生命周期和维护需求,保证结构的安全性和性能。
断裂力学概述及应用定义:断裂力学(fracture mechanics) 是为解决机械结构断裂问题而发展起来的力学分支,它将力学、物理学、材料学以及数学、工程科学紧密结合,是一门涉及多学科专业的力学专业课程。
起源:1957年,美国科学家G.R.Irwin提出应力强度因子的概念, 线弹性断裂理论的重大突破,应力强度因子理论作为断裂力学的最初分支——线弹性断裂力学建立起来。
发展:现代断裂理论大约是在1948—1957年间形成,它是在当时生产实践问题的强烈推动下,在经典Griffith理论的基础上发展起来的,上世纪60年代是其大发展时期。
我国断裂力学工作起步至少比国外晚了20年,直到上世纪70年代,断裂力学才广泛引入我国,一些单位和科技工作者逐步开展了断裂力学的研究和应用工作。
从上世纪五十年代中期以来,断裂力学发展很快,目前线性理论部分已比较成熟,在工程方面,已广泛应用于宇航、航空、海洋、兵器、机械、化工和地质等许多领域。
分类:断裂力学的类型分为:线性断裂力学、弹塑性断裂力学、断裂动力学。
研究的内容包括了:裂纹的起裂条件、裂纹在外部载荷和(或)其他因素作用下的扩展过程、裂纹扩展到什么程度物体会发生断裂。
1.线性断裂力学:应用线弹性理论研究物体裂纹扩展规律和断裂准则。
1921年格里菲斯通过分析材料的低应力脆断,提出裂纹失稳扩展准则格里菲斯准则。
1957年G.R.欧文通过分析裂纹尖端附近的应力场,提出应力强度因子的概念,建立了以应力强度因子为参量的裂纹扩展准则。
线弹性断裂力学可用来解决脆性材料的平面应变断裂问题,适用于大型构件(如发电机转子、较大的接头、车轴等)和脆性材料的断裂分析。
实际上,裂纹尖端附近总是存在塑性区,若塑性区很小(如远小于裂纹长度),则可采用线弹性断裂力学方法进行分析。
2.弹塑性断裂力学:应用弹性力学、塑性力学研究物体裂纹扩展规律和断裂准则,适用于裂纹体内裂纹尖端附近有较大范围塑性区的情况。
损伤:在外载或环境作用下,由细观结构缺陷(如微裂纹、微孔隙等)萌生、扩展等不可逆变化引起的材料或结构宏观力学性能的劣化称为损伤。
损伤力学:研究材料或构件在各种加载条件下,其中损伤随变形而演化发展并最终导致破坏的过程中的力学规律。
损伤变量:把含有众多分散的微裂纹区域看成是局部均匀场,在场内考虑裂纹的整体效应,试图通过定义一个与不可逆相关的场变量来描述均匀场的损伤状态,这个场变量就是损伤变量。
损伤力学发展:损伤力学是近二十年才开始形成和发展的一门新的固体力学分支,它是将固体物理学、材料强度理论和连续介质力学统一起来进行研究的理论,弥补了微观研究和断裂力学研究的不足,越来越多地应用于航天航空、高温高压热力设备寿命评估和混凝土、复合材料、高分子材料质量评估计算,是一门有着无限广阔用途的新学科。
1958年,卡钦诺夫(Kachanov)在研究金属的蠕变破坏时,为了反映材料内部的损伤,第一次提出了“连续性因子”和“有效应力”的概念。
后来,拉博诺夫(Rabotnov)又引入了“损伤因子”的概念。
他们为损伤力学的建立和发展做了开创性的工作。
但在很长的一段时间内,这些概念和方法除了应用于蠕变问题的研究外,并未引起人们的广泛重视。
70年代初,“损伤”概念被重新提出来了。
值得指出的是法国学者勒梅特在这方面做出了卓越的贡献。
1971年勒梅特将损伤概念用于低周疲劳研究,1974年英国学者勒基(Leckie)和瑞典学者赫尔特(Hult)在蠕变的研究中将损伤理论的研究向前推进了一步。
70年代中期和末期各国学者相继采用连续介质力学的方法,把损伤因子作为一种场变量,并称为损伤变量;逐步形成了连续损伤力学的框架和基础。
80年代中期,能量损伤理论和几何损伤理论相继形成。
各国学者相继的研究成果,对损伤理论的形成和发展都做出了有益的贡献。
损伤力学与断裂力学的关系:断裂力学分析是假设结构内已存在一个或多个宏观裂纹,忽略裂纹扩展过程中材料性能的劣化及所导致的应力重分布,这种劣化在裂纹尖端区域尤其明显,故给结构强度与寿命预估带来较大的误差。
损伤力学是引入一个连续场变量来描述材料性能的劣化,由微裂纹和微孔洞的生长与聚合产生的宏观裂纹的临界状态来描述。
若建立起有效的分析模型,即可进行宏观裂纹尖端的损伤分析,当裂纹尖端单元的损伤值达到临界值,宏观裂纹就会扩展。
断裂的整个过程,即宏观裂纹的形成、起裂和扩展,都可用损伤力学分析。
损伤本构方程:宏观断口学:宏观断口学是利用肉眼或低倍放大镜,通过分析断口的色泽、粗糙度、各种条纹(例如发射状条纹、贝壳状条纹等)和宏观变形来确定分析裂纹源的位置、裂纹扩展方向、受力状态级可能的环境介质等,并进一步推断断口的性质和断裂的原因等显微断口学:是利用光学显微镜、投射电子显微镜和扫描电子显微镜来研究断口的显微形貌特征、形成机制及影响因素等。
它和宏观断口学研究结果互相补充及佐证,使人们能对断裂的全部过程有更深入和正确的了解。
韧性断裂:特点:材料断裂前发生明显的塑形变形。
也可以说塑形变形时韧断的前奏,而韧断是大量塑形变形的结果。
定义:构件经过大量变形后发生的断裂。
主要条件是超过工作压力,主要特征是发生了明显的宏观塑性变形(不包括压缩失稳),且产生延性断裂。
如杆件的过量伸长或弯曲、容器的过量鼓胀。
断口的尺寸(如直径、厚度)比原始尺寸也明显变化。
解理断裂:解理断裂是在正应力作用产生的一种穿晶断裂,即断裂面沿一定的晶面(即解理面)分离。
疲劳裂纹的萌生:表面(次表面、内部)疲劳裂纹的扩展:疲劳裂纹扩展机理:1、Laird—Smith裂纹扩展模型认为裂纹的亚临界扩展过程是裂纹尖端反复锐化和钝化过程。
也就是裂纹尖端金属材料在交变应力作用下,产生反复塑性变形的过程。
2、裂纹尖端“弱点”凝聚模型在正交的剪应力作用下,裂纹尖端出现一个弱化区。
这个弱化区可能是由于在晶界前的位错塞积所形成(图);也可能是由于夹杂物或第二相质点在交变应力作用下发生断裂,或夹杂物与基体界面发生开裂形成微孔(VOID)所致,出于局部交变剪切作用,使弱化区与裂纹前沿凝聚起来,从而使裂纹向前扩展如的长度。
疲劳裂纹扩展速率:对于疲劳裂纹扩展速率的研究,主要在于寻求裂纹扩展速率与有关各种力学参量之间的数学表达式。
如果在应力循环ΔN次之后,裂纹扩展量为Δa ,则应力每循环一周,裂纹扩展为Δa/ΔN (mm/周),这称为“裂纹扩展速率”,在极限条件下.用微分da/dN表示。
I Imax Imin max min )K K K ασασσσ∆=-==-在高周恒幅载荷下,将试验测得的数据经过整理画在lg da /dN —lg ΔKI 坐标系中,得到如图所示的曲线.这条曲线大致可以划分为三个阶段。
1.在第I 阶段内,应力强度因子幅度ΔKI 值很低。
当ΔKI 值小于某一界限值ΔKth 时,裂纹基本上不扩展[da /dN ≤10-7—10-8 mm/周)。
该界限值ΔKth 称为裂纹扩展的门槛值。
2. 随着ΔKI 继续增大,当ΔKI >ΔKth ,裂纹开始扩展到直线与曲线的转折点B1,这时裂纹扩展进入第II 区域。
在这一阶段,一般认为lg( da /dN)—lg Δ KI 关系是一条直线。
这是一个研究得最广泛、最深入的区域,也是最重要的裂纹扩展区域。
描述这一阶段da /dN 的表达式有数十个之多,其中最简单,用得最广泛的是Paris 提出的表达式:Paris 公式表明:疲劳裂纹扩展是由裂纹尖端弹性应力强度因子的变化幅度所控制的。
应力强度因子幅度,其定义为:3. 当应力强度因子幅度ΔK I 再继续增大,超过第II 区域的转折点B 2,而进入第III 阶段,这时的足K Imax 已接近材料的K l c (或K c ),裂纹扩展速率将急剧增快直至断裂。
影响疲劳裂纹扩展速率的因素:通过实验发现,除了ΔKI 是控制裂纹亚临界扩展的重要物理量之外,其它因素如平均应力、应力条件、加载频率、温度和环境等,对da /dN 均有影响。
弹塑性断裂力学:弹塑性断裂力学是断裂力学的一个新分支,它用弹性力学和塑性力学的理论研究变形体中裂纹的扩展规律。
弹塑性断裂力学在焊接结构的缺陷评定、核电工程的安全性评定、压力容器的断裂控制以及结构物的低周疲劳和蠕变断裂的研究等方面起着重要的作用。
裂纹尖端的张开位移(简称COD)正是裂纹顶端塑性应变的一种度量。
J ()()σR sW a t -≥在中低强度钢焊接结构和压力容器断裂安全分析中,广泛应用简单而实用的COD 准则。
C0D 判据:Wells 首先提出弹塑性情况下的COD 断裂判据。
即:当裂纹张开位移δ达到某一临界值δc 时,裂纹将会开裂。
即δ=δcδc 是材料弹塑性断裂韧性指标,是材料常数,可以由实验测得,它与温度有关。
δ=δc必须注意,δc 是裂纹开裂的临界值,而不是裂纹最后失稳的临界值。
一般用δi (initiation)表示裂纹开裂的张开位移临界值,用δm (maximum)表示裂纹失稳的张开位移临界值。
对于COD 判据,需要着重研究以下三个问题:(1) δ的表达式,即裂尖张开位移δ与裂纹几何以及外加裁荷之间的关系式;(2)材料的裂尖张开位移临界值δc 的实验测定;(3)COD 判据的工程应用。
J 积分:是弹塑性断裂力学的另一个十分重要的参量。
它既能描述裂纹尖端区域应力应变场的强度,又容易通过试验来测定。
J 积分的两种定义:(1) 回路积分定义:即围绕裂纹尖端周围区域的应力应变和位移所组成的围线积分。
J 积分具有场强度的性质。
不仅适用于线弹性,而且适用于弹塑性。
但J 积分为一平面积分,只能解决二维问题。
(2) 形变功率定义:外加载荷通过施力点位移对试样所做的形变功率给出。
试件要求:试样尺寸的要求,一般是以J 积分的有效性条件和平面应变条件来考虑。
有效性条件要求试样韧带宽(W -a )应满足KIC是材料在平面应变状态下抵抗裂纹失稳扩展能力的度量,是材料本身的性能。
线弹性断裂力学:线弹性断裂力学研究的对象是线弹性裂纹固体,认为裂纹体内各点的应力和应变的关系都是线性的(遵守Hooke定律),即其基础是线弹性理论。
在金属材料中,严格的线弹性断裂问题几乎不存在,因为裂纹的扩展总伴随着有裂纹尖端的塑性变形。
练习:用标准紧凑拉伸试样测定某种钢材的平面应变断裂韧度。
已知材料的屈服强度σs=1340MPa,试样尺寸B=35mm,W=70mm。
从P—V 曲线上查得P Q=78kN,P max=83.5kN。
从试样断口上测得裂纹尺寸a1=36.9mm,a2=37.1mm,a3=38.1mm,a4=37.8mm,a5=37.0mm。
试计算该试样K Q值,并校核此K Q值是否为材料的有效K IC值。
能量释放率断裂理论能量释放率断裂理论:根据能量理论,当裂纹发生扩展时,裂纹体内将有两种能量发生变化。
1.裂纹体的位能降低而释放出一部分弹性能;2. 裂纹扩展形成了新裂纹表面而增加了表面能,因而要吸收一部分能量。
因此,裂纹扩展的条件是裂纹体在裂纹扩展中能释放出足够的弹性能,足以提供增加表面能的需要。
研究裂纹扩展有两种观点:1. 能量平衡的观点认为裂纹扩展的动力是构件在裂纹扩展中所释放出的弹性应变能,它补偿了产生新裂纹表面所消耗的能量,如Griffith理论;2.应力场强度的观点认为裂纹扩展的临界状态是裂纹尖端的应力场强度达到材料的临界值,如Irwin理论。
1) K I:I型裂纹应力强度因子(SIF,Stress Intensity Factor),简称K 因子。
衡量裂尖应力场强弱的唯一指标。
应变、位移、应变能密度均可用K因子表示。